%% プログラミングの楽しみ

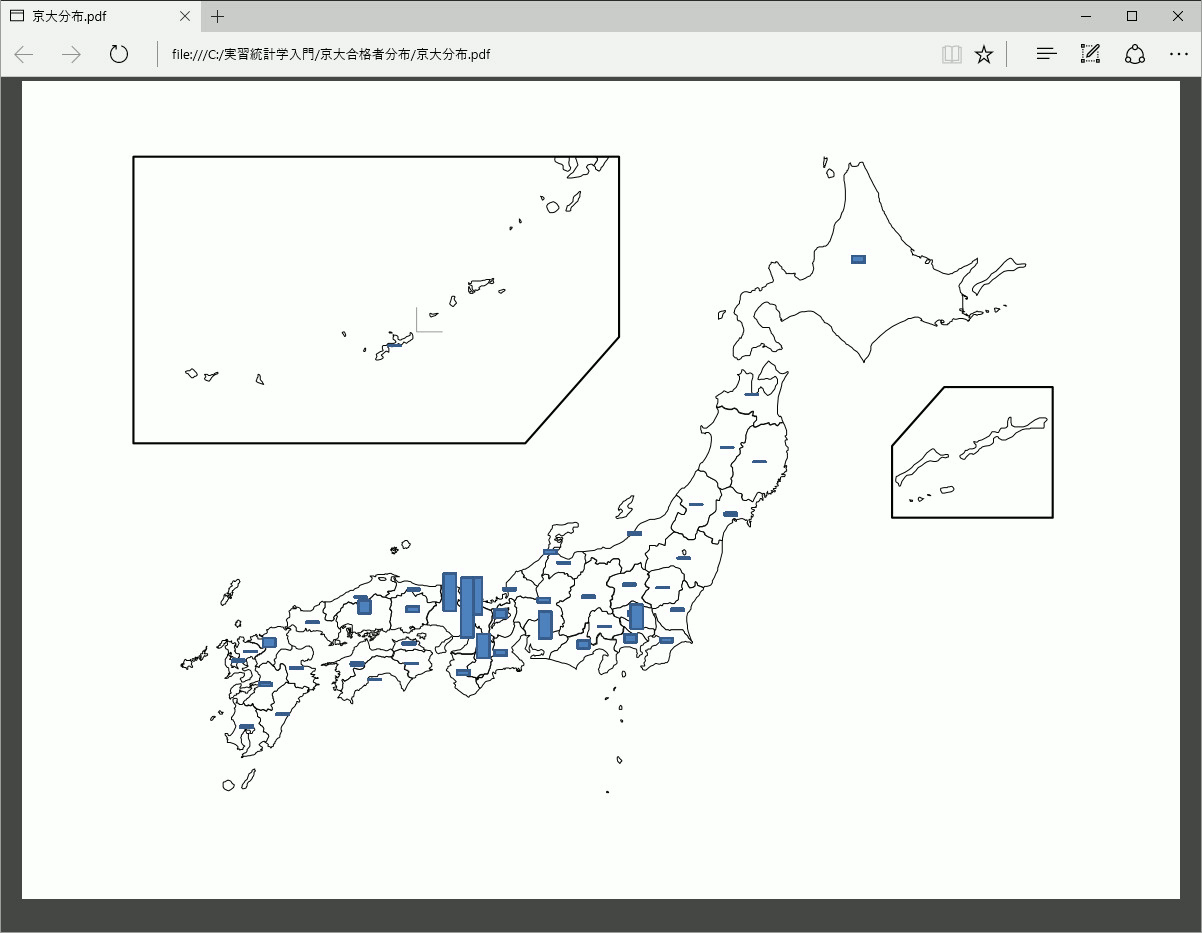
スマホ初心者の初めての Android アプリ公開




スマホを持ってないのに「遊んで作るスマホゲームプログラミング」や「Android ゲームプログラミング A to Z」など 購入していましたが、読むこともなく、環境が変化し、無価値な本になってしまいましたが、 スマホのプログラミングに興味を持ってから何年も経ってやっとガラ携からスマホに変え、 若者にとってはスマホが必需品になっているので Android のアプリのプログラミングをしてみました。 日本では、 iPhone を使っている人が多いみたいですが、 Android にしたのは、Windows 10 のパソコンを使って無料の Android Studio で、プログラミング言語は昔学んだ Java でプログラミング出来、 一度 25 ドル出せば、何回でも公表できるからです。iPhone のプログラミングは、高額な Apple のパソコンと iPhone の購入や Object C の勉強や公開の為の 費用が高額であることなど、スマホで稼いで生活しようと考えているわけではなく、スマホのプログラミングがどんなものか、 ちょっとやってみたいだけの人間には負担が大きすぎるからです。

Android のプログラミングの適応範囲は広範囲に及びますから、書籍には色々なことが書いてある（インターネットの普及で、書籍の役割が変化し、 多分、網羅的な情報を載せた本しか売れなくなっている）ので、順番に読んでいくのは大変ですから、最新の方法ではなく、 すでに理解している Python での tkinter の Game のプログラミング経験の類比が可能な Andproid の Canvas での 図形描画の方法をインターネットで調べて、矩形や円を描く方法や .png ファイルの表示の仕方を学び、スマホに矩形や円や画像だけを表示し、 次に、source code が見える you tube （英語ならあります）の 単純な迷路の Game 「MazeGame」の作り方をなぞりなぞりました。（英語でも本を読むより（適切な日本語の本はまだ出版されていないと思いますが）、 講義を見る方がはるかに楽です。 但し、you tube では、時間的な制約？があり、基本的に、断片的な、導入部分しか学べないように思います。）、 忘れている Java のプログラミングを思い出しながら、図形を描く方法、動かす方法、タッチした時の処理の仕方を理解しながら、一つ簡単なゲームを作ります。

その後、まとまった知識が得られる「Beginning Android Games Development」（数年で、本に書いてある技術が全く使えなくなること （例えば、「Android ゲームプログラミング A to Z」に書いてあるやり方は深刻なセキュリティの問題が見つかったとかで使えなくなりました）がありますから 最新の本を購入します: Crazy Eight という Card Game の作り方と Ballon Popper Game と言う基本的な2種類のゲームの作り方が丁寧に解説されています）の Card Game の作り方の部分を 読みました。 Ballon Popper Game と言うゲームの作り方は画像処理など面倒くさそうだったので、まだ読んでいません。 しかし、2020年の刊行で最新だと思ったこの本のサンプルプログラムをダウンロードしても Android Studio の仕様が変更になりそのままでは実行できません。 実行するにはどうすればいいか分からないというのが正確な表現です。 この本に書いていることの何が実行でき、何が実行できないか、ミスプリントもありますから、コードを打ち込み一つ一つ確かめながら、 Android Studio でゲームを作るための知識を増やしていかなければならない。例えば Dialog の作り方もこの本に書いてある通りでは動かない （実際は本を見て打ち込んだソースコードの打ち間違いで、ダウンロードしたコードのその部分は正しいことに、Dialog の作り方を 色々試した後に気づきました。失敗を繰り返して出来るようになります。）ので、 Dialog の作り方だけに焦点をあて、その方法を他の書籍やインターネットで調べました。

インターネットは例えば、 「Android Toast とは何か？」のように調べなければならないので、調べたい Toast と言う言葉を知っていなければなりませんし、部分的な情報が多いので プログラムにどのように組み込めばいいか考えなくてはいけません。例えば ArrayList の使い方を調べるとき、欲しい情報が得られるまで 探索の言葉を工夫して探す必要があります。 今は大学の宣伝やプログラミング教室の宣伝の為など色々な理由で、色々な情報がインターネット上にあります。 「Ballon Popper Game」を読む代わりに、 今回は運良く 「Android ゲーム開発」で検索して、CatchTheBall という簡単なゲームのプログラムの解説が you tube でプログラムを実際に作っている動画と共に、画像、ソースコード付きのの文章による解説のある分かりやすいページ達にぶつかりました。 かなりの大作です。 こまめにインターネットで調べてみると良いです。Python のプログラミングでは簡単だったですが、 Android の Timer の処理はかなり複雑です。

コンピュータやスマホは人工的に作ったものなので考えれば仕組みが分かるというものではなく、 誰か正確に理解している人に教わる必要があります。この Sara さんのページにはゲームの作り方の分かりやすい解説があります。 昔は大学・専門学校で習うか書籍で独学するしかなかったことが、今はインターネットで必要な情報が得られるので本が売れなくなっている理由が分かります。 今までのプログラミングと大きく変わったことは、.xml ファイルで View （どのように見えるか）を記述し、プログラムのロジックは .java ファイルで記述するように なっていることです。それぞれの書き方と連携の仕方を頭の中に入れなければなりません。 新しいことに挑戦するたびに、頭の中に蓄えた「スキーマ」を次々と改良する必要があります。それが学ぶと言うことみたいです。 ここでも自分なりの学び方を見つける必要があります。

このようにして「Canvas を使う方法」と「 TextView や ImageView を使う方法」の二通りのゲームの作り方を学んだので、それらの技法を定着させるために、 後は Python 等で学んだマンカラやカードゲームのプログラム達を Android のプログラムに翻訳していきます。 Google Play に既にいくつかありますが、Python でつくったことがあり、カードゲームより簡単だと思った （スマホでも見やすいカードの画像を準備しなければいけないので）マンカラのカラハのゲームを作りました。 良く知られているマンカラのベーシックのゲームはコンピュータを強くする方法が私には分かりません（ゲームのαβ探索の 適切な評価関数を思いつかない。どっちかと言うと三山崩しのようなゲームで、必勝形の法則を発見する必要がありますが、 後一手で勝てる局面などの必勝形を見つけるプログラムは簡単に書けますが、動的なアルゴリズムではなく、その結果を静的に数学的に表現することは複雑すぎて、 単純な数学的な表現を私は発見できなかった。勿論、ポケットの数や石の数が小さければ、パソコンで先手後手どちらが必勝か判定できます。）が、 マンカラのカラハのゲームのαβ探索はゴールの石の数の差という 単純な評価関数でも私より強くなり、そのアルゴリズムもちょっとした工夫が必要で面白いと思ったからです。 実際はこのように順調に事が進んだわけではありません。

Android Studio をインストールした時、バーチャルマシンが動かず Android のプログラミングを諦めかけていましたが、 私のパソコンのような hp のパソコンは起動時の設定を変える必要があるとの英文の解説を見つけ、シミュレーションが可能になったり、 慣れないプログラミングで疲れ果てていたのでバーチャルマシンを動かしたまま強制シャットダウンしてしまたのか、バーチャルマシンが 動かなくなって、修復する方法が分からず、諦めて単純なアンインストールをして再度インストールしても過去の設定が残っていてバーチャルマシンが動かず 途方に暮れていましたが、Android Studio を完全にアンインストールする方法というインターネットの記述を見つけ、 android に関連すると思われるファイルを片っ端から削除して、再度インストールすると矢張り昔の設定は残りましたが、 偶然バーチャルマシンに関する設定だけは初期化されて、AVD マネージャーで再設定するとシミュレーションが可能になりました。 後から本を読んでいて気づいたことですが、本当は再インストールの時、オプションをちゃんと読むべきでした。 このようにハプニングが頻発し、どうすればいいか適切に教えてくれる先生がいない中で独学で勉強するのは大変ですが、 今はインターネットがあるので何とかなります。良い世の中になりました。

更に、作ったアプリを Google Play で公表する方法を調べるのも独学で調べるのは大変です。 C++ ではコンパイルするのを debug から release に変更するだけでしたが、android のソフトもリリース版の apk ファイルを作ったり、 Google Play に登録したり、沢山のアプリから選んでもらうための魅力的な画像の準備など複雑で初心者が先生も共に学ぶ仲間もいない私にとっては大仕事です。 一番信用できる「Beginning Android Games Development」の chapter 11 Publishing the Game を読んで、それでも分からないことを 書籍やインターネットで調べますが、既に使われなくなった Eclipse の ADT による 解説などもインターネットにはあるし、高解像度アイコンやスクリーンショットと言っても、情報を書いた人にとっては常識でも、 初心者には画像のサイズはどれくらいで、拡張子は何か、どうやって作ればいいかも調べなければいけないし、更にデジタル署名と言った初めて経験することも出てくるので、 書籍やインターネットで色々な情報を集め判断する必要があります。

更に、Google Play で公表する前に、パソコンと自分のスマホを繋いで、作ったソフトが実機でちゃんと動くか確かめる必要があります。 これも大仕事でした。USB ケーブルをドコモショップで買ってきて、本やインターネットで調べた方法を確かめますが、その説明と実際の状況は 全然違います。何で Android Studio がスマホを認識しないかエラーを調べると -ADB reports that the device is in the 'unauthorized' state but Android Studio reports that it is in the 'offline' state となっています。これが何を言っているのか、ADB とは何かから、インターネットで調べる必要があります。日本語の解説はないので、英文の解説を探すことになります。 書いてあると通りやってもうまくいきません。上手くいかなければ adb を最新のものにしてみたらと書いてあり、インストールしてみますが、 単独のインストールでは Android Studio には反映しません。SDK マネージャーを調べているとアップデート可能なものがあることに気づきました。 スマホは日常的には電話しか使ってなかったので、「設定」のやり方から調べ、「開発者向けオプション」と「USB デバッグ」のチェックは比較的早く分かりましたが、 大事な「提供元不明のアプリ」にチェックを入れるがどこにあるかも最後まで不明でした。 「設定」の「アプリと通知」の「特別なアプリアクセス」の「不明なアプリのインストール」の「ドライブ」を ON にすれば良いにたどり着くまで、 USB ケーブルをドコモショップで買って来てから、丸三日かかりました。 本当は何をすべきだったか分かりませんが兎も角、やっと自分のスマホで Mancala_Kalah を実行できました。自分のスマホでゲームの画面が表示された瞬間は感激しました。 自分の持っているパソコンやスマホやソフトのバージョンによって、何をしなければいけないかがみんな違ってきます。 只管、試行錯誤の繰り返しです。環境を整えるのに凄く時間が掛かります。

後は公表するために、Google Play の要求するオリジナルな画像を作成しなければなりません。 フリーソフトの GIMP の使い方を学ぶ必要があります。この際ですから、本格的に GIMP の勉強をしてみます。 Eテレで漫画家がレイヤーを駆使して作品を作っていましたがプロが使っている高価なソフトを使わなくても GIMP でも今はレイヤーが使えます。 今は本を読まなくても you tube で解説してくれていますから楽ですが、GIMP の全体像を知るには本が便利です。 現在は動画による解説が増え、本の果たすべき役割が変わってきて、本と動画が完全に役割を分けています。上手く使い分けます。GIMP 2.10 対応 で素材がダウンロードできる適当に選んだ2冊を手に入れます。 差し当たって知りたいことは、サイズを指定した画像の作り方、レイヤーの使い方、写真等の切り抜き方、写真からイラストを作る方法、 手書きのイラストを読み込み色を塗る方法、 文字の追加の仕方、合成の仕方、ぼかしの入れ方などです。素材がダウンロードできる動画で、時間はかかりますが、素材をダウンロードして、動画の通り実際にやってみます。 しかし、GIMP のバージョンが違うのか、作者が常識と思っていることを私が知らないせいか、動画で説明する通りにはなりません。 同じことが出来るはずですから、考え、試行錯誤して、自分のパソコンで出来る方法を見つける必要があります。 一つの動画だけでなく、同じことをする方法は何通りもあるので探索ワードを変えて色々な動画を観ます。上には上の人がいて嫌になりますが、自分でも出来る技術を 少しずつ習得します。同時に本も読みます。誰が作っても同じ物が出来るプログラミングと異なり、 熟練者と初心者では大きな差が出るので練習を繰り返さないとなかなか上達しません。 将棋や囲碁が何級・何段になったというように、このような趣味の世界も知識・技術獲得を競う熾烈な競争の世界です。 私のような凡人はすぐには出来るようになりませんから気長に楽しみながら続けます。 一通り出来るようになったら、アイコンの作り方を幾つかの方法で試します。

何とか実機でのテストもし、 apk ファイルも作り、Google Play で公表しようとするとパッケージ名がデフォルトの com.example.*** では駄目だと受け付けて貰えません。パケージ名の変更の仕方が分かりません。 パッケージ名を変えてプログラミングすると今度はバーチャルマシンで動かそうとすると 「Allow USB debuging? 」と 言う表示が出て OK を押しても上手くいきません。 どうすればいいか分からないので Android Studio を再インストールします。 今度は「The application could not be installed: INSTALL_FAILED_MISSING_SHARED_LIBRARY」とエラーメッセージがでます。 何でか分かりませんが、インターネットの対策にあった AndroidManifest.xml の 「＜uses-library android:name="com.google.android.things" /＞」 の記述の削除によって、プログラムが実行できるようになりました（これはなんかの拍子に付け加わったもので、通常はないものです。）が、 ボタンのクリックに反応しなくなった。 困り果てて実行時のログを調べていると Caused by: java.lang.ClassNotFoundException: Didn't find class "android.view.View$OnUnhandledKeyEventListener" と言うのがあった。これを検索ワードにすると「これはどうも SDK 28 の問題らしく 27 にしたらエラーが無くなった」と言う記述を見つけた。 誰かが上での述べた「The application could not be installed: INSTALL_FAILED_MISSING_SHARED_LIBRARY」の解決に SDK 28 にしたら 良いのではとの記述を見て、 SDK 28 も可能にしたが問題が解決しなかったことが影響しています。 Android Studio を再インストールし、 SDK 27 だけにします。テストの為に作ったアプリが縦にすればボタンが反応しますが、 シミュレーションでスマホを横にすれば反応しません。私の作ったソフトは横固定だからボタンに反応しません。 パッケージ名を変えなければ Google Play で 公表できないが、パッケージ名を変えればボタンに反応しない。私が最後に購入した「はじめての Android アプリ開発　第3版」には ボタンに関する記述がない。注意していなかったので分からないが、パッケージ名がデフォルトの com.example.*** でもこうだったかな？これが仕様だろうか？これはどう考えても Android Studio のバグではないか？ 次に何をすべきか？適用スマホのバージョンを上げてみるか？私にスマホと同じ API 29 Android 10 用にしてみる。 テストの為に作ったアプリが縦にすればボタンが反応しますが、 横にすれば反応しません。私の作ったソフトは横固定だが、シミュレーションではスマホを縦にすればボタンに反応するが、 横にすればボタンに反応しません。実際にゲームをする画面が縦に表示されている。最初のプログラムをコピーペーストしたが 何処かで間違えた見たいです。再びゼロからやり直して見るしかないです。疲れたので又明日。 有難いことに最初のプログラムの作成過程の詳細をプログラムリストと共に Tex の原稿で残して置いたので、それを見ながら問題点を見つけます。 原因が分かりました。 コピーペーストしなかった、manifests/AndroidManifest.xm で 「 ＜activity android:name=".MainActivity" android:screenOrientation="landscape" ＞」 とすべき所で、 「 ＜activity android:name=".MainActivity"> android:screenOrientation="landscape" ＞」 となっていました。実機でどのように動くか確かめます。実機でゲームが出来ます。 Android Studio を再インストールを繰り返している内に、コピーペーストした残っていた元のプログラムが最終のものではなかったみたいです。 最終のプログラムと等しくなるように修正し。他のバグがないか暫くテストを続ける必要があります。 まだバグが残っています。これは厄介です。 先手で始め、3番目のポケットを選択し、続けて４番目のポケットを選択するとゲームを中断しスタートの画面に戻ります。 しかし、同じことをしたつもりでもおかしいことが起こったり、起こらなかったりします。不安定な動作をします。 今日はもうやめて、Perry Mason を読みます。A bottle floated into the cave. のような「様態動詞＋前置詞」が英語では多用されると 教わり今まで良く分からなかった句動詞に目が向くようになり、なんとなく意味が取れるようになりました。教えて貰わないと私のような凡人には このようなことは自分では発見できません。 どのような本や人に出会うか人生は運です。 be right with you のようなものも今はインターネットで意味を調べることが出来るようになりました。 小中高校の生徒全員が親の貧富にかかわらず、一日中いつでもパソコン（スマホやタブレットではプログラミング出来ません）で インターネットが自由に使えるようになると良いですが。 学生の時は難しかった英語のミステリーが今は楽しく読めるようになりました。全５５巻の Perry Mason のシリーズを読み終われば 英語がもっと出来るようになるのでしょうか？ I wish I were young.

バグの探求を続けます。上のような致命的なバグは C 言語でプログラミングしていた時、配列の範囲外をアクセスした場合に良く起きていました。 現在のプログラムでは ArrayList でそのようなことが 起きていないか調べます。実行時のログを調べると矢張り ArrayIndexOutOfBoundsException が起きていました。 原因が分かりました。コンピュータの戦略を単純なランダムに手を選ぶ方法から、αβ探索に切り替えた時、強くなりすぎたので、 単純なランダムに手を選ぶ方法も追加しましたが、その時、なにも考えずに元の単純なランダムに手を選ぶ方法のプログラムを コピーペーストしたので、新たな関数の引数に合わせてboard の入れ替えをするのを忘れていました。 しかし、これは多分本質的では無く元のままでも分かり難いプログラムになるが間違いとも言えなくて、if 文の条件が間違っていることが 決定的でした。 変なことが起こったり、起こらなかったりしていたのは、乱数でどの値を選ぶかによって起きていました。 元々間違っていたのに、バグがあることに気づいていませんでした。 独学なので優秀な人のことは知りませんが、私は或る程度以上の長さのプログラムを作るときは、 バグ（思い違いによる単純な論理的な違いだけでなく、コピーペーストを多用したりするので、変更しなければいけない個所の 修正し残りなどがどうしてもあります）が残るのは仕方がないことで、 プログラムが出来たと思ってから実際にバグがなくなったと確信出来る（バグがないとは証明は出来ません）プログラムが出来上がるまで、 それまで費やした時間の倍の時間がかかります。 会社では分業でソフトをテストする専門の人がいるみたいですが、個人でプログラミングするには、 自分で上のような「バグに気づき、発生場所を特定し、修正し続ける」根気が続くかが、私のような凡人がプログラミングが出来る ようになるかどうかの分かれ道ではないかと思います。多くの人がそれが出来ずにプログラミングを断念するように思います。 プログラミングはあくまでアルゴリズムを計算機が理解できる言語にデータ構造を使って翻訳する技術です。 アルゴリズムとプログラミングは密接に関連していますが、別のものです。 アルゴリズムは古代のエジプトでも考案されていて、アルゴリズムを考案するのは数学の問題です。実現したいアルゴリズムを 持っていれば、プログラミングの出番になります。アルゴリズム自体の難しさをプログラミングの難しさだと誤解してはいけません。 例えば、ホームページを作成する言語を学べば、それを知っている人が少なければ、ホームページ作成のやり方を暗記することで大金を稼げました。 しかし、ホームページを作成する言語を知っている人が多くり、知らなくてもホームページが作れるソフトが出てくると 単にホームページを作れれると言うこと以外に何を持っているかが問われるようになります。 今は芸術的センスを生かしてホームページ作成を職業にしている人もいます。また、インターネット上に商店を開設する Java のシステムが公開されると いち早くそのやり方を暗記し、必要な部分だけ修正することにより、お金が稼げます。 これも同様に直ぐそれ以外の何かを持っていないと稼げなくなります。このように、何らかの革新的技術が開発されるとそれを暗記することにより、 多くに人が食べていけます、しかし、そのようなイノベーションを起こす革新的アルゴリズムを新たに開発し、国を豊かにするには、 国の政策として、（実際には、「女子学生には三角関数など教える必要はない」と発言する東大卒の知事（自分自身は数学の恩恵を受け、例えば、 現在、多くの女性が大活躍している文科系だと考えられている外国語教育の分野でも、 「人間が音声を使ってコミュニケーションをとる時に何が起きているか」を科学的に学ぶためには、波動である音声の勉強もしなければいけないので、 その場合、三角関数の理解がまず最初にあり、 その後フーリエ変換などの勉強が続く訳であり、文科系とされている人でも三角関数ぐらいは高校で学んでいれば、 その時よく理解できなくても、改めて勉強しようと思った時のハードルは大きくないと思います。 当然、この人は無知での発言ではなく、数学の重要性を分かった上での 発言だと思われるので、その意図は何か分かりませんが、更に悪質だと思います）が出てくる国ですが）数学的能力を持った人を大幅に増やす必要があります。 欧州が世界中を植民地に出来たのは、数量化革命が原動力だと言われています。どんぶり勘定ではなく、お金の出入りを正確に記録することから始め、 物理現象や社会現象を数値的・数量的に記録することにより、 問題点や法則を発見できるようになったと言われています。現在は画像や音声も数値化することにより、コンピュータで処理することが出来るようになっています。 その結果、「深層学習」や「強化学習」や「探索」といった AI の技術の発達・普及で、コンピュータのソフトが将棋や囲碁のプロ棋士に勝つようになり、 画像認識、音声認識の能力も大幅に拡大し、AI の新たなブームが起きています。 現在、お金になることが分かっていることを勉強する人たちも確かに必要ですが、将来、お金を生み出す可能性のあることの元になる 基礎的な研究を好き勝手に勉強している人も沢山いる必要が あります。将来大きなお金を生み出すことになったマイコンチップを考え出した嶋さんを「発明はアメリカから来る」と思い込んでいる日本人経営者・指導者は理解出来ず、 アメリカの小さな企業：インテルに 話を持ち込むことで実用化された話は余りにも有名です。このような失敗を日本は繰り返しているように思います。 最も、沢山の人が豊かになるのではなく、現在、自分一人ががお金持ちになる方法は全然別みたいですが。

Google Play で公表する前に見つかって幸運でした。 兎も角、ひとまず完成しました。何かを新たに始める時にはあらゆる失敗を経験する必要があるみたいです。Google Play に無料で公表し、様子を見て、次のソフトを 開発します。 所が、公開の仕方が分からない。パッケージ名がデフォルトの com.example.*** では駄目だと受け付けて貰えなかった続きをしようと思ったが、下書きと言う形で残っていて、パッケージ名を 入れ替えたものに変更し続ける方法も、一旦削除する方法も分からない。削除は出来ないみたいです。 新たに公開の手続きをしようとすると普通は順番に、こうしなさい、入力が間違っていなければ、次にこれをしなさい、 入力に不備があれば、再度入力を促すというように、 公開の手順を導いてくれるようになっているはずだが、書籍やインターネットで調べたようになっていない。下書き1/3完了とか、 あがいてみると、下書き2/3完了とかなるが、基本的に次どうすれば良いか分からない。 どうも色々なパターンの画像のテストをしてやると言っているが私のソフトは キャンパスに絵や文字を描いているだけで画像を貼り付けていないのでどのような画像処理をしたらいいかのアドバイスは 必要ない。困り果てて数日過ごすが解決策を思いつかない。

windows ではプログラムを自由に発表出来、 一種の無法地帯になった反省から、 Android のスマホのアプリは公表するかどうか Google がチェックして、かってに公表できないように完全な 管理体制を敷いています。結局、休み休み、一週間ぐらい試行錯誤して、色々な設定をして、 公表の可否をチェックしてもらう段階まできました。Google がチェックしているのは、子供に見せてはいけないものが、 広告を含め含まれていないか、年齢制限が正しく行われているか、ナチスのようなファシストを称賛してないか、 なりすましが行われていないかなどだと思います。勿論、ウィルスチェックもしていると思います。 Google のチェックが終わって、自分のスマホでダウンロード出来るまで、まだしばらく時間がかかります。 「チェックに時間が掛かっています」と表示がありましたが、数日かかって、公開中の表示に 変わりました。Google Play でダウンロードしようとするとダウンロード数０なので、 普通の探し方では表示されません。どうすればダウンロード出来るかその方法を探さなければなりません。 まだまだ、試行錯誤が続きます。これは間違っていました。スマホを電話にしか使わないので、 どうすれば良いか、私よりスマホに詳しい大学の同僚に尋ねましたが、良く分かりませんでした。 私は Play ストアの使い方も理解できておらず、認識不足でした。 アプリ名にマンカラ（カラハ）と括弧を使ったせいで上手く探索出来ていませんでした。 「マンカラ」ではなく「カラハ」で探索すればよかった です。色々不明なことがあったので、大分前に、認可されなかった理由を Google とやり取りしたという インターネットの記述を見たことを思い出し、Google に質問できるページを見つけたので、質問しました。 その結果、Google が改善してくれたのかどうか分かりませんが、Play ストアで探索しやすくなりました。 「マンカラ（カラハ）　作者　佐川の隠居」　でダウンロード出来るそうです。長い戦いが終わりました。 あらゆる失敗を経験したので、次はスムーズに作れるはずです。 所がスマホにインストールして、遊んで見ると1勝１敗のはずなのに、1勝８敗と表示されます。 パッケージ名がデフォルトの com.example.*** では駄目だと言われ、パケージ名を変えて、新たにプログラミングし、 元のプログラムをコピーペーストしましたが、 Android Studio を再インストールするために、別のフォルダーに保存しておいたプログラムが最新のものでなく、 このバグを修正する前のものだった見たいです。現在のアプリを修正したアプリと入れ替える方法があるかな？ 新しく登録し入れ替えなければいけないか、調べなければいけなくなりました。疲れ果てます。 Android Studio を開いてみると正しいプログラムがセットされていました。古いプログラムをなんかの手違いで 公開してしまったかも分かりません。疲れて判断力が衰えているので休息が必要みたいです。山口先生からコンピュータの反応が速すぎるので、 時間をおいた方が臨場感が出るのではないかとのアドバイスを貰いました。 （今日、令和4年4月18日、電話が掛けれなくなって、ドコモショップで見てもらうと「原因不明だが、時々、そのようなお客さんが来るが 電源を一旦切って、入れなおすと直ることが多い」と言われ、 やってみると直りました。その時、私の対応してくれた若い女の子がこのゲームに興味を持ったので、やり方を簡単に教えて、やってもらいましたが、 自分の手を選ぶと瞬時にコンピュータが手を選ぶので、自分が何をやっているのか、自分の行動の結果が瞬時にコンピュータの手で上書きされるので、 何が起こっているか理解するのが難しかったみたいでした。 矢張り山口先生が言うようにコンピュータの反応を数秒後とかに変えないと駄目みたいです。 他人に使ってもらうアプリ作るにも経験を積むことが必要です。しかし、グーグルのスマホのアプリだけでも 280万個以上あるそうなので、注目してもらうのは難しいし、世の中には100万人単位でスマホのアプリを作れる人がいるので、 スマホのアプリを単に作れるだけでは何ということもないので、何か面白いアイデアを思いつくまで、 スマホのプログラミングはお休みです。） 更に、 コンピュータが強すぎる気もするので、囲碁や将棋のソフトのようにヒントを出すように修正して、 バージョンアップするか、暫く、休息をとって考えます。 私のスマホに、実機のテストで確かめた「MazeGame」が入っていることを見つけた。これは Play ストアで取ってきたものではない。 公開されたマンカラ（カラハ）と思っていたものは、実機でテストした古いアプリで、Play ストアで取ってきたものでなかった。 アンインストールして、Play ストアで取得するとちゃんと動いているみたいです。名前は MancalaKalah になっている。 もっとスマホの基本的な使い方を勉強しなといけない。知らないことが多すぎる！

更に、Google に質問して 「この度は Google Play デベロッパー サポートにお問い合わせいただきありがとうございます。 状況がわからないため一般的なご案内となりますがリリースの方法につきましては、下記ヘルプページで詳細をご案内しておりますので、どうぞご利用ください。

https://support.google.com/googleplay/android-developer/answer/9859348?hl=ja

https://support.google.com/googleplay/android-developer/answer/9859751?hl=ja

他にご不明な点などございましたらお知らせください。」 と教えて貰いました。最初から、この情報を知って、良く読んでいれば、上のような無駄な努力をせずに済んだのですが。 「組織的に「マンカラ（カラハ）」のダウンロード数を増やす方法を教えてやろうか」と言う英文のメールが来ました。 増やしても、本当に無料のアプリ（広告も内部課金もないアプリ）なので、意味もないですが、世の中には 色々な人がいます。騙されないように注意しなければ。巧妙な詐欺メールも頻繁に送られて来るようになりました。 失敗ばかりしてきたので、慎重になっているつもりでしたが、また、誰かの気に障ることをしたり、言ったりのだろうか？ 危うく騙されるところでしたが、怪我の功名で何とか逃れることが出来ました。常に細心の注意をしていないと酷い目に遭います。 大学に入学して最初の飲み会で凄く人当たりの良い上級生に「お前は会社では使い物にならないから、一生懸命勉強して大学に残らないといけないぞ」と 忠告されましたが、どうしてだろうとずっと思っていましたが、この年になって、今までの身の回りに起こった出来事を振り返るとやっと意味が理解できた気がします。 生きていくことは大変です。

センター試験の出題官をしていた時、分科会のネットワークを担当していた教授に、分科会長が「どのようにして コンピュータが出来るようになったか」と聞いた時、その教授は「あらゆる失敗を経験したから出来るようになった。だから人には教えたくない。」 と答えていました。（この二人の教授が本当は何を話したのか、数年たってやっと気が付きました。 頭の良い人たちの会話は本当は何を言っているのか、言葉通りのことを必ずしも言っている訳ではないので、将棋や囲碁をしている時と同様、 あらゆる可能性を考慮して良く考えないといけません。） この教授が言ったように、技術を身に着けるには、基本的には自分で試行錯誤して学ぶしかないのでしょうが、 先生がいないと矢張り大変です。50年以上前、高校の古文で習った「少しのことにも、先達はあらまほしき事なり」を思い出しました。 しかし、特別な個別の問題では、先達を見つけるのも結構大変です。誰に聞けばいいか分かりません。 例えば、American accent training Fourh edition の downloadable audio をゲットするのも大変でした。 本に書いているアドレスにアクセスして、言われる通りやっていくとパスワードをメールで送ってきますが、次にパスワードを変更しろと 指示されます。パスワードに必要な条件をすべて満たしているはずなのに何度やってもエラーになって先に進めません。 最初からやると

WE'RE SORRY

THE WEBPAGE YOU REQUESTED IS NOT AVAILABLE AT THE MOMENT

TO GO TO THE BARRON'S MAIN SCREEN, CLICK HERE.

IF THE PROBLEM PERSISTS, PLEASE CONTACT CUSTOMER SUPPORT AT

support@??????

WE APOLOGIZE FOR THE INCONVENIENCE

と表示します。如何すればいいか分からないので、指示されたメール・アドレスに、何をしたか英作文して送るとすぐ、 大量のメールが来ていて大変で多くのメールには48時間以内に返事をしたいというメールが来ましたが、 2日待っても返事は来ません。もう一度、本に書いているアドレスにアクセスするとサーバーの情報を修正して くれたみたいで、パスワードを変更しろと言うページまで到達しました。色々なパスワードを入力してみて、 ちょうど8文字のパスワードを入力すると次のページに移動しました。パスワードは普通の場合と同様、 8文字以上で長いほど良いと思い込んでいましたが、ちょうど８文字でないといけなかった見たいです。 所がここは音声ファイルをダウンロード出来るページではなく、オンラインで音声を聞けるページでした。 amozon の書評に「良書ですが、音声ダウンロードはちょっとした冒険です！」と言うのがあったので、 音声ダウンロードの方法があるはずだとインターネットで色々検索すると出版社 BARRON'S の音声ダウンロードのページを見つけることが 出来、無事、音声の.mp3 ファイルをゲットできました。 これで、Python のプログラム(http://www.cc.kochi-u.ac.jp/~tyamag/jyohou/kifumodify.pdf にそのプログラムの解説があります。 伝統的に「数学」や「プログラム」は「推敲された最終結果」だけを提示し、弟子でなければ何を考えたかを教えてもらえない （「じっと眺めていれば分かる」としか答えて貰えないかも分かりませんが）ですが、 このpdfファイルで備忘録のように制作過程をだらだら書いていては私でも普通は読む気がしないと思います。 しかし、私は琉球大学では理工学部でしたが、高知大学では教育学部でしたから、教員になる学生さんには、優秀な人がどのように考えてものを 作っているかは及びもつきませんが、私のような凡人でもこのように考えを進めていけば何とかそれなりの物が作れるということを 示したくて、「無知で愚か者」の考えかも分かりませんが、「魚」を与えるのではなく「魚を取る方法」を示そうと努力してきた結果です。 サッと目を通し、必要なプログラムだけコピーして使ってください。 そこには書いていませんが、例えば、4枚のCDで提供された音声（それぞれ、例えば、フォルダ D8sc1, Disc2, Disc3, Disc4 に 01.mp3, 02.mp3, ... と名前がふられている時）を 一つのフォルダ AllDisc に纏めるには、次のようなプログラムが役に立ちます。 


Python Program{
import os
import shutil

##data_list = os.listdir('./Disc1')    #ソースディレクトリを指定
##data_list = os.listdir('./Disc2')    #ソースディレクトリを指定
##data_list = os.listdir('./Disc3')    #ソースディレクトリを指定
data_list = os.listdir('./Disc4')    #ソースディレクトリを指定

for file in data_list:
    base, ext = os.path.splitext(file)
    if ext == '.mp3':
        print(file)
        print(base)
##        src = './Disc1/{}'.format(file)     #ソースファイル名を指定
##        tag = './AllDisc/1{}'.format(file)  #ターゲットファイル名を指定
##        src = './Disc2/{}'.format(file)     #ソースファイル名を指定
##        tag = './AllDisc/2{}'.format(file)  #ターゲットファイル名を指定
##        src = './Disc3/{}'.format(file)     #ソースファイル名を指定
##        tag = './AllDisc/3{}'.format(file)  #ターゲットファイル名を指定
        src = './Disc4/{}'.format(file)     #ソースファイル名を指定
        tag = './AllDisc/4{}'.format(file)  #ターゲットファイル名を指定
        shutil.copyfile(src,tag)
}

フォルダのファイルの名前の名前の付け方に応じてプログラムを作り変えます。 更に、例えば、Haydn Symphonies のように33枚のCDがあって、上のようにフォルダーの名前を自分で打ち込み、プログラムを作り直すのが大変だと思うようになれば、 


Python Program{
import os
import shutil
import re
import subprocess

ind = 0
for file in os.listdir():
    if os.path.isdir(file):
        if file == 'AllSymphonies':
            continue
        ind += 1
##        print('ind=', ind, file)
        data_list = os.listdir(file)
        for file2 in data_list:
            base, ext = os.path.splitext(file2)
            if ext == '.mp3':
                print(file2)
                print(base)
                src = './{}/{}'.format(file, file2)
##                print(src)
                if ind < 10:
                    tag = './AllSymphonies/0{}_{}'.format(ind, file2)
                else:
                    tag = './AllSymphonies/{}_{}'.format(ind, file2)                    
                shutil.copyfile(src, tag)
}

のようにプログラムに存在する全てのフォルダーを探させ、見つかった各フォルダーに対して上のプログラムでした処理をするように、 プログラムを作り変えれば良いです。また、 


Python Program{
                if ind < 10:
                    tag = './AllSymphonies/0{}_{}'.format(ind, file2)
                else:
                    tag = './AllSymphonies/{}_{}'.format(ind, file2)                    
}

は、他の言語（例えば、C の書式指定）の場合の様に、調べれば1行で済ます方法があるかもしれませんが、 学生さんに対する教育なら中には変な学生さんもいてそんなことも知らないのかと攻撃してくる場合もありますから調べておくべきですが、 我々素人は自分の為のプログラミングでは余り神経質にならなくても良いです。 我々凡人は前もって起こりうるすべての場合を想定して一気に理想的なプログラムは作れないので、これは不便だと感じたら、 このように少しづつ改良していけば良いです。他人との競争ではなく、自分に自信の無い人が良く言う「俺はあいつより偉い」ではなく、自分のしたいことをします。

このようにすれば、二つのフォルダにまたがって配置されているいるひとまとまりの内容を上記 pdf に書いている Python のプログラム 


Python Program{
import os
import re
import subprocess

print('from pydub import AudioSegment')
print('from pydub.playback import play')
print()
print('n = 1')
print()
print('for i in range(3):')
print('    print("No.", i+1)')
for file in os.listdir():
    base, ext = os.path.splitext(file)
    if ext == '.mp3':
        print('    print("{}")'.format(file))
        print('    sound = AudioSegment.from_mp3("{}")'.format(file))
        print('    for k in range(n):')
        print('        play(sound)')
}

を使って、 再生するためのプログラムを作れば、 人の介入なしに何度でも繰り返し再生することも出来ますし、4枚すべての音声を人の介入なしに自動的に再生したりできます。 私のように音楽の素養のないものが例えば、Haydn Symphonies を全部聞こうと思った時、持っているファイル全部を一つのフォルダーに纏め、 どこまで聞いたか覚えておかなくても、 順番に聞いた部分をコメントアウトしていけば、全部聞くことが出来ますし、気に入ったものだけを残してコメントアウトして聞くことも出来ます。 優秀な人達が作ってくれたモジュールを Python で組み合わせることにより、我々凡人でも、自分の欲しい道具をこのように作ることが出来る 良い時代に今はなっています。単なる消費者でなく、自分で何か作ってみることは楽しいことです。今はそれが簡単に出来ます。 更に、必要のない部分をプログラミングで削除して再生することも会話の一部分だけを繰り返し再生することも出来ます。 


Python Program{
from pydub import AudioSegment
from pydub.playback import play

n = 3
m = 3

for i in range(15):
    print("No.", i+1)
    
##    print("001 - Read This First.mp3")
##    sound = AudioSegment.from_mp3("001 - Read This First.mp3")
##    for k in range(n):
##        play(sound)
        
    print("002 - A Few Words on Pronunciation.mp3")
    sound = AudioSegment.from_mp3("002 - A Few Words on Pronunciation.mp3")
    for k in range(n):
        play(sound)

        sound1 = sound[:232500]
        sound1 = sound1*m
        play(sound1)
        
        sound2 = sound[232500:]
        sound2 = sound2*m
        play(sound2)

　　＜以下省略＞
}

Python のライブラリー tkinter を使って、再生したい mp3 ファイルを選んで、再生させるプログラムを作ることも出来ます。 例えば、 


Python Program{
import tkinter as tk
import os
from pydub import AudioSegment
from pydub.playback import play

 
win = tk.Tk()
win.title('mp3 Player')

n = 1

#----------------------------------------
#ボタンを押した時の反応用関数
def select_lb():
    for i in lb.curselection():
        print(str(i)+"番目を選択中")
        for k in range(n):
            print(listarray[i])
            sound = AudioSegment.from_mp3(listarray[i])
            play(sound)
    print("")
#----------------------------------------

#----------------------------------------
#リストボックス
listarray = []
for file in os.listdir():
    base, ext = os.path.splitext(file)
    if ext == '.mp3':
        listarray.append(file)
txt = tk.StringVar(value=listarray)
lb= tk.Listbox(win, listvariable=txt,width=30,height=6)
lb.grid(row=0, column=1)
lb.configure(selectmode="multiple")
#----------------------------------------
 
#----------------------------------------
#スクロールバー
scrollbar = tk.Scrollbar(win,orient=tk.VERTICAL,command=lb.yview)
scrollbar.grid(row=0,column=2,sticky=(tk.N,tk.S))
#----------------------------------------

# スクロールバーをListboxに反映
lb["yscrollcommand"] = scrollbar.set

#----------------------------------------
# ボタンの作成と配置
button = tk.Button(
    win,
    text="Play",
    command=select_lb
)
button.grid(row=1, column=1, padx=10, pady=10)
#----------------------------------------

win.mainloop()
}

と言うプログラムを再生したい mp3 ファイル達のいるフォルダで実行すれば、リストボックスに表示された（複数の）ファイル名をクリックして、 ボタンを押せば、順に再生してくれます。これを元に、tkinter に関する知識を増やしながら、欲しい機能を追加していけば良いです。 このようなプログラムは、誰でも作れるプログラムで、作り方を知っている人は星の数ほどいますから、知っている人について習うのが一番良いですが、 高知のような田舎で、そのような人に出会うことが難しい環境でも、時間はかかりますが、このような枯れた技術に関しては、 インターネットに情報が溢れていますから、私のように独学で学ぶことも出来ます。

このようにプログラミングが出来るとソフトの単なる消費者ではなく、自分が必要とする道具を自分で作ることが出来るようになります。 コロナで、保育園でも保母さんがマスクを付けなくてはならなくなり、園児は保母さんの口元を見て学んでいたので、大変困惑しているとの 報道を視ました。母語でもそうですから、外国語の発音はネイティブ・スピーカー に直接教えてもらうのが良いですが、個人レッスンなどは高額のお金が掛かりますから、 貧乏人が独学するには、自分の暇なときに動画が見れる DVD は有難いです。 比較的沢山手に入る音声だけで独学で勉強するのは難しいですが、 独学でアラビア語を学んでいても、「Alif Baa」の Drill Dictation の動画の口や舌の動きを何度も観ているとどの音を発音しているか分かってきます。 Georgetown University の文字と発音を学ぶための教科書ですが、DVD にもプロテクトが掛っていなくて、パソコンに取り込み、 


Python Program{
import pyglet
import os
 
### width of window
##width = 1280
##   
### height of window
##height = 768

 
# width of window
width = 640
   
# height of window
height = 480
 
# caption i.e title of the window
title = "Alif Baa : Unit One"
   
# creating a window
 
def mp4Play(vidPath):
 
    window = pyglet.window.Window(width, height, title)

    # creating a media player object
    player = pyglet.media.Player()
 
    # creating a source object
    source = pyglet.media.StreamingSource()
 
    # load the media from the source
    MediaLoad = pyglet.media.load(vidPath)
 
    # add this media in the queue
    player.queue(MediaLoad)
 
    # play the video
    player.play()
 
    # on draw event
    @window.event
    def on_draw():
     
        # clea the window
        window.clear()
     
        # if player source exist
        # and video format exist
        if player.source and player.source.video_format:
         
            # get the texture of video and
            # make surface to display on the screen
            player.get_texture().blit(0, 0)
         
    # key press event    
    @window.event
    def on_key_press(symbol, modifier):
   
        # key "p" get press
        if symbol == pyglet.window.key.P:
         
            # printing the message
            print("Key : P is pressed")
         
            # pause the video
            player.pause()
         
            # printing message
            print("Video is paused")
         
         
        # key "r" get press
        if symbol == pyglet.window.key.R:
         
            # printing the message
            print("Key : R is pressed")
         
            # resume the video
            player.play()
         
            # printing message
            print("Video is resumed")
 
    # run the pyglet application
    pyglet.app.run()
##    window.close()

n = 30

for i in range(3):
    print("No.", i+1)
    
##    print('Drill 1. Hearing frontal and deep alif')
##    print("U02D01.mp4")
##    vidPath = "U02D01.mp4"
##    for k in range(n):
##        mp4Play(vidPath)
##        
##    print('Writing alif')
##    print("U02_Writing_alif.mp4")
##    vidPath = "U02_Writing_alif.mp4"
##    for k in range(n):
##        mp4Play(vidPath)
##
##    print("Writing baa")
##    print("U02_Writing_baa.mp4")
##    vidPath = "U02_Writing_baa.mp4"
##    for k in range(n):
##        mp4Play(vidPath)
##
##    print("Writing taa")
##    print("U02_Writing_taa.mp4")
##    vidPath = "U02_Writing_taa.mp4"
##    for k in range(n):
##        mp4Play(vidPath)

    print("Dril 2 Dictation")
    print("U02D02.mp4")
    vidPath = "U02D02.mp4"
    for k in range(n):
        mp4Play(vidPath)
        
    print("Writing thaa")
    print("U02_Writing_thaa.mp4")
    vidPath = "U02_Writing_thaa.mp4"
    for k in range(n):
        mp4Play(vidPath)

    print("Writing uu")
    print("U02_Writing_uu.mp4")
    vidPath = "U02_Writing_uu.mp4"
    for k in range(n):
        mp4Play(vidPath)

    print("Drill 4 Dictation")
    print("U02D04.mp4")
    vidPath = "U02D04.mp4"
    for k in range(n):
        mp4Play(vidPath)
        
    print("Writing ii")
    print("U02_Writing_ii.mp4")
    vidPath = "U02_Writing_ii.mp4"
    for k in range(n):
        mp4Play(vidPath)

    print("Drill 5 Dictation")
    print("U02D05.mp4")
    vidPath = "U02D05.mp4"
    for k in range(n):
        mp4Play(vidPath)

    print("U02D11.mp4")
    vidPath = "U02D11.mp4"
    for k in range(n):
        mp4Play(vidPath)
    print("U02D17_Scene2_Egyp.mp4")
    vidPath = "U02D17_Scene2_Egyp.mp4"
    for k in range(n):
        mp4Play(vidPath)
    print("U02D17_Scene2_Lev.mp4")
    vidPath = "U02D17_Scene2_Lev.mp4"
    for k in range(n):
        mp4Play(vidPath)
    print("U02_Writing_ShVowels.mp4")
    vidPath = "U02_Writing_ShVowels.mp4"
    for k in range(n):
        mp4Play(vidPath)

}

のような Python のプログラムで、VLC media player や CyberLink Media Suite 10 のように 中断し、マウスで適当な所まで戻し、再開するなどは出来ませんが、中断し（p を押す）、続きを再開する（r を押す）は出来、 一緒に視たい動画を一つのフォルダに集め、繰り返し視ることが出来ます。 VLC media player と使い分ければ良いです。日本だけでなく、外国の本も探してみるとこのような良い教材が見つかることがあります。有難い世の中になりました。

このプログラムのように優秀な人が作ってくれた ffmpeg や pyglet や opencv というソフトやライブラリーを使うことにより、 誰でも ffmpeg や pyglet や opencv の中身の構造を理解しなくても、 自分が欲しいプログラムが容易に作れるので、現在は Python という 汎用性が高く、無料の有用なライブラリーが完備していて、しかも短期間で修得できるプログラミング言語を勉強することが大切です。 何を勉強すれば良いかは常に変化していて、これを勉強して置けば一生安泰ということは残念ながらないです。 （復帰直後の琉大の助手時代に、学生さんがコンピューターを学びたいと言っていると笠原先生に報告するとプログラミングの集中講義が始まり、 助手だった高久さんが「東京から来て「いろは」だけ教えてもらうのは勿体無い。講師の先生にはもっと難しいことを教えてもらおう」と言い出し、 助手が分担して学生さんと一緒に、実質独学で、 FORTRAN の演習書を勉強し、高知大学に移って、コンピュータに自由に触らせて貰え、、 琉大時代のプログラムを紙に書いて、窓口に出し、一週間後に結果が分かるのではなく、パンチカードに穴をあけ、コンピュータにセットし、 コンピュータが計算する様子を眺め、結果を打ち出すのを見ると言う一連の動作を全部一人で勝手にすることが自由に出来たので、 FORTRAN の参考書を手当たり次第に読んだと言うことも、また、 当時は、数学者にとっては簡単で、今のように複雑で難しいことは誰もプログラミングしていなかったことも勿論ありますが、、 FORTRAN のプログラミングがそこそこ出来るようになりました。そうこうするうちに、マイコンが売り出され、 菅原先生と石川先生がマイコンが面白いと話しているのを聞いて、 そうなんだと思い、当時高価だったマイコンを購入し、BASIC と機械語・アセンブリ言語を勉強したり、 代数的トポロジーの計算をしていたので、コンピューターで計算したいと手計算で面倒であった微分の計算結果の整理の為のプログラミングをしてみたり、 段々パソコンの性能も向上し、使うプログラミング言語もCからC++と強力かつ使い易くなり、私でも長いプログラムが作れるようになったので、 最終的にはホップ・アルジェブラのコホモロジーを計算するプログラムを自力で作ることが出来ました。 しかし、地方国立大学の教育学部にいる私の使える非力なコンピュータでは、 ホップ・アルジェブラのコホモロジーの簡単な結果や部分的な結果しか計算できず、 思い描いていた結果が出せず、失敗だったと言えると思います。恵まれた環境にいる方で、興味があれば、プログラムを公開しているので、 続きをやってみてください。もう老人なので、私に報告はいりません。

大分前から、Python のライブラリーを C++ で作ってみたいと思っていましたが、このような技術は linux でまず開発され、 その後、windows でも使えるようになります。boost を使えば、 VC++ で、Python のライブラリーを作れると言う記事を インターネットで見つけたので、やってみました。

まず、Python を最新の Python 39 と入れ替えます。今回は Anaconda 3 をインストールしました。 pydub と pyglet は　pip でインストール出来ますが、pyaudio は駄目です。

まず最初に PyAudio-0.2.11-cp39-cp39m-win_amd64.whl をダウンロードします。

そして pip install PyAudio-0.2.11-cp39-cp39m-win_amd64.whl すると、あっさりインストールできます。

と書いてあったと思いますが、出来ません。 Python 36 (Python 38 でも可能です) もインストールしないと .mp3 ファイルの 再生が出来ません。 Python 36 では、pip install pyaudio で大丈夫です。

C++ で Python のライブラリーを作ってみましょう。 まず最初に boost_1_77_0.zip を手に入れます。そしてダウンロードしたフォルダをカレントフォルダにして以下を実行します。

cd (解凍したディレクトリ)

bootstrap.bat

mkdir stage

b2.exe install -j2 --prefix=stage toolset=msvc-14.2 link=static,shared address-model=64 --with-python

VC++ のプログラムは、空のプロジェクトを選択し、とりあえずプロジェクト名を hello_ext2 とします。 追加する .cpp ファイルの名前は hello_ext2.cpp としなければいけません。 

#include < c:\boost_1_77_0\boost\python.hpp >
char const* greet()
{
    return "hello, world";
}

BOOST_PYTHON_MODULE(hello_ext2)
{
    using namespace boost::python;
    def("greet", greet);
}
のようにします。上で address-model=64 としたので、x64 でライブラリーを作ります。

次にプロジェクトのプロパティを設定します。構成プロパティの全般の構成の種類をダイナミック・ライブラリー(.dll)にし、 ターゲット名を拡張子(.pyd)で、今の場合、hello_ext2.pyd とします。

VC++ ディレクトリのインクルードディレクトリに、c:\Anaconde3\include と c:\boost_1_77_0 を

ライブラリーディレクトリに、c:\Anaconde3\libs と c:\boost_1_77_0\stage\lib

を追加します。Visual Studio 2018 でコンパイルすると hello_ext2.pyd を作ってくれる所までは何とか行きつきましたが、 
import hello_ext2

print(hello_ext2.greet())
が 
Traceback (most recent call last):
  File "C:\C++src\PythonModule\hello_ext2\x64\Release\hello_ext2_test.py", line 1, in 
    import hello_ext2
ImportError: DLL load failed while importing hello_ext2: 指定されたモジュールが見つかりません。
とエラーになってしまいます。古いバージョンの Python を使えば、出来るかも分かりませんが、 丸二日、無駄な努力で疲れ果てました。先生や朋友がいないと大変です。 次の日、 boost_1_66_0.zip と古い Python で確かめてみますが stage\lib を作ってくれず上手くいきません。 VC++ をアンインストールし、再度、インストールして。やってみると上で出来たことも出来なくなりました。 大学では、学生全員に windows パソコンを持たせていたので仕方がなかったのですが、今度、デスクトップが壊れたら、 Ubuntu のデスクトップにしようと思います。最新の技術を学ぶには Ubuntu でないといけません。

久しぶりに、C++ で Python のライブラリーを作ることに再挑戦してみました。 https://isolution.pro/t/python/python-further-extensions/python-c-o-shiyoshita-kakucho-puroguramingu の解説（多分、これは英文のAIによる翻訳で、 可笑しな処があります。例えば、i や double や float や long と英文そのままにすべき所が、「私」や「ダブル」や「浮く」や「長い」と訳されています。）を見て、 まず、VC++ 2022 で、載っていたプログラム 


C Program{
#include ＜Python.h＞

static PyObject* helloworld(PyObject* self) {
   return Py_BuildValue("s", "Hello, Python extensions!!");
}


static char helloworld_docs[] =
   "helloworld( ): Any message you want to put here!!\n";

static PyMethodDef helloworld_funcs[] = {
   {"helloworld", (PyCFunction)helloworld, 
      METH_NOARGS, helloworld_docs},
      {NULL}
};

void inithelloworld(void) {
   Py_InitModule3("helloworld", helloworld_funcs,
                  "Extension module example!");
}

}

をコンパイルしてみました。（＜＞は全角を表示の為使っています。） まず、Python.h が無いと言うので、 https://docs.microsoft.com/ja-jp/visualstudio/python/working-with-c-cpp-python-in-visual-studio?view=vs-2022 をみて、（オリジナルは https://docs.microsoft.com/en-us/visualstudio/python/working-with-c-cpp-python-in-visual-studio?view=vs-2022 です）、 「Python 開発ワークロードがインストールされた Visual Studio 2017 以降。 ワークロードには Python ネイティブ開発ツールが含まれており、 ネイティブ拡張機能に必要な C++ ワークロードとツールセットが提供されます。」に従って、 visual studio 2022 を再インストールし、変更するが上手くいかない。 Python.h は Python が持っているみたいなので、新たに Python の最新版 Python310 をインストールする。 今度は、Py_InitModule3 が分からないと言うので、（コンピュータの世界は物凄いスピードで技術革新が進んでいるので、 Py_InitModule3 は最早使われなくなったと言っているので、どの様に変化したか調べなければならない。）、 インターネットで検索し、 https://stackoverflow.com/questions/43621948/c-python-module-import-error-undefined-symbol-py-initmodule3-py-initmodu に書かれている質問に対する解答を参考に 


C Program{
#include ＜Python.h＞

static PyObject* helloworld(PyObject* self) {
    return Py_BuildValue("s", "Hello, Python extensions!!");
}


static char helloworld_docs[] =
"helloworld( ): Any message you want to put here!!\n";

static PyMethodDef  module_methods[] = {
   {"helloworld", (PyCFunction)helloworld,
      METH_NOARGS, helloworld_docs},
      {NULL}
};

static struct PyModuleDef helloworld_def =
{
    PyModuleDef_HEAD_INIT,
    "helloword", /* name of module */
    "usage: helloworld.helloworld\n", /* module documentation, may be NULL */
    -1,   /* size of per-interpreter state of the module, or -1 if the module keeps state in global variables. */
    module_methods
};

PyMODINIT_FUNC PyInit_helloworld(void)
{
    return PyModule_Create(&helloworld_def);
}

}

と書き直す。（＜＞は全角を表示の為使っています。）python310_d.lib が無いと言うので、 「Python を別個にインストールする場合は、そのインストーラーの [詳細オプション] で [Download debugging symbols](デバッグ シンボルのダウンロード) を必ず選択してください。 このオプションは、Python コードとネイティブ コードの間で混合モードのデバッグを使用する場合に必要です。」 の記述をインターネットで調べて、Python を再インストールする。 main が無いと言うが一様コンパイル出来るようになる。 .dll ファイルを作るものと思っていたので、兎も角、VC++ でコンパイルしてみましたが、こうすることで Py_InitModule3 が今は使えないことが速く分かって、ここまで到達出来ました。何が幸いするか分かりません。

.dll を作るかと思ったが、そうではなく、 上のプログラムを hello.c とすると 


Python Program{
from distutils.core import setup, Extension
setup(name='helloworld', version='1.0',  \
      ext_modules=[Extension('helloworld', ['hello.c'])])
}

を setup.py と言う名前で作り、 


$ python setup.py install

をコマンドプロンプトで実行すると 


build
dist
helloworld.egg-info

のように、VC++ 2022 でコンパイルして、ライブラリーを作ってくれました。 しかし、これはダミーで、本当に必要なライブラリーは Python 本体にセットされています。 


Python Program{
import helloworld

print(helloworld.helloworld())
}

を実行すると 


c:\PythonSrc\C_Extension>python mytest.py
Hello, Python extensions!!

と表示されました。二日がかりで、やっと、出発点に立てました。しかし、この方法も 廃止が計画されていて、直ぐに使えなくなるみたいです。兎も角。こうすれば、Python のプログラムを高速化出来るみたいです。 諦めずに、時間を置いて、頭を冷やして、改めて調べてみると新しいやり方をインターネットで見つけることが出来ました。

上のプログラムを .cpp と名前だけ変え、 


from distutils.core import setup, Extension
setup(name='helloworld', version='1.0',  \
      ext_modules=[Extension('helloworld', ['hello.cpp'])])
}

として、同じことをしても大丈夫です。

続いて、 https://isolution.pro/t/python/python-further-extensions/python-c-o-shiyoshita-kakucho-puroguramingu の続きを読んで、引き数と戻り値のある関数を定義してみます。

C++ には、リスト、タプル、辞書は無いので、引き数には使えないですが、戻り値には使えます。 この解説の例はモジュール名と関数名が同じですが、 モジュール名と関数名をどの様に区別すれば良いか、これを読んだだけでは分かりません。

思いつく全ての組み合わせを片っ端から虱潰しにやって見れば、何が正しいかはコンピュータが教えてくれるので、正解に到達します。 


#include ＜Python.h＞

static PyObject* add_subtract(PyObject* self, PyObject* args) {
    int a;
    int b;

    if (!PyArg_ParseTuple(args, "ii", &a, &b)) {
        return NULL;
    }
    return Py_BuildValue("[ii]", a+b, a-b);
}

static char foo_add_subtract_docs[] =
"add_subtract(int, int ): Any message you want to put here!!\n";

static PyMethodDef  module_methods[] = {
   {"add_subtract", (PyCFunction)add_subtract,
      METH_VARARGS, foo_add_subtract_docs},
      {NULL}
};

static struct PyModuleDef foo_add_subtract_def =
{
    PyModuleDef_HEAD_INIT,
    "foo", /* name of module */
    "usage: foo.add_subtract(int, int)\n", /* module documentation, may be NULL */
    -1,   /* size of per-interpreter state of the module, or -1 if the module keeps state in global variables. */
    module_methods
};

PyMODINIT_FUNC PyInit_foo(void)
{
    return PyModule_Create(&foo_add_subtract_def);
}

を add_subtract.cpp とし、（＜＞は全角を表示の為使っています。） 


from distutils.core import setup, Extension
setup(name='foo', version='1.0',  \
      ext_modules=[Extension('foo', ['add_subtract.cpp'])])

を setup.py とし、 


c:\PythonSrc\C_Extension\add_subtract>python setup.py install

で、コンパイルし、 


Python Program{
import foo

print(foo.add_subtract(5, 3))
}

を実行すると 


c:\PythonSrc\C_Extension\add_subtract>python mytest.py
[8, 2]

と表示されました。これで正しいみたいです。また、 


static PyMethodDef  module_methods[] = {
   {"add_subtract", (PyCFunction)add_subtract,
      METH_VARARGS, foo_add_subtract_docs},
      {NULL}
};

は 


static PyMethodDef  module_methods[] = {
   {"add_subtract", (PyCFunction)add_subtract,
      METH_VARARGS, NULL},
      {NULL}
};

と foo_add_subtract_docs 無しでも大丈夫です。そもそも、これの実際の使い方がまだ分からないです。 まだ、複数の関数を纏めて定義するには如何するかとか、やってみなければいけないことが残っています。兎も角、これで、一様、仕組みを理解できましたが、 「関数のC実装のシグネチャは、常に次の3つの形式のいずれかを取ります」と書いてありますが、 


static PyObject *MyFunction( PyObject *self, PyObject *args );

static PyObject *MyFunctionWithKeywords(PyObject *self,
                                 PyObject *args,
                                 PyObject *kw);

static PyObject *MyFunctionWithNoArgs( PyObject *self );

の真ん中のものに関する解説がありません。このような人工的なものは、我々凡人は考えても分からず、誰かに教えてもらわなければ使えるようにはなりませんが、 差し合たって障害にはならないと思います。ここまでで分かったことで、十分高速なプログラムが作れるはずです。 やっと、気になっていた 「Python の拡張を皆はどうやっているのだろうと言う」疑問が解決しました。

引き続き 、 https://docs.microsoft.com/ja-jp/visualstudio/python/working-with-c-cpp-python-in-visual-studio?view=vs-2022 を読んで見ます。 Visual Studio for Python もインストールして置くと Visual Studio で [ファイル]>[新規]>[プロジェクト] の順に選択して、新しい Python プロジェクトを作成し、 今までに作った Python のプログラムを 打ち込むと [デバッグ]>[デバッグの開始]を選ぶと実行してくれますが、 [デバッグ]>[デバッグなしで開始]だと実行してくれない場合が殆どです。 「 Python を別個にインストールする場合は、そのインストーラーの [詳細オプション] で [Download debugging symbols](デバッグ シンボルのダウンロード) を必ず選択してください。 このオプションは、Python コードとネイティブ コードの間で混合モードのデバッグを使用する場合に必要です。」との関係も今一つ理解できないですが、 兎も角、Visual Studio for Python を使って、Python のプログラミングも出来ます。 この解説では、同時に2つのやり方を解説しているので、戸惑いますが、兎も角、解説通り、 途中まで、このマイクロソフトの VC++ を使った2通りの方法をやってみましたが、 マイクロソフトの解説だから VC++ だけで出来るように面倒くさいことをやっているが上でやったことの真似が出来るのではないかと思いやってみると 可能でした。

CPython 拡張機能 (superfastcode プロジェクト) の場合: 


C++ Program{
#include ＜Windows.h＞
#include ＜cmath＞
#include ＜Python.h＞

const double e = 2.7182818284590452353602874713527;

double sinh_impl(double x) {
    return (1 - pow(e, (-2 * x))) / (2 * pow(e, -x));
}

double cosh_impl(double x) {
    return (1 + pow(e, (-2 * x))) / (2 * pow(e, -x));
}


/*
double tanh_impl(double x) {
    return sinh_impl(x) / cosh_impl(x);
}
*/

PyObject* tanh_impl(PyObject* /* unused module reference */, PyObject* o) {
    double x = PyFloat_AsDouble(o);
    double tanh_x = sinh_impl(x) / cosh_impl(x);
    return PyFloat_FromDouble(tanh_x);
}

static PyMethodDef superfastcode_methods[] = {
    // The first property is the name exposed to Python, fast_tanh
    // The second is the C++ function with the implementation
    // METH_O means it takes a single PyObject argument
    { "fast_tanh", (PyCFunction)tanh_impl, METH_O, nullptr },

    // Terminate the array with an object containing nulls.
    { nullptr, nullptr, 0, nullptr }
};

static PyModuleDef superfastcode_module = {
    PyModuleDef_HEAD_INIT,
    "superfastcode",                        // Module name to use with Python import statements
    "Provides some functions, but faster",  // Module description
    0,
    superfastcode_methods                   // Structure that defines the methods of the module
};

PyMODINIT_FUNC PyInit_superfastcode() {
    return PyModule_Create(&superfastcode_module);
}
}

を module.cpp とし、（＜＞は全角を表示の為使っています。） 


Python Program{
from setuptools import setup, Extension

sfc_module = Extension('superfastcode', sources = ['module.cpp'])

setup(
    name='superfastcode',
    version='1.0',
    description='Python Package with superfastcode C++ extension',
    ext_modules=[sfc_module]
)
}

を setup.py とし、 


python setup.py install

を実行し、 


Python Program{
from random import random
from time import perf_counter

COUNT = 500000  # Change this value depending on the speed of your computer
DATA = [(random() - 0.5) * 3 for _ in range(COUNT)]

e = 2.7182818284590452353602874713527

def sinh(x):
    return (1 - (e ** (-2 * x))) / (2 * (e ** -x))

def cosh(x):
    return (1 + (e ** (-2 * x))) / (2 * (e ** -x))

def tanh(x):
    tanh_x = sinh(x) / cosh(x)
    return tanh_x

def test(fn, name):
    start = perf_counter()
    result = fn(DATA)
    duration = perf_counter() - start
    print('{} took {:.3f} seconds\n\n'.format(name, duration))

    for d in result:
        assert -1 <= d <= 1, " incorrect values"

if __name__ == "__main__":
    print('Running benchmarks with COUNT = {}'.format(COUNT))

    test(lambda d: [tanh(x) for x in d], '[tanh(x) for x in d] (Python implementation)')

    from superfastcode import fast_tanh
    test(lambda d: [fast_tanh(x) for x in d], '[fast_tanh(x) for x in d] (CPython C++ extension)')
}

を PythonApplication1.py として、 


python PythonApplication1.py

を実行すれば、 


Running benchmarks with COUNT = 500000
[tanh(x) for x in d] (Python implementation) took 0.486 seconds


[fast_tanh(x) for x in d] (CPython C++ extension) took 0.096 seconds

と表示されました。

PyBind11 (superfastcode2 プロジェクト) の場合: 


C++ Program{
#include ＜Windows.h＞
#include ＜cmath＞
#include ＜pybind11\pybind11.h＞

const double e = 2.7182818284590452353602874713527;

double sinh_impl(double x) {
    return (1 - pow(e, (-2 * x))) / (2 * pow(e, -x));
}

double cosh_impl(double x) {
    return (1 + pow(e, (-2 * x))) / (2 * pow(e, -x));
}


double tanh_impl(double x) {
    return sinh_impl(x) / cosh_impl(x);
}

namespace py = pybind11;

PYBIND11_MODULE(superfastcode2, m) {
    m.def("fast_tanh2", &tanh_impl, R"pbdoc(
        Compute a hyperbolic tangent of a single argument expressed in radians.
    )pbdoc");

#ifdef VERSION_INFO
    m.attr("__version__") = VERSION_INFO;
#else
    m.attr("__version__") = "dev";
#endif
}
}

を module.cpp とし、（＜＞は全角を表示の為使っています。） 


Python Program{
from setuptools import setup, Extension
import pybind11

cpp_args = ['-std=c++11', '-stdlib=libc++', '-mmacosx-version-min=10.7']

sfc_module = Extension(
    'superfastcode2',
    sources=['module.cpp'],
    include_dirs=[pybind11.get_include()],
    language='c++',
    extra_compile_args=cpp_args,
    )

setup(
    name='superfastcode2',
    version='1.0',
    description='Python package with superfastcode2 C++ extension (PyBind11)',
    ext_modules=[sfc_module],
)
}

を setup.py とし、 


python setup.py install

を実行し、 


Python Program{
from random import random
from time import perf_counter

COUNT = 500000  # Change this value depending on the speed of your computer
DATA = [(random() - 0.5) * 3 for _ in range(COUNT)]

e = 2.7182818284590452353602874713527

def sinh(x):
    return (1 - (e ** (-2 * x))) / (2 * (e ** -x))

def cosh(x):
    return (1 + (e ** (-2 * x))) / (2 * (e ** -x))

def tanh(x):
    tanh_x = sinh(x) / cosh(x)
    return tanh_x

def test(fn, name):
    start = perf_counter()
    result = fn(DATA)
    duration = perf_counter() - start
    print('{} took {:.3f} seconds\n\n'.format(name, duration))

    for d in result:
        assert -1 <= d <= 1, " incorrect values"

if __name__ == "__main__":
    print('Running benchmarks with COUNT = {}'.format(COUNT))

    test(lambda d: [tanh(x) for x in d], '[tanh(x) for x in d] (Python implementation)')

    from superfastcode2 import fast_tanh2
    test(lambda d: [fast_tanh2(x) for x in d], '[fast_tanh2(x) for x in d] (PyBind11 C++ extension)')
}

を PythonApplication1.py として、 


python PythonApplication1.py

を実行すれば、 


Running benchmarks with COUNT = 500000
[tanh(x) for x in d] (Python implementation) took 0.485 seconds


[fast_tanh2(x) for x in d] (PyBind11 C++ extension) took 0.277 seconds

と表示されました。

CPython 拡張機能 (superfastcode プロジェクト) の場合でも、 PyBind11 (superfastcode2 プロジェクト) の場合でも実行でき、前者の場合が後者より高速で、共にオリジナルの Python より高速です。 このマイクロソフトの解説では float の場合、しかも、引き数一個、戻り値1個の場合しか分からないので、更なる解説を探さなければなりませんが、 別の方法もあることが分かりました。 https://isolution.pro/t/python/python-further-extensions/python-c-o-shiyoshita-kakucho-puroguramingu の前に、 https://docs.microsoft.com/ja-jp/visualstudio/python/working-with-c-cpp-python-in-visual-studio?view=vs-2022 を見つけていたら、私の実力ではこのようにすんなり学習することが出来なかったと思います。 実際は、「努力より運」が物事を決めているみたいです。 コンピューターの世界は物凄いスピードで技術革新が行われていて、学んだことがすぐ陳腐化・使われなくなるので、私のような貧乏な老人には付いていくのが大変です。

この関数を上の最初にやった方法に書き直すと 


C++ Program{
#include ＜Windows.h＞
#include ＜cmath＞
#include ＜Python.h＞

const double e = 2.7182818284590452353602874713527;

double sinh_impl(double x) {
    return (1 - pow(e, (-2 * x))) / (2 * pow(e, -x));
}

double cosh_impl(double x) {
    return (1 + pow(e, (-2 * x))) / (2 * pow(e, -x));
}


/*
double tanh_impl(double x) {
    return sinh_impl(x) / cosh_impl(x);
}
*/

PyObject* tanh_impl(PyObject* self, PyObject* args) {
    double x;
    if (!PyArg_ParseTuple(args, "f", &x)) {
        return NULL;
    }
    double tanh_x = sinh_impl(x) / cosh_impl(x);
    return Py_BuildValue("f", tanh_x);
}

static PyMethodDef superfastcode_methods[] = {
    // The first property is the name exposed to Python, fast_tanh
    // The second is the C++ function with the implementation
    // METH_O means it takes a single PyObject argument
    { "fast_tanh", (PyCFunction)tanh_impl, METH_VARARGS, nullptr },

    // Terminate the array with an object containing nulls.
    { nullptr, nullptr, 0, nullptr }
};

static PyModuleDef superfastcode_module = {
    PyModuleDef_HEAD_INIT,
    "superfastcode",                        // Module name to use with Python import statements
    "Provides some functions, but faster",  // Module description
    0,
    superfastcode_methods                   // Structure that defines the methods of the module
};

PyMODINIT_FUNC PyInit_superfastcode() {
    return PyModule_Create(&superfastcode_module);
}
}

を modulo.cpp とし、（-1 と 0 の違いがまだ分かりませんが）（＜＞は全角を表示の為使っています。） 


Python Program{
from setuptools import setup, Extension

sfc_module = Extension('superfastcode', sources = ['module.cpp'])

setup(
    name='superfastcode',
    version='1.0',
    description='Python Package with superfastcode C++ extension',
    ext_modules=[sfc_module]
)
}

を setup.py として、同じことをすれば、同じ結果を得ます。。

C++ と Python を組み合わせてのプログラミングの骨組みだけは理解出来るようになり、プログラミングの幅が広がりました。 又。勉強する順序が大切で、上手い具合に簡単で網羅的な解説から読むことが出来て、勉強時間の短縮になり運が良かったです。

更に、python.org に依る解説が https://docs.python.org/3/extending/index.html にあることが分かりました。膨大な資料で読むのは大変ですが、本で解説を書くような人はチャンと読むんだろうと思います。 C++ のプログラミングの中で、Python を実行する方法も解説しているみたいです。

マンデルブロ集合 （英: Mandelbrot set ）を描くプログラムにこの技法を使ってみましょう。 


C++ Program{
#include ＜Python.h＞
#include ＜complex＞

using namespace std;

PyObject* mb_impl(PyObject* self, PyObject* args) {
    float x, y, K;
    int LOOP;

    if (!PyArg_ParseTuple(args, "fffi", &x, &y, &K, &LOOP)) {
        return NULL;
    }
    complex z, c;
    z = complex(0.0, 0.0);
    c = complex(x, y);
    int n = 0;
    while (abs(z) < K && n < LOOP) {
        z = z*z + c;
        n = n +1;
    }
    return Py_BuildValue("i", n);
}

static PyMethodDef mymb_methods[] = {
    { "mb", (PyCFunction)mb_impl, METH_VARARGS, nullptr },
    { nullptr, nullptr, 0, nullptr }
};

static PyModuleDef mymb_module = {
    PyModuleDef_HEAD_INIT,
    "mymb",                        // Module name to use with Python import statements
    "Provides some functions, but faster",  // Module description
    -1,
    mymb_methods                   // Structure that defines the methods of the module
};

PyMODINIT_FUNC PyInit_mymb(void) {
    return PyModule_Create(&mymb_module);
}
}

を mandel.cpp とし、ここで、＜＞をこのページの表示の為に使っています。プログラムをコピーペーストする時は、変更してください。 そして、 


Python Program{
from setuptools import setup, Extension

sfc_module = Extension('mymb', sources = ['mandel.cpp'])

setup(
    name='mymb',
    version='1.0',
    description='Python Package with superfastcode C++ extension',
    ext_modules=[sfc_module]
)
}

を setup.py とし、 


python setup.py install

をコマンドプロンプトで実行し、 


Python Program{
from tkinter import *
import math
import time
import mymb

root = Tk()
canvas = Canvas(root, width = 480, height=400)
sx , sy = 0.0, 0.0
def setsource(event):
    global sx, sy
    sx = (xmax-xmin)/480.0*event.x + xmin
    sy = ymax - (ymax-ymin)/400.0*event.y
canvas.bind("", setsource)
tx, ty = 0.0, 0.0
def drawline(event):
    global sx, sy, tx, ty
    tx = (xmax-xmin)/480.0*event.x + xmin
    ty = ymax - (ymax-ymin)/400.0*event.y
    if xmin == xmax or ymin == ymax :
        return
    gsx = 480/(xmax-xmin)*(sx-xmin)
    gsy = 400/(ymax-ymin)*(ymax-sy)
    gtx = 480/(xmax-xmin)*(tx-xmin)
    gty = 400/(ymax-ymin)*(ymax-ty)
    canvas.create_rectangle(gsx, gsy, gtx, gty)
canvas.bind("", drawline)
def redraw(event):
    start_time = time.time()
    global sx, sy, tx, ty
    global xmax, xmin, ymax, ymin
    global dx, dy
    tx = (xmax-xmin)/480.0*event.x + xmin
    ty = ymax - (ymax-ymin)/400.0*event.y
    if tx < sx:
        sx, tx = tx, sx
    if ty < sy:
        sy, ty = ty, sy
    xmin, xmax = sx, tx
    ymin, ymax = sy, ty
    dx = (xmax-xmin)/480.0
    dy = (ymax-ymin)/400.0
    x = xmin
    while x < xmax:
        y = ymin
        while y < ymax:
            ##c = x + y*1j
            n = mymb.mb(x, y, K, LOOP)
            plot(x, y, n, LOOP)
            y += dy
        x += dx
    end_time = time.time()
    print( "time = %f" % (end_time-start_time) )
    
canvas.bind("", redraw)

##def mb(c, K, LOOP):
##    z = 0.0 + 0.0*1j
##    n = 0
##    while (abs(z) < K and n < LOOP):
##        z = z**2 + c
##        n = n +1
##    return n
def plot(x, y, n, LOOP):
    #gx = 200*x + 370
    #gy = -180*y + 200
    gx = 480/(xmax-xmin)*(x-xmin)
    gy = 400/(ymax-ymin)*(ymax-y)
    if n == LOOP:
       canvas.create_line(gx, gy, gx+1, gy+1, fill = 'black')
    elif n % 8 == 0:
       canvas.create_line(gx, gy, gx+1, gy+1, fill = 'yellow')
    elif n % 8 == 1:
       canvas.create_line(gx, gy, gx+1, gy+1, fill = 'orange')
    elif n % 8 == 2:
       canvas.create_line(gx, gy, gx+1, gy+1, fill = 'cyan')
    elif n % 8 == 3:
       canvas.create_line(gx, gy, gx+1, gy+1, fill = 'white')
    elif n % 8 == 4:
       canvas.create_line(gx, gy, gx+1, gy+1, fill = 'green')
    elif n % 8 == 5:
       canvas.create_line(gx, gy, gx+1, gy+1, fill = 'coral')
    elif n % 8 == 6:
       canvas.create_line(gx, gy, gx+1, gy+1, fill = 'blue')
    elif n % 8 == 7:
       canvas.create_line(gx, gy, gx+1, gy+1, fill = 'red')
dx, dy = 0.005, 0.005
xmin, xmax = -1.8, 0.6
ymin, ymax = -1.0, 1.0

K = 3.0
LOOP = 255
start_time = time.time()
x = xmin
while x < xmax:
    y = ymin
    while y < ymax:
        ##c = x + y*1j
        n = mymb.mb(x, y, K, LOOP)
        plot(x, y, n, LOOP)
        y += dy
    x += dx
end_time = time.time()
print( "time = %f" % (end_time-start_time) )
canvas.pack()
root.mainloop()
}

を new_mandel.py として、 


python new_mandel.py

を実行すれば、マンデルブロ集合を描いてくれます。マウスで次に描きたい範囲をドラッグで指示すれば


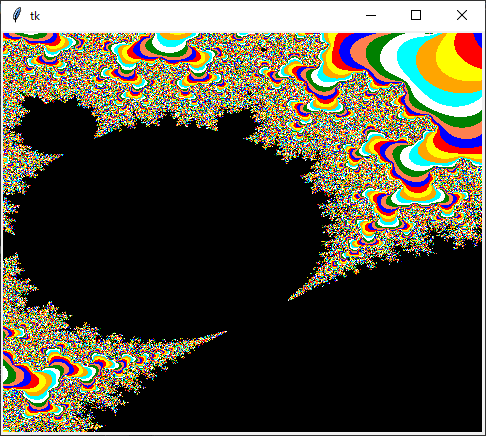
のような図が得られます。繰り返して、範囲が小さくなりすぎると ZeroDivisionError: float division by zero になり、 表示してくれません。プログラムのバグか、float の限界か調べていません。 上の 


##def mb(c, K, LOOP):
##    z = 0.0 + 0.0*1j
##    n = 0
##    while (abs(z) < K and n < LOOP):
##        z = z**2 + c
##        n = n +1
##    return n

を C++ のモジュールにしてみました。

https://qiita.com/supersaiakujin/items/ebc093dd04fe2b49517e

の　pythonからcの関数を呼び出す方法(ctypes編) と言う記事を見つけたので、やってみました。 書いてある通りにやれば出来るものもあれば、出来ないものもあります。 単なるミスプリントか少なくとも記事をかいた時は実行できた可能性が高く、基本的には間違っていないはずですから、 インターネットを調べたり、丸一日、試行錯誤して、何とか、欲しかったプログラムを作り上げました。 VC++ 2022 で、DLL を作り、Python で呼び出す方法です。上でやったモジュールを作る方法のように、インターフェースが スマートではないですが、高速化が計れる拡張方法の一つです。

C++ 2022 で空のプロジェクト Mandelbrort を作り、 


#pragma once

#ifdef CTYPES_SAMPLE1_EXPORTS
#define CTYPES_SAMPLE1_API __declspec(dllexport)
#else
#define CTYPES_SAMPLE1_API __declspec(dllimport)
#endif

extern "C" CTYPES_SAMPLE1_API bool copy(double xmax, double xmin, double ymax, double ymin, double K, int LOOP, int* narry);

の Mandelbrort.h と 


#include "Mandelbrot.h"
#include ＜complex＞ 

using namespace std;

bool copy(double xmax, double xmin, double ymax, double ymin, double K, int LOOP, int* narry)
{
    double x, y;
    double dx = (xmax - xmin) / 480.0;
    double dy = (ymax - ymin) / 400.0;

    for (int i=0; i<480; i++) {
        x = xmin + i * dx;
        for (int k=0; k<400; k++) {
            y = ymin + k * dy;

            complex z, c;
            z = complex(0.0, 0.0);
            c = complex(x, y);
            int n = 0;
            while (abs(z) < K && n < LOOP) {
                z = z * z + c;
                n = n + 1;
            }
            narry[480 * k + i] = n;
        }
    }    
    return true;
}

の Mandelbrot.cpp をプロジェクトに追加し、プロパティで dll 作成に変更し、ビルドします。 


Pyton Program{
from tkinter import *
import math
import time
import mymb
import ctypes

mydll=ctypes.cdll.LoadLibrary('./Mandelbrot.dll')

root = Tk()
canvas = Canvas(root, width = 480, height=400)
sx , sy = 0.0, 0.0
def setsource(event):
    global sx, sy
    sx = (xmax-xmin)/480.0*event.x + xmin
    sy = ymax - (ymax-ymin)/400.0*event.y
canvas.bind("", setsource)
tx, ty = 0.0, 0.0
def drawline(event):
    global sx, sy, tx, ty
    tx = (xmax-xmin)/480.0*event.x + xmin
    ty = ymax - (ymax-ymin)/400.0*event.y
    if xmin == xmax or ymin == ymax :
        return
    gsx = 480/(xmax-xmin)*(sx-xmin)
    gsy = 400/(ymax-ymin)*(ymax-sy)
    gtx = 480/(xmax-xmin)*(tx-xmin)
    gty = 400/(ymax-ymin)*(ymax-ty)
    canvas.create_rectangle(gsx, gsy, gtx, gty)
canvas.bind("", drawline)
def redraw(event):
    start_time = time.time()
    global sx, sy, tx, ty
    global xmax, xmin, ymax, ymin
    global dx, dy
    tx = (xmax-xmin)/480.0*event.x + xmin
    ty = ymax - (ymax-ymin)/400.0*event.y
    if tx < sx:
        sx, tx = tx, sx
    if ty < sy:
        sy, ty = ty, sy
    xmin, xmax = sx, tx
    ymin, ymax = sy, ty

    size = 480 * 400
    arr = (ctypes.c_int*size)(*([0]*size))
    copy1d=mydll.copy
    copy1d.argtypes=(ctypes.c_double,ctypes.c_double,ctypes.c_double,ctypes.c_double,ctypes.c_double,ctypes.c_int,ctypes.POINTER(ctypes.c_int))
    copy1d.restype=ctypes.c_bool
    copy1d(xmax, xmin, ymax, ymin, K, LOOP, ctypes.cast(arr, ctypes.POINTER(ctypes.c_int)))

    dx = (xmax-xmin)/480.0
    dy = (ymax-ymin)/400.0
    for i in range(480):
        x = xmin + i * dx;
        for k in range(400):
            y = ymin + k * dy;
            plot(x, y, arr[480 * k + i], LOOP)
    end_time = time.time()
    print( "time = %f" % (end_time-start_time) )

canvas.bind("", redraw)

def plot(x, y, n, LOOP):
    #gx = 200*x + 370
    #gy = -180*y + 200
    gx = 480/(xmax-xmin)*(x-xmin)
    gy = 400/(ymax-ymin)*(ymax-y)
    if n == LOOP:
       canvas.create_line(gx, gy, gx+1, gy+1, fill = 'black')
    elif n % 8 == 0:
       canvas.create_line(gx, gy, gx+1, gy+1, fill = 'yellow')
    elif n % 8 == 1:
       canvas.create_line(gx, gy, gx+1, gy+1, fill = 'orange')
    elif n % 8 == 2:
       canvas.create_line(gx, gy, gx+1, gy+1, fill = 'cyan')
    elif n % 8 == 3:
       canvas.create_line(gx, gy, gx+1, gy+1, fill = 'white')
    elif n % 8 == 4:
       canvas.create_line(gx, gy, gx+1, gy+1, fill = 'green')
    elif n % 8 == 5:
       canvas.create_line(gx, gy, gx+1, gy+1, fill = 'coral')
    elif n % 8 == 6:
       canvas.create_line(gx, gy, gx+1, gy+1, fill = 'blue')
    elif n % 8 == 7:
       canvas.create_line(gx, gy, gx+1, gy+1, fill = 'red')
dx, dy = 0.005, 0.005
xmin, xmax = -1.8, 0.6
ymin, ymax = -1.0, 1.0

K = 3.0
LOOP = 255
start_time = time.time()

size = 480 * 400
arr = (ctypes.c_int*size)(*([0]*size))
copy1d=mydll.copy
copy1d.argtypes=(ctypes.c_double,ctypes.c_double,ctypes.c_double,ctypes.c_double,ctypes.c_double,ctypes.c_int,ctypes.POINTER(ctypes.c_int))
copy1d.restype=ctypes.c_bool
copy1d(xmax, xmin, ymax, ymin, K, LOOP, ctypes.cast(arr, ctypes.POINTER(ctypes.c_int)))

dx = (xmax-xmin)/480.0
dy = (ymax-ymin)/400.0
for i in range(480):
    x = xmin + i * dx;
    for k in range(400):
        y = ymin + k * dy;
        plot(x, y, arr[480 * k + i], LOOP)

end_time = time.time()
print( "time = %f" % (end_time-start_time) )
canvas.pack()
root.mainloop()
}

を Mandelbrot.dll のあるフォルダーに置いて、実行すれば、上のプログラムと同じことをしてくれます。 


c:\C++src\Python_C\mandelbrot>python mandel.py
time = 5.553392
time = 7.464182
time = 8.693346
c:\C++src\Python_C\mandelbrot>python new_mandel.py
time = 1.341250
time = 1.367817
time = 1.366326
c:\C++src\Python-ctypes\Mandelbrot\Mandelbrot\x64\Release>python new_mandel.py
time = 1.268953
time = 1.321883
time = 1.404821
c:\C++src\Python-ctypes\Mandelbrot\Mandelbrot2\x64\Release>python new_mandel.py
time = 1.273677
time = 1.483736
time = 1.444526

が、純粋な Python のプログラムから順に、最後はプログラムは同様に作れるので挙げていませんが、 (x, y, n) の配列を VC++ 2022 で作って戻す場合まで、 範囲選択を２回行った時までの時間を計測してみましたが、 どの方法も大した差はないみたいです。但し、この表示があってから、暫くして図の描画が終わります。描き終わるまでの時間ではないです。 知らないことばかりですが、インターネットには色々な情報があり、古いものもありますが、それを手掛かりに調べると、色々なことが出来るようになります。 私のような先生も共に学ぶ朋友もいないし、何処かに習いに行くお金もないけど、時間だけある老人にも有難い世の中になりました。

忘れない内に、練習してみましょう。「確率・統計」では、Excel を使うことも多く、私も Excel を使って、「確率・統計」の講義も していましたが、 Excel はヴァージョンアップアがしょっちゅうあり、経済的負担が大きいです。ここでは、Python を使ってみます。

先ずは、簡単なガリレオやカルダーノの時代の確率の話の問題です。


この問題を調べるには2通りの方法があります。 実際にサイコロを多数回振ってみて、統計を取る方法が一つです。人間が実際にサイコロを多数回振るのは大変なので、 現在はコンピュータのシミュレーションで行います。 このような場合、確率を数学的に議論する時には、Laplace による「同等に確からしい」が仮定されています。 即ち、今の場合は、サイコロを一回振った時、それぞれの目の出る確率は 1/6 である 理想的なサイコロに対して何が言えるかを議論しています。このような仮定がなされていることは忘れてはいけません。 


Python Program {
import numpy as np
import matplotlib.pyplot as plt
from time import perf_counter
import random


def f(N):
    dic = {}
    xs = []
    ys = []
    for i in range(N):
        x = random.randrange(1, 7)+random.randrange(1, 7)+random.randrange(1, 7)
        dic[x] = dic.get(x, 0) + 1
    for x, freq in dic.items():
        xs.append(x)
        ys.append(freq)
    return xs, ys

start = perf_counter()
N = 100000
xs, ys = f(N)
plt.bar(xs, ys)
plt.show()
duration = perf_counter() - start
print('{} took {:.3f} seconds\n\n'.format('Python', duration))
}

で


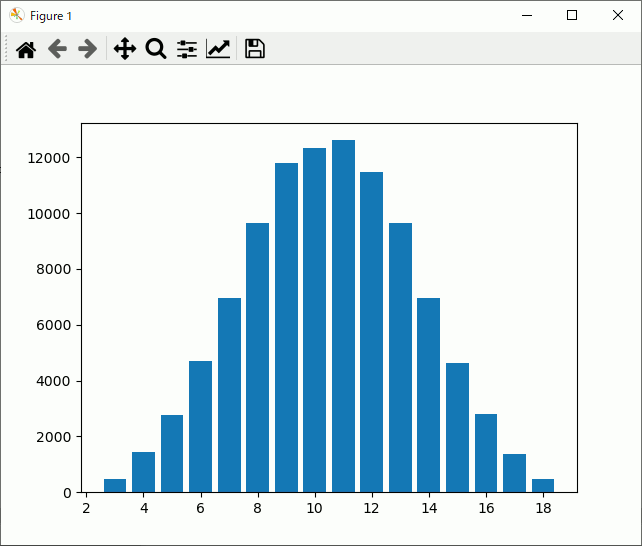
を得ます。プログラミングで使う乱数は、数学的に作った疑似乱数ですが、研究が進んで良いものが使われだしているので、 我々凡人は気にしなくても良いと思います。

別の方法は全ての数字1，2，3，4，5，6が等確率で現れる理想的なサイコロの存在を仮定し、数学的・理論的に考察する方法です。 物理に、「実験物理」と「理論物理」が在るようなものだと考えれば良いです。数学でも「実験数学」として、 上のような実験・シミュレーションがコンピュータの発達で簡単にすることが可能になってきました。 さて、３個のサイコロを投げた時の場合分けを 


 3: 1+1+1
 4: 1+1+2, 1+2+1, 2+1+1
 5: 1+1+3, 1+3+1, 3+1+1, 1+2+2, 2+1+2, 2+2+1
 6: 1+1+4, 1+4+1, 4+1+1, 1+2+3, 1+3+2, 2+1+3, 2+3+1, 3+1+2, 3+2+1, 2+2+2
 7: 1+1+5, 1+5+1, 5+1+1, 1+2+4, 1+4+2, 2+1+4, 2+4+1, 4+1+2. 4+2+1,
    1+3+3, 3+1+3, 3+3+1, 2+2+3, 2+3+2, 3+2+2,
 8: 1+1+6, 1+6+1, 6+1+1, 1+2+5, 1+5+2, 2+1+5, 2+5+1, 5+1+2, 5+2+1,
    1+3+4, 1+4+3, 3+1+4, 3+4+1, 4+1+3, 4+3+1, 2+2+4, 2+4+2, 4+2+2,
    2+3+3, 3+2+3, 3+3+2
 9: 1+2+6, 1+6+2, 2+1+6, 2+6+1, 6+1+2, 6+2+1, 
    1+3+5, 1+5+3, 3+1+5, 3+5+1, 5+1+3, 5+3+1, 1+4+4, 4+1+4, 4+4+1,
    2+2+5, 2+5+2, 2+2+5, 2+3+4, 2+4+3, 3+2+4, 3+4+2, 4+2+3, 4+3+2, 3+3+3
10: 1+3+6, 1+6+3, 3+1+6, 3+6+1, 6+1+3, 6+3+1,
    1+4+5, 1+5+4, 4+1+5, 4+5+1, 5+1+4, 5+4+1, 2+2+6, 2+6+2, 6+2+2,
    2+3+5, 2+5+3, 3+2+5, 3+5+2, 5+2+3, 5+3+2, 2+4+4, 4+2+4, 4+4+2,
    3+3+4, 3+4+3, 4+3+3
11: 1+4+6, 1+6+4, 4+1+6, 4+6+1, 6+1+4, 6+4+1,1+5+5, 5+1+5, 5+5+1,
    2+3+6, 2+6+3, 3+2+6, 3+6+2, 6+2+3, 6+3+2,
    2+4+5, 2+5+4, 4+2+5, 4+5+2, 5+2+4, 5+4+2, 3+3+5, 3+5+3, 5+3+3,
    3+4+4, 4+3+4, 4+4+3
12: 1+5+6, 1+6+5, 5+1+6, 5+6+1, 6+1+5, 6+5+1,
    2+4+6, 2+6+4, 4+2+6, 4+6+2, 6+2+4, 6+4+2, 2+5+5, 5+2+5, 5+5+2,
    3+4+5, 3+5+4, 4+3+5, 4+5+3, 5+3+4, 5+4+3, 3+3+6, 3+6+3, 6+3+3, 4+4+4
13: 1+6+6, 6+1+6, 6+6+1, 2+5+6, 2+6+5, 5+2+6, 5+6+2, 6+2+5, 6+5+2,
    3+4+6, 3+6+4, 4+3+6, 4+6+3, 6+3+4, 6+4+3, 3+5+5, 5+3+5, 5+5+3,
    4+4+5, 4+5+4, 5+4+4
14: 2+6+6, 6+2+6, 6+6+2, 3+5+6, 3+6+5, 5+3+6, 5+6+3, 6+3+5, 6+5+3,
    4+4+6, 4+6+4, 6+4+4, 4+5+5, 5+4+5, 5+5+4
15: 3+6+6, 6+3+6, 6+6+3, 4+5+6, 4+6+5, 5+4+6, 5+6+4, 6+4+5, 6+5+4, 5+5+5
16: 4+6+6, 6+4+6, 6+6+4, 5+5+6, 5+6+5, 6+5+5
17: 5+6+6, 6+5+6,6+6+5
18: 6+6+6

と手計算ですることも出来るし、 順序は無視し目の出方だけ求め、2+2+2 なら一通り、1+1+5 なら３通り、1+2+3 なら６通りと計算すれば、 もっと早く計算できますが、どっちにしろ結構大変です。カルダーノやガリレオの時代はこうするしかなかったのですが、 現在はコンピュータという人間の思考を手助けしてくれる機械があります。 そして、見てわかるように、グラフにします。面倒なことはコンピュータにやってもらいます。

サイコロを3個振った時の分布図を Python で作ってみましょう。 


C++ Program{
#include 
#include 

static PyObject* get_count(PyObject* self) {
    std::vector v{ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 };
    for (int i = 1; i < 7; i++) {
        for (int j = 1; j < 7; j++) {
            for (int k = 1; k < 7; k++) {
                v[i + j + k] += 1;
            }
        }
    }
    return Py_BuildValue("[iiiiiiiiiiiiiiiiiii]", v[0], v[1], v[2], v[3], v[4], v[5], v[6], v[7], v[8], 
	v[9], v[10], v[11], v[12], v[13], v[14], v[15], v[16], v[17], v[18] );
}

static PyMethodDef  module_methods[] = {
   {"get", (PyCFunction)get_count,
      METH_NOARGS, NULL},
      {NULL}
};

static struct PyModuleDef get_count_def =
{
    PyModuleDef_HEAD_INIT,
    "dice", /* name of module */
    "usage: dice.get())\n",
    -1,
    module_methods
};

PyMODINIT_FUNC PyInit_dice(void)
{
    return PyModule_Create(&get_count_def);
}
}

を module.cpp とし、 


Python Program{
from distutils.core import setup, Extension
setup(name='dice', version='1.0',  \
      ext_modules=[Extension('dice', ['module.cpp'])])
}

を setup.py とします。 


Python Program{
import numpy as np
import matplotlib.pyplot as plt
from time import perf_counter

start = perf_counter()
A = [i+j+k for i in range(1,7) for j in range(1,7) for k in range(1,7)]
dic = {}
for x in A:
    dic[x] = dic.get(x, 0) + 1
xs = []
ys = []
for x, freq in dic.items():
    xs.append(x)
    ys.append(freq)
plt.bar(xs, ys)
plt.show()
duration = perf_counter() - start
print('{} took {:.3f} seconds\n\n'.format('Python', duration))

import dice

start = perf_counter()
xs = [i for i in range(19)]
ys = dice.get()
plt.bar(xs, ys)
plt.show()
duration = perf_counter() - start
print('{} took {:.3f} seconds\n\n'.format('C++ module', duration))
}

を dive3.py として、 


python setup.py install

を実行した後、 


python dice3.py

を実行すると


を2回表示した後、 


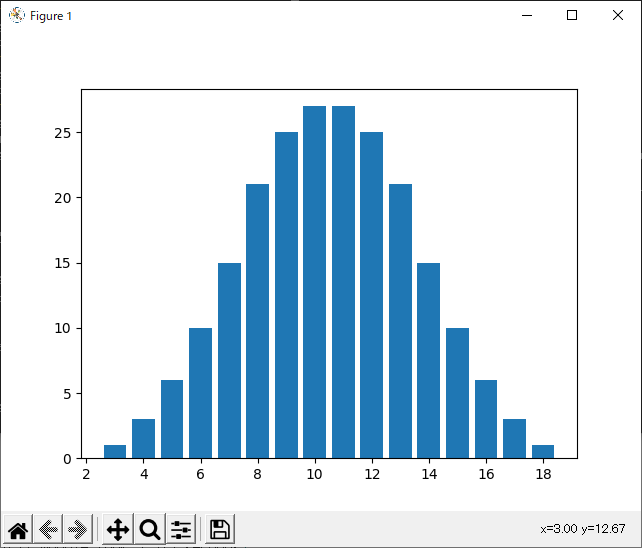
Python took 6.264 seconds

C++ module took 3.379 seconds

と表示します。C++ module を使った方が速いです。 値の受け渡しが原始的で、もっと上手い方法が無いか調べてみる価値があります。

インターネットで調べてみましたが、C++ には良い統計のパッケージは無くて、R か Python を使うのが良いみたいです。 R は統計に特化した奇妙な言語で、教育学部に統計の専門家がいなくて、昔は理学部の授業を学生が聴講させて貰っていましたが、 ある時から、文部省の意向で、数学教員には高度な数学より学ぶべきことがあると教育学部の数学教員免許の為の必修の数学の単位数が半減され、 教育学部の学生は授業時間が理学部の学生より少ないので、 数学の実力が当然落ち、その結果、 、教育学部の学生は勉強しないから理学部の学生に悪影響を与えるから一緒に教えるのは嫌だと言い出し、 仕方がないので教育学部の教官が交代で講義をすることになり、 「確率または統計」が教員免許の為には必修で、話し合って「確率論」と言う名前を付けていたのに、 私はそれを失念して、「確率・統計」の講義を最後まで続けていましたが、教育学部では数学の知識を十分教える時間的余裕がないので、 数学・解析の理論で公式を導くのではなく、コンピュータによるシミュレーションで、統計の公式を理解させるため、 私は講義で Excel を使い始め、そのついでに、 私自身は R を学び、最後の方の講義では知識も増え、しかし、R そのものを教える時間的余裕は無く、講義では、 興味があれば自分で勉強してくださいと Python と R のプログラムと結果を示すだけでしたが、 R は綺麗で細かい統計のグラフが作れるプログラミング言語です。（BASIC, PASCAL, C, Java, C++ と色々変遷しましたが、 教員生活の終盤は、 Python を必須の「コンピュータ」の為の「情報数学」で 私が教えていました。最も小学校で情報が必修科目になると言う話になって、最後は Scratch に変えましたが。） 文部省は時々、妙なことを言い出します。例えば、教育学部の教員は全員学校教育に特化した研究をするべきだと言い出し、 弱小大学の高知大学は平成１１年から平成１６年の間、教育実践共同研究という 教育学部および 付属校園全員参加が建前の教育実践の研究組織が作られました。 仕方がないので、私一人の研究組織を作り、過去に作っていたソフトを その成果として発表していると共同研究なのに一人でやっているのは怪しからんと言う人がでてきて、当時の学部長から構成員を増やせと言う 命令が来て、 研究員は一人から始まり、少しづつ増えて、最後には当時の所属で、 織田　進（教育学部）、小沢和子（付属中）、 苅谷尚子（四国日立ソリューションズ高知支店）、 佐藤淳郎（教育学部）、 下村宏彰（教育学部）、中村　治（教育学部）、久武大介（観音寺第一高）、福島勝成（潮江中）、 山口俊博（教育学部） の構成になりました。優秀な教え子の一人でしたが、小沢和子さんが若くして乳癌でお亡くなりになりました。ご冥福をお祈りします。 発表の場が無かったので、 http://www.cc.kochi-u.ac.jp/~tyamag/sugaku.html にその研究組織の一つ「数学教育を改善するためのソフト開発」の記録を載せています。しかし、教育学部の数学の教員の研究業績の評価も 理学部の数学教員の評価基準が使われるので、このような文部省の「教育学部の教員は教育学部らしい研究をしろ」と言う 気まぐれで思い付きの指示 （これで利益を受ける集団があり、その要請に答えた可能性も無いとは言えませんが）を真に受けると馬鹿を見ます。 数学そのものは世界共通で一つであり、教育学部に於ける数学研究なぞと言うものはありません。数学教員養成に必要な数学教育は、 現在の日本の置かれている現状・惨状に応じて、今までの公式を覚え、それを使う練習をすると言う詰め込み教育ではなく、 自分で考えることの出来る数学的能力を養成するように変えていくべきですが、 教育学部にいる数学教員の数学研究そのものに枠をはめるべきではなく、自由にやりたいことをやらせるべきです。 教育学部の何周年かの記録の数学教室の担当になった時、数学の単位数が半減されたと書くと編集委員が都合が悪いと思ったのか、 添付していた写真が無くなったので書き直せと言ってきましたが、写真のデータは保存していたので、言われたことだけ修正すると 後は何も言ってきませんでした。弱小大学は文部省に忖度ばかりしています。高知大学に「海洋コア研究センター」が出来、これで潰されることが 無くなったと皆喜んでいました。


定年退職した後、ピンチヒッターで１０年ぶりに「確率論」の講義を持つことになった時、 何か講義の導入の目玉になる話題はないかと思って、週刊誌（週刊朝日４月８日特大号）の高等学校の 東大・京大・旧帝大・一橋大・東工大の合格者のデータを使って、合格者の出身高校の所在地別の分布を調べてみました。 結構大変で、データを高校別のデータを都道府県別に整理し、打ち込むのに、それぞれの大学ごとに丸一日掛かりました。 優秀な人は、多分、自分ではせず、授業の一環として、学生さんに手分けして集計させ、このようなグラフを作ることを 授業内容とすると思いますが、私のような凡人は、自分で全部作ってみないと出来るかどうか分からなし、 どれだけ時間が掛かるものか分からないので、自分でやってみて、 結果だけ学生さんに見せました。今考えると一校だけ自分でやってみて、学生さんにやらしたら良かったかなとも思いますが、 結構時間が掛かる作業なので、一コマだけの講義で、他のことが出来なくなるので、 （昔、一度だけ、家庭科の食物専攻の女子学生さんたちと合同で卒論発表会をやったことがありますが、食物専攻なので自分で考えた 料理のレシピの発表をするのかと思えば、付属校園で集めたデータの検定結果の発表ばかりするので、驚きましたが、 更に驚いたことは、数学の学生が「カイ2乗検定とは何ですか？」と 質問したことです。数学の学生なのに、そんなことも知らないかと愕然としました。 （勿論、この質問がやらせである可能性もないではないです。数学の卒論発表会で後輩（３年生）にこう言う質問をしてくれと頼み、 いい格好をするつもりが、「後輩（３年生）は言いつけ通りに質問したのに、答えられなかった、馬鹿だ！」と卒論発表会の後、 ４年生たちが話しているのを聞いたことがあります。） 大分前から数学の必須の単位数は半分で良いことになり、 「確率・統計」の講義は教育学部では30時間で良い・しか出来ないので、 この限られた時間で何を教えるべきか、吟味する必要があります。）「講義の目標」が何かを考える必要もあり、 学生さんに興味を持って受講してもらうには、自分が興味があり、面白いと思ったことをやればいいのではとも思いますが、難しい判断が必要です。 データがそろっているのは上記有名国立大学のものだけでしたが、 調べてみると、面白い結果が出ました。最もこれは私が知らなかっただけで、 インターネットには私が気づいたのは東大の場合ですが、上のような図（東京大学の結果）は載っていませんが、 データそのものは掲載されていました。東北大、京大、阪大以外は所在地の都府県の合格者が高校生数に対して異常に多いです。












これはインターネットで見つけた白地図を使って、Excel で計算し、描いたグラフです。Excel の VB も統計処理に必要なモジュールは 揃っていますが、多数抱えている従業員を食べらせる為にしょっちゅうヴァージョンアップするので経済的にも、 また何処が変わったか調べるのも大変だし、 教育学部の数学教員志望の「確率・統計」のような初心者教育には作業過程が具体的に目で見ることが出来るので、 分り易いと言う面も確かにありますが、慣れるとその作業がめんどくさくなるので、好みが分かれる処です。

「あみだくじは不公平である」と言う記述を何度か読みましたが、根拠を書いてなかったので、何故だろうと不思議に思っていましたが、 西内啓著「統計学が最強の学問であるーデータ社会を生き抜くための武器と教養」ダイヤモンド社２０１３年という本の著者の自慢話

卑近な例では、私はかって大学院生時代、研究室の友人としばしばコンビニへの買い出し役を賭けてあみだくじをした。 あみだくじの形式はさまざまだが、ある日に行ったあみだくじは、 私を含む参加者４名の倍の数である８本の縦の線を引き、 私が残りの参加者に見えないよう左から４番目の縦棒の下に星印をつけ、 残り３人の友人には逆に私には見えないように４本ずつ横の線を引いてもらうといったルールで行った。 参加者はジャンケンで勝った順番に１・・・８の 縦棒の中からまず１か所ずつを選び、ひと通り選び終わった後はその逆順で選ぶ。 そして★印に当たった者がコンビニへと全員の使い走りに行くことになるのである。 もし何のためらいもなく直感のみを頼りにしてこのあみだくじに参加したとしたら、あなたはかなり分の悪い勝負をすることになるだろう。 試しにこのルールで１０００回繰り返したとして、縦棒ごとの当たる回数をシミュレーションしてみると図表２のような結果になる。

と図表２の

1=81, 2=122, 3=182, 4=210, 5=194, 6=100, 7=69, 8=33

のグラフを見て、自分でそれを検証する以下のプログラムを作ってみて、「あみだくじは不公平である」はそう言うことかと納得がいきました。

良い問題を思いつくことは、世間で言われているほど簡単なことではなく、 実際は大変難しいことで、昔、「良い数学の問題を思いついたら、弟子にやらすのではなく、勿体ないので自分で解く」と話している若い数学者の話を聞いたこともあります。 1億円の懸賞金の懸かった大問題も勿論数学にはありますが、我々凡人が手を出せるような問題ではありません。 ささやかな問題を見つけて、幸運にも解ければ大満足です。 さて、これだけの情報があれば、凡人の私でもこの本の著者がやったことを再現してみることが出来ます。 歴史を調べても、何事も偉大な先人の業績を模倣することから始まります。 このような場合、推敲した最終のプログラムだけ提示するのが数学やプログラミングのお決まりですが、 教育学部の数学教員志望の学生の為の授業で示すプログラムですから、 私の拙い作成過程を示します。 始めて作るプログラムですから、次のように作っていきました。

まず縦棒８本を引き、左から４番目の縦棒の下に○印をつける。 プログラムは 


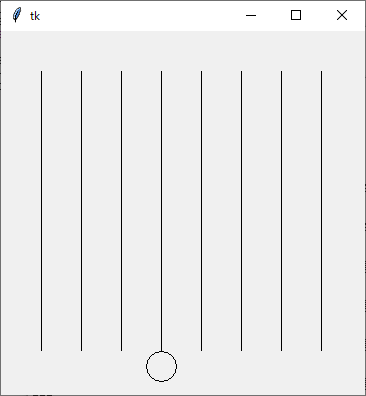
Python Program {
from tkinter import *
from math import *
root = Tk()
canvas = Canvas(root, width=360, height=360)
for i in range(8):
    canvas.create_line(40+40*i,40,40+40*i, 40+40*7)
canvas.create_oval(40+40*3-15,40+40*7,40+40*3+15,40+40*7+30)
canvas.pack()
root.mainloop()
}

です。


次にランダムに横線を引かなければなりません。これをするために次のようにします。 プログラムは 


Python Program {
from tkinter import *
from math import *
root = Tk()
canvas = Canvas(root, width=360, height=360)
for i in range(8):
    canvas.create_line(40+40*i,40,40+40*i, 40+40*7)
canvas.create_oval(40+40*3-15,40+40*7,40+40*3+15,40+40*7+30)
for i in range(7):
    for k in range(12):
        canvas.create_line(40+40*i-10,61+21*k, 40+40*i+10, 61+21*k)
canvas.pack()
root.mainloop()
}

です。


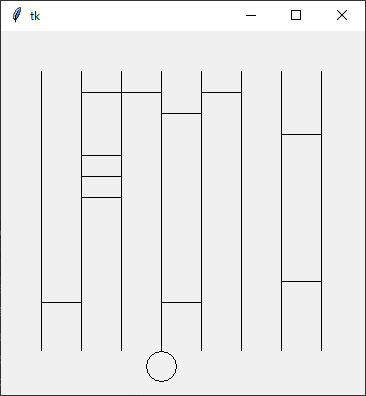
このあみだくじをシミュレーションする方法（計算のモデル）はいろいろ考えられますが、 ここでは 左側７本の縦線上に上図のように１２か所づつ８４か所に印をつけ、ランダムに１２か所選び横線を引くことにします。 （横線を引く位置を半分くらいにした方が実際のあみだくじの実情に合っていると思うかもしれませんが、 ランダムに線を引く場合理論的には左端の棒にすべての横線を引くことも考えられるのでこのようにします。 これは数学者の習性で、必ずこのような極端な場合も大丈夫なように考えます。起こる可能性のあることは、必ず起こり、 極端な場合でも動くようにしておかなかったことがプログラムがクラッシュする原因になり、発見の難しいバグの一つになります。 各自で、シミュレーションして確かめてください。不注意で不公平なモデルを使うと全く違った結果が出ます。 色々やってみることが勉強になります。） プログラムは 


Python Program {
from tkinter import *
from math import *
import random

root = Tk()
canvas = Canvas(root, width=360, height=360)
for i in range(8):
    canvas.create_line(40+40*i,40,40+40*i, 40+40*7)
canvas.create_oval(40+40*3-15,40+40*7,40+40*3+15,40+40*7+30)
for j in range(12):
    n = random.randint(0,83)
    i = n // 12
    k = n % 12
    canvas.create_line(40+40*i,61+21*k, 40+40*i+40, 61+21*k)
canvas.pack()
root.mainloop()
}



です。実はこのプログラムにはバグ（プログラムの間違いのことをバグと言います）があります。 同じ線を２度以上選択する可能性や同じレヴェルに線が並ぶ可能性があることを見落としています。 プログラミングにはバグはつきもので、自分では見つけにくいもので、 バグがあることに気が付かず、あるいはバグを探す根気が続かなくてプログラミングを 諦める人も多いと思いますが、このように結果を視覚化して、図にすると容易に見つけることができます。 間違いに気づけば直せばいいです。 横線を引くための基本図を描くプログラムを 


Python Program {
from tkinter import *
from math import *
import random

root = Tk()
canvas = Canvas(root, width=360, height=360)
for i in range(8):
    canvas.create_line(40+40*i,40,40+40*i, 40+40*7)
canvas.create_oval(40+40*3-15,40+40*7,40+40*3+15,40+40*7+30)
for i in range(7):
    for k in range(12):
        if i % 2 == 0:
            canvas.create_line(40+40*i-10,61+21*k, 40+40*i+10, 61+21*k)
        else:
            canvas.create_line(40+40*i-10,51+21*k, 40+40*i+10, 51+21*k)
canvas.pack()
root.mainloop()
}

として図の左の目印に合わせて横線を引くと公平性に問題が出ます。 これは直感的にそうではないかと思っただけで、確かめたわけでもなく、実際は問題ないかも分かりません。 以下のプログラムでは、どこに横線を引いたか覚えて置き、このようなことが起きないようにしています。 


Python Program {
from tkinter import *
from math import *
import random

root = Tk()
canvas = Canvas(root, width=360, height=360)
for i in range(8):
    canvas.create_line(40+40*i,40,40+40*i, 40+40*7)
canvas.create_oval(40+40*3-15,40+40*7,40+40*3+15,40+40*7+30)
canvas.pack()

hline = [False]*84
j=0
while j < 12:
    n = random.randint(0,83)
    if hline[n] == True: continue
    i = n // 12
    k = n % 12
    if i == 0:
        if hline[n+12] == False:
            hline[n] = True
            canvas.create_line(40+40*i,61+21*k, 40+40*i+40, 61+21*k)
            j += 1
    elif i == 6:
        if hline[n-12] == False:
            hline[n] = True
            canvas.create_line(40+40*i,61+21*k, 40+40*i+40, 61+21*k)
            j += 1
    else:    
        if hline[n-12] == False and hline[n+12] == False:
            hline[n] = True
            canvas.create_line(40+40*i,61+21*k, 40+40*i+40, 61+21*k)
            j += 1

root.mainloop()
}

を実行するとランダムに


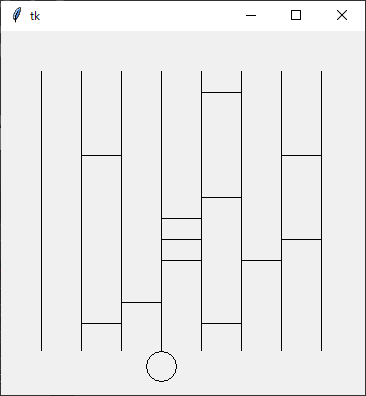
のようなあみだくじを描いてくれます。このあみだくじをモデルに確率分布をシミュレーションします。 このあみだでは左から２番目の縦線が当たりです。 次に当たりの線を計算するようにします。人間がやるように、当たりの位置から上に線を辿れば良いです。 プログラムは、例えば、 


Python Program {
from tkinter import *
from math import *
import random

root = Tk()
canvas = Canvas(root, width=360, height=360)
for i in range(8):
    canvas.create_line(40+40*i,40,40+40*i, 40+40*7)
canvas.create_oval(40+40*3-15,40+40*7,40+40*3+15,40+40*7+30)
canvas.pack()

hline = [False]*84
j=0
while j < 12:
    n = random.randint(0,83)
    if hline[n] == True: continue
    i = n // 12
    k = n % 12
    if i == 0:
        if hline[n+12] == False:
            hline[n] = True
            canvas.create_line(40+40*i,61+21*k, 40+40*i+40, 61+21*k)
            j += 1
    elif i == 6:
        if hline[n-12] == False:
            hline[n] = True
            canvas.create_line(40+40*i,61+21*k, 40+40*i+40, 61+21*k)
            j += 1
    else:    
        if hline[n-12] == False and hline[n+12] == False:
            hline[n] = True
            canvas.create_line(40+40*i,61+21*k, 40+40*i+40, 61+21*k)
            j += 1

n = 3
k = 11
while k >= 0:
    if n == 0:
        if hline[12*n+k] == False:
            k -= 1
        else:
            n = 1
            k -= 1
    elif n == 7:
        if hline[12*(n-1)+k] == False:
            k -= 1
        else:
            n = 6
            k -= 1
    else:
        if hline[12*n+k] == True:
            n += 1
            k -= 1
        elif hline[12*(n-1)+k] == True:
            n -= 1
            k -= 1
        else:
            k -= 1
canvas.create_oval(40+40*n-15, 5,40+40*n+15,35)

root.mainloop()
}

のようなプログラムで良いです。或いは、あみだを作る部分と当たりを調べる部分をそれぞれ関数にした 


Python Program {
from tkinter import *
from math import *
import random

root = Tk()
canvas = Canvas(root, width=360, height=360)
for i in range(8):
    canvas.create_line(40+40*i,40,40+40*i, 40+40*7)
canvas.create_oval(40+40*3-15,40+40*7,40+40*3+15,40+40*7+30)
canvas.pack()

def make_amida():
    hline = [False]*84
    j=0
    while j < 12:
        n = random.randint(0,83)
        if hline[n] == True: continue
        i = n // 12
        k = n % 12
        if i == 0:
            if hline[n+12] == False:
                hline[n] = True
                canvas.create_line(40+40*i,61+21*k, 40+40*i+40, 61+21*k)
                j += 1
        elif i == 6:
            if hline[n-12] == False:
                hline[n] = True
                canvas.create_line(40+40*i,61+21*k, 40+40*i+40, 61+21*k)
                j += 1
        else:    
            if hline[n-12] == False and hline[n+12] == False:
                hline[n] = True
                canvas.create_line(40+40*i,61+21*k, 40+40*i+40, 61+21*k)
                j += 1
    return hline

def which_line(hline, n, k):
    while k >= 0:
        if n == 0:
            if hline[12*n+k] == False:
                k -= 1
            else:
                n = 1
                k -= 1
        elif n == 7:
            if hline[12*(n-1)+k] == False:
                k -= 1
            else:
                n = 6
                k -= 1
        else:
            if hline[12*n+k] == True:
                n += 1
                k -= 1
            elif hline[12*(n-1)+k] == True:
                n -= 1
                k -= 1
            else:
                k -= 1
    canvas.create_oval(40+40*n-15, 5,40+40*n+15,35)

amida = make_amida()
which_line(amida, 3, 11)

root.mainloop()
}

を作った方がお行儀の良いプログラムかも分かりませんが、そんなに長いプログラムではないので、どっちでも良いと思います。 マジックナンバーの３は今の場合、左から4番目が当たり（数字は０からふっているので、一つズレます。）と言うことで、 １１は今の場合、あみだの階段の一番下の11番目の段から上に辿って当たりの線を探せば良いと言うことです。 実行すると


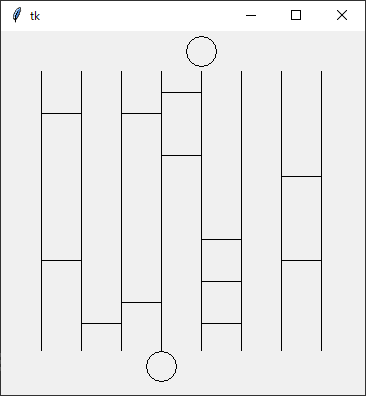
のようにランダムにあみだを作り、当たりの線を示してくれます。正しいプログラムになっているか、何回か実行して確かめます。

ここまで出来るともう今後はバグがないか調べるためのあみだの図は描かなくても良いです。何番目の線が当たりだったかの情報だけが欲しいです。 この操作を１０００回繰り返して、統計を取ります。 


Python Program {
import random
amida = [0] * 8
for m in range(1000):
    hline = [False]*84
    j = 0
    while j < 12:
        n = random.randint(0,83)
        if hline[n] == True:
            continue
        g = n // 12
        if g == 0:
            if hline[n+12] == False:
                hline[n] = True
                j += 1
        elif g == 6:
            if hline[n-12] == False:
                hline[n] = True
                j += 1
        else:
            if hline[n-12] == False and hline[n+12] == False:
                hline[n] = True
                j += 1                
    n = 3
    k = 11
    while k >= 0:
        if n == 0:
            if hline[12*n+k] == False:
                k -= 1
            else:
                n = 1
                k -= 1
        elif n == 7:
            if hline[12*(n-1)+k] == False:
                k -= 1
            else:
                n = 6
                k -= 1
        else:
            if hline[12*n+k] == True:
                n += 1
                k -= 1
            elif hline[12*(n-1)+k] == True:
                n -= 1
                k -= 1
            else:
                k -= 1
    amida[n] += 1  
for i in range(8):
   print( i+1, "=", amida[i])}

を実行するたびにばらつきがあるので、 


===================== RESTART: C:/C++src/statics/amida6.py =====================
1 = 102
2 = 124
3 = 200
4 = 198
5 = 184
6 = 117
7 = 57
8 = 18
>>> 
===================== RESTART: C:/C++src/statics/amida6.py =====================
1 = 85
2 = 140
3 = 205
4 = 205
5 = 166
6 = 111
7 = 65
8 = 23
>>> 
===================== RESTART: C:/C++src/statics/amida6.py =====================
1 = 80
2 = 122
3 = 174
4 = 226
5 = 193
6 = 119
7 = 62
8 = 24
>>>

１００回繰り返して、平均を取ってみます。 


Python Program {
import random
import matplotlib.pyplot as plt
result = [0.0]*8
for p in range(100):
    amida = [0.0] * 8
    for m in range(1000):
        hline = [False]*84
        j = 0
        while j < 12:
            n = random.randint(0,83)
            if hline[n] == True:
                continue
            g = n // 12
            if g == 0:
                if hline[n+12] == False:
                    hline[n] = True
                    j += 1
            elif g == 6:
                if hline[n-12] == False:
                    hline[n] = True
                    j += 1
            else:
                if hline[n-12] == False and hline[n+12] == False:
                    hline[n] = True
                    j += 1                
        n = 3
        k = 11
        while k >= 0:
            if n == 0:
                if hline[12*n+k] == False:
                    k -= 1
                else:
                    n = 1
                    k -= 1
            elif n == 7:
                if hline[12*(n-1)+k] == False:
                    k -= 1
                else:
                    n = 6
                    k -= 1
            else:
                if hline[12*n+k] == True:
                    n += 1
                    k -= 1
                elif hline[12*(n-1)+k] == True:
                    n -= 1
                    k -= 1
                else:
                    k -= 1
        amida[n] += 1
    for i in range(8):
        result[i] += amida[i]
for i in range(8):
    result[i] /= 100
xs = [i for i in range(len(result))]
plt.bar(xs, result)
plt.show()
}

を実行すると


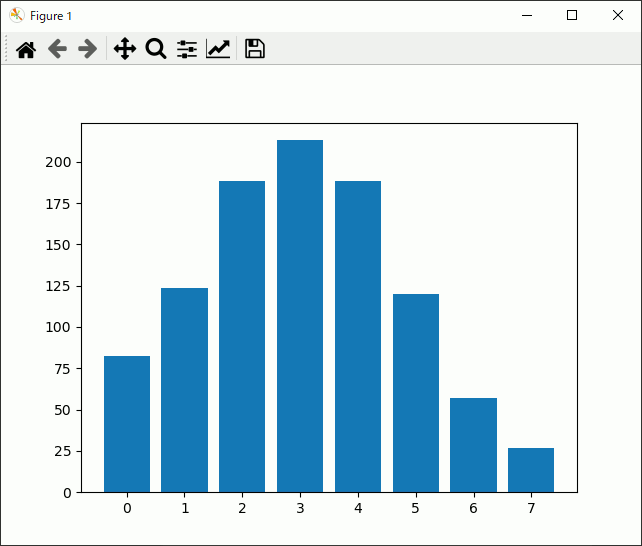
で、○印を付けた左から4番目が当たりやすいです。 確かに本に書いてあると通り中央付近に○印を付けた場合、その縦線の近所が当たりやすいみたいです。 そこで、このプログラムのを○印をつける位置 


        n = 3
        k = 11

を左の端にするように 


        n = 0
        k = 11

に変更すると


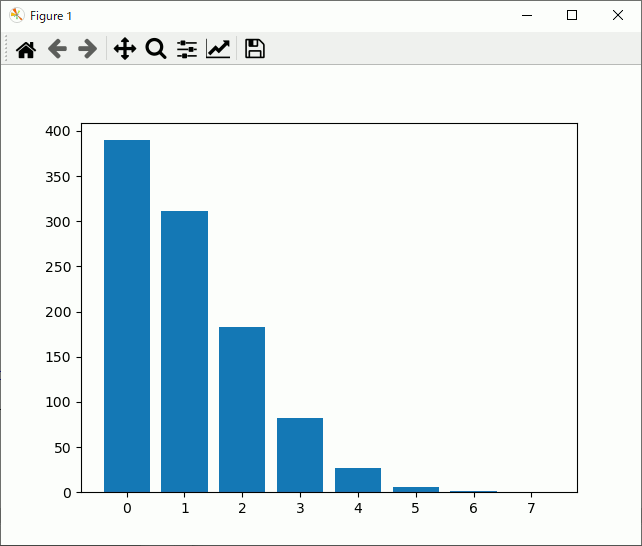
で、今度は左端が最も当たりやすくなりました。「あみだくじは不公平である」と言うのは、○印を付けた人がくじに参加していたら、 その人が有利だと言う意味だったのでした。ランダムに、○印を付け、平均を取れば、勿論、一様分布になります。 その為には、○印をつける位置をランダムに選択するように 


        n = random.randint(0,7)
        k = 11

と変えて実行すると


で、すべての場所が等確率で当たる様子が見て取れます。

基本的には人間がやっていることをコンピュータにやらす訳ですが、人間のようにフリーハンドで横線を引くことをそのまま模倣すると 横線の位置を実数で表現することになって厄介なので、あみだにとって大事なのは、横線の絶対的な位置ではなく、その相対的な位置だけが重要なので、 縦に等間隔に線を引く目安の位置を配置し、その位置をランダムに選択することであみだを作ることにして、上のプログラムを作りました。 本当は、これで良いのかと言う疑問があります。「人間なら、二本の小さい隙間に更に横線を複数引くこともあるのに、上のような設定は 本当にあみだを人間が作る実情に合っているか？」と考え出すとプログラムが作れないので、このような理想的なモデルを仮定して考察すると 以下のようなことがわかると言っているだけだと理解して下さい。数学は全て、「このような仮定をすれば、このようなことが言える」と言っているだけです。 数学だけでなく、すべてのことが何らかの仮定の下にこういうことが言えると言うだけなのに、その仮定を知らされないまま、結論を信じ込まされている ことが多いように思います。 これでは、実際のあみだのモデルになってないので、俺は納得しないという方は、横線の位置を実数で表すモデルで例えば次のようにプログラミングします。 


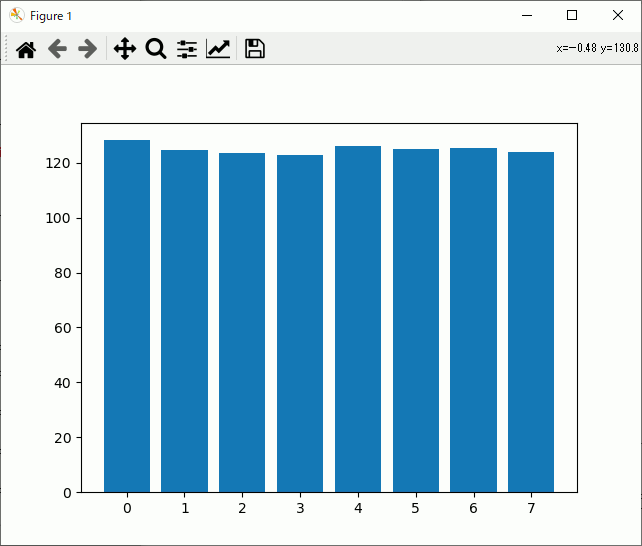
Python Program {
from tkinter import *
from math import *
import random

root = Tk()
canvas = Canvas(root, width=360, height=360)
for i in range(8):
    canvas.create_line(40+40*i,40,40+40*i, 40+40*7)
canvas.create_oval(40+40*3-15,40+40*7,40+40*3+15,40+40*7+30)
canvas.pack()

def check(hline, pos, limit):
    w = int(pos / 200)
    h = int(pos - w*200)
    for p in hline:
        if abs(p-pos) < limit:
            return False, w, h
        if pos-200>0 and abs(p-pos+200) < limit:
            return False, w, h
        if pos+200<1400 and abs(p-pos-200) < limit:
            return False, w, h
    return True, w, h    
    
def make_amida():
    hline = []
    dic = {}
    j=0
    while j < 12:
        pos = random.uniform(0, 1400)
        flag, w, h = check(hline, pos, 2)
        if flag == True:
            j += 1
            hline.append(pos)
            canvas.create_line(40+40*w,80+h, 40+40*(w+1), 80+h)
            inf = dic.get(str(w), [])
##            print('inf=', inf, w)
            dic[str(w)] = inf + [h]
    amida = []
    for w in range(7):
        inf = dic.get(str(w), [])
        inf.sort()
        if inf != []:
            inf.reverse()
        amida.append(inf)
    return amida

def next_h(l, h):
    for p in l:
        if p >= h:
            continue
        return p
    return 0

def which_line(amida, n):
    h = 200
    while h > 0:
        if n == 0:
            my_h = next_h(amida[n], h)
            if my_h == 0:
                h = 0
            else:
                h = my_h
                n += 1
        elif n == 7:
            left_h = next_h(amida[n-1], h)
            if left_h == 0:
                h = 0
            else:
                h = left_h
                n -= 1
        else:
            my_h = next_h(amida[n], h)
            left_h = next_h(amida[n-1], h)
            if my_h > left_h:
                h = my_h
                n += 1
            elif left_h > my_h:
                h = left_h
                n -= 1
            else:
                h = 0
    canvas.create_oval(40+40*n-15, 5,40+40*n+15,35)

amida = make_amida()
##print(amida)
which_line(amida, 3)

root.mainloop()
}

を実行すると


です。 このプログラムでも 


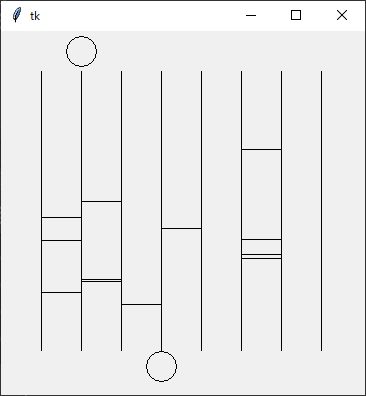
    while j < 12:
        pos = random.uniform(0, 1400)
        flag, w, h = check(hline, pos, 2)
        if flag == True:
            j += 1
            hline.append(pos)
            canvas.create_line(40+40*w,80+h, 40+40*(w+1), 80+h)
            inf = dic.get(str(w), [])
##            print('inf=', inf, w)
            dic[str(w)] = inf + [h]

と既に書き込んでいる横線と近ければ、横線を改めて取り直していますが、 「Monty Hall problem」のように、取り直すと結果が変化するのではないかと思えば、近くで同じ結果になる処に横線を引くように プログラムを修正すれば良いです。これは、このようなことが起こる確率が小さいので、問題ないと予想は付くと思いますが、 何でも疑問に思ったら、そのようにモデルを作り変えて、確かめれば良いです。 今の場合は、下の結果を見ればわかるように、細かなモデルの違いは結果に影響していませんが、問題によっては、 モデルの取り方によって、当然、結果が異なる場合もあります。何でも疑問に思ったら気が済むまでやってみれば良いです。 ひょっとしたら新しい発見があるかも分かりません。少なくともプログラミングの経験値を上げることにはなります。 更に、 


Python Program {
import random
import matplotlib.pyplot as plt

def check(hline, pos, limit):
    w = int(pos / 200)
    h = int(pos - w*200)
    for p in hline:
        if abs(p-pos) < limit:
            return False, w, h
        if pos-200>0 and abs(p-pos+200) < limit:
            return False, w, h
        if pos+200<1400 and abs(p-pos-200) < limit:
            return False, w, h
    return True, w, h    
    
def make_amida():
    hline = []
    dic = {}
    j=0
    while j < 12:
        pos = random.uniform(0, 1400)
        flag, w, h = check(hline, pos, 2)
        if flag == True:
            j += 1
            hline.append(pos)
            inf = dic.get(str(w), [])
            dic[str(w)] = inf + [h]
    amida = []
    for w in range(7):
        inf = dic.get(str(w), [])
        inf.sort()
        if inf != []:
            inf.reverse()
        amida.append(inf)
    return amida

def next_h(l, h):
    for p in l:
        if p >= h:
            continue
        return p
    return 0

def which_line(amida, n):
    h = 200
    while h > 0:
        if n == 0:
            my_h = next_h(amida[n], h)
            if my_h == 0:
                h = 0
            else:
                h = my_h
                n += 1
        elif n == 7:
            left_h = next_h(amida[n-1], h)
            if left_h == 0:
                h = 0
            else:
                h = left_h
                n -= 1
        else:
            my_h = next_h(amida[n], h)
            left_h = next_h(amida[n-1], h)
            if my_h > left_h:
                h = my_h
                n += 1
            elif left_h > my_h:
                h = left_h
                n -= 1
            else:
                h = 0
    return n

result = [0.0]*8
for p in range(100):
    amida = [0.0] * 8
    for m in range(1000):
        a = make_amida()
        n = which_line(a, 3)
        amida[n] += 1
    for i in range(8):
        result[i] += amida[i]
for i in range(8):
    result[i] /= 100
xs = [i for i in range(len(result))]
plt.bar(xs, result)
plt.show()
}

を実行すると


です。

実は、これであみだの解析は終わったと思っていましたが、今日、丸山儀四郎著「確率および統計」基礎数学講座１０をパラパラ見ていたら、 西内啓著「統計学が最強の学問であるーデータ社会を生き抜くための武器と教養」の著者は上の図（確率分布）を知っていれば どれくらい有利かキチンと調べないと「あみだは不公平だ」と結論付けることは出来ないと言う考えがふと浮かびました。 （また、「村の駅ひだか」でオムライスを食べました。美味しかったです。 日高村は村の特産物のトマトを宣伝するために 「オムライス街道」と言って、オムライスを提供する店がたくさんあります。 そこで、「たぬきの油」を売っていました。火傷の薬だそうです。）

卑近な例では、私はかって大学院生時代、研究室の友人としばしばコンビニへの買い出し役を賭けてあみだくじをした。 あみだくじの形式はさまざまだが、ある日に行ったあみだくじは、 私を含む参加者４名の倍の数である８本の縦の線を引き、 私が残りの参加者に見えないよう左から４番目の縦棒の下に星印をつけ、 残り３人の友人には逆に私には見えないように４本ずつ横の線を引いてもらうといったルールで行った。 参加者はジャンケンで勝った順番に１・・・８の 縦棒の中からまず１か所ずつを選び、ひと通り選び終わった後はその逆順で選ぶ。 そして★印に当たった者がコンビニへと全員の使い走りに行くことになるのである。 もし何のためらいもなく直感のみを頼りにしてこのあみだくじに参加したとしたら、あなたはかなり分の悪い勝負をすることになるだろう。

のあみだを実際に多数回シミュレーションして平均を取ってみる（期待値を求めることで判断することが普通行われています）必要があります。所がこれは厄介です。 このルールであみだを行うにしても、 実際にプログラミングするには色々な仮定をする必要があります。 ここでは、★印を付ける人はいつも０番目の人（著者）とします。０番目の人の「★印を付ける戦略は 何か？」も考えなければなりません。単純な戦略・戦術を何度も繰り返すと友人たちも馬鹿ではないですから、著者の戦略・戦術を見抜くはずです。 ここでは見抜かれてもダメージを受けないとゲーム理論が教えてくれている、「単純にランダムに選ぶ」ことにします。０番目の人が横線を選ぶ戦略は「単純に ★印を付けた線から遠い線を選ぶ」ようにします。残りの人の戦略も色々考えられますが、ここでは「単純に乱数で選ぶ」ようにしてみます。 完全情報ゲームの数学理論しか勉強したことがないので、このような不完全情報ゲームの取り扱いは、カードゲームのプログラムの 作り方も公表していますが、カードゲームを含めお手上げです。 実際は、ゲームの進行を見ながら戦略を変更していくはずだし、面白い問題だと思いますが、このような問題に関して何が知られているか、 既に解決しているのか、私は知りません。若ければやってみるかも分かりませんが、読みたい本が既に沢山本箱に残っているし、年を取りすぎました。 I wish I were young. プログラミングの練習の為に、ジャンケンを実装してみても良いですが、ジャンケンは4人の線を選ぶ順番を決めるためですから、 ０，１，２，３の順列の一つを乱数で選ぶことで代用できます。ここでもジャンケンも色々な戦略が考えられ、 乱数で選べば、損はしないと言うゲーム理論の結果もありますが、著者はジャンケンが弱くて常に4番目に線を選ぶことになっても、 或いはルールを変えて、印を付けた著者は最後に線を選ぶことにしても、 「確率分布を知っていれば有利なのか」と考え出すとやってみることは色々ありますが、今回は これだけの条件を付けてプログラミングしてみると例えば 


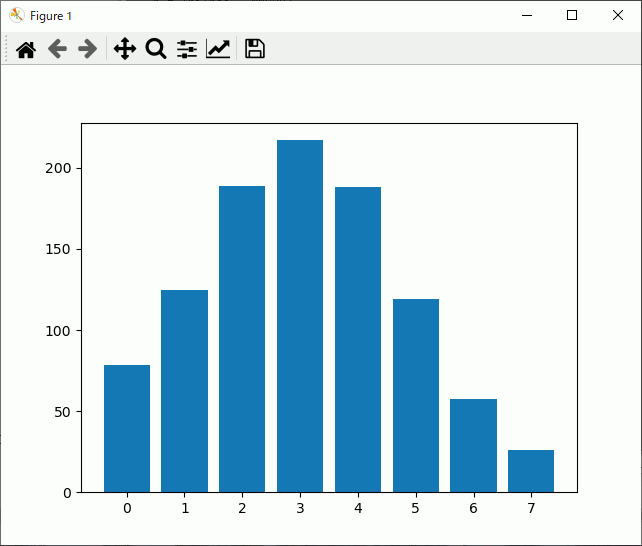
Python Program {
import random
import matplotlib.pyplot as plt

def check(hline, pos, limit):
    w = int(pos / 200)
    h = int(pos - w*200)
    for p in hline:
        if abs(p-pos) < limit:
            return False, w, h
        if pos-200>0 and abs(p-pos+200) < limit:
            return False, w, h
        if pos+200<1400 and abs(p-pos-200) < limit:
            return False, w, h
    return True, w, h    
    
def make_amida():
    hline = []
    dic = {}
    j=0
    while j < 12:
        pos = random.uniform(0, 1400)
        flag, w, h = check(hline, pos, 2)
        if flag == True:
            j += 1
            hline.append(pos)
            inf = dic.get(str(w), [])
            dic[str(w)] = inf + [h]
    amida = []
    for w in range(7):
        inf = dic.get(str(w), [])
        inf.sort()
        if inf != []:
            inf.reverse()
        amida.append(inf)
    return amida

def next_h(l, h):
    for p in l:
        if p >= h:
            continue
        return p
    return 0

def which_line(amida, n):
    h = 200
    while h > 0:
        if n == 0:
            my_h = next_h(amida[n], h)
            if my_h == 0:
                h = 0
            else:
                h = my_h
                n += 1
        elif n == 7:
            left_h = next_h(amida[n-1], h)
            if left_h == 0:
                h = 0
            else:
                h = left_h
                n -= 1
        else:
            my_h = next_h(amida[n], h)
            left_h = next_h(amida[n-1], h)
            if my_h > left_h:
                h = my_h
                n += 1
            elif left_h > my_h:
                h = left_h
                n -= 1
            else:
                h = 0
    return n

l = []
r = []
def get_perm(l, s, k):
    global r
    if len(s)==k:
        r.append(s)
        return
    for e in l:
        old_s = s[:]
        s.append(e)
        new_l = l[:]
        new_l.remove(e)
        get_perm(new_l, s, k)
        s = old_s
n = 4
k = 4
l = [i for i in range(0, n)]
get_perm(l, [], k)
##print(len(r))
##print(r)

def stategy_0(cand, t, n): ## t : target
    l = 0
    u = 7
    while True:
        if t-l < u-t and cand[u]:
            cand[u] = False
            if u == n:
                return True, cand
            else:
                return False, cand
        elif t-l >= u-t and cand[l]:
            cand[l] = False
            if l == n:
                return True, cand
            else:
                return False, cand
        if t-l < u-t:
            u -= 1
        else:
            l += 1

def stategy_1(cand, t, n): ## t : target
    new_cand = []
    for cnt, item in enumerate(cand):
        if item == True:
            new_cand.append(cnt)
    c = new_cand[random.randint(0, len(new_cand)-1)]
    cand[c] = False
    if c == n:
        return True, cand
    else:
        return False, cand
           
result = [0.0]*4
for p in range(100):
    lost = [0] * 4
    for m in range(1000):
        t = random.randint(0,7)
        a = make_amida()
        n = which_line(a, t)
        order = r[random.randint(0, 23)]
        cand =[True]*8
        F = True
        for k in order:
            if k == 0:
                flag, cand = stategy_0(cand, t, n)
                if flag == True:
                    lost[k] += 1
                    F = False
                    break
            else:
                flag, cand = stategy_1(cand, t, n)
                if flag == True:
                    lost[k] += 1
                    F = False
                    break
        if F == True:
            order.reverse()
            for k in order:
                if k == 0:
                    flag, cand = stategy_0(cand, t, n)
                    if flag == True:
                        lost[k] += 1
                        break
                else:
                    flag, cand = stategy_1(cand, t, n)
                    if flag == True:
                        lost[k] += 1
                        break
    for i in range(4):
        result[i] += lost[i]
for i in range(4):
    result[i] /= 100
xs = [i for i in range(len(result))]
label = ['author', 'friendA', 'friendB', 'friendC']
plt.bar(xs, result, tick_label=label)
plt.show()
}

を実行すると


です。これでハッキリと「あみだは当たりの印を付けた人があみだに参加していれば、当たりの印を付けた人が有利で不公平である」が納得いったのではないでしょうか？ まだ納得のいかない人は、それぞれの戦略を自分の思うものに変えて、プログラミングしてみて、納得が行くまでやってみて下さい。

最後に、「あみだは当たりの印を付けた人があみだに参加していなければ、公平だ」と思い込んでいる常識を検証してみましょう。 


Python Program {
import random
import matplotlib.pyplot as plt

def check(hline, pos, limit):
    w = int(pos / 200)
    h = int(pos - w*200)
    for p in hline:
        if abs(p-pos) < limit:
            return False, w, h
        if pos-200>0 and abs(p-pos+200) < limit:
            return False, w, h
        if pos+200<1400 and abs(p-pos-200) < limit:
            return False, w, h
    return True, w, h    
    
def make_amida():
    hline = []
    dic = {}
    j=0
    while j < 12:
        pos = random.uniform(0, 1400)
        flag, w, h = check(hline, pos, 2)
        if flag == True:
            j += 1
            hline.append(pos)
            inf = dic.get(str(w), [])
            dic[str(w)] = inf + [h]
    amida = []
    for w in range(7):
        inf = dic.get(str(w), [])
        inf.sort()
        if inf != []:
            inf.reverse()
        amida.append(inf)
    return amida

def next_h(l, h):
    for p in l:
        if p >= h:
            continue
        return p
    return 0

def which_line(amida, n):
    h = 200
    while h > 0:
        if n == 0:
            my_h = next_h(amida[n], h)
            if my_h == 0:
                h = 0
            else:
                h = my_h
                n += 1
        elif n == 7:
            left_h = next_h(amida[n-1], h)
            if left_h == 0:
                h = 0
            else:
                h = left_h
                n -= 1
        else:
            my_h = next_h(amida[n], h)
            left_h = next_h(amida[n-1], h)
            if my_h > left_h:
                h = my_h
                n += 1
            elif left_h > my_h:
                h = left_h
                n -= 1
            else:
                h = 0
    return n

def stategy_1(cand, t, n): ## t : target
    new_cand = []
    for cnt, item in enumerate(cand):
        if item == True:
            new_cand.append(cnt)
    c = new_cand[random.randint(0, len(new_cand)-1)]
    cand[c] = False
    if c == n:
        return True, cand
    else:
        return False, cand
           
result = [0.0]*8
for p in range(100):
    lost = [0] * 8
    for m in range(1000):
        t = random.randint(0,7)
        a = make_amida()
        n = which_line(a, t)
        cand =[True]*8
        for k in range(8):
            flag, cand = stategy_1(cand, t, n)
            if flag == True:
                lost[k] += 1
                break
            
    for i in range(8):
        result[i] += lost[i]
for i in range(8):
    result[i] /= 100
xs = [i for i in range(len(result))]
label = ['no.1', 'no.2', 'no.3', 'no.4', 'no.5', 'no.6', 'no.7', 'no.8']
plt.bar(xs, result, tick_label=label)
plt.show()
}

を実行すると


です。あみだの当たりの印を付けた人があみだに参加していなくて、印を付ける位置に偏りがなければ、何番目に選んでも差はないみたいで、公平なように見えます。 従って、あみだの当たりの印を付けた人があみだに参加していても、あみだの当たりの印を付けた人は他の人が選んだ後 、残っている線を自動的に選ぶようにルールを決めれば、 当たる線の確率分布の知識を使う余地がないので公平にくじ引きできます。 このように、パソコンを使えば多くの場合、自分で検証できる時代になっているので、、納得いくまでやってみると良いです。

「確率論」の講義で、段階的に、あみだを作り、表示するプログラムから順に、 上のプログラム（当たる線の確率分布を求めるプログラム）まで、何段階にも分け、どの様に考えてプログラムを作るか理解できるように、 プログラムと結果の図を描いた資料を学生さんに 渡しましたが、これも、理学部数学科と異なり、教員養成に特化した学部なので、それなりの異なる授業をすべきで、 実際に学生さんにプログラムを作る過程を経験させる べきだったかなとも思いますが、やり方によっては凄く時間が掛かるので、 これだけは「確率・統計」の常識として教えておきたいと言うこともあり、判断が難しいです。 一人で教える30人以上の講義ではなく、2・3人のゼミでは可能ですが。プログラミングのような技術を教えると能力差と言うか、 上手くできない学生さんが数人は必ずいて、それに掛かりきりになると全然授業が進まなくなります。 理学部だとプログラミング言語の基本など難しくは無いが、環境設定など時間が掛かり面倒なことは、 「夏休みにこの本を読んでおきなさい。それを前提に後期の授業をします。」で、多分、良いです。 教育学部は複数の教育実習など行事が目白押しです。

昨日のNHKの「笑わない数学」の「Monty Hall problem」を Python でシミュレーションしてみるプログラムの例は、例えば 


Python Program{
import matplotlib.pyplot as plt
import numpy as np
import random
import time

def one_try():
    n = random.randrange(0, 3)
    c = random.randrange(0, 3)
    if n == c:
        return 1
    else:
        return 0

def trial(n):
    t = 0
    for i in range(n):
        t += one_try()
    return t

start_time = time.time()
n = 10000
t = trial(n)
f = n - t
X = np.array([1, 2])
Y = np.array([t, f])
label = ['no change', 'change']
plt.bar(X, Y, color='blue', width=0.9,tick_label=label)
plt.title('Monty Hall problem')
plt.xlabel('behavior')
plt.ylabel('Number of Gain')
end_time = time.time()
print( "time = %f" % (end_time-start_time) )
plt.show()
}

を実行すると


です。

先日、高知新聞の2022年6月8日の「声　ひろば」の読者の投稿に赤岡町の宇田英一さん７５が「真に地方に思いやりのある施策を」と題して、 「先日、本紙記事で浜田省司知事が、鉄道網維持は基本的に国鉄改革実行者の国が責任をもって対処すべきであると所信を述べられていた。 全くその通りであると強く思った。不採算の鉄道網が切り捨てられれば、地域の人々の生活が一段と不便になり、過疎化も一層進むだろう。 国は地方創生などと声高に唱えてはいるが、していることは、それに逆行することばかりのような気がする。郵政民営化もそうだった。 本気で地方のことを憂えているのであれば、地方の生活が不便になるようなことをすべきでない。（中略） この愛すべき日本の国土のよりよい活用と、都市と地方の調和のとれた発展のために、政府は地方の声にもっともっと耳を傾けるべきでは ないだろうか。浜田知事のお考えの記事から、このようなことを思った。」と投稿しています。 これを読んで、ふと、次のようなことを思いました。経済産業省に採用された上級公務員は、直ぐにアメリカに留学させられ、アメリカが日本に何を 求めているかを学んでくることが要求されていると聞いたことがあります。戦後、一貫して社会主義的な政策を取ってきた自民党政権が、 社会党の消滅で、アメリカの無茶な要求を社会党が政権を取るようなことになるとアメリカも困るだろうと何とかしのいでいたのが出来なくなったり、 アメリカに逆らって独自の石油確保を狙った田中角栄さんが失脚させられたことなどもあって、国鉄民営化や郵政民営化などの「富の再配分」を やめる政策を次々に取り出し、一気に地方が衰退し、更に、株式上場で大金が手に入ることが分かり、会社は株主のものだとの意識変化も生まれ、 政府による人為易な株高選出で、大量の資金を分散投資できる金持ちだけが益々金持ちになり、 GAFAなどの情報を支配出来るものだけが有利な社会になり、情報弱者は置いてけぼりになり、経済格差が一層増大したのではないかと。 「100分 de 名著」でナオミ・クライン著「ショック・ドクトリン」をやっています。ロシアがアメリカを恨んでいる理由が分かり面白い本です。

「小一時間でゲームをつくる　７つの定番ゲームのプログラミングを体験」と言う本を最近高知市内の本屋で見つけました。 昔、このようなゲームの本格的な解説の本を一式購入していましたが、 読まないうちに使われている技術が時代遅れになり、もはやコンパイル出来なく、添付の実行ファイルも実行できなくなりました。 私が興味を持って勉強したのはオセロのような思考ゲームだけで、 基本的にこのようなゲームで遊んだこともなかったので、どの様にプログラミングしているか興味がありましたが、 この本はコマンドラインに表示する単純なソフトですが、私の知らない技術が一杯あり、とてもとても小一時間では作れないし、 今は英語ぐらいにはなりたいと上手くいかない外国語の習得に興味が移っているので、 時間を見て少しづつ読んでいます。他人の書いたプログラムを読むのは大変なので、本に書いてある通り順番に 少しずつ機能を増やしながらプログラミングしていきますが、 途中で本に書いているようには動かなくなります。どっかで、間違えたのですが、普通に考えれば一歩一歩確かめながらプログラミングしているので、 直前に修正した個所が間違っているはずですが、初めて作るプログラムで、そのアルゴリズムを理解していなければ、慌てます。 この本には、このように初めてのゲームのプログラムの仕組みを学ぶ時、何処を次に修正するかが分り易い工夫がされていますが、 それでも集中力が切れて間違えてしまいます。 このような場合、ダウンロードした正しいプログラムと現時点で作っているプログラムの違いを表示させてみれば良いです。 昔はコマンドプロンプトで 使う diff が有名でしたが、現在は無料のソフトとして WinMerge と TextDiff が有名みたいです。どちらも、デフォルトでは期待していたものと違っていました。 このような多機能なソフトは、デフォルトではなく、どの様なオプションがあるか調べ、 使い勝手が良いように自分なりの設定をする必要があり、 使い方に慣れれば便利な道具ですが、今回は二つのプログラムをプリントアウトして、手動で間違いを見つけました。 久しぶりの C のプログラミングなので、時間が掛かります。 何が目的でこの本を読んでいるかにもよりますが、例えば、第5章「ドットイートゲームを作成する」（昔、大流行した「パックマン」のようなゲームです）を読んだら、 最後に書いてあるように 「ダイクストラ法」や「A スター探索」のアルゴリズムを実装してみるとか、 迷路をコンピューターに作らせるにはどうすれば良いか調べて実装してみるとか、 確か東大生が作り売り出されて、私も遊んだことのある「平安京エイリアン」もどきに改良してみるとか、 別の言語、例えば、Python の Pygame を使ったプログラムに翻訳してみるとか思いつくことを色々時間を掛けてやってみるとゲームの作り方が我々凡人でも身につきます。 現代は何事も如何に時間を掛けずに成果をあげるかの効率の競争みたいですが、我々凡人がプログラミングが出来るようになるかどうかは矢張り費やした時間の関数でもあり、 エジソンが「この子の為になることを何か話して下さい」と母親に乞われた時、答えたとされる「坊や、何かを始めたら時計を見たらいけないよ」で、 夢中になっていて気が付いたら夜が明けていたと言う経験が何度もないと多分駄目じゃないかと私は思います。 Python でのゲームのプログラミングの参考書は、田中賢一郎著「ゲームを作りながら楽しく学べる Python プログラミング」や 廣瀬豪著「Python でつくるゲーム開発入門講座」及び「Python でつくるゲーム開発入門講座　実践編」がお勧めです。

更に、AI 関連の読んでいない本が一杯本箱で埃を被っています。「PythonによるAI・機械学習・深層学習アプリのつくり方」を本屋で見つけ購入すると 本箱に既に購入していた同じ本が並んでいました。これではいけないと思って、この本も少しづつ読んでいます。理論が分かる本ではないですが、今の処、 私の貧弱なパソコンでも実行できています。所が、人物の顔認識の例題で、この本の画像では確かに認識してくれますし、 顔認識の為のソフトをゲットした所に何に使うか分からないソフトが いっぱいありましたが、これは目を認識するものだろうと判断してダウンロードした訓練済みのソフトを使えば、本の例題の画像達では目を認識しますが、 自分で撮った写真では顔も目も認識しません。これらの画像の何がいけないのか・何が違うか分かりません。 矢張り、その原理・使っているアルゴリズムの理解なしには AI は素人には使えません。 （これは、前もって shogi.jpg 画像を小さくリサイズし、画像の大きさを調べ、顔の大きさがどれくらいの矩形で覆えるか計算して、 


Python Program{
import cv2
import matplotlib.pyplot as plt

# カスケードファイルを指定して検出器を作成
cascade_file = "haarcascade_frontalface_alt.xml"
cascade = cv2.CascadeClassifier(cascade_file)

# 画像を読み込んでグレースケールに変換する
img = cv2.imread("shogi.jpg")
img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

# 顔認証を実行
face_list = cascade.detectMultiScale(img_gray, minSize=(150, 150))

# 結果を確認
if len(face_list) == 0:
    print("失敗")
    quit()

# 認識した部分に印を付ける
for (x, y, w, h) in face_list:
    print("顔の座標=", x, y, w, h)
    red = (0, 0, 255)
    cv2.rectangle(img, (x, y), (x+w, y+h), red, thickness=20)

# 画像を出力
cv2.imwrite("face-detect.png", img)

# 画像を表示
plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB))
plt.show()
}

と言うプログラムを 

# 顔認証を実行
face_list = cascade.detectMultiScale(img_gray, minSize=(50, 50))

のように minSize の設定を小さく変えれば、二人の人の一方の顔を認識してくれました。更に、 

# 顔認証を実行
face_list = cascade.detectMultiScale(img_gray, minSize=(30, 30))

と更に、 minSize の設定を小さく変えれば、二人の顔を認識してくれました。プログラムの意味が良く分かっていませんでした。 p.133 の顔検出器の仕組みの画像を見ると minSize で設定した矩形の大きさまで、順番に切り取る画像を小さくしながら虱潰しに調べ、鼻、目、口の明暗パターン が顔の形の配置に合致するものがないか詮索している見たいです。だから、調べる画像の顔の大きさの矩形をここに設定した時だけ、 画像の顔を認識したんだと思います。 この矩形を小さくすれば取りこぼしはないけれども探索に時間が掛かります。このソフトは画像を調べて、 探索すべき最適な最小の矩形を推定できるほどには賢くないので、人間が探索する最小の矩形のサイズを指定しちゃらなければ いけないと言うことみたいです。更に、デジタルカメラで撮ったそのままの画像では検索に時間が掛かりすぎるので、小さな画像にリサイズしないと パソコンでは顔認識できないです。） 「数学を知らなくても AI は分かる」と言う本などの宣伝文句に騙されずに、時間は掛かっても 「何をやっているか」：　基本からきちんと勉強する必要があります。 ある国会議員の発言の「車の構造を知らなくても、車の運転は出来る」と言う訳には残念ながらいかないみたいです。

このページで途中から数式がチャンと表示されていないことに気づきました。原因を調べるのに半日掛かりましたが、何がいけないのか分かりません。 一行ごとに削除して調べれば分かるはずですが、めんどくさくなって、問題を起こしている部分を削除しました。 キチンと html の仕組みを理解していないので、問題が発生した時、大変です。

升田幸三さんも趣味を整理し、将棋だけに集中しなさいと書いていましたが、現役時代と違い、本当は現役時代もその傾向がありましたが、一つのことに集中せず、 散歩に行く公園で見かける小さな女の子達（どう言う訳か弥右衛門公園に来ているのは女の子が多いような気がします）のように他の人が面白そうなことをしていたら、 真似をしてなんにでも手を出し、何一つものになりませんが、老人の良い暇つぶしになっています。

フーリエ解析の本は沢山有るけど、プリンストン解析学講義１の「フーリエ解析入門」が目に留まって、購入して少し読んで見た。 「解析学の全体像を述べようとするならば、まずはじめに次の問いに取り組まなければならない。どこからはじめればよいか？ 最初に取り上げるべきテーマは何か？関連する概念と基本的な技法をどのような順序で展開すべきか？ この問いに対する私たちの答えは、フーリエ解析が解析学の中心に位置しているという視点に立っている。実際、フーリエ解析は解析学の発展の中で 歴史的に重要な役割を果たしてきたし、またそのアイデアは今日の解析学に広く浸透している。これらの理由から私たちは、この最初の巻にフーリエ級数の 基本的な事柄の解説、併せてフーリエ変換、有限フーリエ解析の初歩的な解説を充てることにした。このように始めることにより、解析学の 他の諸科学への応用を、偏微分方程式や数論のような話題との繋がりと併せてわかりやすく学ぶことができる。後の巻において、これらの関連の多くは より体系的な観点から取り上げられ、複素解析、実解析、ヒルベルト空間論、そしてその他の分野の間の連係がさらに探られることになる。」と書いてあります。

この本の最初で、 一松信著「解析学序説　上巻」の定理 5.22 の f(x)がx=aにおいて２回微分可能ならば limh→0f(a+h)+f(a−h)−2f(a)h2=f″(a) を使って、物理の微分方程式の導き方ってこんなんで良いのかなとも思いますが、弦の波動方程式 1c2∂2u∂t2=∂2u∂x2 を導いていました。 何でこんな定理があるんだろう？どうやって見つけたんだろうとずっと思っていました。 この本には、まだ十数ページ読んだだけですが、私が知りたかったことが書いてあります。大学で学んだ解析学の知識があるから読めるような気もしますが、 読んで見ようと言う手頃な本に出会うことが出来れば、我々凡人には解析学の理解・イメージが違っていたような気がします。 優秀な人達と違い、我々凡人には、自分にとって、理解しやすい本に出会うかも結局運みたいです。

絵を描くことが好きな大人？には現在は、絵を描くことに特化した Processing がお勧めです。古く、題名が内容とかけ離れていますが、西田竜太著「遊んで作る スマホゲームプログラミング」や西田竜太著「遊んで学ぶはじめてのプログラミング」と言う Processing によるお決まりのゲームの解説書もありますが、 Processing の面白さは別のところにあります。三井和男著「デザイン言語 Processing 入門　楽しく学ぶコンピュテーショナルデザイン」が 理解するに必要な数学的な基本的な知識は持っていましたから、面白くて久しぶりに集中して2日で読み終わりました。 もう手遅れですが、才能のある人達は学んだ数学的知識をこのように活用していくんだと学ぶことが出来ました、 C++ か java の本格的なプログラミングの経験は必要なく、ちょっと齧っただけのプログラミングの経験があれば、 簡単に理解できるので、Scratch はどうも子供じみていると言う人にもお勧めです。プログラミングが初めてなら、 Casey Reas, Ben Fry 著「Processing をはじめよう」のプログラムを本を読みながら打ち込んで勉強するのが良いと思います。私はサンプルプログラムを 昔購入して読まずに（昔ちょっと触って見た Arduino の関連で購入していました）本箱でずっと埃を被っていたせいか、本に書いている方法ではゲットすることが出来ませんでした。 この本を読んで数学とアートの関係に目覚めれば、その後、興味に応じて、「数学から創るジェネラティブアート - Processingで学ぶかたちのデザイン」や 「[普及版]ジェネラティブ・アート―Processingによる実践ガイド」のアート系の参考書や 目先を変えて「作って動かす ALife」（サンプルのプログラムは Python で書かれていて、見たことのないライブラリーが使われています。）や 「反応拡散方程式」の専門書などをお小遣いと相談して購入すれば良いです。 更に Processing（プロセッシング）のPython（パイソン)モードと言うものもインターネットで調べるとあり、既に学んだことが有機的に繋がっていて、 Python の知識が無駄にはなりません。 Processing はデフォルトは java が元になっていて、プログラムの書き方がと言うか構文が違いますが大きな違いがあるわけではないみたいです。 例えば、java では 


Processing Program{
void setup() {
  size(480, 480);
  smooth();
  noLoop();
}

void draw() {
    translate(100, 100);
    sierpinski(300, 5);
}

void fd(float d) {
  line(0, 0, d, 0);
  translate(d, 0);
}

void rt(float a) {
  float t = radians(a);
  rotate(t);
}

void sierpinski(float s, int n) {
  if (n > 0) {
    for (int i=0; i<3; i++) {
      fd(s);
      rt(120);
      sierpinski(s/2, n-1);
    }
  }
}
}

と言うプログラムが、python では 


Processing Program{
def setup():
  size(480, 480)
  smooth()
  noLoop()

def draw():
    translate(100, 100)
    sierpinski(300, 5)

def fd(d) :
  line(0, 0, d, 0)
  translate(d, 0)

def rt(a) :
  t = radians(a)
  rotate(t)

def sierpinski(s, n) :
  if n > 0 :
    for i in range(3):
      fd(s)
      rt(120)
      sierpinski(s/2, n-1)
}

となります。実行すると


です。このようにタートルグラフィックスが簡単に実現できます。 また、昔は苦労して3Dの静止画を作っていましたが、まだ意味のある華麗な動画のプログラムは作れませんが、3Dの照明、カメラ付きの動画が 


Processing Program{
float n = 0;

void setup() {
  size(600, 600, P3D);
}

void draw() {
  background(0);
  camera(mouseX, mouseY, 300, width/2, height/2, 0, 0, 1, 0);
  translate(width/2, height/2, n);
  rotateY(radians(60+n)); 
  rotateX(radians(60+n)); 
  pointLight(random(0, 255), random(0, 255), random(0, 255), width/3, height/2, 100); 
  pointLight(0, 255, 255,  width/4, height/4, -100);
  ambientLight(10, 10, 100); 
  box(100, 200, 50);
  n -= 1;
}
}

のように簡単に作れます。 このように、現在は面白そうな事が一杯で、時間がなんぼあっても足りませんが、高知のような、東京で優雅な生活をしている政治家・官僚に見放された地方に 住んでいる退職した暇な老人でも地方新聞とテレビとパソコンとインターネットがあれば、 お金を大して使わなくても暇つぶしが出来る面白い時代になりました。私の持っている非力なパソコンでも、 「AI の流れに乗れない、他の人がやっている探索が上手くいかない」と嘆かなくても、 今まで難しそうで手が出なかった数学・偏微分方程式の楽しい応用が 容易に確かめることが出来るように現在はなっています。 「NUMERICAL RECIPES in C」も購入してから読んでいなかったのですが、しかも2冊本箱にあります（久しぶりに、 Grunbaum and Shephard 著「Tilings and Patterns」を持っていたはずだと佐川の実家の本箱を見に行くと更にもう一冊ハードカバーの本が隣で埃を被っていました。 今まで数値計算に興味がなかったので読んでいませんでしたが、基本的な参考書は揃えていました。）が、この本だけで、 常微分方程式の Runge-Kutta 法を見つけた人が何を考えたか読み取るのは難しいですが、私にも理解できるように解説してくれている youtube の動画がありました。若い人の勉強量は半端ないですね。単純な Euler 法も高階の常微分方程式だと「NUMERICAL RECIPES in C」に 書いていることと小高知宏著「Pythonによる数値計算とシミュレーション」の24頁に書いてあることと異なりますが、 gfreefall.py を書き直して、両方の公式のグラフを描かせてみるとほぼ重なりどちらでも大した差がないですが、 小高知宏著「Pythonによる数値計算とシミュレーション」の公式をどうして出したか疑問で、早々とここでまず躓いてしまいましたが、 三井和男著「Processing入門」の偏微分方程式に関する116ページの解説を読んで、2階常微分方程式に直接単純な Euler 法を適応すれば、 小高知宏著「Pythonによる数値計算とシミュレーション」の公式が出せることに気づきました。 私のような解析学の初心者はちょっとしたことで、解析学が分からなくなります。 これだと言う参考書を見つけることのできない広範囲な解析学は私にとっては矢張り難しいですが、面白い学問でもあります。 プログラミングで生計を立てたい若い人は、求人の要求している言語は何かを調べて、有利な言語を選択するのも一つの戦略ではありますが、 必要とされる技能は常に変化しています。

巴山竜来著「数学から創るジェネラティブアート - Processingで学ぶかたちのデザイン」は昔から興味のあった準周期タイリングに関する記述があると言うので 購入しましたが、１４ページ分しかありませんでした。しかし、数学を視覚化する試みで面白いものです。 この本の Processing のプログラムに翻訳しながら、読んで見ました。 「分割(TL, FS)の繰り返しによる分割」のプログラミングは次のようにすれば良いです。 


Python Program{
import turtle
import tkinter as tk
import numpy as np
import random

W = 500
H = 500

root = tk.Tk()
root.title('ClassGoldenTriangle')

canvas = tk.Canvas(root)
canvas.config(width=W, height=H)
canvas.pack()
screen = turtle.TurtleScreen(canvas)
screen.bgcolor("cyan")

t = turtle.RawTurtle(screen, shape="turtle")
t.color("red")
t.width(3)

turtle_stop = False

class Triangle:
    def __init__(self, v1, v2, v3, type):
        self.v1 = v1
        self.v2 = v2
        self.v3 = v3
        self.type = type
    def print(self):
        print('v1', self.v1, 'v2', self.v2, 'v3', self.v3, 'type=', self.type)
    def draw(self):
        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
        canvas.create_polygon(self.v1[0], self.v1[1], self.v2[0], self.v2[1], \
                               self.v3[0], self.v3[1],fill = color1, width = 3)
    def draw_line(self):
        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
        canvas.create_polygon(self.v1[0], self.v1[1], self.v2[0], self.v2[1], \
                               self.v3[0], self.v3[1],fill='', \
                              outline = color1, width = 3)
    def turtle_draw(self):
        global t
        if turtle_stop == True:
            return
        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
        t.color(color1)
        t.begin_fill()
        t.penup()
        t.setpos(self.v1)
        t.pendown()
        t.setpos(self.v2)
        t.setpos(self.v3)
        t.setpos(self.v1)
        t.end_fill()
        t.pendown()

    def turtle_draw_line(self):
        global t
        if turtle_stop == True:
            return
##        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
##        t.color(color1)
        t.color('blue')
        t.penup()
        t.setpos(self.v1)
        t.pendown()
        t.setpos(self.v2)
        t.setpos(self.v3)
        t.setpos(self.v1)
        t.pendown()
        
    def split(self, ind):
        if self.type == 0: ## 狭い(type=0)の二等辺三角形
            m = 0.5*(self.v3-self.v2)+self.v2
            x = np.sqrt((self.v2[0]-self.v1[0])**2+(self.v2[1]-self.v1[1])**2)
            y = np.sqrt((m[0]-self.v1[0])**2+(m[1]-self.v1[1])**2)
            alpha = 2*np.arccos(y/x)
##            print(alpha*180/np.pi)
            r = 1 / (2*np.cos(alpha))
            w = r*(self.v3-self.v1)+self.v1
            tr_list = []
            tr_list.append(Triangle(w, self.v1, self.v2, 1)) ## Ts 1 RU
            tr_list.append(Triangle(self.v2, self.v3, w, 0)) ## Ts 0 RD
            w = r*(self.v2-self.v1)+self.v1
            tr_list.append(Triangle(w, self.v1, self.v3, 1)) ## Ts' 1 LU
            tr_list.append(Triangle(self.v3, self.v2, w, 0)) ## Ts' 0 LD
            beta = (np.pi-alpha)/2
##            print('beta=', beta*180/np.pi)
            z = np.sqrt((self.v2[0]-self.v3[0])**2+(self.v2[1]-self.v3[1])**2)
            r = z / x
            w = r*(self.v1-self.v2)+self.v2
            r2 = 2*z*np.cos(beta)/x
            u = r2*(self.v1-self.v3)+self.v3
            tr_list.append(Triangle(self.v2, self.v3, u, 0)) ## TL 0 RD
            tr_list.append(Triangle(self.v2, u, w, 0))       ## TL 0 LM
            tr_list.append(Triangle(w, u, self.v1, 1))       ## TL 1 LU
            w = r*(self.v1-self.v3)+self.v3
            u = r2*(self.v1-self.v2)+self.v2
            tr_list.append(Triangle(self.v3, u, self.v2, 0)) ## TL' 0 LD
            tr_list.append(Triangle(self.v3, w, u, 0))       ## TL' 0 RM
            tr_list.append(Triangle(u, w, self.v1, 1))       ## TL' 1 RU
            return tr_list
        elif self.type == 1: ## 広い(type=1)の二等辺三角形
            x = np.sqrt((self.v2[0]-self.v1[0])**2+(self.v2[1]-self.v1[1])**2)
            y = np.sqrt((self.v2[0]-self.v3[0])**2+(self.v2[1]-self.v3[1])**2)
            r = (y-x)/y
            w = r*(self.v3-self.v2)+self.v2
            tr_list = []
            tr_list.append(Triangle(self.v3, self.v1, w, 0)) ## Fs 0 R
            tr_list.append(Triangle(w, self.v1, self.v2, 1)) ## Fs 1 L
            w = r*(self.v2-self.v3)+self.v3
            tr_list.append(Triangle(self.v2, w, self.v1, 0)) ## Fs' 0 L
            tr_list.append(Triangle(w, self.v3, self.v1, 1)) ## Fs' 1 R
            z = y-x
            r = z/y
            w = r*(self.v3-self.v2)+self.v2
            tr_list.append(Triangle(w, self.v1, self.v2, 1)) ## FL 1 L
            r2 = z/x
            u = r2*(self.v1-self.v3)+self.v3
            tr_list.append(Triangle(w, u, self.v1, 0))       ## FL 0 M
            tr_list.append(Triangle(u, w, self.v3, 1))       ## FL 1 R
            w = r*(self.v2-self.v3)+self.v3
            tr_list.append(Triangle(w, self.v3, self.v1, 1)) ## FL' 1 R
            u = r2*(self.v1-self.v2)+self.v2
            tr_list.append(Triangle(w, self.v1, u, 0))       ## FL' 0 M
            tr_list.append(Triangle(u, self.v2, w, 1))       ## FL' 1 L
            return tr_list
        
    def Ts(self, ind): ## 狭い(type=0)の二等辺三角形
        if ind == 0:
            triangle_list = self.split(ind)
            return triangle_list[0: 2]
        elif ind == 1:
            triangle_list = self.split(ind)
            return triangle_list[2: 4]
    def Tl(self, ind): ## 狭い(type=0)の二等辺三角形
        if ind == 0:
            triangle_list = self.split(ind)
            return triangle_list[4: 7]
        elif ind == 1:
            triangle_list = self.split(ind)
            return triangle_list[7: ]
        elif ind == 2:
            triangle_list = self.split(ind)
            tri_list = triangle_list[4:7]
            triangle = tri_list[1]
            v2 = triangle.v2
            v3 = triangle.v3
            tri_list[1].v2 = v3
            tri_list[1].v3 = v2
            return tri_list
    def Fs(self, ind): ## 広い(type=1)の二等辺三角形
        if ind == 0:
            triangle_list = self.split(ind)
            return triangle_list[0: 2]
        elif ind == 1:
            triangle_list = self.split(ind)
            return triangle_list[2: 4]
        elif ind == 2:
            triangle_list = self.split(ind)
            tri_list = triangle_list[0:2]
            triangle = tri_list[0]
            v2 = triangle.v2
            v3 = triangle.v3
            tri_list[0].v2 = v3
            tri_list[0].v3 = v2
            return tri_list
            
            
class Pentagon:
    
    def __init__(self, v1, v2, v3, v4, v5, type):
        self.v1 = v1
        self.v2 = v2
        self.v3 = v3
        self.v4 = v4
        self.v5 = v5
        self.type = type
    def print(self):
        print('v1', self.v1, 'v2', self.v2, 'v3', self.v3, \
               'v4', self.v4, 'v5', self.v5, 'type=', self.type)
    def draw(self):
        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
        canvas.create_polygon(self.v1[0], self.v1[1], \
                              self.v2[0], self.v2[1], \
                              self.v3[0], self.v3[1], \
                              self.v4[0], self.v4[1], \
                              self.v5[0], self.v5[1], \
                              fill = color1, width = 3)
    def draw_line(self):
        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
        canvas.create_polygon(self.v1[0], self.v1[1], \
                              self.v2[0], self.v2[1], \
                              self.v3[0], self.v3[1], \
                              self.v4[0], self.v4[1], \
                              self.v5[0], self.v5[1], \
                              fill = '', outline = color1, width = 3)
    def turtle_draw(self):
        global t
        if turtle_stop == True:
            return
        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
        t.color(color1)
        t.begin_fill()
        t.penup()
        t.setpos(self.v1)
        t.pendown()
        t.setpos(self.v2)
        t.setpos(self.v3)
        t.setpos(self.v4)
        t.setpos(self.v5)
        t.setpos(self.v1)
        t.end_fill()
        t.pendown()

    def turtle_draw_line(self):
        global t
        if turtle_stop == True:
            return
        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
        t.color(color1)
        t.penup()
        t.setpos(self.v1)
        t.pendown()
        t.setpos(self.v2)
        t.setpos(self.v3)
        t.setpos(self.v4)
        t.setpos(self.v5)
        t.setpos(self.v1)
        t.pendown()
        
    def split_3_triangles(self):
        tr = []
        tr.append(Triangle(self.v1, self.v3, self.v4, 0))
        tr.append(Triangle(self.v2, self.v3, self.v1, 1))
        tr.append(Triangle(self.v5, self.v1, self.v4, 1))
        return tr

def turtle_draw_coordinate_axis():
    t.pensize(1)
    t.penup()
    t.setpos(0, 0)
    t.pendown()
    t.color('red')
    t.setpos(W/2, 0)
    t.penup()
    t.setpos(0, 0)
    t.pendown()
    t.color('blue')
    t.setpos(-W/2, 0)
    t.penup()
    t.setpos(0, 0)
    t.pendown()
    t.color('yellow')
    t.setpos(0, H/2)
    t.penup()
    t.setpos(0, 0)
    t.pendown()
    t.color('green')
    t.setpos(0, -H/2)
    
def F(tr, level):
    tr.turtle_draw_line()
    if tr.type == 0:
        triangle_list = tr.Tl(2)
        if level == 0:
            for triangle in triangle_list:
                triangle.turtle_draw_line()
        else:
            for triangle in triangle_list:
                F(triangle, level-1)
    elif tr.type == 1:
        triangle_list = tr.Fs(2)
        if level == 0:
            for triangle in triangle_list:
                triangle.turtle_draw_line()
        else:
            for triangle in triangle_list:
                F(triangle, level-1)
level = 5

def main():
    global t
    global turtle_stop
    turtle_stop = False
    turtle_draw_coordinate_axis()
    t.pensize(3)
    p = np.zeros(10).reshape(5, 2)
    for i in range(5):
        p[i] = np.array([np.cos(i*2*np.pi/5+np.pi/2), np.sin(i*2*np.pi/5+np.pi/2)])
    p = 240*p
    poly = Pentagon(p[0], p[1], p[2], p[3], p[4], 0)
    tr_lst = poly.split_3_triangles()
    F(tr_lst[0], level)
    
if __name__ == "__main__":
    lbl = tk.Label(text='Level')
    lbl.pack()
    txt = tk.Entry(width=20)
    txt.pack()
    # テキストボックスをクリア
    txt.delete(0, tk.END)
    # テキストボックスに文字「1234」を入力
    txt.insert(tk.END, str(level))

    def button_click():
        global level
        global turtle_stop
        turtle_stop = True
        # テキストボックスの文字を取得
        level = int(txt.get())
        print(level)
        canvas.create_rectangle(-W/2, -H/2, W/2, H/2, fill='cyan')
        root.after(1000, main)
    
    # button1ウィジェットを作成
    button1 = tk.Button(root ,text="描画", command=button_click)
    button1.pack() # button1ウィジェットを配置
    main()
    
root.mainloop()
}

で、これを実行すると


です。今は亀が動き回って図を描くので、どの様な順序で図を描いているか目で見ることが出来ます。 素早く図を描きたければ、関数 def F(tr, level): の turtle_draw_line() と turtle_draw_line() を draw_line() と draw_line() に それぞれ変更して下さい。

次は、この本のクライマックスである「図14.13 黄金三角形タイリングから得られる五角形ペンローズタイリング(PenroseTiling)」を描く Python のプログラムを作ることです。今まで作ってきたプログラムを修正して、


を描くプログラムは直ぐ作れました。しかし、正五角形が分離していません。分離する線をどの様に描くかを考える必要があります。 大した考えもなく、上の模様を描く途中で必要と思う頂点の座標を配列に保存して置いて、最後に、区分けの線分を描けば良いと考えました。 しかし、これは馬鹿な考えで、


のようなスケッチを描いて、必要な頂点を探す羽目になりました。level=3 の模様まで何とか力技で分離の線を描けるようになりましたが、 この方法では、私の能力では、一般的な法則は見つけることが出来ません。巴山さんの processing のプログラムをざっと眺めると そんなに難しいことをやってないみたいです。キチンと読むのは、processing 特有の技法を使っているので、厄介なので、自分で何とかしようと します。この模様を描くための補助線を全て描いてみると


です。この中の必要な線だけ描けば良いことが分かります。これで、上手く


が描けました。ペンローズタイリングが何で可能なのか疑問でしたが、自分でペンローズタイリングを描くプログラムを作ってみることにより、 やっと疑問が解消しました。レベルを上げると同時に拡大するという操作を無限回繰り返せば、平面を覆うことが出来るでしょうと言うことでした。 教科書をなぞるだけでは駄目だと教えてくれた先生は、佐川小学校4年生（ひょっとしたら、5年生）の時、 担任だった山中乙彦先生ですが、 「確か自由研究で、何かやって（何だったか忘れました）、教科書に書いている通りになった」と得意になって提出すると 「自分で考えたことをやれ」と先生に叱られました。その時は、小学生の私にそんなこと言ってもと思いましたが、時々思い出します。 どうしても速く参考書を勉強したという成果を出したくて、おざなりに単に参考書をなぞるだけになりがちですが、この本のように本当に 何をしているか知りたいと思う本に出会って、今回やったような読み方をすれば、得ることが多かったように思います。 最終的なプログラムは 


Python Program{
import turtle
import tkinter as tk
import numpy as np
import random

W = 500
H = 500

phi = (1+np.sqrt(5))/2

root = tk.Tk()
root.title('TS_FL_repeat')

canvas = tk.Canvas(root)
canvas.config(width=W, height=H)
canvas.pack()
screen = turtle.TurtleScreen(canvas)
screen.bgcolor("white")

t = turtle.RawTurtle(screen, shape="turtle")
t.color("red")
t.width(3)

turtle_stop = False

class Triangle:
    def __init__(self, v1, v2, v3, type):
        self.v1 = v1
        self.v2 = v2
        self.v3 = v3
        self.type = type
    def print(self):
        print('v1', self.v1, 'v2', self.v2, 'v3', self.v3, 'type=', self.type)
    def draw(self):
        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
        canvas.create_polygon(self.v1[0], self.v1[1], self.v2[0], self.v2[1], \
                               self.v3[0], self.v3[1],fill = color1, width = 3)
    def draw_line(self):
        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
        canvas.create_polygon(self.v1[0], self.v1[1], self.v2[0], self.v2[1], \
                               self.v3[0], self.v3[1],fill='', \
                              outline = color1, width = 3)

    def turtle_draw2(self):
        global pentagon_Point_list
        global t
        if turtle_stop == True:
            return
        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
        t.color(color1)
        t.begin_fill()
        t.penup()
        t.setpos(self.v1)
        t.pendown()
        t.setpos(self.v2)
        t.setpos(self.v3)
        t.setpos(self.v1)
        t.end_fill()
        t.pendown()

    def turtle_draw(self):
        global pentagon_Point_list
        global t
        if turtle_stop == True:
            return
##        ## 三角形の裏表を調べる
##        t.penup()
##        t.setpos(self.v1)
####        t.setheading(0)
##        dir = t.towards(self.v2[0], self.v2[1])
##        dir2 = t.towards(self.v3[0], self.v3[1])
##        print('dir=', dir, 'dir2=', dir2, 'dir2-dir=', dir2-dir)
        if self.type == 0:
            x = 1 / phi
            y = 1 / 2
            z = 1 - phi/2
            v4 = x * (self.v2-self.v1)+self.v1
            v5 = z * (self.v3-self.v2)+self.v2
            v6 = y * (self.v3-self.v1)+self.v1
            
            t.color('cyan')
            t.begin_fill()
            t.penup()
            t.setpos(self.v1)
            t.pendown()
            t.setpos(v4)
            t.setpos(v6)
            t.setpos(self.v1)
            t.pendown()
            t.end_fill()
            
            t.color('cyan')
            t.begin_fill()
            t.penup()
            t.setpos(v4)
            t.pendown()
            t.setpos(v5)
            t.setpos(self.v3)
            t.setpos(v6)
            t.setpos(v4)
            t.pendown()
            t.end_fill()
            
            t.color('yellow')
            t.begin_fill()
            t.penup()
            t.setpos(self.v2)
            t.pendown()
            t.setpos(v5)
            t.setpos(v4)
            t.setpos(self.v2)
            t.pendown()
            t.end_fill()
                
        elif self.type == 1:
            x = 1 / phi
            y = 1 / 2
            z = phi / (1+phi)
            v4 = x * (self.v2-self.v1)+self.v1
            v5 = z * (self.v3-self.v2)+self.v2
            v6 = y * (self.v3-self.v1)+self.v1
            
            t.color('cyan')
            t.begin_fill()
            t.penup()
            t.setpos(self.v1)
            t.pendown()
            t.setpos(v4)
            t.setpos(v5)
            t.setpos(v6)
            t.setpos(self.v1)
            t.pendown()
            t.end_fill()
            
            t.color('cyan')
            t.begin_fill()
            t.penup()
            t.setpos(v6)
            t.pendown()
            t.setpos(v5)
            t.setpos(self.v3)
            t.setpos(v6)
            t.pendown()
            t.end_fill()
            
            t.color('yellow')
            t.begin_fill()
            t.penup()
            t.setpos(self.v2)
            t.pendown()
            t.setpos(v5)
            t.setpos(v4)
            t.setpos(self.v2)
            t.pendown()
            t.end_fill()

    def turtle_draw_line2(self):
        global t
        if turtle_stop == True:
            return
##        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
##        t.color(color1)
        t.pensize(3)
        t.color('red')
        t.penup()
        t.setpos(self.v1)
        t.pendown()
        t.setpos(self.v2)
        t.setpos(self.v3)
        t.setpos(self.v1)
        t.pendown()

    def turtle_draw_line(self):
        global t
        if turtle_stop == True:
            return
##        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
##        t.color(color1)
##        t.color('blue')
##        t.penup()
##        t.setpos(self.v1)
##        t.pendown()
##        t.setpos(self.v2)
##        t.setpos(self.v3)
##        t.setpos(self.v1)
##        t.pendown()
        t.pensize(3)
        if self.type == 0:
            x = 1 / phi
            y = 1 / 2
            z = 1 - phi/2
            v4 = x * (self.v2-self.v1)+self.v1
            v5 = z * (self.v3-self.v2)+self.v2
            v6 = y * (self.v3-self.v1)+self.v1
##            t.color('blue')
##            t.penup()
##            t.setpos(self.v1)
##            t.pendown()
##            t.setpos(v4)
##            t.setpos(v6)
##            t.setpos(self.v1)
##            t.pendown()
##            t.penup()
##            t.setpos(v4)
##            t.pendown()
##            t.setpos(v5)
##            t.setpos(self.v3)
##            t.setpos(v6)
##            t.setpos(v4)
##            t.pendown()
##            t.penup()
##            t.setpos(self.v2)
##            t.pendown()
##            t.setpos(v5)
##            t.setpos(v4)
##            t.setpos(self.v2)
##            t.pendown()
            t.color('blue')
            t.penup()
            t.setpos(v5)
            t.pendown()
            t.setpos(v4)
            t.setpos(v6)
            t.pendown()
        elif self.type == 1:
            x = 1 / phi
            y = 1 / 2
            z = phi / (1+phi)
            v4 = x * (self.v2-self.v1)+self.v1
            v5 = z * (self.v3-self.v2)+self.v2
            v6 = y * (self.v3-self.v1)+self.v1
##            t.color('blue')
##            t.penup()
##            t.setpos(self.v1)
##            t.pendown()
##            t.setpos(v4)
##            t.setpos(v5)
##            t.setpos(v6)
##            t.setpos(self.v1)
##            t.pendown()
##            t.penup()
##            t.setpos(v6)
##            t.pendown()
##            t.setpos(v5)
##            t.setpos(self.v3)
##            t.setpos(v6)
##            t.pendown()
##            t.penup()
##            t.setpos(self.v2)
##            t.pendown()
##            t.setpos(v5)
##            t.setpos(v4)
##            t.setpos(self.v2)
##            t.pendown()
            t.color('blue')
            t.penup()
            t.setpos(v4)
            t.pendown()
            t.setpos(v5)
            t.setpos(v6)
            t.pendown()
        
    def split(self, ind):
        if self.type == 0: ## 狭い(type=0)の二等辺三角形
            m = 0.5*(self.v3-self.v2)+self.v2
            x = np.sqrt((self.v2[0]-self.v1[0])**2+(self.v2[1]-self.v1[1])**2)
            y = np.sqrt((m[0]-self.v1[0])**2+(m[1]-self.v1[1])**2)
            alpha = 2*np.arccos(y/x)
##            print(alpha*180/np.pi)
            r = 1 / (2*np.cos(alpha))
            w = r*(self.v3-self.v1)+self.v1
            tr_list = []
            tr_list.append(Triangle(w, self.v1, self.v2, 1)) ## Ts 1 RU
            tr_list.append(Triangle(self.v2, self.v3, w, 0)) ## Ts 0 RD
            w = r*(self.v2-self.v1)+self.v1
            tr_list.append(Triangle(w, self.v1, self.v3, 1)) ## Ts' 1 LU
            tr_list.append(Triangle(self.v3, self.v2, w, 0)) ## Ts' 0 LD
            beta = (np.pi-alpha)/2
##            print('beta=', beta*180/np.pi)
            z = np.sqrt((self.v2[0]-self.v3[0])**2+(self.v2[1]-self.v3[1])**2)
            r = z / x
            w = r*(self.v1-self.v2)+self.v2
            r2 = 2*z*np.cos(beta)/x
            u = r2*(self.v1-self.v3)+self.v3
            tr_list.append(Triangle(self.v2, self.v3, u, 0)) ## TL 0 RD
            tr_list.append(Triangle(self.v2, u, w, 0))       ## TL 0 LM
            tr_list.append(Triangle(w, u, self.v1, 1))       ## TL 1 LU
            w = r*(self.v1-self.v3)+self.v3
            u = r2*(self.v1-self.v2)+self.v2
            tr_list.append(Triangle(self.v3, u, self.v2, 0)) ## TL' 0 LD
            tr_list.append(Triangle(self.v3, w, u, 0))       ## TL' 0 RM
            tr_list.append(Triangle(u, w, self.v1, 1))       ## TL' 1 RU
            return tr_list
        elif self.type == 1: ## 広い(type=1)の二等辺三角形
            x = np.sqrt((self.v2[0]-self.v1[0])**2+(self.v2[1]-self.v1[1])**2)
            y = np.sqrt((self.v2[0]-self.v3[0])**2+(self.v2[1]-self.v3[1])**2)
            r = (y-x)/y
            w = r*(self.v3-self.v2)+self.v2
            tr_list = []
            tr_list.append(Triangle(self.v3, self.v1, w, 0)) ## Fs 0 R
            tr_list.append(Triangle(w, self.v1, self.v2, 1)) ## Fs 1 L
            w = r*(self.v2-self.v3)+self.v3
            tr_list.append(Triangle(self.v2, w, self.v1, 0)) ## Fs' 0 L
            tr_list.append(Triangle(w, self.v3, self.v1, 1)) ## Fs' 1 R
            z = y-x
            r = z/y
            w = r*(self.v3-self.v2)+self.v2
            tr_list.append(Triangle(w, self.v1, self.v2, 1)) ## FL 1 L
            r2 = z/x
            u = r2*(self.v1-self.v3)+self.v3
            tr_list.append(Triangle(w, u, self.v1, 0))       ## FL 0 M
            tr_list.append(Triangle(u, w, self.v3, 1))       ## FL 1 R
            w = r*(self.v2-self.v3)+self.v3
            tr_list.append(Triangle(w, self.v3, self.v1, 1)) ## FL' 1 R
            u = r2*(self.v1-self.v2)+self.v2
            tr_list.append(Triangle(w, self.v1, u, 0))       ## FL' 0 M
            tr_list.append(Triangle(u, self.v2, w, 1))       ## FL' 1 L
            return tr_list
        
    def Ts(self, ind): ## 狭い(type=0)の二等辺三角形
        if ind == 0:
            triangle_list = self.split(ind)
            return triangle_list[0: 2]
        elif ind == 1:
            triangle_list = self.split(ind)
            return triangle_list[2: 4]
    def Tl(self, ind): ## 狭い(type=0)の二等辺三角形
        if ind == 0:
            triangle_list = self.split(ind)
            return triangle_list[4: 7]
        elif ind == 1:
            triangle_list = self.split(ind)
            return triangle_list[7: ]
        elif ind == 2:
            triangle_list = self.split(ind)
            tri_list = triangle_list[4:7]
            triangle = tri_list[1]
            v2 = triangle.v2
            v3 = triangle.v3
            tri_list[1].v2 = v3
            tri_list[1].v3 = v2
            return tri_list
    def Fs(self, ind): ## 広い(type=1)の二等辺三角形
        if ind == 0:
            triangle_list = self.split(ind)
            return triangle_list[0: 2]
    def Fl(self, ind): ## 広い(type=1)の二等辺三角形
        if ind == 0:
            triangle_list = self.split(ind)
            return triangle_list[4: 7]
        elif ind == 1:
            triangle_list = self.split(ind)
            return triangle_list[7: ]
        elif ind == 2:
            triangle_list = self.split(ind)
            tri_list = triangle_list[4:7]
            triangle = tri_list[1]
            v2 = triangle.v2
            v3 = triangle.v3
            tri_list[1].v2 = v3
            tri_list[1].v3 = v2
            triangle = tri_list[2]
            v2 = triangle.v2
            v3 = triangle.v3
            tri_list[2].v2 = v3
            tri_list[2].v3 = v2            
            return tri_list
            
            
class Pentagon:
    
    def __init__(self, v1, v2, v3, v4, v5, type):
        self.v1 = v1
        self.v2 = v2
        self.v3 = v3
        self.v4 = v4
        self.v5 = v5
        self.type = type
    def print(self):
        print('v1', self.v1, 'v2', self.v2, 'v3', self.v3, \
               'v4', self.v4, 'v5', self.v5, 'type=', self.type)
    def draw(self):
        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
        canvas.create_polygon(self.v1[0], self.v1[1], \
                              self.v2[0], self.v2[1], \
                              self.v3[0], self.v3[1], \
                              self.v4[0], self.v4[1], \
                              self.v5[0], self.v5[1], \
                              fill = color1, width = 3)
    def draw_line(self):
        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
        canvas.create_polygon(self.v1[0], self.v1[1], \
                              self.v2[0], self.v2[1], \
                              self.v3[0], self.v3[1], \
                              self.v4[0], self.v4[1], \
                              self.v5[0], self.v5[1], \
                              fill = '', outline = color1, width = 3)
    def turtle_draw(self):
        global t
        if turtle_stop == True:
            return
        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
        t.color(color1)
        t.begin_fill()
        t.penup()
        t.setpos(self.v1)
        t.pendown()
        t.setpos(self.v2)
        t.setpos(self.v3)
        t.setpos(self.v4)
        t.setpos(self.v5)
        t.setpos(self.v1)
        t.end_fill()
        t.pendown()

    def turtle_draw_line(self):
        global t
        if turtle_stop == True:
            return
        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
        t.color(color1)
        t.penup()
        t.setpos(self.v1)
        t.pendown()
        t.setpos(self.v2)
        t.setpos(self.v3)
        t.setpos(self.v4)
        t.setpos(self.v5)
        t.setpos(self.v1)
        t.pendown()
        
    def split_3_triangles(self):
        tr = []
        tr.append(Triangle(self.v1, self.v3, self.v4, 0))
        tr.append(Triangle(self.v2, self.v3, self.v1, 1))
        tr.append(Triangle(self.v5, self.v1, self.v4, 1))
        return tr

def turtle_draw_coordinate_axis():
    t.pensize(1)
    t.penup()
    t.setpos(0, 0)
    t.pendown()
    t.color('red')
    t.setpos(W/2, 0)
    t.penup()
    t.setpos(0, 0)
    t.pendown()
    t.color('blue')
    t.setpos(-W/2, 0)
    t.penup()
    t.setpos(0, 0)
    t.pendown()
    t.color('yellow')
    t.setpos(0, H/2)
    t.penup()
    t.setpos(0, 0)
    t.pendown()
    t.color('green')
    t.setpos(0, -H/2)

def F(tr, level):
    global pentagon_Point_list    
##    tr.turtle_draw_line()
    if tr.type == 0:
        if level == 0:
##            tr.turtle_draw_line()
            tr.turtle_draw()
        else:
            triangle_list = tr.Ts(0)
            for triangle in triangle_list:
                F(triangle, level-1)
    elif tr.type == 1:
        if level == 0:
##            tr.turtle_draw_line()
            tr.turtle_draw()
        else:
            triangle_list = tr.Fl(2)
            for triangle in triangle_list:
                F(triangle, level-1)
##    tr.turtle_draw_line2()
    if level == 0:
        tr.turtle_draw_line()
            

level = 3

def modify_list():
    global pentagon_Point_list, pentagon_Point_list2
    correct_list = []
    if len(pentagon_Point_list)==2:
        correct_list.append(pentagon_Point_list)
    elif len(pentagon_Point_list)==6:
        v = pentagon_Point_list[3]
        pentagon_Point_list[3] = pentagon_Point_list[5]
        pentagon_Point_list[5] = v
        correct_list.append(pentagon_Point_list)
    elif len(pentagon_Point_list)==16:
        ind_list = [2, 4, 3, 6, 7, 2]
        p_list = []
        for k, ind in enumerate(ind_list):
            p_list.append(pentagon_Point_list[ind])
        correct_list.append(p_list)
        ind_list = [10, 12, 13, 14, 15, 10]
        p_list = []
        for k, ind in enumerate(ind_list):
            p_list.append(pentagon_Point_list[ind])
        correct_list.append(p_list)
        ind_list = [1, 2, 4, 9, 10, 12]
        for k, ind in enumerate(ind_list):
            pentagon_Point_list2.append(pentagon_Point_list[ind])      
        return correct_list
    elif len(pentagon_Point_list)==42:
        ind_list = [6, 7, 19, 28, 22, 6]
        p_list = []
        for k, ind in enumerate(ind_list):
            p_list.append(pentagon_Point_list[ind])
        correct_list.append(p_list)
        p_list = []
        ind_list = [12, 10, 7, 1, 11, 12]
        for k, ind in enumerate(ind_list):
            p_list.append(pentagon_Point_list[ind])
        correct_list.append(p_list)
        p_list = []
        ind_list = [19, 16, 17, 13, 20, 19]
        for k, ind in enumerate(ind_list):
            p_list.append(pentagon_Point_list[ind])
        correct_list.append(p_list)
        p_list = []
        ind_list = [28, 34,38, 37, 19, 28]
        for k, ind in enumerate(ind_list):
            p_list.append(pentagon_Point_list[ind])
        correct_list.append(p_list)
        p_list = []
        ind_list = [26, 33, 29, 28, 22, 26]
        for k, ind in enumerate(ind_list):
            p_list.append(pentagon_Point_list[ind])
        correct_list.append(p_list)
        p_list = []
        ind_list = [4, 21, 22, 1, 2, 4]
        for k, ind in enumerate(ind_list):
            p_list.append(pentagon_Point_list[ind])
        correct_list.append(p_list)
        ind_list = [3, 4, 2, 12, 8, 9, 21, 25, 24, 30, 31, 33]
        for k, ind in enumerate(ind_list):
            pentagon_Point_list2.append(pentagon_Point_list[ind])      

    else:
        correct_list.append(pentagon_Point_list)        
    return correct_list

def modify_list2():
    global pentagon_Point_list2
    correct_list = []
    if len(pentagon_Point_list2)==30:
        for i in range(5):
            ind_list = [(6+i*6)%30, (7+i*6)%30, (8+i*6)%30, \
                    (4+i*6)%30, (3+i*6)%30, (6+i*6)%30]
            p_list = []
            for k, ind in enumerate(ind_list):
                p_list.append(pentagon_Point_list2[ind])
            correct_list.append(p_list)
    elif len(pentagon_Point_list2)==60:
        for i in range(5):
            ind_list = [(6+i*12)%60, (7+i*12)%60, (8+i*12)%60, \
                    (13+i*12)%60, (14+i*12)%60, (6+i*12)%60]
            p_list = []
            for k, ind in enumerate(ind_list):
                p_list.append(pentagon_Point_list2[ind])
            correct_list.append(p_list)
            ind_list = [(9+i*12)%60, (10+i*12)%60, (11+i*12)%60, \
                    (16+i*12)%60, (17+i*12)%60, (9+i*12)%60]
            p_list = []
            for k, ind in enumerate(ind_list):
                p_list.append(pentagon_Point_list2[ind])
            correct_list.append(p_list)
    return correct_list

scalar = 240

def main():
    global t, pentagon_Point_list
    global turtle_stop
    turtle_stop = False
    turtle_draw_coordinate_axis()
    t.pensize(2)
    p = np.zeros(22).reshape(11, 2)
    for i in range(10):
        p[i] = np.array([np.cos(i*2*np.pi/10), np.sin(i*2*np.pi/10)])
    p[10] = np.array([0, 0])
    p = scalar * p
    for i in range(10):
        if i % 2 == 0:
            F(Triangle(p[10], p[i], p[(i+1)%10], 0), level)
        else:
            F(Triangle(p[10], p[(i+1)%10], p[i], 0), level)
##            ## pentagon_Point_listを描く：外側
####            if i == 1:
####                print(len(pentagon_Point_list), pentagon_Point_list)
##            correct_list = modify_list()
##            t.color('blue')
##            for pentagon in correct_list:
##                t.penup()
##                for k, pentagon_p in enumerate(pentagon):
##                    t.setpos(pentagon_p)
##                    if k == 0:
##                        t.pendown()
##            t.penup()
##    ##  pentagon_Point_listを描く：内側
##    correct_list = modify_list2()
####    print('pentagon_Point_list2=', pentagon_Point_list2)
####    print('correct_list=', correct_list)
##    t.color('blue')
##    for pentagon in correct_list:
####        print('pentagon=', pentagon)
##        t.penup()
##        for k, pentagon_p in enumerate(pentagon):
##            t.setpos(pentagon_p)
##            if k == 0:
##                t.pendown()
##    t.penup()

if __name__ == "__main__":
    lbl = tk.Label(text='Level')
    lbl.pack()
    txt = tk.Entry(width=20)
    txt.pack()
    # テキストボックスをクリア
    txt.delete(0, tk.END)
    # テキストボックスに文字「1234」を入力
    txt.insert(tk.END, str(level))

    def button_click():
        global level
        global turtle_stop
        turtle_stop = True
        # テキストボックスの文字を取得
        level = int(txt.get())
        print(level)
        canvas.create_rectangle(-W/2, -H/2, W/2, H/2, fill='cyan')
        root.after(1000, main)
    
    # button1ウィジェットを作成
    button1 = tk.Button(root ,text="描画", command=button_click)
    button1.pack() # button1ウィジェットを配置
    main()

    
root.mainloop()
}

です。残りの菱形タイリングとカイト＆ダートタイリングはそれぞれ(TS_FL)型の黄金三角形タイリングと (TL_FS)型の黄金三角形タイリングから簡単に作れます。 実行結果は、それぞれ、


と


です。プログラムは 


Python Program{
import turtle
import tkinter as tk
import numpy as np
import random

W = 500
H = 500

root = tk.Tk()
root.title('RecurRhombusTS_FL')

canvas = tk.Canvas(root)
canvas.config(width=W, height=H)
canvas.pack()
screen = turtle.TurtleScreen(canvas)
screen.bgcolor("cyan")

t = turtle.RawTurtle(screen, shape="turtle")
t.color("red")
t.width(3)

turtle_stop = False

class Triangle:
    def __init__(self, v1, v2, v3, type):
        self.v1 = v1
        self.v2 = v2
        self.v3 = v3
        self.type = type
    def print(self):
        print('v1', self.v1, 'v2', self.v2, 'v3', self.v3, 'type=', self.type)
    def draw(self):
        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
        canvas.create_polygon(self.v1[0], self.v1[1], self.v2[0], self.v2[1], \
                               self.v3[0], self.v3[1],fill = color1, width = 3)
    def draw_line(self):
        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
        canvas.create_polygon(self.v1[0], self.v1[1], self.v2[0], self.v2[1], \
                               self.v3[0], self.v3[1],fill='', \
                              outline = color1, width = 3)
    def turtle_draw(self):
        global t
        if turtle_stop == True:
            return
##        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
##        t.color(color1)
        if self.type == 0:
            t.color('cyan')
        else:
            t.color('red')
        t.begin_fill()
        t.penup()
        t.setpos(self.v1)
        t.pendown()
        t.setpos(self.v2)
        t.setpos(self.v3)
        t.setpos(self.v1)
        t.end_fill()
        t.pendown()
        
        t.pensize(2)
        t.color('black')
        t.penup()
        t.setpos(self.v2)
        t.pendown()
        t.setpos(self.v1)
        t.setpos(self.v3)
        t.pendown()
        
    def turtle_draw_line(self):
        global t
        if turtle_stop == True:
            return
##        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
##        t.color(color1)
        t.color('black')
        t.penup()
##        t.setpos(self.v1)
##        t.pendown()
##        t.setpos(self.v2)
##        t.setpos(self.v3)
##        t.setpos(self.v1)
##        t.pendown()
        
        t.setpos(self.v2)
        t.pendown()
        t.setpos(self.v1)
        t.setpos(self.v3)
        t.pendown()
        
    def split(self, ind):
        if self.type == 0: ## 狭い(type=0)の二等辺三角形
            m = 0.5*(self.v3-self.v2)+self.v2
            x = np.sqrt((self.v2[0]-self.v1[0])**2+(self.v2[1]-self.v1[1])**2)
            y = np.sqrt((m[0]-self.v1[0])**2+(m[1]-self.v1[1])**2)
            alpha = 2*np.arccos(y/x)
##            print(alpha*180/np.pi)
            r = 1 / (2*np.cos(alpha))
            w = r*(self.v3-self.v1)+self.v1
            tr_list = []
            tr_list.append(Triangle(w, self.v1, self.v2, 1)) ## Ts 1 RU
            tr_list.append(Triangle(self.v2, self.v3, w, 0)) ## Ts 0 RD
            w = r*(self.v2-self.v1)+self.v1
            tr_list.append(Triangle(w, self.v1, self.v3, 1)) ## Ts' 1 LU
            tr_list.append(Triangle(self.v3, self.v2, w, 0)) ## Ts' 0 LD
            beta = (np.pi-alpha)/2
##            print('beta=', beta*180/np.pi)
            z = np.sqrt((self.v2[0]-self.v3[0])**2+(self.v2[1]-self.v3[1])**2)
            r = z / x
            w = r*(self.v1-self.v2)+self.v2
            r2 = 2*z*np.cos(beta)/x
            u = r2*(self.v1-self.v3)+self.v3
            tr_list.append(Triangle(self.v2, self.v3, u, 0)) ## TL 0 RD
            tr_list.append(Triangle(self.v2, u, w, 0))       ## TL 0 LM
            tr_list.append(Triangle(w, u, self.v1, 1))       ## TL 1 LU
            w = r*(self.v1-self.v3)+self.v3
            u = r2*(self.v1-self.v2)+self.v2
            tr_list.append(Triangle(self.v3, u, self.v2, 0)) ## TL' 0 LD
            tr_list.append(Triangle(self.v3, w, u, 0))       ## TL' 0 RM
            tr_list.append(Triangle(u, w, self.v1, 1))       ## TL' 1 RU
            return tr_list
        elif self.type == 1: ## 広い(type=1)の二等辺三角形
            x = np.sqrt((self.v2[0]-self.v1[0])**2+(self.v2[1]-self.v1[1])**2)
            y = np.sqrt((self.v2[0]-self.v3[0])**2+(self.v2[1]-self.v3[1])**2)
            r = (y-x)/y
            w = r*(self.v3-self.v2)+self.v2
            tr_list = []
            tr_list.append(Triangle(self.v3, self.v1, w, 0)) ## Fs 0 R
            tr_list.append(Triangle(w, self.v1, self.v2, 1)) ## Fs 1 L
            w = r*(self.v2-self.v3)+self.v3
            tr_list.append(Triangle(self.v2, w, self.v1, 0)) ## Fs' 0 L
            tr_list.append(Triangle(w, self.v3, self.v1, 1)) ## Fs' 1 R
            z = y-x
            r = z/y
            w = r*(self.v3-self.v2)+self.v2
            tr_list.append(Triangle(w, self.v1, self.v2, 1)) ## FL 1 L
            r2 = z/x
            u = r2*(self.v1-self.v3)+self.v3
            tr_list.append(Triangle(w, u, self.v1, 0))       ## FL 0 M
            tr_list.append(Triangle(u, w, self.v3, 1))       ## FL 1 R
            w = r*(self.v2-self.v3)+self.v3
            tr_list.append(Triangle(w, self.v3, self.v1, 1)) ## FL' 1 R
            u = r2*(self.v1-self.v2)+self.v2
            tr_list.append(Triangle(w, self.v1, u, 0))       ## FL' 0 M
            tr_list.append(Triangle(u, self.v2, w, 1))       ## FL' 1 L
            return tr_list
        
    def Ts(self, ind): ## 狭い(type=0)の二等辺三角形
        if ind == 0:
            triangle_list = self.split(ind)
            return triangle_list[0: 2]
        elif ind == 1:
            triangle_list = self.split(ind)
            return triangle_list[2: 4]
    def Tl(self, ind): ## 狭い(type=0)の二等辺三角形
        if ind == 0:
            triangle_list = self.split(ind)
            return triangle_list[4: 7]
        elif ind == 1:
            triangle_list = self.split(ind)
            return triangle_list[7: ]
        elif ind == 2:
            triangle_list = self.split(ind)
            tri_list = triangle_list[4:7]
            triangle = tri_list[1]
            v2 = triangle.v2
            v3 = triangle.v3
            tri_list[1].v2 = v3
            tri_list[1].v3 = v2
            return tri_list
    def Fs(self, ind): ## 広い(type=1)の二等辺三角形
        if ind == 0:
            triangle_list = self.split(ind)
            return triangle_list[0: 2]
    def Fl(self, ind): ## 広い(type=1)の二等辺三角形
        if ind == 0:
            triangle_list = self.split(ind)
            return triangle_list[4: 7]
        elif ind == 1:
            triangle_list = self.split(ind)
            return triangle_list[7: ]
        elif ind == 2:
            triangle_list = self.split(ind)
            tri_list = triangle_list[4:7]
            triangle = tri_list[1]
            v2 = triangle.v2
            v3 = triangle.v3
            tri_list[1].v2 = v3
            tri_list[1].v3 = v2
            triangle = tri_list[2]
            v2 = triangle.v2
            v3 = triangle.v3
            tri_list[2].v2 = v3
            tri_list[2].v3 = v2            
            return tri_list
            
            
class Pentagon:
    
    def __init__(self, v1, v2, v3, v4, v5, type):
        self.v1 = v1
        self.v2 = v2
        self.v3 = v3
        self.v4 = v4
        self.v5 = v5
        self.type = type
    def print(self):
        print('v1', self.v1, 'v2', self.v2, 'v3', self.v3, \
               'v4', self.v4, 'v5', self.v5, 'type=', self.type)
    def draw(self):
        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
        canvas.create_polygon(self.v1[0], self.v1[1], \
                              self.v2[0], self.v2[1], \
                              self.v3[0], self.v3[1], \
                              self.v4[0], self.v4[1], \
                              self.v5[0], self.v5[1], \
                              fill = color1, width = 3)
    def draw_line(self):
        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
        canvas.create_polygon(self.v1[0], self.v1[1], \
                              self.v2[0], self.v2[1], \
                              self.v3[0], self.v3[1], \
                              self.v4[0], self.v4[1], \
                              self.v5[0], self.v5[1], \
                              fill = '', outline = color1, width = 3)
    def turtle_draw(self):
        global t
        if turtle_stop == True:
            return
        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
        t.color(color1)
        t.begin_fill()
        t.penup()
        t.setpos(self.v1)
        t.pendown()
        t.setpos(self.v2)
        t.setpos(self.v3)
        t.setpos(self.v4)
        t.setpos(self.v5)
        t.setpos(self.v1)
        t.end_fill()
        t.pendown()

    def turtle_draw_line(self):
        global t
        if turtle_stop == True:
            return
        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
        t.color(color1)
        t.penup()
        t.setpos(self.v1)
        t.pendown()
        t.setpos(self.v2)
        t.setpos(self.v3)
        t.setpos(self.v4)
        t.setpos(self.v5)
        t.setpos(self.v1)
        t.pendown()
        
    def split_3_triangles(self):
        tr = []
        tr.append(Triangle(self.v1, self.v3, self.v4, 0))
        tr.append(Triangle(self.v2, self.v3, self.v1, 1))
        tr.append(Triangle(self.v5, self.v1, self.v4, 1))
        return tr

def turtle_draw_coordinate_axis():
    t.pensize(1)
    t.penup()
    t.setpos(0, 0)
    t.pendown()
    t.color('red')
    t.setpos(W/2, 0)
    t.penup()
    t.setpos(0, 0)
    t.pendown()
    t.color('blue')
    t.setpos(-W/2, 0)
    t.penup()
    t.setpos(0, 0)
    t.pendown()
    t.color('yellow')
    t.setpos(0, H/2)
    t.penup()
    t.setpos(0, 0)
    t.pendown()
    t.color('green')
    t.setpos(0, -H/2)
    

def F(tr, level):
##    tr.turtle_draw_line()
    if tr.type == 0:
        triangle_list = tr.Ts(0)
        if level == 0:
            for triangle in triangle_list:
##                triangle.turtle_draw_line()
                triangle.turtle_draw()
        else:
            for triangle in triangle_list:
                F(triangle, level-1)
    elif tr.type == 1:
        triangle_list = tr.Fl(2)
        if level == 0:
            for triangle in triangle_list:
##                triangle.turtle_draw_line()
                triangle.turtle_draw()
        else:
            for triangle in triangle_list:
                F(triangle, level-1)

level = 3

def main():
    global t
    global turtle_stop
    turtle_stop = False
    turtle_draw_coordinate_axis()
    t.pensize(2)
    p = np.zeros(22).reshape(11, 2)
    for i in range(10):
        p[i] = np.array([np.cos(i*2*np.pi/10), np.sin(i*2*np.pi/10)])
    p[10] = np.array([0, 0])
    p = 240*p
    for i in range(10):
        if i % 2 == 0:
            F(Triangle(p[10], p[i], p[(i+1)%10], 0), level)
        else:
            F(Triangle(p[10], p[(i+1)%10], p[i], 0), level)
    
if __name__ == "__main__":
    lbl = tk.Label(text='Level')
    lbl.pack()
    txt = tk.Entry(width=20)
    txt.pack()
    # テキストボックスをクリア
    txt.delete(0, tk.END)
    # テキストボックスに文字「1234」を入力
    txt.insert(tk.END, str(level))

    def button_click():
        global level
        global turtle_stop
        turtle_stop = True
        # テキストボックスの文字を取得
        level = int(txt.get())
        print(level)
        canvas.create_rectangle(-W/2, -H/2, W/2, H/2, fill='cyan')
        
        root.after(1000, main)
    
    # button1ウィジェットを作成
    button1 = tk.Button(root ,text="描画", command=button_click)
    button1.pack() # button1ウィジェットを配置
    main()

root.mainloop()
}

と 


Python Program{
import turtle
import tkinter as tk
import numpy as np
import random

W = 500
H = 500

root = tk.Tk()
root.title('RecurKateDartTL_FS')

canvas = tk.Canvas(root)
canvas.config(width=W, height=H)
canvas.pack()
screen = turtle.TurtleScreen(canvas)
screen.bgcolor("white")

t = turtle.RawTurtle(screen, shape="turtle")
t.color("red")
t.width(3)

turtle_stop = False

class Triangle:
    def __init__(self, v1, v2, v3, type):
        self.v1 = v1
        self.v2 = v2
        self.v3 = v3
        self.type = type
    def print(self):
        print('v1', self.v1, 'v2', self.v2, 'v3', self.v3, 'type=', self.type)
    def draw(self):
        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
        canvas.create_polygon(self.v1[0], self.v1[1], self.v2[0], self.v2[1], \
                               self.v3[0], self.v3[1],fill = color1, width = 3)
    def draw_line(self):
        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
        canvas.create_polygon(self.v1[0], self.v1[1], self.v2[0], self.v2[1], \
                               self.v3[0], self.v3[1],fill='', \
                              outline = color1, width = 3)
    def turtle_draw(self):
        global t
        if turtle_stop == True:
            return
        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
        t.color(color1)
        t.begin_fill()
        t.penup()
        t.setpos(self.v1)
        t.pendown()
        t.setpos(self.v2)
        t.setpos(self.v3)
        t.setpos(self.v1)
        t.end_fill()
        t.pendown()

    def turtle_draw_line2(self):
        global t
        if turtle_stop == True:
            return
##        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
##        t.color(color1)
        t.color('blue')
        t.penup()
        t.setpos(self.v1)
        t.pendown()
        t.setpos(self.v2)
        t.setpos(self.v3)
        t.setpos(self.v1)
        t.pendown()

    def turtle_draw_line(self):
        global t
        if turtle_stop == True:
            return
##        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
##        t.color(color1)
        if self.type == 1:
            t.color('blue')
            t.penup()
            t.setpos(self.v1)
            t.pendown()
            t.setpos(self.v2)
            t.setpos(self.v3)
            t.pendown()
        elif self.type == 0:
##            t.color('red')
##            t.penup()
##            t.setpos(self.v1)
##            t.pendown()
##            t.setpos(self.v2)
##            t.setpos(self.v3)
##            t.setpos(self.v1)
##            t.pendown()
            t.color('red')
            t.penup()
            t.setpos(self.v1)
            t.pendown()
            t.setpos(self.v2)
            t.setpos(self.v3)
            t.pendown()
        
    def split(self, ind):
        if self.type == 0: ## 狭い(type=0)の二等辺三角形
            m = 0.5*(self.v3-self.v2)+self.v2
            x = np.sqrt((self.v2[0]-self.v1[0])**2+(self.v2[1]-self.v1[1])**2)
            y = np.sqrt((m[0]-self.v1[0])**2+(m[1]-self.v1[1])**2)
            alpha = 2*np.arccos(y/x)
##            print(alpha*180/np.pi)
            r = 1 / (2*np.cos(alpha))
            w = r*(self.v3-self.v1)+self.v1
            tr_list = []
            tr_list.append(Triangle(w, self.v1, self.v2, 1)) ## Ts 1 RU
            tr_list.append(Triangle(self.v2, self.v3, w, 0)) ## Ts 0 RD
            w = r*(self.v2-self.v1)+self.v1
            tr_list.append(Triangle(w, self.v1, self.v3, 1)) ## Ts' 1 LU
            tr_list.append(Triangle(self.v3, self.v2, w, 0)) ## Ts' 0 LD
            beta = (np.pi-alpha)/2
##            print('beta=', beta*180/np.pi)
            z = np.sqrt((self.v2[0]-self.v3[0])**2+(self.v2[1]-self.v3[1])**2)
            r = z / x
            w = r*(self.v1-self.v2)+self.v2
            r2 = 2*z*np.cos(beta)/x
            u = r2*(self.v1-self.v3)+self.v3
            tr_list.append(Triangle(self.v2, self.v3, u, 0)) ## TL 0 RD
            tr_list.append(Triangle(self.v2, u, w, 0))       ## TL 0 LM
            tr_list.append(Triangle(w, u, self.v1, 1))       ## TL 1 LU
            w = r*(self.v1-self.v3)+self.v3
            u = r2*(self.v1-self.v2)+self.v2
            tr_list.append(Triangle(self.v3, u, self.v2, 0)) ## TL' 0 LD
            tr_list.append(Triangle(self.v3, w, u, 0))       ## TL' 0 RM
            tr_list.append(Triangle(u, w, self.v1, 1))       ## TL' 1 RU
            return tr_list
        elif self.type == 1: ## 広い(type=1)の二等辺三角形
            x = np.sqrt((self.v2[0]-self.v1[0])**2+(self.v2[1]-self.v1[1])**2)
            y = np.sqrt((self.v2[0]-self.v3[0])**2+(self.v2[1]-self.v3[1])**2)
            r = (y-x)/y
            w = r*(self.v3-self.v2)+self.v2
            tr_list = []
            tr_list.append(Triangle(self.v3, self.v1, w, 0)) ## Fs 0 R
            tr_list.append(Triangle(w, self.v1, self.v2, 1)) ## Fs 1 L
            w = r*(self.v2-self.v3)+self.v3
            tr_list.append(Triangle(self.v2, w, self.v1, 0)) ## Fs' 0 L
            tr_list.append(Triangle(w, self.v3, self.v1, 1)) ## Fs' 1 R
            z = y-x
            r = z/y
            w = r*(self.v3-self.v2)+self.v2
            tr_list.append(Triangle(w, self.v1, self.v2, 1)) ## FL 1 L
            r2 = z/x
            u = r2*(self.v1-self.v3)+self.v3
            tr_list.append(Triangle(w, u, self.v1, 0))       ## FL 0 M
            tr_list.append(Triangle(u, w, self.v3, 1))       ## FL 1 R
            w = r*(self.v2-self.v3)+self.v3
            tr_list.append(Triangle(w, self.v3, self.v1, 1)) ## FL' 1 R
            u = r2*(self.v1-self.v2)+self.v2
            tr_list.append(Triangle(w, self.v1, u, 0))       ## FL' 0 M
            tr_list.append(Triangle(u, self.v2, w, 1))       ## FL' 1 L
            return tr_list
        
    def Ts(self, ind): ## 狭い(type=0)の二等辺三角形
        if ind == 0:
            triangle_list = self.split(ind)
            return triangle_list[0: 2]
        elif ind == 1:
            triangle_list = self.split(ind)
            return triangle_list[2: 4]
    def Tl(self, ind): ## 狭い(type=0)の二等辺三角形
        if ind == 0:
            triangle_list = self.split(ind)
            return triangle_list[4: 7]
        elif ind == 1:
            triangle_list = self.split(ind)
            return triangle_list[7: ]
        elif ind == 2:
            triangle_list = self.split(ind)
            tri_list = triangle_list[4:7]
            triangle = tri_list[1]
            v2 = triangle.v2
            v3 = triangle.v3
            tri_list[1].v2 = v3
            tri_list[1].v3 = v2
            return tri_list
    def Fs(self, ind): ## 広い(type=1)の二等辺三角形
        if ind == 0:
            triangle_list = self.split(ind)
            return triangle_list[0: 2]
        elif ind == 1:
            triangle_list = self.split(ind)
            return triangle_list[2: 4]
        elif ind == 2:
            triangle_list = self.split(ind)
            tri_list = triangle_list[0:2]
            triangle = tri_list[0]
            v2 = triangle.v2
            v3 = triangle.v3
            tri_list[0].v2 = v3
            tri_list[0].v3 = v2
            return tri_list
            
            
class Pentagon:
    
    def __init__(self, v1, v2, v3, v4, v5, type):
        self.v1 = v1
        self.v2 = v2
        self.v3 = v3
        self.v4 = v4
        self.v5 = v5
        self.type = type
    def print(self):
        print('v1', self.v1, 'v2', self.v2, 'v3', self.v3, \
               'v4', self.v4, 'v5', self.v5, 'type=', self.type)
    def draw(self):
        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
        canvas.create_polygon(self.v1[0], self.v1[1], \
                              self.v2[0], self.v2[1], \
                              self.v3[0], self.v3[1], \
                              self.v4[0], self.v4[1], \
                              self.v5[0], self.v5[1], \
                              fill = color1, width = 3)
    def draw_line(self):
        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
        canvas.create_polygon(self.v1[0], self.v1[1], \
                              self.v2[0], self.v2[1], \
                              self.v3[0], self.v3[1], \
                              self.v4[0], self.v4[1], \
                              self.v5[0], self.v5[1], \
                              fill = '', outline = color1, width = 3)
    def turtle_draw(self):
        global t
        if turtle_stop == True:
            return
        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
        t.color(color1)
        t.begin_fill()
        t.penup()
        t.setpos(self.v1)
        t.pendown()
        t.setpos(self.v2)
        t.setpos(self.v3)
        t.setpos(self.v4)
        t.setpos(self.v5)
        t.setpos(self.v1)
        t.end_fill()
        t.pendown()

    def turtle_draw_line(self):
        global t
        if turtle_stop == True:
            return
        color1 = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])]                  
        t.color(color1)
        t.penup()
        t.setpos(self.v1)
        t.pendown()
        t.setpos(self.v2)
        t.setpos(self.v3)
        t.setpos(self.v4)
        t.setpos(self.v5)
        t.setpos(self.v1)
        t.pendown()
        
    def split_3_triangles(self):
        tr = []
        tr.append(Triangle(self.v1, self.v3, self.v4, 0))
        tr.append(Triangle(self.v2, self.v3, self.v1, 1))
        tr.append(Triangle(self.v5, self.v1, self.v4, 1))
        return tr

def turtle_draw_coordinate_axis():
    t.pensize(1)
    t.penup()
    t.setpos(0, 0)
    t.pendown()
    t.color('red')
    t.setpos(W/2, 0)
    t.penup()
    t.setpos(0, 0)
    t.pendown()
    t.color('blue')
    t.setpos(-W/2, 0)
    t.penup()
    t.setpos(0, 0)
    t.pendown()
    t.color('yellow')
    t.setpos(0, H/2)
    t.penup()
    t.setpos(0, 0)
    t.pendown()
    t.color('green')
    t.setpos(0, -H/2)
    
def F(tr, level):
##    tr.turtle_draw_line()
    if tr.type == 0:
        triangle_list = tr.Tl(2)
        if level == 0:
            for triangle in triangle_list:
##                triangle.turtle_draw_line2()
                triangle.turtle_draw_line()
        else:
            for triangle in triangle_list:
                F(triangle, level-1)
    elif tr.type == 1:
        triangle_list = tr.Fs(2)
        if level == 0:
            for triangle in triangle_list:
##                triangle.turtle_draw_line2()
                triangle.turtle_draw_line()
        else:
            for triangle in triangle_list:
                F(triangle, level-1)
level = 3

def main():
    global t
    global turtle_stop
    turtle_stop = False
    turtle_draw_coordinate_axis()
    t.pensize(2)
    p = np.zeros(22).reshape(11, 2)
    for i in range(10):
        p[i] = np.array([np.cos(i*2*np.pi/10), np.sin(i*2*np.pi/10)])
    p[10] = np.array([0, 0])
    p = 240*p
    for i in range(10):
        if i % 2 == 0:
            F(Triangle(p[10], p[i], p[(i+1)%10], 0), level)
        else:
            F(Triangle(p[10], p[(i+1)%10], p[i], 0), level)
    
if __name__ == "__main__":
    lbl = tk.Label(text='Level')
    lbl.pack()
    txt = tk.Entry(width=20)
    txt.pack()
    # テキストボックスをクリア
    txt.delete(0, tk.END)
    # テキストボックスに文字「1234」を入力
    txt.insert(tk.END, str(level))

    def button_click():
        global level
        global turtle_stop
        turtle_stop = True
        # テキストボックスの文字を取得
        level = int(txt.get())
        print(level)
        canvas.create_rectangle(-W/2, -H/2, W/2, H/2, fill='cyan')
        root.after(1000, main)
    
    # button1ウィジェットを作成
    button1 = tk.Button(root ,text="描画", command=button_click)
    button1.pack() # button1ウィジェットを配置
    main()
    
root.mainloop()
}

です。 やっと、2か月ぐらいでこの本も読み終わりました。随分、勉強になりました。 しかし、この方法はプログラミングの勉強だから通用することで、Python の練習にはなりましたが、Processing の勉強にはなっていません。 プログラミング言語はどのプログラミング言語でも基本的にすべてのパソコンが理解してくれますが、外国語は任意の外国語をすべての人が理解する訳ではないので、 「類比」が利きません。外国語の勉強は厄介です。例えば、アルハンブラ宮殿で各国語のパンフレットがあり、日本語版は日本で印刷したもので、 記念にはならないので、スペイン語版が欲しかったですが、スペイン語が喋れないので、「違う！違う！日本人はこれだろう。」と言って渡された日本語版を貰うしかありませんでした。 尤も、現在は携帯できるそれ程高額でない通訳機があるので簡単な会話はスペイン語が喋れなくても機械が助けてくれるますが。 又、スペインで特急列車に乗っている時、窓から見える草みたいな植物が何だろうと思って、向いに座った人に英語で何かと聞くと変な奴がいると思ったのか、 別の席に移動しましたが、暫くして新たに座った人に今度は「?Que es esto? 」 と聞くと一言「Vine」と英語で答えてくれました。日本の様に棚を作って栽培しているのではなく、 そのまま地面に這わして栽培していました。 又、ソ連で、ツアーの人達が銅像を見て、何をした人だろうと話し合っていたので、周りに居た地元の人に「Кто　это？」と聞くと 一言大声で「поэт」と教えてくれました。 後は「Спасибо」と言えばいいです。英語だけでなく、その国の言葉を片言でも話せると情報を得ることが出来ることもあります。 似たような本に、岡本健太郎著「アートで魅せる数学の世界」と古堅真彦著「Designing Math.」がありますが、 前者は Excel で、しかも、プログラムのダウンロードなし、ですが、面白そうな図の詳しい解説があります。 後者は Javascript のプログラムのダウンロードはありますが今一つ良く分からない本です。 次は、興味があったが学ぶ時間がなかった 「OpenGL で3次元図形」の勉強か「偏微分方程式」の勉強をしてみたいです。

処で、日本の指導階級の人達は、お金で食料を外国から買いあさり、 外国の技術をパクればいい時代は終わったことを理解していないのでしょうか？ IT 人材が足りないと指導者層が騒ぎ出しましたが、 元になる数学を軽視し続けた報いではないでしょうか？。ある調査によると日本のIT技術者の賃金は世界で最低クラスで、 最も高い国の数分の１だそうです。 「ソースコードを書くことは単純作業」との大会社の上層部の発言から分かるように、 「ITは非正規の派遣に低賃金でやらせれば良い、IT 人材はいくらでも交換可能な消耗品だ。（パソナが懇意な政府関係者から受注し、下請けに仕事を割り振るだけで、 ７５％中抜きし、中小企業には２５％のお金しか渡していなかったことが氷山の一角としてバレてしまいましたが、 自分たち大企業の人間は旨い汁を吸い、実際の辛い仕事は下請けに分散して低賃金でやらせば良いとの考えを最近流行りの誤解を受けたならと言いながら述べていたように思います。 これは先進国の何処もがやっていることで、例えば、最近はフェアトレード（Fair Trade : 公平貿易）と言って、他人を搾取することを考え直す人達も増え、 コーヒーの生豆の購入時に、フェアトレードかどうか確かめる人達も増えてきています。）」 と文系の政治家・官僚を始めとする支配者階級が考えているなら、 IT 人材は小学校から情報教育を行っても増えないのではないでしょうか？優秀な若い人達は、日本の現状に絶望し、日本を捨てて外国へ逃げていくと思います。 「GAFAに就職できるのはとびっきり優秀な限られる人だけだ！」と言う人もいますが、日本より高給を払ってくれるのはGAFAだけではなく、 普通の若い日本人の給料が世界の最低クラスになって久しいです。かって、「高額所得者から税金を取ると彼らは外国に逃げていく！」とテレビで盛んに アナウンサーが自分を含む高額所得者に増税することに反対していましたが、増税しなくても、実際は、 外国で生活するのはお金持ちでないと結構大変だと思いますが、有名人たちが外国に出ていくだけでなく、 今は「外国語をそこそこ話せ、手に職がある若者たちが結構な数、外国に逃げ出している」みたいです。 勿論、数学を学ぶこと及びプログラミングが出来ることだけが、 お金を稼ぐ唯一の手段ではなく、それぞれ各人が自分の信じることで努力していますが。 昨日、「土佐の里」の通路で、自分で作ったふわふわの梟を並べて売っているご婦人が居て、可愛らしかったので一つ購入しました。 ドングリを拾ってきて、加工して 売っている老人もいました。女性用のアクセサリーの出店が主で、時々開かれていて、 お金になるかどうか分かりませんが、皆、思い思いに思いついた創作を楽しんでいます。

巴山竜来著「数学から創るジェネラティブアート - Processingで学ぶかたちのデザイン」は 子供たちに数学とプログラミングに興味を持ってもらいたい小中高校の数学の先生にとっては面白い本です。 私も美しい図が一杯でどうやってプログラミングしているだろうと久しぶりに夢中になって読んでいます。 若い頃、「外国の著名なトポロジーの専門家（名前は忘れました）は、他の人の発表を聞くと自分の持っているモデル・例で、 その新しく聞いた理論の検証を必ずするそうだよ。」とシンポジュウムに参加していた若い数学者達が噂しているのを聞いたことがあります。 どの分野でも勉強の仕方は同じです。自分が理解していることから、関連付けて知識を広げていきます。 何をするべきだと言うことが無くなったので、昔購入してそのままになっていた古く厚い本ですが、 Grunbaum and Shephard 著「Tilings and Patterns」もやっと Processing のプログラミングを参考に、 この本の大量のタイリングの図を描きながら読んで見ようと言う気になりました。 教育学部の教育は何をすべきだろうとずっと思っていました。教育学部には色々な教員がいて、例えば、自分は方言の専門家だからと言って自分の専門の方言の教育を する人もいますし、そのような先生ばかりみたいですし、その方が研究と教育が一致し、自分の売りである専門分野を深めることに専念でき、 教員にとっては楽だと思います。 しかし、高知大学のような小さい大学の教育学部には沢山の教員がいるわけではなく、教育学部全体の数学の講義数も極めて少数で、 私の専門がホモトピー論だからと言って、ホモトピー論の講義をするのはどうだろうかと思いました。様々試行錯誤を繰り返した後、 私自身にとっては研究の為と教育の為の二重の勉強をしなくてはならず負担は大きくなりますが、小中高の先生になった時、役に立ちそうな数学的知識として、 例えば、壁紙群の英文の解説書を学会の数学書販売会場で見つけ、これは教育学部の数学の教育に良いのではないかと思い、壁紙群の教育を始め、 その本の図以外の図を自分で作れるように、、壁紙群の各種の図形を描くための ESCHER, ESCHER2 を作りました。 その後、Grunbaum and Shephard 著「Tilings and Patterns」を 見つけ、購入しましたが、膨大な情報量の本で、教育に差し当たって使えるとも思わなかったし、これを読み切るのは大変だと、本箱で埃を被ることになりました。 しかし、これでチャンスを逃してしまったみたいです。 しかし、巴山竜来著「数学から創るジェネラティブアート - Processingで学ぶかたちのデザイン」を読んで見るとコンピュータを使えば、 数学と言うものの考え方・物事を改良・発展させる方法を平易に示せる教材だと教えてもらうことが出来ました。ここが我々凡人と優秀な人との違いです。 巴山竜来著「数学から創るジェネラティブアート - Processingで学ぶかたちのデザイン」の processing のプログラムを Python のプログラムに 片っ端から翻訳してみることにより、そのアルゴリズムを理解することが出来、 Grunbaum and Shephard 著「Tilings and Patterns」を読み始めるためのハードルを超えることが出来ました。 世界史の啓蒙書を読んで見ると世界史だけ学んでも駄目で、その地域の地理も同時に学ばなければ真の理解は出来ないし、地理を正確に 理解するためには、地学や語学や宗教・人種や科学。産業の知識もなければ真の理解が出来ないことを https://www.youtube.com/watch?v=tXm004R2MNo などの youtube で教えてもらいました。地球の緯度によって、雨が降ったり、乾燥したりする 帯があるということを大分前にテレビで見て知っていましたが、本当は高校で習っていたが、私に興味なかったので記憶に残らなかったかもしれませんが、 それが地理で昔習った気候帯と結びつきませんでした。 夏と冬では太陽の位置が違うので、季節によってこの降雨帯と乾燥帯が南北に移動し、複雑になり、更に、地球上にはマントルの衝突で大山脈や高原が出来ているので、 様々な気候帯があるそうです。 我々凡人は習わないと気づきません。この人は実に面白い講義をしてくれています。 更に、昔購入して読まずに本箱で埃を被っていた橋本陽介著「7ヶ国語をモノにした人の勉強法」を読んで見て、数学やプログラミングは 困難なく学ぶことが出来るのに、何で語学は時間とお金を費やしたつもりになっていたのに成果が出ない理由が分かった気がします。 私の学生時代と比べると様々な新たな知見が得られたのか、間違った勉強法を繰り返していた気がします。あらゆることが有機的に繋がっていることに 気が付いていませんでした。社交的な人は積極的に様々な優秀な人の話を聴き、或いは共同で研究することで道を開いて行きますが、 非社交的な私のような人間は工夫して必要な情報を得る方法を努力して探さなければなりません。やっとこの年になって何が本質的なことであるか 理解できるようになってきました。長生きも悪いものではありません。「知ることは楽しいこと、知らないことは悲しいこと」です。

Clayton Walnum 著「Win32 OpenGL プログラミング」を眺めていて、movetoex と言う命令が PyOpenGL にあるだろうかとインターネットで 検索していて https://docs.hektorprofe.net/opengl/03-programando-una-tortuga/ ： Programando una tortuga con OpenGL と言うページを見つけました。 スペイン語のページだけど今は AI が翻訳してくれます。誤訳も一杯ありますが、必要な情報は Python のプログラムとどの様な図がそれで描けるかであり、 スペイン語のままでも問題はありません。大学院の時、スペイン語の論文を読む必要があり少し齧りましたが役に立ちません。 LSystem と反復関数系（Iterated function system、IFS）のプログラミングの例が示されていました。 これは良いものを見つけたと書かれているプログラムをコピーペーストして実行すると 


pygame 2.1.2 (SDL 2.0.18, Python 3.9.7)
Hello from the pygame community. https://www.pygame.org/contribute.html
Traceback (most recent call last):
  File "C:\PythonSrc\OpenGL\TurtleGraphics\ex1.py", line 6, in 
    from res.App import App
  File "C:\Anaconda3\Scripts\res.py", line 70
    	except SyntaxError, e:
    	                  ^
SyntaxError: invalid syntax

のようなエラーメッセージがでます。私のパソコンでは実行できないみたいです。 Linux で出来ても Windows10 では出来ないことが色々あるみたいです。すべてのプログラムを実行できるように書き直します。 具体的には、表示されるエラーメッセージを読んで、出なくなるように、ローカル変数で宣言されているのをグローバル変数に変えてみるなど エラーメッセージに応じて一つ一つ潰していけば良いです。 例えば 


Python Program{
import time
import tkinter
from OpenGL import GL
from OpenGL.GL import *
from OpenGL.GLU import *
from pyopengltk import OpenGLFrame
import numpy as np
from copy import copy

##https://docs.hektorprofe.net/opengl/03-programando-una-tortuga/
##
##リンデンマイヤーシステムは、
##植物の成長過程とさまざまな生物の形態をモデル化するために使用される
##正式な文法(規則と記号のセット)です。
##それらは1968年にハンガリーの理論生物学者で植物学者の
##アリスティッドリンデンマイヤーによって導入され開発されました。
##
##L系の規則の再帰的性質は自己相似性をもたらし、
##したがってフラクタルのような形式の記述を容易にする。
##自然に見える植物モデルと有機的な形状は簡単に定義できます
##:再帰のレベルが上がるにつれて、形状はゆっくりと成長し、より複雑になります。
##リンデンマイヤーシステムは、人工生命生成でも人気があります。

##導入はさておき、カメがさまざまな数字を描くために従う一連のルールと指示を
##定義する独自のLシステムを開発します
##(詳細な説明については、ウィキペディアをご覧ください)。
##
##私たちのシステムには、初期状態を表す文字列を持つ公理変数と、
##公理値を置き換える方法を説明する一連のルールがあります。
##
##たとえば、公理と規則が与えられた場合、
##たとえば「F」が前方に移動するか、「+」が特定の角度を回転します。
##数回の反復で、Lシステムは複雑な命令キットを含む最終チェーンを
##再帰的に生成します。
##"F""F=F[+F]F"
##
##1: F
##2: F[+F]F
##3: F[+F]F[+F[+F]F]F[+F]F
##4: F[+F]F[+F[+F]F]F[+F]F[+F[+F]F[+F[+F]F]F[+F]F]F[+F]F[+F[+F]F]F[+F]F

##ここでの目標は、結果のチェーンを解析して、
##カメが各文字を解釈する方法を認識できるようにすることです。
##
##F:一定量前進します。
##[: 現在の位置と回転をスタックに格納します。
##+:方向を時計回りに一定回転させます。
##-:方向を反時計回りに一定回転させます。
##]: スタックの最後の位置と回転を取得します。
##
##カメにメソッドを追加し、そこから生成されたチェーンの各命令を処理できます。

class LSystem:

    def __init__(self, axiom, rules):
        self.axiom = axiom
        self.rules = rules

    def Generate(self, times):
        print(f"===== Generando sistema-L en {times} ciclos =====")
        # El valor inicial de las instrucciones es el axioma base
        instructions = self.axiom
        # Aplicamos las reglas de forma recursiva N repeticiones
        for i in range(times):
            # Copiamos las instrucciones actuales
            previous_instructions = instructions
            # Reiniciamos las instrucciones actuales para reprocesarlas
            instructions = ""
            # Para cada caracter en las instrucciones guardadas
            for instruction_char in previous_instructions:
                # Si se encuentra definido en las reglas
                if instruction_char in self.rules:
                    # Sumamos la porcion substituida de las regglas
                    instructions += self.rules[instruction_char]
                else:
                    # Sino simplemente sumamos el caracter
                    instructions += instruction_char
        # Debugeamos la regla generada en esa iteracion
        print("Resultado: ", instructions)
        return instructions
    
class Vector3:
    def __init__(self, x=0, y=0, z=0):
        self.x = x
        self.y = y
        self.z = z
    def RotateZ(self, angle):
        angle = np.radians(angle)  # angulo a radianos
        rotatedX = self.x * np.cos(angle) - self.y * np.sin(angle)
        rotatedY = self.x * np.sin(angle) + self.y * np.cos(angle)
        self.x = rotatedX
        self.y = rotatedY
        
class Point():
    def __init__(self, x, y):
        self.x = x
        self.y = y
    
class Turtle:
    stack = []

    pos = Point(0, 0)
    dir = Vector3(0, 1, 0)
    def Reset(self):
        self.pos = Point(0, 0)
        self.dir = Vector3(0, 1, 0)
        ##    def LineTo(cls, x, y):
    def LineTo(self, x, y):
        glLineWidth(2)
        glBegin(GL_LINE_STRIP)
        glVertex2f(self.pos.x, self.pos.y)
        glVertex2f(x, y)
        glEnd()
        self.pos.x = x
        self.pos.y = y
    def Forward(self, distance):
        dest = Point(0, 0)
        dest.x = self.pos.x + self.dir.x * distance
        dest.y = self.pos.y + self.dir.y * distance
        self.LineTo(dest.x, dest.y)
        self.pos.x = dest.x
        self.pos.y = dest.y
    def Rotate(self, angle):
        self.dir.RotateZ(-angle)
    def MoveTo(self, x, y):
        self.pos.x = x
        self.pos.y = y
    def ExecuteLSystem(self, system, distance, angle):
        for instruction in system:
            if instruction == 'F':
                self.Forward(distance)
            elif instruction == '[':
                self.stack.append((copy(self.pos), copy(self.dir)))
            elif instruction == '+':
                self.Rotate(angle)
            elif instruction == '-':
                self.Rotate(-angle)
            elif instruction == ']':
                self.pos, self.dir = self.stack.pop()
    
t = Turtle()

class AppOgl(OpenGLFrame):
    global t

    def initgl(self):
        """Initalize gl states when the frame is created"""
        GL.glViewport(0, 0, self.width, self.height)
        GL.glClearColor(0.0, 0.0, 0.0, 0.0)    
        self.start = time.time()
        self.nframes = 0
##        self.system = LSystem(
##            "F", {
##                "F": "F[+F]F"
##            }).Generate(5)
        
##        self.system = LSystem(
##            "F", {
##            "F": "F[+F][-F]F"
##            }).Generate(5)

##        self.system = LSystem(
##            "F", {
##            "F": "FF[+F][--FF][-F+F]"
##        }).Generate(4)

        self.system = LSystem(
            "X", {
            "F": "FF",
            "X": "F+[-F-XF-X][+FF][--XF[+X]][++F-X]"
            }).Generate(4)

    def Setup(self):
        GL.glLoadIdentity() ## 投影変換の変換行列を単位行列で初期化
        glOrtho(-300, 300, 0, 600, -1.0, 1.0)

    def redraw(self):
        global t
        """Render a single frame"""
##        GL.glClear(GL.GL_COLOR_BUFFER_BIT)
##        tm = time.time() - self.start
        self.nframes += 1
##        print("fps",self.nframes / tm, end="\r" )
        glClear(GL_COLOR_BUFFER_BIT)
        glColor3f(1.0, 1.0, 1.0)
##        glOrtho(0.0, 1.0, 0.0, 1.0, -1.0, 1.0)
        
        glOrtho(-300.0, 300.0, -300.0, 300.0, -1.0, 1.0)
        
##        t.Reset()
##        t.LineTo(250, 100)
##        t.LineTo(200, 0)
        t.Reset()
##        t.LineTo(100, 100)
##        t.LineTo(100, 200)
##        t.LineTo(200, 100)
##        t.LineTo(100, 100)
        
##        t.Forward(100)
##        t.LineTo(200, 100)
##        t.Forward(100)
##        t.Rotate(90)
##        t.Forward(200)
        
##        t.Forward(100)
##        t.Rotate(90)
##        t.Forward(200)
##        t.MoveTo(-50, -100)
##        t.Rotate(180)
##        t.Forward(100)
##        t.Rotate(45)
##        t.Forward(100)
##        t.Rotate(45)
##        t.Forward(100)

##        t.MoveTo(-150, -50)
##        for i in range(10):
##            t.Forward(100)
##            t.Rotate(360/10)

##        t.MoveTo(0, -150)
##        for i in range(20):
##            t.Forward(300)
##            t.Rotate(170)

##        t.ExecuteLSystem(self.system, 10, 90)

##        GL.glViewport(0, 0, self.width, self.height)
##        GL.glMatrixMode(GL_PROJECTION) ## 投影変換モードへ
##        GL.glLoadIdentity() ## 投影変換の変換行列を単位行列で初期化
##        glOrtho(-300, 300, 0, 600, -1.0, 1.0)
##	glOrtho(-1.0, 1.0, -1.0, 1.0, 1.0, -1.0) ## 各軸-1.0～1.0で囲まれる立方体の範囲を平行投影
        self.Setup()
        t.Reset()
##        t.ExecuteLSystem(self.system, 10, 90) ## for 1, 2
        t.ExecuteLSystem(self.system, 10, 25) ## for 3

if __name__ == '__main__':
##    LSystem("F", {"F": "F[+F]F"}).Generate(3)
##    F[+F]F[+F[+F]F]F[+F]F[+F[+F]F[+F[+F]F]F[+F]F]F[+F]F[+F[+F]F]F[+F]F
##ここでの目標は、結果のチェーンを解析して、カメが各文字を解釈する方法を
##認識できるようにすることです。
##
##F:一定量前進します。
##[: 現在の位置と回転をスタックに格納します。
##+:方向を時計回りに一定回転させます。
##-:方向を反時計回りに一定回転させます。
##]: スタックの最後の位置と回転を取得します。

    root = tkinter.Tk()
    app = AppOgl(root, width=600, height=600)
    app.pack(fill=tkinter.BOTH, expand=tkinter.YES)
##    app.animate = 1
    app.animate = 0
##    app.after(100, app.printContext)
    app.mainloop()
}

のように修正すれば、


を描きます。 


Python Program{
import time
import tkinter
from OpenGL import GL
from OpenGL.GL import *
from OpenGL.GLU import *
from pyopengltk import OpenGLFrame
import numpy as np
from copy import copy

class Point:
    def __init__(self, x=0, y=0):
        self.x = x
        self.y = y

    def __str__(self):
        return f"({self.x}, {self.y})"

points = []

class AppOgl(OpenGLFrame):
    
    def initgl(self):
        """Initalize gl states when the frame is created"""
        GL.glViewport(0, 0, self.width, self.height)
        GL.glClearColor(0.0, 0.0, 0.0, 0.0)    
        self.start = time.time()
        self.nframes = 0
        self.point = Point()

##    def Init(self):
##        global points
##        points = []
##        # Generamos 100 puntos de prueba
##        for _ in range(100):
##            points.append(
##                Point(np.random.randint(-300, 300),
##                      np.random.randint(0, 400)))

    def Setup(self):
        GL.glLoadIdentity() ## 投影変換の変換行列を単位行列で初期化
        glOrtho(-300, 300, 0, 400)

##    def Update(self): ## tree
##        global points
##        # Generamos un numero para modificar el punto usando condiciones
##        r = np.random.rand()
##        if r < 0.1:
##            self.point.x = 0.00 * self.point.x + 0.00 * self.point.y + 0.00
##            self.point.y = 0.00 * self.point.x + 0.16 * self.point.y + 0.00
##        elif r < 0.86:
##            self.point.x = 0.85 * self.point.x + 0.04 * self.point.y + 0.00
##            self.point.y = -0.04 * self.point.x + 0.85 * self.point.y + 1.60
##        elif r < 0.93:
##            self.point.x = 0.20 * self.point.x - 0.26 * self.point.y + 0.00
##            self.point.y = 0.23 * self.point.x + 0.22 * self.point.y + 1.60
##        else:
##            self.point.x = -0.15 * self.point.x + 0.28 * self.point.y + 0.00
##            self.point.y = 0.26 * self.point.x + 0.24 * self.point.y + 0.44
##
##        # Anadimos el nuevo punto a la lista
##        points.append(Point(self.point.x, self.point.y))


##私たちが構築できるもう一つの非常に有名なフラクタルは
##シェルピンスキの三角形です、
##私たちはただこのように条件を変更する必要があります:

    def Update(self):
        global points
        # Generamos un numero para modificar el punto usando condiciones
        r = np.random.rand()
        if r < 0.33:
            self.point.x = 0.5 * self.point.x + 0.00 * self.point.y + 0.0
            self.point.y = 0.0 *self.point.x  + 0.50 * self.point.y + 0.5
        elif r < 0.66:
            self.point.x = 0.5 * self.point.x + 0.0 * self.point.y + 0.5
            self.point.y = 0.0 * self.point.x + 0.5 * self.point.y + 0.0
        else:
            self.point.x = 0.5 * self.point.x + 0.0 * self.point.y + 0.0
            self.point.y = 0.0 * self.point.x + 0.5 * self.point.y + 0.0

        # Anadimos el nuevo punto a la lista
        points.append(Point(self.point.x, self.point.y))
    


       
    def redraw(self):
        global points
        glMatrixMode(GL_PROJECTION)
        glLoadIdentity()
        gluOrtho2D(-300.0, 300.0, 400, 0)
##        GLUtils.DrawPoints(self.points, 5)
##        self.Init()
##        glPointSize(5)
##        glBegin(GL_POINTS)
##        for point in points:
##            glVertex2f(point.x, point.y)
##        glEnd()

##        glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
##        glMatrixMode(GL_MODELVIEW)
##        glLoadIdentity()
##        glScaled(80, 40, 1) # <-----

        glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
        glMatrixMode(GL_MODELVIEW)
        glLoadIdentity()
        glTranslate(-300, 0, 0) # <----
        glScaled(600, 400, 1) # <----

        self.Update()
        glPointSize(5)
        glBegin(GL_POINTS)
        for point in points:
            glVertex2f(point.x, point.y)
        glEnd()
        self.nframes += 1

if __name__ == '__main__':
    root = tkinter.Tk()
    app = AppOgl(root, width=600, height=600)
    app.pack(fill=tkinter.BOTH, expand=tkinter.YES)
    app.animate = 1

    app.mainloop()
}

のように修正すれば、


を描きます。こちらはアニメーションです。 知らないことばかりです。偶然、知りたいことを解説しているホームページに出会えました。 ウイキペディアで調べると面白い図が一杯載っています。どうやってプログラミングしているのだろう？ 調べてやってみたいことが増えました。優秀な数学者が目指している高度な数学ではなく、誰でも理解できる数学の範囲でも面白いことが一杯あります。 この人はまずロボット言語を作っていたので、昔作った、3次元 LOGO のようなものをまず作ってみようかな？ 語学の勉強で失敗ばかりしているように、目的もなく、入門書ばかり読んでも時間の無駄です。

3次元の LSystem の画像を作れるように、上のプログラムを修正した。 


Python Program{
import time
import tkinter
from OpenGL import GL
from OpenGL.GL import *
from OpenGL.GLU import *
from pyopengltk import OpenGLFrame
import numpy as np
from copy import copy

class LSystem:

    def __init__(self, axiom, rules):
        self.axiom = axiom
        self.rules = rules

    def Generate(self, times):
        print(f"===== Generando sistema-L en {times} ciclos =====")
        # El valor inicial de las instrucciones es el axioma base
        instructions = self.axiom
        # Aplicamos las reglas de forma recursiva N repeticiones
        for i in range(times):
            print("Resultado: i= ", i, instructions)
            # Copiamos las instrucciones actuales
            previous_instructions = instructions
            # Reiniciamos las instrucciones actuales para reprocesarlas
            instructions = ""
            # Para cada caracter en las instrucciones guardadas
            for instruction_char in previous_instructions:
                # Si se encuentra definido en las reglas
                if instruction_char in self.rules:
                    # Sumamos la porcion substituida de las regglas
                    instructions += self.rules[instruction_char]
                else:
                    # Sino simplemente sumamos el caracter
                    instructions += instruction_char
        # Debugeamos la regla generada en esa iteracion
##        print("Resultado: ", instructions)
        return instructions

class Vector3:
    def __init__(self, x=0.0, y=0.0, z=0.0):
        self.x = x
        self.y = y
        self.z = z
    def Rotate(self, angle, n):
        r = Point()
        cp = np.zeros(3)
        angle = angle*np.pi/180
        ip = n.x*self.x+n.y*self.y+n.z*self.z
        cp[0] = n.y*self.z-n.z*self.y
        cp[1] = n.z*self.x-n.x*self.z
        cp[2] = n.x*self.y-n.y*self.x
##        print('cp=', cp)
##        print('self: ', self.x, self.y, self.z)
##        print('n: ', n.x, n.y, n.z)
        r.x = n.x*ip+cp[0]*np.sin(angle)+(cp[1]*n.z-cp[2]*n.y)*np.cos(angle)
        r.y = n.y*ip+cp[1]*np.sin(angle)+(cp[2]*n.x-cp[0]*n.z)*np.cos(angle)
        r.z = n.z*ip+cp[2]*np.sin(angle)+(cp[0]*n.y-cp[1]*n.x)*np.cos(angle)
        norm = np.sqrt(r.x*r.x+r.y*r.y+r.z*r.z)
##        print('norm=', norm, 'r: ', r.x, r.y, r.z)
        self.x = r.x/norm
        self.y = r.y/norm
        self.z = r.z/norm
        
        
class Point():
    def __init__(self, x=0, y=0, z=0):
        self.x = x
        self.y = y
        self.z = z
    
class Turtle:
    stack = []

    def __init__(self, x=0, y=0, z=0):
        self.pos = Point(x, y, z)
        self.e1 = Vector3(1, 0, 0)
        self.e2 = Vector3(0, 1, 0)
        self.e3 = Vector3(0, 0, 1)

    def print(self):
        print('pos=', self.pos.x, self.pos.y, self.pos.z)
        print('e1=', self.e1.x, self.e1.y, self.e1.z)
        print('e2=', self.e2.x, self.e2.y, self.e2.z)
        print('e3=', self.e3.x, self.e3.y, self.e3.z)
        
    def Reset(self):
        self.pos = Point(0, 0, 0)
        self.e1 = Vector3(1, 0, 0)
        self.e2 = Vector3(0, 1, 0)
        self.e3 = Vector3(0, 0, 1)
        ##    def LineTo(cls, x, y):
        
    def LineTo(self, x, y, z):
        glLineWidth(2)
        glBegin(GL_LINE_STRIP)
        glVertex3f(self.pos.x, self.pos.y, self.pos.z)
        glVertex3f(x, y, z)
        glEnd()
        self.pos.x = x
        self.pos.y = y
        self.pos.z = z
        
    def fd(self, distance):
        dest = Point(0, 0, 0)
        dest.x = self.pos.x + self.e1.x * distance
        dest.y = self.pos.y + self.e1.y * distance
        dest.z = self.pos.z + self.e1.z * distance
        self.LineTo(dest.x, dest.y, dest.z)
        self.pos.x = dest.x
        self.pos.y = dest.y
        self.pos.z = dest.z
    def bk(self, distance):
        self.fd(-distance)       
        
    def yaw(self, angle):
        self.e1.Rotate(angle, self.e3)
        self.e2.Rotate(angle, self.e3)
    def lt(self, angle):
        self.yaw(angle)
    def rt(self, angle):
        self.yaw(-angle)
        
    def pitch(self, angle):
        self.e1.Rotate(angle, self.e2)
        self.e3.Rotate(angle, self.e2)
    def up(self, angle):
        self.pitch(angle)
    def down(self, angle):
        self.pitch(-angle)
        
    def roll(self, angle):
        self.e2.Rotate(angle, self.e1)
        self.e3.Rotate(angle, self.e1)
        
    def ExecuteLSystem(self, system, distance, angle):
        for instruction in system:
            if instruction == 'F':
                self.fd(distance)
            elif instruction == '[':
                self.stack.append((copy(self.pos), \
                copy(self.e1), copy(self.e2), copy(self.e3)))
            elif instruction == '+':
                self.lt(angle)
            elif instruction == '-':
                self.rt(angle)
            elif instruction == ']':
                self.pos, self.e1, self.e2, self.e3 = self.stack.pop()

    def ExecuteLSystem3D(self, system, distance, angle, size_scale, angle_scale):
        self.pitch(60)
        self.yaw(30)
        for instruction in system:
            if instruction == 'F':
                self.fd(distance)
            elif instruction == '[':
                self.stack.append((copy(self.pos), \
                copy(self.e1), copy(self.e2), copy(self.e3), \
                                   distance, angle))
            elif instruction == '+':
                self.lt(angle)
            elif instruction == '-':
                self.rt(angle)
            elif instruction == ']':
                self.pos, self.e1, self.e2, self.e3, distance, angle = \
                          self.stack.pop()
            elif instruction == '&':
                self.up(angle)
            elif instruction == '^':
                self.down(angle)
            elif instruction == '_':
                self.roll(angle)
            elif instruction == '/':
                self.roll(-angle)
            elif instruction == 'N':
                distance *= size_scale
            elif instruction == 'K':
                angle *= angle_scale

def cube(length):
    global t
    for i in range(4):
        t.fd(length)
        t.lt(90)
    t.yaw(90)
    for i in range(4):
        t.fd(length)
        t.rt(90)
    t.pitch(90)
    t.fd(length)
    t.pitch(-90)
    for i in range(4):
        t.fd(length)
        t.rt(90)
    

    
t = Turtle()

class AppOgl(OpenGLFrame):##
    global t

    def initgl(self):
        """Initalize gl states when the frame is created"""
        GL.glViewport(0, 0, self.width, self.height)
        GL.glClearColor(0.0, 0.0, 0.0, 0.0)    
        self.start = time.time()
        self.nframes = 0

    
##        self.system = LSystem(
##            "F", {
##                "F": "F[+F]F"
##            }).Generate(5)
        
##        self.system = LSystem(
##            "F", {
##            "F": "F[+F][-F]F"
##            }).Generate(5)

##        self.system = LSystem(
##            "F", {
##            "F": "FF[+F][--FF][-F+F]"
##        }).Generate(4)

##        self.system = LSystem(
##            "X", {
##            "F": "FF",
##            "X": "F+[-F-XF-X][+FF][--XF[+X]][++F-X]"
##            }).Generate(4)

##    self.system = LSystem(
##        "A", {
##         "A": "AB",
##        "B": "A"
##        }).Generate(4)

##        self.system = LSystem( ## 3d
##            "F-F-F-F", {
##            "F": "F-F+F+FF-F-F+F"
##            }).Generate(3)

##        self.system = LSystem( ## 3d
##            "FFFA", {
##            "A": "N[&FFFA]////[&FFFA]////[&FFFA]"
##            }).Generate(6)

        self.system = LSystem( ## 3d hilbert curve
            "A", {
            "A": "^/AF^/AFA-F^__AFA&F+__AFA-F_A-_"
            }).Generate(3)

    def Setup(self):
        GL.glLoadIdentity() ## 投影変換の変換行列を単位行列で初期化
        glOrtho(-100, 500, -100, 500, -300.0, 300.0)


    def redraw(self):
        global t
        """Render a single frame"""
        self.nframes += 1
        glClear(GL_COLOR_BUFFER_BIT)
        glColor3f(1.0, 1.0, 1.0)
        glOrtho(-300.0, 300.0, -100.0, 500.0, -300.0, 300.0)
        
##        self.Setup()
##        t.Reset()
##
##        t.ExecuteLSystem(self.system, 10, 90) ## for 1, 2

##        GL.glViewport(0, 0, self.width, self.height)
##        GL.glMatrixMode(GL_PROJECTION) ## 投影変換モードへ
##        GL.glLoadIdentity() ## 投影変換の変換行列を単位行列で初期化
##        glOrtho(-300, 300, 0, 600, -1.0, 1.0)
##        self.Setup()
##        t.Reset()
##        t.ExecuteLSystem(self.system, 10, 90) ## for 1, 2
####        t.ExecuteLSystem(self.system, 10, 25) ## for 3

        self.Setup()
        t.Reset()
        t.ExecuteLSystem3D(self.system, 40, 90, 1, 1)

   
if __name__ == '__main__':
    root = tkinter.Tk()
    app = AppOgl(root, width=600, height=600)
    app.pack(fill=tkinter.BOTH, expand=tkinter.YES)
##    app.animate = 1
    app.animate = 0
##    app.after(100, app.printContext)
    app.mainloop()
}

で、インターネットで見つけた 3D Hilbert Curve と言う LSystem を実行すると


を描きます。文字の解釈は
F distance 進み、線を描画
+ angle だけ回転
- angle だけ逆回転
[ turtle の状態をスタックに保存
] turtle の状態をスタックから復元
& ピッチアップ
^ ピッチダウン
/ ロールアップ
_ ロールダウン
N distance に size_scale を掛ける
K angle に angle_scale を掛ける
としてあります。前進しても線を描かない解釈の文字も追加するべきかも。 このプログラムのように Rotate(self, angle, n) を多数回、連続して呼ぶと、誤差が大きくなり、上手く動かないので、 turtle の姿勢を表す3つのベクトルは、次のように意識的に正規化しておく必要があります。 


    def Rotate(self, angle, n):
        r = Point()
        cp = np.zeros(3)
        angle = angle*np.pi/180
        ip = n.x*self.x+n.y*self.y+n.z*self.z
        cp[0] = n.y*self.z-n.z*self.y
        cp[1] = n.z*self.x-n.x*self.z
        cp[2] = n.x*self.y-n.y*self.x
##        print('cp=', cp)
##        print('self: ', self.x, self.y, self.z)
##        print('n: ', n.x, n.y, n.z)
        r.x = n.x*ip+cp[0]*np.sin(angle)+(cp[1]*n.z-cp[2]*n.y)*np.cos(angle)
        r.y = n.y*ip+cp[1]*np.sin(angle)+(cp[2]*n.x-cp[0]*n.z)*np.cos(angle)
        r.z = n.z*ip+cp[2]*np.sin(angle)+(cp[0]*n.y-cp[1]*n.x)*np.cos(angle)
        norm = np.sqrt(r.x*r.x+r.y*r.y+r.z*r.z)
##        print('norm=', norm, 'r: ', r.x, r.y, r.z)
        self.x = r.x/norm
        self.y = r.y/norm
        self.z = r.z/norm

多分、絶対の自信は無いですが、バグは無いと思います。昔作った 3D LOGO のプログラム KITE で。yaw と roll の意味を取り違えていました。 キチンと調べてプログラミングすべきでした。今はインターネットがあるので簡単にチェックできます。Rotate() で使っている計算は 英語版のウイキペディアにも載っています。現在、日本語版のウイキペディアにある公式は間違っていると思います。 このような最も基本的な3次元空間の回転の行列・ベクトルの公式は暗記するのではなく、繰り返し練習して、何も見なくてもスラスラ導けるようになりたいものです。 勿論、「タイパ」から見ても、インターネットで調べれば良い、どうしても試験の為に必要なら、 定義からの導き方ではなく公式そのものを暗記しろと言う意見の人が殆どだと思いますが。 LSystem と目新しい名前を付けていますが、歴史的にはどちらが先か調べていませんが、その本質はロボット言語に依る再帰的プログラミングに過ぎません。 アルゴリズムを静的にプログラムの外部で記述するか。動的にプログラムの内部で記述するかの違いではないかと言う気がしますが、 その違いが本質的に大きいと言う見方も勿論出来ます。このように外部で記述できれば、 生物学者はプログラミングが出来なくても他人の作った汎用のプログラムを使って自分の研究に専念できるし、 LSystem で表現したんデータを解釈し綺麗に表示するプログラムは LSystem のルールは学ばなければなりませんが、 プログラミングの専門家が如何に美しい図を表示できるか腕を競って作れば良いです。分業が可能になります。実際、そのようなプログラムが作られ、講習会が開かれている見たいです。 これで LSystem は理解できたことにして、PyOpenGL の勉強を続けます。

私のパソコンのフォルダーを調べてみると20年以上前に OpenGL で作ったソフトがあることに気が付いた。


私も若かったので、このようなめんどくさいプログラムが作れた見たいです。 Borland C++ Bilder で作っているので、もう修正は出来ないが、すっかり忘れているので、今度はこれを元に Python で作り直してみよう。 一度出来たことなので、簡単に出来るはずである。 20数年前は丁度だと思ったけれど今動かしてみるとスピードを１にしても速すぎる見たいです。 私の作ったプログラムの中では珍しくクラスの継承を使ったかなり整然としたプログラムで幾つかのファイルに分けてプログラミングしていますが、 (この頃作ったこのプログラム Archimedes や壁紙群の Escher は C++ がやっと理解できた時期で、継承や多態性などの新しく学んだ機能を使う練習していたので、 Escher ではや多態性も使っているし、Knuth さんの MIX のプログラムを作った時より技術が向上し、それなりに綺麗なプログラムを作っているみたいです。) このプログラムは全部で9000行位で、思ったほど長くないです。最後に作った各種の鉛筆パズルのプログラムは2万行位あります。 囲碁のプログラムも作ろうとしていましたが、見当違いの方針で、馬鹿げたプログラムを作っていて、私には出来ないと諦めました。 他人に見せることを想定していないので、余りコメントを書いていないので読むのは自分が作ったプログラムであるとは言え、かなり大変です。

昔は、レイトレーシングなど反射による映り込みや影など精巧で美しい静止画を作るための書籍が多数出版されていましたが、最近は見ません。 プロには常識になったのか、VR やアバターが目下の関心事になり、そのような精巧な計算量が多いプログラミングに 対する関心が無くなったのか、分かりませんが、OpenGL のカラーの 3D graphics なども結構複雑で、そのような難しいことを思い出すのは大変ですから、 次は、正多面体から準正多面体を5種類の方法で作る様子を線画でのアニメーションで表示するプログラムの作成です。 Borland C++ Builder のソースコードが残っているので、比較的容易に出来るはずです。

最初に作ったプログラムは 

import tkinter as tk
from OpenGL.GL import *
from OpenGL.GLU import *
import numpy as np
from OpenGL import GL
from pyopengltk import OpenGLFrame

class F444:
    def __init__(self):
        self.v =[]
        self.e = []
        self.f = []
        self.n_vertex = 8
        self.n_edge = 12
        self.n_face = 6

    def set_inf(self):       
        ## 各辺を構成する頂点の番号
        t_edge = [[0,1], [1,2], [2,3], [3,0], [5,4], [6,5], \
                  [7,6], [4,7], [0,4], [1,5], [2,6], [3,7]]
        ## 各面を構成する頂点の番号：反時計回り
        t_face = [[0,1,2,3], [7,6,5,4], \
                  [4,5,1,0], [5,6,2,1], \
                  [3,2,6,7], [0,3,7,4]]
        self.v =[]
        for i in range(4):
            x = np.cos(i*np.pi/2)/2+np.sin(i*np.pi/2)/2
            y = np.sin(i*np.pi/2)/2-np.cos(i*np.pi/2)/2
            z = 0.5
            self.v.append([x,y,z])
        for i in range(4):
            x = np.cos(i*np.pi/2)/2+np.sin(i*np.pi/2)/2
            y = np.sin(i*np.pi/2)/2-np.cos(i*np.pi/2)/2
            z = -0.5
            self.v.append([x,y,z])
        self.e = t_edge
        self.f = t_face
    def print(self):       
        print('v=', self.v)
        print('e=', self.e)
        print('f=', self.f)
        
cube = F444()
cube.set_inf()
##cube.print()

class Sphere:
    def __init__(self, radius, n_longitude, n_latitude):
        self.radius = radius
        self.n_longitude = n_longitude ## 横の分割数
        self.n_latitude = n_latitude   ## 縦の分割数
    def draw(self):
        end = np.pi
        step_longitude = 2 * np.pi/ self.n_longitude
        step_latitude = np.pi / self.n_latitude
        r = self.radius
        for i in range(self.n_latitude):
            arad1 = i * step_latitude
            arad2 = (i+1) * step_latitude
            for k in range( self.n_longitude):
                brad1 = k * step_longitude
                brad2 = (k+1) * step_longitude               
                x1 = r*np.sin(arad1)*np.cos(brad1)
                y1 = r*np.sin(arad1)*np.sin(brad1)
                z1 = r*np.cos(arad1)                
                x2 = r*np.sin(arad2)*np.cos(brad1)
                y2 = r*np.sin(arad2)*np.sin(brad1)
                z2 = r*np.cos(arad2)
                x3 = r*np.sin(arad2)*np.cos(brad2)
                y3 = r*np.sin(arad2)*np.sin(brad2)
                z3 = r*np.cos(arad2)
                x4 = r*np.sin(arad1)*np.cos(brad2)
                y4 = r*np.sin(arad1)*np.sin(brad2)
                z4 = r*np.cos(arad1)
                glNormal3d(x1, y1, z1)
                glBegin(GL_POLYGON)
                glVertex3d(x1, y1, z1)
                glVertex3d(x2, y2, z2)
                glVertex3d(x3, y3, z3)
                glVertex3d(x4, y4, z4)                
                glEnd()
    def draw_wireframe(self):
        end = np.pi
        step_longitude = 2 * np.pi/ self.n_longitude
        step_latitude = np.pi / self.n_latitude
        r = self.radius
        for i in range(self.n_latitude):
            arad1 = i * step_latitude
            arad2 = (i+1) * step_latitude
            for k in range( self.n_longitude):
                brad1 = k * step_longitude
                brad2 = (k+1) * step_longitude               
                x1 = r*np.sin(arad1)*np.cos(brad1)
                y1 = r*np.sin(arad1)*np.sin(brad1)
                z1 = r*np.cos(arad1)                
                x2 = r*np.sin(arad2)*np.cos(brad1)
                y2 = r*np.sin(arad2)*np.sin(brad1)
                z2 = r*np.cos(arad2)
                x3 = r*np.sin(arad2)*np.cos(brad2)
                y3 = r*np.sin(arad2)*np.sin(brad2)
                z3 = r*np.cos(arad2)
                x4 = r*np.sin(arad1)*np.cos(brad2)
                y4 = r*np.sin(arad1)*np.sin(brad2)
                z4 = r*np.cos(arad1)
                glBegin(GL_LINES)
                glVertex3d(x1, y1, z1)
                glVertex3d(x2, y2, z2)
                glVertex3d(x2, y2, z2)
                glVertex3d(x3, y3, z3)
                glVertex3d(x3, y3, z3)
                glVertex3d(x4, y4, z4)                
                glVertex3d(x4, y4, z4)                
                glVertex3d(x1, y1, z1)
                glEnd()
sphere1 = Sphere(0.5, 10, 10)
sphere2 = Sphere(0.5, 10, 5)

rotate = 0

class AppOgl(OpenGLFrame):

    def initgl(self):
        global rotate, cube       
        glViewport(0, 0, self.width, self.height) ## 画面の描画領域       
        glClearColor(1.0, 1.0, 1.0, 1.0) ## 背景色
        self.n_model_list = [0]
        self.n_model = self.n_model_list[0]
        self.old_n_model = -1
        rotate = 0
        self.n_move_list = [0]
        self.n_move = self.n_move_list[0]
           
    def torad(self, deg):
        return deg*(math.pi/180.0)

    def redraw(self):
        global rotate
        self.n_model = self.n_model_list[0]
        glClear(GL_COLOR_BUFFER_BIT)
        
        if self.n_model == 0:
            rotate += 0.1
            if self.n_model != self.old_n_model:
                self.old_n_model = self.n_model
            glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
            glLoadIdentity() ## 投影行列を単位行列で初期化する
##            glOrtho(left, right, bottom, top, near, far) ## 平行投影
            glOrtho(-2.0, 2.0, -2.0, 2.0, -2.0, 2.0)
            glMatrixMode(GL_MODELVIEW)
            glLoadIdentity()
            glRotated(rotate, 1.0, 1.0, 0.0)
        elif self.n_model == 1:
            rotate += 0.1
            if self.n_model != self.old_n_model:
                self.old_n_model = self.n_model
            glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
            glLoadIdentity() ## 投影行列を単位行列で初期化する
##            glFrustum(left, right, bottom, top, near, far) ## 透視投影
            glFrustum(-1.0, 1.0, -1.0, 1.0, 2.0, 10.0) ## 透視投影
            gluLookAt( ## カメラを配置する
                0.0, 0.0, 5.0,
                0.0, 0.0, 0.0,
                0.0, 1.0, 0.0,
            )
            glMatrixMode(GL_MODELVIEW)
            glLoadIdentity()
            glRotated(rotate, 1.0, 1.0, 0.0)
        elif self.n_model == 2:       
            rotate += 0.1
            if self.n_model != self.old_n_model:
                self.old_n_model = self.n_model
            glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
            glLoadIdentity() ## 投影行列を単位行列で初期化する
##            gluPerspective(fovy, aspect, near,far) ## 透視投影
            gluPerspective(30, self.width/self.height, 0.1,100) ## 透視投影
            gluLookAt( ## カメラを配置する
                0.0, 0.0, 5.0,
                0.0, 0.0, 0.0,
                0.0, 1.0, 0.0,
            )
            glMatrixMode(GL_MODELVIEW)
            glLoadIdentity()
            glRotated(rotate, 1.0, 1.0, 0.0)
        elif self.n_model == 3: ## キーイベント      
            rotate = 0.0
            rotate += 0.0
            self.n_move = self.n_move_list[0]
            if self.n_model != self.old_n_model:
                self.old_n_model = self.n_model
                glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
                glLoadIdentity() ## 投影行列を単位行列で初期化する
##                gluPerspective(fovy, aspect, near,far) ## 透視投影
                gluPerspective(30, self.width/self.height, 0.1,100) ## 透視投影
                gluLookAt( ## カメラを配置する
                    0.0, 0.0, 10.0,
                    0.0, 0.0, 0.0,
                    0.0, 1.0, 0.0,
                )
                glMatrixMode(GL_MODELVIEW)
                glLoadIdentity()
                glRotated(rotate, 1.0, 1.0, 0.0)
            if self.n_move != 0:
                self.n_move_list = [0]
                if self.n_move == 37: ## key_left
                    glTranslated(-0.5, 0.0, 0.0)
                elif self.n_move == 38: ## key_up
                    glTranslated(0.0, 0.5, 0.0)
                elif self.n_move == 39: ## key_right
                    glTranslated(0.5, 0.0, 0.0)
                elif self.n_move == 40: ## key_down
                    glTranslated(0.0, -0.5, 0.0)
            if self.n_move != 0:
                self.n_move_list = [0]
                if self.n_move == 37: ## key_left
                    glTranslated(-0.5, 0.0, 0.0)
                elif self.n_move == 38: ## key_up
                    glTranslated(0.0, 0.5, 0.0)
                elif self.n_move == 39: ## key_right
                    glTranslated(0.5, 0.0, 0.0)
                elif self.n_move == 40: ## key_down
                    glTranslated(0.0, -0.5, 0.0)
        elif self.n_model == 4:       
            rotate += 0.1
            if self.n_model != self.old_n_model:
                self.old_n_model = self.n_model
            glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
            glLoadIdentity() ## 投影行列を単位行列で初期化する
##            gluPerspective(fovy, aspect, near,far) ## 透視投影
            gluPerspective(30, self.width/self.height, 0.1,100) ## 透視投影
            gluLookAt( ## カメラを配置する
                0.0, 0.0, 5.0,
                0.0, 0.0, 0.0,
                0.0, 1.0, 0.0,
            )
            glMatrixMode(GL_MODELVIEW)
            glLoadIdentity()
            m = [1,0,0,0, 1,1,0,0, 0,0,1,0, 0,0,0,1]
            glLoadMatrixd(m)
            m2 = [-1,0,0,0, 0,1,0,0, 0,0,1,0, 0,0,0,1]
            glMultMatrixd(m2)
            glScaled(0.5, 0.5, 0.5)
            glRotated(rotate, 1.0, 1.0, 0.0)
        elif self.n_model == 5:       
            rotate += 0.1
            if self.n_model != self.old_n_model:
                self.old_n_model = self.n_model
            glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
            glLoadIdentity() ## 投影行列を単位行列で初期化する
##            gluPerspective(fovy, aspect, near,far) ## 透視投影
            gluPerspective(30, self.width/self.height, 0.1,100) ## 透視投影
            gluLookAt( ## カメラを配置する
                0.0, 0.0, 15.0,
                0.0, 0.0, 0.0,
                0.0, 1.0, 0.0,
            )
        elif self.n_model == 6:       
            rotate += 0.1
            if self.n_model != self.old_n_model:
                self.old_n_model = self.n_model
            glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
            glLoadIdentity() ## 投影行列を単位行列で初期化する
##            gluPerspective(fovy, aspect, near,far) ## 透視投影
            gluPerspective(30, self.width/self.height, 0.1,100) ## 透視投影
            gluLookAt( ## カメラを配置する
                0.0, 0.0, 15.0,
                0.0, 0.0, 0.0,
                0.0, 1.0, 0.0,
            )
        elif self.n_model == 7:       
            rotate += 0.1
            if self.n_model != self.old_n_model:
                self.old_n_model = self.n_model
            glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
            glLoadIdentity() ## 投影行列を単位行列で初期化する
##            gluPerspective(fovy, aspect, near,far) ## 透視投影
            gluPerspective(30, self.width/self.height, 0.1,100) ## 透視投影
            gluLookAt( ## カメラを配置する
                0.0, 0.0, 5.0,
                0.0, 0.0, 0.0,
                0.0, 1.0, 0.0,
            )
        elif self.n_model == 8:       
            rotate += 0.1
            if self.n_model != self.old_n_model:
                self.old_n_model = self.n_model
            glClear(GL_DEPTH_BUFFER_BIT)
            glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
            glLoadIdentity() ## 投影行列を単位行列で初期化する
##            gluPerspective(fovy, aspect, near,far) ## 透視投影
            gluPerspective(30, self.width/self.height, 0.1,100) ## 透視投影
            gluLookAt( ## カメラを配置する
                0.0, 0.0, 15.0,
                0.0, 0.0, 0.0,
                0.0, 1.0, 0.0,
            )
            glMatrixMode(GL_MODELVIEW)
            glLoadIdentity()
            glRotated(rotate, 0.0, 0.0, 1.0)
            glTranslate(3.0, 0.0, 0.0)
            glRotated(30, 1.0, 1.0, 0.0)
        elif self.n_model == 9:       
            rotate += 0.1
            if self.n_model != self.old_n_model:
                self.old_n_model = self.n_model
            glClear(GL_DEPTH_BUFFER_BIT)
            glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
            glLoadIdentity() ## 投影行列を単位行列で初期化する
##            gluPerspective(fovy, aspect, near,far) ## 透視投影
            gluPerspective(30, self.width/self.height, 0.1,100) ## 透視投影
            gluLookAt( ## カメラを配置する
                0.0, 0.0, 15.0,
                0.0, 0.0, 0.0,
                0.0, 1.0, 0.0,
            )
            glMatrixMode(GL_MODELVIEW)
            glLoadIdentity()
            glRotated(rotate, 0.0, 0.0, 1.0)
            glTranslate(3.0, 0.0, 0.0)
            glRotated(30, 1.0, 1.0, 0.0)
        if self.n_model < 5:
            for i in range(12):
                edge_list = cube.e[i]
                glColor(0.0, 0.0, 1.0, 1.0)
                glLineWidth(4.0) ## 線の幅
                glBegin(GL_LINES)
                s_vertex = cube.v[edge_list[0]]
                t_vertex = cube.v[edge_list[1]]
                glVertex3f(s_vertex[0], s_vertex[1], s_vertex[2])
                glVertex3f(t_vertex[0], t_vertex[1], t_vertex[2])
                glEnd()
        elif self.n_model == 5:
            glMatrixMode(GL_MODELVIEW)
            glLoadIdentity()
            glRotated(rotate, 1.0, 1.0, 0.0)
            for i in range(12):
                edge_list = cube.e[i]
                glColor(0.0, 0.0, 1.0, 1.0)
                glLineWidth(4.0) ## 線の幅
                glBegin(GL_LINES)
                s_vertex = cube.v[edge_list[0]]
                t_vertex = cube.v[edge_list[1]]
                glVertex3f(s_vertex[0], s_vertex[1], s_vertex[2])
                glVertex3f(t_vertex[0], t_vertex[1], t_vertex[2])
                glEnd()
            glPushMatrix()
            glTranslated(2.0, 0.0, 0.0)
            sphere1.draw()
            glPopMatrix()
            glTranslated(-3.0, 0.0, 0.0)
            glColor(1.0, 0.0, 0.0, 1.0)
            sphere2.draw_wireframe()
        elif self.n_model == 6:
            glMatrixMode(GL_PROJECTION)
            glLoadIdentity()
            m = [1,0,0,0, 1,1,0,0, 0,0,1,0, 0,0,0,1]
            glLoadMatrixd(m)
            m2 = [-1,0,0,0, 0,1,0,0, 0,0,1,0, 0,0,0,1]
            glMultMatrixd(m2)
            glMatrixMode(GL_MODELVIEW)
            glLoadIdentity()
            glRotated(rotate, 1.0, 1.0, 0.0)
            for i in range(12):
                edge_list = cube.e[i]
                glColor(0.0, 0.0, 1.0, 1.0)
                glLineWidth(4.0) ## 線の幅
                glBegin(GL_LINES)
                s_vertex = cube.v[edge_list[0]]
                t_vertex = cube.v[edge_list[1]]
                glVertex3f(s_vertex[0], s_vertex[1], s_vertex[2])
                glVertex3f(t_vertex[0], t_vertex[1], t_vertex[2])
                glEnd()
        elif self.n_model == 8:
            for i in range(12):
                edge_list = cube.e[i]
                glColor(0.0, 0.0, 1.0, 1.0)
                glLineWidth(4.0) ## 線の幅
                glBegin(GL_LINES)
                s_vertex = cube.v[edge_list[0]]
                t_vertex = cube.v[edge_list[1]]
                glVertex3f(s_vertex[0], s_vertex[1], s_vertex[2])
                glVertex3f(t_vertex[0], t_vertex[1], t_vertex[2])
                glEnd()
            for i in range(6):
                face_list = cube.f[i]
                glColor(1.0, 1.0, 1.0, 1.0)
##                glLineWidth(4.0) ## 線の幅
                glBegin(GL_POLYGON)
                for f in face_list:
                    glVertex3f(cube.v[f][0], cube.v[f][1], cube.v[f][2])
                glEnd()
        elif self.n_model == 9:
            glEnable(GL_DEPTH_TEST)
            glPolygonMode(GL_FRONT_AND_BACK, GL_LINE)
            glColor(0.0, 0.0, 1.0, 1.0)
            for i in range(6):
                face_list = cube.f[i]
                glBegin(GL_POLYGON)
                for f in face_list:
                    glVertex3f(cube.v[f][0], cube.v[f][1], cube.v[f][2])
                glEnd()
            glPolygonMode(GL_FRONT_AND_BACK, GL_FILL)
            glEnable(GL_POLYGON_OFFSET_FILL)
            glPolygonOffset(1.0, 1.0)
            glColor(1.0, 1.0, 1.0, 1.0)
            for i in range(6):
                face_list = cube.f[i]
                glBegin(GL_POLYGON)
                for f in face_list:
                    glVertex3f(cube.v[f][0], cube.v[f][1], cube.v[f][2])
                glEnd()
            glDisable(GL_POLYGON_OFFSET_FILL)
            glDisable(GL_DEPTH_TEST)
        else:
            rotate += 0.1
            glMatrixMode(GL_MODELVIEW)
            glLoadIdentity()
            glRotated(rotate, 1.0, 1.0, 0.0)
            for i in range(6):
                face_list = cube.f[i]
                glColor(0.0, 0.0, 1.0, 1.0)
##                glLineWidth(4.0) ## 線の幅
                glBegin(GL_POLYGON)
                for f in face_list:
                    glVertex3f(cube.v[f][0], cube.v[f][1], cube.v[f][2])
                glEnd()

                        
def change_tesselation():    
    # 現在選択されている項目のインデックスを取得
    indices = listbox.curselection()
    if len(indices) != 1:
        # ２つ以上選択されているor１つも選択されていない
        return
    # 項目を取得
    index = indices[0]
    app.n_model_list = []
    app.n_model_list.append(int(index))
    app._display()
    
def key_handler(e):
    if e.keycode == 38: ## key_up
        app.n_move_list = []
        app.n_move_list.append(38)
        app._display()
    elif e.keycode == 40: ## key_down
        app.n_move_list = []
        app.n_move_list.append(40)
        app._display()
    elif e.keycode == 37: ## key_left
        app.n_move_list = []
        app.n_move_list.append(37)
        app._display()
    elif e.keycode == 39: ## key_right
        app.n_move_list = []
        app.n_move_list.append(39)
        app._display()
    print(e.keycode)

if __name__ == '__main__':
    root = tk.Tk()
    root.title('立方体の表示')
    app = AppOgl(root, width=600, height=600)
    app.pack(fill=tk.BOTH, expand=tk.YES)
##    app.animate = 1
    app.animate = True
    listbox = tk.Listbox(root, height=10) ## default height=10
    listbox.pack(fill=tk.X)
    tesselations = ['平行投影', '透視投影:glFrustum()', \
                    '透視投影:gluPerspective()', \
                    'キーイベント', 'glLoadMatrixd() and glMultMatrix()', \
                    'glPushMatrix() and glPopMatrix()', \
                    '視界変換', '着色', '陰線処理I:SIMPLE', \
                    '陰線処理II:POLYGON OFFSET']
    for item in tesselations:
        listbox.insert(tk.END, item)
    button = tk.Button(root, text='選択', command=change_tesselation)
    button.pack(fill=tk.X)
    root.bind("", key_handler)
##    app.after(100, app.printContext)
    app.mainloop()
です。最後から3行目の root.bind("", key_handler) は "" には＜KeyPress＞が見えないと思いますから無くなっていれば補って下さい。 ＜＞は半角です。 実行すると


などを描きます。

3D Graphics では、正射影（平行投影）と透視法射影（透視投影）の2種類があります。後者は絵画で言う遠近法です。 まず 

        glViewport(0, 0, self.width, self.height) ## 画面の描画領域
の様にビューポート（画面の表示領域）を指示します。通常はこの指示で良いです。 正射影は 

        glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
        glLoadIdentity() ## 投影行列を単位行列で初期化する
##        glOrtho(left, right, bottom, top, near, far) ## 平行投影
        glOrtho(-1.0, 1.0, -1.0, 1.0, -1.0, 1.0) ## 平行投影
の様に指示します。 透視法射影は２通りの方法があります。 

        glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
        glLoadIdentity() ## 投影行列を単位行列で初期化する
##        glFrustum(left, right, bottom, top, near, far) ## 透視投影
        glFrustum(-1.0, 1.0, -1.0, 1.0, 2.0, 10.0) ## 透視投影
と 

        glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
        glLoadIdentity() ## 投影行列を単位行列で初期化する
##        gluPerspective(fovy, aspect, near,far) ## 透視投影
        gluPerspective(30, self.width/self.height, 0.1,100) ## 透視投影
です。透視法射影では、通常、 作ったオブジェクト（今の場合、立方体）を見るためには、カメラを操作するかオブジェクトを上で指定した視体積（クリップされていない領域）に 移動する必要があります。デフォルト（初期設定）では、カメラは gluLookAt(0.0, 0.0, 0.0, 0.0, 0.0, -100.0, 0.0, 1.0, 0.0) で、原点にあり、負のz軸の方向を向いていて、y軸が真上になるようカメラを設置しています。 カメラは 

        gluLookAt( ## カメラを配置する
            0.0, 0.0, 5.0, ## カメラの位置
            0.0, 0.0, 0.0, ## カメラの視点の位置
            0.0, 1.0, 0.0, ## カメラの向き
        )
のように指定します。


オブジェクトに対する変換は、平行移動、スケーリング（拡大・縮小）、回転が可能で、 

        glMatrixMode(GL_MODELVIEW)
        glLoadIdentity()
        glRotated(30, 0.0, 0.0, 1.0)
        glScaled(1.5, 0.5, 1.0)
        glTranslated(0.0, 0.0, -4.0)
のように使います。指示の順番が大切で、間違えると描画が思いがけないものになります。 更に、 

            glMatrixMode(GL_MODELVIEW)
            glLoadIdentity()
            m = [1,0,0,0, 1,1,0,0, 0,0,1,0, 0,0,0,1]
            glLoadMatrixd(m)
            m2 = [-1,0,0,0, 0,1,0,0, 0,0,1,0, 0,0,0,1]
            glMultMatrixd(m2)
            glScaled(0.5, 0.5, 0.5)
            glRotated(rotate, 1.0, 1.0, 0.0)
}
のように、勝手な４×４行列をロードしたり、掛けたり出来ます。行列は m を順番に列から先に並べたものと解釈されます。 オブジェクトに対する適用は最後に指示した行列が最初になります。この機能を使えば、行列が幾何学的図形にどの様に作用するかの図示が簡単に出来ます。 更に、 

        elif self.n_model == 5:
            glMatrixMode(GL_MODELVIEW)
            glLoadIdentity()
            glRotated(rotate, 1.0, 1.0, 0.0)
            for i in range(12):
                edge_list = cube.e[i]
                glColor(0.0, 0.0, 1.0, 1.0)
                glLineWidth(4.0) ## 線の幅
                glBegin(GL_LINES)
                s_vertex = cube.v[edge_list[0]]
                t_vertex = cube.v[edge_list[1]]
                glVertex3f(s_vertex[0], s_vertex[1], s_vertex[2])
                glVertex3f(t_vertex[0], t_vertex[1], t_vertex[2])
                glEnd()
            glPushMatrix()
            glTranslated(2.0, 0.0, 0.0)
            sphere1.draw()
            glPopMatrix()
            glTranslated(-3.0, 0.0, 0.0)
            glColor(1.0, 0.0, 0.0, 1.0)
            sphere2.draw_wireframe()
のように、glPushMatrix() と glPopMatrix() を組にして、モデルビュー行列や射影行列をスタックに push したり、pop したり出来ます。 push したら、pop して、一連の処理が終った時には、スタックを空にしておかなければなりません。 更に、 

        elif self.n_model == 6:
            glMatrixMode(GL_PROJECTION)
            glLoadIdentity()
            m = [1,0,0,0, 1,1,0,0, 0,0,1,0, 0,0,0,1]
            glLoadMatrixd(m)
            m2 = [-1,0,0,0, 0,1,0,0, 0,0,1,0, 0,0,0,1]
            glMultMatrixd(m2)
            glMatrixMode(GL_MODELVIEW)
            glLoadIdentity()
            glRotated(rotate, 1.0, 1.0, 0.0)
            for i in range(12):
                edge_list = cube.e[i]
                glColor(0.0, 0.0, 1.0, 1.0)
                glLineWidth(4.0) ## 線の幅
                glBegin(GL_LINES)
                s_vertex = cube.v[edge_list[0]]
                t_vertex = cube.v[edge_list[1]]
                glVertex3f(s_vertex[0], s_vertex[1], s_vertex[2])
                glVertex3f(t_vertex[0], t_vertex[1], t_vertex[2])
                glEnd()
}
のように、射影行列をいじることも出来ます。先ず、モデルビュー行列をオブジェクトに適用した後、射影行列をオブジェクトに適用します。 どちらの行列も最初にセットした行列が最後に適用されます。 

            for i in range(12):
                edge_list = cube.e[i]
                glColor(0.0, 0.0, 1.0, 1.0)
                glLineWidth(4.0) ## 線の幅
                glBegin(GL_LINES)
                s_vertex = cube.v[edge_list[0]]
                t_vertex = cube.v[edge_list[1]]
                glVertex3f(s_vertex[0], s_vertex[1], s_vertex[2])
                glVertex3f(t_vertex[0], t_vertex[1], t_vertex[2])
                glEnd()
のように、glBegin(GL_LINES)を使っていますが、glEnd() との間の glVertex3f() の並びをどの様に解釈するかの指示の仕方に 様々なものがあり、「OpenGLプログラミングガイド」などに解説があります。 glBegin(GL_LINES)は二個づつ線分の始点と終点の座標として線分を描きます。 更に、破線などに関して、好きなパターンの破線の線分を描く指示もありますが、例は上の平面充しん形のプログラムで使っています。 その他では、「クリップ面の追加」がありますが、切断面の表示の為の技法で、線画では必要ないと思います。 現在は GPU を利用した高度な技術なども種々開発されていると思いますが（最新の技術は調べていません）、 我々 GPU のないパソコンを使っている貧乏人は 線画に関しては基本的にはこれだけ知っておけば良いです。 これらを使いこなすだけでも大変ですが、Python だと手軽に実験でき、本当に夢のような時代になっています。 プログラミングでは、このような新たに学んだこと（技法）を直ぐに様々、このように変えればどの様になるか実験してみるのに、 語学などの勉強では只管「覚えなければ」と言う脅迫観念だけで、数学やプログラミングでやっているようなことが出来ていません。 今までのやり方では駄目だと言うことは分かりますが、具体的に何をすれば最も効果的かが分からないことが辛い処です。 本当は「絶対的な勉強時間が足りていないことが一番の原因で、 誰かが良いと言う参考書を次々買い集め、本箱で埃を被っているだけで、本当にチャンと勉強したか」だとは思いますが。 数学とプログラミングは勉強法が違いますが、外国語も勉強法が違うみたいです。更に、外国語は何がしたいかで勉強法が違うみたいです。 最近文庫版が出版され、高知の書店でも山積みになっていた種田輝豊著「20ヶ国語ペラペラ　私の外国語学習法」や最近ブックオフで手に入れた 黒田龍之助著「寝るまえ5分の外国語　語学書評論集」をパラパラめくってみると今まで調べた様々な人達と異なる勉強法もあることが分かります。 若い人がその外国語を生活の糧にする為に学ぶのでなければ、思い思い好きにやればいいみたいです。唯、常にその外国語に何らかの形で触れている必要がありますが。

面に色を 


            for i in range(6):
                face_list = cube.f[i]
                glColor(0.0, 0.0, 1.0, 1.0)
                glBegin(GL_POLYGON)
                for f in face_list:
                    glVertex3f(cube.v[f][0], cube.v[f][1], cube.v[f][2])
                glEnd()
のように単純に付けると綺麗には見えません。

最後の選択肢の陰線処理は「陰線処理I:SIMPLE」では、一番外の輪郭線しか描いてくれません。これは 

        elif self.n_model == 8:       
            rotate += 0.1
            if self.n_model != self.old_n_model:
                self.old_n_model = self.n_model
            glClear(GL_DEPTH_BUFFER_BIT)
            glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
            glLoadIdentity() ## 投影行列を単位行列で初期化する
##            gluPerspective(fovy, aspect, near,far) ## 透視投影
            gluPerspective(30, self.width/self.height, 0.1,100) ## 透視投影
            gluLookAt( ## カメラを配置する
                0.0, 0.0, 15.0,
                0.0, 0.0, 0.0,
                0.0, 1.0, 0.0,
            )
            glMatrixMode(GL_MODELVIEW)
            glLoadIdentity()
            glRotated(rotate, 0.0, 0.0, 1.0)
            glTranslate(3.0, 0.0, 0.0)
            glRotated(30, 1.0, 1.0, 0.0)
        elif self.n_model == 8:
            for i in range(12):
                edge_list = cube.e[i]
                glColor(0.0, 0.0, 1.0, 1.0)
                glLineWidth(4.0) ## 線の幅
                glBegin(GL_LINES)
                s_vertex = cube.v[edge_list[0]]
                t_vertex = cube.v[edge_list[1]]
                glVertex3f(s_vertex[0], s_vertex[1], s_vertex[2])
                glVertex3f(t_vertex[0], t_vertex[1], t_vertex[2])
                glEnd()
            for i in range(6):
                face_list = cube.f[i]
                glColor(1.0, 1.0, 1.0, 1.0)
                glBegin(GL_POLYGON)
                for f in face_list:
                    glVertex3f(cube.v[f][0], cube.v[f][1], cube.v[f][2])
                glEnd()
のように、glClear(GL_DEPTH_BUFFER_BIT) でデプス・バッファ処理を有効化し、 最初、glBegin(GL_LINES) で線画を描き、背景色で面を描きます。 「陰線処理II:POLYGON OFFSET」では、欲しかった図を描いてくれます。これは 

        elif self.n_model == 9:       
            rotate += 0.1
            if self.n_model != self.old_n_model:
                self.old_n_model = self.n_model
            glClear(GL_DEPTH_BUFFER_BIT)
            glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
            glLoadIdentity() ## 投影行列を単位行列で初期化する
##            gluPerspective(fovy, aspect, near,far) ## 透視投影
            gluPerspective(30, self.width/self.height, 0.1,100) ## 透視投影
            gluLookAt( ## カメラを配置する
                0.0, 0.0, 15.0,
                0.0, 0.0, 0.0,
                0.0, 1.0, 0.0,
            )
            glMatrixMode(GL_MODELVIEW)
            glLoadIdentity()
            glRotated(rotate, 0.0, 0.0, 1.0)
            glTranslate(3.0, 0.0, 0.0)
            glRotated(30, 1.0, 1.0, 0.0)
        elif self.n_model == 9:
            glEnable(GL_DEPTH_TEST)
            glPolygonMode(GL_FRONT_AND_BACK, GL_LINE)
            glColor(0.0, 0.0, 1.0, 1.0)
            for i in range(6):
                face_list = cube.f[i]
                glBegin(GL_POLYGON)
                for f in face_list:
                    glVertex3f(cube.v[f][0], cube.v[f][1], cube.v[f][2])
                glEnd()
            glPolygonMode(GL_FRONT_AND_BACK, GL_FILL)
            glEnable(GL_POLYGON_OFFSET_FILL)
            glPolygonOffset(1.0, 1.0)
            glColor(1.0, 1.0, 1.0, 1.0)
            for i in range(6):
                face_list = cube.f[i]
                glBegin(GL_POLYGON)
                for f in face_list:
                    glVertex3f(cube.v[f][0], cube.v[f][1], cube.v[f][2])
                glEnd()
            glDisable(GL_POLYGON_OFFSET_FILL)
            glDisable(GL_DEPTH_TEST)
のように、glClear(GL_DEPTH_BUFFER_BIT) でデプス・バッファ処理を有効化し、glEnable(GL_DEPTH_TEST)でデプス・テストを可能にし、 glPolygonMode(GL_FRONT_AND_BACK, GL_LINE)の設定で、面を描き、 glPolygonMode(GL_FRONT_AND_BACK, GL_FILL)の設定に変更し、 glEnable(GL_POLYGON_OFFSET_FILL)とglPolygonOffset(1.0, 1.0)でポリゴン・オフセットを使って、背景色で、 面を描けば、少し小さい面を描いてくれ、内部の輪郭線も描かれることになります。 最後に、glDisable(GL_POLYGON_OFFSET_FILL)とglDisable(GL_DEPTH_TEST)で環境を元に戻して置きます。 glPolygonOffset(1.0, 1.0)の数値をいじれば、輪郭線の大きさを変更できます。

もう一つ、「ステンシル・バッファ」を 使う複雑な方法もあるみたいですが、上の方法で、差し当たって必要なことは分かったので、必要になれば勉強します。

更に、youtube で、pyopengl を pygame 上で描写する次のようなプログラムを見つけました。 

import pygame
from pygame.locals import *
from OpenGL.GL import *
from OpenGL.GLU import *

verticies = (
    (1, -1, -1),
    (1, 1, -1),
    (-1, 1, -1),
    (-1, -1, -1),
    (1, -1, 1),
    (1, 1, 1),
    (-1, -1, 1),
    (-1, 1, 1)
    )

edges = (
    (0,1),
    (0,3),
    (0,4),
    (2,1),
    (2,3),
    (2,7),
    (6,3),
    (6,4),
    (6,7),
    (5,1),
    (5,4),
    (5,7)
    )

def Cube():
    glBegin(GL_LINES)
    for edge in edges:
        for vertex in edge:
            glVertex3fv(verticies[vertex])
    glEnd()

def main():
    pygame.init()
    display = (800, 600)
    pygame.display.set_mode(display, DOUBLEBUF|OPENGL)

    gluPerspective(45, (display[0]/display[1]), 0.1, 50.0)

    glTranslatef(0.0, 0.0, -10.0)

    glRotatef(0, 0, 0, 0)

    while True:
        for event in pygame.event.get():
            if event.type == pygame.QUIT:
                pygame.quit()
                quit()
            if event.type == pygame.KEYDOWN:
                if event.key == pygame.K_LEFT:
                   glTranslatef(-1.0, 0.0, 0.0) 
                if event.key == pygame.K_RIGHT:
                   glTranslatef(1.0, 0.0, 0.0) 
                if event.key == pygame.K_UP:
                   glTranslatef(0.0, 1.0, 0.0) 
                if event.key == pygame.K_DOWN:
                   glTranslatef(0.0, -1.0, 0.0) 
            if event.type == pygame.MOUSEBUTTONDOWN:
                ## 1:左ボタン, 2:中ボタン, 3:右ボタン
                if event.button == 4: ## ホイールを上にスクロール
                    glTranslatef(0.0, 0.0, 1.0)
                if event.button == 5: ## ホイールを下にスクロール
                    glTranslatef(0.0, 0.0, -1.0)

        glRotatef(1, 3, 1, 1)
        glClear(GL_COLOR_BUFFER_BIT|GL_DEPTH_BUFFER_BIT)
        Cube()
        pygame.display.flip()
        pygame.time.wait(10)

main()
外国の人のプログラムに、このようなプログラムがありますが、3D graphics のゲームを作るのでしょうか？

pyOpenGL で色を使うためには、人間が色をどの様にして認識しているかの一般常識の理解が不可欠です。 大分前、「車の構造を知らなくても、車の運転は出来る」と発言して、数学など勉強するより、投資を学べと発言した政治家がいましたが、 投資もその基本となる数学的基礎を含む仕組みを知らなければ、 (実際、外国の投資家は確率微分方程式などの高度な数学を駆使して株式・金融市場を制圧しています)、 世の中に無数にいる無知に付け込む人達に騙されるだけです。 OpenGL の場合も、勿論 OpenGL のソースコードを読んで見るのが一番良いですが、我々凡人には荷が重いですが、基本的な仕組みを知らなければ、 プログラミング出来ません。 OpenGL は変更されるまで効果が持続する各種のステータス（モード）で使用するステート・マシンであることや 各種バッファの役割や使用法などかなりの程度内部構造を理解していないと理解不能なバグに途方に暮れることになります。 政治家の発言は「宗主国の米国とこんな約束をして、数十年前の役に立たない旧式の兵器を数兆円分買わされ」とか、本当のことを言えないことが 一杯あるので、嘘をつくことが常態化しているので、言葉通りではなく注意して聞かなければなりません。 「防衛力拡大」と「子育て支援」が目下問題になっていますが、後者に関しては、公明党が最初に小さく掲げていたり、れいわ新選組の山本太郎さんが問題視していた、 今まで、成功した有名人たちが声高に「自己責任だ」と叫び、 政治家が切り捨ててきた就職氷河期以降の沢山の人達が経済的に余裕が出来、結婚できる環境を整えることが本当は一番大切なことではないでしょうか？ このような意見に対する反論として、年収2000万円でもこんな人がいる、年収１000万円でもこんな人がいる、 年収800万円でもこんな人がいるとお金に余裕があるのにこんな理由で結婚していな人もいると達数人の結婚していない例を述べ、 結婚しないのは経済的な問題だけではないので、若者の賃上げ・経済的支援をするのは少子化対策にならないと主張します。 これも政治家・官僚及びその支配下にあるマスコミなど支配者層が好んで使う「統計の嘘」です。 100万人単位や1000万人単位の人達に言及しているのに、数人の例外を持ってきて、その主張を潰そうとし、実際、その主張をなるほどと思ってしまう人が多く、 そのような主張をした人達の思い通りになっているのが日本の実情ではないでしょうか？「非正規労働者」の問題も同じ論法を政治家・官僚・経営者・ 連合・マスコミ・お抱え学者など大企業の正社員だけを守りたい人達が揃って、この「統計の嘘」を使ったんだと思います。 また、テレビに出演する老人はお金が有り余っていて、老人はお金を持っていると声高に発言しますが、それはごく一部で、上手く立ち回り天下り出来た 一部官僚などが中心で、大多数の老人は苦しい生活をしています。インターネットには金融資産の6割は老人が持っているとの記事も出ていますが、 すべての老人が豊かなわけでなく、世襲の政治家や大企業の経営者や天下りした官僚や芸能人やスポーツ選手など一部の有名な老人がその金融資産の 殆どを持っているだけで、その分布を示し、論拠を示さなければ一般的に老人が金持ちだと言うのは単なる悪意を持った世論誘導です。 船員を長く勤めて、十分な年金を貰えると思っていたのに、会社が騙して、年金のお金を払ってくれていなくて、 十分な年金を貰えてない、生活保護では自由が無くなると幡多地区から早朝に起きて高知大の付属病院に来ていた自嘲気味に話す可哀そうな老人と話をしたこともあります。 碁会所に行く500円がないと無料の将棋解説会に来ていた老人と話したこともあります。これも数人の例ではないかと反論されそうですが？ 金持ちとしか会食しない政治家や官僚やすべての労働者の味方のふりをする連合も金持ち優遇の政策を次々実行すれだけで、 地方の疲弊した現状を全然理解していないか、 無視しても問題ない、外国と異なり、「君君たらずといえども臣臣たらざるべからず」が日本人には染み付いているから、 中曽根首相や小泉首相により巨大労働組合のあった国鉄、郵政を民営化し、社会党を潰せたから、企業別の組合しか残っていない日本では最早ストライキは起きない、 我々特権階級は好き勝手に振る舞っていいのだと思っていると思います。 テレビでよく視るように弱い魚は大量の数の集団の塊になることで、強い魚の攻撃から被害を最小限度にしています。


この図を頭に入れ、OpenGL のコマンドの仕組みを少しずつ学び、様々な試行錯誤・実験を繰り返し、自分の欲しい画像を得る方法を探す必要があります。 私のような色覚障害者はこの L,M,S の錐体（錐状体）のどれか或いは全部に何らかの問題があるそうです。我々凡人にとってはかなり厄介です。 現在は、インターネットで様々な情報を得ることが出来ますが、書籍は必要な情報を纏めて提供してくれるので、「OpenGL プログラミング　ガイド」は 高額で、分厚いですが、お小遣いと相談して購入して、例えば、第4章「カラー」を最初から読んで見ると良いです。 私の持っているのは２０年以上前の古い英語版と翻訳版ですが、 基本的な知識はこの本と同じ頃購入した「Win32OpenGL プログラミング」で得て、使い方が良く分からないコマンドを PyOpenGL でも使えるか、 ワンポイントでインターネットで検索します。インターネットは そのような使い方に適していると思います。インターネットだけでなく、書籍と使い分けます。具体的には、3.5 インチのフロッピーディスクの時代の本で、 使う参考書名は参考にはならないとは思いますが、基本的な知識を教えてくれる書籍で、華やかな応用を解説した書籍では無いです。 これらを読んでも良く分からない場合は、OpenGL で使われている元になった技術を書いてある、例えば、 DAVID F. ROGERS 著「PROCEDURAL ELEMENTS FOR COMPUTER GRAPHICS」を読んで見るか、読んだ人に知りたいことを聞けば良いですが、 余程他人に教えるのが好きな人かそのような教育を生活の糧にしている人でないと 「あらゆる失敗を経験したから出来るようになった。だから人には教えたくない」と言う発言になり、顰蹙を買うことになります。

巴山竜来さんの参考文献リストにあった「APERIODIC ORDER Volume 1, 2」が手に入った。到着予定日より随分遅かったが、 一つは米国から中古品が、一つは英国から新品が送られてきた。日本円の価値の変動が激しく、洋書の値段も大幅に変動しています。どうも最も円安の時に買ってしまった。 私たちの学生時代のように英語の洋書は高くて買えなく、台湾の海賊版やロシア語や中国語の翻訳本に頼らなければならない時代に逆戻りするのでしょうか？ もうこれが最後で、数学の本を買うこともないと思いますが、パラパラ眺めてみると面白そうな本です。 最初に誰もが知っているペンローズタイリングのノーベル物理学賞受賞者 Roger Penrose さんの Foreword by Roger Penrose があります。 Penrose Tiling を発見した当時の状況が解説されていて、数学研究はどの様に為されているかのサンプルで、 これだけ読むだけでもこの本を購入した価値があります。有名な Hilbert の18番目の問題に端を発する問題だそうで、 数学者だけでなく、と言うか、ノーベル物理学賞受賞者やノーベル化学賞受賞者にとって興味があり、 それぞれ貢献している、位相幾何学や群論を中心とする代数学や解析学の知識が必要な数学の応用分野です。 専門家でないと基本的な定義が説明されてなく途方に暮れる本が多いですが、この本は最初を読んだだけですが、私のような初心者でも読めそうです。 また、予定変更で、この本と「TILINGS AND PATTERNS」を読んで見ます。 しかし、壁紙群を位相幾何学的手法で解説している河野俊丈著「結晶群」を読んで、現代的な手法を学んでから厄介なこれらの本を読むのが良さそうです。 本も読む順番があります。 人が面白そうな事をやっていれば、すぐ何でも小さな子供のように真似をし、この道一筋とならないので、何一つ身につきませんが、人生面白ければそれでいいです。 更に、Interface 2022年6月号には、量子コンピュータの特集記事が掲載されています。一部、実用化され、特殊な問題なら解くことが出来るそうです。 雑誌の特集記事では、完全に理解できる訳では無いですが、面白そうなものが次から次へと出てきます。 又、Interface 2019年3月号にも、量子コンピュータの特集記事があり、こっちの方はハードよりの記事が載っています。 定期購入している訳でなく、常に何が特集されているか本屋でチェックしてないので、その記事を元に出版された単行本の情報を元に古本で手に入れました。 多くの場合、関連するプログラムは単行本ではなく雑誌のダウンロードの場所からゲットできます。 量子力学は才能ある優秀な人達だけが関心・興味のある遠い世界だと言う認識でしたが、量子コンピュータだと我々全員の日々の生活にもろに影響してきます。 面白い世の中になってきました。

河野俊丈著「結晶群」の「課題 1.31」をやってみましょう。手計算は大変だから、Python のプログラミングをやってみます。 一番厄介なのは一般の単位ベクトルの周りの3次元回転の計算です。インターネットで調べると公式を見つけることが出来ますが、 間違っていることもあります。ベクトルの内積と外積を知っていれば、次のような図を描いて見れば、容易に導出出来ます。 x軸、ｙ軸、ｚ軸の回転の公式を先ず導き、あっちこち移動するややこしいことをして導くややこしい公式を暗記するより、この図を覚える方が私には簡単です。 この時。軸 n は単位ベクトル（長さ１のベクトル）と言う条件を忘れると正しい答えは得られません。前提条件はしっかり覚えておかなければいけません。 次の紙の下の方で証明しているように、 n は単位ベクトルという条件があるから、同じ円周上に関係する3つのベクトルの端点が載っているので、関係式が導けます。 尤も覚えていなくても図の正当性（何で3つのベクトルの端点が同じ円周上にあるのだろう？）を調べれば、n は単位ベクトルでなければならないと分かりますが。


小学校で習う「鶴亀算」「旅人算」・・・などめんどくさかったもの（思考力を養成するのに役立つと思いますが）も中学校で学ぶアラビア・イスラム由来の 連立方程式を学べば、問題ごとに個別に考えなくとも、すべて同じ考えで簡単に解けるようになったように、 多分、大学で学ぶベクトルの外積（ベクトル積）を知っていれば、このように楽に暗記出来き、導けます。 （ベクトルの外積（ベクトル積）に関しても、その定義、右手形で、外積は元のベクトル2つと直交することや大きさは平行四辺形の面積とかの幾何学的イメージと その成分はどの様に求めれば良いかといった代数的イメージや幾つかの公式を暗記するか （どの様な公式があったか或いはどの様な公式があるはずかは覚えていて）定義から導けるようにしておかなければいけないと思いますが。） 高校で苦労して丸暗記させられる三角関数の沢山の公式も大学で学ぶオイラーの公式を使い、複素数の計算に還元すれば簡単に導けます。 そして、現在の科学技術（電気・電子回路や音波や地震波や電磁波から量子力学まで）では波の理解が必須で、 特に波を重ねるとどうなるか（干渉）は振幅（大きさ）と位相（ずれ）が大きく関係しているので、両者を一度に表現できる複素数が使われます。 更に、数学だけ学んだ者には、「物理や工学を学んだ人達は数学的対象をこんな風に考えるんだと言う面白い考え・アイデア」を使っていることが良くあります。 以下で考察する正多面体を不変にする回転の集まり（集合）に群構造を入れ、名前を付ければ、簡単に識別できます。 わが町佐川町出身で「春爛漫」の植物学者の牧野富太郎さんが植物に片っ端に名前を付けたように、色々な集合に群構造や位相構造や順序構造などを入れ、名前を付け 整理すると昔苦労したことが簡単に整理して捉え直すことが出来るようになります。このように学べば学ぶほど楽に物事を理解することが可能になります。 更に、行列の計算でも連立方程式を解くアルゴリズムを実際に自分でプログラミングした経験がなく、連立方程式を解くソフトを使って答えだけを求めるだけだと、 行列を変形して解を求めるアルゴリズムを繰り返し使えば、ホップ代数のコホモロジーの生成元などを求めるという非数値計算にも使えると言う発想は浮かばないと思います。 勿論、天才たちが作ってくれた様々なソフトをブラックボックスとして使いこなして、好き勝手に創造的なことをしている人たちが沢山いることも事実で、 天才と言われる人達が何を考えているか分かりませんが、殆どすべての人が過去の偉大な遺産を元に、自分のやりたいこともやりたいようにしているだけです。 何が幸いするか我々凡人には前もって分かりません。 江戸時代の「読み書きそろばん」は現在でも大切で、国語、算数・数学、プログラミング、外国語はあらゆる思考の為の基本技術です。 これは他の分野の学習は不要だと言っている訳ではなく、各人の興味に応じて学べば良いですが、人の話の意図を正確に聴き取り。本の内容を正確に読み取り、 政治家・官僚・評論家など有名人達が好んで使う「統計による嘘」を見抜くには「読み書きそろばん」の知識が基本ですと言っているだけです。

「自分でやらなくても他人がやっているのを見て来たから分かる」と言う人もいますが、これでは駄目で、自分で何でもやってみます。 例えば、「数直線の合同変換全体のなす群を Isom(E^1) で表す。 Isom(E^1) の要素は、実数 b を用いて t(x) = x + b で表される平行移動、または、実数 c についての鏡映 r(x) = - x + 2c である。」と書いてあるとき、 「そうなんだ」とこの事実を丸暗記するのと合同変換の定義から自分で納得できるように・納得できるまで、証明してみるのでは、 長い目でみると大きな違いが出るのではないかと私は思います。 「試験に合格するためや資格を取るためには、兎も角、沢山丸暗記した人が勝ちだ」との意見の人が実際は多いとは思いますが。

他の部分は、定義通りコツコツプログラミングすれば良いです。プログラムは 


import tkinter as tk
from OpenGL.GL import *
from OpenGL.GLU import *
import numpy as np
from OpenGL import GL
from pyopengltk import OpenGLFrame
import copy

class Rotate:
    def rotate(self, n, r, theta):
        n = (1/np.sqrt(np.dot(n, n))) * n
        n_dot = np.dot(r, n)
        n_cross = np.cross(n, r)
        w = np.cos(theta)*r+n_dot*(1-np.cos(theta))*n+np.sin(theta)*n_cross
        return w
    def matrix(self, n, theta):
        mtx = []
        m1 = self.rotate(n, np.array([1.0, 0.0, 0.0]), theta)
        m2 = self.rotate(n, np.array([0.0, 1.0, 0.0]), theta)
        m3 = self.rotate(n, np.array([0.0, 0.0, 1.0]), theta)
        mtx.extend(m1)
        mtx.append(0.0)
        mtx.extend(m2)
        mtx.append(0.0)
        mtx.extend(m3)
        mtx.append(0.0)
        mtx.extend(np.array([0.0, 0.0, 0.0, 1.0]))
        return mtx
                   
    
class F444:
    def __init__(self):
        ## v=[[頂点の座標]]のリスト
        self.v =[]
        ## e=[[辺を構成する頂点の番号]]のリスト
        self.e = []
        ## f=[[面を構成する頂点の番号]]のリスト
        self.f = []
        self.n_vertex = 8
        self.n_edge = 12
        self.n_face = 6
        ## v=[[頂点の座標]]のリスト
        self.t_v =[]
        ## e=[[辺を構成する頂点の番号]]のリスト
        self.t_e = []
        self.t_n_vertex = 4
        self.t_n_edge = 6
        ## f=[[面を構成する頂点の番号]]のリスト
        self.t_f = []
        self.t_n_face = 4
        self.p6 = Rotate()
        self.symm = []
        self.diagonal = []
        self.tetra_v = []
        
        self.index = 0

    def set_inf(self):       
        ## 各辺を構成する頂点の番号
        t_edge = [[0,1], [1,2], [2,3], [3,0], [5,4], [6,5], \
                  [7,6], [4,7], [0,4], [1,5], [2,6], [3,7]]
        ## 各面を構成する頂点の番号：反時計回り
        t_face = [[0,1,2,3], [7,6,5,4], \
                  [4,5,1,0], [5,6,2,1], \
                  [3,2,6,7], [0,3,7,4]]
        vertex = []
        for i in range(4):
            x = np.cos(i*np.pi/2)/2+np.sin(i*np.pi/2)/2
            y = np.sin(i*np.pi/2)/2-np.cos(i*np.pi/2)/2
            z = 0.5
            vertex.append(np.array([x,y,z]))
        for i in range(4):
            x = np.cos(i*np.pi/2)/2+np.sin(i*np.pi/2)/2
            y = np.sin(i*np.pi/2)/2-np.cos(i*np.pi/2)/2
            z = -0.5
            vertex.append(np.array([x,y,z]))
        for i in range(self.n_vertex):
            self.v.append(vertex[i])
        self.e = t_edge
        self.f = t_face
        self.t_v =[self.v[0], self.v[2], self.v[5], self.v[7]]
        t_edge = [[0,1], [0,2], [0,3], [1,2], [1,3], [2,3]]
        self.t_e = t_edge
        ## 各面を構成する頂点の番号：反時計回り
        t_face = [[0,2,1], [0,3,2], [0,1,3], [1,2,3]]
        self.t_f = t_face
        self.symm = self.symmetry()
        self.diagonal = [[0,6],[1,7],[2,4],[3,5]]
        self.tetra_v = [0, 2, 5, 7]
        
    def print(self):       
        print('v=', self.v)
        print('e=', self.e)
        print('f=', self.f)

    def symmetry(self):
        symm_list = []
        for i in range(4):
            symm_list.append([np.array([0.0, 0.0, 1.0]), i*np.pi/2])
        for i in range(1, 4):
            symm_list.append([np.array([0.0, 1.0, 0.0]), i*np.pi/2])
        for i in range(1, 4):
            symm_list.append([np.array([1.0, 0.0, 0.0]), i*np.pi/2])
        pair = [[0,6],[1,7],[2,4],[3,5],[8,10],[9,11]]
        for k in range(4):
            source = self.v[pair[k][0]]
            target = self.v[pair[k][1]]
            for i in range(1, 3):
                symm_list.append([source-target, i*2*np.pi/3])
        for k in range(6):
            source = (self.v[self.e[pair[k][0]][0]]+self.v[self.e[pair[k][0]][1]])
            target = (self.v[self.e[pair[k][1]][0]]+self.v[self.e[pair[k][1]][1]])
            source = 0.5*source
            target = 0.5*target
            symm_list.append([source-target, np.pi])
        return symm_list
    def cube_vertex_move(self, n, theta):
        target_v_list = []
        for k in range(8):
            target_v_list.append([self.p6.rotate(n, self.v[k], theta)])
        return target_v_list
    def get_v_num(self, coordinate):
        for k in range(8):
            flag = True
            for i in range(3):
                if np.abs(self.v[k][i]-coordinate[0][i]) > 0.01:
                    flag = False
                    break
            if flag == True:
                return k
            
    def get_v_permutation(self, target_list):
        perm_list = []
        for i in range(8):
            perm_list.append(self.get_v_num(target_list[i]))
        return perm_list
    
    def get_d_num(self, target):
        for k in range(4):
            if self.diagonal[k][0] == target[0] and self.diagonal[k][1] == target[1]:
                return k
            if self.diagonal[k][0] == target[1] and self.diagonal[k][1] == target[0]:
                return k
        return -1
                    
    def get_d_permutation(self, target_list):
        v_perm_list = self.get_v_permutation(target_list)
        perm_list = []
        for k in range(4):
            source = self.diagonal[k]
            target = [v_perm_list[source[0]], v_perm_list[source[1]]]
            perm_list.append(self.get_d_num(target))
        return perm_list
            
    def even_permutationP(self, d_permutaton):
        p = 1
        for i in range(4):
            for k in range(i+1, 4):
                p = p*(d_permutaton[i]-d_permutaton[k])
        if p > 0:
            return True
        else:
            return False
        
    def get_tetra_v_permutation(self, target_list):
        v_perm_list = self.get_v_permutation(target_list)
        target = []
        for k in range(4):
            target.append(v_perm_list[self.tetra_v[k]])
        perm_list = []
        for k in range(4):
            if target[k] in self.tetra_v:                
                perm_list.append(self.tetra_v.index(target[k]))
            else:
               return []
        return perm_list
        
    def test(self):
        for k in range(24):            
            t_list = self.cube_vertex_move(self.symm[k][0], self.symm[k][1])
            v_perm = self.get_v_permutation(t_list)
            print('v_perm=', v_perm)
            d_perm = self.get_d_permutation(t_list)
            print('d_perm=', d_perm)
            print('even_permutationP:', self.even_permutationP(d_perm))
            t_v_perm = self.get_tetra_v_permutation(t_list)
            print('t_v_perm=', t_v_perm)

cube = F444()
cube.set_inf()
##cube.print()

p6 = Rotate()
cube.test()

rotate = 0

class AppOgl(OpenGLFrame):

    def initgl(self):
        global rotate, cube
        
        glViewport(0, 0, self.width, self.height) ## 画面の描画領域
        
        glClearColor(0.0, 0.0, 0.0, 1.0) ## 背景色
        self.n_model_list = [0]
        self.old_n_model = -1
        rotate = 0
        
    def torad(self, deg):
        return deg*(math.pi/180.0)


    def redraw(self):
        global rotate
        self.n_model = self.n_model_list[0]
        rotate += 0.1
##        rotate += 0.0
        if self.n_model == 0:
            if self.n_model != self.old_n_model:
                self.old_n_model = self.n_model
                rotate = 0.0
            else:
                if rotate >= 360.0:
                    if cube.index >= cube.n_vertex:
                        rotate = 0.0
                    else:
                        rotate = 0.0
        
        glClear(GL_COLOR_BUFFER_BIT)
        
##        glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
##        glLoadIdentity() ## 投影行列を単位行列で初期化する
####        glFrustum(left, right, bottom, top, near, far) ## 透視投影
##        glFrustum(-1.0, 1.0, -1.0, 1.0, 2.0, 10.0) ## 透視投影
####        gluLookAt( ## カメラを配置する
####            0.0, 0.0, 2.0, ## カメラの位置
####            0.0, 0.0, 0.0, ## カメラの視点の位置
####            0.0, 1.0, 0.0, ## カメラの向き
####        )
        
##        glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
##        glLoadIdentity() ## 投影行列を単位行列で初期化する
####        gluPerspective(fovy, aspect, near,far) ## 透視投影
##        gluPerspective(30, self.width/self.height, 0.1,100) ## 透視投影
##        gluLookAt( ## カメラを配置する
##            0.0, 0.0, 5.0,
##            0.0, 0.0, 0.0,
##            0.0, 1.0, 0.0,
##        )
        
        glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
        glLoadIdentity() ## 投影行列を単位行列で初期化する
##        glOrtho(left, right, bottom, top, near, far) ## 平行投影
        glOrtho(-1.0, 1.0, -1.0, 1.0, -1.0, 1.0) ## 平行投影
####        glOrtho(-2.0, 2.0, -2.0, 2.0, -2.0, 2.0)

        glMatrixMode(GL_MODELVIEW)
        glLoadIdentity()
        symm = cube.symm[self.n_model]
        mtx = p6.matrix(symm[0], symm[1])
        glLoadMatrixd(mtx)
        glRotated(rotate, 1.0, 1.0, 0.0)
        
        
        ## v=[[頂点の座標]]のリスト
        ## e=[[辺を構成する頂点の番号]]のリスト
        ## f=[[面を構成する頂点の番号]]のリスト
        clist = [[1.0, 0.0, 0.0], [0.0, 1.0, 0.0], [0.0, 0.0, 1.0],
                     [1.0, 1.0, 0.0], [1.0, 0.0, 1.0], [0.0, 1.0, 1.0],
                     [0.5, 0.0, 0.0], [0.0, 0.5, 0.0], [0.0, 0.0, 0.5],
                     [0.5, 0.5, 0.0], [0.0, 0.5, 0.5], [0.5, 0.0, 0.5],
                     [0.5, 0.7, 0.0], [0.7, 0.5, 0.0], [0.7, 0.0, 0.5],
                     [0.5, 0.2, 0.3], [0.2, 0.5, 0.3], [0.3, 0.2, 0.5]]
                     
        glClear(GL_DEPTH_BUFFER_BIT)
        glPolygonMode(GL_FRONT_AND_BACK, GL_FILL)
        glEnable(GL_DEPTH_TEST)
        glEnable(GL_BLEND)
        glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA)
        for i in range(cube.t_n_face):
            face_list = cube.t_f[i]
            glColor(clist[i+cube.n_face][0], clist[i+cube.n_face][1], \
                        clist[i+cube.n_face][2], 1.0)
            glLineWidth(4.0) ## 線の幅
            glBegin(GL_POLYGON)
            for k in range(3):
                s_vertex = cube.v[cube.tetra_v[face_list[k]]]
                glVertex3f(s_vertex[0], s_vertex[1], s_vertex[2])
            glEnd()
        for i in range(cube.n_face):
            face_list = cube.f[i]
            glColor(clist[i][0], clist[i][1], clist[i][2], 0.5)
            glLineWidth(4.0) ## 線の幅
            glBegin(GL_POLYGON)
            for k in range(4):
                s_vertex = cube.v[face_list[k]]
                glVertex3f(s_vertex[0], s_vertex[1], s_vertex[2])
            glEnd()
        glDisable(GL_DEPTH_TEST)
        glDisable(GL_BLEND)
                        

def next_symmetry():
    global n_symmetry, label, cube
    n_symmetry += 1
    if n_symmetry >= 24:
        n_symmetry = 0
    label['text'] = 'No.'+str(n_symmetry+1)
    symm = cube.symm[n_symmetry]
    mtx = p6.matrix(symm[0], symm[1])
    print('n_symmetry:', n_symmetry)
    print('matrix:', mtx)
    app.n_model_list = []
    app.n_model_list.append(int(n_symmetry))
    app._display()
        
if __name__ == '__main__':
    root = tk.Tk()
    root.title('正6面体群 P(6)')
    app = AppOgl(root, width=600, height=600)
    app.pack(fill=tk.BOTH, expand=tk.YES)
##    app.animate = 0  
##    app.animate = True ## この方が正式  
    app.animate = 1
    label = tk.Label(text='N0.1', font = ('MS Gothic', 20), foreground = '#FF00FF', background = 'cyan' )
    label.pack(fill=tk.X)
    n_symmetry = 0
    symm = cube.symm[n_symmetry]
    mtx = p6.matrix(symm[0], symm[1])
    print('n_symmetry:', n_symmetry)
    print('matrix:', mtx)
    button = tk.Button(root, text='Next', command=next_symmetry)
    button.pack(fill=tk.X)
##    app.after(100, app.printContext)
    app.mainloop()
です。実行すると 

v_perm= [0, 1, 2, 3, 4, 5, 6, 7]
d_perm= [0, 1, 2, 3]
even_permutationP: True
t_v_perm= [0, 1, 2, 3]
v_perm= [1, 2, 3, 0, 5, 6, 7, 4]
d_perm= [1, 2, 3, 0]
even_permutationP: False
t_v_perm= []
v_perm= [2, 3, 0, 1, 6, 7, 4, 5]
d_perm= [2, 3, 0, 1]
even_permutationP: True
t_v_perm= [1, 0, 3, 2]
v_perm= [3, 0, 1, 2, 7, 4, 5, 6]
d_perm= [3, 0, 1, 2]
even_permutationP: False
t_v_perm= []
v_perm= [4, 5, 1, 0, 7, 6, 2, 3]
d_perm= [2, 3, 1, 0]
even_permutationP: False
t_v_perm= []
v_perm= [7, 6, 5, 4, 3, 2, 1, 0]
d_perm= [1, 0, 3, 2]
even_permutationP: True
t_v_perm= [3, 2, 1, 0]
v_perm= [3, 2, 6, 7, 0, 1, 5, 4]
d_perm= [3, 2, 0, 1]
even_permutationP: False
t_v_perm= []
v_perm= [4, 0, 3, 7, 5, 1, 2, 6]
d_perm= [2, 0, 3, 1]
even_permutationP: False
t_v_perm= []
v_perm= [5, 4, 7, 6, 1, 0, 3, 2]
d_perm= [3, 2, 1, 0]
even_permutationP: True
t_v_perm= [2, 3, 0, 1]
v_perm= [1, 5, 6, 2, 0, 4, 7, 3]
d_perm= [1, 3, 0, 2]
even_permutationP: False
t_v_perm= []
v_perm= [0, 3, 7, 4, 1, 2, 6, 5]
d_perm= [0, 3, 1, 2]
even_permutationP: True
t_v_perm= [0, 3, 1, 2]
v_perm= [0, 4, 5, 1, 3, 7, 6, 2]
d_perm= [0, 2, 3, 1]
even_permutationP: True
t_v_perm= [0, 2, 3, 1]
v_perm= [5, 1, 0, 4, 6, 2, 3, 7]
d_perm= [3, 1, 0, 2]
even_permutationP: True
t_v_perm= [2, 0, 1, 3]
v_perm= [2, 1, 5, 6, 3, 0, 4, 7]
d_perm= [2, 1, 3, 0]
even_permutationP: True
t_v_perm= [1, 2, 0, 3]
v_perm= [5, 6, 2, 1, 4, 7, 3, 0]
d_perm= [3, 0, 2, 1]
even_permutationP: True
t_v_perm= [2, 1, 3, 0]
v_perm= [7, 3, 2, 6, 4, 0, 1, 5]
d_perm= [1, 3, 2, 0]
even_permutationP: True
t_v_perm= [3, 1, 0, 2]
v_perm= [2, 6, 7, 3, 1, 5, 4, 0]
d_perm= [2, 0, 1, 3]
even_permutationP: True
t_v_perm= [1, 3, 2, 0]
v_perm= [7, 4, 0, 3, 6, 5, 1, 2]
d_perm= [1, 2, 0, 3]
even_permutationP: True
t_v_perm= [3, 0, 2, 1]
v_perm= [1, 0, 4, 5, 2, 3, 7, 6]
d_perm= [1, 0, 2, 3]
even_permutationP: False
t_v_perm= []
v_perm= [6, 2, 1, 5, 7, 3, 0, 4]
d_perm= [0, 2, 1, 3]
even_permutationP: False
t_v_perm= []
v_perm= [6, 7, 3, 2, 5, 4, 0, 1]
d_perm= [0, 1, 3, 2]
even_permutationP: False
t_v_perm= []
v_perm= [3, 7, 4, 0, 2, 6, 5, 1]
d_perm= [3, 1, 2, 0]
even_permutationP: False
t_v_perm= []
v_perm= [4, 7, 6, 5, 0, 3, 2, 1]
d_perm= [2, 1, 0, 3]
even_permutationP: False
t_v_perm= []
v_perm= [6, 5, 4, 7, 2, 1, 0, 3]
d_perm= [0, 3, 2, 1]
even_permutationP: False
t_v_perm= []
n_symmetry: 0
matrix: [1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 1.0]
n_symmetry: 1
matrix: [6.123233995736766e-17, 1.0, 0.0, 0.0, -1.0, 6.123233995736766e-17, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 1.0]
n_symmetry: 2
matrix: [-1.0, 1.2246467991473532e-16, 0.0, 0.0, -1.2246467991473532e-16, -1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 1.0]
n_symmetry: 3
matrix: [-1.8369701987210297e-16, -1.0, 0.0, 0.0, 1.0, -1.8369701987210297e-16, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 1.0]
のような表示と


のようなアニメーションが表示されます。 立方体の内部に正4面体が含まれているこのような図を綺麗に描くためには、適当に拾い読みした断片的な知識を元に思い付きでこのようなプログラミングしてみるのではなく、 3次元の色の付け方（照明・材質・DEPTH_BUFFER の使い方・法線ベクトルの指定方法・混色のやり方など）基本を キチンと学ばないと思い通りの絵が描けません。 各頂点に番号を付けて表示すればどの様な回転かハッキリ分かりますが簡単な方法は知りません。 自分で線で数字を作れば良いですがめんどくさいです。優秀な人達は次の「課題 1.32」に書いてあるように、力任せでなく、巧妙なアイデアで簡潔に証明しますが、 現在は我々凡人でもコンピュータによる力任せの方法でそれなりのことが出来るようになってきています。この問題のように既に知られていることでなく、 最先端の未知の課題に対して挑戦すべきなのは言うまでもありませんが、まだプログラミングに自信が無ければ、先ずは、このような課題で練習してみると良いです。 次の「課題 1.32」も更に長いプログラムになりますが、同様にプログラミング出来るハズです。上のプログラムが理解できれば、本質的な技法は すべて出ています。プログラミングしてみることに意味があるかどうか分かりませんが、暇ならやってみて下さい。 優秀な人達の真似をして頭の中に図形を描いて考える（或いは参考書の図を見ながら考える）のは我々凡人には結構難しいので正12面体を手に取って考えるのが良いです。 紙風船や紙工作（http://www.cc.kochi-u.ac.jp/~tyamag/sugaku.html に私が作った正多面体の地球儀の展開図や各種多面体の 展開図や型紙を印刷できるソフトをアップしています。




それらを使えば簡単に紙の模型が作れます。）でも 作れますが、私の様に不器用だと綺麗に作れません。各種正多面体のサイコロを購入して、手に取って考えるのが経済的です。 勿論、最先端装置を備えた有名大学や企業など恵まれた環境にいれば、三次元プリンターで各種正多面体、準正多面体、星形多面体を作れますが。 又、セレブのお坊ちゃま、お嬢様ならお父様に頼んで水晶で作ってもらえば完璧ですが。一組すべての正多面体のプログラムを作れば、コピーペーストで 簡単に使い回しが出来るので、双対多面体の図など片っ端に作ってみれば良いです。そして、今度は3次元空間のタイリングに挑戦し、 更には高次元の正多面体へと学習を進めていけば良いです。既に、分かっていることばかりですが、いきなり未知の領域は難しいのでは？ 勿論、こんな虱潰しに調べるのではなく、簡潔な法則を見つけ、簡潔に証明するのがカッコ良いことは言うまでもありませんが、 才能ある優秀な人達はどの様にして発見しているかいるか分からず、我々凡人には、虱潰しに調べてみて何か法則が見つかれば儲けもので、難しいです。

参考になるかどうか知りませんが、今回は私は下手糞な次の様な図を描いてデータが正しいかチェックします。




それでも見落としがあります。困ったものです。見栄を張らず、矢張り20数年前のように紙の模型に番号を振って考える方が結局時間の節約になります。 自分で作っても簡単ですが、例えば、上で紹介したソフトを使って、


（このような自分に必要な道具は自分で作れば良いです。尤も Borland C++ Builder を開発していた天才たちが Borland からいなくなり、古いコンパイラではコンパイルできず、 現在手に入るコンパイラは物凄く高額で年金生活者にはその金額に見合うものか購入をためらう金額で、古いコンパイラとの互換性がなく、しかも昔のように使い易い保証もなく、 昔苦労して習得した使い方の情報を同時に提供する技法もそのまま使える保証もなく、現在無料で使える Microsoft の VC++ や C# では、 他人に使ってもらえるのに必要な技術も一から学び直さなければならず、このようなソフトを私には最早、昔のように簡単には作れないですが。 例えば Python で、展開図なら何でもできる他人に使ってもらうことも考慮したソフトではなく、正12面体の展開図だけを印刷する自分用のプログラムを作るだけなら、勿論、簡単です。 校正が不十分で参考書に載っている展開図が間違っていることも良くありますが印刷して組み立ててみれば、間違っていることやどの様に直せば良いかは直ぐに分かります。 例えば、立方体の本質的な展開図が何種類あるかも考え方（直ぐ思いつくのは、例えば、「紙の模型で辺に番号を振り、各辺に番号の付いた面をばらばらにして、 机の上で辺の番号が一致するように面を並べる並べ方が何通りあるか調べてみなさい。或いは、サイコロを机の上で転がし、すべての面が一回だけ机に付く回転の仕方が 何通りあるかです。」です。 これがコンピュータで正多面体の展開図を虱潰しに探索するアルゴリズムの一つのアイデアで、プログラミング出来るようになるには、コピーペースト専門でなければ、 このようなアイデアを思いつけるかです。プログラミング教育にはそのような能力をどの様にすれば身につけることが出来るかですが、 鳥の掛かった網の部分だけ掲げて鳥が掛かるのを待つのではなく、無駄だと思っても、効率重視出ない大きな網を広げて鳥が掛かるのを待つこと： 国語教育（自発的な大量の読書の奨励）の充実と政治家・有名人の指導者層が「数学の勉強など必要ない」と繰り返し発言する算数・数学教育が本当は基礎では？ コンピュータはアラン・チューリングやフォン・ノイマン等々の数学者たちがもともと考えた出した産物です。 教育学者や心理学者の「果たせぬ夢」である、（子供たちは、経験が少なく、模倣したり、考える材料が乏しく、何故それをしなければいけないか分からないことを、 何も教えなくても子供自らが自発的活動で次々に法則を発見出来るようになるのは 出来るとしてもギフテッドと呼ばれる天才だけなのでは？）を教えると小学生でも全部自分で見つけます。 すべての正多面体の展開図を全て求めることも双対関係を上手く利用してプログラミングで虱潰しに探索することで簡単に出来ます。 どうも高度な数学を使えば論理的に説明でき簡単なことらしいですが、私には理解できていません。 コンピューターの世界は技術革新が凄いスピードで起こっていて、学んだことが直ぐに陳腐化、使えなくなります。諦めて学び続けるしかないです。 先日、高知の地方テレビで、猫が好きで好きで、高知のコンデンサーに使われる高度な紙を作っている会社に勤めていた女性が、CAD を独学で学び、自分で猫の小屋を設計し、 木工の基本を県内の何処かで教えて貰い、後は独学で、1000万円もかけて木工の工作機械を買いそろえ、木製の猫の小屋に特化した商売を始めた女性を紹介していました。 高知の田舎なので、作業場も確保でき、山ばかりの県ですから沢山の木工関係の会社もあるので、量産化に提携してくれる会社もあったみたいですが、 才能のある優秀な凄い女性も高知の田舎にもいます。 保守系の一部政治家の様に若者が結婚できる環境整備もせずに、「速く結婚しろ」とか言って、 （尤も結婚しているかどうか知りませんが）才能を潰す人たちが周りに居なかったのでしょう。 正12面体の展開図を必要な枚数印刷して


のように、美術工芸品を作るわけではないので、紙の模型を作ったり、展開図のまま、正12面体に内接する正6面体の頂点との 対応関係が分かる図を描いてみると良いです。正6面体と正4面体は2通りでしたが、今度は5通りあるのでキチンと絵を描かないと厄介です。 握力が弱くなって、キャップが開けれないペットボトルもあります。困ったものです。ビニール手袋をして開ければよいとのアドバイスもあります。 その為、最近はボールペンは止めて、万年筆かシャープペンシルを使っています。 万年筆は最近様々な色のインクが手に入り楽しいですが、手やノートや参考書がインクで汚れます。 シャープペンシルも 0.2, 0.3, 0.5, 0.7, 0.9, 1.3, 2.0 mm と「大人の鉛筆」とバラエティーに富んでいます。高かったので持っていませんが金属の鉛筆なるものも見ました。 更にピンからキリまでの値段と色数の「色鉛筆」があります。0.7 mm と「大人の鉛筆」には黒・赤（・青）以外にも様々の色があって便利です。 実際に使うのは何をするかによって段々決まっていきますが、全部揃えてみないと何が必要か前もって分かりません。

次の「課題 1.32」用に作ったプログラムは次のようなものです。 

import tkinter as tk
from OpenGL.GL import *
from OpenGL.GLU import *
import numpy as np
from OpenGL import GL
from pyopengltk import OpenGLFrame
import copy
import random

class Rotate:
    def rotate(self, n, r, theta):
        n = (1/np.sqrt(np.dot(n, n))) * n
        n_dot = np.dot(r, n)
        n_cross = np.cross(n, r)
        w = np.cos(theta)*r+n_dot*(1-np.cos(theta))*n+np.sin(theta)*n_cross
        return w
    def matrix(self, n, theta):
        mtx = []
        m1 = self.rotate(n, np.array([1.0, 0.0, 0.0]), theta)
        m2 = self.rotate(n, np.array([0.0, 1.0, 0.0]), theta)
        m3 = self.rotate(n, np.array([0.0, 0.0, 1.0]), theta)
        mtx.extend(m1)
        mtx.append(0.0)
        mtx.extend(m2)
        mtx.append(0.0)
        mtx.extend(m3)
        mtx.append(0.0)
        mtx.extend(np.array([0.0, 0.0, 0.0, 1.0]))
        return mtx
                   
class F555:
    def __init__(self):
        ## v=[次数,[頂点の座標],[[隣接する辺の番号],[隣接する面の番号]]のリスト
        self.v =[]
        self.original_v =[]
        ## e=[[辺を構成する頂点の番号],[隣接する面の番号]]のリスト
        self.e = []
        self.original_e = []
        ## f=[[面を構成する頂点の番号],[面を構成する辺の番号]]のリスト
        self.f = []
        self.original_f = []
        
        self.n_vertex = 20
        self.original_n_vertex = 20
        self.n_edge = 30
        self.original_n_edge = 30
        self.n_face = 12
        self.original_n_face = 12
        self.P = 5
        self.Q = 3
        self.icosa_v = []
        self.icosa_e = []
        self.icosa_f = []
        self.n_icosa_v = 12
        self.n_icosa_e = 30
        self.n_icosa_f = 20
        ## cube_v=[[立方体の頂点の番号]]のリスト
        self.cube_v = []
        ## cube_e=[[立方体の辺を構成する頂点の番号]]のリスト
        self.cube_e = []
        ## cube_f=[[立方体の面を構成する頂点の番号]]のリスト
        self.cube_f = []
        self.n_cube_v = 8
        self.n_cube_e = 12
        self.n_cube_f = 6
        self.p12 = Rotate()
        self.symm = []
        self.normal = []
        self.cube_normal = []
        self.index = 0

    def set_inf(self):       
        ## v=[次数,[頂点の座標],[[隣接する辺の番号],[隣接する面の番号]]のリスト
        ## e=[[辺を構成する頂点の番号],[隣接する面の番号]]のリスト
        ## f=[[面を構成する頂点の番号],[面を構成する辺の番号]]のリスト
        
        ## 各辺を構成する頂点の番号,隣接する面の番号
        t_edge = [[[0,1],[0,4]], [[1,2],[0,5]], [[2,3],[0,1]], \
                  [[3,4],[0,2]], [[4,0],[0,3]], [[0,5],[3,4]], \
                  [[1,6],[4,5]], [[2,7],[5,1]], [[3,8],[1,2]], \
                  [[4,9],[2,3]], [[5,10],[4,10]], [[10,6],[4,6]], \
                  [[6,11],[6,7]], [[11,7],[5,7]], [[7,12],[1,7]], \
                  [[12,8],[1,8]], [[8,13],[2,8]], [[13,9],[2,9]], \
                  [[9,14],[3,9]], [[14,5],[3,10]], [[10,15],[6,10]], \
                  [[11,16],[6,7]], [[12,17],[7,8]], [[13,18],[8,9]], \
                  [[14,19],[9,10]], [[19,15],[10,11]], [[15,16],[6,11]], \
                  [[16,17],[7,11]], [[17,18],[8,11]], [[18,19],[9,11]]]
        ## 各面を構成する頂点の番号,辺の番号：反時計回り
        t_face = [[[0,1,2,3,4],[0,1,2,3,4]], [[2,7,12,8,3],[2,7,14,15,8]], \
                  [[3,8,13,9,4],[3,8,16,17,9]], [[4,9,14,5,0],[4,9,18,19,5]], \
                  [[0,5,10,6,1],[0,5,10,11,6]], [[1,6,11,7,2],[1,6,12,13,7]], \
                  [[6,10,15,16,11],[11,20,26,21,12]], \
                  [[7,11,16,17,12],[13,21,27,22,14]], \
                  [[8,12,17,18,13],[15,22,28,23,16]], \
                  [[9,13,18,19,14],[17,23,29,24,18]], \
                  [[5,14,19,15,10],[19,24,25,20,10]], \
                  [[15,19,18,17,16],[25,29,28,27,26]]]

        ## 各頂点に隣接する辺と面の番号：反時計回り
        t_vertex = [[[0,4,5],[0,3,4]], [[0,6,1],[4,5,0]], \
                    [[1,7,2],[5,1,0]], [[2,8,3],[1,2,0]], \
                    [[3,9,4],[2,3,0]], [[5,19,10],[3,10,4]], \
                    [[6,11,12],[4,6,5]], [[7,13,14],[5,7,1]], \
                    [[8,15,16],[1,8,2]], [[9,18,17],[2,9,3]], \
                    [[10,20,11],[10,6,4]], [[12,21,13],[6,7,5]], \
                    [[14,22,15],[7,8,1]], [[16,23,17],[8,9,2]], \
                    [[18,24,19],[9,10,3]], [[20,25,26],[10,11,6]], \
                    [[21,26,27],[6,11,7]], [[22,27,28],[7,11,8]], \
                    [[23,28,29],[8,11,9]], [[24,29,25],[9,11,10]]]

        vertex = []
        r = np.sqrt(50+22*np.sqrt(5))/4/np.sqrt(5)
        vtx_size = np.sqrt(10+2*np.sqrt(5))/2/np.sqrt(5)
        mid_size = np.sqrt(5+2*np.sqrt(5))/2/np.sqrt(5)
        c_chi = np.sqrt(10-2*np.sqrt(5))/np.sqrt(15)
        s_chi = np.sqrt(5+2*np.sqrt(5))/np.sqrt(15)
        c_psi = (np.sqrt(5)-1)/2/np.sqrt(3)
        s_psi = (1+np.sqrt(5))/2/np.sqrt(3)
        c_phi = np.sqrt(10-2*np.sqrt(5))/2/np.sqrt(5)
        s_phi = np.sqrt(10+2*np.sqrt(5))/2/np.sqrt(5)

        for i in range(5):
            x = vtx_size*np.cos(i*2*np.pi/5)
            y = vtx_size*np.sin(i*2*np.pi/5)
            z = r
            vertex.append(np.array([x, y, z]))
        temp_x = vtx_size - c_chi*c_psi + s_chi*s_psi
##        temp_z = r - c_chi*s_psi + c_psi*s_chi;
        temp_z = r - (vtx_size+mid_size)*2*c_phi*s_phi
        for i in range(5):
            x = temp_x*np.cos(i*2*np.pi/5)
            y = temp_x*np.sin(i*2*np.pi/5)
            z = -temp_z
            vertex.append(np.array([x, y, z]))
        temp = mid_size - (2*c_phi*c_phi-1)*(vtx_size+mid_size)
        temp_x = temp * np.cos(np.pi/5)
        temp_y = temp * np.sin(np.pi/5)
        temp_z = r - (vtx_size+mid_size)*2*c_phi*s_phi
        for i in range(5):
            x = temp_x*np.cos(i*2*np.pi/5)-temp_y*np.sin(i*2*np.pi/5)
            y = temp_x*np.sin(i*2*np.pi/5)+temp_y*np.cos(i*2*np.pi/5)
            z = temp_z
            vertex.append(np.array([x, y, z]))
        temp_x = vtx_size * np.cos(np.pi/5)
        temp_y = vtx_size * np.sin(np.pi/5)
        temp_z = -r
        for i in range(5):
            x = temp_x*np.cos(i*2*np.pi/5)-temp_y*np.sin(i*2*np.pi/5)
            y = temp_x*np.sin(i*2*np.pi/5)+temp_y*np.cos(i*2*np.pi/5)
            z = temp_z
            vertex.append(np.array([x, y, z]))
        for i in range(self.n_vertex):
            self.v.append([3, vertex[i], t_vertex[i]])
        self.original_v = self.v.copy()
        self.e = t_edge
        self.original_e = self.e.copy()
        self.f = t_face
        self.original_f = self.f.copy()
        self.normal = []
        for k in range(self.n_face):
            x = self.v[self.f[k][0][1]][1]-self.v[self.f[k][0][0]][1]
            y = self.v[self.f[k][0][4]][1]-self.v[self.f[k][0][0]][1]
            n = np.cross(x, y)
            norm = np.sqrt(n[0]*n[0]+n[1]*n[1]+n[2]*n[2])
            n = (1/norm)*n     
            self.normal.append(n)
            
        ## 正20面体の頂点
        ## v=[次数,[頂点の座標],[[隣接する辺の番号],[隣接する面の番号]]のリスト
        self.icosa_v = []
        for k in range(self.n_face):
            v_list = self.f[k][0]
            centroid = np.array([0.0, 0.0, 0.0])
            for i in range(5):
                centroid =  centroid + self.v[v_list[i]][1]
            centroid = 0.2 * centroid
            self.icosa_v.append(centroid)
        ## 各辺を構成する頂点の番号
        t_edge = [[0,1], [0,2], [0,3], [0,4], [0,5], [1,2], \
                  [2,3], [3,4], [4,5], [5,1], [1,8], [2,8], \
                  [2,9], [3,9], [3,10], [4,10], [4,6], [5,6], \
                  [5,7], [1,7], [7,8], [8,9], [9,10], [10,6], \
                  [6,7], [8,11], [9,11], [10,11], [6,11], [7,11]]
        ## 各面を構成する頂点の番号：反時計回り
        t_face = [[0,1,2], [0,2,3], [0,3,4], [0,4,5], \
                 [0,5,1], [1,8,2], [2,8,9], [2,9,3], \
                 [3,9,10], [3,10,4], [4,10,6], [4,6,5], \
                 [5,6,7], [1,5,7], [1,7,8], [8,11,9], \
                 [10,9,11], [10,11,6], [6,7,11], [8,7,11]]        
        self.icosa_e = t_edge
        self.icosa_f = t_face
        ## 正6面体の頂点
        ## v=[次数,[頂点の座標],[[隣接する辺の番号],[隣接する面の番号]]のリスト
        ## cube_v=[[立方体の頂点の番号]]のリスト
        self.cube_v = [[0,2,8,9,10,11,17,19],
                       [1,3,9,5,11,12,18,15],
                       [2,4,5,6,12,13,19,16],
                       [3,0,6,7,13,14,15,17],
                       [4,1,7,8,14,10,16,18]]
        ## cube_e=[[立方体の辺を構成する頂点の番号]]のリスト
        self.cube_e = [
            [[0,2],[2,8],[8,9],[9,0],[0,10],[2,11], \
             [8.17],[9,19],[10,11],[11,17],[17,19],[19,10]], \
            [[1,3],[3,9],[9,5],[5,1],[1,11],[3,12], \
             [9,18],[5,15],[11,12],[12,18],[18,15],[15,11]], \
            [[2,4],[4,5],[5,6],[6,2],[2,12],[4,13], \
             [5,19],[6,16],[12,13],[13,19],[19,16],[16,12]], \
            [[3,0],[0,6],[6,7],[7,3],[3,13],[0,14], \
             [6,15],[7,17],[13,14],[14,15],[15,17],[17,13]], \
            [[4,1],[1,7],[7,8],[8,4],[4,14],[1,10], \
             [7,16],[8.18],[14,10],[10,16],[16,18],[18,14]]]
        ## cube_f=[[立方体の面を構成する頂点の番号]]のリスト
        self.cube_f = [
            [[0,2,8,9],[0,10,11,2],[2,11,17,8], \
             [8,17,19,9],[0,9,19,10],[10,19,17,11]],
            [[1,3,9,5],[1,11,12,3],[3,12,18,9], \
             [5,9,18,15],[1,5,15,11],[11,15,18,12]],
            [[2,4,5,6],[2,12,13,4],[5,4,13,19], \
             [6,5,19,16],[2,6,16,12],[12,16,19,13]],
            [[3,0,6,7],[0,3,13,14],[0,14,15,6], \
             [7,6,15,17],[3,7,17,13],[15,14,13,17]],
            [[4,1,7,8],[1,4,14,10],[1,10,16,7], \
             [7,16,18,8],[4,8,18,14],[10,14,18,16]]]
        ## cube_v=[[立方体の頂点の番号]]のリスト
        self.cube_v = [[0,2,8,9,10,11,17,19],
                       [1,3,9,5,11,12,18,15],
                       [2,4,5,6,12,13,19,16],
                       [3,0,6,7,13,14,15,17],
                       [4,1,7,8,14,10,16,18]]
        ## v=[次数,[頂点の座標],[[隣接する辺の番号],[隣接する面の番号]]のリスト
        self.cube_normal = []
        for k in range(self.n_cube_f):
            x1 = self.v[self.cube_f[0][k][1]][1]
            x0 = self.v[self.cube_f[0][k][0]][1]
            x2 = self.v[self.cube_f[0][k][3]][1]
            x = x1 - x0
            y = x2 - x0
            n = np.cross(x, y)
            norm = np.sqrt(n[0]*n[0]+n[1]*n[1]+n[2]*n[2])
            n = (1/norm)*n     
            self.cube_normal.append(n)

        self.symm = self.symmetry()

    def symmetry(self):
        symm_list = []
        ## v=[次数,[頂点の座標],[[隣接する辺の番号],[隣接する面の番号]]のリスト
        pair = [[0,17],[1,18],[2,19],[3,15],[4,16], \
                [5,12],[6,13],[7,14],[8,10],[9,11]]
        for k in range(len(pair)):
            source = self.v[pair[k][0]][1]
            target = self.v[pair[k][1]][1]
            if k == 0:
                for i in range(3):
                    symm_list.append([source-target, i*2*np.pi/3])
            else:
                for i in range(1, 3):
                    symm_list.append([source-target, i*2*np.pi/3])
                
        ## f=[[面を構成する頂点の番号],[面を構成する辺の番号]]のリスト
        pair = [[0,11],[1,10],[2,6],[3,7],[4,8],[5,9]]
        for k in range(len(pair)):
            source = np.array([0.0, 0.0, 0.0])
            for i in range(5):
                source =  source + self.v[self.f[pair[k][0]][0][i]][1]
            source = 0.2 * source
            target = np.array([0.0, 0.0, 0.0])
            for i in range(5):
                target =  target + self.v[self.f[pair[k][1]][0][i]][1]
            target = 0.2 * target
            for i in range(1, 5):
                symm_list.append([source-target, i*2*np.pi/5])
        ## e=[[辺を構成する頂点の番号],[隣接する面の番号]]のリスト
        pair = [[0,28],[1,29],[2,25],[3,26],[4,27], \
                [5,22],[6,23],[7,24],[8,20],[9,21], \
                [10,15],[11,16],[12,17],[13,18],[14,19]]
        for k in range(len(pair)):
            source = self.v[self.e[pair[k][0]][0][0]][1] + \
                     self.v[self.e[pair[k][0]][0][1]][1]
            source = 0.5 * source
            target = self.v[self.e[pair[k][1]][0][0]][1] + \
                     self.v[self.e[pair[k][1]][0][1]][1]
            target = 0.5 * target
            symm_list.append([source-target, np.pi])
        return symm_list
        
    def dodeca_vertex_move(self, n, theta):
        ## v=[次数,[頂点の座標],[[隣接する辺の番号],[隣接する面の番号]]のリスト
        target_v_list = []
        for k in range(self.n_vertex):
            target_v_list.append([self.p12.rotate(n, self.v[k][1], theta)])
        return target_v_list
    def get_v_num(self, coordinate):
        for k in range(self.n_vertex):
            flag = True
            for i in range(3):
                if np.abs(self.v[k][1][i]-coordinate[0][i]) > 0.01:
                    flag = False
                    break
            if flag == True:
                return k           
    def get_v_permutation(self, target_list):
        perm_list = []
        for i in range(self.n_vertex):
            perm_list.append(self.get_v_num(target_list[i]))
        return perm_list

    def test(self):
        for k in range(60):
            t_list = self.dodeca_vertex_move(self.symm[k][0], self.symm[k][1])
            v_perm = self.get_v_permutation(t_list)
            print('k=', k, ' v_perm=', v_perm)
##            d_perm = self.get_d_permutation(t_list)
##            print('d_perm=', d_perm)
##            print('even_permutationP:', self.even_permutationP(d_perm))
##            t_v_perm = self.get_tetra_v_permutation(t_list)
##            print('t_v_perm=', t_v_perm)

    def get_new_cube(self, v_perm, v_list):
        new_list = []
        for n in v_list:
            new_list.append(v_perm[n])
        return new_list

    def get_num_of_new_cube(self, new_cube):
        for k in range(5):
            curent_cube = self.cube_v[k]
            if set(new_cube) == set(curent_cube):
                return k
        return -1
   
    def get_cube_permutation(self, v_perm):
##        ## cube_v=[[立方体の頂点の番号]]のリスト
##        self.cube_v = [[0,2,8,9,10,11,17,19],
##                       [1,3,9,5,11,12,18,15],
##                       [2,4,5,6,12,13,19,16],
##                       [3,0,6,7,13,14,15,17],
##                       [4,1,7,8,14,10,16,18]]
        perm_list = []
        for k in range(5):
            curent_cube = self.cube_v[k]
            new_cube = self.get_new_cube(v_perm, curent_cube)
            perm_list.append(self.get_num_of_new_cube(new_cube))
        return perm_list
        
    def cube_move_test(self):
        cube_perm_gr = []
        for k in range(60):
            t_list = self.dodeca_vertex_move(self.symm[k][0], self.symm[k][1])
            v_perm = self.get_v_permutation(t_list)
            cube_perm = self.get_cube_permutation(v_perm)
            print('k=', k, 'cube_perm=', cube_perm)
            cube_perm_gr.append(cube_perm)
        alter_gr = self.get_alternative_group(5)
        if cube_perm_gr.sort() == alter_gr.sort():
            print('P(12)は交代群と一致する')
            

    def cyclic_permutation_of_length3P(self, cube_perm):
        c_list = []
        flag_list = [False, False, False, False, False]
        for k in range(5):
            if flag_list[k] == True:
                continue
            n = cube_perm[k]
            if k == n:
                flag_list[k] = True
                continue
            i = k
            while flag_list[i] == False:
                c_list.append(n)
                flag_list[i] = True
                i = n
                n = cube_perm[n]
        if len(c_list) == 3:
            return True
        else:
            return False

    def get_perm(self, r, l, s, k):
        if len(s)==k:
            r.append(s)
            return
        for e in l:
            old_s = s[:]
            s.append(e)
            new_l = l[:]
            new_l.remove(e)
            self.get_perm(r, new_l, s, k)
            s = old_s
            
    def get_symmetry_group(self, n):
        l = []
        r = []
        k = n
        l = [i for i in range(n)]
        self.get_perm(r, l, [], k)
        return r
    
    def get_length_3_ciclic_permutatin(self, n):
        r = self.get_symmetry_group(n)
        a = []
        i = 0
        for p in r:
            if self.cyclic_permutation_of_length3P(p)==True:
                print('i=', i, p)
                a.append(p)
                i = i+1
        return a
        
    def cube_move_test_by_first_21_rotation(self):
        three_cicles = []
        for k in range(21):
            t_list = self.dodeca_vertex_move(self.symm[k][0], self.symm[k][1])
            v_perm = self.get_v_permutation(t_list)
            cube_perm = self.get_cube_permutation(v_perm)
            flag = self.cyclic_permutation_of_length3P(cube_perm)
            print('k=', k, 'cube_perm=', cube_perm, ':', flag)
            if flag == True:
                three_cicles.append(cube_perm)
        alternative = self.get_length_3_ciclic_permutatin(5)
        if three_cicles.sort()==alternative.sort():
            print('一致する：すべての長さ３の巡回置換を与える')
    def even_permutationP(self, permutaton):
        p = 1
        for i in range(len(permutaton)):
            for k in range(i+1, len(permutaton)):
                p = p*(permutaton[i]-permutaton[k])
        if p > 0:
            return True
        else:
            return False

    def get_alternative_group(self, n):
        symm_gr = self.get_symmetry_group(n)
        alter_gr = []
        j = 0
        for p in symm_gr:
            if self.even_permutationP(p)==True:
                print('j=', j, 'p', p)
                j += 1
                alter_gr.append(p)
        return alter_gr

    def perm_product(self, g, h):
        p = []
        for i in range(len(g)):
            p.append(g[h[i]])
        return p
        
    def check_problem(self):
        alter_gr = self.get_alternative_group(5)
        generator = alternative = self.get_length_3_ciclic_permutatin(5)
        flag = True
        G = [[0,1,2,3,4]]
        NG = copy.deepcopy(G)
        while flag == True:
            flag = False
            for g in generator:
                for h in G:
                    k = self.perm_product(g, h)
                    if k not in NG:
                        flag = True
                        NG.append(k)
            G = copy.deepcopy(NG)
        if alter_gr.sort() == NG.sort():
            print('長さ３の巡回置換は交代群を生成した')
        
    def print(self):       
        print('v=', self.v)
        print('e=', self.e)
        print('f=', self.f)
                  
dodeca = F555()
dodeca.set_inf()
##dodeca.print()
p12 = Rotate()
##dodeca.cube_move_test_by_first_21_rotation()
##dodeca.get_symmetry_group(5)
##dodeca.get_alternative_group(5)

##dodeca.check_problem()
print(dodeca.normal)

rotate = 0

clist = []
for k in range(50):
    clist.append([random.random(), random.random(), random.random(), 1.0])

class AppOgl(OpenGLFrame):

    def initgl(self):
        global rotate, cube
        
        glViewport(0, 0, self.width, self.height) ## 画面の描画領域
        
        glClearColor(0.0, 0.0, 0.0, 1.0) ## 背景色
        self.n_model_list = [1]
        self.old_n_model = -1
        self.n_symm_list = [0]
        self.old_n_symm = -1
        rotate = 0
        
    def torad(self, deg):
        return deg*(math.pi/180.0)

    def redraw(self):
        global rotate
        self.n_model = self.n_model_list[0]
        self.n_symm = self.n_symm_list[0]
        rotate += 0.1
##        rotate += 0.0
        if self.n_model == 0 or self.n_model == 1:
            if self.n_model != self.old_n_model:
                self.old_n_model = self.n_model
                rotate = 0.0
            else:
                if rotate >= 360.0:
                    if dodeca.index >= dodeca.n_vertex:
                        rotate = 0.0
                    else:
                        rotate = 0.0
        
        glClear(GL_COLOR_BUFFER_BIT)
        
##        glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
##        glLoadIdentity() ## 投影行列を単位行列で初期化する
####        glFrustum(left, right, bottom, top, near, far) ## 透視投影
##        glFrustum(-1.0, 1.0, -1.0, 1.0, 2.0, 10.0) ## 透視投影
####        gluLookAt( ## カメラを配置する
####            0.0, 0.0, 2.0, ## カメラの位置
####            0.0, 0.0, 0.0, ## カメラの視点の位置
####            0.0, 1.0, 0.0, ## カメラの向き
####        )
        
##        glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
##        glLoadIdentity() ## 投影行列を単位行列で初期化する
####        gluPerspective(fovy, aspect, near,far) ## 透視投影
##        gluPerspective(30, self.width/self.height, 0.1,100) ## 透視投影
##        gluLookAt( ## カメラを配置する
##            0.0, 0.0, 5.0,
##            0.0, 0.0, 0.0,
##            0.0, 1.0, 0.0,
##        )
        
        glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
        glLoadIdentity() ## 投影行列を単位行列で初期化する
##        glOrtho(left, right, bottom, top, near, far) ## 平行投影
##        glOrtho(-1.0, 1.0, -1.0, 1.0, -1.0, 1.0) ## 平行投影
        glOrtho(-2.0, 2.0, -2.0, 2.0, -2.0, 2.0)

        glMatrixMode(GL_MODELVIEW)
        glLoadIdentity()
        symm = dodeca.symm[self.n_model]
        mtx = p12.matrix(symm[0], symm[1])
        glLoadMatrixd(mtx)
        glRotated(rotate, 1.0, 1.0, 0.0)
        
        
        ## v=[[頂点の座標]]のリスト
        ## e=[[辺を構成する頂点の番号]]のリスト
        ## f=[[面を構成する頂点の番号]]のリスト
                     
##        glClear(GL_DEPTH_BUFFER_BIT)
##        glPolygonMode(GL_FRONT_AND_BACK, GL_FILL)
##        glEnable(GL_DEPTH_TEST)
##        for i in range(cube.t_n_face):
##            face_list = cube.t_f[i]
##            glColor(clist[i+cube.n_edge][0], clist[i+cube.n_edge][1], \
##                        clist[i+cube.n_edge][2], 1.0)
##            glLineWidth(4.0) ## 線の幅
##            glBegin(GL_POLYGON)
##            s_vertex = cube.t_v[face_list[0]]
##            m_vertex = cube.t_v[face_list[1]]
##            t_vertex = cube.t_v[face_list[2]]
##            glVertex3f(s_vertex[0], s_vertex[1], s_vertex[2])
##            glVertex3f(m_vertex[0], m_vertex[1], m_vertex[2])
##            glVertex3f(t_vertex[0], t_vertex[1], t_vertex[2])
##            glEnd()
##        glDisable(GL_DEPTH_TEST)
##        for i in range(cube.n_edge):
##            edge_list = cube.e[i]
##            glColor(clist[i][0], clist[i][1], clist[i][2], 1.0)
##            glLineWidth(4.0) ## 線の幅
##            glBegin(GL_LINES)
##            s_vertex = cube.v[edge_list[0]]
##            t_vertex = cube.v[edge_list[1]]
##            glVertex3f(s_vertex[0], s_vertex[1], s_vertex[2])
##            glVertex3f(t_vertex[0], t_vertex[1], t_vertex[2])
##            glEnd()
                     
        if self.n_model == 0:
            glClear(GL_DEPTH_BUFFER_BIT)
            glPolygonMode(GL_FRONT_AND_BACK, GL_FILL)
            glEnable(GL_DEPTH_TEST)
            for i in range(dodeca.n_icosa_f):
                face_list = dodeca.icosa_f[i]
                glColor(clist[i][0], clist[i][1], \
                        clist[i][2], 1.0)
                glLineWidth(4.0) ## 線の幅
                glBegin(GL_POLYGON)
                s_vertex = dodeca.icosa_v[face_list[0]]
                m_vertex = dodeca.icosa_v[face_list[1]]
                t_vertex = dodeca.icosa_v[face_list[2]]
                glVertex3f(s_vertex[0], s_vertex[1], s_vertex[2])
                glVertex3f(m_vertex[0], m_vertex[1], m_vertex[2])
                glVertex3f(t_vertex[0], t_vertex[1], t_vertex[2])
                glEnd()
            glDisable(GL_DEPTH_TEST)
            for i in range(dodeca.n_edge):
                edge_list = dodeca.e[i][0]
##                print('edge_list = ', edge_list)
                glColor(0.0, 0.0, 1.0, 1.0)
##                glColor3f(1.0, 0.0, 1.0)
                glLineWidth(4.0) ## 線の幅
                glBegin(GL_LINES)
                for k in range(2):
                    s_vertex = dodeca.v[edge_list[0]][1]
                    t_vertex = dodeca.v[edge_list[1]][1]
                    glVertex3f(s_vertex[0], s_vertex[1], s_vertex[2])
                    glVertex3f(t_vertex[0], t_vertex[1], t_vertex[2])
                glEnd()
        if self.n_model == 1:
            glClear(GL_DEPTH_BUFFER_BIT)
            glPolygonMode(GL_FRONT, GL_FILL)
            glPolygonMode(GL_BACK, GL_LINE)
            glEnable(GL_DEPTH_TEST)
            glEnable(GL_BLEND)
            glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA)
            for i in range(dodeca.n_cube_f):
                face_list = dodeca.cube_f[0][i]
##                print('face_list=', face_list)
                glColor(clist[i][0], clist[i][1], \
                        clist[i][2], 1.0)
                glLineWidth(4.0) ## 線の幅
##                x1 = dodeca.cube_normal[i][0]
##                y1 = dodeca.cube_normal[i][1]
##                z1 = dodeca.cube_normal[i][2]
##                glNormal3d(x1, y1, z1)
                glBegin(GL_POLYGON)
                for k in range(4):
                    s_vertex = dodeca.v[face_list[k]][1]
                    glVertex3f(s_vertex[0], s_vertex[1], s_vertex[2])
                glEnd()
            ## f=[[面を構成する頂点の番号],[面を構成する辺の番号]]のリスト
            for i in range(dodeca.n_face):
                face_list = dodeca.f[i][0]
##                print('edge_list = ', edge_list)
##                glColor(0.0, 0.0, 1.0, 0.5)
##                glColor3f(1.0, 0.0, 1.0)
                glColor(clist[i][0], clist[i][1], \
                        clist[i][2], 0.5)
                glLineWidth(4.0) ## 線の幅
                x1 = dodeca.normal[i][0]
                y1 = dodeca.normal[i][1]
                z1 = dodeca.normal[i][2]
                glNormal3d(x1, y1, z1)
                glBegin(GL_POLYGON)
                for k in range(5):
                    s_vertex = dodeca.v[face_list[k]][1]
                    glVertex3f(s_vertex[0], s_vertex[1], s_vertex[2])
                glEnd()
            glDisable(GL_DEPTH_TEST)
            glDisable(GL_BLEND)
                        

def next_symmetry():
    global n_symmetry, label, cube
    n_symmetry += 1
    if n_symmetry >= 60:
        n_symmetry = 0
    label['text'] = 'No.'+str(n_symmetry+1)
    symm = dodeca.symm[n_symmetry]
    mtx = p12.matrix(symm[0], symm[1])
    print('n_symmetry:', n_symmetry)
    print('matrix:', mtx)
    app.n_symm_list = []
    app.n_symm_list.append(int(n_symmetry))
    app._display()
                        
def change_mode():
    
    # 現在選択されている項目のインデックスを取得
    indices = listbox.curselection()
    if len(indices) != 1:
        # ２つ以上選択されているor１つも選択されていない
        return
    # 項目を取得
    index = indices[0]
    if index < 2:
        app.n_model_list = []
        app.n_model_list.append(int(index))
        app._display()
    elif index == 2:
        dodeca.test()
    elif index == 3:
        dodeca.cube_move_test()
    elif index == 4:
        dodeca.cube_move_test_by_first_21_rotation()
    elif index == 5:
        dodeca.check_problem()
        
      
if __name__ == '__main__':
    root = tk.Tk()
    root.title('正6面体群 P(6)')
    app = AppOgl(root, width=600, height=600)
    app.pack(fill=tk.BOTH, expand=tk.YES)
    app.animate = 1 
##    app.animate = True ## この方が正式  
##    app.animate = 1
    listbox = tk.Listbox(root, height=6) ## default height=10
    listbox.pack(fill=tk.X)
    tesselations = ['双対多面体', '内接立方体', \
                    '正12面体の頂点の置換', '内接する立方体の置換', \
                    '向かい合う頂点の回転による内接する立方体の置換', \
                    '長さ３の巡回置換が5次の交代群を生成する？']
    for item in tesselations:
        listbox.insert(tk.END, item)
    button2 = tk.Button(root, text='選択', command=change_mode)
    button2.pack(fill=tk.X)
    label = tk.Label(text='N0.1', font = ('MS Gothic', 20), foreground = '#FF00FF', background = 'cyan' )
    label.pack(fill=tk.X)
    n_symmetry = 0
    symm = dodeca.symm[n_symmetry]
    mtx = p12.matrix(symm[0], symm[1])
    print('n_symmetry:', n_symmetry)
    print('matrix:', mtx)
    button = tk.Button(root, text='Next', command=next_symmetry)
    button.pack(fill=tk.X)
##    app.after(100, app.printContext)
    app.mainloop()
実行すると


のようなアニメーションが表示されます。まだ、分り易い図が描けません。法線ベクトルを追加しただけです。 課題は力任せで証明しています。それぞれの項目を選択し、上のボタンをクリックしてみて下さい。 但し、章末問題　問1.5 のような「n を3以上の自然数とする。交代群 An は、長さ３の巡回置換によって生成されることを示せ」のような 問題は n が具体的に与えられていないので、パソコンでは多分解けません。 無限個の n に対して成り立つことを示せるのが人間の偉い処ですが、これを最初に見つけた人はどうやって見つけたのでしょうか？ ここでやったような計算を（手計算で）沢山やって見て、帰納で予想を立て、証明したのでしょうか？ 或いは、じっと眺めていれば、閃くのでしょうか？昔からの疑問です。 我々凡人にはそうするしかないですが。又、参考書を読んでいて、証明が何を言っているか分からない時は、 (将棋に関して、米長邦雄さんが確か対談で話していたと思いますが)、自分の力ではこれは分からないと保留にしておくことも 一つの方法ですが、（女子学生が部屋のドアを開けようとして、開かずに苦労している時、 その大学（琉球大学）の数学の先生がぼそっと「押して駄目なら、引いて見な！」と言っていましたが）、 参考書のその証明を一旦忘れ、その定理以前の定義や定理をもう一度読み直してみれば、手掛かりが得られ、自分で証明できることもあります。 何を言っているかと言うと、カッコいい証明でなくても、命題XXXの証明の議論を用いることによりと書いてなくても、同じ議論で証明できることもあります。 数学は答えは一つと良く言われますが、証明方法は一般に何通りもあります。簡潔な証明がカッコいいですが、泥臭い方法でもキチンと正しく証明出来れば良いです。

上でやろうとしていた20数年前の Archimedes.exe を Python に翻訳するのは、ソースコードを読んで見ると全然コメントも書いてないし、何をやっているか自分の 書いたプログラムなのに、線画の Archimedes で練習して、 （更に、ゼミ生だった豊田祐子さんと松永弘子さんが作った星形小十二面体や大十二面体や星形大十二面体や大二十面体などのKITEによるプログラムを インターネットの同じ処で公開しています。




本来、チャンとプログラムを読んで指導すべきでしたが、面倒くさかったので、 私が作ったKITEのバグか彼女が作ったプログラムのバグか調べていませんが、 バグを除いていないものもあります。（正確は彼女たちが卒業した後、おかしいものもあることに気づいた。 彼女たちも勿論、このプログラムを作る前に、多面体の紙風船や紙の模型も作りました。 唯、「君たちはこれでも作って他の人の邪魔をしないように大人しくしていなさい。」と言われてやっているみたいと呟きながら作っていましたが。 高知の高岡高校出身の高知出身者としては最後のゼミ生も Kite が遅いと文句言いながら、同様のしかし広範囲の多面体のプログラムを自分で作りましたが、 そのプログラムは私は持っていません。） 参考になるなら覗いて見て下さい。） この新たなプログラムで出来ることを可能にするためにかなり一般化して、 汎用的に使えるようクラスを作っているみたいで、（例えば、平面と直線の交点を求める必要がありますが、交点が求まる場合だけでなく、平面と直線が平行の場合、 平面に直線が含まれる場合も区別して判定する必要があり、この場合、数学的に厳密に正確である必要はないですが、数値計算では誤差が必ず出るので、 誤差を考慮したアルゴリズムを使う必要があり、標準的な参考書に載っているガウスの消去法のプログラムをコピーするだけでは対処出来ません。 通常、例外として扱われる部分の理解が必要で、キチンとガウスの消去法の数学的理解が必要です。原発の事故でも想定外のことが起こったと言って、責任逃れを良くしますが、 起こる可能性のあることは必ず起こるので、そういうことを研究している人も必要です。無駄の排除のつもりか、国立大学の予算も年々削除していますが、 無駄だと思うことを許容している社会が健全です。 一方、コンピュータの技術が大衆化してきて、個人で色々なことが出来るようになってきたので、 先日も CAD を独学で学び、3D プリンターで物づくりをする会社を立ち上げ、高知大学や東京大学とも取引している女性が高知にもいると言う記事が高知新聞に載っていました。 一人で起業すれば、他人の生活を考えなくても良いので、失敗しても元々で、冒険が出来るので、色々な分野で、金儲けを第一に考えない、 自分が面白いと思うこと・独創的なことをする人達が出てきているそうです。何が成長分野か、官僚が頭で考えて、コントロールしても上手くいかないのではないでしょうか？ 研究開発は東京だけだではなく、全国各地で、色々な人達が思い思いに好きなことが出来れば、何処かで有望な研究成果が上がるのではないでしょうか？ 高校の古文で、網で鳥を取っている人が「鳥が引っかかった部分だけあれば良い、他の部分は無駄だと、鳥が引っかかった部分だけを持って、鳥が掛かるのを待っている」と言う 逸話を習い、その時の先生の顔の表情も覚えていますが、国立大学の予算を削り続け、政府・官僚のコントール下に大学の教育・研究を置こうとしている日本の現在の政策は、 まさに、この鳥が掛かった網の部分だけを掲げて、鳥が掛かるのを待っている状態と同じではないかと感じるのは私だけでしょうか？ （政府・官僚の論理は、「国民の税金を使っているので、国民に役に立つ大学でなければなければならない。国民を代表しているのは選挙で選ばれ、 国会議員の多数を握っている我々政府であり、無条件に、国立大学は政府・官僚の言うことを聞かなければならない。 その為に、大学の判断で使える大学の交付金は毎年減らすので 、研究・教育の為の予算は政府・官僚が募集するプロジェクトに応募することや 産学共同研究を進め民間から得なさい。「企業から研究資金を得ることのできない研究者は無能である」と言うキャンペンをマスコミが大々的にやったので国民は理解するはずだ。 大学の運営は経済界の有識者を入れた理事会に任せ、政府・官僚が大学の実績を評価するので、資金が欲しければ、民間企業の様に官僚の天下りを受け入れなさい。 そうすれば、容易に研究・教育資金が得られますよ。」ではないでしょうか？不安定な予算で運営していかなければならない国立大学で現在色々な問題が噴出しています。 産業に関係ない芸術分野の最高学府：東京芸大が交付金が減らさせた結果、電気代の高騰もあって、ピアノを廃棄したことがニュースになっていますが、マスコミも馬鹿で、 学長に質問している映像をテレビで流していましたが意味がないでしょう。現職の学長が本音を言う訳ないでしょう。 昔、九大のコンピューターの為の建設中の建物に米軍の戦闘機が墜落炎上した時、学長が不用意な発言をした為、学長を首になり、卒業式も中止になりました。 政府の政策の必然の結果なのですから、政府・官僚に聞くべきです。マスコミも自分も加担した結果なのに、こんなに阿保だと思いませんでした。 例えば文部省の政策がどの様に決められているか、有識者による各種委員会の委員は自分の学者生命を掛けて、 そこで自分がどの様な発言をしたか、今はインターネットがあるので、 実名付きで全て公表すべきです。そうすれば変な癒着・忖度を疑われる事は無くなります。それが有識者と言われる人たちの国民に対する最低限度の責任です。 更に、国民の大部分を占める恵まれない経済的弱者のことを真剣に考えてくれる政党が皆無で、投票率も低く、本当に国民の代表かという政府が勝手なことをしているのでは？） 例えば、青色発光ダイオードで2014年のノーベル物理学賞を受賞した中村修二さんは徳島大学工学部で学んでいますし、京セラ・KDI の稲盛 和夫さんは鹿児島県立大学 （後に鹿児島大学に統合）の工学部応用科学科で学んでいます。東京の大学だけが有意なな人材を必ずしも輩出している訳ではありません。 東京で生活し、東京中心でしか考えられない政府・官僚が、無駄な大学だとして、切り捨てようとしている規模が小さく卒業生も少なくどうしても 東京の大規模大学と比べると見劣りのする地方弱小国立大学も 今まで鳥を取る網の必要な部分として一定の役割を果たしてきています。国の政策は無駄の排除の効率重視で農業政策でも常に失敗しているように思います。）、 プログラミングしている時は他が何も見えない一種の興奮状態になっているので、適切なコメントも書いていないので、どの様にプログラミングしているのか 今となっては自分が書いたプログラムでも、ボトムアップで一つ一つ細部から辿っていかないと理解するのが大変です。 困ったものです。 我々凡人でもこのように順番に練習しながら努力すれば、それなりのものが出来ることもありますが、悲しいことに、昔読んだ本で瀬越健作さんも書いていましたが、 才能ある優秀な人達が本気で努力をするととても太刀打ちできず、お手上げで、才能ある人達には所詮かないませんが、面白いと思うことを気ままにやってみるだけです。 先ず、正多面体の5種類の削り取りのプログラミングをしようと思いましたが、Python に翻訳するのではなく、本質的な部分は特別なコンパイラに依存しない 標準の C++ のクラスで表現されているので、Python のモジュールとして、Python に読み込んで使う方が遥かに楽みたいだし、今までやったことがないことです。 そうすると完全に理解しなくてもブラックボックスみたいに使えます。 まだ、簡単なモジュールしか作れないので、こんな複雑なモジュールを作れる自信は無いですが、 どうせ暇だし、身近な人達を観察していると人間は役割が終れば死ぬんだと思っているので、 もう少し生きているために、上の本たちも読みながら、これもやってみようかな。不幸な死を迎えた人たちは神様が判断を間違えたのでは無いかな？尤も私は信心深くないですが。

C++ で Python のモジュールを作ることを久しぶりにやってみましたが、分からないことだらけです。インターネットで情報を探しますが、インターネットの情報は 断片的な情報が多いです。pybind11 を使うのが楽みたいですが、読んでいるインターネットの情報は macOS を使ったものや、Linux を使ったものであれば、 Windows10 では通用しないことが殆どだし、Windows10 用の記事でも、VC++ のバージョンと Python のバージョンの組み合わせが違えば、記事に書いてある通りにならないですが、 使ったバージョンが明記されていない場合が殆どです。VC++ 2022 で Python 3.9.7 用の pybind11 のヘッダーファイルなどを使ってコンパイルすると 私の思い違いかも分かりませんが、他のバージョンの Python ではモジュールとして認識してくれないみたいだし、インターネットの記事には C++ のクラスを使うプログラミングの例も載っていますが、単なる C++ の関数はモジュールとして使えますが、私がやってみると C++ のクラスを使う例は エラーメッセージが出てきて実行してくれません。この記事を書いた人は実行できたのでしょうから、VC++ と Python のバージョンの組み合わせが違うのでしょう。 多分。エラーメッセージも意味が分からず、簡単な例を確かめるだけでもまだまだ時間が掛かりそうです。 他の本も一杯同時に読んでいるので、別に急ぐ必要はないですが、独学で学ぶのは矢張り結構大変です。 例えば、cmake も全然理解していなかったので、インターネットでググってやってみようとしても、インターネットに書いてある通りにすれば、上手くいくとは限りません。 そのままでは上手くいかないので、cmake の最新版をインストールしますが、二種類あります。setup が必要なものと既に展開されているものです。 両方ダウンロードしてみて、どうすれば良いか考えます。インターネットの記事を読んでも setup の仕方が分からないし、setup するためのコマンドのファイルも見つからないので、 展開されているものを古い cmake が何処にあるか調べて、こっぽり入れ替えると最初のエラーメッセージは消えました。次は、AI の翻訳したコードを不注意でそのまま使い、エラーメッセージが何か分からず悩みます。 これは英語のままでなければいけないところを勝手に日本語に翻訳していることにうっかりして気が付かないことが原因です。 英語のページを AI で翻訳すると思わぬエラーに悩むことになります。更に、インターネットのコードをコピーペーストするとエラーが良く起こります。 この原因は、見た目では判断が付きませんが、半角のスペースでなければいけないのに、全角のスペースになっていて、コンパイル出来ないことです。 全然、学習していません。困ったものです。 「hello World!」の C++ で最初に学ぶプログラムを cmake でコンパイルするのに、何をして、どうであったかの記録を LaTeX の文章で残しながらなので、半日掛かりました。 これは、pybind11 の使い方を説明しているページで、cmake を使っていて、肝心の部分の説明が省略されていて、記事に書いてあることと自分のコンピュータの表示が まるっきり異なり何をすればいいか全然理解できなかったので、昔から気になっていた事でもあったので、寄り道して学んでみました。まだ、最初の一歩だけですが。 昔に比べれば、隔世の感がありますが、それでも新しいことを学ぶのはなかなか大変です。

最初に調べたのは https://qiita.com/SatoshiTerasaki/items/6e318910cd0060ef301d で、class を使った例は上で述べたように上手くいかなかった。 https://www.iwaxlab.com/articles?id=10 にある例は上手くいった。VC++ 2022 で、.pyd ファイルを作り、Python で読み込む方法です。 CMakeLists.txt を作って、cmake する方法はまだ成功していないですが、pybind11 で、クラスをモジュールに組み込む一つの方法は理解できました。 この方法では Python のバージョンが異なると実行できないのは、リンカーの追加のライブラリーディレクトリを指定しないと 「LINK : fatal error LNK1104: ファイル 'python310.lib' を開くことができません。」のエラーメッセージが出る事から想像できるように、 puthon のどの python???.lib を使うかによって、どのバージョンの Python で実行できるか決まるみたいです。 実際、Python3.10 をインストールする前のPython3.9 の為にインストールした pybind11.h のあるフォルダを追加のインクルードディレクトリに指定すると 「LNK1104: ファイル 'python39.lib' を開くことができません。」のエラーメッセージが出ます。このように実験してみるとコンピュータが答えを教えてくれます。 我々凡人は根を詰めてがむしゃらに努力すれば次々とアイデアが浮かぶわけでなく、嫌になったら、 安くて美味しいコーヒーが飲めるのでやっている（可愛い女の子が入れてくれるコーヒーの25分の１？）自家焙煎したコーヒーを入れて一服したり、 タバコ休憩してみるなり、（敷地内禁煙と言う処もありますが、決められた喫煙場所に行くと場合によっては、普段話をすることのできない、 雲の上の人と話す機会もあります。尤もこれは過去のことで、私などは何をしているのだろうと思いますが、 現在は煙草を吸っている間も、打ち合わせをしている人達も時には見かけますが、多くの場合、取り付かれたように皆、黙々とスマホをいじっています。）、 別のことをしたり、ボーっとしていたりすれば、実際は無意識下で考え続けているので、 ドアを開けた瞬間や眠る前に思いを巡らすとふと思いつくこともあります。 両方とも POINT と言うクラスを使っているので、共通のもとになった情報があるのではと思って調べると https://qiita.com/SatoshiTerasaki/items/6e318910cd0060ef301d の References に書いてある。 https://pybind11.readthedocs.io/en/latest/ に pybind11 documentation があることが分かった。 これが pybind11 の基本文献みたいで、これを読めば良いことにやっと気が付いた。随分、遠回りしました。 単独のクラスを使ったモジュール作成の実行できる例を一つ得ることが出来たので、 pybind11 documentation の目次を眺めると、上の上手くいかなかった例も、試行錯誤を繰り返せば、何処に問題があるか？分からないことはコンピュータが教えてくれるので、 クラスの継承などを使ったモジュール作成など最終的にやろうとしていることが出来そうな気がしてきました。 このような人工的なものは基本は教えて貰わなけば使えるようにはなりません。基本が分かれば、その応用は自分で考えることが出来る様になります。 このように、独学で学ぶのは、プログラミングが一番楽です。コンピュータが家庭教師の役割を果たしてくれるし、必要な情報がインターネットに溢れています。 数学は、独学では、「分かった！」という感覚だけが頼りです。外国語は厄介です。その外国語の話されている国に行けば良いですが、高知では、 昨日の新聞に「高新文化教室」の「春の講座」の広告が載っていて、「英会話」、「フランス語」、「ドイツ語」、「中国語」、「イタリア語」、「スペイン語」の 講座が開講されるみたいです。「韓国語」は講師の高齢化（？：私より若い韓国人の老婦人ですが。）で止めた見たいです。 十数人程度の募集で、外出機会の減った老人が人と接するいい機会ですが、 受講料で何冊も参考書が購入できると思うと私のような貧乏人は躊躇します。 色々な外国語に手を出しますが、何をやっても続かず、ちっとも成果が上がらない私のような者は、中学校の英語の学習でやったように、 プログラミングでは新しいことを学ぶとそれを確かめる簡単なプログラムを自分で色々作ってみるように、 新たに学んだことを確かめ、適切な回数練習できる問題集を片っ端から解いてみるのも一つの方法みたいな気がします。これなら成果が数字で目に見えるし、 動詞の人称変化や名詞・形容詞の格変化や単語の暗記も余り苦にならず繰り返し復習できそうです。 高知では英語すら話す機会がないし、 数学・コンピュータ関連・物理学書や外国の推理小説などの小説やインターネットのプログラミング関連の情報・記事を読むぐらいですが、 今は AI による翻訳も随分性能が良くなってきました。無駄な努力をしているような気もしますが不思議な文字を使う外国語が少し読めるようになると嬉しいです。 量子力学も数千円で出来る「偏光板とレーザーポインターと0.2mm のシャープペンシルの芯」を 使って、簡単な実験をすることで、光が粒子でありかつ波であることなどを理解できるそうです。やってみて、私は分かったような、騙されたような気がしましたが。

https://www.iwaxlab.com/articles?id=10 にある例wを CMakeLists.txt を作って、cmake する方法は次の様にすれば、コンパイル出来た。 CMakeLists.txt を 

cmake_minimum_required(VERSION 3.4)
project(pybindtest LANGUAGES CXX)
add_subdirectory(pybind11)
include_directories(c:/python/python310/include)
pybind11_add_module(pybindtest mylibs.cpp)
とし、最も簡単な方法は mylibs.cpp, mylibs.h, CMakeLists.txt のあるフォルダーに 

 mkdir build
 cd build
 cmake ..
 cmake --build .
を実行しますが、 

add_subdirectory(pybind11)
と指示している ので、同じフォルダーにダウンロードした pybind11 の展開したフォルダー pybind11_master を pybind11 と名前を変えてコピーして置く必要があります。 use_mylibs_module.py をここにコピーすれば、


の様になるので、pybindtest.pyd が出来ている訳ではないですが、 

python use_mylibs_module.py
を実行すれば、 

c:\C++src\cmake_test\pybindtest\build\Debug>python use_mylibs_module.py
48
[2, 4, 8, 10]
[[1, 2, 3], [1, 3, 6, 10, 15], [1, 0, 1, 0, 1, 0], [1, 3, 7, 15, 31, 63, 127]]
5 10 15
15 20 35
の様に実行できました。VC++ で .pyd を作る方法が分かったので、最早無意味ですが、意地になって出来る方法を見つけました。 mylibs.cpp と mylibs.h は勿論、変更する必要はありません。更に、この時、 use_mylibs_module.py を TeraPad のようなエディターで作ると 文字コードが違うので実行できません。他のファイルは TeraPad で大丈夫だったと思います。

これまでやって来た知識があれば、 https://pybind11.readthedocs.io/en/latest/ の pybind11 documentation に書いてあることは大体理解できます。差し合ったって必要なことを拾い読みすれば良いです。 やりたいことの第一歩は次のようなモジュール作成でした。 VC++ 2022 のプロジェクト名を simplecube とし、source.h を 

#pragma once

#include 

#define MAXDEG  50
#define MAXVERTEX 500
#define MAXEDGE 500


struct CVertex {
    double x, y, z;
    int degree;
    int e[MAXDEG];
};

class CPolyhedron {
public:
    CVertex vertex[MAXVERTEX];
    int n_vertex;
    int edge[MAXEDGE][2];
    int n_edge;

    CPolyhedron(int n);
    virtual ~CPolyhedron() {};
    void f444();
    std::vector> get_edge();
    std::vector> get_vertex();
};
とし、source.cpp を 

#include 
#include 

#include "source.h"

using namespace std;

CPolyhedron::CPolyhedron(int n)
{
    n_edge = 12;
    n_vertex = 8;
    f444();
}

void CPolyhedron::f444()
{
    int t_edge[][2] =
    { {0,1}, {1,2}, {2,3}, {3,0}, {5,4}, {6,5}, {7,6}, {4,7}, {0,4}, {1,5}, {2,6}, {3,7} };
    int t_face[][4] =
    { {0,1,2,3}, {7,6,5,4}, {8,4,9,0}, {9,5,10,1}, {10,6,11,2}, {11,7,8,3} };
    int i, j;
    int P = 4;
    int Q = 3;
    double PI = 3.14159265358979;

    n_vertex = 8;
    for (i = 0; i < 4; i++) {
        vertex[i].x = cos(i * PI / 2) / 2 + sin(i * PI / 2) / 2;
        vertex[i].y = sin(i * PI / 2) / 2 - cos(i * PI / 2) / 2;
        vertex[i].z = 0.5;
    }
    for (i = 0; i < 4; i++) {
        vertex[i + 4].x = cos(i * PI / 2) / 2 + sin(i * PI / 2) / 2;
        vertex[i + 4].y = sin(i * PI / 2) / 2 - cos(i * PI / 2) / 2;
        vertex[i + 4].z = -0.5;
    }
    n_edge = 12;
    for (i = 0; i < n_edge; i++)
        for (j = 0; j < 2; j++)
            edge[i][j] = t_edge[i][j];
    vertex[0].e[0] = 0; vertex[0].e[1] = 3; vertex[0].e[2] = 8;
    vertex[1].e[0] = 0; vertex[1].e[1] = 9; vertex[1].e[2] = 1;
    vertex[2].e[0] = 1; vertex[2].e[1] = 10; vertex[2].e[2] = 2;
    vertex[3].e[0] = 2; vertex[3].e[1] = 11; vertex[3].e[2] = 3;
    vertex[4].e[0] = 7; vertex[4].e[1] = 4; vertex[4].e[2] = 8;
    vertex[5].e[0] = 4; vertex[5].e[1] = 5; vertex[5].e[2] = 9;
    vertex[6].e[0] = 5; vertex[6].e[1] = 6; vertex[6].e[2] = 10;
    vertex[7].e[0] = 6; vertex[7].e[1] = 7; vertex[7].e[2] = 11;

    for (i = 0; i < this->n_vertex; i++)
        vertex[i].degree = Q;
}

std::vector> CPolyhedron::get_edge()
{
    std::vector> result;
    for (int i = 0; i < n_edge; i++) {
        std::vector v{ edge[i][0], edge[i][1] };
        result.push_back(v);
    }
    return result;
}


std::vector> CPolyhedron::get_vertex()
{
    std::vector> result;
    for (int i = 0; i < n_vertex; i++) {
        std::vector v{ vertex[i].x,  vertex[i].y,  vertex[i].z };
        result.push_back(v);
    }
    return result;
}

namespace py = pybind11;

//python側で使用するときのモジュール名になる。この場合"simplecube"となる
PYBIND11_MODULE(simplecube, m) {
    //モジュールの各種設定
    //このモジュールの説明
    m.doc() = "simplecube made by pybind11";
    //使用するクラスを指定
    py::class_(m, "CPolyhedron")
        .def_readwrite("n_edge", &CPolyhedron::n_edge)
        .def(py::init())
        .def("get_edge", &CPolyhedron::get_edge)
        .def("get_vertex", &CPolyhedron::get_vertex);
}
として、simplecube.pyd を作ります。 そして、 

import tkinter as tk
from OpenGL.GL import *
from OpenGL.GLU import *
import numpy as np
from OpenGL import GL
from pyopengltk import OpenGLFrame
import simplecube

cube = simplecube.CPolyhedron(0)
e_list = cube.get_edge()
v_list = cube.get_vertex()

##for i in range(cube.n_edge):
##    print(e_list[i])
##    print(v_list[e_list[i][0]])
##    print(v_list[e_list[i][1]])
    
rotate = 0

class AppOgl(OpenGLFrame):

    def initgl(self):
        global rotate, cube       
        glViewport(0, 0, self.width, self.height) ## 画面の描画領域       
        glClearColor(1.0, 1.0, 1.0, 1.0) ## 背景色
        self.n_model_list = [0]
        self.n_model = self.n_model_list[0]
        self.old_n_model = -1
        rotate = 0
        self.n_move_list = [0]
        self.n_move = self.n_move_list[0]
           
    def torad(self, deg):
        return deg*(math.pi/180.0)

    def redraw(self):
        global rotate
        self.n_model = self.n_model_list[0]
        glClear(GL_COLOR_BUFFER_BIT)
        
        if self.n_model == 0:
            rotate += 0.05
            if self.n_model != self.old_n_model:
                self.old_n_model = self.n_model
            glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
            glLoadIdentity() ## 投影行列を単位行列で初期化する
##            glOrtho(left, right, bottom, top, near, far) ## 平行投影
            glOrtho(-2.0, 2.0, -2.0, 2.0, -2.0, 2.0)
            glMatrixMode(GL_MODELVIEW)
            glLoadIdentity()
            glRotated(rotate, 1.0, 1.0, 0.0)
        elif self.n_model == 1:
            rotate += 0.05
            if self.n_model != self.old_n_model:
                self.old_n_model = self.n_model
            glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
            glLoadIdentity() ## 投影行列を単位行列で初期化する
##            glFrustum(left, right, bottom, top, near, far) ## 透視投影
            glFrustum(-1.0, 1.0, -1.0, 1.0, 2.0, 10.0) ## 透視投影
            gluLookAt( ## カメラを配置する
                0.0, 0.0, 4.0, ## カメラの位置
                0.0, 0.0, 0.0, ## カメラの視点の位置
                0.0, 1.0, 0.0, ## カメラの向き
            )
            glMatrixMode(GL_MODELVIEW)
            glLoadIdentity()
            glRotated(rotate, 1.0, 1.0, 0.0)
        elif self.n_model == 2:
            rotate += 0.05
            if self.n_model != self.old_n_model:
                self.old_n_model = self.n_model
            glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
            glLoadIdentity() ## 投影行列を単位行列で初期化する
##            gluPerspective(fovy, aspect, near,far) ## 透視投影
            gluPerspective(30, self.width/self.height, 0.1,100) ## 透視投影
            gluLookAt( ## カメラを配置する
                0.0, 0.0, 5.0,
                0.0, 0.0, 0.0,
                0.0, 1.0, 0.0,
            )
            glMatrixMode(GL_MODELVIEW)
            glLoadIdentity()
            glRotated(rotate, 1.0, 1.0, 0.0)
        if self.n_model < 5:
            for i in range(12):
                glColor(0.0, 0.0, 1.0, 1.0)
                glLineWidth(4.0) ## 線の幅
                glBegin(GL_LINES)
                s_vertex = v_list[e_list[i][0]]
                t_vertex = v_list[e_list[i][1]]
                glVertex3f(s_vertex[0], s_vertex[1], s_vertex[2])
                glVertex3f(t_vertex[0], t_vertex[1], t_vertex[2])
                glEnd()
                        
def change_tesselation():    
    # 現在選択されている項目のインデックスを取得
    indices = listbox.curselection()
    if len(indices) != 1:
        # ２つ以上選択されているor１つも選択されていない
        return
    # 項目を取得
    index = indices[0]
    app.n_model_list = []
    app.n_model_list.append(int(index))
    app._display()
    

if __name__ == '__main__':
    root = tk.Tk()
    root.title('立方体の表示')
    app = AppOgl(root, width=600, height=600)
    app.pack(fill=tk.BOTH, expand=tk.YES)
##    app.animate = 1
    app.animate = True
    listbox = tk.Listbox(root, height=3) ## default height=10
    listbox.pack(fill=tk.X)
    tesselations = ['平行投影', '透視投影:glFrustum()', \
                    '透視投影:gluPerspective()']
    for item in tesselations:
        listbox.insert(tk.END, item)
    button = tk.Button(root, text='選択', command=change_tesselation)
    button.pack(fill=tk.X)
    app.mainloop()
を simplecube.pyd のあるフォルダーで実行すると


のようなアニメーションが表示されます。vector の＜＞の表示や＿の後ろなど所どころ消えていますが、本当は何が書いているか分からなけれな、このページのソースコードを 表示して見ると良いです。キチンと表示する方法を本当は学ぶべきですが、見る人も殆どいなし、見る人は私よりこれらの知識があると思いますので、そのままにしています。 次は、例えば、「立方体の中央切り」のアニメーションの為の情報を作ってくれるモジュール作成をします。 C++ のプログラムの内部の処理は C++ のロジックで作り、Python とのインターフェースを vector で受け渡しをすれば、Python ではリストで受け取ってくれます。 このように、自分に出来ることを、自分の能力に応じて、理解できたことを使って段階的に作っていけば良いです。 何とか欲しいモジュールをどの様に作れば良いか分かってきましたが、Archimedes 全体のモジュール作成はまだまだ結構大変です。 しかも、この方法では特定の Python のバージョンのモジュールごとに作らなければならないですが、 自分の暇つぶしの為に、もう学生さんの教育をすることもないので、自分の為のプログラムを楽しみで作っているので問題はないです。

昔の Archimedes の C++ のプログラムを Python のモジュールとして作成してみました。 素人が一人で作ったプログラムですから、それぞれの準正多面体や星形多面体などを描画するのに必要なデータを計算し、 描画するだけの単純な構造をしているプログラムなので簡単に Python のモジュール（ライブラリー）に出来ます。 Visual Studio 2020 を立ち上げ、「新しいプロジェクトの作成(N)」を選択し、C++ の「CLR 空のプロジェクト」を選択し、 プロジェクト名を archimedes とし、「プロジェクト」の「新しい項目の追加」で、「source.h」、「source.cpp」、「Polyhedra.h」、「Polyhedra.cpp」を 作り、それぞれ以下のプログラムをコピーします。「Polyhedra.cpp」は長いのでここでは提示していません。 C++ と Python のインターフェースの為に 

#pragma once
#include "Polyhedra.h"
#include 

using namespace std;

class POLY {
	CModel* pmyModel;

public:
	int length;
	int base_n_edge;
	vector> base_edge;
	int base_n_vertex;
	vector> base_vertex;
	int n_face;
	vector> face;
	vector> normal;
	int n_vertex;
	vector> vertex;

	POLY(int type, int kind, int index);
	vector> get_base_edge();
	vector> get_base_vertex();
	vector> get_face();
	vector> get_normal();
	vector> get_vertex();
};
を source.h とし、 

#include 
#include 

#include "source.h"

using namespace std;

void CalcNormal(double p1[], double p2[], double p3[], double n[]);

POLY::POLY(int type, int kind, int index) {
	pmyModel = new CModel(type, (KIND) kind, index);
	// number of loop
	length = pmyModel->get_length((KIND)kind);
	// pmyModel::base's inf
	base_n_edge = pmyModel->base.n_edge;
	for (int i = 0; i < base_n_edge; i++) {
		vector e{ pmyModel->base.edge[i][0], pmyModel->base.edge[i][1] };
		base_edge.push_back(e);
	}
	base_n_vertex = pmyModel->base.n_vertex;
	for (int i = 0; i < base_n_vertex; i++) {
		vector v{ pmyModel->base.vertex[i].x, pmyModel->base.vertex[i].y, pmyModel->base.vertex[i].z };
		base_vertex.push_back(v);
	}
	// pmyModel::current's inf
	CPolyInf tmp = pmyModel->current.get_inf();
	n_face = tmp.n_face;
	for (int i = 0; i < n_face; i++) {
		vector f;
		for (int k = 0; k < tmp.face[i].size(); k++) {
			f.push_back(tmp.face[i][k]);
		}
		face.push_back(f);
		double p1[3], p2[3], p3[3], n[3];
		p1[0] = tmp.vertex[(tmp.face[i])[0]][0];
		p1[1] = tmp.vertex[(tmp.face[i])[0]][1];
		p1[2] = tmp.vertex[(tmp.face[i])[0]][2];
		p2[0] = tmp.vertex[(tmp.face[i])[1]][0];
		p2[1] = tmp.vertex[(tmp.face[i])[1]][1];
		p2[2] = tmp.vertex[(tmp.face[i])[1]][2];
		p3[0] = tmp.vertex[(tmp.face[i])[2]][0];
		p3[1] = tmp.vertex[(tmp.face[i])[2]][1];
		p3[2] = tmp.vertex[(tmp.face[i])[2]][2];
		CalcNormal(p1, p2, p3, n);
		vector nv{ n[0], n[1], n[2] };
		normal.push_back(nv);
	}
	n_vertex = tmp.n_vertex;
	for (int i = 0; i < n_vertex; i++) {
		vector v{ tmp.vertex[i][0], tmp.vertex[i][1], tmp.vertex[i][2] };
		vertex.push_back(v);
	}
	if (pmyModel != NULL) {
		delete pmyModel;
		pmyModel = NULL;
	}
}

vector> POLY::get_base_edge() {
	return base_edge;
}
vector> POLY::get_base_vertex() {
	return base_vertex;
}
vector> POLY::get_face() {
	return face;
}
vector> POLY::get_normal() {
	return normal;
}
vector> POLY::get_vertex() {
	return vertex;
}

namespace py = pybind11;

//python側で使用するときのモジュール名になる。この場合"archimedes"となる
PYBIND11_MODULE(archimedes, m) {
	//モジュールの各種設定
	//このモジュールの説明
	m.doc() = "archimedes made by pybind11";
	//使用するクラスを指定
	py::class_(m, "POLY")
		.def_readwrite("length", &POLY::length)
		.def_readwrite("n_base_edge", &POLY::base_n_edge)
		.def_readwrite("n_base_vertex", &POLY::base_n_vertex)
		.def_readwrite("n_face", &POLY::n_face)
		.def_readwrite("n_vertex", &POLY::n_vertex)
		.def(py::init())
		.def("get_base_edge", &POLY::get_base_edge)
		.def("get_base_vertex", &POLY::get_base_vertex)
		.def("get_face", &POLY::get_face)
		.def("get_normal", &POLY::get_normal)
		.def("get_vertex", &POLY::get_vertex);
}
を source.cpp とて新たに作り、C++ の本体として20数年前に作った193行のPolyhedra.h 

#ifndef POLYHEDRA_H
#define POLYHEDRA_H
#include 
#include 
#include 

#define MAXDEG  50
#define MAXVERTEX 500
#define MAXEDGE 500
#define MAXFACE 500
#define INNERPOINT 0
#define ENDPOINT 1
#define CONTAINED 2
#define ENDPOINT1 3
#define ENDPOINT2 4
#define ENDPOINT3 5
#define PI 3.14159265
#define MAXCOLOR 500

using namespace std;

enum {tetrahedron, cube, octahedron, dodecahedron, icosahedron};

typedef enum {tetrasimple, tetraatama, tetramiddle, tetraedgecut,
    tetradouble, tetratwist,
    cubesimple, cubeatama, cubemiddle, cubeedgecut,
    cubedouble, cubetwist,
    octasimple, octaatama, octamiddle, octaedgecut,
    octadouble, octatwist,
    dodecasimple, dodecaatama, dodecamiddle, dodecaedgecut,
    dodecadouble, dodecatwist,
    icosasimple, icosaatama, icosamiddle, icosaedgecut,
    icosadouble, icosatwist,
    tetradual, cubedual, octadual, dodecadual, icosadual,
    starsmalldodeca, starsmalldodeca2, starlargedodeca,
    starlargedodeca2, starlargedodeca3, largedodeca,
    largedodeca2, largeicosa, largeicosa2, starocta,
    starocta2, greatdodeca, stargreatdodeca, greaticosa,
    fiveocta, fiveocta2, fivetetra, fivetetra2, tentetra,
    tentetra2, triakisicosa, secondstar, thirdstar, fourthstar} KIND;

struct plain_vtx {
	int flag;
	int vtx;
	int se, te, sf, tf;
};

struct CVertex {
	double x, y, z;
	int degree;
	int e[MAXDEG];
	int f[MAXDEG];
};

struct CFace {
    int edge_n;
	CFace *next;
	CFace();
	CFace(int num);
};


struct CPolyInf {
    double vertex[MAXVERTEX][3];
    int n_vertex;
    vector face[MAXFACE];
    int n_face;
    int oldP[MAXFACE];
};

struct CPolyhedron {
    CVertex vertex[MAXVERTEX], j_vertex[MAXVERTEX];
    int n_vertex, n_j_vertex;
    int edge[MAXEDGE][2];
    int n_edge;
    CFace *face[MAXFACE];
    int n_face;
    float materialAmbient[MAXCOLOR][4];
    float materialSpecular[MAXCOLOR][4];
    int oldP[MAXFACE];
    UINT kind;
    plain_vtx V[MAXVERTEX];
    int n_V;
    int E[MAXDEG];
    int n_E;
    int j_vtx[MAXFACE][MAXDEG];
    int n_j_vtx;
    int C[MAXDEG];
    int n_C;

    CPolyhedron(UINT type);
    virtual ~CPolyhedron();
    void f333();
    void f444();
    void f3333();
    void f555();
    void f33333();
    void resize(double ratio);
    void reset();
    CPolyInf get_inf();
    int get_vertices(int face_n, int v[]);
    int get_target(int edge_n, int source);
    void cut(double K[][3], double G[], double n[], int ind);
    int get_V(double K[][3], double G[],  double n[]);
    void get_living_edge(bool e[]);
    int set_V(int ind, int vtx, double n[], int edge_n);
    bool outP(int v0, int v1, double n[]);
    int get_faces(int vtx, int e_num, int f[]);
    double inner_product(int edge_n, int vtx, double n[]);
    int get_source(int v0, int v1, double G[], double n[]);
    void modify_edges(double n[]);
    void set_new_edges();
    void modify_faces();
    void Delete(int face_n, int source, int target, int new_edge);
    void change();
    void del_faces(double G[], double n[]);
    void set_new_face(double n[], int ind);
    void sort_V();
    bool containedCP(int v0, int v1, int *edge_n);
    void set_new_edges2();
    void modify_faces2();
    void change2();
    void set_new_face2(double n[], int ind);
    void change(int ind, double *M, int i, int p, int n);
    void arrange(double *M, int var[], int n);
    double solution(int n, double *M, double eps, int *ans);
};

struct ConvexPolyhedron : public CPolyhedron {
    ConvexPolyhedron(UINT type);
    virtual ~ConvexPolyhedron();
    void truncated(int vertex_n, double K[3][3], double G[], double n[]);
    void middle(int vertex_n, double K[3][3], double G[], double n[]);
    int get_edges(int vtx, int top_e, int e[]);
    void get_coord(int source, int target, double t, double *px, double *py, double *pz);
    void cut_edge(int ind, int edge_n, double K[3][3], double G[], double n[]);
    void edge_cut(int ind, int vertex_n, double K[3][3], double G[], double n[]);
    void twist(int vertex_n, double K[3][3], double G[], double n[]);
    void set_key_point();
    int get_order_in_face(int face_n, int vtx);
    void twist2(int face_n, double K[3][3], double G[], double n[], int j, int v[], int n_v, int e);
    int get_adj_face(int vtx, int edge_n, int face_n);
    void dual(int vertex_n, double K[3][3], double G[], double n[]);

    void get_vertex(int v0, int v1, int v2, int v3, double P[]);
    void getSmallDodeca(int face_n, double K[5][3]);
    int getVertexNumber(double P[]);
    int getEdgeNumber(int v0, int v1);
    void addSmallDodeca(int face_n, double K[6][3]);
    void getLargeDodeca(int vertex_n, double K[6][3]);
    void addLargeDodeca(int vertex_n, double K[6][3]);
    void addDodecaLarge(int vertex_n, double K[6][3], CPolyhedron &base);
    void addDodecaLarge2(int vertex_n, ConvexPolyhedron &base);
    int get_adj(int face_n, int edge_n);
    void addIcosaLarge(int face_n, ConvexPolyhedron &base);
    void addSmallDodeca2(int vertex_n, ConvexPolyhedron &base);
    int get_adj_vertex(int vertex_n, int edge_n);
    void addLargeDodeca2(int face_n, ConvexPolyhedron &base);
    void addIcosaLarge2(int face_n, ConvexPolyhedron &base);
    int get_face_num(int vertex_n, int face_n, int ind);
    void get_intersection(double X[4][3], double Y[4][3], double Z[4][3], double K[3]);
    void get_coefficient(double X[4][3], double A[4]);
    void addLargeDodeca3(int face_n, ConvexPolyhedron &base);
    int get_face_num2(int vertex_n, int face_n, int ind, int ind2);
    void addStarOcta(int face_n, ConvexPolyhedron &base);
    void addStarOcta2(int face_n, ConvexPolyhedron &base);
    void addGreatDodeca(int face_n, double K[6][3], CPolyhedron &base);
    void addGreatIcosa(int face_n, ConvexPolyhedron &base);
    double get_crossing(double X[], double Y[], double A[], double B[]);
    void addFiveOcta(int face_n, ConvexPolyhedron &base);
    void addFiveOcta2(int face_n, ConvexPolyhedron &base);
    void addFiveTetra(int face_n, ConvexPolyhedron &base);
    void addFiveTetra2(int face_n, ConvexPolyhedron &base);
    void addTenTetra(int face_n, ConvexPolyhedron &base);
    void addTenTetra2(int face_n, ConvexPolyhedron &base);
    void addTriakisIcosa(int face_n, ConvexPolyhedron &base);
    void addSecondStar(int face_n, ConvexPolyhedron &base);
    void addThirdStar(int face_n, ConvexPolyhedron &base);
    void addStarGreatDodeca(int face_n, ConvexPolyhedron &base);
    void addFourthStar(int face_n, ConvexPolyhedron &base);

};

class CModel {
public:
    ConvexPolyhedron base;
    ConvexPolyhedron current;
    CModel(UINT type);
    CModel(UINT type, KIND kind, int index);
    ~CModel();
    int get_length(KIND type);
};
#endif
とこれらの関数を実装した 7703 行の Polyhedra.cpp を使って、「プロジェクト」の「archimedes のプロパティ」で、「構成プロパティ」の 「全般」の「構成の種類」を「ダイナミックライブラリ(.dll)」に変更し、「詳細」の「ターゲットファイルの拡張子」を「.pyd」とし、 「C/C++」 の「全般」の「追加のインクルードディレクトリ」と「リンカー」の「全般」の「追加のライブラリディレクトリ」に pybind11 のそれぞれの所在するディレクトリを教え、ビルド（コンパイル）して、 archimedes.pyd を作り、 

import tkinter as tk
from OpenGL.GL import *
from OpenGL.GLU import *
import numpy as np
from OpenGL import GL
from pyopengltk import OpenGLFrame
import archimedes

##cube = archimedes.POLY(1, 8, 0)
##print(cube.n_base_edge)
##e_face = cube.ger_face()
##n_face = cube.n_face

type = 1
kind = 7
cube = archimedes.POLY(type, kind, 0)

rotate = 0
index = 0
n_face = 0
length = 8

class AppOgl(OpenGLFrame):

    def initgl(self):
        global rotate, cube       

        cube = archimedes.POLY(type, kind, index)
        f_list = cube.get_face()
        n_face = cube.n_face
        n_list = cube.get_normal()
        v_list = cube.get_vertex()
        glViewport(0, 0, self.width, self.height) ## 画面の描画領域       
        glClearColor(1.0, 1.0, 1.0, 1.0) ## 背景色
        self.n_model_list = [0]
        self.n_model = self.n_model_list[0]
        self.old_n_model = -1
        rotate = 0
        glShadeModel(GL_FLAT)
        glEnable(GL_NORMALIZE)
        glEnable(GL_DEPTH_TEST)
        glClearColor(0.0, 0.0, 0.0, 1.0)
        ambientLight0 = [0.7, 0.7, 0.7, 1.0]
        diffuseLight0 = [1.0, 1.0, 0.0, 1.0]
        specularLight0 = [1.0, 1.0, 0.0, 1.0]
        positionLight0 = [500.0, 50.0, 100.0, 1.0]

        glMatrixMode(GL_MODELVIEW)
        glLoadIdentity();
        glLightfv(GL_LIGHT0, GL_AMBIENT, ambientLight0)
        glLightfv(GL_LIGHT0, GL_DIFFUSE, diffuseLight0)
        glLightfv(GL_LIGHT0, GL_SPECULAR, specularLight0)
        glLightfv(GL_LIGHT0, GL_POSITION, positionLight0)
        glEnable(GL_LIGHTING)
        glEnable(GL_LIGHT0)
           
    def torad(self, deg):
        return deg*(math.pi/180.0)

    def redraw(self):
        global rotate, index, cube, length, type, kind
        
        self.n_model = self.n_model_list[0]
        glClear(GL_COLOR_BUFFER_BIT)
        
        if self.n_model >= 0 and self.n_model < 20:
            if self.n_model != self.old_n_model:
                print('n_model=', self.n_model)
                self.old_n_model = self.n_model
                rotate = 0.0
                index = 0
                glClearColor(0.0, 0.0, 0.0, 1.0)
                
                print('A:type=', type, 'kind=', kind, 'length=', length, 'index=', index)
                cube = archimedes.POLY(type, kind, index)
                length = cube.length
                f_list = cube.get_face()
                n_face = cube.n_face
                n_list = cube.get_normal()
                v_list = cube.get_vertex()
            else:
                if rotate >= 360.0:
                    if index < length-1:
                        rotate = 0.0
                        index += 1
                        print('C:type=', type, 'kind=', kind, 'length=', length, 'index=', index)
                        cube = archimedes.POLY(type, kind, index)
                        length = cube.length
                        f_list = cube.get_face()
                        n_face = cube.n_face
                        n_list = cube.get_normal()
                        v_list = cube.get_vertex()
                    else:
                        rotate = 0.0
                        index = 0
                        print('B:type=', type, 'kind=', kind, 'length=', length, 'index=', index)
                        cube = archimedes.POLY(type, kind, index)
                        length = cube.length
                        f_list = cube.get_face()
                        n_face = cube.n_face
                        n_list = cube.get_normal()
                        v_list = cube.get_vertex()
        rotate += 0.1
        glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
        glLoadIdentity() ## 投影行列を単位行列で初期化する
##        glFrustum(left, right, bottom, top, near, far) ## 透視投影
        glFrustum(-1.0, 1.0, -1.0, 1.0, 2.0, 10.0) ## 透視投影
        gluLookAt( ## カメラを配置する
                0.0, 0.0, 4.0, ## カメラの位置
                0.0, 0.0, 0.0, ## カメラの視点の位置
                0.0, 1.0, 0.0, ## カメラの向き
        )
        glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
##        glMaterialfv(GL_FRONT, GL_AMBIENT_AND_DIFFUSE, materialAmbient[0])
##        glMaterialfv(GL_FRONT, GL_SPECULAR, materialSpecular[0])
	
        glMatrixMode(GL_MODELVIEW)
        glLoadIdentity()
        glRotated(rotate, 1.0, 1.0, 0.0)
        if self.n_model < 20:
            f_list = cube.get_face()
            n_face = cube.n_face
            n_list = cube.get_normal()
            v_list = cube.get_vertex()
                
            for i in range(n_face) :
##            glMaterialfv(GL_FRONT, GL_AMBIENT_AND_DIFFUSE, materialAmbient[tmp.oldP[i]]);
##          glMaterialfv(GL_FRONT, GL_SPECULAR, materialSpecular[tmp.oldP[i]]);
                glBegin(GL_POLYGON)
                glNormal3d(n_list[i][0], n_list[i][1], n_list[i][2])
                for k in range(len(f_list[i])):
                    glVertex3dv(v_list[f_list[i][k]])
                glEnd()
                        
def change_tesselation():
    global type, kind
    
    # 現在選択されている項目のインデックスを取得
    indices = listbox.curselection()
    if len(indices) != 1:
        # ２つ以上選択されているor１つも選択されていない
        return
    cut_kind = 0
    for language, val in languages: # ループ開始
        if val == select_var.get(): # 選択されている言語とlanguagesリストの言語を照合
            cut_kind = val
            
    # 項目を取得
    index = indices[0]
    if int(index) == 0:
        type = 0
        if cut_kind < 6:
            kind = cut_kind
        else: ## dual
           kind = 30
    elif int(index) == 1:
        type = 1
        if cut_kind < 6:
            kind = 6 + cut_kind
        else: ## dual
           kind = 31
    elif int(index) == 2:
        type = 2
        if cut_kind < 6:
            kind = 12 + cut_kind
        else: ## dual
           kind = 32
    elif int(index) == 3:
        type = 3
        if cut_kind < 6:
            kind = 18 + cut_kind
        else: ## dual
           kind = 33
    elif int(index) == 4:
        type = 4
        if cut_kind < 6:
            kind = 24 + cut_kind
        else: ## dual
           kind = 34
    elif int(index) == 5:
        type = 3
        if cut_kind == 7:
            kind = 35
        elif cut_kind == 8:
         type = 4
         kind = 36
        else:
            kind = 35            
    elif int(index) == 6:
        type = 3
        kind = 37
        if cut_kind == 7:
            kind = 37
        elif cut_kind == 8:
            kind = 38
        elif cut_kind == 9:
            type = 4
            kind = 39
        elif cut_kind == 10:
            type = 3
            kind = 47
        else:
            kind = 37            
    elif int(index) == 7:
        type = 3
        if cut_kind == 7:
            kind = 40
        elif cut_kind == 8:
            type = 4
            kind = 41
        elif cut_kind == 9:
            type = 3
            kind = 46
        else:
            kind = 40            
    elif int(index) == 8:
        type = 4
        if cut_kind == 7:
            kind = 42
        elif cut_kind == 8:
            kind = 43
        elif cut_kind == 9:
            type = 4
            kind = 48
        else:
            kind = 42            
    elif int(index) == 9:
        type = 2
        if cut_kind == 7:
            kind = 44
        elif cut_kind == 8:
            type = 1
            kind = 45
        else:
            kind = 44           
    elif int(index) == 10:
        type = 4
        if cut_kind == 7:
            kind = 49
        elif cut_kind == 8:
            kind = 50
        else:
            kind = 49           
    elif int(index) == 11:
        type = 4
        if cut_kind == 7:
            kind = 51
        elif cut_kind == 8:
            kind = 52
        else:
            kind = 51          
    elif int(index) == 12:
        type = 4
        if cut_kind == 7:
            kind = 53
        elif cut_kind == 8:
            kind = 54
        else:
            kind = 53          
    elif int(index) == 13:
        type = 4
        kind = 55
    elif int(index) == 14:
        type = 4
        kind = 56
    elif int(index) == 15:
        type = 4
        kind = 57
    elif int(index) == 16:
        type = 4
        kind = 58
        
    print('type=', type, 'kind=', kind, 'cut_kind=', cut_kind)
            
    app.n_model_list = []
    app.n_model_list.append(int(index))
    app._display()
    

if __name__ == '__main__':
    root = tk.Tk()
    root.title('立方体の表示')
    root.geometry("800x600") 
    app = AppOgl(root, width=600, height=600)
    app.place(x=0, y=0)
##    app.animate = 1
    app.animate = True
    listbox = tk.Listbox(root, height=17, width=25) ## default height=10
    listbox.place(x=620, y=20)
    tesselations = ['正四面体', '立方体',
                    '正八面体', '正十二面体',
                    '正二十面体', '星形小十二面体',
                    '星形大十二面体', '大十二面体', '大二十面体',\
                    '星形八面体', '五個の正八面体の複合体', \
                    '五個の正四面体の複合体', '十個の正四面体の複合体', \
                    '六十面体', '第二の星形', '第三の星形', '第四の星形']
    
    for item in tesselations:
        listbox.insert(tk.END, item)
    select_var = tk.IntVar() # ウィジェット変数select_varを作成
    select_var.set(0) # select_var変数に数値をセット
    languages = [("そのまま",0),("載頭(切隅)",1),("中央切り",2),\
                 ("削辺",3),("二重切り",4),("捩じり切り",5), ("双対",6), \
                 ("標準形",7), ("変種",8), ("変種２",9), ("変種３",10)]
 
    for language, val in languages: # ループ開始
        radio1 = tk.Radiobutton(root, text=language, value=val, \
                                variable=select_var) # languagesリストを選択肢とするradio1ウィジェットを生成
        radio1.place(x=620, y = 300+val*20) # radio1ウィジェットを配置
     
    button = tk.Button(root, text='選択', command=change_tesselation)
    button.place(x=650, y=550)
    app.mainloop()
を実行すると








のようなアニメーションをしてくれます。静止画だと何をしているか分からないと思いますが、まだ pyopengl の照明の仕方を理解していないので、綺麗な画像になりません。 基本的には、高知大学教育学部数学教室の山口俊博教授のホームページに載せていて、 誰でも無料で使える Archimedes.exe の単純なアニメーションがすべてこのような Python のプログラムで実行できるようになったのです。 但し、枠の表示などを可能にするためには、まだ調べていませんが更なる情報を取り出せるように　source.h と source.cpp を書き直さなければならないかも？ Archimedes.exe は教育実践共同研究を私一人でやっているのは怪しからんという人が出てきて、学部長から研究員を増やせと命令され、困って、 私のゼミ出身の久武大介（室戸高）と福島勝成（西部中）（当時の所属）の両君に急遽グループに加わって貰い、使用感や使い易さに関する意見を 出して貰いました。 一つのコンピュータで開発していたので気が付かなかったことですが、スピードの調節が 必要なことやビデオレコーダの様に停止したり、再実行したり、逆回転する機能を付け加えたらいいのではとの提案をいただき、 そのようにソフトを作り直しました。 自分の講義で使うだけなら、受講生の反応を見て、修正できますが、一般に公表するには、一人で開発していると自己満足で終る可能性はあります。 故人を悪く言うのは慎むべきですが、この学部長は誰かの圧力があったのか、全員参加と言いながら、 共同研究に参加していない教授や外部の高校の先生との二人で研究している先生もいるのに、 最後は付属校園の教員が参加していないのは怪しからんから増やせと命令してきて、仕方がないので、唯一面識のある、付属中学に採用されたばかりの数学教室の卒業生に 名前だけでいいから参加してほしいと頼みました。リーダーに必要なカリスマ性もコミュニケーション能力もなく、「長」と付くものは、小学校で先生が勝手に決めた 「級長」を一回やっただけで、選挙でえらばれる「長」と付くものは一度もやったことの無い人間は、一人で好きなことをやっていたいのに、 次々と色々押し付けられても困惑します。 超有名大学も大変だと聞きますが、弱小地方大学で生きていくのも様々なことが次々起こりそれなりに大変です。 このページも整理して古い余計なたわ言は消して、最近のものだけにしないと 19MB になっているので、現在の契約は 20MB なのでメモリー不足です。 メモリーを増やすには基本料金では駄目で、追加る料金が必要で、これで広告収入などの利益を得ている訳ではないので、年金生活者にはきついです。 Python のモジュール作成をやってみたいと思って、調べ始めてから随分時間が 掛かりましたが何とか自分が使うためのモジュール作成は出来るようになりました。 現在は、Python のモジュール作成のような既に良く知られている技術は、インターネットに沢山の情報があり、間違っていたり、時代遅れになっているものも多いですが、 コンピュータが何が正しいか教えてくれるので、高知のような田舎で、先生も共に学ぶ朋友もいなくても学ぶことが出来ます。良い世の中になりました。 このようなモジュールを作っても大した意味はなく、 今回のモジュールは使い方がどの立体を描かせるか二つの数字 

enum {tetrahedron, cube, octahedron, dodecahedron, icosahedron};

typedef enum {tetrasimple, tetraatama, tetramiddle, tetraedgecut,
    tetradouble, tetratwist,
    cubesimple, cubeatama, cubemiddle, cubeedgecut,
    cubedouble, cubetwist,
    octasimple, octaatama, octamiddle, octaedgecut,
    octadouble, octatwist,
    dodecasimple, dodecaatama, dodecamiddle, dodecaedgecut,
    dodecadouble, dodecatwist,
    icosasimple, icosaatama, icosamiddle, icosaedgecut,
    icosadouble, icosatwist,
    tetradual, cubedual, octadual, dodecadual, icosadual,
    starsmalldodeca, starsmalldodeca2, starlargedodeca,
    starlargedodeca2, starlargedodeca3, largedodeca,
    largedodeca2, largeicosa, largeicosa2, starocta,
    starocta2, greatdodeca, stargreatdodeca, greaticosa,
    fiveocta, fiveocta2, fivetetra, fivetetra2, tentetra,
    tentetra2, triakisicosa, secondstar, thirdstar, fourthstar} KIND;
で指定しなければいけなくて誰も使う気のしないモジュールですが、勿論、一つの数字： 

typedef enum {tetrasimple, tetraatama, tetramiddle, tetraedgecut,
    tetradouble, tetratwist,
    cubesimple, cubeatama, cubemiddle, cubeedgecut,
    cubedouble, cubetwist,
    octasimple, octaatama, octamiddle, octaedgecut,
    octadouble, octatwist,
    dodecasimple, dodecaatama, dodecamiddle, dodecaedgecut,
    dodecadouble, dodecatwist,
    icosasimple, icosaatama, icosamiddle, icosaedgecut,
    icosadouble, icosatwist,
    tetradual, cubedual, octadual, dodecadual, icosadual,
    starsmalldodeca, starsmalldodeca2, starlargedodeca,
    starlargedodeca2, starlargedodeca3, largedodeca,
    largedodeca2, largeicosa, largeicosa2, starocta,
    starocta2, greatdodeca, stargreatdodeca, greaticosa,
    fiveocta, fiveocta2, fivetetra, fivetetra2, tentetra,
    tentetra2, triakisicosa, secondstar, thirdstar, fourthstar} KIND;
だけで、指示するように変更できますが。この表を見ながら、どれを表示するか指示する必要があります。 ちょっとやってみていましたが、このようなプログラムを全部 Python で作るのは大変で、 20数年前に私が作った Borland C++ Builder で作り、今となっては VC++ 2022 で作り直そうと言う気がしなかった C++ のプログラムの再利用が、 Python のモジュールとして復活でき、良い勉強・良い暇つぶしになりました。プログラミングは高知のような僻地でも誰にでも手軽にできる物づくりです。 Archimedes.exe のような単体の完全なソフトであれば作者が意図した使い方しか出来ませんが、このような Python のモジュールであれば、 ある意味怖いことでもありますが、その中身で何をしているか（ひょっとしたら「トロイの木馬」が組み込まれているかもしれません）を理解できなくても、 インターフェースだけ分かれば、 これをつかう Python のプログラムを自分の欲しいものにすることにより、もし良いアイデアがあれば、さまざまなソフトを簡単に作ることが出来るようになります。 昔は将棋のソフトも一つ1万円で売れるので、何をしているか秘密にされることも多かったし、私が鳴門教育大学で、プログラミングの集中講義をした時、 呼んでくれた兄弟子に、「せっかく苦労して作ったプログラムを全部学生に見せても良いのか？」と聞かれ、「えっ！」と思いましたが、 画期的な強い将棋のソフトのソースコードを公開する人が現れ、一気に将棋ソフトの実力が向上し、プロ棋士を負かす様になりました。 プログラミングによって、お金を稼ぐことも名声を得ることも有利な就職を得る手段にもなりますが、このようにプログラミングの世界では、 才能ある優秀な人達がフリーソフトに関するルールをキチンと作り、ソフトそのものではなくても、そのソフトを解説する書籍の出版などでも収入を得る手段もあるので、 ソースコードを公表する文化を徐々に作り上げ、ソースコードを見ることの出来るフリーソフトがインターネット上に溢れるようになり、 インターネットにアクセスできる環境にいれば、住んでいる国や地域・貧富に関わらず、誰でも競争に参加でき、プログラミングの世界は物凄いスピードで技術革新が進んでいます。 この archimedes.pyd は欲しい人がいれば、差し上げますが、インターネットでどう配布すれば良いかまだ分かりません。 インターネットの解説は archimedes.pyd を更に加工して、一般にモジュールとして配布されている形にする方法ばかり解説していますがまだ理解できません。 「.exe ファイルは、どうすれば良いかわからん」と在職中ある学生さんに話すと「簡単なことで単純に一行で済むよ！」と教えて貰ったのですが、 .pyd も単純に同様にすれば、兎も角、ダウンロード出来るようになるのかな？やってみれば分かることですがこのホームページの容量がなくなった。

Knuth さんの Mix もこのようなことが出来ないかと思って、ソースコードを調べてみましたが、Archimedes は画像の為のデータ作成の数値計算がプログラミングの 大部分で完全に分離したクラスとして標準な C++ で書かれていて、データ作成を C++ で作り、表示を Python で行うと言う形態で分離しやすかったので、 上で述べたようなモジュール化が簡単に出来ましたが、Mix はこのような計算はほとんどなく、メインの7611行のプログラムは 各々の処理すべてに画面の表示の更新が必要で Borland C++ Builder 固有の 記述が為されているので、完全に VC++ か C# で書き直す必要があり、上の方で縷々書いたように楽な仕事ではなし、最初の50０個の素数を計算するプログラムを アセンブルし、実行している MIX の動作を観察できるので、 それで計算機の仕組みは説明できるので、作り直押すのは止めです。 上の多面体のプログラミングの続きは、私が持っていて読んでない H.S.M.Coxeter 著「Regular Polytopes」や Peter R. Cromwell 著「POLYHEDRA」 を読む必要があります。 更に、種々の外国語達の勉強と Feynman さんの有名な本（原著）とタイリングの本などを読みたいので、 プログラミングは何か面白そうなことを思いつくかプログラミングしてみようと思う新しいタイリングの例を見つけるまでお休みです。 数学やプログラミングや外国語はそれそのものを研究する専門家以外の一般の人達にとっては、 金槌やノコギリのような物づくりの為の必要不可欠なものですが、物づくりの単なる道具であって、 道具の使い方だけ幾ら学んでも、 それで何を作るか、何を作りたいか、作りたいものに関する知識・情熱がないと何にもなりません。これも「鶏が先か、卵が先か」ではあります。 プログラミングに関しては、アルゴリズムを実装するのがプログラミングなので、 先ずはアルゴリズムの作成・理解が大切だと言うことで、 フィンランド人の若い女性が作った 絵本 Linda Liukas 著「HELLO RUBY」（翻訳：「ルビーの冒険」、RUBY はプログラミング言語 の RUBY ではなく、主人公の女の子の名前です）がプログラミング言語を 使わず、小さな子供たちにプログラミングの考え方・子供向けのアルゴリズムを身に着けさせようという本が世界的な大ヒットしました。

例えば、 アラビア語はまだまだ小説（コーランでなく千夜一夜物語）を辞書を引き引きすらすら読めるレベルになってないので、 （著者も書いているように初級・中級文法の参考書で、入門書ではなく、丸暗記するのでなければ、入門書を読んで基本的な文法の知識がないと 印欧語の様に単語が必ずしも分かち書きされていないので、 （例えば、アラビア語では lilmu'minIna は前置詞 li + 冠詞 'al（続けて書く時 'a　が消えている） + 名詞 mu'minuN の（男性規則）複数の属格：mu'minIna を 一つの単語の様に続けて書いています。 インターネットにはアラビア文字の表示の仕方も書いてありますが、たまたま見つけたその情報だけでは不十分でまだ上手くいきません。） 最初から正確には読めない参考書だし、音声も僅かですが、） 大阪大学外国語学部の「世界の言語シリーズ１７　アラビア語」＋「アラビア語　別冊」が初級のアラビア語の学習に必要な物がすべてセットになっていて、 練習問題も沢山あるし、パソコンや電卓やスマホやリモコンやスーパーマンといった古本で集めた有名な古い日本の参考書にはない単語もあり、 同じ単語が繰り返し出てきて自然に覚えられる様に配慮された、（それでも私には不十分で、覚えようと努力しないとなかなか覚えられないですが） 日本で出版されたアラビア語参考書では私の知る限りでは唯一の貴重なもので、 単語も纏めて100語・200語覚えろではないので、私には現時点の丁度の参考書みたいで、 「Alif Baa」などと併用すれば、アラビア語の勉強を細々と続けることが出来そうです。 アラビア語の私が手に入れた「千夜一夜物語」には母音の記号が書いてないですが、これでは古代の暗号にも使われていた技法と同じで、こんなもの読めるだろうかと 思っていましたが、（初心者は語尾の母音の違いによって、主格・属格・対格を判断しますが、母音がないと別のことで判断しなければなりません。）、 アラビア語の力が少しは付いてきたせいか、この本の練習問題の「母音記号等を付けよ」を解き続けていると段々母音記号無しでも読めるようになります。 但し、例えば、「女性教師」と「学校」は語根が同じで母音記号等（重子音記号：シャッダ）無しでは同じになるし、 「教師」の双数形と複数形の属格・対格は母音記号無しでは全く同じで、発音は異なるので文脈で判断する必要があります。 また、「男」と「脚・足」も母音記号無しでは同じですが、rajulun と rijlun と発音が異なります。 このように基本単語にもこんなのが一杯あります。ヘブライ語も母音記号無しで、昔専門家も誤訳して、 聖人だったかの肖像画に角を生やしてしまったと言う例があるそうです。 Al Jazeera Arabic のライブ動画も母音記号が付いていません。何を言っているかは shukraN や 日本語と同じ発音のバングラデシュやワシントンやデモクラシーやリビアやアメリキーヤ（アメリカのこと：日本はヤーバーニィヤですが重要視されていないので出てきません）や バイデンや僅かに暗記しているアラビア語の単語など以外は勿論全く分かりませんが、 動かない大きい文字を見ると今はスーダン（よく聞くとスーダンもスーダンと言っています）を話題にしていることやサッカーが大好きだということ位は 分かります。日本のテレビでは話題にされない国々もあり。彼らは何処の国に興味があるかぐらいは分かります。天気予報も面白いです。 何を言っているか分かる日が来ると良いですが。文字も表示されていますが凄いスピードで流れていきます。しかし、インターネットでライブ画像が見える良い時代になっています。 今日（4月18日）も私が見ていた時間はスーダンの内戦の映像ばかり放送しています、残念ながら、詳しいことは新聞（高知新聞）の記事以上のことは分かりませんが。 今日（4月20日）は大きいディスプレイを使い日本のテレビの囲碁講座の様にアイコンを色々選びながら、地図上で戦闘の状況も説明しています。 各国の見慣れた顔も出てきます。アラブ世界では現在はウクライナよりスーダンの戦況が重要見たいです。 今日（4月21日）は米国や英国やフランスの新聞が何を報じているかもその国の言語のまま（英語やフランス語で）、 掲載されている写真もそのままだと思いますが表示していましたが、あっという間に流れていき消えます。 余程、ネイティブのような語学に堪能な人でないとそれだけでは何て書いているか読めません。 今日（4月23日）はジブチに日本の自衛隊が来たことも地図や飛行機の絵（日の丸を描いているので日本の自衛隊のことだと分かります。 日の丸に対して色々な意見がありますが、他の国の国旗に比べ、単純な図案で、小さく一瞬の表示でも日の丸だと認識できます。）も示しながら報道しています。 又、スーダンから周辺の国々へ脱出ルートなど地図と絵（空港や飛行機やヘリコプタなど）を表示しながら分り易く説明していますが、 アラビア語を聴き取れないので（まだ文字で書いてあっても読めないので：文字の無い言語も多いし、文字の使用は最近のことで、歴史が遥かに長い、 音声での理解が基本だとの主張もあります。）正確なことは残念ながら理解できません。こうだろうと想像するだけです。 今日（4月24日）は各国がヘリコプターや船舶を使って、どの様に救出しているか、地図とヘリコプターや船舶や車のイラスト（プロペラが回転しています）と 写真を苦に合わせ何処にヘリコプターを付けたか何処から避難人がヘリコプターに乗ったかも 示しながら日本のテレビより遥かに分り易く報道しています。何を言っているか幾つかの単語（特に国名）しか分からなくても画面を見ていればおおよそのことは分かります。 ロシアやスーダンと隣接国のエチオピアやリビアなとの関係をイラストも示しながら話題にしていますが、何を言っているかは残念ながら分かりません。

今日（4月30日）はスーダンの情勢が落ち着いているのか、ウクライナやパトリオットの映像やキリル文字の表示もあります。 中国は「アッスィーン」と言いますが、聞きなれない言葉なので、報道されているかどうかまだ分かりません。アラビア語がもっと分かると良いですが、 何年掛かることやら。

今日（5月3日夜）は多分、ウクライナがモスクワのクレムリンを攻撃したとずっと報道している。 アラビア語の力がないので何を言っているか正確には分からない。地図でウクライナからモスクワへ線を引いて解説していたのでミサイルで、空中で爆破したと思ったのですが、 直後に見たテレビ news23 によるとドローン攻撃だそうです。 よくこんな映像が撮れたなとは思ったが、こんな映像を見たことなかったので凄いことになったと思ったが間違えた。ウクライナの攻撃か真偽不明だそうです。

今日（5月15日）はトルコの大統領選挙の報道をしています。日本にとっては遠い親日国の一つと言うことで、選挙結果しか興味がないみたいですが、 アラブ世界にとっては誰がなるかが大問題みたいで、4人が立候補していてそれぞれの支持率（多分）やエルドアン（アルドアンと言っています）大統領が物凄い人数の大衆の前で、 どんな演説をしているか 延々とその映像と共に、翻訳して放送しています。「アンカラ」などしかアラビア語が分からなくても（有名な井筒俊彦さんのアラビア語の勉強の仕方を読めば、 アラビア語を学ぶことがどれだけ大変か分かります。）映像を見るだけでも色々分かります。トルコの地図でそれぞれの陣営が支持を得ている地域を図示して 「イスタンブール」での得票率や「アンカラ」での得票率などを次々解説しています。 日本がアメリカの大統領選挙に関心があるように、アラブ世界は隣接するトルコの変化に重大な関心があるみたいです。 アラビア語のアラビア数字でなく、普通のアラビア数字を使って表示していることに今日初めて気が付きました。 文字を読むと「開票率」だと思いますが９７％と出ていますが、今はエルドアン：49.35%、その他の人：44,97%、5.25%、 0.43%と表示されていますが、この数字が しょっちゅう変化しているように思います。開票が１００％でないので大票田の値で変化するのだろうか、そんなことはあり得ないので、 ある地域の得票率を全体の得票率だと私が勘違いしたと言うことかな？多分、そうです。 開票風景も放送しています。候補者4名の写真付きの紙に丸印を付けるみたいで、投票箱から取り出し、手作業で一枚ずつ、多分、管理人達（？）に見せながら、 一瞬でそれで分かるとは思えないですが、集計しています。 日本に住んでいる外国人で無くてもピーター・フランクルさんが書いていた様に色々な情報を得る手段を持っていることが必要みたいです。 日本はアメリカに助けてもらわないと生きていけないと政治家が意味ありげにニヤニヤ笑いながら発言していましたが、 隣接する超大国中国・ロシアにも助けてもらわないと生きてはいけません。日本はアメリカだけでなく、今まで平和国家として、戦争をしない国であると言う 信頼で、世界各国の助けで、外交努力だけで、生き延びてきたはずです。 スーダンではアメリカは軍用ヘリコプターで真っ先に自国民を救出しましたが、私の思い違いでなければ、他国民の救出に協力したとの報道はなかったのではと思いますし、 日本は国連や米以外の他の国々に助けられ救出したと報道していたと思います。アメリカに必死で尽くしていてこの結果です。 日本が生き延びるには何が本当は大切か一人一人自分の頭で考えることが大切です。 アメリカだけに従っているとアメリカの奴隷にされるだけです。最近の韓国と日本に対するアメリカの扱いに注目してください。 その微妙なバランスの中でに、ニューヨークタイムズが報道した（政府は慌てふためいて書き換えを頼み込み、有名人が「売るために刺激的な表題を付けるものだ」と 援護射撃していましたが）アメリカの危険な役割の先陣を務める、国民を満足に食べらしていけない国が外国に目を向けらすための「軍事大国」としてではなく 今まで通り「平和国家」として外交努力でしたたかに生きていく必要があります。 今すべきことは、「ウクライナ戦争を止めらせる事であり、日本人は犠牲になっていないからといって、戦いを長引かせ死人を増やすことではありません。 スーダンでは停戦させるのにウクライナではそれをしないのは何故でしょう？ロシアがけしからんかどうかは後世の人達が検証すれば良いことです。 戦争が兎も角終わればロシアの核兵器使用の心配も無くなります。何が本質か考える必要があります。」。 それが再び戦争に巻き込まれず、再び核兵器で国土が破壊されない唯一の方法です。 従って、日本や英米だけでなく、例えば、イスラム世界のような異なる立場の国々の 報道にも注目していないと戦前の日本のような状態（大本営発表だけで誘導される）に日本は置かれます。日本で余り報道されていないことが報道されています。 19日にはゼレンスキー大統領がサウジアラビアで演説している様子が大々的に報道されていました。 こんなことを書くと、ロシアを潰したい人達に、何か潰すための落ち度がないか・なんかでっち上げることが出来ないか必死で探されますが、 今まで大学でさんざんやられてきたことでもあり、まだ読みたい本も一杯残っていますが、もう十分生きてきたとも言えます。 弱い魚が一匹で、凶暴な魚の集団に対応するのは、神経をすり減らし、身の回りで何が起こっているか常に注意する必要があり、物凄く大変です。 殆ど読む人のいないこんなしょうもない文章を書いてる人間より、もっと重要な・政権に批判的なことを書いている本や情報発信などが現在沢山されていると思いますが、 先日も公園で本を読んでいると男の人が話しかけてきて、長時間話をしましたが、途中、別の人がやってきて、話しているテーブルに来ましたが、 前に来た人との話に気を取られるうちにいなくなっていましたが、 家に帰って見ると持っていたはずのシャープペンシルが 無くなっていました。どっかで落とした可能性もありますが、疑い出すとキリがないですが、二人で組んで、私の指紋が欲しかった可能性もあります。 推理小説の読みすぎによる妄想だと良いですが。生きていくのは大変です。

矢張り、適切な参考書を、適切な順序で読む必要があります。唯、若くなく独学なので、色々試行錯誤してみないと自分にとって良い方法が分かりませんが。 もう、年金生活者の「かくあらねばならない」の無い趣味の暇つぶしですから、根を詰めてする必要もなく、嫌になったら別のことをし、気楽に続けることが出来ます。 欠点は、老人には文字が小さすぎて虫メガネ（ルーペ）が必要なことですが、文字を大きくすればページ数が更に多くなり持ち運びに不便になります。 更に、例えば、名詞や形容詞の複数形の作り方は他の言語と比べ、翻訳を禁じられた絶対的な存在の「コーラン」があり、 （日本語の翻訳は翻訳ではなく、コーランの解説書と言うことで存在を認められているそうです。宗教は「奇跡」の存在が普及に不可欠みたいで、 先日も近くの札場公園で本を読んでいると2人連れの老婦人（一人は高齢ではなかったかも？主にしゃべっていたのは老婦人でした。）がやってきて、 「日蓮何とか教」の勧誘を始めました。「日蓮」なら「創価学会か？」と聞くと あれは邪教だから止めた、「池田会長を崇拝しているだけだ。」と言い、鬱で自殺も考えていたがこの宗教に入信して道が開けた。 金儲けだけ考えている仏教界からの反発・憎悪を受け、処刑されることになるがと、日蓮の龍ノ口の奇跡（法難）の話をし、当時の元寇と同じく、 現在は中国の台湾・尖閣諸島侵攻の危機が迫り、 日本も無傷で済むはずも無く、南海地震もいつ起きても不思議ではない。必ず起こるんですと若い方が口をはさんでいました。我々は統一教会や他の宗教のような金儲けでなく、 信者からお金を集めて建てた立派な建物がある訳ではなく、お金は必要なく、質素な3階建ての建物で、 毎日２０分お経を一心に唱えれば、このような災難から逃れることが出来る。○○高校や○○高校の生徒など高校生に入信者が多く、進学や就職で成果を挙げて、皆感謝している。 先ずはこの新聞を読んで見なさい。こんな感じの話をしていました。「私は忙しいからそんなことしよりけにいかない。」といって帰りましたが、 「奇跡」や「迫害」が心に響くみたいです。 又、最近の世界情勢を契機に、色々な動きが色々な処で出てきているみたいです。） 他の言語で起きた簡略化が文語では起こらず、 複雑怪奇で、 有名な古い本には不規則な名詞の複数形が細かく分類して解説されていて、これは覚えきれないと思い、カードを作りましたが、 このような覚え方も上級になればあると言うことだけ頭の片隅に入れて置き、初級レベルでは、この本に書いてある基本的な法則を 先ず繰り返し練習して覚えるのが良いような気がします。 才能ある優秀な人達は、自分で何が必要か考え出し、工夫して必要なものを手に入れる手段を考え、手に入れ、そして学び、暗記しますが、 我々凡人にはそれを助けてくれる学ぶべき事柄を解説した解答付きの例題が提示され、それを練習する適切な個数の解答付きの問題が提示されている参考書が必要です。 私は中学校の数学や英語はそのような参考書にたまたま出会うことが出来て学ぶことが出来ました。語学は更に、その前に、「20ヶ国語ペラペラ」に 「鸚鵡（オウム）返しと言うが、観察してみると鸚鵡は一回聴いて喋るのではなく、何回も何回も同じことを聴いて初めて喋る」と書いてあるように、その言語の音に慣れるまで、 意味がわからなくても只管聴く必要があるみたいです。 中学生時代に、「先ず、数学全体でなく、数学のどれか一つの領域・単元を完全に勉強して、その単元の問題は完全に解ける様にして自信を付けなさい。」と言う先生もいましたが、 先生はこのスローガンだけで十分だと思ったと思いますが、 それだけでは数学の苦手な生徒はどうすれば良いか分かりません。その為に先生自身はどのようにしたか、どのな方法があるか、 経験の乏しく考える材料を持ち合わせていない普通の中学生には、その為の考えられる様々な勉強方法を具体的に提示する必要があったのではと思います。 それを自分で考え出せるようになるのが勉強で、考える力を養うことだと言う主張も勿論ありますが。 昔、中学校で野球部の監督をしていた数学教室の卒業生が、「今の子供は単にこう言う練習しろと言っても駄目で、何故その練習をしなければいけないか説明し、 納得しないと練習しない。」と言っていました。 「Alif Baa」には日本語の参考書に書いてない文字の書き方が動画で説明されています。 Alladin と言うオンライン辞書（アラビア語辞書では普通の語根順ではなく、パスポート初級アラビア語辞典の様に、アルファベット順で引けます。 パスポート初級アラビア語辞典も語数が多いわけでないので、刀(swords)：saifun の複数形：suyu-fun などその単語を出て来た時に暗記する能力がない私などは、 単数形を予想してパスポート初級アラビア語辞典などをひくか、その語根を予想して、 池田修・竹田新編「現代アラビア語小辞典」などの語根順の辞書で調べる必要があります。アラビア語の場合、上達して来ると語根順の辞書の方が色々と便利みたいです。 大阪大学外国語学部の「アラビア語　別冊」の巻末の単語集はアルファベット順ですが、世界中に植民地を持っていた民族のアラビア語の参考書： J.A.Haywood and H.M.Nahmed 著「A new Arabic grammar of the Written Language」の巻末の単語集は語根順になっていることから分かるように、アラビア語は、 語根が同じものを纏めて覚えること・私の様に覚えられなくとも「アラビア語の語彙の仕組みはどの様になっているか」毎回眺めておくことが重要だと言うことみたいです。 では、英語やロシア語はどうだろうと考えてみる必要があるみたいです。若い時は考えもしなかった。 勿論、あれ！と思えば、複数の紙の辞書や文法書で調べる必要があります。 例えば、maktabuN を Alladin で引くと語根：kataba 意味：[男]事務所とだけ出てきますが、それでは意味が通じなければ、「机:desk」という意味もあることを 別の辞書で調べる必要があります。但し、青色の「事務所」をクリックすれば、「机:desk」を含む沢山の意味や熟語が出てきます。ソフトの使い方を知ることも大事です。 語根：kataba の単語は「書く」ことに関係していて、ma- で始まる単語は場所に関係していることが多いといったことを少しづつ覚えていきます。 記憶力の良い人は単語一つ一つばらばらに片っ端から丸暗記した方が効率が良いとは思いますし、入門期は先ず重要単語の丸暗記だと思いますが。 日本語の過分数は「過」が余分だと言うことで、分子が分母より大きい、帯分数は「帯」が帯びるで整数がくっ付いたものと覚えるのと多分同じことです。 算数・数学が分かるようになるには、先ず日本語・国語が分かるようにする必要があります。その為には本（漫画でも良いかも？）を沢山読む必要があります。 その為には .... です。）も使えるし、 アラビア語も随分独学できる環境が整ってきました。 スマホのカメラで写すだけでも翻訳してくれます（高知大付属病院のお医者さんがやって見せてくれました）が、アラビア語はまだまだ翻訳の精度が良くないみたいです。 有難いことです。唯、日常語は「デイリー・日本語・アラビア語・英語辞典」は出版されましたが、「デイリー・アラビア語・日本語・英語辞典」はまだ出版されていません。 データをコンピュータに入れていれば、並べ替えだけで出版出来るはずですが、需要が見込めないのでしょうか？ 例えば。ghalyu-n:パイプ（「管の」と「煙草の」で違う単語を使うみたいですが）の訳語を辞書で探すのに （「世界の言語シリーズ１７　アラビア語」には載っているので暗記すれば良いだけですが）苦労します。 J.A.Haywood and H.M.Nahmed 著「A new Arabic grammar of the Written Language」+ 「Key to A new Arabic grammar of the Written Language」も面白い本です。 特に、大量の練習問題（各セクションごとにアラビア語から英語へと英語からアラビア語へが20問づつ） と transcription の練習が前半にかなりあること（p.62 まで：著者はアラビア文字が自由に読めるまで、 transcription も載せていると 思いますが、 transcription からアラビア文字への変換の練習にも使えます。）と合字が使われていることと語尾の ya-' に点々がない（？）ことに特徴があります。 transcription からアラビア文字への変換が自由に出来だすと有名な井筒俊彦さんの参考書を読んで見ようという気になるかも？ 「読みもしない・読めない本を一杯集めてどうするんだ！チャンと一冊づつ読め！」ですが、時々思い出して眺めるだけだったのが、やっと、 どう言う訳か、最近このような本が時間は物凄く掛かりますが読めるように・読んで見ようという気になってきました。もう手遅れですが。 プログラミング言語は人工的なもので、構文も意味も例外は無く、正しいかどうかはコンピュータが教えてくれるので、独学が出来ますが、外国語は文法が先にあるのではなく、 言語が先にあり、それを合理的に説明するために学者が試行錯誤しているもので例外も多く、才能ある優秀な人は「20ヶ国語ペラペラ」の著者の様に、 どの様に学べば良いか自分で考え出しますが、我々凡人は「解答付きの練習問題集」で強制的に文法規則が身につくまで必要な回数練習を繰り返し学ばないと 普通の参考書のような文法規則の羅列を何回も繰り返し読むのは苦行で、本に書いてない単語の活用・変化の答えが正かどうかも自信がなく、 辞書でいちいち調べるのもめんどくさいし、調べても分からないことも多いし、直ぐ飽きて、学ぶことを止めてしまう様に思います。 原理的には四則計算位しかできないコンピュータが AI として現在脚光を浴びているのは、大量のデータを与え、これは正しい、これは間違いと教えているからで、 絶対的に正しい答えではないですが、統計的に妥当で十分実用に足ると思われる答えを出すことが可能になって来ているのだと思います。 インターネットの情報を元にした AI はインターネットの情報は間違いも多いので、正しい答えが出る保証はないので、使い方に注意が必要です。 ある意味、人工的な仮定を置いて、演繹的・論理的に議論を展開する数学やプログラミングと異なり、厄介な外国語の学習は我々凡人には、「類比」が成り立つとすれば、 同じように「解答付きの問題」による大量の練習が必要見たいです。 黒田龍之助さんも高校時代の愛読書だったと言う種田輝豊著「20ヶ国語ペラペラ」にあるように、 「世界の言語シリーズ１７　アラビア語」＋「アラビア語　別冊」を他のことは一時制限して（私は根気が続かないので、息抜きも必要なので）兎も角 少なくとも一回は最後まで読んで見たいです。 この本(「20ヶ国語ペラペラ」)をこの年になって読むのではなく、若い時に出会っていれば、違った人生だった気もします。 シュリーマンの「古代への情熱」が私たちの世代が高校生の時知ることの出来た外国語の勉強法で、同級生も凄いと言っていましたが、マネできるものではなかったです。 ずっと後になって、ロンブ・カトー著　米原万里訳「わたしの外国語学習法」やピーター・フランクル著「ピーター流外国語修得術」なども読みましたが、 置かれている環境・境遇が違い、殆どマネできるようなものではなかったです。また、このような本には自慢話ばかりのものも、特に、政治家の話には多いです。 名横綱が必ずしも名親方でないように、我々凡人は才能ある優秀な人の真似をすれば必ず上手くいく訳ではないので、 一人の人のアドバイスで上手くいかなければ、「単語ではなく、文章を暗記せよ！」（野口悠紀雄さんなど多数）とか 「多分、嫌になったら（？）別の複数の本も同時に読んでみよ！」（ピーター・フランクルさん）とか「Al Jazeera Arabic のライブ動画を一日中バックランドで流しておく」 （誰だったか忘れましたが、外国のラジオ放送 BBC を只管聞いたと書いていました。 これらの議論で注意すべきは、「前提条件を明示せずに、結論だけ示されている」ことです。ゼロからの勉強法が示されている訳ではありません。 それぞれの人の「前提条件が何か」を考える必要があります。本当は、例えば、「中学（或いは高校）で学ぶ単語の暗記や文法の知識は待っていることが暗黙に前提とされていないか？」 前提条件が間違っていれば、どんな命題でも証明できます。 現代は、私の様に貧乏人で、留学することや有名芸能人の様に大学・大学院に（再）入学することが出来なくとも、インターネットがあるので、 一日中ネイティブの外国語に触れることが可能です。） とかと色々組み合わせて自分に合った方法を探せば良いです。 そうすることが楽しいか、或いは、どうしても何らかの理由で自分の欲望を満たすのに必要で、大量の時間を費やす価値があると思うなら。 更に、同じ本を読んで素晴らしいと言っても、人によって、何に感激したか、全然違っていて、全く違うことを素晴らしいと思っていると知って愕然としますが。

東京新聞「賃金上がらず予想外」アベノミクス指南役・浜田宏一氏証言　トリクルダウン起こせず…「望ましくない方向」 2023年3月14日 06時00分　には

大規模な金融緩和を中心とした首安倍晋三元相の経済政策「アベノミクス」の指南役として、 当時内閣官房参与を務めた浜田宏一米エール大学名誉教授（87）は本紙のインタビューで、 10年に及ぶ政策の効果について「賃金が上がらなかったのは予想外。 私は上がると漠然と思っていたし、安倍首相（当時）も同じだと思う」と証言した。 大企業の収益改善を賃上げへとつなげる「トリクルダウン」を起こせなかったことを認めた。　（渥美龍太、原田晋也、畑間香織）

とあります。言っていることは「「富める者が富めば、貧しい者にも自然に富がこぼれ落ち、経済全体が良くなる」とする経済理論は正しいが、 条件の「富める者が富めば、」は実現できたが、結論の「貧しい者にも自然に富がこぼれ落ち、経済全体が良くなる」は実現できなかった。」みたいですが、 頭の良い人の言い訳を理解するのが難しいです。論理的には「A→B」が偽なのはA:真かつ B:偽の時で、それ以外は真です。 米エール大学名誉教授である浜田宏一さんのような偉い人の言うことは何時も正しいと思考停止した人達は気にも止めないでしょうが、 条件の「富める者が富めば、」は実現できたが、結論の「貧しい者にも自然に富がこぼれ落ち、経済全体が良くなる」は実現できなかった。」は 普通に論理的に考えれば、「富める者が富めば、貧しい者にも自然に富がこぼれ落ち、経済全体が良くなる」は偽であるとなると思いますが、 「トリクルダウン」は正しいとすれば、条件の「富める者が富めば、」の他に、例えば、「非正規労働者を増やせば」の条件もアベノミクスでは付いたのが、 失敗の原因だったと言うことでしょうか？

最近、議論されている「少子化」も誰にとって問題なのでしょうか？本当に「少子化」が問題なら、「少子化」を防ぐには、「子供が増えればいい」。 その為には、一つの方法として、「結婚している人がもっと子供を増やせるようにすれば良い」とか「結婚していない人に結婚してもらえば良い」とかが出てき、 「結婚していない人に結婚してもらえば良い」を実現するには、「結婚しない理由」を調べたら、「経済的理由」はそれ程多くないぞ」とかやっていますが、 支配階級にとては「少子化」は大問題でも、現在の日本にとって、「少子化」が本当に差し当たっての大問題でしょうか？ 領主さまは参勤交代では半分はお江戸で半分はお国元で生活しましたが、今は東京にずっと住んでいます。東京を魅力ある街にすること、 「富める者が富めば、」の条件を満たすこと、東京と地方の格差を付けること、例えば、「東京に来ればお金が稼げますよ」 と若者・特に女性を東京に引き寄せいています。 最高権力者であった故安倍晋三元相の地元山口県でも、地元民を桜を見る会に呼んで、如何に、東京が素晴らしいかを見せるだけでは、山口県は発展せず、 衰退の一途で、議員定数削減に追い込まれました。地方でも、東京と同じ金額のお金が稼げるようにすべきです。若者も老人の投票率が高いから、 自分が投票しても無駄だと思わず、（「今日のパンにも事欠いている人達」に投票されると困る人達に誘導されている可能性もあります。 発言力の大きい人が何でそんなことを言っているのか、表面上の言葉の断片でなく本当は何を言っているか、自分で考える必要が あります。頭の良い人の発言は、多くの場合、裏があります。又、スタンフォード大の心理学者、ミシェル・ワルタさんの「マシュマロ・テスト」があります。 子供達はより多くのマシュマロをもらうために、目の前にあるマシュマロを食べることを15分間我慢するように言われます。 半数の子供達はできました。半数の子供たちは目の前のマシュマロを食べてしまいました。その子供たちを追跡調査をすると ご褒美や満足することを、より大きい収穫のために先に延ばすことができることと、学力、その他の能力の高さとの関係が明らかになったのです。 「マシュマロ・テスト」の正確なことは自分で調べて下さい。 関係ないことをもとに言っている可能性もありますが,「今日のパンにも事欠いているのに、将来の利益に賭けろと言われても」と思うかも分かりませんが、 現在の日本の指導者たちの多くは、「自己責任」と言って、「今日のパンにも事欠いている人達」のことなど眼中にありません。 日本は民主主義という価値観を共有している国の一つだそうですから、「自分たちもいること」を投票行動で示す必要があります。 そうでないと「今日のパンにも事欠いている人達」は日本にはいないことにされてしまいます。 ） 「NHK党・政治家女子48党」でも議席が持てるのだから、その手法を真似し、 例えば、（現在の状況に危機感を覚えているお金持ちも少しはいるはずですから）クラウドファンディングのような選挙資金を集める方法がないか或いは 2000万人が一人10円づつでも2億円になるので選挙資金も調達できそうだし、 非正規労働者全体が一つの塊になり、非正規労働者など眼中にない既成政党・組織に頼るのではなく、 自分たちの候補者を一人区でない当選の可能性の高い所で立て、（間違えました、一人区でも勝つ可能性があります。） （過去の選挙の当選者の得票数を調べ、その選挙区に非正規労働者が何人いるかと比較し、上回る所を探せば良いです。 それが算数・数学を生活に生かすと言うことです。上回らないところでも、非正規労働者のことも考えてくれると約束してくれた 自分たち全員が支援すれば当選する候補者を全員で支援してみれば良いです。これは例えば、薬剤師の団体などが実際にやっていることで、薬剤師の待遇改善に 成功していることは、周知の事実です。尤も、院外処方が普通になり薬局経営者が多大の利益を得ただけかも分かりませんが、薬剤師も利益のおこぼれを得ています。） 戦ってみれば、 2000万人いると言われているので全員が万難を排して投票すれば、かなりの数の当選が見込めることは小学生でも分かることで、少しは、世の中変わるのではないでしょうか？ それが、菅前首相がこうしたらいいと助言してくれている（？）「先ず「自助」だ！」と言うことだと思います。

今日（4月27日）弥右衛門公園で犬2匹と豚を散歩させている多分夫婦を又見ました。前回、こんな豚を見たことなかったので、「猪ですか？」と聞くと「豚だ」と言っていました。 公園への道路で小さい豚が走り出すと小犬より力が強くかつ速くて引いていた女性が必死で走っていました。 高知市でもペットの豚が飼えるみたいです。全国的に有名になった佐川町の「山椒餅」は私が子供の頃は母親も作っていました。 祖母に作り方を教わったと聞きました。かなりめんどくさく、基本的には、米を煎って、山椒と共に（手動の）ミルで粉にし、（私がやっていました）、蒸せば良いそうです。 秘伝ではないので、今はインターネットにも作り方が確か載っていると思います。好き嫌いがあるようです。 「うな丼大臣」と騒がれている谷国家公安委員長が我を忘れて食べたのは「最後の清流四万十川の天然ウナギ」だと思います。 余計なことを言ってしまったと思いますが、唯のウナギではないです。失言するほど美味しかったと言うことです。是非、食べに来て下さい。 高知県は天然ウナギが色々の所で食べれますが、今話題の牧野富太郎さんの佐川町でも「多分、 「仁淀ブルー」や細田守監督の「竜とそばかすの姫」の舞台で有名な仁淀川の天然ウナギ」が食べれます。 高知で一番有名な店「大正軒」があります。予約が必要だと思います。 高知県には女流棋士戦「リコー杯女流王座戦」


が、里見香奈さんの師匠が今は高知にいるせいかもしれませんが、連続して開催され、 全国を巡り美味しいものを食べて尽くしているはずの男性トップ棋士が入れ替わり次々やって来たことでもわかるように美味しいものが一杯あります。 私の家の周りには小さな子供の遊べる遊具付きの公園も一杯あります。 観光や移住に是非お越しください。良い処ですよ。

昨日、一部有志の佐川小学校の同窓会があり、そこで、「仁淀ブルー」を現地調査など随分勉強している人がいて、「仁淀ブルー」と言っても、 今有名になって観光客が詰めかけている一ヶ所だけでなく、仁淀川の色々な支流にそれぞれの「仁淀ブルー」があり、 支流・地層・構造帯の岩石の組成によっては「グリーン」にしかみえないと地元の人が言うところもあり、木を伐採した後、植林してなかったので 台風５号で随分変わってしまい、淵に流れ込んだ岩石を地元住民が協力して取り除いたりしている。 民間の個人では限界があるので、 「仁淀ブルー」ブームの今、「高知観光の促進の為にも高知大学が中心になって、「仁淀ブルー」の解明に取り組んでくれないかな。自分も協力したい。」 と言っていました。私は相談されても高知大学の適切な先生との知り合いがないのですが、高知の大切な観光資源の一つなので 高知県やNHKなどマスコミも一緒に検討してもらえると有難いです。

私の苦労して作ったスマホのソフトは Google が Google Pay で公開する条件を変更したので作り直せと言うメールが来ましたが、 数百万あると言うソフトの中の一つで別に素晴らしいものでもなく誰にでも作れるものなので、 2通、意図の良く分からないメール(我々のグループに参加しないかなのかな？)やダウンロード数を増やす方法を教えてやろうかと言う外国からのメールが来ましたが、誰もダウンロードしないので、 作り直しても無駄だと思い条件に合うように作り直さなかったので、 Google Pay から消えました。自分で作って、自分のスマホで使うだけなら、 パソコンでソフトを作り、スマホとコードで繋ぎ、スマホで実行すれば、自動的にスマホにソフトが保存されます。 更に、 Google Pay から消えたせいか、「お前のゲームソフトをプロモートしてやろうか？お金は我々が出すから必要ない」という外国の企業からのメールも来ました。 


Promoting and Investing in Your Apps 

Hi,

How are you?

I wanted to reach out and discuss with you regarding your games.

I reviewed some of the games in your portfolio and I would like to
discuss how we can help you promote them on a large scale.

....
残念ながら私は若くないです。I wish I were young. 若い人には面白いと思ったことを何かやっていればチャンスがあります。多分。

水取コーヒーの新しい器具を購入しました。今までのものと違い、数千円で高いものではありません。


今まで購入した水取コーヒーの器具と全く異なるアイデアによるものでした。 私が学生の頃は、SFは新しいものがずっと出るはずだけれども、（SFは「太陽の反対側に地球と同じ惑星があるとか嘘ばっかり書いている」から読まないと言う学生さんもいましたし、 また「手品には必ず種があると父親が言っていたので興味がない」と言っている女子学生もいましたが、色々な人がいます。）、推理小説はトリックが出尽くすと終るので、 今は推理小説を読むんだと言っていましたが、 推理小説も「社会派ミステリー」とか「ユーモアミステリー」とか色々新しい視点のものが出てきてずっと続いています。 それぞれの分野に才能ある優秀な人達がいて、次々新しいことを考え出しています。凄いもんです。

「数学の未解決問題「アインシュタイン問題」を“完全解決”する新図形発見　「The hat」を改良」と言う記事を見て、 関連する記事を調べているとその論文の他に「TILINGS AND PATTERNS」の「10 APERIODIC TILINGS」の補足の記事も見つけたので、そこにある図形の印刷をする Python の プログラムを作ろうとして、http://www.cc.kochi-u.ac.jp/~tyamag/jyohou/pythonsudoku.pdf で印刷の仕方を書いてあったと思い出し実行してみましたが、 


Traceback (most recent call last):
  File "C:\TilingsAndPatterns\sudoku6.py", line 9, in 
    import win32ui
ImportError: DLL load failed while importing win32ui: ダイナミック リンク ライブラリ (DLL) 初期化ルーチンの実行に失敗しました。
となり、実行できなくなっていました。今の処、直接印刷する解決策が私には分かりません。 多分、Ruby 版の「数独」でやったように、パズルの局面を html ファイルで打ち出すようにするのが一番簡単です。 もし Python 版を使いたければ、印刷の部分を削除するか、又は、Ruby 版を参考に、自分で修正して下さい。

尚、プログラムの修正が面倒くさければ、プログラムの印刷の部分を削除し、盤面を、例えば GIMP にコピーペーストし、印刷するのが多分最も簡単です。

「TILINGS AND PATTERNS」を最初から読むのは大変ですが、興味のある「10 APERIODIC TILINGS」の図を Python のプログラムで描いてみることは パズルを解くみたいで面白いです。簡単には描けないものもありますが、Figure 10.1.5 は「A 4-similarity tiling」というのがまだ理解できていませんが、




のような図で level を増大すると同時に拡大すえば良いのではと思います。次のプログラムは上のプログラムの骨組みの再利用ですが 

import tkinter
import tkinter as tk
from OpenGL.GL import *
from OpenGL.GLU import *
import numpy as np
from OpenGL import GL
from pyopengltk import OpenGLFrame

W = 600
H = 600

num = 1  ## 描画するタイルの行の数
##tile = np.zeros(14).reshape(2, 7)  ## そのままのタイル
tile = np.zeros(12).reshape(2, 6)  ## そのままのタイル
base = np.zeros(4).reshape(2, 2)  ## 格子を張るベクトル

scalar = H * 1.0 / num ## 描画ウィンドウと行の数からタイルの大きさを決定


def makeHexVector():
    global base
##    base[0] = np.array([np.cos(np.pi / 2), np.sin(np.pi/2)])
##    base[1] = np.array([np.cos(np.pi / 6), np.sin(np.pi/6)])
    base[1] = np.array([1, 0])
    base[0] = np.array([0, 1])
makeHexVector()  ## 四角格子を張るベクトルの生成

m = int(np.ceil(num / base[1][0]))  ## 列の数
lattice = np.zeros((num + 1)*(m + 1)*2).reshape(num+1, m+1, 2)  ## 格子点ベクトル

def makeLattice():
    global lattice
    m = int(np.ceil(num / base[1][0]))  ## 列の数
    for i in range(num+1):
        for j in range(m+1):
            v = (i*scalar)*base[0]
            v = v + (j*scalar)*base[1]
            lattice[i][j] = np.array([v[0], (v[1]) % (H+scalar)])

makeLattice()  ## 格子点ベクトルを生成

def makeHexTriangle():
    global tile, scalar
    tile[0][0] = 0
    tile[1][0] = 0
    tile[0][1] = scalar
    tile[1][1] = 0
    tile[0][2] = scalar
    tile[1][2] = scalar/2
    tile[0][3] = scalar/2
    tile[1][3] = scalar/2
    tile[0][4] = scalar/2
    tile[1][4] = scalar
    tile[0][5] = 0
    tile[1][5] = scalar
    
makeHexTriangle()

def drawMotif(level, vec, tile, scalar, orient):
    if level == 0:
        if orient == 0:
            t = tile.copy()
            glColor3f(0.0, 0.0, 1.0)
            glLineWidth(3.0)
            glBegin(GL_POLYGON)
            for j in range(6):
                glVertex3d(vec[0]+t[0][j], vec[1]+t[1][j], 0)
            glEnd()
        elif orient == 1:
            t = tile.copy()
            rotate_mtx = np.array([[np.cos(np.pi/2), -np.sin(np.pi/2)],\
                    [np.sin(np.pi/2), np.cos(np.pi/2)]])
            t = t.transpose()
            t = t - scalar/2
            t = t.transpose()
            t = np.dot(rotate_mtx, t)
            t = t + scalar/2
            glColor3f(0.0, 0.0, 1.0)
            glLineWidth(3.0)
            glBegin(GL_POLYGON)
            for j in range(6):
                glVertex3d(vec[0]+t[0][j], vec[1]+t[1][j], 0)
            glEnd()
        elif orient == 2:
            t = tile.copy()
            rotate_mtx = np.array([[np.cos(-np.pi/2), -np.sin(-np.pi/2)],\
                    [np.sin(-np.pi/2), np.cos(-np.pi/2)]])
            t = t.transpose()
            t = t - scalar/2
            t = t.transpose()
            t = np.dot(rotate_mtx, t)
            t = t + scalar/2
            glColor3f(0.0, 0.0, 1.0)
            glLineWidth(3.0)
            glBegin(GL_POLYGON)
            for j in range(6):
                glVertex3d(vec[0]+t[0][j], vec[1]+t[1][j], 0)
            glEnd()
        elif orient == 3:
            t = tile.copy()
            rotate_mtx = np.array([[np.cos(np.pi), -np.sin(-np.pi)],\
                    [np.sin(-np.pi), np.cos(-np.pi)]])
            t = t.transpose()
            t = t - scalar/2
            t = t.transpose()
            t = np.dot(rotate_mtx, t)
            t = t + scalar/2
            glColor3f(0.0, 0.0, 1.0)
            glLineWidth(3.0)
            glBegin(GL_POLYGON)
            for j in range(6):
                glVertex3d(vec[0]+t[0][j], vec[1]+t[1][j], 0)
            glEnd()
    else:
        newtile = tile/2
        if orient == 0:
            drawMotif(level-1, vec, newtile, scalar/2, 0)
            drawMotif(level-1, vec+np.array([scalar/2, 0]), newtile, scalar/2, 1)
            drawMotif(level-1, vec+np.array([0, scalar/2]), newtile, scalar/2, 2)
            drawMotif(level-1, vec+np.array([scalar/2, scalar/2]), newtile, scalar/2, 0)
        elif orient == 1:
            drawMotif(level-1, vec, newtile, scalar/2, 0)
            drawMotif(level-1, vec+np.array([scalar/2, 0]), newtile, scalar/2, 1)
            drawMotif(level-1, vec+np.array([0, scalar/2]), newtile, scalar/2, 1)
            drawMotif(level-1, vec+np.array([scalar/2, scalar/2]), newtile, scalar/2, 3)
        elif orient == 2:
            drawMotif(level-1, vec, newtile, scalar/2, 0)
            drawMotif(level-1, vec+np.array([scalar/2, 0]), newtile, scalar/2, 2)
            drawMotif(level-1, vec+np.array([0, scalar/2]), newtile, scalar/2, 2)
            drawMotif(level-1, vec+np.array([scalar/2, scalar/2]), newtile, scalar/2, 3)
        elif orient == 3:
            drawMotif(level-1, vec, newtile, scalar/2, 3)
            drawMotif(level-1, vec+np.array([scalar/2, 0]), newtile, scalar/2, 1)
            drawMotif(level-1, vec+np.array([0, scalar/2]), newtile, scalar/2, 2)
            drawMotif(level-1, vec+np.array([scalar/2, scalar/2]), newtile, scalar/2, 3)

level = 3

class AppOgl(OpenGLFrame):
    
    def initgl(self):
        global level
        """Initalize gl states when the frame is created"""
        GL.glViewport(0, 0, self.width, self.height)
        GL.glClearColor(1.0, 1.0, 1.0, 1.0)    
        self.n_tiling_list = [level]

    def redraw(self):
        global num, lattice, tile, level
        level = self.n_tiling_list[0]
        GL.glClear(GL.GL_COLOR_BUFFER_BIT)
        glColor3f(0.0, 0.0, 1.0)
        glLineWidth(2.0) ## 線の幅
        glMatrixMode(GL_PROJECTION)
        glLoadIdentity()
        glOrtho(0, W, 0, H, -1.0, 1.0)
        glPolygonMode(GL_FRONT, GL_LINE) ## 表面をワイヤーフレームで
        for k, vecArr in enumerate(lattice):
            for l, vec in enumerate(vecArr):
                drawMotif(level, vec, tile, scalar, 0)
                
def button_click():
    global level
    level = int(txt2.get())
    print(level)
    app.n_tiling_list = []
    app.n_tiling_list.append(level)
    app._display()

if __name__ == '__main__':
    root = tkinter.Tk()
    root.title('TILINGS AND PATTERNS Figure 10.1.5')
    app = AppOgl(root, width=600, height=600)
    app.pack(fill=tkinter.BOTH, expand=tkinter.YES)
    lbl2 = tk.Label(text='level')
    lbl2.pack()
    txt2 = tk.Entry(width=20)
    txt2.pack()
    # テキストボックスをクリア
    txt2.delete(0, tk.END)
    # テキストボックスに文字「1234」を入力
    txt2.insert(tk.END, str(level))
    button1 = tk.Button(root ,text="描画", command=button_click)
    button1.pack() # button1ウィジェットを配置

    app.mainloop()
で良いと思います。私はこのようなプログラムを作ってみれば、その構造が理解でき、良い暇つぶしになります。


もう一つの non-periodic 4-similarity tiling の例である Figure 10.1.6 は


ですが、上の場合と同様、ヒントのグレイの部分に注目すれば


のような図で level を増大すると同時に拡大すえば良いのではと思います。プログラムは 

import tkinter
import tkinter as tk
from OpenGL.GL import *
from OpenGL.GLU import *
import numpy as np
from OpenGL import GL
from pyopengltk import OpenGLFrame

W = 600
H = 600

tile = np.zeros(12).reshape(2, 6)  ## そのままのタイル
scalar = W * 0.8 
level = 4

def makeHexTriangle():
    global tile, scalar
    temp = np.zeros(12).reshape(6, 2)
    temp[0][0] = 0
    temp[0][1] = 0
    temp[1][0] = scalar
    temp[1][1] = 0
    temp[5][0] = 1/2 * scalar
    temp[5][1] = np.sqrt(3) * scalar / 2
    temp[3] = (temp[0]+temp[1]+temp[5])/3
    temp[2] = temp[1]+(temp[5]-temp[1])*2/3
    temp[4] = temp[0]+(temp[5]-temp[0])/3
    tile = np.transpose(temp)
       
makeHexTriangle()

def makeM1(tile, scalar):
    t = tile.copy()
    rotate_mtx = np.array([[np.cos(2*np.pi/3), -np.sin(2*np.pi/3)],\
                [np.sin(2*np.pi/3), np.cos(2*np.pi/3)]])
    t = np.dot(rotate_mtx, t)
    temp = np.transpose(t)
    temp = temp + np.array([scalar, 0])
    t = np.transpose(temp)
    return t

def makeM2(tile, scalar):
    t = tile.copy()
    rotate_mtx = np.array([[-1.0, 0.0], [0.0, 1.0]])
    t = np.dot(rotate_mtx, t)
    temp = np.transpose(t)
    temp = temp + np.array([scalar, 0])
    t = np.transpose(temp)
    return t

def makeM3(tile, scalar):
    t = tile.copy()
    rotate_mtx = np.array([[np.cos(np.pi), -np.sin(np.pi)],\
                [np.sin(np.pi), np.cos(np.pi)]])
    t = np.dot(rotate_mtx, t)
    rotate_mtx = np.array([[-1.0, 0.0], [0.0, 1.0]])
    t = np.dot(rotate_mtx, t)
    temp = np.transpose(t)
    temp = temp + np.array([0, np.sqrt(3)*scalar/3])
    t = np.transpose(temp)
    return t

def makeM4(tile, scalar):
    t = tile.copy()
    rotate_mtx = np.array([[np.cos(np.pi/3), -np.sin(np.pi/3)],\
                [np.sin(np.pi/3), np.cos(np.pi/3)]])
    t = np.dot(rotate_mtx, t)
    temp = np.transpose(t)
    temp = temp + np.array([scalar/2,  -np.sqrt(3)*scalar/6])
    t = np.transpose(temp)
    return t

def makeM5(tile, scalar):
    t = tile.copy()
    rotate_mtx = np.array([[np.cos(4*np.pi/3), -np.sin(4*np.pi/3)],\
                [np.sin(4*np.pi/3), np.cos(4*np.pi/3)]])
    t = np.dot(rotate_mtx, t)
    temp = np.transpose(t)
    temp = temp + np.array([scalar/2, np.sqrt(3)*scalar/2])
    t = np.transpose(temp)
    return t

def makeM6(tile, scalar):
    t = tile.copy()
    rotate_mtx = np.array([[np.cos(np.pi/3), -np.sin(np.pi/3)],\
                [np.sin(np.pi/3), np.cos(np.pi/3)]])
    t = np.dot(rotate_mtx, t)
    rotate_mtx = np.array([[1.0, 0.0], [0.0, -1.0]])
    t = np.dot(rotate_mtx, t)
    temp = np.transpose(t)
    temp = temp + np.array([scalar/2,  np.sqrt(3)*scalar/2])
    t = np.transpose(temp)
    return t

def makeM7(tile, scalar):
    t = tile.copy()
    rotate_mtx = np.array([[np.cos(np.pi/3), -np.sin(np.pi/3)],\
                [np.sin(np.pi/3), np.cos(np.pi/3)]])
    t = np.dot(rotate_mtx, t)
    rotate_mtx = np.array([[-1.0, 0.0], [0.0, 1.0]])
    t = np.dot(rotate_mtx, t)
    temp = np.transpose(t)
    temp = temp + np.array([scalar/2,  -np.sqrt(3)*scalar/6])
    t = np.transpose(temp)
    return t

def makeM8(tile, scalar):
    t = tile.copy()
    rotate_mtx = np.array([[np.cos(5*np.pi/3), -np.sin(5*np.pi/3)],\
                [np.sin(5*np.pi/3), np.cos(5*np.pi/3)]])
    t = np.dot(rotate_mtx, t)
    rotate_mtx = np.array([[1.0, 0.0], [0.0, -1.0]])
    t = np.dot(rotate_mtx, t)
    return t

def makeM9(tile, scalar):
    t = tile.copy()
    rotate_mtx = np.array([[np.cos(np.pi), -np.sin(np.pi)],\
                [np.sin(np.pi), np.cos(np.pi)]])
    t = np.dot(rotate_mtx, t)
    temp = np.transpose(t)
    temp = temp + np.array([scalar,  np.sqrt(3)*scalar/3])
    t = np.transpose(temp)
    return t

def makeM10(tile, scalar):
    t = tile.copy()
    rotate_mtx = np.array([[np.cos(5*np.pi/3), -np.sin(5*np.pi/3)],\
                [np.sin(5*np.pi/3), np.cos(5*np.pi/3)]])
    t = np.dot(rotate_mtx, t)
    rotate_mtx = np.array([[-1.0, 0.0], [0.0, 1.0]])
    t = np.dot(rotate_mtx, t)
    temp = np.transpose(t)
    temp = temp + np.array([scalar,  np.sqrt(3)*scalar/3])
    t = np.transpose(temp)
    return t

def makeM11(tile, scalar):
    t = tile.copy()
    rotate_mtx = np.array([[np.cos(-np.pi/3), -np.sin(-np.pi/3)],\
                [np.sin(-np.pi/3), np.cos(-np.pi/3)]])
    t = np.dot(rotate_mtx, t)
    temp = np.transpose(t)
    temp = temp + np.array([0,  np.sqrt(3)*scalar/3])
    t = np.transpose(temp)
    return t

def drawMotif(level, vec, tile, scalar, orient):
##    t = tile.copy()
    if level == 0:
        if orient == 0:
            t = tile.copy()
        elif orient == 1:
            t = makeM1(tile, scalar)
        elif orient == 2:
            t = makeM2(tile, scalar)
        elif orient == 3:
            t = makeM3(tile, scalar)
            glBegin(GL_LINE_LOOP)
            for j in range(5):
                glVertex3d(vec[0]+t[0][j], vec[1]+t[1][j], 0)
            glEnd()
        elif orient == 4:
            t = makeM4(tile, scalar)
        elif orient == 5:
            t = makeM5(tile, scalar)
        elif orient == 6:
            t = makeM6(tile, scalar)
        elif orient == 7:
            t = makeM7(tile, scalar)
        elif orient == 8:
            t = makeM8(tile, scalar)
        elif orient == 9:
            t = makeM9(tile, scalar)
        elif orient == 10:
            t = makeM10(tile, scalar)
        elif orient == 11:
            t = makeM11(tile, scalar)
        glBegin(GL_LINE_LOOP)
        for j in range(5):
            glVertex3d(vec[0]+t[0][j], vec[1]+t[1][j], 0)
        glEnd()
    else:
        if orient == 0:
            newvec = vec + np.array([5*scalar/12, np.sqrt(3)*scalar/12])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 1)
            newvec = vec + np.array([scalar/2, 0])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 2)
            newvec = vec + np.array([scalar/6, 0])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 3)
            newvec = vec
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 2)
        elif orient == 1:
            newvec = vec + np.array([scalar/6, np.sqrt(3)*scalar/6])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 5)
            newvec = vec + np.array([scalar/4, np.sqrt(3)*scalar/4])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 6)
            newvec = vec + np.array([5*scalar/12, np.sqrt(3)*scalar/12])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 7)
            newvec = vec + np.array([scalar/2, 0])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 6)
        elif orient == 2:
            newvec = vec + np.array([scalar/12, np.sqrt(3)*scalar/12])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 8)
            newvec = vec
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 0)
            newvec = vec + np.array([scalar/3, 0])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 9)
            newvec = vec + np.array([scalar/2, 0])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 0)
        elif orient == 3:
            newvec = vec + np.array([0, np.sqrt(3)*scalar/6])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 9)
            newvec = vec + np.array([scalar/6, np.sqrt(3)*scalar/6])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 0)
            newvec = vec + np.array([scalar/2, np.sqrt(3)*scalar/6])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 9)
            newvec = vec + np.array([5*scalar/12, np.sqrt(3)*scalar/12])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 10)
        elif orient == 4:
            newvec = vec + np.array([scalar/3, np.sqrt(3)*scalar/6])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 9)
            newvec = vec + np.array([scalar/2, np.sqrt(3)*scalar/6])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 10)
            newvec = vec + np.array([scalar/3, 0])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 8)
            newvec = vec + np.array([scalar/4, -np.sqrt(3)*scalar/12])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 10)
        elif orient == 5:
            newvec = vec + np.array([scalar/4, np.sqrt(3)*scalar/4])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 8)
            newvec = vec + np.array([scalar/6, np.sqrt(3)*scalar/6])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 10)
            newvec = vec
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 8)
            newvec = vec + np.array([scalar/6, 0])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 0)
            t = makeM5(tile, scalar)
            glBegin(GL_LINE_LOOP)
            for j in range(5):
                glVertex3d(vec[0]+t[0][j], vec[1]+t[1][j], 0)
            glEnd()
        elif orient == 6:
            newvec = vec + np.array([scalar/4, np.sqrt(3)*scalar/4])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 1)
            newvec = vec + np.array([scalar/3, np.sqrt(3)*scalar/6])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 11)
            newvec = vec + np.array([scalar/2, 0])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 1)
            newvec = vec + np.array([scalar/3, 0])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 2)
        elif orient == 7:
            newvec = vec + np.array([scalar/6, np.sqrt(3)*scalar/6])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 3)
            newvec = vec + np.array([0, np.sqrt(3)*scalar/6])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 11)
            newvec = vec + np.array([scalar/6, 0])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 1)
            newvec = vec + np.array([scalar/4, -np.sqrt(3)*scalar/12])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 11)
            t = makeM7(tile, scalar)
            glBegin(GL_LINE_LOOP)
            for j in range(5):
                glVertex3d(vec[0]+t[0][j], vec[1]+t[1][j], 0)
            glEnd()
        elif orient == 8:
            newvec = vec + np.array([scalar/4, np.sqrt(3)*scalar/4])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 5)
            newvec = vec + np.array([scalar/3, np.sqrt(3)*scalar/6])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 6)
            newvec = vec + np.array([scalar/12, np.sqrt(3)*scalar/12])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 4)
            newvec = vec + np.array([0, 0])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 5)
        elif orient == 9:
            newvec = vec + np.array([scalar/2, np.sqrt(3)*scalar/6])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 3)
            newvec = vec + np.array([scalar/3, np.sqrt(3)*scalar/6])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 2)
            newvec = vec + np.array([0, np.sqrt(3)*scalar/6])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 3)
            newvec = vec + np.array([scalar/12, np.sqrt(3)*scalar/12])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 11)
        elif orient == 10:
            newvec = vec + np.array([scalar/2, np.sqrt(3)*scalar/6])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 4)
            newvec = vec + np.array([5*scalar/12, np.sqrt(3)*scalar/12])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 5)
            newvec = vec + np.array([scalar/4, -np.sqrt(3)*scalar/12])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 4)
            newvec = vec + np.array([scalar/6, 0])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 7)
        elif orient == 11:
            newvec = vec + np.array([0, np.sqrt(3)*scalar/6])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 7)
            newvec = vec + np.array([scalar/12, np.sqrt(3)*scalar/12])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 6)
            newvec = vec + np.array([scalar/4, -np.sqrt(3)*scalar/12])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 7)
            newvec = vec + np.array([scalar/3, 0])
            newtile = (1/2)*tile
            drawMotif(level-1, newvec, newtile, scalar/2, 4)

class AppOgl(OpenGLFrame):
    
    def initgl(self):
        global num
        """Initalize gl states when the frame is created"""
        GL.glViewport(0, 0, self.width, self.height)
        GL.glClearColor(1.0, 1.0, 1.0, 1.0)    
        self.n_tiling_list = [level]

    def redraw(self):
        global level, tile
        level = self.n_tiling_list[0]
        vec = np.zeros(2)
        vec[0] = W / 2 - scalar / 2
        vec[1] = H / 2 - scalar * np.sqrt(3) / 6
        
        GL.glClear(GL.GL_COLOR_BUFFER_BIT)
        glColor3f(0.0, 0.0, 1.0)
        glLineWidth(2.0) ## 線の幅
        glMatrixMode(GL_PROJECTION)
        glLoadIdentity()
        glOrtho(0, W, 0, H, -1.0, 1.0)
        glPolygonMode(GL_FRONT, GL_LINE) ## 表面をワイヤーフレームで
        drawMotif(level, vec, tile, scalar, 0)

def button_click():
    global level
    level = int(txt2.get())
    print(level)
    app.n_tiling_list = []
    app.n_tiling_list.append(level)
    app._display()

if __name__ == '__main__':
    root = tkinter.Tk()
    root.title('TILINGS AND PATTERNS Figure 10.1.6')
    app = AppOgl(root, width=600, height=600)
    app.pack(fill=tkinter.BOTH, expand=tkinter.YES)
    lbl2 = tk.Label(text='level')
    lbl2.pack()
    txt2 = tk.Entry(width=20)
    txt2.pack()
    # テキストボックスをクリア
    txt2.delete(0, tk.END)
    # テキストボックスに文字「1234」を入力
    txt2.insert(tk.END, str(level))
    button1 = tk.Button(root ,text="描画", command=button_click)
    button1.pack() # button1ウィジェットを配置

    app.mainloop()
です。今度はモチーフが12パターンあるので、同じことの繰り返しですが、数学の様に以下同様と言う訳にはいかないので、 プログラミングに丸一日掛かりました。再帰の素晴らしさです。 このようなプログラムを作ってみれば、どの様に考えれば、このようなタイリングが出来るか、その構造が理解でき、良い暇つぶしになります。 知ることは楽しいことです。プログラミングが出来れば、このようなに私のような凡人でも複雑な数学が理解できる様になります。 尤もプログラミングで出来ることは無数にあるので、 個人があらゆることに精通することは不可能なので、自分がやりたいと思うこと・価値があると思うことに特化しなければ、努力してみただけになりますが。 様々な分野の成功した才能ある優秀な人達が言っていることは、多分、「具体的に何がしたいか？その為に何をすべきか？自分で考え、実行してみなさい。 良く考えて適切な努力をしないと唯がむしゃらに努力しても上手くいく保証はないですが。」だと思います。

プログラミングは「アルゴリズム」をコンピュータが理解できるように翻訳・通訳する技術で、最初に「アルゴリズム」があり、 自分が実現したい「アルゴリズム」を翻訳・通訳する技術だけ学べば良いように、 （私はアラビア語で書かれた全4巻の「千夜一夜物語」を読みたいだけで、読めれば良いと思ってアラビア語を学び始めましたが）、 中川浩一著「総理通訳の外国語勉強法」によると その類比で、「外国人と話すために外国語を学ぶのであれば、まず、日本語で話す内容を考え、それから外国語に「置き換え」ましょう」と書いてあります。 最小の努力で効果を上げるには「先ずは自分の興味・専門に応じて、自分が話す必要のあることだけを外国語に置き換える努力だけしなさい」と言うことみたいです。 アラビア語関連の本と言うことで手に取った本ですが、今まで読んだ本と全然違うことを書いてある本も読んで見るものです。 これが難しければ、山下太郎さんが「しっかり学ぶ初級ラテン語」に書いてある、「本書が想定するラテン語の学習法を述べます。それは、 教科書を広げ、(1)変化表を暗記し、(2)例文の文法的説明を理解し、(3)日本語訳から元の例文が 再現できるまで練習を繰り返すことです。」の（３）を他の外国語でもやってみれば、 「押しても駄目なら、引いて見な！」で、今までと逆のことをやってみるとまた違った景色が見えてくるかもしれません？ この年になると英語でも話す必要があるとは思えませんが、聴くのはニュースが聴けるようになると良いですが、それなりに勉強しないと出来るように なりません。車を運転するために、早く車に乗った時放送していた「ニュースで学ぶ「現代英語」」がテキスト代も必要ない、ウエブに全て載せてくれている 教材であることに気が付きました。「反訳トレーニング」が上で書いたことの練習みたいです。 直訳しているせいかも、まだ易しい文章しか学んでないせいかもしれませんが、英語とアラビア語は語順が同じような気がしますが、 日本語と英語は語順が逆なので、「反訳トレーニング」が有効みたいで、毎日、30分でもこの放送内容を勉強すると良いみたいな気がします。 教えて貰って良いと思ったことは何でもやってみれば良いですが、長続きしません。困ったものです。

例えば、「TILINGS AND PATTERNS」の P.527 の 


Now tile D must be an arm (for a cross has only arrowheads on its sides) and to fit ajaiust A it must be of type (c), (d) or (e).
In any case its right side will carry the tail of one or two arrows and the same will clearly be true of the left side of tile F.
We deduce that E must be a cross, and we shall suppose that it faces upwards and to the right as shown. 
The choice for E faces B and D to be of type (e) and F to be of type (c).
Of course the cross E is necessarilly cornerless.

....
と言う英文は私は英語の実力ではなく、数学の素養を元に読んでいます。自分の専門分野の本であれば、自分の専門分野の知識と専門用語の知識で英文が正確に読めてしまいます。 （勿論、学校教育における中学・高校・大学の一般教養で学ぶ英語の文法・基本単語・英文解釈の知識がそれなりにあることは前提条件として仮定しています。 プロの同時通訳者も国際会議の通訳をする時は、 何でも知っている訳ではないので、その会議の議題に関する資料・論文など提示してもらい議論を理解するに必要な専門用語を一夜漬けで暗記するそうです。） それで日本にいるだけではこれで十分だと思ってしまいます。これが多分留学した人達との違いです。更なる上を目指すなら、意識して、上に書いたような 日本語から他の外国語に変換する努力をすべきでした。 又、こう言う考察をすれば、適切な探索プログラムが作れますが、闇雲に探索プログラミングを作ると反って時間の無駄になってしまうのではとの懸念もあります。 又、「TILINGS AND PATTERNS」の P.528 の 


10.2.1 The set R1 of six Robinson prototiles is aperiodic

To prove this we first remark that if the tiles of a tiling 
are basically square tiles with modified edges (like the 
Robinson tiles) and the tiling is peiodic, then translations 
parallel to the sides of the squares necessarily occur 
among the symmetries of the tiling (see Exercise 10.2.2).
も 「peiodic」が何を意味しているか、迷いました。平面の模様の対称群は、 私のソフト Escher.exe でそれぞれの模様が描けるように ROSE 群、FRIEZE 群 、WALLPAPER 群がありますが、WALLPAPER 群が作用していると言う 意味だと思いますが、そうであれば、（29ページに periodic の定義が書いてありました）、この場合は平行移動を表す行列の成分が整数ですから簡単に示せます。 更に、「TILINGS AND PATTERNS」の直後の 


However, the method of construction implies that for 
each n we can find facing crosses which are at distance 2^n 
apart (namely the central crosses of (2^n-1)x(2^n-1) blocks) 
in both rows and columns. But clearly this implies 
that no translation parallel to the sides of the squares 
through a distance less than 2^n is a symmetry of the tiling.
ince 2^n can be arbitarily large, no translative symmetry 
of the tiling exists. Thus the tiling is non-periodic, the 
tiles form an aperiodic set, and Statement 10.2.1 is proved.
も日本語に訳すのではなく、何を書いているかキチンとチェックしようとすると私の様な凡人にとっては結構厄介です。 注意深く無かったので気がつきませんでしたが、この後に載せてある図は本の図と微妙に異なります。 このページの最後に掲載してあるプログラムで全て発見できるはずでしたが、まだバグがあるみたいで、本に載っている図が出てきません。 プログラミングは、自分では実際に意味のあるプログラムを自分で全て一から考えてプログラミングしたことの無いと思われる文系の経営者や政治家や官僚が考えるような 「幾らでも代わりの利く、非正規労働者に、孫請け、ひ孫請けで、消耗品扱いで低賃金でやらせば良い単純作業ではない」みたいです。 （だから、プログラマーの業績を作成したプログラムの長さで評価したり、実際は優秀なプログラマーほど同じことを短いプログラムで実装しますが、 上司が馬鹿だから、わざと長いプログラムを作ったり、徹夜徹夜のブラックな環境で、必要な勉強も出来ない中で、 経験を積み給料を上げざるを得なくなると燃え尽きたと追い出します。困ったことに、それら経営者の言い分を多くの人が信じています。） 私のような凡人はこの様な単純なプログラムでも出来たと思ってから実際に出来上がるまで、それまで掛った時間の倍の時間が掛かります。 途中で拙いことが見つかり方針を変更して、小手先の部分的な修正で、プログラムを仕上げようとすると私は良く泥沼に陥ります。 Ammann's tiling の同様な探索のプログラミングで何度も失敗したので、Robinson's tiling のプログラミングも間違っているのではと自信を無くしていましたが、 一日掛でプログラムが何をしているかを調べて、私のプログラムの間違いでなく、本に載っている図 Figure 10.2.5 が（多分）間違っていて、この図では １×１，３×3、７×７と拡張している方法だと私が考える自然な形では１５×１５に拡張できないことに気が付きました。 だから、最後に提示しているプログラムでこの図 Figure 10.2.5 のデータが出てきませんでした。本にはミスプリントが付き物で、私の勘違いでした。 この後に私が提示している図のように拡張していかないと簡単なパターンは見えてきません。本は自分が納得するまで粘って理解しようとする必要があります。 更に、Ammann's tiling のパターンを見つける為には、 どうも最初に思いついた一つの拡張方法に固定するのではなく、可能だと言うことは既に分かっているので、上手くいかなければ、 思いつく様々な拡張方法で探索するプログラムを作ってみる必要があります。拘りだすと結構大変ですが、 ひょっとしたら新しい発見があるかもしれません。

矢張り、面白そうな図が一杯あるので、最早、雇われの身で何らかの業績をと時間に追われている訳ではないので、 最も私が大学に就職した頃は時間がゆったりと流れていた様に思いますが、「貧すれば鈍する」で急に「金、金、金」の世知辛い世の中になりましたが、 基本的なことは既に学んでいると焦らず、知らないことが一杯書いてあるので、本質的な部分だけ学んで、最先端に到達するのが大切だとの考えも勿論ありますが、 僅か700頁の本なので最初から






のような tiling を描きながらチャンと読んだ方が その歴史も分かり反って時間の節約になりそうです。 昔は専門家にこの様な図を描いてもらっていましたが、現在は素人がパソコンを使って自分で描くことが出来る・描かなければいけない時代になっています。 それぞれ練習の為、tkinter だけの使用、tkinter と turtle の併用、tkinter と pyopengl の併用で作成しています。一番下の tiling は、例えば 

from tkinter import *
import tkinter
import tkinter as tk
from OpenGL.GL import *
from OpenGL.GLU import *
import numpy as np
from OpenGL import GL
from pyopengltk import OpenGLFrame

W = 500
H = 500

num = 5  ## 描画するタイルの行の数
base = np.zeros(4).reshape(2, 2)  ## 格子を張るベクトル

def makeSqVector():
    global base
    base[0] = np.array([0, 1])
    base[1] = np.array([1, 0])
makeSqVector()

def makeSqLattice(num, scalar):
    m = int(np.ceil(num / base[1][0]))  ## 列の数
    lattice = np.zeros((num + 1)*(num + 1)*2).reshape(num+1, num+1, 2)  ## 格子点ベクトル
    for i in range(num+1):
        for j in range(num+1):
            v = (i*scalar)*base[0]  ## 正方形を描画する位置ベクトル
            v = v + (j*scalar)*base[1]
            lattice[i][j] = np.array([v[0], v[1]])
    return lattice

def makeSquare(scalar):
    tile = np.zeros(20).reshape(10, 2)  ## 
    rtile = np.zeros(20).reshape(10, 2)  ## 
    tile[0] = np.array([0, 0])
    tile[1] = np.array([1/3, 0])
    tile[2] = np.array([1/3, 1/6])
    tile[3] = np.array([2/3, 1/2])
    tile[4] = np.array([5/6, 1/2])
    tile[5] = np.array([5/6, 5/6])
    tile[6] = np.array([1/2, 5/6])
    tile[7] = np.array([1/2, 2/3])
    tile[8] = np.array([1/6, 1/3])
    tile[9] = np.array([0, 1/3])    
    tile = scalar * tile
    rtile[0] = np.array([1/2, 1/3])
    rtile[1] = np.array([1/2, 0])
    rtile[2] = np.array([2/3, 0])
    rtile[3] = np.array([1, -1/3])
    rtile[4] = np.array([1, -1/2])
    rtile[5] = np.array([4/3, -1/2])
    rtile[6] = np.array([4/3, -1/6])
    rtile[7] = np.array([7/6, -1/6])
    rtile[8] = np.array([5/6, 1/6])
    rtile[9] = np.array([5/6, 1/3])    
    rtile = scalar * rtile
    return tile, rtile    
    
class AppOgl(OpenGLFrame): 
    def initgl(self):
        GL.glViewport(0, 0, self.width, self.height)
        GL.glClearColor(1.0, 1.0, 1.0, 1.0)    
    def redraw(self):
        global num, base
        scalar = H * 1.0 / num  ## 描画ウィンドウと行の数からタイルの大きさを決定
        m = int(np.ceil(num / base[1][0]))  ## 列の数
        lattice = makeSqLattice(num, scalar)  ## 正方格子の格子点ベクトルを生成
        tile, rtile  = makeSquare(scalar)
        GL.glClear(GL.GL_COLOR_BUFFER_BIT)
        glColor3f(0.0, 0.0, 1.0)
        glLineWidth(2.0) ## 線の幅
        glMatrixMode(GL_PROJECTION)
        glLoadIdentity()
        glOrtho(0, W, 0, H, -1.0, 1.0)
        glPolygonMode(GL_FRONT, GL_LINE) ## 表面をワイヤーフレームで
        glPolygonMode(GL_BACK, GL_FILL) ## 裏面を中身の詰まった多角形で
        glFrontFace(GL_CCW) ## 表は反時計回り（デフォルト）
##        glFrontFace(GL_CW) ## 表は時計回り
        for vecArr in lattice:
            for k, vec in enumerate(vecArr):
                glLineWidth(2.0)
                glColor3f(0.0, 0.0, 1.0)
                t = tile.copy()
                glBegin(GL_LINE_LOOP)
                for i in range(10):
                    glVertex3d(vec[0]+t[i][0], vec[1]+t[i][1], 0)
                glEnd()
                t = rtile.copy()
                glBegin(GL_LINE_LOOP)
                for i in range(10):
                    glVertex3d(vec[0]+t[i][0], vec[1]+t[i][1], 0)
                glEnd()
                if k == 0:
                    t = rtile.copy()
                    glBegin(GL_LINE_LOOP)
                    for i in range(10):
                        glVertex3d(vec[0]-scalar+t[i][0], vec[1]+t[i][1], 0)
                    glEnd()
                   
def button_click():
    global num   
    num = int(txt.get())
    app._display()

if __name__ == '__main__':
    root = tkinter.Tk()
    root.title('Figure1.3.9 by tkinter with pyopengl')
    app = AppOgl(root, width=600, height=600)
    app.pack(fill=tkinter.BOTH, expand=tkinter.YES)
    lbl = tk.Label(text='num')
    lbl.pack()
    txt = tk.Entry(width=20)
    txt.pack()
    # テキストボックスをクリア
    txt.delete(0, tk.END)
    # テキストボックスに文字「1234」を入力
    txt.insert(tk.END, str(num))
    # button1ウィジェットを作成
    button1 = tk.Button(root ,text="描画", command=button_click)
    button1.pack() # button1ウィジェットを配置
##    app.animate = 1  
##    app.animate = True ## この方が正式  
    app.animate = 0
    app.mainloop()
のようなプログラムをでっち上げれば大丈夫です。 この様な模様は市販のデザイン用ソフトや私の Escher.exe、Escher2.exe でも描けるはずですが、大変な労力が要ります。 個人的な意見ですが、普遍性のあるプログラミングの方が自由にプログラミング出来るようになれば便利でかつ有用です。昔、教えていた女子学生さんに あるタイリングの作成方法を聞かれましたが、 その時には経験に乏しく適切な答えが出来ませんでした。その当時はこのソフトをやっとこさ作り上げましたが、単なるプロトタイプで、商品として使ってもらうためには、 色々考えて改良すべきだと言うことがこの年になってやっと分かりました。単に作ってみただけで、単なる自己満足で、私も使わないソフトでした。 退職して、タイリングの図を沢山プログラミングしてみると少しづつ色々なことが見えてきます。残念なのは昔作成した C++ の言語のソフト Borland C++ Builder が今は使えないので その当時よりプログラミング能力はそれなりに向上しているはずですが、全部最初から作り直す必要があり、簡単には改良できません。 公共インフラと異なり、利益追求の民間企業は色々な理由で、利益にならないと思えば、簡単に切り捨て撤退するので、それまでの努力が無になり力のない我々凡人は困惑します。 更に、インターネット上に大量の画像が溢れる時代になったので AI が探索技術の向上でインターネット上にこの様な画像がないか探し、 あれば見つけて、要求に応じた適切な処理をしてくれる様になる・なったみたいです。 AI のそのような助けで人間の本質的な能力が上がる訳では決して無いですが、人間が本来すべきことのハードルが次々と上がってきています。 「必要な所を拾い読みすれば良い」と言う現在の風潮のタイパ重視の意見もありますが、「あれ？」と思えば、別のこともしてみます。

（第72回高知市「夏期大学」で、尾池和夫さんが、Goldberg の tiling のプログラミングの作成で睡眠不足の状態で講演を聞いていたので 、 聞き間違えたのか知れませんが「やなせたかしさんは高知に何らかの関係はあるが、厳密には本人は高知出身ではない」と言っていた様に思いました。） 土佐黒潮鉄道奈半利線の各駅のキャラクターを作成した時に、「キャラクターを作るのにどれだけ時間が掛かるか」と聞かれた時に、 確か、「昔は随分時間が掛ったけれども、今は一つ数分だ」と答えていたと思いますが、 「探索」と言う応用範囲の広い一つの分野に限定して練習を繰り返せば、我々凡人でもそれなりに上達し、自分の武器にすることが出来ます。 自分にとって必要なことは努力できます。努力できないこと・長続きしないことは、それは自分にはまだ必要ないことです。多分。 或いは、読んでいる才能ある優秀な人達が書いた参考書が不適切で、才能ある優秀な人達はその方法で良くても、 我々凡人にはその方法では、例えば、「理解できないことは暗記出来ない」 で努力できない可能性があります。唯、最近は、多分、若い人達の書いた（この人達も才能ある優秀な人達ですが）我々凡人でも理解できる 参考書が多数出版されだしましたから、自分に合った参考書を探せば良いです。

最近話題の NAOMI KLEIN 著「THE SHOCK DOCTORINE」(Penguin Books) を手に入れました。翻訳より安いと思ったので購入しましたが、活字が小さくて老人には 大変です。Eテレの「100分で名著」や日本語の解説書の堤未果さんの解説もあり、大体内容は把握できているので、今まで読んできた英文の本とは全然分野の違う本ですが、 英語の勉強の為、これも少しづつ読んで見たいです。 メアリー・L・グレイ、シッダールタ・スリ著「ゴースト・ワーク」も「身の回りで最近起こっている事の意味・何が起こっているか」を教えてくれる本です。 例えば、「最近話題の AI が信用できるか？」が話題になった時、「最近話題のAI は単にインターネット上の情報を使っているのではなく、 人間が修正している」と AIの研究者がテレビの対談でポロっと漏らしたのですが、「これは何を言ったのか？」が書いてあります。 例えば、下のタイル張りの画像が「タイル張りの画像」であると直接判定するアルゴリズムは開発されていません。人間が一つ一つ判断して、インターネットで見つけた 画像にこれは「タイル張りの画像」であると言った紐づけをし、その「タイル張りの画像」と紐づけされた大量の画像を AI が学習することにより、 「タイル張りの画像」が欲しいと 命令すれば、下のような画像が表示されるようになります。脚光を浴びている AI の裏で大量の人間の仕事が生み出されています。 それがどの様な新たな問題を引き起こしているか解説してくれるのがこの「ゴースト・ワーク」です。 大学紛争が盛んな頃、学生に「専門バカ」と言われた大学教授が「専門バカでなければ唯のバカだ」と答えたと言われていましたが、 「専門バカ」ではアメリカや中国と言った巨大な国が仕掛けている新たなステルスな「新植民地政策」で再び世界が完膚なきまでに略奪・蹂躙され、 そうなれば再び元の自由な世界には戻ることが出来なくなりそうです。 知らないうちに大変な世の中になりつつあるみたいです。 したいことが一杯あって、健康の為に必須の散歩が疎かになりそうで困ったもんです。

弥右衛門公園でトンボを見ました。今までそんな余裕が無かったかも分かりませんが、トンボは久しぶりに見たような気がします。

今までやって来た作業は誰もやったことのない分野・最先端の研究ですべきですが、 aperiodic tiling と言う私にとって今まで学んだことの無い新たな分野を学ぶためにはこの様な基本的手法を学ぶ為の訓練が多分必要です。 「帰納」と「類比」と「パソコン」を使い別の Robinson's tiling を探します。自分でもこの様に考えることが出来れば、同じことが出来たんだなあと言うものを探します。



のような対称群（変換群）が Wallpaper 群（平面結晶群と訳している参考書もあります）であるタイル張りは 経験を積めば「ルーチンワーク」で簡単にプログラミング出来ますが、 TILINGS AND PATTERNS の Figure 1.3.6 (a) の対称群が C6 のタイル張りは 規制が少ないので、本で与えられた図をじっと眺めるだけでパターンを見つける人もいるとは思いますが、 この図の外側はどの様なアルゴリズムで生成されているかを知るのは 我々凡人にとっては厄介です。「Frieze 群（フリーズ群）」も同様ですが、「aperiodic tiling」 なら更に厄介です。 このタイル張りを見つけた M.GOLDBERG 1955 : Central tessellations. Scripta Math. 21(1955), 253-260 を手に入れる事が出来れば良いですが、出来なくてもこの図があれば、 自分で何とか調べて見ることが出来ます。内角が「60度、150度、45度、105度」の四角形の紙片を沢山作って並べてみるのが一つの方法ですが、 画家・工芸作家のような根気はないので、直ぐ嫌になりますが、今はパソコンガあるので、探索プログラムを作って調べることが出来ます。 興味があればやってみて下さい。試行錯誤の過程を書いていましたが、削除しました。

今年インターネットで報道された「数学の未解決問題「アインシュタイン問題」を“完全解決”する新図形発見「The hat」を改良」で 平面のタイリングの主要な問題は多分終わったので、 （安易な考えでは、巴山竜来著「数学から創るジェネラティブアート - Processingで学ぶかたちのデザイン」でやって見せてくれたように、例えば、 Goldberg tiling の矩形を複雑な形に変形することにより、美術的に美しい模様を探すような作業は勿論残されていますし、誰かが何らかの新しい視点を 発見する可能性が無いわけで無いですが）、これからは我々素人でも予備知識なく理解出来る研究は「3次元のタイリング」の研究だとおもいます。 小学生でも何を研究しているか理解できる幾何学の分野ですが、現在知られている結果（平面や高次元 Euclid 空間の periodic tiling を 制御する結晶群の構造が解明され、低次元の場合には分類表も得られていますが、Euclid 空間の代わりに、 Rieman 対称空間と呼ばれる「曲がった空間」の上で periodic tiling を考えると、 実簡約 Lie 群の格子と呼ばれる群が現れるそうです。更に、非 Rieman 等質空間の periodic tiling の研究などといった難しいことを 本物の現役の数学者は現在研究しているそうです。）からも複雑なことが予想され、 老後の暇つぶしで　Python のプログラムを作っていますが、上で少し正多面体や準正多面体単独の描画を思い出してやってみましたが、 この年になると結構大変で、テーマはタイリングなので手始めに空間充しん形からでしょうが、昔買い集めた本達を佐川の本箱から見つけることから 始めなければいけないし、日本語の関連する参考書も最近出版されているみたいだし。 多面体単独の表示のプログラミングもさわりをやってみただけで有名な本に載っている膨大な数の不思議な多面体、 （例えば、ゾーン多面体とかもあるそうで、この分野では常識とされている事も全く知らないので一つ一つ勉強しなければならず、 知らなかったことを知ることは楽しいことですが一人で独学するのは矢張り大変です。 尾池和夫さんは夏期大学で100歳まで生きるつもりであると言って、 自分の生涯年表を発表していましたが、3次元の何らかの綺麗な（出来たら非周期的なものだと良いですが:既に見つかっていると書いている人がいます）タイリングを幸運にも見つけることが 出来たら、実際は、3次元のタイリングは簡単に何らかの面白い図形が私如きに見つけれるとは思えないのですが、 生きている内に誰かの参考になるかもと思えるプログラムを何か作ることが出来たら、また余計なたわ言を削除して書いてみます。 手塚治虫さんの「鉄腕アトム」と石ノ森章太郎さんの「サイボーグ009」を比較して、コンピュータとの付き合い方は、「サイボーグ009」の方式で 行くべきだとの意見を最近読みました。この人の意見の様に人間の能力を拡大してくれるものとして AI も捉え、活用すれば思い悩むこともなさそうです。 老人のたわ言かもしれませんが、例えば、11+x4 の不定積分の答えだけを数式処理ソフトで直接得るのと 複素数の範囲と実数の範囲の部分分数分解をそれぞれ求める為に Python の プログラミングして、（この年になって計算してみると能力の衰えは隠しようがなく手計算では間違えてばかりなので、 参考書に載っている人間が計算する通りの方法でコンピュータの助けを借りて計算していますが）、 過去の偉人たちの業績を辿ってみるのとでは「何をしているか理解しているか？」で、長い目で見ると得るものが違うように思います。 本に載っている複雑な多面体の図も専門家しか描けない図だと思わず、コンピュータの力を借りれば我々凡人のプログラミングの素人でも 高校の数学の知識＋α位で描けるはずですから挑戦してみると良いです。 多面体を描くプログラムは様々な方法で作れますし、又、様々な多面体の紙の模型を作るための本も2冊出版されていて、一冊の翻訳は持っていてどっかにあるはずですが、 今調べて見ると円安のせいか英語の原本は凄く高価で、しかも、他人に写真などが流用されないようにわざと不鮮明にしているなどと不評ですが、参考になります。 上でやったように昔の Archimedes の C++ のプログラムを Python のモジュールとし、既に作っている準正多面体や星形多面体などはそれを使って描画し、 それ以外の不思議な・奇妙な形状の各種多面体を描けるよう拡張していく方法やこれは正多面体を元に他の多面体を構成する方法を知りたくて作ったものでしたが、 直接各種多面体を MAGNUS J. WENNINGER 著「Polyhedron Models」（これはどうゆう訳か原著も持っていました）などの情報と その多面体の変換群の情報とを元に描くことも可能ですし、 H.S.M. Coxeter 著「Regular Complex Polytopes」にもどうやって描いただろうと思う図が沢山載っています。 また、私の過去のプログラム： 「 https://www.cc.kochi-u.ac.jp/~tyamag/kite/kite_pro2.html のプログラム」 を再利用するには、タートル・グラフィックスが使えます。 私の昔技術が未熟な時作った出来損ないの Kite ではなく、上で示した「3次元の LSystem の画像を作れるプログラム」を https://www.cc.kochi-u.ac.jp/~tyamag/kite/kite_pro2.html のプログラムを参考に、単純な多面体を描ける様に作り直して、 更に、星形多面体などを描くために面を描く機能や色を付ける機能や連立方程式を解く機能など必要になるたびに追加すれば、様々な多面体を描くことが可能になるはずです。 例えば、第一歩は 

import time
import tkinter as tk
from OpenGL import GL
from OpenGL.GL import *
from OpenGL.GLU import *
from OpenGL import GLU
##from pyopengltk import OpenGLFrame
import numpy as np
import pygame
pygame.init()

W = 600
H = 600

class Vector3:
    def __init__(self, x=0.0, y=0.0, z=0.0):
        self.x = x
        self.y = y
        self.z = z
    def Rotate(self, angle, n):
        r = Point()
        cp = np.zeros(3)
        angle = angle*np.pi/180
        ip = n.x*self.x+n.y*self.y+n.z*self.z
        cp[0] = n.y*self.z-n.z*self.y
        cp[1] = n.z*self.x-n.x*self.z
        cp[2] = n.x*self.y-n.y*self.x
        r.x = n.x*ip+cp[0]*np.sin(angle)+(cp[1]*n.z-cp[2]*n.y)*np.cos(angle)
        r.y = n.y*ip+cp[1]*np.sin(angle)+(cp[2]*n.x-cp[0]*n.z)*np.cos(angle)
        r.z = n.z*ip+cp[2]*np.sin(angle)+(cp[0]*n.y-cp[1]*n.x)*np.cos(angle)
        norm = np.sqrt(r.x*r.x+r.y*r.y+r.z*r.z)
        self.x = r.x/norm
        self.y = r.y/norm
        self.z = r.z/norm
        
class Point():
    def __init__(self, x=0, y=0, z=0):
        self.x = x
        self.y = y
        self.z = z
    
class Turtle:
    stack = []

    def __init__(self, x=0, y=0, z=0):
        self.pos = Point(x, y, z)
        self.e1 = Vector3(1, 0, 0)
        self.e2 = Vector3(0, 1, 0)
        self.e3 = Vector3(0, 0, 1)

    def print(self):
        print('pos=', self.pos.x, self.pos.y, self.pos.z)
        print('e1=', self.e1.x, self.e1.y, self.e1.z)
        print('e2=', self.e2.x, self.e2.y, self.e2.z)
        print('e3=', self.e3.x, self.e3.y, self.e3.z)
        
    def Reset(self):
        self.pos = Point(0, 0, 0)
        self.e1 = Vector3(1, 0, 0)
        self.e2 = Vector3(0, 1, 0)
        self.e3 = Vector3(0, 0, 1)
        ##    def LineTo(cls, x, y):
        
    def LineTo(self, x, y, z):
        glLineWidth(2)
        glBegin(GL_LINE_STRIP)
        glVertex3f(self.pos.x, self.pos.y, self.pos.z)
        glVertex3f(x, y, z)
        glEnd()
        self.pos.x = x
        self.pos.y = y
        self.pos.z = z
        
    def fd(self, distance):
        dest = Point(0, 0, 0)
        dest.x = self.pos.x + self.e1.x * distance
        dest.y = self.pos.y + self.e1.y * distance
        dest.z = self.pos.z + self.e1.z * distance
        self.LineTo(dest.x, dest.y, dest.z)
        self.pos.x = dest.x
        self.pos.y = dest.y
        self.pos.z = dest.z
    def bk(self, distance):
        self.fd(-distance)       
        
    def yaw(self, angle):
        self.e1.Rotate(angle, self.e3)
        self.e2.Rotate(angle, self.e3)
    def lt(self, angle):
        self.yaw(angle)
    def rt(self, angle):
        self.yaw(-angle)
        
    def pitch(self, angle):
        self.e1.Rotate(angle, self.e2)
        self.e3.Rotate(angle, self.e2)
    def up(self, angle):
        self.pitch(angle)
    def down(self, angle):
        self.pitch(-angle)
        
    def roll(self, angle):
        self.e2.Rotate(angle, self.e1)
        self.e3.Rotate(angle, self.e1)
        

##TO TETRA :A :B :C :D :E :F
##  FD :A
##  RT 180 - ACOS (:A*:A+:B*:B-:C*:C)/(2*:A*:B)
##  FD :B
##  RT 180 - ACOS (:B*:B+:C*:C-:A*:A)/(2*:B*:C)
##  FD :C
##  RT 180 - ACOS (:C*:C+:A*:A-:B*:B)/(2*:C*:A)
##  LOCAL :X :Y :Z
##  :X = ACOS  (:C*:C+:A*:A-:B*:B)/(2*:C*:A)
##  :Y =  ACOS (:D*:D+:A*:A-:E*:E)/(2*:D*:A)
##  :Z = ACOS (:D*:D+:C*:C-:F*:F)/(2*:D*:C)
##  YAW 180 - ACOS ((COS :Z)-(COS :X)*(COS :Y))/((SIN :X)*(SIN :Y))
##  FD :A
##  LT 180 - ACOS (:A*:A+:E*:E-:D*:D)/(2*:A*:E)
##  FD :E
##  LT 180 - ACOS (:E*:E+:D*:D-:A*:A)/(2*:E*:D)
##  FD :D
##  LT 180 - ACOS (:D*:D+:A*:A-:E*:E)/(2*:D*:A)
##  LT :Y
##  YAW 180 - ACOS ((COS :X)-(COS :Y)*(COS :Z))/((SIN :Y)*(SIN :Z))
##  FD :D
##  LT 180 - ACOS (:D*:D+:F*:F-:C*:C)/(2*:D*:F)
##  FD :F
##  LT 180 - ACOS (:F*:F+:C*:C-:D*:D)/(2*:F*:C)
##  FD :C
##  LT 180 - ACOS (:C*:C+:D*:D-:F*:F)/(2*:C*:D)
##  YAW -180 + ACOS ((COS :X)-(COS :Y)*(COS :Z))/((SIN :Y)*(SIN :Z))
##  RT :Y
##  YAW -180 + ACOS ((COS :Z)-(COS :X)*(COS :Y))/((SIN :X)*(SIN :Y))
##END

def tetra(a, b, c, d, e, f):
    global t
    
    t.fd(a)
    t.rt(180-np.arccos((a*a+b*b-c*c)/(2*a*b))*180/np.pi)
    t.fd(b)
    t.rt(180-np.arccos((b*b+c*c-a*a)/(2*b*c))*180/np.pi)
    t.fd(c)
    t.rt(180-np.arccos((c*c+a*a-b*b)/(2*c*a))*180/np.pi)
    x = np.arccos((c*c+a*a-b*b)/(2*c*a))
    y = np.arccos((d*d+a*a-e*e)/(2*d*a))     
    z = np.arccos((d*d+c*c-f*f)/(2*d*c))
    t.roll(180-np.arccos((np.cos(z)-np.cos(x)*np.cos(y))/\
                      (np.sin(x)*np.sin(y)))*180/np.pi)
    t.fd(a)
    t.lt(180-np.arccos((a*a+e*e-d*d)/(2*a*e))*180/np.pi)
    t.fd(e)
    t.lt(180-np.arccos((e*e+d*d-a*a)/(2*e*d))*180/np.pi)
    t.fd(d)
    t.lt(180-np.arccos((d*d+a*a-e*e)/(2*d*a))*180/np.pi)
    t.lt(y*180/np.pi)
    t.roll(180-np.arccos((np.cos(x)-np.cos(y)*np.cos(z))/\
                      (np.sin(y)*np.sin(z)))*180/np.pi)
    t.fd(d)
    t.lt(180-np.arccos((d*d+f*f-c*c)/(2*d*f))*180/np.pi)
    t.fd(f)
    t.lt(180-np.arccos((f*f+c*c-d*d)/(2*f*c))*180/np.pi)
    t.fd(c)
    t.lt(180-np.arccos((c*c+d*d-f*f)/(2*c*d))*180/np.pi)
    t.roll(-180+np.arccos((np.cos(x)-np.cos(y)*np.cos(z))/\
                      (np.sin(y)*np.sin(z)))*180/np.pi)
    t.rt(y*180/np.pi)
    t.roll(-180+np.arccos((np.cos(z)-np.cos(x)*np.cos(y))/\
                      (np.sin(x)*np.sin(y)))*180/np.pi)

t = Turtle()

display = (W, H)

screen = pygame.display.set_mode(display, pygame.DOUBLEBUF|pygame.OPENGL)

GL.glMatrixMode(GL.GL_PROJECTION)
GL.glLoadIdentity()
GLU.gluPerspective(90, (display[0]/display[1]), 0.1, 100.0)

angle = 0
game = 1
clock = pygame.time.Clock()
while game:
    for event in pygame.event.get():
        if event.type == pygame.QUIT:
            game = 0

    GL.glMatrixMode(GL.GL_MODELVIEW)
    GL.glLoadIdentity()
    GLU.gluLookAt(0, 0, 0, -1.0, 0, 0, 0, 1, 0)

    GL.glClearColor(0, 0, 0, 1)
    GL.glClear(GL.GL_COLOR_BUFFER_BIT|GL.GL_DEPTH_BUFFER_BIT)

    GL.glTranslatef(-5, 0, 0)
    GL.glRotatef(angle, 0, 1, 0)
    angle += 1

    GL.glPolygonMode(GL.GL_FRONT_AND_BACK, GL.GL_LINE)
    tetra(10, 8, 7, 6, 6.5, 7.5)

    pygame.display.flip()
    clock.tick(50)
    
pygame.quit()
のようなプログラムを作れば良いです。 何時も同じようなプログラムを作っていても技術が向上しないので、 https://stackoverflow.com/questions/66501839/pyopengl-does-not-redraw-triangle-strip-more-than-once-after-glclear で見つけたプログラムを参考に、pyopengl + pygame を使ってみました。アニメーションですが、気に入るようにプログラムを修正してください。 勉強になると思います。 上で示した「3次元の LSystem の画像を作れるプログラム」をそのまま使ったプログラムは、例えば、第一歩は 

import time
import tkinter
from OpenGL import GL
from OpenGL.GL import *
from OpenGL.GLU import *
from pyopengltk import OpenGLFrame
import numpy as np
from copy import copy

W = 600
H = 600

class Vector3:
    def __init__(self, x=0.0, y=0.0, z=0.0):
        self.x = x
        self.y = y
        self.z = z
    def Rotate(self, angle, n):
        r = Point()
        cp = np.zeros(3)
        angle = angle*np.pi/180
        ip = n.x*self.x+n.y*self.y+n.z*self.z
        cp[0] = n.y*self.z-n.z*self.y
        cp[1] = n.z*self.x-n.x*self.z
        cp[2] = n.x*self.y-n.y*self.x
        r.x = n.x*ip+cp[0]*np.sin(angle)+(cp[1]*n.z-cp[2]*n.y)*np.cos(angle)
        r.y = n.y*ip+cp[1]*np.sin(angle)+(cp[2]*n.x-cp[0]*n.z)*np.cos(angle)
        r.z = n.z*ip+cp[2]*np.sin(angle)+(cp[0]*n.y-cp[1]*n.x)*np.cos(angle)
        norm = np.sqrt(r.x*r.x+r.y*r.y+r.z*r.z)
        self.x = r.x/norm
        self.y = r.y/norm
        self.z = r.z/norm
        
class Point():
    def __init__(self, x=0, y=0, z=0):
        self.x = x
        self.y = y
        self.z = z
    
class Turtle:
    stack = []

    def __init__(self, x=0, y=0, z=0):
        self.pos = Point(x, y, z)
        self.e1 = Vector3(1, 0, 0)
        self.e2 = Vector3(0, 1, 0)
        self.e3 = Vector3(0, 0, 1)

    def print(self):
        print('pos=', self.pos.x, self.pos.y, self.pos.z)
        print('e1=', self.e1.x, self.e1.y, self.e1.z)
        print('e2=', self.e2.x, self.e2.y, self.e2.z)
        print('e3=', self.e3.x, self.e3.y, self.e3.z)
        
    def Reset(self):
        self.pos = Point(0, 0, 0)
        self.e1 = Vector3(1, 0, 0)
        self.e2 = Vector3(0, 1, 0)
        self.e3 = Vector3(0, 0, 1)
        ##    def LineTo(cls, x, y):
        
    def LineTo(self, x, y, z):
        glLineWidth(2)
        glBegin(GL_LINE_STRIP)
        glVertex3f(self.pos.x, self.pos.y, self.pos.z)
        glVertex3f(x, y, z)
        glEnd()
        self.pos.x = x
        self.pos.y = y
        self.pos.z = z
        
    def fd(self, distance):
        dest = Point(0, 0, 0)
        dest.x = self.pos.x + self.e1.x * distance
        dest.y = self.pos.y + self.e1.y * distance
        dest.z = self.pos.z + self.e1.z * distance
        self.LineTo(dest.x, dest.y, dest.z)
        self.pos.x = dest.x
        self.pos.y = dest.y
        self.pos.z = dest.z
    def bk(self, distance):
        self.fd(-distance)       
        
    def yaw(self, angle):
        self.e1.Rotate(angle, self.e3)
        self.e2.Rotate(angle, self.e3)
    def lt(self, angle):
        self.yaw(angle)
    def rt(self, angle):
        self.yaw(-angle)
        
    def pitch(self, angle):
        self.e1.Rotate(angle, self.e2)
        self.e3.Rotate(angle, self.e2)
    def up(self, angle):
        self.pitch(angle)
    def down(self, angle):
        self.pitch(-angle)
        
    def roll(self, angle):
        self.e2.Rotate(angle, self.e1)
        self.e3.Rotate(angle, self.e1)
        

##TO TETRA :A :B :C :D :E :F
##  FD :A
##  RT 180 - ACOS (:A*:A+:B*:B-:C*:C)/(2*:A*:B)
##  FD :B
##  RT 180 - ACOS (:B*:B+:C*:C-:A*:A)/(2*:B*:C)
##  FD :C
##  RT 180 - ACOS (:C*:C+:A*:A-:B*:B)/(2*:C*:A)
##  LOCAL :X :Y :Z
##  :X = ACOS  (:C*:C+:A*:A-:B*:B)/(2*:C*:A)
##  :Y =  ACOS (:D*:D+:A*:A-:E*:E)/(2*:D*:A)
##  :Z = ACOS (:D*:D+:C*:C-:F*:F)/(2*:D*:C)
##  YAW 180 - ACOS ((COS :Z)-(COS :X)*(COS :Y))/((SIN :X)*(SIN :Y))
##  FD :A
##  LT 180 - ACOS (:A*:A+:E*:E-:D*:D)/(2*:A*:E)
##  FD :E
##  LT 180 - ACOS (:E*:E+:D*:D-:A*:A)/(2*:E*:D)
##  FD :D
##  LT 180 - ACOS (:D*:D+:A*:A-:E*:E)/(2*:D*:A)
##  LT :Y
##  YAW 180 - ACOS ((COS :X)-(COS :Y)*(COS :Z))/((SIN :Y)*(SIN :Z))
##  FD :D
##  LT 180 - ACOS (:D*:D+:F*:F-:C*:C)/(2*:D*:F)
##  FD :F
##  LT 180 - ACOS (:F*:F+:C*:C-:D*:D)/(2*:F*:C)
##  FD :C
##  LT 180 - ACOS (:C*:C+:D*:D-:F*:F)/(2*:C*:D)
##  YAW -180 + ACOS ((COS :X)-(COS :Y)*(COS :Z))/((SIN :Y)*(SIN :Z))
##  RT :Y
##  YAW -180 + ACOS ((COS :Z)-(COS :X)*(COS :Y))/((SIN :X)*(SIN :Y))
##END

def tetra(a, b, c, d, e, f):
    global t
    
    t.fd(a)
    t.rt(180-np.arccos((a*a+b*b-c*c)/(2*a*b))*180/np.pi)
    t.fd(b)
    t.rt(180-np.arccos((b*b+c*c-a*a)/(2*b*c))*180/np.pi)
    t.fd(c)
    t.rt(180-np.arccos((c*c+a*a-b*b)/(2*c*a))*180/np.pi)
    x = np.arccos((c*c+a*a-b*b)/(2*c*a))
    y = np.arccos((d*d+a*a-e*e)/(2*d*a))     
    z = np.arccos((d*d+c*c-f*f)/(2*d*c))
    t.roll(180-np.arccos((np.cos(z)-np.cos(x)*np.cos(y))/\
                      (np.sin(x)*np.sin(y)))*180/np.pi)
    t.fd(a)
    t.lt(180-np.arccos((a*a+e*e-d*d)/(2*a*e))*180/np.pi)
    t.fd(e)
    t.lt(180-np.arccos((e*e+d*d-a*a)/(2*e*d))*180/np.pi)
    t.fd(d)
    t.lt(180-np.arccos((d*d+a*a-e*e)/(2*d*a))*180/np.pi)
    t.lt(y*180/np.pi)
    t.roll(180-np.arccos((np.cos(x)-np.cos(y)*np.cos(z))/\
                      (np.sin(y)*np.sin(z)))*180/np.pi)
    t.fd(d)
    t.lt(180-np.arccos((d*d+f*f-c*c)/(2*d*f))*180/np.pi)
    t.fd(f)
    t.lt(180-np.arccos((f*f+c*c-d*d)/(2*f*c))*180/np.pi)
    t.fd(c)
    t.lt(180-np.arccos((c*c+d*d-f*f)/(2*c*d))*180/np.pi)
    t.roll(-180+np.arccos((np.cos(x)-np.cos(y)*np.cos(z))/\
                      (np.sin(y)*np.sin(z)))*180/np.pi)
    t.rt(y*180/np.pi)
    t.roll(-180+np.arccos((np.cos(z)-np.cos(x)*np.cos(y))/\
                      (np.sin(x)*np.sin(y)))*180/np.pi)

t = Turtle()

class AppOgl(OpenGLFrame):##
    global t

    def initgl(self):
        """Initalize gl states when the frame is created"""
        GL.glViewport(0, 0, self.width, self.height)
        GL.glClearColor(0.0, 0.0, 0.0, 0.0)    
##        self.start = time.time()
##        self.nframes = 0


    def Setup(self):
        GL.glLoadIdentity() ## 投影変換の変換行列を単位行列で初期化
        glOrtho(-300, 300, -300, 300, -300.0, 300.0)


    def redraw(self):
        global t, loop_step, degree
        
        """Render a single frame"""
        degree  += loop_step 
        glClear(GL_COLOR_BUFFER_BIT)
        glColor3f(1.0, 1.0, 1.0)
        glOrtho(-300.0, 300.0, -300.0, 300.0, -300.0, 300.0)
        
        self.Setup()
        t.Reset()
        t.pitch(degree)
        t.yaw(degree)
        tetra(250, 170, 140, 120, 170, 150)
           
if __name__ == '__main__':
    root = tkinter.Tk()
    app = AppOgl(root, width=W, height=H)
    app.pack(fill=tkinter.BOTH, expand=tkinter.YES)
##    app.animate = 1
    degree = 0
    loop_step = 0.1
    app.animate = 1
##    app.after(100, app.printContext)
    app.mainloop()
で良いと思います。 但し、 https://www.cc.kochi-u.ac.jp/~tyamag/kite/kite_pro2.html のプログラムの yaw() と roll() は上でやっている様に入れ替える必要があります。 この tetra() のプログラムは山口先生に「一般に四面体になる６個の辺の長さの条件」を質問された時、作ったものです。 確か球面幾何学の知識が必要だったと思います。 私は何か新しいことを学びたい時、3，4年生のゼミや一般教養の講義で私がしたいことをテーマにすることで学んできました。 ある意味、色々の書籍で沢山の優秀な先生たちに間接的に指導を受け、またゼミの学生さん達に助けられて新しことを今まで学んできました。 又、目で見る「風景・絵・図・模様・文字等」と同様、耳で聴く「音全般・言語・音楽等」が我々に身近ですが、 何度やっても中途半端で上手くいかなかった「音のプログラミング」も、 書籍を読んでの独学では、大学等で専門の先生について学ぶようにはいきませんが、 別の本を探しに行って偶々本屋で最近出版された青木直史著「Python ではじめる音のプログラミング」を見つけたので、 難解な理論をプログラミングで一つ一つやってみないと理解するのが難しい我々凡人でも、 （「What I cannot create, I do not understand.」と言うファインマンさんの言葉もあるそうです。）、 実験してみるのに参考になる理解できるプログラムを提示してくれているので、既に集めている本と一緒にもう一度基礎からやってみたいです。 音の勉強（外国語の発音等や音楽・MIDI及びそのフーリエ解析などの数学理論・アルゴリズム）の細部を解説した様々な解説書で、迷子になっていたのですが、 この本の前半：第5章ディジタル信号処理までで大雑把な見取り図・散歩道を与えてくれているので、 （また、評判になっている今井むつみ・秋田喜実著「言語の本質」も面白い本です）、自分は本当は何をしたいのか考えることが出来ます。

例えば、青木直史著「Python ではじめる音のプログラミング」のプログラムと https://pythonnumericalmethods.berkeley.edu/notebooks/chapter24.04-FFT-in-Python.html　で見つけたプログラムを使って 

import numpy as np
##from wave_file import wave_write_16bit_mono
import matplotlib.pyplot as plt
from wave_file import wave_read_16bit_mono
from numpy.fft import fft, ifft

fs, s = wave_read_16bit_mono('trumpet.wav')

length_of_s = len(s)
print('length_of_s=', length_of_s)

offset = 20000
fs = 44100

ts = 1.0/fs
t = np.arange(0,1,ts)

x = np.zeros(fs)
for n in range(fs):
    x[n] = s[n+offset]

X = fft(x)
N = len(X)
n = np.arange(N)
T = N/fs
freq = n/T 

plt.figure(figsize = (12, 6))
plt.subplot(121)

plt.stem(freq, np.abs(X), 'b', \
         markerfmt=" ", basefmt="-b")
plt.xlabel('Freq (Hz)')
plt.ylabel('FFT Amplitude |X(freq)|')
plt.xlim(0, 1000)

plt.subplot(122)
plt.plot(t, ifft(X), 'r')
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.xlim(0, 0.02)
plt.tight_layout()
plt.show()
で、 

Warning (from warnings module):
  File "C:\Anaconda3\lib\site-packages\numpy\core\_asarray.py", line 102
    return array(a, dtype, copy=False, order=order)
ComplexWarning: Casting complex values to real discards the imaginary part
のような警告がでますが、


を描いてくれます。トランペットの音声の一部を周波数分析したもののつもりですが急いで作ったので間違っているかも？ライブラリーを使えば簡単です。 青木直史さんのプログラムをそのまま使わず、この様に変えたのは、青木直史さんのプログラムは実際の音の研究している専門家が使っている「窓関数」を使っているので、 サイン関数の単純な単振動の音の周波数分析でも余計な周波数成分が表示されるので、 そうではなく純粋な数学的な理論通りの周波数分析をしてみたかったからです。これなら単振動は周波数成分は一個だけ表示されます。 音のプログラミングに興味がある私のような初心者は、例えば、青木直史著「Python ではじめる音のプログラミング」で与えられているプログラムで、 様々な数式を与えて音を作り、.wav ファイルを作ったり、 青木直史著「ゼロからはじめる音響学」のサポートページの音声を Praat で録音して、.wav ファイルを作りながら、 青木直史著「ゼロからはじめる音響学」を上のプログラムで確かめながら読めば良いです。多分。 何で私が音に興味があるかと言うと音痴だし外国語の発音も自信がないからです。アラビア語で「saaf」と「.saaf」は最初の子音が違うだけで、 発音し分けるにはこれら子音を発音し分けなければいけないと殆どの参考書には書いてありますが、CD で発音を聞くと次の母音が異なっている様にしか 聞こえません。アルファベットの「qaaf」と「kaaf」 の発音も参考書に書いてあるような子音の違いは分かりませんが 「カーフ」と「ケーフ」と母音の発音の違いが耳に残ります。アラビア語の母音は「あ」と「い」と「う」だけだと参考書には書いてありますが、 独学で学んでいる私には「え」と発音している様に聞こえます。 David James Young 著「Arabic Grammar」の NOTE には、文字は発音を正確に表現するものではなく、外国人は多分、子音＋母音で発音を考えれば 良いと書いてあると思います。外国語の勉強は私には難しいです。

サヘル・ローズさんが「高知市　夏期大学」の講演に来ると言うので、確か広中 平祐さんが講演した時に聞きに行った時以来、 数十年ぶり（？）に夏期大学に行きました。イラン・イラク戦争の戦争孤児で過酷な半生を過ごしてきた方で、貴重な話を聴くことが出来ました。 昔、テレビで初めて見た時は、凄い美人だと思いましたが、前日までの北海道でのアイヌ人の役の撮影があり、そのまま駆け付けた言っていましたので、 疲れていたのかもしれませんが、随分疲れ果ている印象を受けましたが、最後に２，３階席の聴衆に笑顔で手を振り続けていたのが印象に残りました。 サイン付きの著書も販売していましたが、 昔から有名人の書籍では常識とされているゴーストライターに依る本ではなく、「自分で書きました」とわざわざ話し笑いを誘っていましたが、 多くの人が感銘を受けたであろう・色々考えさせられた素晴らしい講演で、講演後、沢山の人が書籍の購入を希望し、 長蛇の列を作りましたが私のすぐ前の人までで売り切れてしまいました。

一松信著「正多面体を解く」に載っている星形大十二面体、星形小十二面体、大十二面体や大二十面体を描くには、座標を求めて描くのが普通ですが、 昔作ったKITE のプログラムがあるので、それらを再利用するために、3次元タートルグラフィックスもどきでプログラミングしてみました。 kite.py を 

import time
import tkinter
from OpenGL import GL
from OpenGL.GL import *
from OpenGL.GLU import *
from pyopengltk import OpenGLFrame
import numpy as np
from copy import copy
import random

W = 600
H = 600

class Vector3:
    def __init__(self, x=0.0, y=0.0, z=0.0):
        self.x = x
        self.y = y
        self.z = z
    def Rotate(self, angle, n):
        r = Point()
        cp = np.zeros(3)
        angle = angle*np.pi/180
        ip = n.x*self.x+n.y*self.y+n.z*self.z
        cp[0] = n.y*self.z-n.z*self.y
        cp[1] = n.z*self.x-n.x*self.z
        cp[2] = n.x*self.y-n.y*self.x
        r.x = n.x*ip+cp[0]*np.sin(angle)+(cp[1]*n.z-cp[2]*n.y)*np.cos(angle)
        r.y = n.y*ip+cp[1]*np.sin(angle)+(cp[2]*n.x-cp[0]*n.z)*np.cos(angle)
        r.z = n.z*ip+cp[2]*np.sin(angle)+(cp[0]*n.y-cp[1]*n.x)*np.cos(angle)
        norm = np.sqrt(r.x*r.x+r.y*r.y+r.z*r.z)
        self.x = r.x/norm
        self.y = r.y/norm
        self.z = r.z/norm
        
class Point():
    def __init__(self, x=0, y=0, z=0):
        self.x = x
        self.y = y
        self.z = z
    
class Turtle:
    def __init__(self, x=0, y=0, z=0):
        self.pos = Point(x, y, z)
        self.e1 = Vector3(1, 0, 0)
        self.e2 = Vector3(0, 1, 0)
        self.e3 = Vector3(0, 0, 1)
        self.penFlag = True
        self.lineWidth = 2
        self.stack = []

    def push(self):
        p = (self.pos.x, self.pos.y, self.pos.z)
        e1 = (self.e1.x, self.e1.y, self.e1.z)
        e2 = (self.e2.x, self.e2.y, self.e2.z)
        e3 = (self.e3.x, self.e3.y, self.e3.z)
        
        self.stack.append((p, e1, e2, e3, self.penFlag))
    def pop(self):
        inf = self.stack[len(self.stack)-1]
        self.pos = Point(inf[0][0], inf[0][1], inf[0][2])
        self.e1 = Vector3(inf[1][0], inf[1][1], inf[1][2]) 
        self.e2 = Vector3(inf[2][0], inf[2][1], inf[2][2]) 
        self.e3 = Vector3(inf[3][0], inf[3][1], inf[3][2]) 
        self.penFlag = inf[4]
        del self.stack[len(self.stack)-1]

    def exchange(self):
        top = self.stack.pop(0)
        next = self.stack.pop(0)
        self.stack.insert(0, next)
        self.stack.insert(0, top)

    def duplicate(self):
        top = self.stack[0]
        self.stack.insert(0, top)
        
    def print(self):
        print('pos=', self.pos.x, self.pos.y, self.pos.z)
        print('e1=', self.e1.x, self.e1.y, self.e1.z)
        print('e2=', self.e2.x, self.e2.y, self.e2.z)
        print('e3=', self.e3.x, self.e3.y, self.e3.z)
        print('penFlag=', self.penFlag)
        
    def Reset(self):
        self.pos = Point(0, 0, 0)
        self.e1 = Vector3(1, 0, 0)
        self.e2 = Vector3(0, 1, 0)
        self.e3 = Vector3(0, 0, 1)
        self.penFlag = True
        ##    def LineTo(cls, x, y):
        
    def LineTo(self, x, y, z):
        if self.penFlag:
            glLineWidth(self.lineWidth)
            glBegin(GL_LINE_STRIP)
            glVertex3f(self.pos.x, self.pos.y, self.pos.z)
            glVertex3f(x, y, z)
            glEnd()
        self.pos.x = x
        self.pos.y = y
        self.pos.z = z
        
    def fd(self, distance):
        dest = Point(0, 0, 0)
        dest.x = self.pos.x + self.e1.x * distance
        dest.y = self.pos.y + self.e1.y * distance
        dest.z = self.pos.z + self.e1.z * distance
        self.LineTo(dest.x, dest.y, dest.z)
    def bk(self, distance):
        self.fd(-distance)       
        
    def yaw(self, angle):
        self.e1.Rotate(angle, self.e3)
        self.e2.Rotate(angle, self.e3)
    def lt(self, angle):
        self.yaw(angle)
    def rt(self, angle):
        self.yaw(-angle)
        
    def pitch(self, angle):
        self.e1.Rotate(angle, self.e2)
        self.e3.Rotate(angle, self.e2)
    def up(self, angle):
        self.pitch(angle)
    def down(self, angle):
        self.pitch(-angle)
        
    def roll(self, angle):
        self.e2.Rotate(angle, self.e1)
        self.e3.Rotate(angle, self.e1)

    def toward(self, x, y, z):
        a = np.array([x, y, z])
        b = np.array([self.pos.x, self.pos.y, self.pos.z])
        c = a - b
        norm = np.sqrt(c[0]*c[0]+c[1]*c[1]+c[2]*c[2])
        d = np.array([c[0]/norm, c[1]/norm, c[2]/norm])
        e = np.array([self.e1.x, self.e1.y, self.e1.z])
        ip = e[0]*d[0]+e[1]*d[1]+e[2]*d[2]
        cp = np.zeros(3)
        cp[0] = e[1]*d[2]-e[2]*d[1]
        cp[1] = e[2]*d[0]-e[0]*d[2]
        cp[2] = e[0]*d[1]-e[1]*d[0]
        norm = np.sqrt(cp[0]*cp[0]+cp[1]*cp[1]+cp[2]*cp[2])
        n = Vector3(cp[0]/norm, cp[1]/norm, cp[2]/norm)
        angle = np.arccos(ip)*180/np.pi
        self.e1.x = d[0]
        self.e1.y = d[1]
        self.e1.z = d[2]
        self.e2.Rotate(angle, self.e1)
        self.e3.Rotate(angle, self.e1)

    def penup(self):
        self.penFlag = False
    def pendown(self):
        self.penFlag = True

    def setLineWidth(self, n):
        self.lineWidth = n

class Manager:
    def __init__(self):
        self.t = [Turtle(), Turtle()]
        self.synchroFlag = False
        self.surfaceFlag = False
        self.magazine = []
        self.surfcolor = [1, 0, 1]
        self.polyModeFlag = False
        self.store = []

    def put(self, n, ind):
        m = len(self.magazine)
        if m <= ind:
            for i in range(ind-m+1):
                self.magazine.append((0,))               
        p = (self.t[n].pos.x, self.t[n].pos.y, self.t[n].pos.z)
        e1 = (self.t[n].e1.x, self.t[n].e1.y, self.t[n].e1.z)
        e2 = (self.t[n].e2.x, self.t[n].e2.y, self.t[n].e2.z)
        e3 = (self.t[n].e3.x, self.t[n].e3.y, self.t[n].e3.z)
        
        self.magazine[ind] =(p, e1, e2, e3, self.t[n].penFlag)
    def get(self, n, ind):
        if self.polyModeFlag == False:
            inf = self.magazine[ind]
            self.t[n].pos = Point(inf[0][0], inf[0][1], inf[0][2])
            self.t[n].e1 = Vector3(inf[1][0], inf[1][1], inf[1][2]) 
            self.t[n].e2 = Vector3(inf[2][0], inf[2][1], inf[2][2]) 
            self.t[n].e3 = Vector3(inf[3][0], inf[3][1], inf[3][2]) 
            self.t[n].penFlag = inf[4]
        else:
            if len(self.store) == 0:
                p0 = self.t[n].pos
                x0 = p0.x
                y0 = p0.y
                z0 = p0.z
                self.store.append((x0, y0, z0))
            inf = self.magazine[ind]
            self.t[n].pos = Point(inf[0][0], inf[0][1], inf[0][2])
            self.t[n].e1 = Vector3(inf[1][0], inf[1][1], inf[1][2]) 
            self.t[n].e2 = Vector3(inf[2][0], inf[2][1], inf[2][2]) 
            self.t[n].e3 = Vector3(inf[3][0], inf[3][1], inf[3][2]) 
            self.t[n].penFlag = inf[4]
            p0 = self.t[n].pos
            x0 = p0.x
            y0 = p0.y
            z0 = p0.z
            self.store.append((x0, y0, z0))
               
    def Reset(self, n):
        self.t[n].Reset()
    def push(self, n):
        self.t[n].push()
    def pop(self, n):
        self.t[n].pop()
        
    def LineTo(self, x0, y0, z0, x1, y1, z1):
        if self.t[0].penFlag and self.t[1].penFlag:
            glLineWidth(self.t[0].lineWidth)
            glBegin(GL_LINE_STRIP)
            glVertex3f(x0, y0, z0)
            glVertex3f(x1, y1, z1)
            glEnd()
    def setSurfaceColor(self, c):
        self.surfcolor = c
        
    def DrawTriangle(self, x0, y0, z0, x1, y1, z1, x2, y2, z2):
        glClear(GL_DEPTH_BUFFER_BIT)
        glPolygonMode(GL_FRONT, GL_FILL)
        glPolygonMode(GL_BACK, GL_LINE)
        glEnable(GL_DEPTH_TEST)
        glColor3fv(self.surfcolor)
        glBegin(GL_POLYGON)
        glVertex3f(x0, y0, z0)
        glVertex3f(x1, y1, z1)
        glVertex3f(x2, y2, z2)
        glEnd()
        glDisable(GL_DEPTH_TEST)
        
    def fd(self, n, distance):
        if self.polyModeFlag == False:
            if self.surfaceFlag == False:
                if self.synchroFlag == False:
                    self.t[n].fd(distance)
                else:
                    if n == 1:
                        self.t[n].fd(distance)
                        p0 = self.t[0].pos
                        x0 = p0.x
                        y0 = p0.y
                        z0 = p0.z
                        p1 = self.t[1].pos
                        x1 = p1.x
                        y1 = p1.y
                        z1 = p1.z
                        self.LineTo(x0, y0, z0, x1, y1, z1)
                    else:
                        self.t[n].fd(distance)
            else:
                if self.synchroFlag == False:
                    self.t[n].fd(distance)
                elif self.t[n].penFlag == False or self.t[(n+1)%2].penFlag == False:
                    self.t[n].fd(distance)
                else:    
                    p0 = self.t[n].pos
                    x0 = p0.x
                    y0 = p0.y
                    z0 = p0.z
                    self.t[n].penup()
                    self.t[n].fd(distance)
                    p1 = self.t[n].pos
                    self.t[n].pendown()
                    x1 = p1.x
                    y1 = p1.y
                    z1 = p1.z
                    p2 = self.t[(n+1)%2].pos
                    x2 = p2.x
                    y2 = p2.y
                    z2 = p2.z
                    v=np.array([x1, y1, z1]) - np.array([x0, y0, z0])
                    w=np.array([x2, y2, z2]) - np.array([x0, y0, z0])
                    u = np.cross(v, w)
                    g = np.array([x0, y0, z0])+np.array([x1, y1, z1])+np.array([x2, y2, z2])
                    g = 0.5 * g
                    if np.dot(u, g) >= 0:
                        self.DrawTriangle(x0, y0, z0, x1, y1, z1, x2, y2, z2)
                    else:
                        self.DrawTriangle(x0, y0, z0, x2, y2, z2, x1, y1, z1)
        else: ## self.polyModeFlag = True
            ## 差し当たって fd の行き先を store に保存
            self.t[n].fd(distance)
            p0 = self.t[n].pos
            x0 = p0.x
            y0 = p0.y
            z0 = p0.z
            self.store.append((x0, y0, z0))
            
    def bk(self, n, distance):
        self.fd(n, -distance)
        
    def yaw(self, n, angle):
        self.t[n].yaw(angle)      
    def lt(self, n, angle):
        self.t[n].yaw(angle)
    def rt(self, n, angle):
        self.t[n].yaw(-angle)
        
    def pitch(self, n, angle):
        self.t[n].pitch(angle)
    def up(self, n, angle):
        self.t[n].pitch(angle)
    def down(self, n, angle):
        self.t[n].pitch(-angle)
        
    def roll(self, n, angle):
        self.t[n].roll(angle)
        
    def toward(self, n, x, y, z):
        self.t[n].toward(x, y, z)
        
    def facingto(self, source, target):
        x = self.t[target].pos.x
        y = self.t[target].pos.y
        z = self.t[target].pos.z
        self.t[source].toward(x, y, z)

    def penup(self, n):
        self.t[n].penFlag = False
    def pendown(self, n):
        self.t[n].penFlag = True

    def setLineWidth(self, n, w):
        self.t[n].lineWidth = w
        
    def synchro(self):
        self.synchroFlag = True
    def nonsynchro(self):
        self.synchroFlag = False
        
    def surface(self):
        self.surfaceFlag = True
    def nonsurface(self):
        self.surfaceFlag = False
        
    def polymode(self):
        self.polyModeFlag = True
        del self.store[:]
    def DrawStore(self):
        glClear(GL_DEPTH_BUFFER_BIT)
        glPolygonMode(GL_FRONT_AND_BACK, GL_FILL)
        glEnable(GL_DEPTH_TEST)
        glEnable(GL_BLEND)
        glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA)
        glColor(self.surfcolor[0], self.surfcolor[1], self.surfcolor[2], 0.9)
        glBegin(GL_POLYGON)
        for pos in self.store:            
            glVertex3f(pos[0], pos[1], pos[2])
        glEnd()
        glDisable(GL_DEPTH_TEST)
        glDisable(GL_BLEND)
    def nonpolymode(self):
        self.DrawStore()
        del self.store[:]
        self.polyModeFlag = False
    
    def duplicate(self, n):
        self.t[n].duplicate()

    def exchange(self, n):
        self.t[n].exchange()
とし、mypolyhedron.py を 

import time
import tkinter
from OpenGL import GL
from OpenGL.GL import *
from OpenGL.GLU import *
from pyopengltk import OpenGLFrame
import numpy as np
from copy import copy
import random
from kite import *

def pyramid(m, n, x):
    if n < 3 or n > 5:
        return
    y = x / 2 / np.sin(np.pi/n)
    h = np.sqrt(x * x - y * y)
    m.penup(0)
    m.fd(0, h)
    m.pendown(0)
    m.penup(1)
    m.down(1, 90)
    m.fd(1, y)
    m.rt(1, 90+180/n)
    m.pendown(1)
    for i in range(n):
        m.fd(1, x)
        m.rt(1, 360/n)
    m.synchro()
    for i in range(n):
        m.fd(1, x)
        m.rt(1, 360/n)
    m.nonsynchro()
    m.penup(0)
    m.bk(0, h)
    m.pendown(0)
    m.penup(1)
    m.lt(1, 90+180/n)
    m.fd(1, -y)
    m.up(1, 90)
    m.pendown(1)

def pyramid2(m, n, x):
    if n < 3 or n > 5:
        return
    y = x / 2 / np.sin(np.pi/n)
    h = np.sqrt(x * x - y * y)
    m.penup(0)
    m.fd(0, h)
    m.pendown(0)
    m.penup(1)
    m.down(1, 90)
    m.rt(1, 180/n)
    m.fd(1, y)
    m.rt(1, 90+180/n)
    m.pendown(1)
    for i in range(n):
        m.fd(1, x)
        m.rt(1, 360/n)
    m.synchro()
    for i in range(n):
        m.fd(1, x)
        m.rt(1, 360/n)
    m.nonsynchro()
    m.penup(0)
    m.bk(0, h)
    m.pendown(0)
    m.penup(1)
    m.lt(1, 90+180/n)
    m.fd(1, -y)
    m.rt(1, 180/n)
    m.up(1, 90)
    m.pendown(1)
  
def hexahedron(m, x):
    pyramid(m, 3, x)
    m.rt(0, 180)
    m.rt(1, 180)
    pyramid(m, 3, x)
    m.rt(0, 180)
    m.rt(1, 180)
    
def decahedron(m, x):
    pyramid(m, 5, x)
    m.rt(0, 180)
    m.rt(1, 180)
    pyramid(m, 5, x)
    m.rt(0, 180)
    m.rt(1, 180)
    
def prism(m, n, x):
    y = x/2/np.sin(np.pi/n)
    h = x/2
    m.penup(0)
    m.fd(0, h)
    m.down(0, 90)
    m.fd(0, y)
    m.rt(0, 90+180/n)
    m.pendown(0)
    m.penup(1)
    m.fd(1, -h)
    m.down(1, 90)
    m.fd(1, y)
    m.rt(1, 90+180/n)
    m.pendown(1)
    for _ in range(n):
        m.fd(1, x)
        m.rt(1, 360/n)
    m.synchro()
    for _ in range(n):
        m.fd(0, x)
        m.rt(0, 360/n)
        m.fd(1, x)
        m.rt(1, 360/n)
    m.nonsynchro()
    m.penup(0)
    m.lt(0, 90+180/n)
    m.fd(0, -y)
    m.up(0, 90)
    m.bk(0, h)
    m.pendown(0)
    m.penup(1)
    m.lt(1, 90+180/n)
    m.fd(1, -y)
    m.penup(1)
    m.bk(1, -h)
    m.pendown(1)

def antiprism(m, n, x):
    y = x/2/np.sin(np.pi/n)
    z = 2*y*np.sin(np.pi/2/n)
    h = np.sqrt(x*x-z*z)/2
    m.penup(0)
    m.fd(0, h)
    m.down(0, 90)
    m.fd(0, y)
    m.rt(0, 90+180/n)
    m.pendown(0)
    for _ in range(n):
        m.fd(0, x)
        m.rt(0, 360/n)
    m.penup(1)
    m.fd(1, -h)
    m.down(1, 90)
    m.rt(1, 180/n)
    m.fd(1, y)
    m.rt(1, 90+180/n)
    m.pendown(1)
    for _ in range(n):
        m.fd(1, x)
        m.rt(1, 360/n)
    m.synchro()
    for _ in range(n):
        m.fd(0, x)
        m.rt(0, 360/n)
        m.fd(1, 0)
        m.fd(1, x)
        m.rt(1, 360/n)
    m.nonsynchro()
    m.penup(0)
    m.lt(0, 90+180/n)
    m.fd(0, -y)
    m.up(0, 90)
    m.bk(0, h)
    m.pendown(0)
    m.penup(1)
    m.lt(1, 90+180/n)
    m.fd(1, -y)
    m.lt(1, 180/n)
    m.up(1, 90)
    m.bk(1, -h)
    m.pendown(1)
    
def colorantiprism(m, n, x):
    y = x/2/np.sin(np.pi/n)
    z = 2*y*np.sin(np.pi/2/n)
    h = np.sqrt(x*x-z*z)/2
    m.penup(0)
    m.fd(0, h)
    m.down(0, 90)
    m.fd(0, y)
    m.rt(0, 90+180/n)
    m.pendown(0)
    m.setSurfaceColor([1, 1, 1])
    m.polymode()
    for _ in range(n):
        m.fd(0, x)
        m.rt(0, 360/n)
    m.nonpolymode()
    m.penup(1)
    m.fd(1, -h)
    m.down(1, 90)
    m.rt(1, 180/n)
    m.fd(1, y)
    m.rt(1, 90+180/n)
    m.pendown(1)
    m.polymode()
    for _ in range(n):
        m.fd(1, x)
        m.rt(1, 360/n)
    m.nonpolymode()
    m.synchro()
    m.surface()
    for _ in range(n):
        m.setSurfaceColor([1, 0, 0])
        m.fd(0, x)
        m.rt(0, 360/n)
        m.setSurfaceColor([0, 0, 1])
        m.fd(1, 0)
        m.fd(1, x)
        m.rt(1, 360/n)
    m.nonsynchro()
    m.nonsurface()
    m.penup(0)
    m.lt(0, 90+180/n)
    m.fd(0, -y)
    m.up(0, 90)
    m.bk(0, h)
    m.pendown(0)
    m.penup(1)
    m.lt(1, 90+180/n)
    m.fd(1, -y)
    m.lt(1, 180/n)
    m.up(1, 90)
    m.bk(1, -h)
    m.pendown(1)

def icosahedron(m, x):
    y = x/2/np.sin(np.pi/5)
    z = 2*y*np.sin(np.pi/2/5)
    h = np.sqrt(x*x-z*z)/2
    m.penup(0)
    m.fd(0, h)
    m.pendown(0)
    m.penup(1)
    m.fd(1, h)
    m.pendown(1)
    pyramid(m, 5, x)
    m.penup(0)
    m.fd(0, -h)
    m.pendown(0)
    m.penup(1)
    m.fd(1, -h)
    m.pendown(1)
    antiprism(m, 5, x)
    m.penup(0)
    m.fd(0, -h)
    m.rt(0, 180)
    m.pendown(0)
    m.penup(1)
    m.fd(1, -h)
    m.rt(1, 180)
    m.pendown(1)
    pyramid2(m, 5, x)
    m.penup(0)
    m.rt(0, 180)
    m.fd(0, h)
    m.pendown(0)
    m.penup(1)
    m.rt(1, 180)
    m.fd(1, h)
    m.pendown(1)

def dodeca(m, x):
    z = (np.sin(np.pi/5)*np.sin(np.pi/5)-2*np.cos(np.pi/3)*np.cos(np.pi/3))/\
        (np.sin(np.pi/5)*np.sin(np.pi/5))
    phi = np.arccos(z)*180/np.pi
    d = np.sqrt(1 - np.cos(np.pi/5)*np.cos(np.pi/5)-\
                np.cos(np.pi/3)*np.cos(np.pi/3))
    h = x / np.tan(np.pi/5)*np.cos(np.pi/3)/(2*d)
    r = x * np.sin(np.pi/3)/(2*d)
    y = np.sqrt(r*r-h*h)
    m.push(0)
    m.penup(0)
    m.fd(0, h)
    m.down(0, 90)
    m.fd(0, y)
    m.rt(0, 126)
    m.pendown(0)
    for i in range(5):
        m.fd(0, x)
        m.rt(0, 72)
    m.roll(0, 180-phi)
    m.lt(0, 108)
    for i in range(5):
        for k in range(4):
            m.fd(0, x)
            m.rt(0, 72)
        m.rt(0, 108)
        m.roll(0, -180+phi)
    m.penup(0)
    m.pop(0)
    m.pendown(0)
    
    m.push(0)
    m.penup(0)
    m.fd(0, -h)
    m.down(0, 90)
    m.rt(0, 36)
    m.fd(0, y)
    m.rt(0, 126)
    m.pendown(0)
    for i in range(5):
       m.fd(0, x)
       m.rt(0, 72)
    m.roll(0, -180+phi)
    m.lt(0, 108)
    for i in range(5):
        for k in range(4):
            m.fd(0, x)
            m.rt(0, 72)
        m.rt(0, 108)
        m.roll(0, 180-phi)
    m.penup(0)
    m.pop(0)
    m.pendown(0)

def cube(m, x):
    for _ in range(4):
        m.fd(0, x)
        m.down(0, 90)
        m.fd(0, x)
        m.bk(0, x)
        m.up(0, 90)
        m.rt(0, 90)
    m.down(0, 90)
    m.fd(0, x)
    m.up(0, 90)
    for _ in range(4):
        m.fd(0, x)
        m.rt(0, 90)
    m.down(0, 90)
    m.bk(0, x)
    m.up(0, 90)

def polygon(m, r, n):
    m.push(1)
    m.put(0, 0)
    m.penup(1)
    m.get(1, 0)
    m.pendown(1)
    m.penup(0)
    m.fd(0, r)
    m.rt(0, 90)
    m.pendown(0)
    m.rt(0, 360/n/2)
    m.synchro()
    m.surface()
    for _  in range(n):
        m.setSurfaceColor([random.random(), random.random(), random.random()])
        m.fd(0, 2*np.pi*r/n)
        m.rt(0, 360/n)
    m.nonsynchro()
    m.nonsurface()
    m.penup(0)
    m.lt(0, 360/n/2)
    m.lt(0, 90)
    m.bk(0, r)
    m.pendown(0)
    m.penup(1)
    m.pop(1)
    m.pendown(1)
    
def thing(m):
    polygon(m, 100, 20)
    m.rt(0, 90)
    m.penup(0)
    m.fd(0, 150)
    m.pendown(0)
    polygon(m, 40, 6)
    m.penup(0)
    m.bk(0, 300)
    polygon(m, 40, 12)
    
def colorcube(m, size):
    m.penup(0)
    m.push(0)
    m.penup(1)
    m.push(1)
    m.put(0, 0)
    m.get(1, 0)
    m.penup(0)
    m.fd(0, size)
    m.down(0, 90)
    m.fd(0, size)
    m.rt(0, 90)
    m.fd(0, size)
    m.rt(0, 90)
    m.pendown(0)
    m.penup(1)
    m.fd(1, size)
    m.down(1, 90)
    m.fd(1, size)
    m.lt(1, 90)
    m.fd(1, size)
    m.pendown(1)
    m.synchro()
    m.surface()
    m.setSurfaceColor([1, 0, 0])
    m.fd(0, 2*size)
    m.rt(0, 90)
    m.fd(0, 2*size)
    m.setSurfaceColor([0, 1, 0])
    m.down(0, 90)
    m.fd(0, 2*size)
    m.rt(0, 90)
    m.fd(0, 2*size)
    m.setSurfaceColor([0, 0, 1])
    m.down(0, 90)
    m.fd(0, 2*size)
    m.rt(0, 90)
    m.fd(0, 2*size)
    m.penup(0)
    m.pop(0)
    m.push(0)
    m.penup(1)
    m.put(0, 0)
    m.get(1, 0)
    m.penup(0)
    m.bk(0, size)
    m.up(0, 90)
    m.fd(0, size)
    m.lt(0, 90)
    m.fd(0, size)
    m.down(0, 90)
    m.roll(0, -90)
    m.pendown(0)
    m.penup(1)
    m.bk(1, size)
    m.up(1, 90)
    m.fd(1, size)
    m.rt(1, 90)
    m.fd(1, size)
    m.pendown(1)
    m.setSurfaceColor([1, 1, 0])
    m.fd(0, 2*size)
    m.rt(0, 90)
    m.fd(0, 2*size)
    m.setSurfaceColor([1, 0, 1])
    m.down(0, 90)
    m.fd(0, 2*size)
    m.rt(0, 90)
    m.fd(0, 2*size)
    m.setSurfaceColor([0, 1, 1])
    m.down(0, 90)
    m.fd(0, 2*size)
    m.rt(0, 90)
    m.fd(0, 2*size)
    m.nonsynchro()
    m.nonsurface()
    m.penup(1)
    m.pop(1)
    m.penup(0)
    m.pop(0)
    m.pendown(0)
    m.pendown(1)
    
def colorpentagon(m, size):
    m.polymode()
    for _ in range(5):
        m.fd(0, size)
        m.rt(0, 72)
    m.nonpolymode()
    m.polymode()
    for _ in range(4):
        m.fd(0, size/2)
        m.lt(0, 90)
    m.nonpolymode()
        
def kaleidoscopecube(m, size):
    m.push(1)
    m.penup(1)
    m.put(0, 0)
    m.get(1, 0)
    for _ in range(4):
        colorsubcube(m, size)
        m.rt(0, 90)
    m.up(0, 90)
    colorsubcube(m, size)
    m.up(0, 180)
    colorsubcube(m, size)
    m.up(0, 90)
    m.penup(1)
    m.pop(1)
    m.pendown(1)
    
def towardtest(m, x, y, z):
    m.toward(0, x, y, z)
    for _ in range(4):
        m.fd(0, 100)
        m.lt(0, 90)
        
    
def facingtotest(m, source, target):
    m.fd(target, 100)
    m.lt(target, 90)
    m.fd(target, 100)    
    m.facingto(source, target)
    for _ in range(4):
        m.fd(source, 100)
        m.lt(source, 90)
   
def subpyramid(m, n, x):
    if n < 3 or n > 5:
        return
    y = x / 2 / np.sin(np.pi/n)
    h = np.sqrt(x * x - y * y)
    m.penup(0)
    m.fd(0, h)
    m.pendown(0)
    m.penup(1)
    m.down(1, 90)
    m.fd(1, y)
    m.rt(1, 90+180/n)
    m.pendown(1)
    for i in range(n):
        m.fd(1, x)
        m.rt(1, 360/n)
    m.put(0, 0)
    m.synchro()
    for i in range(n):
        m.fd(1, x)
        m.rt(1, 360/n)
        m.put(1, i+1)
    m.nonsynchro()
    m.penup(0)
    m.bk(0, h)
    m.pendown(0)
    m.penup(1)
    m.lt(1, 90+180/n)
    m.fd(1, -y)
    m.up(1, 90)
    m.pendown(1)
    
def subpyramid2(m, n, x):
    if n < 3 or n > 5:
        return
    y = x / 2 / np.sin(np.pi/n)
    h = np.sqrt(x * x - y * y)
    m.penup(0)
    m.fd(0, h)
    m.pendown(0)
    m.penup(1)
    m.down(1, 90)
    m.rt(1, 180/n)
    m.fd(1, y)
    m.rt(1, 90+180/n)
    m.pendown(1)
    for i in range(n):
        m.fd(1, x)
        m.rt(1, 360/n)
        m.put(1, i+6)
##        m.t[1].print()
    m.synchro()
    for i in range(n):
        m.fd(1, x)
        m.rt(1, 360/n)
    m.nonsynchro()
    m.put(0, 11)
##    m.t[0].print()
    m.penup(0)
    m.bk(0, h)
    m.pendown(0)
    m.penup(1)
    m.lt(1, 90+180/n)
    m.fd(1, -y)
    m.rt(1, 180/n)
    m.up(1, 90)
    m.pendown(1)

def starpentagon(m, l):
    p = np.zeros(3*5).reshape([5, 3])
    p[0] = m.magazine[l[0]][0]
    p[1] = m.magazine[l[1]][0]
    p[2] = m.magazine[l[2]][0]
    p[3] = m.magazine[l[3]][0]
    p[4] = m.magazine[l[4]][0]
    o = (p[0]+p[1]+p[2]+p[3]+p[4])
    o = 0.2 * o
    store = []
    result = []
    for i in range(5):
        del store[:]
        store.append((o[0], o[1], o[2]))
        store.append((p[(2*i)%5][0], p[(2*i)%5][1], p[(2*i)%5][2]))
        store.append((p[(2*i+2)%5][0], p[(2*i+2)%5][1], p[(2*i+2)%5][2]))
        result.append(tuple(store))
    return result
        
def smallstellateddodecahedron(m, x):
    y = x/2/np.sin(np.pi/5)
    z = 2*y*np.sin(np.pi/2/5)
    h = np.sqrt(x*x-z*z)/2
    m.penup(0)
    m.fd(0, h)
    m.pendown(0)
    m.penup(1)
    m.fd(1, h)
    m.pendown(1)
    subpyramid(m, 5, x)
    m.penup(0)
    m.fd(0, -h)
    m.pendown(0)
    m.penup(1)
    m.fd(1, -h)
    m.pendown(1)
    antiprism(m, 5, x)
    m.penup(0)
    m.fd(0, -h)
    m.rt(0, 180)
    m.pendown(0)
    m.penup(1)
    m.fd(1, -h)
    m.rt(1, 180)
    m.pendown(1)
    subpyramid2(m, 5, x)
    m.penup(0)
    m.rt(0, 180)
    m.fd(0, h)
    m.pendown(0)
    m.penup(1)
    m.rt(1, 180)
    m.fd(1, h)
    m.pendown(1)

    index_list = []
    index_list.append((1, 2, 3, 4, 5))
    index_list.append((0, 1, 8, 7, 3))
    index_list.append((0, 2, 7, 6, 4))
    index_list.append((0, 3, 6, 10, 5))
    index_list.append([0, 4, 10, 9, 1])
    index_list.append((0, 5, 9, 8, 2))
    index_list.append((6, 7, 8, 9, 10))
    index_list.append((11, 6, 3, 2, 8))
    index_list.append((11, 7, 2, 1, 9))
    index_list.append((11, 8, 1, 5, 10))
    index_list.append((11, 9, 5, 4, 6))
    index_list.append((11, 10, 4, 3, 7))

    clist = [[1.0, 0.0, 0.0], [0.0, 1.0, 0.0], [0.0, 0.0, 1.0],
                     [1.0, 1.0, 0.0], [1.0, 0.0, 1.0], [0.0, 1.0, 1.0],
                     [0.5, 0.0, 0.0], [0.0, 0.5, 0.0], [0.0, 0.0, 0.5],
                     [0.5, 0.5, 0.0], [0.0, 0.5, 0.5], [0.5, 0.0, 0.5],
                     [0.5, 0.7, 0.0], [0.7, 0.5, 0.0], [0.7, 0.0, 0.5],
                     [0.5, 0.2, 0.3], [0.2, 0.5, 0.3], [0.3, 0.2, 0.5],
                     [0.7, 0.2, 0.8], [0.2, 0.9, 0.3], [0.7, 0.2, 0.9],
                 ]
    glClear(GL_DEPTH_BUFFER_BIT)
    glPolygonMode(GL_FRONT_AND_BACK, GL_FILL)
    glEnable(GL_DEPTH_TEST)
    glEnable(GL_BLEND)
    glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA)
    for n in range(12):               
        surf = starpentagon(m, index_list[n])
        glColor(clist[n][0], clist[n][1], clist[n][2], 0.5)
        glLineWidth(4.0) ## 線の幅
        for i in range(5):
            face_list = surf[i]
            glBegin(GL_POLYGON)
            for k in range(3):
                glVertex3f(face_list[k][0], face_list[k][1], face_list[k][2])
            glEnd()
    glDisable(GL_DEPTH_TEST)
    glDisable(GL_BLEND)


def pentagon(m, l):
    p = np.zeros(3*5).reshape([5, 3])
    p[0] = m.magazine[l[0]][0]
    p[1] = m.magazine[l[1]][0]
    p[2] = m.magazine[l[2]][0]
    p[3] = m.magazine[l[3]][0]
    p[4] = m.magazine[l[4]][0]
    result = []
    for i in range(5):
        result.append(tuple(p[i]))
    return result
        
def greatdodecahedron(m, x):
    y = x/2/np.sin(np.pi/5)
    z = 2*y*np.sin(np.pi/2/5)
    h = np.sqrt(x*x-z*z)/2
    m.penup(0)
    m.fd(0, h)
    m.pendown(0)
    m.penup(1)
    m.fd(1, h)
    m.pendown(1)
    subpyramid(m, 5, x)
    m.penup(0)
    m.fd(0, -h)
    m.pendown(0)
    m.penup(1)
    m.fd(1, -h)
    m.pendown(1)
    antiprism(m, 5, x)
    m.penup(0)
    m.fd(0, -h)
    m.rt(0, 180)
    m.pendown(0)
    m.penup(1)
    m.fd(1, -h)
    m.rt(1, 180)
    m.pendown(1)
    subpyramid2(m, 5, x)
    m.penup(0)
    m.rt(0, 180)
    m.fd(0, h)
    m.pendown(0)
    m.penup(1)
    m.rt(1, 180)
    m.fd(1, h)
    m.pendown(1)

    index_list = []
    index_list.append((1, 2, 3, 4, 5))
    index_list.append((0, 1, 8, 7, 3))
    index_list.append((0, 2, 7, 6, 4))
    index_list.append((0, 3, 6, 10, 5))
    index_list.append([0, 4, 10, 9, 1])
    index_list.append((0, 5, 9, 8, 2))
    index_list.append((6, 7, 8, 9, 10))
    index_list.append((11, 6, 3, 2, 8))
    index_list.append((11, 7, 2, 1, 9))
    index_list.append((11, 8, 1, 5, 10))
    index_list.append((11, 9, 5, 4, 6))
    index_list.append((11, 10, 4, 3, 7))


    clist = [[1.0, 0.0, 0.0], [0.0, 1.0, 0.0], [0.0, 0.0, 1.0],
                     [1.0, 1.0, 0.0], [1.0, 0.0, 1.0], [0.0, 1.0, 1.0],
                     [0.5, 0.0, 0.0], [0.0, 0.5, 0.0], [0.0, 0.0, 0.5],
                     [0.5, 0.5, 0.0], [0.0, 0.5, 0.5], [0.5, 0.0, 0.5],
                     [0.5, 0.7, 0.0], [0.7, 0.5, 0.0], [0.7, 0.0, 0.5],
                     [0.5, 0.2, 0.3], [0.2, 0.5, 0.3], [0.3, 0.2, 0.5],
                     [0.7, 0.2, 0.8], [0.2, 0.9, 0.3], [0.7, 0.2, 0.9],
                 ]
    glClear(GL_DEPTH_BUFFER_BIT)
    glPolygonMode(GL_FRONT_AND_BACK, GL_FILL)
    glEnable(GL_DEPTH_TEST)
    glEnable(GL_BLEND)
    glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA)
    for n in range(12):               
        surf = pentagon(m, index_list[n])
        glColor(clist[n][0], clist[n][1], clist[n][2], 0.5)
        glLineWidth(4.0) ## 線の幅
        glBegin(GL_POLYGON)
        for k in range(5):
            glVertex3f(surf[k][0], surf[k][1], surf[k][2])
        glEnd()
    glDisable(GL_DEPTH_TEST)
    glDisable(GL_BLEND)

def triangle(m, l):        
    p = np.zeros(3*5).reshape([5, 3])
    p[0] = m.magazine[l[0]][0]
    p[1] = m.magazine[l[1]][0]
    p[2] = m.magazine[l[2]][0]
    result = []
    for i in range(3):
        result.append(tuple(p[i]))
    return result

def greaticosahedron(m, x):
    y = x/2/np.sin(np.pi/5)
    z = 2*y*np.sin(np.pi/2/5)
    h = np.sqrt(x*x-z*z)/2
    m.penup(0)
    m.fd(0, h)
    m.pendown(0)
    m.penup(1)
    m.fd(1, h)
    m.pendown(1)
    subpyramid(m, 5, x)
    m.penup(0)
    m.fd(0, -h)
    m.pendown(0)
    m.penup(1)
    m.fd(1, -h)
    m.pendown(1)
    antiprism(m, 5, x)
    m.penup(0)
    m.fd(0, -h)
    m.rt(0, 180)
    m.pendown(0)
    m.penup(1)
    m.fd(1, -h)
    m.rt(1, 180)
    m.pendown(1)
    subpyramid2(m, 5, x)
    m.penup(0)
    m.rt(0, 180)
    m.fd(0, h)
    m.pendown(0)
    m.penup(1)
    m.rt(1, 180)
    m.fd(1, h)
    m.pendown(1)

    index_list2 = []
    index_list2.append((3, 5, 8))
    index_list2.append((1, 7, 4))
    index_list2.append((2, 6, 5))
    index_list2.append((1, 3, 10))
    index_list2.append((2, 4, 9))
    index_list2.append((0, 9, 7))
    index_list2.append((1, 11, 3))
    index_list2.append((0, 8, 6))
    index_list2.append((2, 11, 4))
    index_list2.append((0, 7, 10))
    index_list2.append((3, 11, 5))
    index_list2.append((0, 6, 9))
    index_list2.append((1, 4, 11))
    index_list2.append((0, 10, 8))
    index_list2.append((2, 5, 11))
    index_list2.append((2, 9, 6))
    index_list2.append((3, 8, 10))
    index_list2.append((4, 7, 9))
    index_list2.append((5, 6, 8))
    index_list2.append((1, 10, 7))


    clist = [[1.0, 0.0, 0.0], [0.0, 1.0, 0.0], [0.0, 0.0, 1.0],
                     [1.0, 1.0, 0.0], [1.0, 0.0, 1.0], [0.0, 1.0, 1.0],
                     [0.5, 0.0, 0.0], [0.0, 0.5, 0.0], [0.0, 0.0, 0.5],
                     [0.5, 0.5, 0.0], [0.0, 0.5, 0.5], [0.5, 0.0, 0.5],
                     [0.5, 0.7, 0.0], [0.7, 0.5, 0.0], [0.7, 0.0, 0.5],
                     [0.5, 0.2, 0.3], [0.2, 0.5, 0.3], [0.3, 0.2, 0.5],
                     [0.7, 0.2, 0.8], [0.2, 0.9, 0.3], [0.7, 0.2, 0.9],
                 ]
    glClear(GL_DEPTH_BUFFER_BIT)
    glPolygonMode(GL_FRONT_AND_BACK, GL_FILL)
    glEnable(GL_DEPTH_TEST)
    glEnable(GL_BLEND)
    glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA)
    for n in range(20):               
        surf = triangle(m, index_list2[n])
        glColor(clist[n][0], clist[n][1], clist[n][2], 0.5)
        glLineWidth(4.0) ## 線の幅
        glBegin(GL_POLYGON)
        for k in range(3):
            glVertex3f(surf[k][0], surf[k][1], surf[k][2])
        glEnd()
    glDisable(GL_DEPTH_TEST)
    glDisable(GL_BLEND)

def greatstellateddodecahedron(m, x):
    cnt = 0
    z = (np.sin(np.pi/5)*np.sin(np.pi/5)-2*np.cos(np.pi/3)*np.cos(np.pi/3))/\
        (np.sin(np.pi/5)*np.sin(np.pi/5))
    phi = np.arccos(z)*180/np.pi
    d = np.sqrt(1 - np.cos(np.pi/5)*np.cos(np.pi/5)-\
                np.cos(np.pi/3)*np.cos(np.pi/3))
    h = x / np.tan(np.pi/5)*np.cos(np.pi/3)/(2*d)
    r = x * np.sin(np.pi/3)/(2*d)
    y = np.sqrt(r*r-h*h)
    m.push(0)
    m.penup(0)
    m.fd(0, h)
    m.down(0, 90)
    m.fd(0, y)
    m.rt(0, 126)
    m.pendown(0)
    for i in range(5):
        m.put(0, cnt)
        cnt += 1
        m.fd(0, x)
        m.rt(0, 72)
    m.roll(0, 180-phi)
    m.lt(0, 108)
    for i in range(5):
        for k in range(4):
            m.fd(0, x)
            if k < 2:
                m.put(0, cnt)
                cnt += 1                
            m.rt(0, 72)
        m.rt(0, 108)
        m.roll(0, -180+phi)
    m.penup(0)
    m.pop(0)
    m.pendown(0)
    
    m.push(0)
    m.penup(0)
    m.fd(0, -h)
    m.down(0, 90)
    m.rt(0, 36)
    m.fd(0, y)
    m.rt(0, 126)
    m.pendown(0)
    for i in range(5):
        m.put(0, cnt)
        cnt += 1
        m.fd(0, x)
        m.rt(0, 72)
    m.roll(0, -180+phi)
    m.lt(0, 108)
    for i in range(5):
        for k in range(4):
            m.fd(0, x)
            m.rt(0, 72)
        m.rt(0, 108)
        m.roll(0, 180-phi)
    m.penup(0)
    m.pop(0)
    m.pendown(0)

    index_list = []
    index_list.append((5, 7, 9, 11, 13))
    index_list.append((4, 14, 15, 8, 2))
    index_list.append((0, 6, 16, 10, 3))
    index_list.append((1, 8, 17, 12, 4))
    index_list.append((2, 10, 18, 14, 0))
    index_list.append((1, 3, 12, 19, 6))
    index_list.append((0, 13, 18, 16, 7))
    index_list.append((5, 19, 17, 9, 1))
    index_list.append((7, 15, 18, 11, 2))
    index_list.append((9, 16, 19, 13, 3))
    index_list.append((11, 17, 15, 5, 4))
    index_list.append((6, 14, 12, 10, 8))

    clist = [[1.0, 0.0, 0.0], [0.0, 1.0, 0.0], [0.0, 0.0, 1.0],
                     [1.0, 1.0, 0.0], [1.0, 0.0, 1.0], [0.0, 1.0, 1.0],
                     [0.5, 0.0, 0.0], [0.0, 0.5, 0.0], [0.0, 0.0, 0.5],
                     [0.5, 0.5, 0.0], [0.0, 0.5, 0.5], [0.5, 0.0, 0.5],
                     [0.5, 0.7, 0.0], [0.7, 0.5, 0.0], [0.7, 0.0, 0.5],
                     [0.5, 0.2, 0.3], [0.2, 0.5, 0.3], [0.3, 0.2, 0.5],
                     [0.7, 0.2, 0.8], [0.2, 0.9, 0.3], [0.7, 0.2, 0.9],
                 ]
    glClear(GL_DEPTH_BUFFER_BIT)
    glPolygonMode(GL_FRONT_AND_BACK, GL_FILL)
    glEnable(GL_DEPTH_TEST)
    glEnable(GL_BLEND)
    glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA)
    for n in range(12):               
        surf = starpentagon(m, index_list[n])
        glColor(clist[n][0], clist[n][1], clist[n][2], 0.5)
        glLineWidth(4.0) ## 線の幅
        for i in range(5):
            face_list = surf[i]
            glBegin(GL_POLYGON)
            for k in range(3):
                glVertex3f(face_list[k][0], face_list[k][1], face_list[k][2])
            glEnd()
    glDisable(GL_DEPTH_TEST)
    glDisable(GL_BLEND)
とし、usegeneralkite.py を 

import time
import tkinter
from OpenGL import GL
from OpenGL.GL import *
from OpenGL.GLU import *
from pyopengltk import OpenGLFrame
import numpy as np
from copy import copy
import random
from kite import *
##from tetra import *
from mypolyhedron import *

W = 600
H = 600

m = Manager()

class AppOgl(OpenGLFrame):##
    global m

    def initgl(self):
        GL.glViewport(0, 0, self.width, self.height) ## 画面の描画領域
        GL.glClearColor(0.0, 0.0, 0.0, 1.0)  ## 背景色   

    def Setup(self):
        GL.glLoadIdentity() ## 投影変換の変換行列を単位行列で初期化
        glOrtho(-300, 300, -300, 300, -300.0, 300.0)

    def redraw(self):
        global m, loop_step, degree
        
        degree  += loop_step 
        glClear(GL_COLOR_BUFFER_BIT)
        glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
        glLoadIdentity() ## 投影行列を単位行列で初期化する
        glColor3f(1.0, 1.0, 1.0)
        glOrtho(-300.0, 300.0, -300.0, 300.0, -300.0, 300.0) ## 平行投影
        
        self.Setup()
        m.t[0].Reset()
        m.t[0].pitch(degree)
        m.t[0].yaw(degree)
        m.t[1].Reset()
        m.t[1].pitch(degree)
        m.t[1].yaw(degree)
        
        dodeca(m, 100)
##        hexahedron(m, 100)
##        decahedron(m, 100)
##        prism(m, 5, 100)
##        antiprism(m, 5, 100)
##        icosahedron(m, 100)
##        thing(m)
##        colorcube(m, 100)
##        colorpentagon(m, 150)
##        colorantiprism(m, 5, 100)
##        towardtest(m, 100, 100, 0)
##        facingtotest(m, 0, 1)
##        smallstellateddodecahedron(m, 200)
##        greatdodecahedron(m, 200)
##        greaticosahedron(m, 200)        
##        greatstellateddodecahedron(m, 200)
        
if __name__ == '__main__':
    root = tkinter.Tk()
    app = AppOgl(root, width=W, height=H)
    app.pack(fill=tkinter.BOTH, expand=tkinter.YES)
##    app.animate = 1
    degree = 0
    loop_step = 0.1
    app.animate = 1
##    app.after(100, app.printContext)
    app.mainloop()
とし、 

        dodeca(m, 100)
##        hexahedron(m, 100)
##        decahedron(m, 100)
##        prism(m, 5, 100)
##        antiprism(m, 5, 100)
##        icosahedron(m, 100)
##        thing(m)
##        colorcube(m, 100)
##        colorpentagon(m, 150)
##        colorantiprism(m, 5, 100)
##        towardtest(m, 100, 100, 0)
##        facingtotest(m, 0, 1)
##        smallstellateddodecahedron(m, 200)
##        greatdodecahedron(m, 200)
##        greaticosahedron(m, 200)        
##        greatstellateddodecahedron(m, 200)
のどれかを有効にして、（今は dodeca(m, 100）が有効になっています。smallstellateddodecahedron(m, 200) を描きたいなら、 dodeca(m, 100）を コメントにし、smallstellateddodecahedron(m, 200) のコメントを外します。）、usegeneralkite.py を実行すれば良いです。 上のプログラム　usegeneralkite.py で 

##from tetra import *
とすべきでした。 今考えると KITE は随分奇妙なプログラミング言語で、LOGO に凝っていて、小学校の教員志望の学生さんの教育に使っていると、 立方体を描くにはどうすれば良いか女子学生さん（高知大学教育学部は女子学生の方が多いです）に聞かれ、 彼女のような高度の数学の素養が無い人でも簡単に立方体の様々な方向から見た正確な図が描けるように、 自分で3次元LOGO もどきを作り、 思い付きで変な拡張を続けたもので、参考にならないと思いますが、一松信著「正多面体を解く」で球面幾何学を学べば、 この様なプログラムでも色々な立体をパズル感覚で描くことが出来ます。 https://www.cc.kochi-u.ac.jp/~tyamag/kite/kite_pro2.html の私のゼミの女子学生たちの星形大十二面体、星形小十二面体、大十二面体や大二十面体のプログラムは、 正二十面体や正十二面体の座標を計算して描く直ぐ思い付くものでないもの（？）を作るように言って作ってもらったものなので、 正二十面体や正十二面体の紙の模型を例えば https://www.cc.kochi-u.ac.jp/~tyamag/tenkaizu/tenkaizu.html のソフト （一松信著「正多面体を解く」東海大学出版会　とマグナス　J. ウェニンガー著茂木勇・横手一郎共訳「多面体の模型 その作り方と鑑賞」教育出版を参考に 代表的な各種多面体の展開図が作れるものは展開図をそうでないものはパーツを打ち出せるようにしたソフトです。展開図は問題ないと思いますが、 パーツを組み立てる方法が分からなければ 上記の翻訳本か原著「Polyhedron Models」を見て下さい。古い本で古本で購入するか大学等の図書館で借りてくるかしかないかもしれませんが？ 例えば、高知大学の図書館は高知大学の名誉教授や卒業生でなくても確か一般の人も利用できるのではと思いますが、この本は私は私費で購入したので、 高知大学の図書館が購入していて廃棄していないか知りません。場合によっては他大学から借りてもらうことや実費で一部をコピーしてもらうことも可能なはずです。 アルキメデスの純正多面体なども本の図を眺めるだけより、このソフトで打ち出した展開図を組み立て紙の模型を手に取って眺める方が得ることが多いと思います。 全ての純正多面体の外接球の大きさも一定に揃える事も出来ますから暇ならやってみて下さい。紙のサイズは A4 です。 今は少し高いですが黄色や緑や青などのコピー用紙もあります。勿論、自分でこの様なプログラムを実際に作ってみることが他人の作ったソフトを使うより勉強に なることは言うまでもありません。これは面白い・これぐらいなら自分でも出来そうだと思えば何でもやってみるといいです。 ）で打ち出した展開図から作って、 眺めながらでないと理解するのが難しいかも。 上の私が今回作ったものは日和って最後の詰を kite.py のコマンドではなく、 kite.py の外側で Python で書いています。 KITE の全てのコマンドを kite.py に翻訳している訳ではなく、差し当たって必要なものだけ実装してみました。 唯、pyopengl の使い方が今一つ分からないので、奇妙な図（ このプログラムでは面の裏表を正確に把握できない（嘘です。模型を作り、眺めてみれば分かりますが（法線の計算など）面倒だからやってないだけです。）ので、応急処置で、 ある意味、幻想的な（？）図を描きます。 又、単純なプグラムで、意図したわけではないのに偶然面白い動きをするものもあります。 こんなマニアアックなプログラムが理解できなくても良いですが、暇なら上の3個のプログラムをコピーして実行してみて下さい。 そのままではなく、ソースコードを表示してコピーペーストしないとプログラムの修正が必要かも？ 多くの人がやっているそのままコピーペースト出来るプログラムの提示の仕方が今一つ理解できていません。 図形の回転スピードは、usegeneralkite.py の下から4行目の loop_step = 0.1 を自分のパソコンの性能に合わせて変えて下さい。 又 mypolyhedron.py の clist のRGB の数値０～１を自分の好きな色になるよう変更すれば、違った雰囲気の図になります。 私は芸術家ではないので、計算して決めたわけではなく、適当に決めているだけで、偶然この様な表示になっているだけです。 芸術的なセンスのある人ならこの様なプログラミングでも面白い作品が作れるかも？） を描きます。


実行途中を Cntl+Alt+Print Sc で GIMP で静止画にすると変なつまらない絵になりましたが、実際の実行結果はこの絵よりずっと綺麗なアニメーションです。

本には陰面処理（陰線処理（？））をした線画の図が多いですが、凸多面体でなければ難しそうです。 連立方程式を解いたり、（正）多面体の変換群などの数学の知識を駆使する必要があるのか？一時期 POV RAY などでも利用されていたレイトレーシングを使うのか？ 或いは上手く処理してくれるライブラリーがあるのか？ 私はまだ欲しい図形を描くプロぐラミイングが出来ないですが、そのような凸でない多面体が集めた書籍には無数に載っています。 例えば、「Polyhedron Models」には１１９個の多面体が載っていて、「Dual Models は前著と異なり図解が多いですが複雑な多面体ばかりで、 更に多面体と言うより寄せ木細工の ようなものも沢山載っていますが私は余り綺麗な立体では無いと思います。 これらの本の解説を読んで、紙の模型を作るのも大変そうですが、コンピュータグラフィックスにするのは更に大変そうです。 全部やってみるのは大変です。 例えば、101ページの６７Tetrahemihexahedron は模型の写真を見ても、解説を読んでも良く分からないので、まず、紙の模型を作ります。 三角定規と鉛筆と紙があれば出来ますが面倒ですからプログラムを作ります。 紙を無駄にしないように、ここでは VC++ 2022 を使います。Windows フォームに PictureBox と2個の button と printDialog と printDocument （印刷の項目にあります）を配置し、PictureBox のプロパティで Size を印刷する用紙と相似な図形になるよう 調整します。 次のようにプログラミングします。 

#pragma endregion
	private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {
		Graphics^ g = pictureBox1->CreateGraphics();
		Brush^ brush = gcnew SolidBrush(Color::White);
		g->FillRectangle(brush, 0, 0, pictureBox1->Width, pictureBox1->Height);
		Pen^ pen = gcnew Pen(Color::Black, 1);
		int K = 9;
		int s1 = pictureBox1->Width / (K + 2);
		int s2 = pictureBox1->Height / (K + 2);
		int s = (s1 > s2) ? s2 : s1;
		int w = (pictureBox1->Width - s * 9) / 2;
		int h = (pictureBox1->Height - s * 9) / 2;

		pen = gcnew Pen(Color::Black, 3);
		double b = 3 * s;
		int X = w + s;
		int Y = h + s;
		for (int k = 0; k < 2; k++) {
			Y = Y + (4 * s + s / 2) * k;
			g->DrawLine(pen, X, Y, X + b, Y);
			g->DrawLine(pen, X, Y, X + b / 2, Y - sqrt(3) / 2 * b);
			g->DrawLine(pen, X + b / 2, Y - sqrt(3) / 2 * b, X + b, Y);
			g->DrawLine(pen, X, Y, X + b / 2, Y + b / 2);
			g->DrawLine(pen, X + b / 2, Y + b / 2, X + b, Y);
			g->DrawLine(pen, X, Y, X + b / 4 - sqrt(3) / 4 * b, Y - sqrt(3) / 4 * b - b / 4);
			g->DrawLine(pen, int(X + b / 4 - sqrt(3) / 4 * b), Y - sqrt(3) / 4 * b - b / 4, X + b / 2, Y - sqrt(3) / 2 * b);
			g->DrawLine(pen, X + b, Y, X + 3 * b / 4 + sqrt(3) / 4 * b, Y - sqrt(3) / 4 * b - b / 4);
			g->DrawLine(pen, int(X + 3 * b / 4 + sqrt(3) / 4 * b), Y - sqrt(3) / 4 * b - b / 4, X + b / 2, Y - sqrt(3) / 2 * b);

			g->DrawLine(pen, X + 5 * s, Y, X + 5 * s + b, Y);
			g->DrawLine(pen, X + 5 * s, Y, X + 5 * s + b / 2, Y - b / 2);
			g->DrawLine(pen, X + 5 * s + b, Y, X + 5 * s + b / 2, Y - b / 2);
			g->DrawLine(pen, X + 5 * s + b, Y, X + 5 * s + b, Y - b);
			g->DrawLine(pen, int(X + 5 * s + b / 2), Y - b / 2, X + 5 * s + b, Y - b);
			g->DrawLine(pen, int(X + 5 * s), Y - b, X + 5 * s + b, Y - b);
			g->DrawLine(pen, int(X + 5 * s), Y - b, X + 5 * s + b / 2, Y - b / 2);
		}

		Y = int(Y + 4 * s + s / 2);
		for (int i = 0; i < 2; i++) {
			X = X + 4 * s * i;
			g->DrawLine(pen, X, Y, X + b, Y);
			g->DrawLine(pen, X, Y, X + b / 2, Y - sqrt(3) / 2 * b);
			g->DrawLine(pen, X + b / 2, Y - sqrt(3) / 2 * b, X + b, Y);
		}
	}
	int pCount;
	private: System::Void button2_Click(System::Object^ sender, System::EventArgs^ e) {
		if (printDialog1->ShowDialog() == System::Windows::Forms::DialogResult::OK) {
			printDocument1->PrinterSettings = printDialog1->PrinterSettings;
		}
		else {
			return;
		}
		pCount = 1;
		printDocument1->Print();
		}
private: System::Void printDocument1_PrintPage(System::Object^ sender, System::Drawing::Printing::PrintPageEventArgs^ e) {
	if (pCount > 0) {
		Graphics^ g = e->Graphics;
		int K = 9;
		int s1 = e->PageBounds.Width / (K + 2);
		int s2 = e->PageBounds.Height / (K + 2);
		int s = (s1 > s2) ? s2 : s1;
		int w = (e->PageBounds.Width - s * 9) / 2;
		int h = (e->PageBounds.Height - s * 9) / 2;

		Pen^ pen = gcnew Pen(Color::Black, 1);
		pen = gcnew Pen(Color::Black, 3);
		double b = 3 * s;
		int X = w + s;
		int Y = h + s;
		for (int k = 0; k < 2; k++) {
			Y = Y + (4 * s + s / 2) * k;
			g->DrawLine(pen, X, Y, X + b, Y);
			g->DrawLine(pen, X, Y, X + b / 2, Y - sqrt(3) / 2 * b);
			g->DrawLine(pen, X + b / 2, Y - sqrt(3) / 2 * b, X + b, Y);
			g->DrawLine(pen, X, Y, X + b / 2, Y + b / 2);
			g->DrawLine(pen, X + b / 2, Y + b / 2, X + b, Y);
			g->DrawLine(pen, X, Y, X + b / 4 - sqrt(3) / 4 * b, Y - sqrt(3) / 4 * b - b / 4);
			g->DrawLine(pen, int(X + b / 4 - sqrt(3) / 4 * b), Y - sqrt(3) / 4 * b - b / 4, X + b / 2, Y - sqrt(3) / 2 * b);
			g->DrawLine(pen, X + b, Y, X + 3 * b / 4 + sqrt(3) / 4 * b, Y - sqrt(3) / 4 * b - b / 4);
			g->DrawLine(pen, int(X + 3 * b / 4 + sqrt(3) / 4 * b), Y - sqrt(3) / 4 * b - b / 4, X + b / 2, Y - sqrt(3) / 2 * b);

			g->DrawLine(pen, X + 5 * s, Y, X + 5 * s + b, Y);
			g->DrawLine(pen, X + 5 * s, Y, X + 5 * s + b / 2, Y - b / 2);
			g->DrawLine(pen, X + 5 * s + b, Y, X + 5 * s + b / 2, Y - b / 2);
			g->DrawLine(pen, X + 5 * s + b, Y, X + 5 * s + b, Y - b);
			g->DrawLine(pen, int(X + 5 * s + b / 2), Y - b / 2, X + 5 * s + b, Y - b);
			g->DrawLine(pen, int(X + 5 * s), Y - b, X + 5 * s + b, Y - b);
			g->DrawLine(pen, int(X + 5 * s), Y - b, X + 5 * s + b / 2, Y - b / 2);
		}

		Y = int(Y + 4 * s + s / 2);
		for (int i = 0; i < 2; i++) {
			X = X + 4 * s * i;
			g->DrawLine(pen, X, Y, X + b, Y);
			g->DrawLine(pen, X, Y, X + b / 2, Y - sqrt(3) / 2 * b);
			g->DrawLine(pen, X + b / 2, Y - sqrt(3) / 2 * b, X + b, Y);
		}
	}
の様なプログラムを作れば良いです。何度か失敗して、紙を無駄にするとより良いプログラムが何か分かってきます。 図形を印刷する VC++ のプログラムの作り方は https://www.cc.kochi-u.ac.jp/~tyamag/jyohou/suudoku2.pdfを見て下さい。 VC++ 2019 を対象に書いていますが VC++ 2022 でも通用します。 （次々と多面体の型紙を印刷する為には、menuStrip を使って、メニューを作り、画面を描くものと印刷するものそれぞれのプログラムをコピーペーストし、 必要な修正をすれば、素早くプログラミング出来ます。参考書を読んで、どの様な型紙が何枚必要か考えなければいけませんが、 プログラミングそのものは別に難しいプログラミングではありません。） このプログラムで型紙を作り、組み立てれば良いです。この多面体に関しては参考書には２種類の作り方が解説してあります。 私は凡人だから、勿論、最初からこの様なプログラムを作った訳ではありません。ろくに解説も読まず、 この本で初めて出て来たタイプの多面体ですから読んでも良く分からないですが、目に付いた二つの大きいパーツを３個づつ印刷するプログラムを数独を 解説した私の pdf ファイルを見ながら作り、それぞれ貼り付けれる処は貼り付けて組み立てて見ると正八面体の模型を見ながらでもどうすれば良いか分かりません。 解説をちゃんと読むとすべてを貼り付けては駄目で、貼り付ける時も「のりしろの一方は外に出しなさい」と書いてあることに気が付きます。やり直しです。 どれを貼り付けるか書いてないので、正八面体の模型を眺めながら、 糊付けする前に色々組み合わせを試して、やっと4個の三角形からなるパーツ4個で多面体が作れました。 これが出来ると何を作れば良いか分かったので他の3個の三角形のパーツは正三角形のパーツと4個づつで直ぐ作ることが出来ます。 どおゆう訳か作るのが難しい方法から先に説明しています。 誰にでも理解できる作り方を説明しようとすれば、沢山の図を使って何ページにも渡って解説する必要があることも理解できましたが、 写真が他人に無断転載・利用されない様、不鮮明にしてあるので模型を作るのは結構大変です。

これでどの様な多面体か理解できたので、 上の mypolyhedron.py に 

def stored_pyramid(m, n, x):
    if n < 3 or n > 5:
        return
    y = x / 2 / np.sin(np.pi/n)
    h = np.sqrt(x * x - y * y)
    m.penup(0)
    m.fd(0, h)
    m.put(0, 0)
    m.pendown(0)
    m.penup(1)
    m.down(1, 90)
    m.fd(1, y)
    m.rt(1, 90+180/n)
    m.pendown(1)
    for i in range(n):
        m.fd(1, x)
        m.put(1, i+1)
        m.rt(1, 360/n)
    m.synchro()
    for i in range(n):
        m.fd(1, x)
        m.rt(1, 360/n)
    m.nonsynchro()
    m.penup(0)
    m.bk(0, h)
    m.pendown(0)
    m.penup(1)
    m.lt(1, 90+180/n)
    m.fd(1, -y)
    m.up(1, 90)
    m.pendown(1)
    
def stored_pyramid3(m, n, x):
    if n < 3 or n > 5:
        return
    y = x / 2 / np.sin(np.pi/n)
    h = np.sqrt(x * x - y * y)
    m.penup(0)
    m.fd(0, -h)
    m.pendown(0)
    m.put(0, 5)
    m.penup(1)
    m.down(1, 90)
    m.fd(1, y)
    m.rt(1, 90+180/n)
    m.pendown(1)
    for i in range(n):
        m.fd(1, x)
        m.rt(1, 360/n)
    m.synchro()
    for i in range(n):
        m.fd(1, x)
        m.rt(1, 360/n)
    m.nonsynchro()
    m.penup(0)
    m.bk(0, -h)
    m.pendown(0)
    m.penup(1)
    m.lt(1, 90+180/n)
    m.fd(1, -y)
    m.up(1, 90)
    m.pendown(1)

def tetrahemiheahedron(m, x):
    stored_pyramid(m, 4, x)
    stored_pyramid3(m, 4, x)
    p = np.zeros(3*6).reshape([6, 3])
    p[0] = m.magazine[0][0]
    p[1] = m.magazine[1][0]
    p[2] = m.magazine[2][0]
    p[3] = m.magazine[3][0]
    p[4] = m.magazine[4][0]
    p[5] = m.magazine[5][0]
    clist = [[1.0, 0.0, 0.0], [0.0, 1.0, 0.0], [0.0, 0.0, 1.0],
                     [1.0, 1.0, 0.0], [1.0, 0.0, 1.0], [0.0, 1.0, 1.0],
                     [0.5, 0.0, 0.0], [0.0, 0.5, 0.0], [0.0, 0.0, 0.5],
                     [0.5, 0.5, 0.0], [0.0, 0.5, 0.5], [0.5, 0.0, 0.5],
                     [0.5, 0.7, 0.0], [0.7, 0.5, 0.0], [0.7, 0.0, 0.5],
                     [0.5, 0.2, 0.3], [0.2, 0.5, 0.3], [0.3, 0.2, 0.5],
                     [0.7, 0.2, 0.8], [0.2, 0.9, 0.3], [0.7, 0.2, 0.9],
                 ]
    rect = [[0,1,3], [0,2,4], [5,1,3],[5,2,4],[1,2,4],[2,1,3],[3,2,4],[4,1,3]]
    glClear(GL_DEPTH_BUFFER_BIT)
    glPolygonMode(GL_FRONT_AND_BACK, GL_FILL)
    glEnable(GL_DEPTH_TEST)
    glEnable(GL_BLEND)
    glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA)
    for n in range(len(rect)):               
        glColor(clist[n][0], clist[n][1], clist[n][2], 0.7)
        glLineWidth(4.0) ## 線の幅
        glBegin(GL_POLYGON)
        for k in range(3):
            glVertex3f(p[rect[n][k]][0], p[rect[n][k]][1], p[rect[n][k]][2])       
        glEnd()
    tri = [[0,1,2],[0,3,4],[5,1,4], [5,3,2]]
    for n in range(len(tri)):               
        glColor(1.0, 1.0, 1.0, 0.9)
        glLineWidth(4.0) ## 線の幅
        glBegin(GL_POLYGON)
        for k in range(3):
            glVertex3f(p[tri[n][k]][0], p[tri[n][k]][1], p[tri[n][k]][2])       
        glEnd()
    glDisable(GL_DEPTH_TEST)
    glDisable(GL_BLEND)
を追加し、usegeneralkite.py に 

・・・
##        greatstellateddodecahedron(m, 200)
        tetrahemiheahedron(m, 300)
               
if __name__ == '__main__':
・・・
を追加して、実行すると


のアニメーションをしてくれます。この一様多面体は実際に紙の模型を作って、手に取って眺めてみないとどの様な構造になっているのか、 写真を見るだけでは我々凡人には分かりません。トポロジーの解説書には必ず出てくるメビウスの帯やクラインの壺や射影曲面の様な裏表の無い曲面です。 どの面が繋がっていて裏と表が入れ替わっている様子が分かるアニメーションを作ってみるとか、 正八面体からこの多面体を作る様子が分かるアニメーションや 正方形の上下に三角錐を並べてこの多面体を作る様子が分かるアニメーションを作ってみるとプログラミングの良い練習になります。 この4面半6面体 (tetrahemihexahedron) は正8面体の三角形の面の半分を互い違いに陥没させて出来る曲面で、3次元で実現すると面が交差してしまいます。 同様に６８番の8面半８面体 (octahemioctahedron) と78番の立方半8面体 (cubohemioctahdron) はそれぞれ正8面体（立方体）の各辺の中央で削って出来る 立方8面体 (cuboctahedron) の正方形の面を陥没させて出来る曲面と三角形の面を陥没させて出来る曲面です。 この様な解説があれば、理解しやすかったです。三角定規と（分度器と）鉛筆と紙とハサミと糊があれば、不器用な私でも何とか作ることが出来ますので、 小中学生の幾何の自由研究の教材に適しているのではと思います。別に高価な教材を購入する必要はありません。 https://www.cc.kochi-u.ac.jp/~tyamag/tenkaizu/tenkaizu.html のフリーソフト TENKAIZU.EXE を使って、正8面体や立方8面体や 69番の小立方立方8面体（small cubicuboctahedron）の作り方を考える為には 小菱形立方8面体（rhombbicubocctahedron：斜方立方8面体：人によって訳語が異なります）の模型を作って 眺めながら、どの様に模型を作れば良いかやこれらの立体を思い付いた人は何を考えたか考えて見ると良いです。 69番の小立方立方8面体も作ってみましたが、プリンターで型紙を打ち出し組み立てて見ましたが、コピー用紙では薄すぎて、私の様に不器用だと 本に書いている方法（見た目の美しい模型の作り方）では上手く出来ません。 のりしろが表に出ることを気にしなければ、小菱形立方8面体の模型を眺めながら、何とか不格好な模型を組み立てることが出来て、写真を眺めるだけでは分からなかった、 どの様な立体かやっと理解できました。これは小菱形立方8面体の正方形の面を互い違いに二つ折りした陥没面が垂直になるまで陥没させて出来る立体でした。 立体が理解できると何で写真を見るだけで理解できなかったのかと落ち込みますが。私のような凡人はこんなもんです。 沢山の多面体の模型の作り方を紹介するため一つ一つの解説が簡潔で実際に作ってみるのは結構大変ですが 誰でも知っている古代のプラトン・アルキメデス・ケプラーの多面体から多面体の概念がどの様に拡大してきたかの歴史を知ることが出来きて面白いです。 86番の小斜方6面体(small rhombihexahedron)も小菱形立方8面体のすべての正三角形を三角錐の形に又正方形を互い違いに正四角柱の形に陥没させて 出来る立体です。まるでパズルで試行錯誤で不格好な模型が何とか出来て初めて本の解説がこれはそうゆうことかと理解できます。 2つの立体を見比べてみると小斜方6面体は小立方立方8面体の陥没した面と陥没してない面とを逆にしたものです。そう書いてくれていれば楽に作れるのですが、 全く不親切な本です。しかし、これは図工の参考書として読んでいればまっとうな意見ですが、数学書として読んでいるのであれば、 立方8面体から６８番の8面半８面体と78番の立方半8面体と2種類作れたので、類比で、 小立方立方8面体の模型を作った時、小菱形立方8面体から他に一様多面体が作れないか考えるべきで、考えれば小斜方6面体の存在にも気が付くはずだと 言う意見も成立し、不当な言いがかりだと言えます。ただ、多面体の順番が不明です。 余裕を持って本を読む必要があります。更に、PETER R. CROMWELL 著「 POLYHEDRA」の .175 Uniform polyhedra にも これらを含む簡単な幾つかの一様多面体の分り易い陰面処理の図が載っていることに気が付きました。この本も購入したまま本箱で埃を被っていました。 不格好な模型でも手に取って眺めて見ると誰でもどの面がどの様に繋がっているか、裏と表の面が交互に表面に現れている事が理解できます。 三角定規と（分度器と）鉛筆と紙とハサミと糊があればとは書きましたが、プログラムを作り、印刷しなければ、 私は作ることが出来ないと思います。矢張り、文明の利器を使う方が楽です。失敗しても簡単にやり直すことが出来ます。これで小立方立方8面体の コンピュータグラフィックスも作れそうです。 コンピュータグラフィックスにするためにはこれらの立体の座標を 求める必要があり、中学校・高校で学ぶルートや三角関数の知識が必要になります。 マグナス　J. ウェニンガー著茂木勇・横手一郎共訳「多面体の模型 その作り方と鑑賞」教育出版には大量の多面体の模型を作るための方法が 解説されていますが、重要なすべての多面体が網羅されている訳ではありません。PETER R. CROMWELL 著「 POLYHEDRA」を読んでいると 「The kernels of some nuts and fruits contain many small seeds which grow in a restricted space. Pomegranates are one example. As each seed grows it presses up sgainst its neighbours. The seeds prevent each other from expanding uniformly and they grow to fill the available space producing flat-faced seeds with sharp corners. If the seeds had a perfectly uniform distribution before they began to grow and were subjected to isotropic compression forces they would end up as rhombic dodecahedra.」 と果物の種は菱形十二面体の形の分布になると書いてあります。「菱形十二面体」は重要な多面体ですが上記の本には載っていません。 「菱形十二面体」とはどんな多面体だろうと思えば、模型を作って、手に取って眺めて見るのが一番良いです。 更に、複数個作ってくっ付けて見れば、色々な事が分かります。この様なことを繰り返し、数学的センスが身につくと参考書の図を見るだけで 理解できるようになるそうです。 インターネットで検索すると画像や展開図が出てき、その展開図を印刷すると簡単に模型が作れ、誰もが自分で画像や展開図を描くプログラムを 作る必要があるか（作ろうと思えば作れる能力は必要だと思いますが）自信が無くなってきます。 しかし、これらの情報を提供してくれているのはあくまでも利益を追求する私企業です。ライバルを蹴散らし市場を独占できれば、 利用に高額のお金を要求しだすはずです。アメリカと中国のせめぎあいもそこにあると思います。全面対立では米中共倒れになるので 属国の日本を巻き込み複雑な駆け引きがここでも為されているみたいです。アメリカも基本的には敵を見つけ、直接・間接を問わず戦争ばかりしている国です。 この展開図をコンピュータを使わず正確さを意識して手作業で描こうとすると（ルート２や）ルート３倍の線を引く必要があるのでコンパスも 必要になり、かなり複雑な操作が必要になります。 コンピュータで描くにも主として高校で学ぶルートや三角関数やベクトルや行列の知識が無いと作れないのではないかと思います。 少なくとも私にはそれらの知識を使わないと作れません。 この様に検索で直ぐ画像が出てくるのは、これは「菱形十二面体」の画像ですと一つ一つの画像にラベルを付ける仕事を低賃金でしている人達が 実は沢山いるからだそうです。AIの影の部分です。 現在は上の英文もコンピュータがそれなりに翻訳してくれるので、（翻訳もありますが正二十面体を正十二面体と誰でも気が付く誤訳をしていたりしています）、 英語が世界標準だと言っても全世界のすべての人が英語を話すわけでなく話すのは エリートや観光産業関係者だけだし、今更、小学校で国語や算数教育を差し置いて、日本はアメリカの植民地・属国では無いと首相は表向きは言っているので、 全員に英語や情報教育をする必要があるのか甚だ疑問です。矢張り、そこに政治家が目を付ける利権があり、それで利益を得る人達がいて推進しているのでしょうが。 実際は、英語より中国語を話せればより利益を挙げれるはずの日本人も沢山いるはずですが。日本語を話せる中国人が日本での中国人関連の利益を独占しているとも 言われています。

模型を作るのとコンピュータグラフィックスを作るのとの最大の違いは出来上がるものが各人の才能によって差が出るか出ないかの違いです。 模型作成では経験値や型紙の作り方や使う用紙の材質や手先の器用さなどにより出来上がるものに天と地の差が出ますが コンピュータグラフィックスは誰が作ったプログラムでもプログラムが同じなら誰が作ったものでも全く同じものが出来上がることです。 綺麗な模型の作り方は、PETER R. CROMWELL 著「 POLYHEDRA」に丁寧に解説されています。私はそんな面倒なことは出来ないので、 パソコンで正確な型紙を作り、 プリンターに打ち出し、コピー用紙を使って、不恰好な模型を作り、満足していますが、人に自慢したい美しい模型を作る人がどの様に作っているか 解説してくれています。兎も角、その多面体がどんなものかを知りたいだけなら、私のような安易な方法で良いです。 どうせ、不器用ですから私には本に載っているような綺麗な模型は作れませんから。 思い通りのプログラムが作れるようになるためには数学の勉強が基本です。数学が出来るようになる為には小学校の国語の勉強（本を沢山読むこと） が必要です。日本人は日本語で考えています。 そうすれば、頭の良い人たちの嘘（例えば、電気・ガス料金の値上がり対策として、貧困者への直接現金配布はマイナンバーカードが １００パーセント普及せず、マイナンバーカードと預金口座の紐づけが出来ていなくて全国民の個人個人の収入・財産の把握が「政権」に出来ていないから、 電気・ガスの大企業に対する助成しかないと政治家やコメンテーターが熱弁しますが、本音は貧困者への直接給付では 政治家・官僚へのキックバックがないから（大企業に対する助成なら政治家への政治献金や官僚の天下りが期待出来る）言っている可能性があります。 優秀な人達が官僚になっているはずだから、貧困者への直接現金配布の速やかな方法もやろうと思えば考え出せるはずです。 ） も見破れるようになります。 「数学だけは遺伝との関係がない・少ない」と言われています。 手先の器用さも遺伝しないみたいです。父親は自分でチャンと動く実用的な木工の水車も作って、 田圃の横の低い水路から田圃に水を入れていましたが、私にはそんなことは多分出来ません。 私の様に何をやっても駄目だと思う人は、現在はコンピュータがあるので、ちょっとしたコツがありますが、 （数学の参考書の読み方も、PETER R. CROMWELL 著「 POLYHEDRA」にも解説されています。この本は昔山口教授に教えて貰った本で、 英文の原著と翻訳を私費で購入しただけで読まずに本箱で埃を被っていたのを引っ張り出し、 今頃になってチャンと読んでいますが、翻訳も高価で、翻訳は所どころ誤訳もあるように思いますが凄く良い本です。 基本的には多面体に関する数学史の本です。やっと、日本でも我々凡人が読んでも理解できる数学史の書籍の翻訳本が複数出版されるようになって良い時代になっています。 「持っているだけで強くなる」と書いてある囲碁の本も持っていますが、（数学の）本は持っているだけでは出来るようにはならないみたいです。 習った先生達のようには短時間では私は（数学の）本が読めないので、本は直ぐ絶版になるので、私の家に来たがっている本たちをとりあえず購入するだけで、 読んでない・読む時間的余裕・根性がなく持っているだけの本が一杯あります。生きている内にどれだけ読めるかです。）、 中学校の数学から一生懸命勉強してみれば良いです。プロの数学者になることはどの分野でもそうだと思いますが難しいでしょうが、 既に知られている数学を理解することは誰にでも出来ます。そうなれば道は開けます。多分。

小立方立方8面体の模型の為の型紙を切り貼りして無理やり作った不細工な小斜方6面体の模型を眺めていて、もっと綺麗な模型模型を作ろうと 小斜方6面体の模型用の3種類の型紙を印刷するプログラムを作り、組み立ててみましたが、不器用な私が綺麗な模型を作るためには、 出来るだけ型紙に沢山の長方形や正方形や直角二等辺三角形を詰め込んで、必要な型紙の数を減らせば良いことに気が付きました。 最低限、何枚の型紙があれば良いか？ 又、そのような型紙は何種類あるか？小中学生でも解けそうな数学的パズルで、既に誰かが答えを見つけているかも分かりませんが、 凸でない多面体は沢山知られているので、沢山の問題があります。ある程度、手計算でやってみれば、私の非力なパソコンでも解決できそうな・ 出来るかもしれないプログラミングの練習問題だと思います。こんなことやっていたのでは、読みたい本がちっとも読めなくなりますが、ふと頭に浮かびました。 面白そうだと思ったらやってみて下さい。年金生活なので、もうこれを絶対しなければと言うことはないので、私も少しは考えてみますが。

一晩寝て、基本的な数値を数えてみました。67番：4面半6面体は正三角形4個と直角二等辺三角形12個で表の面が出来ています。 68番：8面半８面体は正三角形32個です。78番：立方半８面体は正方形6個と正三角形２４個です。 69番：小立方立方8面体は正方形6個と長方形24個と正三角形8個と直角二等辺三角形24個です。 86番：小斜方6面体は正方形18個と長方形24個と直角二等辺三角形２４個です。 67番は出来そうな気がします。68番と78番は私の能力と私のパソコンの性能でも何日も何か月も動かせばひっよとすれば可能かも。 微妙でやってみないと何とも言えません。 69番と86番は多分、私の能力と私のパソコンの性能では絶望的です。 最初の問題は、凸多面体（展開図が作れるので、答えは1個）でないので、最低2個です。答えが2個なら、手作業で例を見つければ良いです。 答えが３以上の n なら、ｎ 個からなる例を見つけるだけでなく、n 未満の例がないことを検証する必要があるのでコンピュータを使いたくなります。 次の問題は見落としがどうしても出るのでコンピュータで検証したいです。 勿論、糊で貼り付ける個所をすくなくする為になるべく大きい型紙のセットの一つを見つけることは模型を見ながら絵を描けば出来き、 それで楽な模型作成の為には十分ですが。

プログラムを作るためには本に与えられているデータを使えば良いだけですが、一般的な方針だけで、個々の具体的な計算を書いてくれていませんから、 我々凡人が穴埋めするのは結構大変ですが、現在はパソコンがあるので、プログラミングが出来れば、 楽に考えるための正確な結果の図を印刷したものを何枚でも使えるので、必要な方程式を見つける時間を短縮することが出来ます。 更に、見つけた方程式が正しいものか数値計算して確かめることも出来ます。図が正しく大きなものであれば、三角定規と分度器で 小学生の様に計ってみて考える事も出来ます。この様に既に知られている数学を学ぶことは、 結果を既に知っているし、我々の子供・学生時代と異なり、コンピュータで正確な図を自分で描かせることも出来るので、時間を掛ければ、 これを発見した人達はどの様に考えたかは分かりませんが、この様にすれば自分でも発見できるのではないかと言う方法を見つけることが出来ます。 これが出来たのは一松信著「正多面体を解く」に図を正確に描くためのデータがあったからで、（正三角形と正四面体に対する数値は 何処にも書いてないように思います）、正確な結果の図を描けたならこんな計算を わざわざしてみる必要があるか？それより最先端の事を早くやりたいと思う人が実際は殆どだとは思いますが。 既に解決していることだから、一松信著「正多面体を解く」の図を正確に描くためのデータを使って平面充填形の捩り切りの結果を描くプログラムが 簡単に作れ、それを眺めたり、データを変えるとどの様な図形になるか眺める事により、そのデータを見つけた人は何を考えただろうと 逆に考えてみる事が出来るので、時間は掛かり、無駄な努力だと思うかもしれませんが、このデータを見つけた人よりは多分誰でも素早く見つけることが出来ます。、 唯、コンピュータの技術が必要不可欠な時代になったから言っても、小学生から情報教育だと言うのは今一つ良く分かりません。 プログラミングの基礎のアルゴリズムを理解・開発出来るよう日本人は英語ではなく日本語で考えますから、キチンと日本語教育と算数教育を すべきだと思います。数学だけ算数・数学と使い分けているのは、琉球大学の前原先生（弟：名前の漢字が難しい）も「小学校の算数は アルゴリズムを習っただけだよね」と言っていました。考えるより、計算のアルゴリズムを覚えるだけだった様に私も思います。 プログラミングの基礎になるアルゴリズムは、算数教育でアルゴリズムの重要性を叩きこんでいるのだと私は思います。 唯、私が理解できないことは丸暗記できない三角形、平行四辺形。台形などの面積の公式などは父親が新聞紙を切って、それらを並べて理屈を教えてくれて、 覚えることが出来ました。九九の暗記も同様で、足せばいいことに気づいて、暗算で足し算しながら唱えることで覚えました。小学生に自分で公式を 発見しろと言っても駄目ではないかと思います。子供の自由な発想を小学校の先生が画一的なアルゴリズム・ルールに固執して潰していると言う意見もあります。 これは日教組を潰すために、教育学部の教育でもこれも教えろ、これもやらせろと次々教師に必要とされるとされることを増やし、 教科そのものの学習時間を減らし、 教員になってもあらゆることを教員に求め、教員が算数教育について十分に研究する時間的余裕を奪ってきたことの必然の結果なのかも知れません。 算数を理解するためには日本語の理解が必要だと子供に気づかせ・納得させてから、日本語教育をしっかりすれば良い、情報教育をしてみて、更なる上達を目指すには、 キチンと算数・数学を学ばなけれいけないと子供に気づかせる必要がある、そうなれば自発的に算数・数学の勉強をしだすとの主張も勿論成り立つと思いますが。 また、心理学者や教育学者は諦めずに、それ（小学生が自分で発見できること）を目指すのでしょうが。）、 準正多面体の構成法など正確に理解する為に 上で紹介した様々なプログラム達を作りました。行方不明っだた一松信著「正多面体を解く」（見つかったのは最初に購入した旧版でなく新版でした。）を 本箱から見つけて眺めてみましたが、 準正多面体の双対多面体や空間充填形も解説されていますが、チャンと読んでいませんでした。この本には必要最小限度の情報は載せてくれているので、 準正多面体の双対多面体も見栄を張らず誰でも作れる展開図を先ず作り、準正多面体と対応する双対多面体の模型を見ながら準正多面体の双対多面体の構成法の解説を読めば、 時間は掛かりますが誰でも理解出来るのではないでしょうか？そうすることが自分にとって意味があると思えばですが。 更に、数学の教師になるのでなるのでなければ、数学が仕事で使えるようになる為には、理解なしの丸暗記では駄目だと思いますが、 チャンとは説明できませんが、それなりの勉強法があるような気もします。 例えば、英語の学習法など、次から次へとこうすれば良いと言う勉強法が考案され、我々凡人は何が良いか分からず振り回されますが、 推理小説を読むことが好きなら、「アガサ・クリスティー」や「シャーロック・ホームズ」より「ペリー・メイスン」が良いと言う専門家もいますが、 （イギリス英語かアメリカ英語かでもありますが、「エラリイ・クイーン」をありますし、私の学生時代に流行っていた本ばかりで、すべて古典ですが、 実際、越前敏弥著「名作ミステリで学ぶ英文読解」を読めば、「名作ミステリは、原文も謎だらけ！」のコピー通りこれらが難解であることが分かります。） 例えば、合計で数千円で済みますから、 「英語で読む　シャーロック・ホームズ傑作短編２０選」の易しく書き直した「ボヘミアの醜聞」と「英語で味わう　シャーロック・ホームズ名作短編集」の 元のままの「ボヘミアの醜聞」の音声など共通している短編を聞き比べて、自分には何が足りないか調べて、足りないことを補う勉強をすれば良いです。多分。 数学はギリシャ時代から 「幾何学に王道なし」と言われていたように、平凡なことの積み重ねしか学ぶ方法がないのではないでしょうか？ だから、既に知られている数学を理解することは平凡なことの積み重ねで誰でもできます。 それに対して、新しい数学の発見をすることは我々凡人には物凄く大変ですが。 「コスパ」且つ「タイパ」重視なら、多分、最初に読むべき本です。菱形十二面体もインターネットで見つけた展開図から模型を作って見たり、インターネットで画像を 観るだけではなく、優秀な人達はそれだけで理解すると思いますが、我々凡人は見栄を張っても理解できないものは理解できませんから。 自分で展開図を作り、模型を作り、どの多面体から構成出来るか調べ、画像を表示するプログラムを作りと、自分でこれらのプログラミングをしてみて、 初めて理解できたと言えるのではないかと思いますが、これは昭和の人間の考えかもしれませんが？自分が理解できたと思うまでやってみれば良いです。 唯、我々凡人でもここまでは誰でも出来ますが、そこで息切れしてしまい、その後、これらの知識・技術を元に何をすれば良いかにいきません。 多分、そこが我々凡人と才能ある優秀な人達との違いです。） 多面体に関する直ぐに試せるそれ以外の手持ちの材料は尽きたので、 3次元空間の230個の結晶群の表が解説されている「INTERNATIONAL TABLES for CRYSTALLOGRAPHY」（シリーズで Volume A, A1, B, C, D, E, F, G, H, I と様々な本がありますが、Teaching edition だと個別に数学者養成の為の群論の参考書を読むなどしなくても空間結晶群の理解に必要な数学はすべて基本を解説してくれています。 但し、必要な定義と定理は解説してくれていますが、証明は難しくはありませんが、 いちいち与えてくれてはいません。その代わり大量の例を与えてくれているので、 その例を研究して、定理を理解すれば良いですし、 参考文献もセクションごとに提示してくれています。 標準的な群論の参考書になじめなかった人でも、結晶学などで群論を必要とする人達の為に書いているので何の為に学んでいるか分かり、勉強しやすいように思います。 「線形代数」も標準的な参考書になじめなかった人も高価な本ですが「行列プログラマー Pythonプログラムで学ぶ線形代数」を本屋でパラパラめくってみれば良いです。 或いは、空間の回転や鏡映の行列を Python でどの様に求めたらいいかと言った具体的な目的を持って、線形代数の本やインターネットの解説を探し、 学べば楽しく学べます。多分。 更に、ギルバート・ストラング著「ストラング：線形代数イントロダクション」は 8000円＋税と高額ですが、広範に線形代数の応用分野の解説もあり、 絶望的な程の膨大な演習問題もあり、我々日本人の大学生と異なり、アメリカ人の大学生になってからの精力的・広範囲の学習量が垣間見える参考書です。 どの様な本に出会うかも運です。 更にこの本（「INTERNATIONAL TABLES for CRYSTALLOGRAPHY」）の数学を Python のプログラミングで一つ一つチェックできれば完璧だと思いますが、 具体的な例で理解するためには計算力が必要ですが、私の様に計算力に自信が無くなれば、パソコンで Python のプログラムを ちょこちょこと作れば良いです。自分が手作業で出来ることを Python のプログラムに置き換えれるようになるには一か月も練習すれば良いです。多分。 唯、次に掲げているプログラムを作りたいと思う人が何人いるか甚だ疑問ではあります。 自分の仕事に直結した、お金を直ぐに生み出すプログラミングを教えろと言う人達ばかりだと思います。 自分の仕事を分析し、何をすべきかは、その人や同僚など実際にその仕事をしている人達にしか多分分かりません。 やりだせば面白いものですが、それだけの時間の投資が自分にとって意味があると思えば やってみれば良いです。

何を言っているかと言うと、例えば、正 P 角形の対称群の性質を調べる 

import numpy as np
import copy

class G:
    def __init__(self, P): #コンストラクタ
        self.P = P
        
        self.rotate_mtx = np.array([[np.cos(2*np.pi/self.P), \
                                -np.sin(2*np.pi/self.P)],\
                            [np.sin(2*np.pi/self.P), \
                             np.cos(2*np.pi/self.P)]])
        self.vertices = np.zeros(2*self.P).reshape(self.P, 2)
        self.vertices[0] = np.array([1, 0])
        for i in range(self.P-1):
            self.vertices[i+1] = np.dot(self.rotate_mtx, self.vertices[i])        

        self.A = [np.array([[1, 0], [0, 1]])]    
        for i in range(self.P-1):
            self.A.append(np.dot(self.rotate_mtx, self.A[i]))
        self.A.append(np.array([[1, 0], [0, -1]]))
        for i in range(self.P-1):
            self.A.append(np.dot(self.rotate_mtx, self.A[i+self.P]))

        self.table = self.get_table()
        self.index = []
        for i in range(2*self.P):
            self.index.append(self.convert_permutation(i))
        self.group = self.get_group()
        self.subgroups = self.get_subgroup()
        self.normal_subgroups = self.get_normal_subgroup()
        
    def same(self, d1, d2):
        if np.abs(d1-d2) < 0.0001:
            return True
        else:
            return False
    def multi(self, i, j):
        R = np.dot(self.A[i], self.A[j])
        for k in range(2*self.P):
            if self.same(R[0][0], self.A[k][0][0]) and \
               self.same(R[1][0], self.A[k][1][0]) and \
               self.same(R[0][1], self.A[k][0][1]) and \
               self.same(R[1][1], self.A[k][1][1]):
                return k
    
    def get_table(self):
        self.table = []
        for k in range(2*self.P):
            t = []
            for i in range(2*self.P):
                t.append(self.multi(k, i))
            self.table.append(t)
        return self.table
    def show_table(self):
        for k in range(len(self.table)):
            print(self.table[k])
        print()
        
    def convert_permutation(self, i):
        v = np.zeros(2*self.P).reshape(self.P, 2)
        for k in range(self.P):
            v[k] = np.dot(self.A[i], self.vertices[k])
        result = []
        for k in range(self.P):
            for j in range(self.P):
                if self.same(v[k][0], self.vertices[j][0]) and \
                   self.same(v[k][1], self.vertices[j][1]):
                    result.append(j)
                    break
        return result
    
    def get_group(self):
        G = []
        for i in range(2*self.P):
            G.append(self.convert_permutation(i))
        return G
    
    def perm_product(self, g, h):
##        print('g=', g, ' h=', h)
        p = []
        for i in range(len(g)):
            p.append(g[h[i]])
        return p
    
##    def inverse(self, g):
##        for k in range(2*self.P):
##            if g == self.index[k]:
##                i = k
##                break
##        if i < self.P:
##            return self.index[(self.P -i) % self.P]
##        else:
##            return self.index[i]
    
    def inverse(self, g):
        inv = []
        for i in range(len(g)):
            inv.append(g.index(i))
        return inv
                
    def generate_subgroup(self, generator):
        flag = True
        G = [self.convert_permutation(0)]
        NG = copy.deepcopy(G)
        while flag == True:
            flag = False
            for f in generator:
                g = self.convert_permutation(f)
                for h in G:
                    k = self.perm_product(g, h)
                    if k not in NG:
                        flag = True
                        NG.append(k)
            G = copy.deepcopy(NG)
        return G

    def sub_get_combination(self, r, l, s, k):
        if len(s) == k:
            r.append(s)
            return
        new_l = l[:]
        for e in l:
            old_s = s[:]
            s.append(e)
            new_l.remove(e)
            self.sub_get_combination(r, new_l, s, k)
            s = old_s
    def get_combination(self, n, k):
        l = [i for i in range(n)]
        r = []
        self.sub_get_combination(r, l, [], k)
        return r
                      
    def get_subset(self, n):
        result = [[]]
        for k in range(1, n+1):
            result.extend(self.get_combination(n, k))
        return result

    def sub_get_all_subset(self, r, l, s):
        if len(l) == 0:
            return
        new_l = copy.deepcopy(l)
        for e in l:
            new_s = copy.deepcopy(s)
            new_s.append(e)
            r.append(new_s)
            new_l.remove(e)
            self.sub_get_all_subset(r, new_l, new_s)
            
    def get_all_subset(self, n):
        l = [i for i in range(n)]
        r = [[]]
        self.sub_get_all_subset(r, l, [])
        return r
    
    def show_all_subset(self, n):
        S = self.get_all_subset(n)
        for s in S:
            print(s)
        print()
        
    def lessP(self, g1, g2):
        for e1, e2 in zip(g1, g2):
            if e1 < e2:
                return -1
            elif e1 > e2:
                return 1
        return 0
    
    def arrange(self, G):
        for i in range(1, len(G)):
            x = copy.copy(G[i])
            j = i-1
            while self.lessP(x, G[j]) == -1:
                G[j+1] = copy.copy(G[j])
                j = j-1
            G[j+1] = copy.copy(x)
        return G  
        
    def get_subgroup(self):
        SG = []
        cand = self.get_subset(2*self.P)
        for gen in cand:
          G = self.generate_subgroup(gen)
          NG = self.arrange(G)
          if NG not in SG:
              SG.append(NG)
        return SG
    def show_subgroups(self):
        for G in self.subgroups:
            print(G)
        print()
    
    def g_time_H(self, g, H):
        NH = []
        for h in H:
           NH.append(self.perm_product(g, h))
        return NH
    
    def get_left_cosets(self, i):
        H = self.subgroups[i]
        LC = [H]
        flag = True
        for g in self.group:
            flag = True        
            for C in LC:
                if g in C:
                    flag = False
                    break
            if flag:
                LC.append(self.g_time_H(g, H))
        return LC
    def show_left_cosets(self, i):
        LC = self.get_left_cosets(i)
        for c in LC:
            print(c)
        print()
                
    def H_time_g(self, g, H):
        NH = []
        for h in H:
           NH.append(self.perm_product(h, g))
        return NH
    
    def get_right_cosets(self, i):
        H = self.subgroups[i]
        LC = [H]
        flag = True
        for g in self.group:
            flag = True        
            for C in LC:
                if g in C:
                    flag = False
                    break
            if flag:
                LC.append(self.H_time_g(g, H))
        return LC
    def show_right_cosets(self, i):
        LC = self.get_right_cosets(i)
        for c in LC:
            print(c)
        print()

    def get_normal_subgroup(self):
        G = self.group
        NG = []
        for SG in self.subgroups:
            flag = True
            for g in G:
                for h in SG:
                    x = self.perm_product(g, h)
                    y = self.inverse(g)
                    z = self.perm_product(x, y)
                    if z not in SG:
                        flag = False
                        break
            if flag:
                NG.append(SG)
        return NG
    def show_normal_subgroup(self):
        NG = self.get_normal_subgroup()
        for G in NG:
            print(G)
        print()
    def permutation2index(self, perm):
        for i in range(2*self.P):
            if perm == self.index[i]:
                return i
    def index_rep_of_subgroup(self, SG):
        IG = []
        for g in SG:
            IG.append(self.permutation2index(g))
        return IG
    
    def index_rep_of_all_subgroup(self):
        G = []
        for g in self.subgroups:
            G.append(self.index_rep_of_subgroup(g))
        return G
    
    def index_rep_of_all_normal_subgroup(self):
        G = []
        for g in self.normal_subgroups:
            G.append(self.index_rep_of_subgroup(g))
        return G
        
        

P = 4
m44 = G(P)
print('乗積表')
m44.show_table()
print('置換に変換')
for i in range(2*P):
    print('i=', i, ' : ', m44.convert_permutation(i))
print('対応する置換群')
print(m44.group)
print('生成元で生成される部分群')
print(m44.generate_subgroup([2,4]))
print('すべての部分集合')
m44.show_all_subset(P)
print('全部分群')
m44.show_subgroups()
print('left cosets')
m44.show_left_cosets(2)
print('right cosets')
m44.show_right_cosets(2)
print('全正規部分群')
m44.show_normal_subgroup()
print('all subgroup')
print(m44.index_rep_of_all_subgroup())
print('all normal subgroups')
print(m44.index_rep_of_all_normal_subgroups())
のようなプログラムを作って、P=4 で実行すると 

乗積表
[0, 1, 2, 3, 4, 5, 6, 7]
[1, 2, 3, 0, 5, 6, 7, 4]
[2, 3, 0, 1, 6, 7, 4, 5]
[3, 0, 1, 2, 7, 4, 5, 6]
[4, 7, 6, 5, 0, 3, 2, 1]
[5, 4, 7, 6, 1, 0, 3, 2]
[6, 5, 4, 7, 2, 1, 0, 3]
[7, 6, 5, 4, 3, 2, 1, 0]

置換に変換
i= 0  :  [0, 1, 2, 3]
i= 1  :  [1, 2, 3, 0]
i= 2  :  [2, 3, 0, 1]
i= 3  :  [3, 0, 1, 2]
i= 4  :  [0, 3, 2, 1]
i= 5  :  [1, 0, 3, 2]
i= 6  :  [2, 1, 0, 3]
i= 7  :  [3, 2, 1, 0]
対応する置換群
[[0, 1, 2, 3], [1, 2, 3, 0], [2, 3, 0, 1], [3, 0, 1, 2], [0, 3, 2, 1], [1, 0, 3, 2], [2, 1, 0, 3], [3, 2, 1, 0]]
生成元で生成される部分群
[[0, 1, 2, 3], [2, 3, 0, 1], [0, 3, 2, 1], [2, 1, 0, 3]]
すべての部分集合
[]
[0]
[0, 1]
[0, 1, 2]
[0, 1, 2, 3]
[0, 1, 3]
[0, 2]
[0, 2, 3]
[0, 3]
[1]
[1, 2]
[1, 2, 3]
[1, 3]
[2]
[2, 3]
[3]

全部分群
[[0, 1, 2, 3]]
[[0, 1, 2, 3], [1, 2, 3, 0], [2, 3, 0, 1], [3, 0, 1, 2]]
[[0, 1, 2, 3], [2, 3, 0, 1]]
[[0, 1, 2, 3], [0, 3, 2, 1]]
[[0, 1, 2, 3], [1, 0, 3, 2]]
[[0, 1, 2, 3], [2, 1, 0, 3]]
[[0, 1, 2, 3], [3, 2, 1, 0]]
[[0, 1, 2, 3], [0, 3, 2, 1], [1, 0, 3, 2], [1, 2, 3, 0], [2, 1, 0, 3], [2, 3, 0, 1], [3, 0, 1, 2], [3, 2, 1, 0]]
[[0, 1, 2, 3], [0, 3, 2, 1], [2, 1, 0, 3], [2, 3, 0, 1]]
[[0, 1, 2, 3], [1, 0, 3, 2], [2, 3, 0, 1], [3, 2, 1, 0]]

left cosets
[[0, 1, 2, 3], [2, 3, 0, 1]]
[[1, 2, 3, 0], [3, 0, 1, 2]]
[[0, 3, 2, 1], [2, 1, 0, 3]]
[[1, 0, 3, 2], [3, 2, 1, 0]]

right cosets
[[0, 1, 2, 3], [2, 3, 0, 1]]
[[1, 2, 3, 0], [3, 0, 1, 2]]
[[0, 3, 2, 1], [2, 1, 0, 3]]
[[1, 0, 3, 2], [3, 2, 1, 0]]

全正規部分群
[[0, 1, 2, 3]]
[[0, 1, 2, 3], [1, 2, 3, 0], [2, 3, 0, 1], [3, 0, 1, 2]]
[[0, 1, 2, 3], [2, 3, 0, 1]]
[[0, 1, 2, 3], [0, 3, 2, 1], [1, 0, 3, 2], [1, 2, 3, 0], [2, 1, 0, 3], [2, 3, 0, 1], [3, 0, 1, 2], [3, 2, 1, 0]]
[[0, 1, 2, 3], [0, 3, 2, 1], [2, 1, 0, 3], [2, 3, 0, 1]]
[[0, 1, 2, 3], [1, 0, 3, 2], [2, 3, 0, 1], [3, 2, 1, 0]]

all subgroups
[[0], [0, 1, 2, 3], [0, 2], [0, 4], [0, 5], [0, 6], [0, 7], [0, 4, 5, 1, 6, 2, 3, 7], [0, 4, 6, 2], [0, 5, 2, 7]]
all normal subgroups
[[0], [0, 1, 2, 3], [0, 2], [0, 4, 5, 1, 6, 2, 3, 7], [0, 4, 6, 2], [0, 5, 2, 7]]
を表示してくれます。P=3 と書き直すと 

乗積表
[0, 1, 2, 3, 4, 5]
[1, 2, 0, 4, 5, 3]
[2, 0, 1, 5, 3, 4]
[3, 5, 4, 0, 2, 1]
[4, 3, 5, 1, 0, 2]
[5, 4, 3, 2, 1, 0]

置換に変換
i= 0  :  [0, 1, 2]
i= 1  :  [1, 2, 0]
i= 2  :  [2, 0, 1]
i= 3  :  [0, 2, 1]
i= 4  :  [1, 0, 2]
i= 5  :  [2, 1, 0]
対応する置換群
[[0, 1, 2], [1, 2, 0], [2, 0, 1], [0, 2, 1], [1, 0, 2], [2, 1, 0]]
生成元で生成される部分群
[[0, 1, 2], [2, 0, 1], [1, 0, 2], [1, 2, 0], [0, 2, 1], [2, 1, 0]]
すべての部分集合
[]
[0]
[0, 1]
[0, 1, 2]
[0, 2]
[1]
[1, 2]
[2]

全部分群
[[0, 1, 2]]
[[0, 1, 2], [1, 2, 0], [2, 0, 1]]
[[0, 1, 2], [0, 2, 1]]
[[0, 1, 2], [1, 0, 2]]
[[0, 1, 2], [2, 1, 0]]
[[0, 1, 2], [0, 2, 1], [1, 0, 2], [1, 2, 0], [2, 0, 1], [2, 1, 0]]

left cosets
[[0, 1, 2], [0, 2, 1]]
[[1, 2, 0], [1, 0, 2]]
[[2, 0, 1], [2, 1, 0]]

right cosets
[[0, 1, 2], [0, 2, 1]]
[[1, 2, 0], [2, 1, 0]]
[[2, 0, 1], [1, 0, 2]]

全正規部分群
[[0, 1, 2]]
[[0, 1, 2], [1, 2, 0], [2, 0, 1]]
[[0, 1, 2], [0, 2, 1], [1, 0, 2], [1, 2, 0], [2, 0, 1], [2, 1, 0]]

all subgroups
[[0], [0, 1, 2], [0, 3], [0, 4], [0, 5], [0, 3, 4, 1, 2, 5]]
all normal subgroups
[[0], [0, 1, 2], [0, 3, 4, 1, 2, 5]]
です。有限巡回群や n 次置換群（この為に必要な順列のすべての要素を書きだす　Python のプログラムは、例えば、「Python による数値計算」： https://www.cc.kochi-u.ac.jp/~tyamag/jyohou/console3.pdf の p.97 から解説しています。 ）の性質を調べるプログラムにも この様に自分でプログラミングしていれば自由に作り変える事ができます。集合のすべての部分集合を求める関数は2種類書いておきました。 直接求める方法と組み合わせを求めて（これも上記順列を求める Python の解説の後ろにあります。）合算する方法です。 Python の学び始めなら、この様なプログラムを作り変えて、全部分群の表示や全正規部分群の表示を小さい順に綺麗に並べ替えるようにしてみたり、 部分群が正規部分群か判定する機能や部分群と元が与えられたとき conjugate group （共役群）を計算する機能を追加してみたり、 部分群や正規部分群の表示を置換や０から2P-1 の数値ではなく自分に分り易い記号で表示するように変えてみるなど自分が使い易いように作り変えてみると良いです。 理解しやすい単純なアルゴリズムだけ使って作っているので、P が大きければ使い物にならないです。我々凡人はこの様なプログラムが作れれば十分です。 どの分野も自分の分野がプロとアマの差が一番大きいと思っていると思いままが、一般にはプログラミングの世界がプロとアマチアの差が最も大きいと言われていて、 プロの作ったプログラムは一瞬で答えを出すが、我々凡人の作ったプログラムは 一か月経っても答えが出ないと言うことも良くあります。多分、使っているアルゴリズムが違っています。 例えば、同じソートのプログラムでも使うアルゴリズムによってデータの量が多くなれば物凄い差が出るので、Knuth さんの本でも大型の分厚い本の半分を 使ってソートのアルゴリズムが解説されています。 ここで作っているプログラムは簡単な群の例で群論の理論を理解するために作っているだけなので この様な誰でも作れる単純なプログラムで良いです。商品のプログラムを作っている訳ではないので、見栄を張らず、 使っているすべての部分群を求めるアルゴリズムなど明らかに無駄な計算をしていますが、 （例えば、正多面体群のプログラムでこんなことをすれば、立方体の回転群では 16777216 個の部分集合を試すことになり、幾ら待っても答えが出ないので、 我々凡人でも生成元は本当は何個あれば良いか考えるようになります。 即ち、「すべての部分集合を求める」ではなく「k 個から成るすべての組み合わせ（部分集合）を求める」を使って、 何個の元からなる生成元まで調べればよいか考えるようになります。それでも駄目なら、更に探索を精密にするにはどうすればよいか、失敗するたび考えます。 才能ある優秀な人達は最初から完璧な解を求めるとは思いますが、我々凡人は最初に思い付いたことから拙いことに気が付くたびにこの様に改良して行けば良いです。）、 単純で自信のあるアルゴリズムだけを使って、 定義に忠実に、兎も角、正しいプログラムかどうか自分で確かめられる正三角形や正方形のような簡単な例で正しい答えの出るプログラムを作ってみることです。 自分で手作業で出来ないことは、コンピュータに代わりにやらすことは基本的に出来ません。自分に出来ることを高速にやってもらうことから プログラミングの勉強は始まると私は思います。先ずは自分が良く知っていること・自分が手作業で出来る事 をコンピュータにやらせてみることからプログラミングの学習を始めます。 これは上のような正 P 角形の対称群と言った誰も作っていないだろう特殊なプログラムは、自分で考えるしかないものは、 やらせたいこと（正 P 角形の対称群を置換群に変換する、生成元から部分群を作る、群の部分群や正規部分群を求める）が 自分で手作業で出来なければ作ることが出来ないと言っているだけです。誰かが作っていて公表していれば、それを参考にすれば良いです。 これは「魚の捕り方」の解説で、自分でアルゴリズムを考え、プログラムを組み立てれるようになる方法です。 現在のプログラミングは、流れ図を描く昔のやり方でなく、ブロックの組み合わせなので、 「すべての順列」や「すべての組み合わせ」や「すべての部分集合」を計算する必要あれば、 「車輪を再発見するな」と言う言葉もあるので、自分でアルゴリズムを苦労して考えるのではなく、誰かアルゴリズムやそれを実装したプログラムを 公表していないか探してみれば良いです。「すべての順列」や「すべての組み合わせ」のアルゴリズムは昔、 このような組み合わせ論のアルゴリズムだけを解説した本が出版され、読んで見ましたが、 再帰を使ってないアルゴリズムで高速に実行してくれるアルゴリズムですが、 複雑すぎて私には本を閉じて見ずにアルゴリズムを書いたり、暗記できるようなものではないので、 再帰を使った少なくとも私にとっては理解し易い、何時でも再現可能なものを昔作って、 https://www.cc.kochi-u.ac.jp/~tyamag/jyohou/console3.pdf に「順列」や「組み合わせ」を計算するプログラムを載せているので、 「組み合わせ」を計算するプログラムをコピーして「すべての部分集合」を計算するプログラムを先ず作りました。 「すべての部分集合」を計算するプログラムを直接作ろうとしましたが、上手くいかず、「組み合わせ」を計算するプログラムを使って 「すべての部分集合」を計算するプログラムをまず作りました。私にも見栄もあるので、 「組み合わせ」を計算するプログラムの類比で（真似をして）、 直接「すべての部分集合」を計算するプログラムをでっち上げそれも載せています。再帰のプログラムには決まったパターンがあり、 理解しやすい「タートルグラフィックス」で練習すれば誰でも作れるようになります。多分。 万能のコーチがついていれば別ですが、独学で上手くいくかどうかは、多分、 「LOGO」や「タートルグラフィックス」の本を偶然本屋で手に取り、これは面白い、勉強してみようと思うことなど、 「努力」ではなく「運」です。面白いと思ったことを小さい子供の様にやっているだけか或いは無意識に博打をしています。偶々、上手くいっただけです。 「NUMERICAL RECIPES in C」や「Python コードレシピ集」のような本で、必要なプログラムの部品を探したり、インターネットにも、例えば、上で書いたように https://www.cc.kochi-u.ac.jp/~tyamag/jyohou/console3.pdf にも「順列」や「組み合わせ」を計算するプログラムを載せているので、 使いたいアルゴリズムを実装したプログラムが既に誰かが考えていて本やインターネットに載せているのが運よく見つかれば、 それが信頼できるプログラムかどうか確かめるテスト用のプログラムを作って、自分の欲しいものであれば、 それををコピーして使えば良いですし、新しいアルゴリズムの開発者になりたい訳でなければ、 差し当たってそれでも十分だとも言えます。これは「魚を貰う」事に当たります。 又、例えば、、 よくあるゲームのプログラムを作りたいなら、自分の作りたい種類のゲームのプログラムコードの載っている本やインターネットの記事が沢山あるので、 それを見つけ、そのコードを読み、 真似して自分の欲しいプログラムに改良していけば良いです。そして、プログラミングに自信がついてきたら、段々、 複雑な高速に実行してくれるアルゴリズムにも挑戦してみれば良いです。 更に、プログラミングの特殊性で、技量が上がってくると他人の作ったライブラリーを上手く使って、そのライブラリーのアルゴリズムが理解できなくても、 ライブラリーの使い方が理解できれば、自分の能力以上の事が出来るようになります。多分。 「車の構造を知らなくても、車の運転は出来る」と言う政治家の発言は、その意味では正しいと言えますが、それでは車を作れるようにはならず、 お金を生み出し、それによって沢山の日本人が食べていけるライブラリーを作れる人が日本では生まれず、 そのライブラリーを購入することで短期的には企業は利益を挙げることは出来き、 アメリカと現在の中国のような摩擦を起こすこともないでしょうが、常にアメリカ（や今後は中国）を中心とする外国に主導権を取られ、 文化的・技術的な植民地・属国の地位から抜け出せません。色々な考えで、好きなことをしている人を許容する社会であることが必要です。 目標が高ければ、最初から訓練の仕方が異なると主張する有名人も勿論いますが、独学ならこの様にすれば、誰でもプログラミングが出来るようになります。多分。。 本格的な群論の研究をしたければ、GAP と言う（群論とプログラミングの）プロの作ったソフトがあります。 この様なプログラムを作る事が出来れば、手計算で上のような部分群をすべて求めてみる厄介な作業を代わりにやってくれます。 手作業で確かめるのとプログラミングで確かめるのとどっちが自分にとって良いかは私には分かりません。 勿論、両方できるのが理想的ですが、例えば、正規部群をこの様に定義を元に力ずくで求めるのではなく、 参考書に書いてあるように、この部分群　H の index（指数） が２だから正規部分群だとか conjugate（共役元） が H に含まれない g, h の組を見つけるとか、 頭を使って楽に結論を出すことを学ぶことも重要で、それで上手くいかない時、定義通り力ずくで判定するのが多分普通の考えです。 答えが本に書いてあるので「そうなんだ！」で結論だけ覚えれば十分だと言う意見も勿論あります。 何を目指しているかで答えは異なると思います。 「貧すれば鈍する」で「金、金。金」の世の中になり、政治家を筆頭に、他人を（無知に付け込み、言葉巧みに、合法的に）騙し、 他人から如何に搾取するかに皆必死で余裕のない世の中になってしまったので、 「そんな時間はない」が本音かも分かりませんが。 この様なプログラムが作れるようになる為には、数学の基本知識とアルゴリズムの基本知識と Python の基本知識が必要です。アルゴリズムの基本知識を学ぶための本は Donald E. Knuth著「The Art of Computer Programming」が最も有名だと私は思いますが、この本は本箱に飾って置き、どうしても分からないことが 出て来た時読む本で、私は Niklaus Wirth 著「Algorithms+Data Struvtures = Programs」を読んでプログラミングの基本を学びましたが、 アマチアのプログラマーに必要かつ十分なプログラミングの技術が懇切丁寧に解説されていると私は思いますが、 インターネットの「史上最もおすすめされているプログラミング本 25冊」と言う記事には載っていないので今は手に入れる事が多分不可能です。 この様な記事を参考に読む本を決めれば良いですが、自分にあった本に出会うかどうかは「運」です。 GAP と言う群論専用のフリーソフトもありますが、群論に精通している人が使うもので、群論を学び始めた人には使うのが難しいと思います。 この様なソフトが無かった時代の昭和の人間の考えかも知れませんが、群論を学び始めた時、 GAP のような高級なソフトが何を内部でやっているか分からないうちに使うのではなく、手作業で出来るようになった簡単なことを 例えば、Python のプログラミングで一つ一つやらせてみることを繰り返し、コンピュータが何をやっているか理解できたことに対して、 複雑で、時間が掛かることを GAP のようなプロの作ったソフトを使ってやってもらうと言うのが有効な戦略ではないでしょうか？ 将棋ソフトがプロの実力を超えたからと言って、将棋を学び始めた時、定跡を覚えたり、詰将棋を只管解くと言った作業が不要になる訳では無いと 言うことと同じではないかと思います。数式ソフトで積分の計算が出来るからと言って、最早、基本的な積分の技法を手計算で学ぶ必要は無くなった、 積分を知らなくても、積分は使えるは暴論だと思います。 統計ソフトも同様で、数学や確率・統計を学ばなくても、統計やデータ分析は出来るも甚だ疑問です。

更に、この様なプログラミングに興味があれば、一松信著「正多面体を解く」の第3章正多面体群の解説と大分上で提示しているプログラムを参考にして、 正多面体群を調べて見るプログラムを作ってみれば良いです。更に、平面では鏡映を考えるのに、空間では鏡映から生成される群を解説した参考書が 何故ないだろうと思っていましたが、78ページに「正多面体の対称面」の解説があります。「鏡映」を元に幾何学的に合同変換を解説した参考書も あります。そのような参考書で私は平面の結晶群を最初に学びました。 パソコンを使えば、「空間の鏡映から生成される群」を調べることも簡単ですから興味があればやってみれば良いです。 私の学生時代には出来なかった事が色々出来て面白いですが、 老人の暇つぶしには良い時代になっていますが、即ち、自分でパソコンの力を借りて、 インターネットの有用な情報（例えば、http://web.econ.keio.ac.jp/staff/tose/cours/2016/slin/STlin107Chapter09_20160920a.pdf （所どころミスプリントがありますが、3次元の回転を表す行列が具体的にどんな回転か決定する方法などが丁寧に解説されています）とか https://zenn.dev/mebiusbox/articles/8e765148576919 （opengl を理解するための線形代数が解説されています））も沢山あるので、 足りない・不確かな知識・忘れてしまった事などを補い、 疑問に思ったことを色々確かめてみることが出来ますが、 必要最小限度の知識を仕入れて、最前線の戦場に到達するのが遅くなり、若い人たちには大変な時代になっているのかも知れません。 「カエルを食べてしまえ！」（原著の「EAT THAT FRG!」も高額ではなく、日本で活躍しているタイ人の人もこの本で英語を学んだそうです。）には 「「カエル」とは一番大きく重要なこと　一番重要でやっかいな事からすませなさい！！」と書いています。 すぐ忘れて、横道にそれてしまします。しかも中途半端に終わります。困ったものです。

何が良いかはある意味博打です。アメリカの大統領に気に入られる為に大阪万博の後に作る予定のカジノで運を試して必然的に自己破産しなくても、 皆、意識していないだけで、例えば、だれに投票するかなど日常的に博打をしています。日本の現状を変えたければ、社会的弱者の沢山いる貧乏人は、 スキルを上げもっと稼げるようにすべきは当然ですが、 最近は「道の駅」やインターネットなど生産者が自分で値段を付けることが出来る販売方法・場所も増えてきましたが、 実際はそれだけではなかなか稼げるようにならない既得権益者や富裕層や大企業有利（生産者が値段を付けれず搾取される）の仕組みが色々有り、 それを改善する合法的で直ぐ出来き、効果があるのは、富裕層の意見しか聞かない政治家を投票で入れ替えることだけです。 若者のお前達が一票入れても世の中変わらないと富裕層に騙されていますが、我々団塊の世代が何かする時は必ず制度が代わり、最初は高校受験の時、 高知県は特別で、一つ前までは「全員入学の小学区制」で、進学できる公立高校が一校に決まっていて、佐川の私達は伝統のある高知市内の追手前高校や 小津高校には進学できなかったのですが、私達からは「全員入学」は維持できないから、希望者の多分、8５パーセント進学で、 入学定員の数パーセントは郡部からでも高知市内の公立高校に進学できるようにすると制度が代わりました。最近でも、75歳になると1割負担が2割負担のままに 据え置かれ、更に、良く分からない払い込み請求書が送られてくるようになり、これから毎年、その金額が上がっていくそうです。しかも、これは増税ではないそうです。 年寄りが保守だから投票しても無駄ではなく、 我々団塊の世代が後期高齢者になってきたので、今まで通りには行かなくなってきたので、老人いじめが始まり、 老人も段々追い詰められているので、今まで保守にしか投票しなかったと言う人達も保守から離れていきだしています。 老人が増えたから、消費税を増やさなければいけないと支配者階級は主張しますが、一般財源ですから、そのお金が福祉目的だけに使われているようにはどうしても思えません。 現在の政権を支持している人達の割合も50パーセントの遥か下ですから、現状に不満のある人達がこぞって投票すれば、小選挙区制度の下でも簡単に政権交代が起きます。 インターネットで不満を晴らすだけで、何で投票しないのか理解に苦しみます。「投票しても無駄だ」と支配者階級に完全に洗脳されているのでしょうか？ 経済連会長の「自分たちの利益だけを考え、消費税を大幅に上げろ！法人税を下げろ！」と言う発言が気に入らないと言っても簡単に会長を変えることは我々には出来ませんが、 政治家は我々に入れ替える権利が与えられていますし、幸いなことに、現在はまだ完全な独裁政権ではないので、実際、それが可能です。。 「現状に不満があれば、自分より下だと思う人達を叩け！増えすぎた老人を叩け！」と煽動するのが支配階級の常套手段ですが、騙されてはいけません。 本当の敵は誰かキチンと見極める必要があります。） など私自身が学ぶ為の膨大な時間が必要です。本当に暫くお休みです。

家の近所のパチンコ屋が「かめや」と言う全国チエーンの釣具屋に代わっていました。 年金が出ればパチンコ店に入り浸っていた老人もパチンコをする余裕も無くなったのでしょうか？ インターネットの有識者の解説では最近はパチンコ業界は大変だそうです。何もない辺鄙な場所にカジノを作る諸外国と異なり、大都会の大阪にカジノを 作るために、ギャンブル依存との批判をかわすために、パチンコの規制強化で、貧乏人にとって身近なギャンブルであったパチンコを潰そうと画策しているのでしょうか？ 地元資本の大きな「かつら」という釣具屋が随分前に閉店したのに、「かめや」はその後、有名な釣り人も高知に移住しているし、 高知は「釣り」が有望と見ている訳ですね。 海釣りの道具も無くなり、昔、誘ってくれていた大学の同僚達も随分前に故人になり、海釣りも随分やっていません。車があるので、大してお金を掛けなくても、 高知市内近辺の堤防釣りなら出かけることが出来ますが、なんとなくおっこうです。何も考えずに、釣れなくても、時間をゆったり過ごすのも良いもんではありますが。

涼しくなったので、弥右衛門公園の健康遊具（器具）を使いに行った帰りに、いつもより遅く暗くなって家の近くの公園の側のベンチに座っていると、 頭にヘッドランプを付けた爺さんが数人の叔母さん達を引き連れ、「ブランコが独りでに動いている」、「そんなこともある」とか言いながら、 公園内のゴミ拾いをして、次の場所へ移動していきました。 又、それぞれの公園にボランティア活動の老人がいて、草取りをしたり、季節ごとの草花を植えたりしています。唯、多分、 公園内や近くにトイレや水道の無い公園もあり、主として犬の散歩の人達や時に中学生達が来るだけで、 他の公園の様に小さな子供を遊ばせている人はいないみたいですが、 テーブルやベンチが汚れたままの所が残念ながらあります。「そう思えば、お前がやれ！」ですが、家から結構遠いし、水も無いし、・・・です。

復帰直後の琉球大学に就職した時、田村先生と笠原先生が「この講義を聴けば、こう言う事が出来るようになると最初に学生に提示しなければいけない」と 話していたように記憶しています。私の学生時代は私のような凡人は何も分からず、只管論理を追っていただけでした。 直感は間違えることも多いから、「図を描くことは証明ではない！論理的に証明しなさい！」と言われてきましたが、 我々凡人でも理解できるためには頭の中にイメージを持つことが必要ではないでしょうか？ たまたま見た、グラム・シュミットの直交化法を解説する you tube で若い人がやっていたように、先ず、一次元の場合をやり、2次元の場合をやり、 3次元の場合は2次元の場合の「類比（真似をすれば良い）」であることが分かるように絵を描きながら、そして、「帰納」で一般化し、やっていることのイメージを 持たせてから、論理的な完璧な証明も提示していたように思います。この様に、ポリアさんの教え通りすれば、我々凡人でも理解できると思いますし、記憶に残ります。 群論や位相空間論は定義が3個覚えるだけで簡単なので、私のような凡人でも学ぶのに支障は無かったのですが、 線形代数は定義が遥かに複雑で、しかも一般の n 次元空間で実数係数の線形代数だけでなく複素数係数の線形代数をいきなり習います。 私のような凡人には、「平面の回転は複素数で表現できるがハミルトンが4元数を発見して3次元の回転が表現できるようになったが、 その後、線形代数が出てきて、3次元の回転がずっと容易に理解できるようになった」と歴史的な話もしてくれて、先ずは3次元の線形代数の有用性を http://web.econ.keio.ac.jp/staff/tose/cours/2016/slin/STlin107Chapter09_20160920a.pdf で解説されている様に、 「単位ベクトル f1 を軸とする回転角αの回転の行列 R は、正規直交基底 f1, f2, f3 で右手系になるものをグラム・シュミットの直交化法を使って求め、 回転角αの回転の標準的な行列を正規直交基底 f1, f2, f3 で座標変換すれば欲しい行列 R が求まる」と、又、 「3次元の回転の行列 R がどんな回転かは、(R-I)x = 0 が自明でない解 x を持ち、それが回転の軸になり、後は上と同様の計算をし、最後に逆の事をすれば、 回転角αが求まる」と何をしているか頭の中でビジュアルに描ける様な一つの目標を提示してくれて、先ずは3次元の線形代数を始めてくれていれば、 我々凡人でも意欲的に線形代数に取り組めたのではと思います。 我々凡人でもこの様に、やっていることを整理し、頭の中で何をやっているか映像化できれば・出来て初めて、複雑なアルゴリズムを覚えることが出来ます。 最先端の数学に素早く到達するためには出来るだけ一般化した線形代数を教える必要が あったのかも知れませんが。3次元空間の平面への直射影や鏡映の行列の求め方も解説されています。 更に、行列を使わない鏡映は r∈R3suchthat||r||=2に対して Sr(v)=v−(v,r)r で定義できる事も知られています。 より良く理解するためには、例えば、読みやすいプログラムでは無いですが 

import tkinter as tk
from OpenGL.GL import *
from OpenGL.GLU import *
import numpy as np
from OpenGL import GL
from pyopengltk import OpenGLFrame
import sympy

class F444:
    def __init__(self):
        self.v =[]
        self.e = []
        self.f = []
        self.n_vertex = 8
        self.n_edge = 12
        self.n_face = 6

    def set_inf(self):       
        ## 各辺を構成する頂点の番号
        t_edge = [[0,1], [1,2], [2,3], [3,0], [5,4], [6,5], \
                  [7,6], [4,7], [0,4], [1,5], [2,6], [3,7]]
        ## 各面を構成する頂点の番号：反時計回り
        t_face = [[0,1,2,3], [7,6,5,4], \
                  [4,5,1,0], [5,6,2,1], \
                  [3,2,6,7], [0,3,7,4]]
        self.v =[]
        for i in range(4):
            x = np.cos(i*np.pi/2)/2+np.sin(i*np.pi/2)/2
            y = np.sin(i*np.pi/2)/2-np.cos(i*np.pi/2)/2
            z = 0.5
            self.v.append([x,y,z])
        for i in range(4):
            x = np.cos(i*np.pi/2)/2+np.sin(i*np.pi/2)/2
            y = np.sin(i*np.pi/2)/2-np.cos(i*np.pi/2)/2
            z = -0.5
            self.v.append([x,y,z])
        self.e = t_edge
        self.f = t_face
    def print(self):       
        print('v=', self.v)
        print('e=', self.e)
        print('f=', self.f)
        
cube = F444()
cube.set_inf()
##cube.print()


class Rotate:
    def rotate(self, n, r, theta):
        n = (1/np.sqrt(np.dot(n, n))) * n
        n_dot = np.dot(r, n)
        n_cross = np.cross(n, r)
        w = np.cos(theta)*r+n_dot*(1-np.cos(theta))*n+np.sin(theta)*n_cross
        return w
    def matrix(self, n, theta):
        t_mtx = []
        m1 = self.rotate(n, np.array([1.0, 0.0, 0.0]), theta)
        m2 = self.rotate(n, np.array([0.0, 1.0, 0.0]), theta)
        m3 = self.rotate(n, np.array([0.0, 0.0, 1.0]), theta)
        t_mtx.extend(m1)
        t_mtx.extend(m2)
        t_mtx.extend(m3)
        mtx = np.array(t_mtx, dtype=float).reshape(3, 3) 
        return mtx

## 演習９5改

a = np.array([1, 1, 1])
f1 = (1/np.sqrt(3))*a
print('f1=', f1)

e1 = np.array([1, 0, 0])
print(np.dot(f1, e1))

f2 = e1 - np.dot(f1, e1)*f1
print(f2)
f2= (1/np.sqrt(np.dot(f2, f2)))*f2
print('f2=', f2, np.dot(f1, f2), np.dot(f2, f2))

e2 = np.array([0, 1, 0])
f3 = e2 - np.dot(f1, e2)*f1 - np.dot(f2, e2)*f2
print(f3)
f3= (1/np.sqrt(np.dot(f3, f3)))*f3
print('f3=', f3, np.dot(f1, f3), np.dot(f2, f3), np.dot(f3, f3))

p6 = Rotate()

mtx = p6.matrix(f1, np.pi/6)
print('mtx=', mtx)

S = np.array([[1, 0, 0], [0, np.cos(np.pi/6), -np.sin(np.pi/6)], \
             [0, np.sin(np.pi/6), np.cos(np.pi/6)]])
U = np.transpose(np.array([f1, f2, f3]))
print('U=', U)
det = np.linalg.det(U)
print('det(U)=', det)
R = np.dot(np.dot(U, S), np.transpose(U))
print('R=', R)
RR = np.dot(np.dot(np.transpose(U), mtx), U)
print('RR=', RR)

## 演習9.6

R2 = np.array([[4 , -4, 7], [8, 1, -4], [1, 8, 4]])
R2 = (1/9)*R2
print('R2=', R2)
S = np.dot(np.transpose(R2), R2)
print(S)
S = np.dot(R2, np.transpose(R2))
print(S)
det = np.linalg.det(R2)
print('det(R2)=', det)
I = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]])
left = R2-I
det = np.linalg.det(left)
print('det(left)=', det)

right = np.array([0, 0, 0])
print(np.linalg.solve(left, right))

x = sympy.Symbol('x')
y = sympy.Symbol('y')
z = sympy.Symbol('z')

equation1 = -5*x - 4*y + 7*z
equation2 = 8*x - 8*y - 4*z
equation3 = 1*x + 8*y - 5*z

print(sympy.linsolve([equation1, equation2, equation3], (x, y, z)))

print(np.dot(left, np.array([2, 1, 2])))
f1 = np.array([2, 1, 2])
f1 = (1/np.sqrt(np.dot(f1, f1)))*f1
print('f1=', f1)
e1 = np.array([1, 0, 0])
f2 = e1 - np.dot(e1, f1)*f1
f2 =  (1/np.sqrt(np.dot(f2, f2)))*f2
print('f2=', f2)
e2 = np.array([0, 1, 0])
f3 = e2 - np.dot(e2, f1)*f1 - np.dot(e2, f2)*f2
f3 =  (1/np.sqrt(np.dot(f3, f3)))*f3
print('f3=', f3)
U = np.transpose(np.array([f1, f2, f3]))
print('U=', U)
det = np.linalg.det(U)
print('det(U)=', det)
S = np.dot(np.dot(np.transpose(U), R2), U)
print('S=', S)

f1 = np.array([0, 0, 1])

mtx2 = np.transpose(p6.matrix(f1, np.pi/6))
print('mtx=', mtx2)
x = sympy.Symbol('x')
y = sympy.Symbol('y')
z = sympy.Symbol('z')

equation1 = (sympy.sqrt(3)/2-1)*x - 1/2*y
equation2 = 1/2*x + (sympy.sqrt(3)/2-1)*y
equation3 = 0

print(sympy.linsolve([equation1, equation2, equation3], (x, y, z)))
f2 =  np.array([1, 0, 0])
f3 =  np.array([0, 1, 0])
U = np.transpose(np.array([f1, f2, f3]))
print('U=', U)
det = np.linalg.det(U)
print('det(U)=', det)
S = np.dot(np.dot(np.transpose(U), mtx2), U)
print('S=', S)


rotate = 0

n_problem = 0

class AppOgl(OpenGLFrame):

    def initgl(self):
        global rotate, cube       
        glViewport(0, 0, self.width, self.height) ## 画面の描画領域       
        glClearColor(1.0, 1.0, 1.0, 1.0) ## 背景色
        self.n_model_list = [0]
        self.n_model = self.n_model_list[0]
        self.old_n_model = -1
        rotate = 0
        self.n_move_list = [0]
        self.n_move = self.n_move_list[0]
           
    def torad(self, deg):
        return deg*(math.pi/180.0)

    def redraw(self):
        global rotate, mtx, mtx2
        self.n_model = self.n_model_list[0]
        glClear(GL_COLOR_BUFFER_BIT)
        
        if self.n_model == 0:
            rotate += 0.01
            if self.n_model != self.old_n_model:
                self.old_n_model = self.n_model
            glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
            glLoadIdentity() ## 投影行列を単位行列で初期化する
##            glOrtho(left, right, bottom, top, near, far) ## 平行投影
            glOrtho(-1.0, 1.0, -1.0, 1.0, -1.0, 1.0)
            glMatrixMode(GL_MODELVIEW)
            glLoadIdentity()
            glRotated(rotate, 1.0, 1.0, 1.0)
            for i in range(12):
                edge_list = cube.e[i]
                glColor(0.0, 0.0, 1.0, 1.0)
                glLineWidth(4.0) ## 線の幅
                glBegin(GL_LINES)
                s_vertex = cube.v[edge_list[0]]
                t_vertex = cube.v[edge_list[1]]
                glVertex3f(s_vertex[0], s_vertex[1], s_vertex[2])
                glVertex3f(t_vertex[0], t_vertex[1], t_vertex[2])
                glEnd()
            glPushMatrix()
            glMatrixMode(GL_MODELVIEW)
            glLoadIdentity()
            glRotated(rotate, 1.0, 1.0, 1.0)
            m = []
            M = np.transpose(mtx)
            for k in range(3):
                m.extend(M[k])
                m.append(0.0)
            m.extend(np.array([0.0, 0.0, 0.0, 1.0]))
            glMultMatrixd(m)
            for i in range(12):
                edge_list = cube.e[i]
                glColor(1.0, 0.0, 0.0, 1.0)
                glLineWidth(4.0) ## 線の幅
                glBegin(GL_LINES)
                s_vertex = cube.v[edge_list[0]]
                t_vertex = cube.v[edge_list[1]]
                glVertex3f(s_vertex[0], s_vertex[1], s_vertex[2])
                glVertex3f(t_vertex[0], t_vertex[1], t_vertex[2])
                glEnd()
            glPopMatrix()
            glPushMatrix()
            glMatrixMode(GL_MODELVIEW)
            glLoadIdentity()
            glRotated(rotate, 1.0, 1.0, 1.0)
            m = []
            M = np.transpose(R)
            for k in range(3):
                m.extend(M[k])
                m.append(0.0)
            m.extend(np.array([0.0, 0.0, 0.0, 1.0]))
            glMultMatrixd(m)
            for i in range(12):
                edge_list = cube.e[i]
                glColor(0.0, 0.0, 0.0, 1.0)
                glLineWidth(4.0) ## 線の幅
                glBegin(GL_LINES)
                s_vertex = cube.v[edge_list[0]]
                t_vertex = cube.v[edge_list[1]]
                glVertex3f(s_vertex[0], s_vertex[1], s_vertex[2])
                glVertex3f(t_vertex[0], t_vertex[1], t_vertex[2])
                glEnd()
            glPopMatrix()
        if self.n_model == 1:
            rotate += 0.01
            if self.n_model != self.old_n_model:
                self.old_n_model = self.n_model
        
            glClear(GL_COLOR_BUFFER_BIT)
        
        
            glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
            glLoadIdentity() ## 投影行列を単位行列で初期化する
##          glOrtho(left, right, bottom, top, near, far) ## 平行投影
            glOrtho(-1.0, 1.0, -1.0, 1.0, -1.0, 1.0) ## 平行投影
            
            glMatrixMode(GL_MODELVIEW)
            glLoadIdentity()
            glRotated(rotate, 1.0, 1.0, 1.0)
                
            ## v=[[頂点の座標]]のリスト
            ## e=[[辺を構成する頂点の番号]]のリスト
            ## f=[[面を構成する頂点の番号]]のリスト
            clist = [[1.0, 0.0, 0.0], [0.0, 1.0, 0.0], [0.0, 0.0, 1.0],
                     [1.0, 1.0, 0.0], [1.0, 0.0, 1.0], [0.0, 1.0, 1.0],
                     [0.5, 0.0, 0.0], [0.0, 0.5, 0.0], [0.0, 0.0, 0.5],
                     [0.5, 0.5, 0.0], [0.0, 0.5, 0.5], [0.5, 0.0, 0.5],
                     [0.5, 0.7, 0.0], [0.7, 0.5, 0.0], [0.7, 0.0, 0.5],
                     [0.5, 0.2, 0.3], [0.2, 0.5, 0.3], [0.3, 0.2, 0.5]]
                     
            glClear(GL_DEPTH_BUFFER_BIT)
            glPolygonMode(GL_FRONT_AND_BACK, GL_FILL)
            for i in range(cube.n_edge):
                edge_list = cube.e[i]
                glColor(clist[i][0], clist[i][1], clist[i][2], 1.0)
                glLineWidth(4.0) ## 線の幅
                glBegin(GL_LINES)
                s_vertex = cube.v[edge_list[0]]
                t_vertex = cube.v[edge_list[1]]
                glVertex3f(s_vertex[0], s_vertex[1], s_vertex[2])
                glVertex3f(t_vertex[0], t_vertex[1], t_vertex[2])
                glEnd()
            glPushMatrix()
            glMatrixMode(GL_MODELVIEW)
            glLoadIdentity()
            glRotated(rotate, 1.0, 1.0, 1.0)
            m = []
            M = np.transpose(R2)
            for k in range(3):
                m.extend(M[k])
                m.append(0.0)
            m.extend(np.array([0.0, 0.0, 0.0, 1.0]))
            glMultMatrixd(m)
            for i in range(12):
                edge_list = cube.e[i]
                glColor(0.0, 1.0, 1.0, 1.0)
                glLineWidth(4.0) ## 線の幅
                glBegin(GL_LINES)
                s_vertex = cube.v[edge_list[0]]
                t_vertex = cube.v[edge_list[1]]
                glVertex3f(s_vertex[0], s_vertex[1], s_vertex[2])
                glVertex3f(t_vertex[0], t_vertex[1], t_vertex[2])
                glEnd()
            glPopMatrix()
        if self.n_model == 2:
            rotate += 0.01
            if self.n_model != self.old_n_model:
                self.old_n_model = self.n_model
        
            glClear(GL_DEPTH_BUFFER_BIT)
            glPolygonMode(GL_FRONT, GL_FILL)
            glPolygonMode(GL_BACK, GL_LINE)
            glEnable(GL_DEPTH_TEST)
            glEnable(GL_BLEND)
            glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA)
            
            glClear(GL_COLOR_BUFFER_BIT)
                
            glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
            glLoadIdentity() ## 投影行列を単位行列で初期化する
##          glOrtho(left, right, bottom, top, near, far) ## 平行投影
            glOrtho(-1.0, 1.0, -1.0, 1.0, -1.0, 1.0) ## 平行投影

            glMatrixMode(GL_MODELVIEW)
            glLoadIdentity()
            glRotated(rotate, 1.0, 1.0, 0.0)
            clist = [[1.0, 0.0, 0.0], [0.0, 1.0, 0.0], [0.0, 0.0, 1.0],
                     [1.0, 1.0, 0.0], [1.0, 0.0, 1.0], [0.0, 1.0, 1.0],
                     [0.5, 0.0, 0.0], [0.0, 0.5, 0.0], [0.0, 0.0, 0.5],
                     [0.5, 0.5, 0.0], [0.0, 0.5, 0.5], [0.5, 0.0, 0.5],
                     [0.5, 0.7, 0.0], [0.7, 0.5, 0.0], [0.7, 0.0, 0.5],
                     [0.5, 0.2, 0.3], [0.2, 0.5, 0.3], [0.3, 0.2, 0.5]]
                     
            glClear(GL_DEPTH_BUFFER_BIT)
            glPolygonMode(GL_FRONT_AND_BACK, GL_FILL)
            for i in range(cube.n_edge):
                edge_list = cube.e[i]
                glColor(clist[i][0], clist[i][1], clist[i][2], 1.0)
                glLineWidth(4.0) ## 線の幅
                glBegin(GL_LINES)
                s_vertex = cube.v[edge_list[0]]
                t_vertex = cube.v[edge_list[1]]
                glVertex3f(s_vertex[0], s_vertex[1], s_vertex[2])
                glVertex3f(t_vertex[0], t_vertex[1], t_vertex[2])
                glEnd()
            glPushMatrix()
            glMatrixMode(GL_MODELVIEW)
            glLoadIdentity()
            glScaled(0.5, 0.5, 0.5)
            glRotated(rotate, 1.0, 1.0, 1.0)
            m = []
            M = np.transpose(R2)
            for k in range(3):
                m.extend(M[k])
                m.append(0.0)
            m.extend(np.array([0.0, 0.0, 0.0, 1.0]))
            glMultMatrixd(m)
            for i in range(cube.n_face):
                face_list = cube.f[i]
                glColor(clist[i][0], clist[i][1], \
                        clist[i][2], 0.5)
                glLineWidth(4.0) ## 線の幅
                glBegin(GL_POLYGON)
                for k in range(4):
                    s_vertex = cube.v[face_list[k]]
                    glVertex3f(s_vertex[0], s_vertex[1], s_vertex[2])
                glEnd()
            glPopMatrix()
        if self.n_model == 3:
            rotate += 0.01
            if self.n_model != self.old_n_model:
                self.old_n_model = self.n_model
        
            glClear(GL_DEPTH_BUFFER_BIT)
            glPolygonMode(GL_FRONT, GL_FILL)
            glPolygonMode(GL_BACK, GL_LINE)
            glEnable(GL_DEPTH_TEST)
            glEnable(GL_BLEND)
            glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA)
            
            glClear(GL_COLOR_BUFFER_BIT)
        
        
            glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
            glLoadIdentity() ## 投影行列を単位行列で初期化する
##          glOrtho(left, right, bottom, top, near, far) ## 平行投影
            glOrtho(-1.0, 1.0, -1.0, 1.0, -1.0, 1.0) ## 平行投影

            glMatrixMode(GL_MODELVIEW)
            glLoadIdentity()
            glRotated(rotate, 1.0, 1.0, 1.0)
            clist = [[1.0, 0.0, 0.0], [0.0, 1.0, 0.0], [0.0, 0.0, 1.0],
                     [1.0, 1.0, 0.0], [1.0, 0.0, 1.0], [0.0, 1.0, 1.0],
                     [0.5, 0.0, 0.0], [0.0, 0.5, 0.0], [0.0, 0.0, 0.5],
                     [0.5, 0.5, 0.0], [0.0, 0.5, 0.5], [0.5, 0.0, 0.5],
                     [0.5, 0.7, 0.0], [0.7, 0.5, 0.0], [0.7, 0.0, 0.5],
                     [0.5, 0.2, 0.3], [0.2, 0.5, 0.3], [0.3, 0.2, 0.5]]
                     
            glClear(GL_DEPTH_BUFFER_BIT)
            glPolygonMode(GL_FRONT_AND_BACK, GL_FILL)
            for i in range(cube.n_edge):
                edge_list = cube.e[i]
                glColor(clist[i][0], clist[i][1], clist[i][2], 1.0)
                glLineWidth(4.0) ## 線の幅
                glBegin(GL_LINES)
                s_vertex = cube.v[edge_list[0]]
                t_vertex = cube.v[edge_list[1]]
                glVertex3f(s_vertex[0], s_vertex[1], s_vertex[2])
                glVertex3f(t_vertex[0], t_vertex[1], t_vertex[2])
                glEnd()
            glPushMatrix()
            glMatrixMode(GL_MODELVIEW)
            glLoadIdentity()
            glScaled(0.5, 0.5, 0.5)
            glRotated(rotate, 1.0, 1.0, 01.0)
            m = []
            M = np.transpose(mtx2)
            for k in range(3):
                m.extend(M[k])
                m.append(0.0)
            m.extend(np.array([0.0, 0.0, 0.0, 1.0]))
            glMultMatrixd(m)
            for i in range(cube.n_face):
                face_list = cube.f[i]
                glColor(clist[i][0], clist[i][1], \
                        clist[i][2], 0.5)
                glLineWidth(4.0) ## 線の幅
                glBegin(GL_POLYGON)
                for k in range(4):
                    s_vertex = cube.v[face_list[k]]
                    glVertex3f(s_vertex[0], s_vertex[1], s_vertex[2])
                glEnd()
            glPopMatrix()
        glDisable(GL_DEPTH_TEST)
        glDisable(GL_BLEND)

def next_symmetry():
    global n_problem
    
    n_problem = (n_problem+1) % 4
    if n_problem == 0:
        label['text'] = '演習 9.5 改'
    elif n_problem == 1:
        label['text'] = '演習 9.6 I'
    elif n_problem == 2:
        label['text'] = '演習 9.6 II'
    else:
        label['text'] = '演習 9.6 改'
    app.n_model_list = []
    app.n_model_list.append(int(n_problem))
    app._display()
        

if __name__ == '__main__':
    root = tk.Tk()
    root.title('立方体の表示')
    app = AppOgl(root, width=600, height=600)
    app.pack(fill=tk.BOTH, expand=tk.YES)
    app.animate = 1
    label = tk.Label(text='演習９5改', font = ('MS Gothic', 20),
                     foreground = '#FF00FF', background = 'cyan' )
    label.pack(fill=tk.X)
    button = tk.Button(root, text='Next', command=next_symmetry)
    button.pack(fill=tk.X)
    app.mainloop()
のようなプログラムを作ってみれば良いです。 現在なら、この様なアニメーションをまず最初に学生さん達に見せてから、 この様な事が出来るようになるには、線形代数を学ぶ必要があると提示して、線形代数の講義を始めれば、学生さんのモチベーションも 上がるのではないでしょうか？ 一松信著「正多面体を解く」の「正多面体の対称面」の解説とで、次のプログラムが作れます。

立方体の対称群（9個の鏡映で生成される群）と回転群（正六面体群＝正八面体群で4次の対称群）を調べるプログラムは、例えば、ごちゃごちゃ書いていますが、 

####import time
####import tkinter
##import tkinter as tk
##from OpenGL.GL import *
##from OpenGL.GLU import *
import numpy as np
##from OpenGL import GL
##from pyopengltk import OpenGLFrame
import copy


class Rotate:
    def rotate(self, n, r, theta):
        n = (1/np.sqrt(np.dot(n, n))) * n
        n_dot = np.dot(r, n)
        n_cross = np.cross(n, r)
        w = np.cos(theta)*r+n_dot*(1-np.cos(theta))*n+np.sin(theta)*n_cross
        return w
    def matrix(self, n, theta):
        t_mtx = []
        m1 = self.rotate(n, np.array([1.0, 0.0, 0.0]), theta)
        m2 = self.rotate(n, np.array([0.0, 1.0, 0.0]), theta)
        m3 = self.rotate(n, np.array([0.0, 0.0, 1.0]), theta)
        t_mtx.extend(m1)
        t_mtx.append(0.0)
        t_mtx.extend(m2)
        t_mtx.append(0.0)
        t_mtx.extend(m3)
        t_mtx.append(0.0)
        t_mtx.extend(np.array([0.0, 0.0, 0.0, 1.0]))
        mtx = np.array(t_mtx, dtype=float).reshape(4, 4) 
        return mtx
                   
    
class F444:
    def __init__(self):
        ## v=[[頂点の座標]]のリスト
        self.v =[]
        ## e=[[辺を構成する頂点の番号]]のリスト
        self.e = []
        ## f=[[面を構成する頂点の番号]]のリスト
        self.f = []
        self.n_vertex = 8
        self.n_edge = 12
        self.n_face = 6
        ## v=[[頂点の座標]]のリスト
        self.t_v =[]
        ## e=[[辺を構成する頂点の番号]]のリスト
        self.t_e = []
        self.t_n_vertex = 4
        self.t_n_edge = 6
        ## f=[[面を構成する頂点の番号]]のリスト
        self.t_f = []
        self.t_n_face = 4
        self.p6 = Rotate()
        self.mtx = np.zeros(24*4*4).reshape(24, 4, 4)
        self.diagonal = []
        self.tetra_v = []
        self.v_perm = []
        self.d_perm = []
        self.even_permP = []
        self.group = []
        self.subgroups = []
        self.normal_subgroups = []
        self.ref_mtx = []
        self.ref_v_perm = []
        self.full_group = []
        self.full_subgroups = []
        self.full_normal_subgroups = []

    def set_inf(self):       
        ## 各辺を構成する頂点の番号
        t_edge = [[0,1], [1,2], [2,3], [3,0], [5,4], [6,5], \
                  [7,6], [4,7], [0,4], [1,5], [2,6], [3,7]]
        ## 各面を構成する頂点の番号：反時計回り
        t_face = [[0,1,2,3], [7,6,5,4], \
                  [4,5,1,0], [5,6,2,1], \
                  [3,2,6,7], [0,3,7,4]]
        vertex = []
        for i in range(4):
            x = np.cos(i*np.pi/2)/2+np.sin(i*np.pi/2)/2
            y = np.sin(i*np.pi/2)/2-np.cos(i*np.pi/2)/2
            z = 0.5
            vertex.append(np.array([x,y,z]))
        for i in range(4):
            x = np.cos(i*np.pi/2)/2+np.sin(i*np.pi/2)/2
            y = np.sin(i*np.pi/2)/2-np.cos(i*np.pi/2)/2
            z = -0.5
            vertex.append(np.array([x,y,z]))
        for i in range(self.n_vertex):
            self.v.append(vertex[i])
        self.e = t_edge
        self.f = t_face
        self.t_v =[self.v[0], self.v[2], self.v[5], self.v[7]]
        t_edge = [[0,1], [0,2], [0,3], [1,2], [1,3], [2,3]]
        self.t_e = t_edge
        ## 各面を構成する頂点の番号：反時計回り
        t_face = [[0,2,1], [0,3,2], [0,1,3], [1,2,3]]
        self.t_f = t_face
        self.symm = self.symmetry()
        self.diagonal = [[0,6],[1,7],[2,4],[3,5]]
        self.tetra_v = [0, 2, 5, 7]

        for k in range(24):
            self.mtx[k] = self.p6.matrix(self.symm[k][0], self.symm[k][1])
            t_list = self.cube_vertex_move(self.symm[k][0], self.symm[k][1])
            self.v_perm.append(self.get_v_permutation(t_list))
            self.d_perm.append(self.get_d_permutation(t_list))
            self.even_permP.append(self.even_permutationP(self.d_perm[k]))
        self.group = self.get_group()
        self.subgroups = self.get_subgroup()
        self.normal_subgroups = self.get_normal_subgroup()
        self.table = self.get_table()
        self.ref_mtx  = self.full_symmetry()
        for k in range(9):
            t_list = self.full_cube_vertex_move(self.ref_mtx[k])
            self.ref_v_perm.append(self.get_v_permutation(t_list))
        self.full_group = self.ref_generate_subgroup(self.ref_v_perm)
        self.full_subgroups = self.get_full_subgroup()
        self.full_normal_subgroups = self.get_full_normal_subgroup()
        
    def get_group(self):
        return self.d_perm
    
    def perm_product(self, g, h):
##        print('g=', g, ' h=', h)
        p = []
        for i in range(len(g)):
            p.append(g[h[i]])
        return p

    def get_index(self, g):
        for k in range(24):
            if g == self.v_perm[k]:
                return k
            
    def get_table(self):
        self.table = []
        for k in range(24):
            t = []
            for i in range(24):
                g = self.perm_product(self.v_perm[k], self.v_perm[i])
                t.append(self.get_index(g))
            self.table.append(t)
        return self.table

    def print(self):       
        print('v=', self.v)
        print('e=', self.e)
        print('f=', self.f)

    def symmetry(self):
        symm_list = []
        for i in range(4):
            symm_list.append([np.array([0.0, 0.0, 1.0]), i*np.pi/2])
        for i in range(1, 4):
            symm_list.append([np.array([0.0, 1.0, 0.0]), i*np.pi/2])
        for i in range(1, 4):
            symm_list.append([np.array([1.0, 0.0, 0.0]), i*np.pi/2])
        pair = [[0,6],[1,7],[2,4],[3,5],[8,10],[9,11]]
        for k in range(4):
            source = self.v[pair[k][0]]
            target = self.v[pair[k][1]]
            for i in range(1, 3):
                symm_list.append([source-target, i*2*np.pi/3])
        for k in range(6):
            source = (self.v[self.e[pair[k][0]][0]]+self.v[self.e[pair[k][0]][1]])
            target = (self.v[self.e[pair[k][1]][0]]+self.v[self.e[pair[k][1]][1]])
            source = 0.5*source
            target = 0.5*target
            symm_list.append([source-target, np.pi])
        return symm_list
    
    def full_symmetry(self):
        symm_list = []
        ref_lists = [[1, 0, 0], [0, 1, 0], [0, 0, 1],
                     [1, 1, 0], [1, 0, 1], [0, 1, 1],
                     [-1, 1, 0], [-1, 0, 1], [0, -1, 1]]
        I = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]])
        for k in range(len(ref_lists)):
            p1 = np.array(ref_lists[k])
            p1 = (1/np.sqrt(np.dot(p1, p1)))*p1
            Q = np.array([[p1[0]*p1[0], p1[0]*p1[1], p1[0]*p1[2]], \
                  [p1[1]*p1[0], p1[1]*p1[1], p1[1]*p1[2]], \
                  [p1[2]*p1[0], p1[2]*p1[1], p1[2]*p1[2]]])
            S = I - 2*Q
            symm_list.append(S)
        return symm_list            
       
   
    def cube_vertex_move(self, n, theta):
        target_v_list = []
        for k in range(8):
            target_v_list.append([self.p6.rotate(n, self.v[k], theta)])
        return target_v_list
    def full_cube_vertex_move(self, mtx):
        target_v_list = []
        for k in range(8):
            target_v_list.append([np.dot(mtx, self.v[k])])
        return target_v_list
    
    def get_v_num(self, coordinate):
        for k in range(8):
            flag = True
            for i in range(3):
                if np.abs(self.v[k][i]-coordinate[0][i]) > 0.01:
                    flag = False
                    break
            if flag == True:
                return k
            
    def get_v_permutation(self, target_list):
        perm_list = []
        for i in range(8):
            perm_list.append(self.get_v_num(target_list[i]))
        return perm_list
    def get_full_v_permutation(self, target_list):
        perm_list = []
        for i in range(8):
            perm_list.append(self.get_v_num(target_list[i]))
        return perm_list
    
    def get_d_num(self, target):
        for k in range(4):
            if self.diagonal[k][0] == target[0] and self.diagonal[k][1] == target[1]:
                return k
            if self.diagonal[k][0] == target[1] and self.diagonal[k][1] == target[0]:
                return k
        return -1
                    
    def get_d_permutation(self, target_list):
        v_perm_list = self.get_v_permutation(target_list)
        perm_list = []
        for k in range(4):
            source = self.diagonal[k]
            target = [v_perm_list[source[0]], v_perm_list[source[1]]]
            perm_list.append(self.get_d_num(target))
        return perm_list
            
    def even_permutationP(self, d_permutaton):
        p = 1
        for i in range(4):
            for k in range(i+1, 4):
                p = p*(d_permutaton[i]-d_permutaton[k])
        if p > 0:
            return True
        else:
            return False
        
    def get_tetra_v_permutation(self, target_list):
        v_perm_list = self.get_v_permutation(target_list)
        target = []
        for k in range(4):
            target.append(v_perm_list[self.tetra_v[k]])
        perm_list = []
        for k in range(4):
            if target[k] in self.tetra_v:                
                perm_list.append(self.tetra_v.index(target[k]))
            else:
               return []
        return perm_list

    def sub_get_combination(self, r, l, s, k):
        if len(s) == k:
            r.append(s)
            return
        new_l = l[:]
        for e in l:
            old_s = s[:]
            s.append(e)
            new_l.remove(e)
            self.sub_get_combination(r, new_l, s, k)
            s = old_s
            
    def get_combination(self, n, k):
        l = [i for i in range(n)]
        r = []
        self.sub_get_combination(r, l, [], k)
        return r
                      
    def get_subset(self, n, m):
        result = [[]]
        for k in range(1, m+1):
            result.extend(self.get_combination(n, k))
        return result

        
    def sub_get_all_subset(self, r, l, s):
        if len(l) == 0:
            return
        new_l = copy.deepcopy(l)
        for e in l:
            new_s = copy.deepcopy(s)
            new_s.append(e)
            r.append(new_s)
            new_l.remove(e)
            self.sub_get_all_subset(r, new_l, new_s)
            
    def get_all_subset(self, n):
        l = [i for i in range(n)]
        r = [[]]
        self.sub_get_all_subset(r, l, [])
        return r
    
    def show_all_subset(self, n):
        S = self.get_all_subset(n)
        for s in S:
            print(s)
        print()
        
    def lessP(self, g1, g2):
        for e1, e2 in zip(g1, g2):
            if e1 < e2:
                return -1
            elif e1 > e2:
                return 1
        return 0
    
    def arrange(self, G):
        for i in range(1, len(G)):
            x = copy.copy(G[i])
            j = i-1
            while self.lessP(x, G[j]) == -1:
                G[j+1] = copy.copy(G[j])
                j = j-1
            G[j+1] = copy.copy(x)
        return G  
        
        
    def convert_permutation(self, i):
        return self.d_perm[i]
        
    def generate_subgroup(self, generator):
        flag = True
        G = [self.convert_permutation(0)]
        NG = copy.deepcopy(G)
        while flag == True:
            flag = False
            for f in generator:
                g = self.convert_permutation(f)
                for h in G:
                    k = self.perm_product(g, h)
                    if k not in NG:
                        flag = True
                        NG.append(k)
            G = copy.deepcopy(NG)
        return G

    def ref_generate_subgroup(self, generator):
        flag = True
        G = [[0, 1, 2, 3, 4, 5, 6, 7]]
        NG = copy.deepcopy(G)
        while flag == True:
            flag = False
            for g in generator:
                for h in G:
                    k = self.perm_product(g, h)
                    if k not in NG:
                        flag = True
                        NG.append(k)
            G = copy.deepcopy(NG)
        return G

    def get_subgroup(self):
        SG = []
##        cand = self.get_all_subset(24)
        cand = self.get_subset(24, 3)
        for gen in cand:
          G = self.generate_subgroup(gen)
          NG = self.arrange(G)
          if NG not in SG:
              SG.append(NG)
        return SG
    def show_subgroups(self):
        for G in self.subgroups:
            print(G)
        print()

    def perm_in_ref_perm(self, n):
        return self.ref_v_perm[n]


    
    def get_full_subgroup(self):
        SG = []
##        cand = self.get_all_subset(24)
        cand = self.get_all_subset(9)
        for c in cand:
            gen = []
            for n in c:
                gen.append(self.perm_in_ref_perm(n))           
            G = self.ref_generate_subgroup(gen)
            NG = self.arrange(G)
            if NG not in SG:
                SG.append(NG)
        return SG
    def show_full_subgroups(self):
        for G in self.full_subgroups:
            print(G)
        print()

    def permutation2index(self, perm):
        for i in range(24):
            if perm == self.d_perm[i]:
                return i
    def index_rep_of_subgroup(self, SG):
        IG = []
        for g in SG:
            IG.append(self.permutation2index(g))
        return IG
    
    def index_rep_of_all_subgroup(self):
        G = []
        for g in self.subgroups:
            G.append(self.index_rep_of_subgroup(g))
        return G

    def full_permutation2index(self, perm):
        for i in range(48):
            if perm == self.full_group[i]:
                return i
    def index_rep_of_full_subgroup(self, SG):
        IG = []
        for g in SG:
            IG.append(self.full_permutation2index(g))
        return IG
    
    def index_rep_of_all_full_subgroup(self):
        G = []
        for g in self.full_subgroups:
            G.append(self.index_rep_of_full_subgroup(g))
        return G
    
    def inverse(self, g):
        inv = []
        for i in range(len(g)):
            inv.append(g.index(i))
        return inv

    def get_normal_subgroup(self):
        G = self.group
        NG = []
        for SG in self.subgroups:
            flag = True
            for g in G:
                for h in SG:
                    x = self.perm_product(g, h)
                    y = self.inverse(g)
                    z = self.perm_product(x, y)
                    if z not in SG:
                        flag = False
                        break
            if flag:
                NG.append(SG)
        return NG
    
    def show_normal_subgroup(self):
        NG = self.get_normal_subgroup()
        for G in NG:
            print(G)
        print()
    def get_full_normal_subgroup(self):
        G = self.full_group
        NG = []
        for SG in self.full_subgroups:
            flag = True
            for g in G:
                for h in SG:
                    x = self.perm_product(g, h)
                    y = self.inverse(g)
                    z = self.perm_product(x, y)
                    if z not in SG:
                        flag = False
                        break
            if flag:
                NG.append(SG)
        return NG
    
    def show_full_normal_subgroup(self):
        NG = self.full_normal_subgroups
        for G in NG:
            print(G)
        print()
    
     
    def index_rep_of_all_normal_subgroup(self):
        G = []
        for g in self.normal_subgroups:
            G.append(self.index_rep_of_subgroup(g))
        return G
     
    def index_rep_of_all_full_normal_subgroup(self):
        G = []
        for g in self.full_normal_subgroups:
            G.append(self.index_rep_of_full_subgroup(g))
        return G

    
        
    def test(self):
        for k in range(24):            
            t_list = self.cube_vertex_move(self.symm[k][0], self.symm[k][1])
            v_perm = self.get_v_permutation(t_list)
            print('v_perm=', self.v_perm[k])
            d_perm = self.get_d_permutation(t_list)
            print('d_perm=', self.d_perm[k])
            print('even_permutationP:', self.even_permP[k])
            t_v_perm = self.get_tetra_v_permutation(t_list)
            print('t_v_perm=', t_v_perm)

    def test2(self):
        sym = self.symmetry()
        print(sym)


cube = F444()
cube.set_inf()
cube.print()
cube.test()

p6 = Rotate()
cube.test2()
for k in range(24):
 print(cube.mtx[k])
for k in range(24):
    print(cube.table[k])
print('group')
print(cube.group)
print('subsets')
cube.show_all_subset(4)
print('subgroups')
cube.show_subgroups()
sg = cube.index_rep_of_all_subgroup()
for i in range(len(sg)):
    print(sg[i])
print('normal subgroups')    
cube.show_normal_subgroup()
print('normal subgroups')    
nsg = cube.index_rep_of_all_normal_subgroup()
for i in range(len(nsg)):
    print(nsg[i])
print()
print('full symmetry ofcube')
print(cube.full_symmetry())
print(cube.ref_v_perm)
print(len(cube.full_group))
print(len(cube.full_subgroups))
print(len(cube.full_normal_subgroups))
cube.show_full_normal_subgroup()
print('correspondence index to permutation')
for k in range(48):
    if k < 10:
        print(' ', k, ' : ', cube.full_group[k])
    else:    
        print('', k, ' : ', cube.full_group[k])
print('full subgroups')
sg = cube.index_rep_of_all_full_subgroup()
for i in range(len(sg)):
    print(sg[i])
print('full normal subgroups')    
nsg = cube.index_rep_of_all_full_normal_subgroup()
for i in range(len(nsg)):
    print(nsg[i])
で、実行結果は 

v= [array([ 0.5, -0.5,  0.5]), array([0.5, 0.5, 0.5]), array([-0.5,  0.5,  0.5]), 
array([-0.5, -0.5,  0.5]), array([ 0.5, -0.5, -0.5]), array([ 0.5,  0.5, -0.5]), 
array([-0.5,  0.5, -0.5]), array([-0.5, -0.5, -0.5])]
e= [[0, 1], [1, 2], [2, 3], [3, 0], [5, 4], [6, 5], [7, 6], [4, 7], [0, 4], [1, 5], [2, 6], [3, 7]]
f= [[0, 1, 2, 3], [7, 6, 5, 4], [4, 5, 1, 0], [5, 6, 2, 1], [3, 2, 6, 7], [0, 3, 7, 4]]
v_perm= [0, 1, 2, 3, 4, 5, 6, 7]
d_perm= [0, 1, 2, 3]
even_permutationP: True
t_v_perm= [0, 1, 2, 3]
v_perm= [1, 2, 3, 0, 5, 6, 7, 4]
d_perm= [1, 2, 3, 0]
even_permutationP: False
t_v_perm= []
v_perm= [2, 3, 0, 1, 6, 7, 4, 5]
d_perm= [2, 3, 0, 1]
even_permutationP: True
t_v_perm= [1, 0, 3, 2]
v_perm= [3, 0, 1, 2, 7, 4, 5, 6]
d_perm= [3, 0, 1, 2]
even_permutationP: False
t_v_perm= []
v_perm= [4, 5, 1, 0, 7, 6, 2, 3]
d_perm= [2, 3, 1, 0]
even_permutationP: False
t_v_perm= []
v_perm= [7, 6, 5, 4, 3, 2, 1, 0]
d_perm= [1, 0, 3, 2]
even_permutationP: True
t_v_perm= [3, 2, 1, 0]
v_perm= [3, 2, 6, 7, 0, 1, 5, 4]
d_perm= [3, 2, 0, 1]
even_permutationP: False
t_v_perm= []
v_perm= [4, 0, 3, 7, 5, 1, 2, 6]
d_perm= [2, 0, 3, 1]
even_permutationP: False
t_v_perm= []
v_perm= [5, 4, 7, 6, 1, 0, 3, 2]
d_perm= [3, 2, 1, 0]
even_permutationP: True
t_v_perm= [2, 3, 0, 1]
v_perm= [1, 5, 6, 2, 0, 4, 7, 3]
d_perm= [1, 3, 0, 2]
even_permutationP: False
t_v_perm= []
v_perm= [0, 3, 7, 4, 1, 2, 6, 5]
d_perm= [0, 3, 1, 2]
even_permutationP: True
t_v_perm= [0, 3, 1, 2]
v_perm= [0, 4, 5, 1, 3, 7, 6, 2]
d_perm= [0, 2, 3, 1]
even_permutationP: True
t_v_perm= [0, 2, 3, 1]
v_perm= [5, 1, 0, 4, 6, 2, 3, 7]
d_perm= [3, 1, 0, 2]
even_permutationP: True
t_v_perm= [2, 0, 1, 3]
v_perm= [2, 1, 5, 6, 3, 0, 4, 7]
d_perm= [2, 1, 3, 0]
even_permutationP: True
t_v_perm= [1, 2, 0, 3]
v_perm= [5, 6, 2, 1, 4, 7, 3, 0]
d_perm= [3, 0, 2, 1]
even_permutationP: True
t_v_perm= [2, 1, 3, 0]
v_perm= [7, 3, 2, 6, 4, 0, 1, 5]
d_perm= [1, 3, 2, 0]
even_permutationP: True
t_v_perm= [3, 1, 0, 2]
v_perm= [2, 6, 7, 3, 1, 5, 4, 0]
d_perm= [2, 0, 1, 3]
even_permutationP: True
t_v_perm= [1, 3, 2, 0]
v_perm= [7, 4, 0, 3, 6, 5, 1, 2]
d_perm= [1, 2, 0, 3]
even_permutationP: True
t_v_perm= [3, 0, 2, 1]
v_perm= [1, 0, 4, 5, 2, 3, 7, 6]
d_perm= [1, 0, 2, 3]
even_permutationP: False
t_v_perm= []
v_perm= [6, 2, 1, 5, 7, 3, 0, 4]
d_perm= [0, 2, 1, 3]
even_permutationP: False
t_v_perm= []
v_perm= [6, 7, 3, 2, 5, 4, 0, 1]
d_perm= [0, 1, 3, 2]
even_permutationP: False
t_v_perm= []
v_perm= [3, 7, 4, 0, 2, 6, 5, 1]
d_perm= [3, 1, 2, 0]
even_permutationP: False
t_v_perm= []
v_perm= [4, 7, 6, 5, 0, 3, 2, 1]
d_perm= [2, 1, 0, 3]
even_permutationP: False
t_v_perm= []
v_perm= [6, 5, 4, 7, 2, 1, 0, 3]
d_perm= [0, 3, 2, 1]
even_permutationP: False
t_v_perm= []
[[array([0., 0., 1.]), 0.0], [array([0., 0., 1.]), 1.5707963267948966], 
[array([0., 0., 1.]), 3.141592653589793], [array([0., 0., 1.]), 4.71238898038469], 
[array([0., 1., 0.]), 1.5707963267948966], [array([0., 1., 0.]), 3.141592653589793], 
[array([0., 1., 0.]), 4.71238898038469], [array([1., 0., 0.]), 1.5707963267948966], 
[array([1., 0., 0.]), 3.141592653589793], [array([1., 0., 0.]), 4.71238898038469], 
[array([ 1., -1.,  1.]), 2.0943951023931953], [array([ 1., -1.,  1.]), 4.1887902047863905], 
[array([1., 1., 1.]), 2.0943951023931953], [array([1., 1., 1.]), 4.1887902047863905], 
[array([-1.,  1.,  1.]), 2.0943951023931953], [array([-1.,  1.,  1.]), 4.1887902047863905], 
[array([-1., -1.,  1.]), 2.0943951023931953], [array([-1., -1.,  1.]), 4.1887902047863905], 
[array([ 1.00000000e+00, -1.38777878e-16,  1.00000000e+00]), 3.141592653589793], 
[array([8.32667268e-17, 1.00000000e+00, 1.00000000e+00]), 3.141592653589793], 
[array([-1.00000000e+00,  1.38777878e-16,  1.00000000e+00]), 3.141592653589793], 
[array([-8.32667268e-17, -1.00000000e+00,  1.00000000e+00]), 3.141592653589793], 
[array([ 1., -1.,  0.]), 3.141592653589793], [array([1., 1., 0.]), 3.141592653589793]]
[[1. 0. 0. 0.]
 [0. 1. 0. 0.]
 [0. 0. 1. 0.]
 [0. 0. 0. 1.]]
[[ 6.123234e-17  1.000000e+00  0.000000e+00  0.000000e+00]
 [-1.000000e+00  6.123234e-17  0.000000e+00  0.000000e+00]
 [ 0.000000e+00  0.000000e+00  1.000000e+00  0.000000e+00]
 [ 0.000000e+00  0.000000e+00  0.000000e+00  1.000000e+00]]
[[-1.0000000e+00  1.2246468e-16  0.0000000e+00  0.0000000e+00]
 [-1.2246468e-16 -1.0000000e+00  0.0000000e+00  0.0000000e+00]
 [ 0.0000000e+00  0.0000000e+00  1.0000000e+00  0.0000000e+00]
 [ 0.0000000e+00  0.0000000e+00  0.0000000e+00  1.0000000e+00]]
[[-1.8369702e-16 -1.0000000e+00  0.0000000e+00  0.0000000e+00]
 [ 1.0000000e+00 -1.8369702e-16  0.0000000e+00  0.0000000e+00]
 [ 0.0000000e+00  0.0000000e+00  1.0000000e+00  0.0000000e+00]
 [ 0.0000000e+00  0.0000000e+00  0.0000000e+00  1.0000000e+00]]
[[ 6.123234e-17  0.000000e+00 -1.000000e+00  0.000000e+00]
 [ 0.000000e+00  1.000000e+00  0.000000e+00  0.000000e+00]
 [ 1.000000e+00  0.000000e+00  6.123234e-17  0.000000e+00]
 [ 0.000000e+00  0.000000e+00  0.000000e+00  1.000000e+00]]
[[-1.0000000e+00  0.0000000e+00 -1.2246468e-16  0.0000000e+00]
 [ 0.0000000e+00  1.0000000e+00  0.0000000e+00  0.0000000e+00]
 [ 1.2246468e-16  0.0000000e+00 -1.0000000e+00  0.0000000e+00]
 [ 0.0000000e+00  0.0000000e+00  0.0000000e+00  1.0000000e+00]]
[[-1.8369702e-16  0.0000000e+00  1.0000000e+00  0.0000000e+00]
 [ 0.0000000e+00  1.0000000e+00  0.0000000e+00  0.0000000e+00]
 [-1.0000000e+00  0.0000000e+00 -1.8369702e-16  0.0000000e+00]
 [ 0.0000000e+00  0.0000000e+00  0.0000000e+00  1.0000000e+00]]
[[ 1.000000e+00  0.000000e+00  0.000000e+00  0.000000e+00]
 [ 0.000000e+00  6.123234e-17  1.000000e+00  0.000000e+00]
 [ 0.000000e+00 -1.000000e+00  6.123234e-17  0.000000e+00]
 [ 0.000000e+00  0.000000e+00  0.000000e+00  1.000000e+00]]
[[ 1.0000000e+00  0.0000000e+00  0.0000000e+00  0.0000000e+00]
 [ 0.0000000e+00 -1.0000000e+00  1.2246468e-16  0.0000000e+00]
 [ 0.0000000e+00 -1.2246468e-16 -1.0000000e+00  0.0000000e+00]
 [ 0.0000000e+00  0.0000000e+00  0.0000000e+00  1.0000000e+00]]
[[ 1.0000000e+00  0.0000000e+00  0.0000000e+00  0.0000000e+00]
 [ 0.0000000e+00 -1.8369702e-16 -1.0000000e+00  0.0000000e+00]
 [ 0.0000000e+00  1.0000000e+00 -1.8369702e-16  0.0000000e+00]
 [ 0.0000000e+00  0.0000000e+00  0.0000000e+00  1.0000000e+00]]
[[ 2.22044605e-16  1.11022302e-16  1.00000000e+00  0.00000000e+00]
 [-1.00000000e+00  2.22044605e-16  1.11022302e-16  0.00000000e+00]
 [-1.11022302e-16 -1.00000000e+00  2.22044605e-16  0.00000000e+00]
 [ 0.00000000e+00  0.00000000e+00  0.00000000e+00  1.00000000e+00]]
[[-1.11022302e-16 -1.00000000e+00  3.33066907e-16  0.00000000e+00]
 [-3.33066907e-16 -1.11022302e-16 -1.00000000e+00  0.00000000e+00]
 [ 1.00000000e+00 -3.33066907e-16 -1.11022302e-16  0.00000000e+00]
 [ 0.00000000e+00  0.00000000e+00  0.00000000e+00  1.00000000e+00]]
[[ 2.22044605e-16  1.00000000e+00  0.00000000e+00  0.00000000e+00]
 [-1.11022302e-16  1.11022302e-16  1.00000000e+00  0.00000000e+00]
 [ 1.00000000e+00 -1.66533454e-16  2.22044605e-16  0.00000000e+00]
 [ 0.00000000e+00  0.00000000e+00  0.00000000e+00  1.00000000e+00]]
[[-1.11022302e-16  2.22044605e-16  1.00000000e+00  0.00000000e+00]
 [ 1.00000000e+00 -3.33066907e-16  1.11022302e-16  0.00000000e+00]
 [ 4.44089210e-16  1.00000000e+00 -1.11022302e-16  0.00000000e+00]
 [ 0.00000000e+00  0.00000000e+00  0.00000000e+00  1.00000000e+00]]
[[ 2.22044605e-16  1.11022302e-16 -1.00000000e+00  0.00000000e+00]
 [-1.00000000e+00  2.22044605e-16 -1.11022302e-16  0.00000000e+00]
 [ 1.11022302e-16  1.00000000e+00  2.22044605e-16  0.00000000e+00]
 [ 0.00000000e+00  0.00000000e+00  0.00000000e+00  1.00000000e+00]]
[[-1.11022302e-16 -1.00000000e+00 -3.33066907e-16  0.00000000e+00]
 [-3.33066907e-16 -1.11022302e-16  1.00000000e+00  0.00000000e+00]
 [-1.00000000e+00  3.33066907e-16 -1.11022302e-16  0.00000000e+00]
 [ 0.00000000e+00  0.00000000e+00  0.00000000e+00  1.00000000e+00]]
[[ 2.22044605e-16  1.00000000e+00  0.00000000e+00  0.00000000e+00]
 [-1.11022302e-16  1.11022302e-16 -1.00000000e+00  0.00000000e+00]
 [-1.00000000e+00  1.66533454e-16  2.22044605e-16  0.00000000e+00]
 [ 0.00000000e+00  0.00000000e+00  0.00000000e+00  1.00000000e+00]]
[[-1.11022302e-16  2.22044605e-16 -1.00000000e+00  0.00000000e+00]
 [ 1.00000000e+00 -3.33066907e-16 -1.11022302e-16  0.00000000e+00]
 [-4.44089210e-16 -1.00000000e+00 -1.11022302e-16  0.00000000e+00]
 [ 0.00000000e+00  0.00000000e+00  0.00000000e+00  1.00000000e+00]]
[[-2.22044605e-16 -5.21822725e-17  1.00000000e+00  0.00000000e+00]
 [-2.25373484e-16 -1.00000000e+00 -5.21822725e-17  0.00000000e+00]
 [ 1.00000000e+00 -2.25373484e-16 -2.22044605e-16  0.00000000e+00]
 [ 0.00000000e+00  0.00000000e+00  0.00000000e+00  1.00000000e+00]]
[[-1.00000000e+00  1.69862332e-16 -3.32887878e-18  0.00000000e+00]
 [-3.32887878e-18 -2.22044605e-16  1.00000000e+00  0.00000000e+00]
 [ 1.69862332e-16  1.00000000e+00 -2.22044605e-16  0.00000000e+00]
 [ 0.00000000e+00  0.00000000e+00  0.00000000e+00  1.00000000e+00]]
[[-2.22044605e-16 -5.21822725e-17 -1.00000000e+00  0.00000000e+00]
 [-2.25373484e-16 -1.00000000e+00  5.21822725e-17  0.00000000e+00]
 [-1.00000000e+00  2.25373484e-16 -2.22044605e-16  0.00000000e+00]
 [ 0.00000000e+00  0.00000000e+00  0.00000000e+00  1.00000000e+00]]
[[-1.00000000e+00  1.69862332e-16  3.32887878e-18  0.00000000e+00]
 [-3.32887878e-18 -2.22044605e-16 -1.00000000e+00  0.00000000e+00]
 [-1.69862332e-16 -1.00000000e+00 -2.22044605e-16  0.00000000e+00]
 [ 0.00000000e+00  0.00000000e+00  0.00000000e+00  1.00000000e+00]]
[[-2.22044605e-16 -1.00000000e+00  8.65956056e-17  0.00000000e+00]
 [-1.00000000e+00 -2.22044605e-16  8.65956056e-17  0.00000000e+00]
 [-8.65956056e-17 -8.65956056e-17 -1.00000000e+00  0.00000000e+00]
 [ 0.00000000e+00  0.00000000e+00  0.00000000e+00  1.00000000e+00]]
[[ 2.22044605e-16  1.00000000e+00 -8.65956056e-17  0.00000000e+00]
 [ 1.00000000e+00 -2.22044605e-16  8.65956056e-17  0.00000000e+00]
 [ 8.65956056e-17 -8.65956056e-17 -1.00000000e+00  0.00000000e+00]
 [ 0.00000000e+00  0.00000000e+00  0.00000000e+00  1.00000000e+00]]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23]
[1, 2, 3, 0, 14, 22, 10, 12, 23, 16, 18, 9, 19, 6, 20, 7, 21, 4, 13, 15, 17, 11, 8, 5]
[2, 3, 0, 1, 20, 8, 18, 19, 5, 21, 13, 16, 15, 10, 17, 12, 11, 14, 6, 7, 4, 9, 23, 22]
[3, 0, 1, 2, 17, 23, 13, 15, 22, 11, 6, 21, 7, 18, 4, 19, 9, 20, 10, 12, 14, 16, 5, 8]
[4, 12, 18, 11, 5, 6, 0, 17, 20, 14, 7, 22, 23, 9, 19, 3, 1, 21, 8, 13, 2, 10, 15, 16]
[5, 23, 8, 22, 6, 0, 4, 21, 2, 19, 17, 15, 16, 14, 13, 11, 12, 10, 20, 9, 18, 7, 3, 1]
[6, 16, 20, 15, 0, 4, 5, 10, 18, 13, 21, 3, 1, 19, 9, 22, 23, 7, 2, 14, 8, 17, 11, 12]
[7, 10, 21, 17, 12, 19, 15, 8, 9, 0, 22, 4, 18, 3, 1, 20, 6, 23, 11, 2, 16, 5, 14, 13]
[8, 22, 5, 23, 18, 2, 20, 9, 0, 7, 14, 12, 11, 17, 10, 16, 15, 13, 4, 21, 6, 19, 1, 3]
[9, 14, 19, 13, 11, 21, 16, 0, 7, 8, 1, 18, 4, 23, 22, 6, 20, 3, 12, 5, 15, 2, 10, 17]
[10, 21, 17, 7, 1, 14, 22, 18, 13, 6, 11, 0, 2, 15, 16, 8, 5, 12, 3, 20, 23, 4, 9, 19]
[11, 4, 12, 18, 21, 16, 9, 3, 15, 22, 0, 10, 17, 8, 5, 13, 14, 2, 7, 23, 19, 1, 6, 20]
[12, 18, 11, 4, 19, 15, 7, 23, 16, 1, 8, 14, 13, 0, 2, 17, 10, 5, 9, 3, 21, 22, 20, 6]
[13, 9, 14, 19, 3, 17, 23, 6, 10, 18, 16, 2, 0, 12, 11, 5, 8, 15, 1, 4, 22, 20, 21, 7]
[14, 19, 13, 9, 22, 10, 1, 4, 17, 20, 12, 8, 5, 16, 15, 0, 2, 11, 23, 6, 3, 18, 7, 21]
[15, 6, 16, 20, 7, 12, 19, 22, 11, 3, 5, 17, 10, 2, 0, 14, 13, 8, 21, 1, 9, 23, 4, 18]
[16, 20, 15, 6, 9, 11, 21, 1, 12, 23, 2, 13, 14, 5, 8, 10, 17, 0, 19, 22, 7, 3, 18, 4]
[17, 7, 10, 21, 23, 13, 3, 20, 14, 4, 15, 5, 8, 11, 12, 2, 0, 16, 22, 18, 1, 6, 19, 9]
[18, 11, 4, 12, 2, 20, 8, 13, 6, 10, 9, 1, 3, 7, 21, 23, 22, 19, 0, 17, 5, 14, 16, 15]
[19, 13, 9, 14, 15, 7, 12, 5, 21, 2, 23, 20, 6, 1, 3, 4, 18, 22, 16, 0, 11, 8, 17, 10]
[20, 15, 6, 16, 8, 18, 2, 14, 4, 17, 19, 23, 22, 21, 7, 1, 3, 9, 5, 10, 0, 13, 12, 11]
[21, 17, 7, 10, 16, 9, 11, 2, 19, 5, 3, 6, 20, 22, 23, 18, 4, 1, 15, 8, 12, 0, 13, 14]
[22, 5, 23, 8, 10, 1, 14, 11, 3, 15, 4, 7, 21, 20, 6, 9, 19, 18, 17, 16, 13, 12, 0, 2]
[23, 8, 22, 5, 13, 3, 17, 16, 1, 12, 20, 19, 9, 4, 18, 21, 7, 6, 14, 11, 10, 15, 2, 0]
group
[[0, 1, 2, 3], [1, 2, 3, 0], [2, 3, 0, 1], [3, 0, 1, 2], [2, 3, 1, 0], [1, 0, 3, 2], 
[3, 2, 0, 1], [2, 0, 3, 1], [3, 2, 1, 0], [1, 3, 0, 2], [0, 3, 1, 2], [0, 2, 3, 1], 
[3, 1, 0, 2], [2, 1, 3, 0], [3, 0, 2, 1], [1, 3, 2, 0], [2, 0, 1, 3], [1, 2, 0, 3], 
[1, 0, 2, 3], [0, 2, 1, 3], [0, 1, 3, 2], [3, 1, 2, 0], [2, 1, 0, 3], [0, 3, 2, 1]]
subsets
[]
[0]
[0, 1]
[0, 1, 2]
[0, 1, 2, 3]
[0, 1, 3]
[0, 2]
[0, 2, 3]
[0, 3]
[1]
[1, 2]
[1, 2, 3]
[1, 3]
[2]
[2, 3]
[3]

subgroups
[[0, 1, 2, 3]]
[[0, 1, 2, 3], [1, 2, 3, 0], [2, 3, 0, 1], [3, 0, 1, 2]]
[[0, 1, 2, 3], [2, 3, 0, 1]]
[[0, 1, 2, 3], [1, 0, 3, 2], [2, 3, 1, 0], [3, 2, 0, 1]]
[[0, 1, 2, 3], [1, 0, 3, 2]]
[[0, 1, 2, 3], [1, 3, 0, 2], [2, 0, 3, 1], [3, 2, 1, 0]]
[[0, 1, 2, 3], [3, 2, 1, 0]]
[[0, 1, 2, 3], [0, 2, 3, 1], [0, 3, 1, 2]]
[[0, 1, 2, 3], [2, 1, 3, 0], [3, 1, 0, 2]]
[[0, 1, 2, 3], [1, 3, 2, 0], [3, 0, 2, 1]]
[[0, 1, 2, 3], [1, 2, 0, 3], [2, 0, 1, 3]]
[[0, 1, 2, 3], [1, 0, 2, 3]]
[[0, 1, 2, 3], [0, 2, 1, 3]]
[[0, 1, 2, 3], [0, 1, 3, 2]]
[[0, 1, 2, 3], [3, 1, 2, 0]]
[[0, 1, 2, 3], [2, 1, 0, 3]]
[[0, 1, 2, 3], [0, 3, 2, 1]]
[[0, 1, 2, 3], [0, 1, 3, 2], [0, 2, 1, 3], [0, 2, 3, 1], [0, 3, 1, 2], 
[0, 3, 2, 1], [1, 0, 2, 3], [1, 0, 3, 2], [1, 2, 0, 3], [1, 2, 3, 0], 
[1, 3, 0, 2], [1, 3, 2, 0], [2, 0, 1, 3], [2, 0, 3, 1], [2, 1, 0, 3], 
[2, 1, 3, 0], [2, 3, 0, 1], [2, 3, 1, 0], [3, 0, 1, 2], [3, 0, 2, 1], 
[3, 1, 0, 2], [3, 1, 2, 0], [3, 2, 0, 1], [3, 2, 1, 0]]
[[0, 1, 2, 3], [0, 3, 2, 1], [1, 0, 3, 2], [1, 2, 3, 0], [2, 1, 0, 3], [2, 3, 0, 1], [3, 0, 1, 2], [3, 2, 1, 0]]
[[0, 1, 2, 3], [0, 1, 3, 2], [1, 0, 2, 3], [1, 0, 3, 2], [2, 3, 0, 1], [2, 3, 1, 0], [3, 2, 0, 1], [3, 2, 1, 0]]
[[0, 1, 2, 3], [1, 0, 3, 2], [2, 3, 0, 1], [3, 2, 1, 0]]
[[0, 1, 2, 3], [0, 2, 1, 3], [1, 0, 3, 2], [1, 3, 0, 2], [2, 0, 3, 1], [2, 3, 0, 1], [3, 1, 2, 0], [3, 2, 1, 0]]
[[0, 1, 2, 3], [0, 2, 3, 1], [0, 3, 1, 2], [1, 0, 3, 2], [1, 2, 0, 3], 
[1, 3, 2, 0], [2, 0, 1, 3], [2, 1, 3, 0], [2, 3, 0, 1], [3, 0, 2, 1], [3, 1, 0, 2], [3, 2, 1, 0]]
[[0, 1, 2, 3], [0, 3, 2, 1], [2, 1, 0, 3], [2, 3, 0, 1]]
[[0, 1, 2, 3], [0, 1, 3, 2], [1, 0, 2, 3], [1, 0, 3, 2]]
[[0, 1, 2, 3], [0, 2, 1, 3], [3, 1, 2, 0], [3, 2, 1, 0]]
[[0, 1, 2, 3], [0, 1, 3, 2], [0, 2, 1, 3], [0, 2, 3, 1], [0, 3, 1, 2], [0, 3, 2, 1]]
[[0, 1, 2, 3], [0, 1, 3, 2], [2, 1, 0, 3], [2, 1, 3, 0], [3, 1, 0, 2], [3, 1, 2, 0]]
[[0, 1, 2, 3], [0, 3, 2, 1], [1, 0, 2, 3], [1, 3, 2, 0], [3, 0, 2, 1], [3, 1, 2, 0]]
[[0, 1, 2, 3], [0, 2, 1, 3], [1, 0, 2, 3], [1, 2, 0, 3], [2, 0, 1, 3], [2, 1, 0, 3]]

[0]
[0, 1, 2, 3]
[0, 2]
[0, 5, 4, 6]
[0, 5]
[0, 9, 7, 8]
[0, 8]
[0, 11, 10]
[0, 13, 12]
[0, 15, 14]
[0, 17, 16]
[0, 18]
[0, 19]
[0, 20]
[0, 21]
[0, 22]
[0, 23]
[0, 20, 19, 11, 10, 23, 18, 5, 17, 1, 9, 15, 16, 7, 22, 13, 2, 4, 3, 14, 12, 21, 6, 8]
[0, 23, 5, 1, 22, 2, 3, 8]
[0, 20, 18, 5, 2, 4, 6, 8]
[0, 5, 2, 8]
[0, 19, 5, 9, 7, 2, 21, 8]
[0, 11, 10, 5, 17, 15, 16, 13, 2, 14, 12, 8]
[0, 23, 22, 2]
[0, 20, 18, 5]
[0, 19, 21, 8]
[0, 20, 19, 11, 10, 23]
[0, 20, 22, 13, 12, 21]
[0, 23, 18, 15, 14, 21]
[0, 19, 18, 17, 16, 22]
normal subgroups
[[0, 1, 2, 3]]
[[0, 1, 2, 3], [0, 1, 3, 2], [0, 2, 1, 3], [0, 2, 3, 1], [0, 3, 1, 2], [0, 3, 2, 1], 
[1, 0, 2, 3], [1, 0, 3, 2], [1, 2, 0, 3], [1, 2, 3, 0], [1, 3, 0, 2], [1, 3, 2, 0], 
[2, 0, 1, 3], [2, 0, 3, 1], [2, 1, 0, 3], [2, 1, 3, 0], [2, 3, 0, 1], [2, 3, 1, 0], 
[3, 0, 1, 2], [3, 0, 2, 1], [3, 1, 0, 2], [3, 1, 2, 0], [3, 2, 0, 1], [3, 2, 1, 0]]
[[0, 1, 2, 3], [1, 0, 3, 2], [2, 3, 0, 1], [3, 2, 1, 0]]
[[0, 1, 2, 3], [0, 2, 3, 1], [0, 3, 1, 2], [1, 0, 3, 2], [1, 2, 0, 3], [1, 3, 2, 0], 
[2, 0, 1, 3], [2, 1, 3, 0], [2, 3, 0, 1], [3, 0, 2, 1], [3, 1, 0, 2], [3, 2, 1, 0]]

normal subgroups
[0]
[0, 20, 19, 11, 10, 23, 18, 5, 17, 1, 9, 15, 16, 7, 22, 13, 2, 4, 3, 14, 12, 21, 6, 8]
[0, 5, 2, 8]
[0, 11, 10, 5, 17, 15, 16, 13, 2, 14, 12, 8]

full symmetry ofcube
[array([[-1.,  0.,  0.],
       [ 0.,  1.,  0.],
       [ 0.,  0.,  1.]]), array([[ 1.,  0.,  0.],
       [ 0., -1.,  0.],
       [ 0.,  0.,  1.]]), array([[ 1.,  0.,  0.],
       [ 0.,  1.,  0.],
       [ 0.,  0., -1.]]), array([[ 2.22044605e-16, -1.00000000e+00,  0.00000000e+00],
       [-1.00000000e+00,  2.22044605e-16,  0.00000000e+00],
       [ 0.00000000e+00,  0.00000000e+00,  1.00000000e+00]]), array([[ 2.22044605e-16,  0.00000000e+00, -1.00000000e+00],
       [ 0.00000000e+00,  1.00000000e+00,  0.00000000e+00],
       [-1.00000000e+00,  0.00000000e+00,  2.22044605e-16]]), array([[ 1.00000000e+00,  0.00000000e+00,  0.00000000e+00],
       [ 0.00000000e+00,  2.22044605e-16, -1.00000000e+00],
       [ 0.00000000e+00, -1.00000000e+00,  2.22044605e-16]]), array([[2.22044605e-16, 1.00000000e+00, 0.00000000e+00],
       [1.00000000e+00, 2.22044605e-16, 0.00000000e+00],
       [0.00000000e+00, 0.00000000e+00, 1.00000000e+00]]), array([[2.22044605e-16, 0.00000000e+00, 1.00000000e+00],
       [0.00000000e+00, 1.00000000e+00, 0.00000000e+00],
       [1.00000000e+00, 0.00000000e+00, 2.22044605e-16]]), array([[1.00000000e+00, 0.00000000e+00, 0.00000000e+00],
       [0.00000000e+00, 2.22044605e-16, 1.00000000e+00],
       [0.00000000e+00, 1.00000000e+00, 2.22044605e-16]])]
[[3, 2, 1, 0, 7, 6, 5, 4], [1, 0, 3, 2, 5, 4, 7, 6], [4, 5, 6, 7, 0, 1, 2, 3], 
[0, 3, 2, 1, 4, 7, 6, 5], [7, 6, 2, 3, 4, 5, 1, 0], [0, 4, 7, 3, 1, 5, 6, 2], 
[2, 1, 0, 3, 6, 5, 4, 7], [0, 1, 5, 4, 3, 2, 6, 7], [5, 1, 2, 6, 4, 0, 3, 7]]
48
38
4
[[0, 1, 2, 3, 4, 5, 6, 7]]
[[0, 1, 2, 3, 4, 5, 6, 7], [1, 0, 3, 2, 5, 4, 7, 6], [2, 3, 0, 1, 6, 7, 4, 5], 
[3, 2, 1, 0, 7, 6, 5, 4], [4, 5, 6, 7, 0, 1, 2, 3], [5, 4, 7, 6, 1, 0, 3, 2], 
[6, 7, 4, 5, 2, 3, 0, 1], [7, 6, 5, 4, 3, 2, 1, 0]]
[[0, 1, 2, 3, 4, 5, 6, 7], [0, 1, 5, 4, 3, 2, 6, 7], [0, 3, 2, 1, 4, 7, 6, 5], 
[0, 3, 7, 4, 1, 2, 6, 5], [0, 4, 5, 1, 3, 7, 6, 2], [0, 4, 7, 3, 1, 5, 6, 2], 
[1, 0, 3, 2, 5, 4, 7, 6], [1, 0, 4, 5, 2, 3, 7, 6], [1, 2, 3, 0, 5, 6, 7, 4], 
[1, 2, 6, 5, 0, 3, 7, 4], [1, 5, 4, 0, 2, 6, 7, 3], [1, 5, 6, 2, 0, 4, 7, 3], 
[2, 1, 0, 3, 6, 5, 4, 7], [2, 1, 5, 6, 3, 0, 4, 7], [2, 3, 0, 1, 6, 7, 4, 5], 
[2, 3, 7, 6, 1, 0, 4, 5], [2, 6, 5, 1, 3, 7, 4, 0], [2, 6, 7, 3, 1, 5, 4, 0], 
[3, 0, 1, 2, 7, 4, 5, 6], [3, 0, 4, 7, 2, 1, 5, 6], [3, 2, 1, 0, 7, 6, 5, 4], 
[3, 2, 6, 7, 0, 1, 5, 4], [3, 7, 4, 0, 2, 6, 5, 1], [3, 7, 6, 2, 0, 4, 5, 1], 
[4, 0, 1, 5, 7, 3, 2, 6], [4, 0, 3, 7, 5, 1, 2, 6], [4, 5, 1, 0, 7, 6, 2, 3], 
[4, 5, 6, 7, 0, 1, 2, 3], [4, 7, 3, 0, 5, 6, 2, 1], [4, 7, 6, 5, 0, 3, 2, 1], 
[5, 1, 0, 4, 6, 2, 3, 7], [5, 1, 2, 6, 4, 0, 3, 7], [5, 4, 0, 1, 6, 7, 3, 2], 
[5, 4, 7, 6, 1, 0, 3, 2], [5, 6, 2, 1, 4, 7, 3, 0], [5, 6, 7, 4, 1, 2, 3, 0], 
[6, 2, 1, 5, 7, 3, 0, 4], [6, 2, 3, 7, 5, 1, 0, 4], [6, 5, 1, 2, 7, 4, 0, 3], 
[6, 5, 4, 7, 2, 1, 0, 3], [6, 7, 3, 2, 5, 4, 0, 1], [6, 7, 4, 5, 2, 3, 0, 1], 
[7, 3, 0, 4, 6, 2, 1, 5], [7, 3, 2, 6, 4, 0, 1, 5], [7, 4, 0, 3, 6, 5, 1, 2], 
[7, 4, 5, 6, 3, 0, 1, 2], [7, 6, 2, 3, 4, 5, 1, 0], [7, 6, 5, 4, 3, 2, 1, 0]]
[[0, 1, 2, 3, 4, 5, 6, 7], [0, 1, 5, 4, 3, 2, 6, 7], [0, 3, 2, 1, 4, 7, 6, 5], 
[0, 3, 7, 4, 1, 2, 6, 5], [0, 4, 5, 1, 3, 7, 6, 2], [0, 4, 7, 3, 1, 5, 6, 2], 
[2, 1, 0, 3, 6, 5, 4, 7], [2, 1, 5, 6, 3, 0, 4, 7], [2, 3, 0, 1, 6, 7, 4, 5], 
[2, 3, 7, 6, 1, 0, 4, 5], [2, 6, 5, 1, 3, 7, 4, 0], [2, 6, 7, 3, 1, 5, 4, 0], 
[5, 1, 0, 4, 6, 2, 3, 7], [5, 1, 2, 6, 4, 0, 3, 7], [5, 4, 0, 1, 6, 7, 3, 2], 
[5, 4, 7, 6, 1, 0, 3, 2], [5, 6, 2, 1, 4, 7, 3, 0], [5, 6, 7, 4, 1, 2, 3, 0], 
[7, 3, 0, 4, 6, 2, 1, 5], [7, 3, 2, 6, 4, 0, 1, 5], [7, 4, 0, 3, 6, 5, 1, 2], 
[7, 4, 5, 6, 3, 0, 1, 2], [7, 6, 2, 3, 4, 5, 1, 0], [7, 6, 5, 4, 3, 2, 1, 0]]

correspondence index to permutation
  0  :  [0, 1, 2, 3, 4, 5, 6, 7]
  1  :  [3, 2, 1, 0, 7, 6, 5, 4]
  2  :  [1, 0, 3, 2, 5, 4, 7, 6]
  3  :  [4, 5, 6, 7, 0, 1, 2, 3]
  4  :  [0, 3, 2, 1, 4, 7, 6, 5]
  5  :  [7, 6, 2, 3, 4, 5, 1, 0]
  6  :  [0, 4, 7, 3, 1, 5, 6, 2]
  7  :  [2, 1, 0, 3, 6, 5, 4, 7]
  8  :  [0, 1, 5, 4, 3, 2, 6, 7]
  9  :  [5, 1, 2, 6, 4, 0, 3, 7]
 10  :  [2, 3, 0, 1, 6, 7, 4, 5]
 11  :  [7, 6, 5, 4, 3, 2, 1, 0]
 12  :  [3, 0, 1, 2, 7, 4, 5, 6]
 13  :  [4, 5, 1, 0, 7, 6, 2, 3]
 14  :  [3, 7, 4, 0, 2, 6, 5, 1]
 15  :  [1, 2, 3, 0, 5, 6, 7, 4]
 16  :  [3, 2, 6, 7, 0, 1, 5, 4]
 17  :  [6, 2, 1, 5, 7, 3, 0, 4]
 18  :  [5, 4, 7, 6, 1, 0, 3, 2]
 19  :  [6, 7, 3, 2, 5, 4, 0, 1]
 20  :  [1, 5, 6, 2, 0, 4, 7, 3]
 21  :  [1, 0, 4, 5, 2, 3, 7, 6]
 22  :  [4, 0, 3, 7, 5, 1, 2, 6]
 23  :  [4, 7, 6, 5, 0, 3, 2, 1]
 24  :  [6, 5, 4, 7, 2, 1, 0, 3]
 25  :  [5, 6, 2, 1, 4, 7, 3, 0]
 26  :  [0, 4, 5, 1, 3, 7, 6, 2]
 27  :  [0, 3, 7, 4, 1, 2, 6, 5]
 28  :  [7, 3, 2, 6, 4, 0, 1, 5]
 29  :  [7, 4, 0, 3, 6, 5, 1, 2]
 30  :  [2, 6, 7, 3, 1, 5, 4, 0]
 31  :  [2, 1, 5, 6, 3, 0, 4, 7]
 32  :  [5, 1, 0, 4, 6, 2, 3, 7]
 33  :  [6, 7, 4, 5, 2, 3, 0, 1]
 34  :  [5, 4, 0, 1, 6, 7, 3, 2]
 35  :  [2, 6, 5, 1, 3, 7, 4, 0]
 36  :  [2, 3, 7, 6, 1, 0, 4, 5]
 37  :  [7, 3, 0, 4, 6, 2, 1, 5]
 38  :  [7, 4, 5, 6, 3, 0, 1, 2]
 39  :  [5, 6, 7, 4, 1, 2, 3, 0]
 40  :  [6, 5, 1, 2, 7, 4, 0, 3]
 41  :  [3, 7, 6, 2, 0, 4, 5, 1]
 42  :  [3, 0, 4, 7, 2, 1, 5, 6]
 43  :  [4, 0, 1, 5, 7, 3, 2, 6]
 44  :  [4, 7, 3, 0, 5, 6, 2, 1]
 45  :  [1, 5, 4, 0, 2, 6, 7, 3]
 46  :  [1, 2, 6, 5, 0, 3, 7, 4]
 47  :  [6, 2, 3, 7, 5, 1, 0, 4]
full subgroups
[0]
[0, 1]
[0, 2, 10, 1]
[0, 2, 10, 1, 3, 18, 33, 11]
[0, 4, 2, 15, 7, 10, 12, 1, 3, 23, 18, 39, 24, 33, 38, 11]
[0, 8, 4, 27, 26, 6, 2, 21, 15, 46, 45, 20, 7, 31, 10, 36, 35, 30, 12, 42, 
1, 16, 14, 41, 43, 22, 13, 3, 44, 23, 32, 9, 34, 18, 25, 39, 17, 47, 40, 24, 
19, 33, 37, 28, 29, 38, 5, 11]
[0, 8, 2, 21, 10, 36, 1, 16, 13, 3, 34, 18, 19, 33, 5, 11]
[0, 6, 2, 20, 10, 35, 1, 14, 22, 3, 9, 18, 17, 33, 37, 11]
[0, 4, 2, 15, 7, 10, 12, 1]
[0, 1, 3, 11]
[0, 8, 1, 16, 13, 3, 5, 11]
[0, 6, 1, 14]
[0, 6, 1, 14, 9, 18, 17, 33]
[0, 1, 9, 17]
[0, 2]
[0, 2, 3, 18]
[0, 6, 2, 20, 22, 3, 9, 18]
[0, 2, 19, 5]
[0, 8, 2, 21, 19, 33, 5, 11]
[0, 8, 2, 21]
[0, 3]
[0, 4, 3, 23]
[0, 4, 7, 10, 3, 23, 24, 33]
[0, 7, 3, 24]
[0, 4]
[0, 4, 9, 25, 28, 5]
[0, 8, 4, 27, 26, 6, 7, 31, 10, 36, 35, 30, 32, 9, 34, 18, 25, 39, 37, 28, 29, 38, 5, 11]
[0, 8, 4, 27, 26, 6]
[0, 4, 7, 10]
[0, 5]
[0, 6, 7, 30, 29, 5]
[0, 8, 5, 11]
[0, 6]
[0, 6, 9, 18]
[0, 7]
[0, 8, 7, 31, 32, 9]
[0, 8]
[0, 9]
full normal subgroups
[0]
[0, 2, 10, 1, 3, 18, 33, 11]
[0, 8, 4, 27, 26, 6, 2, 21, 15, 46, 45, 20, 7, 31, 10, 36, 35, 30, 12, 42, 1, 16, 14, 41, 
43, 22, 13, 3, 44, 23, 32, 9, 34, 18, 25, 39, 17, 47, 40, 24, 19, 33, 37, 28, 29, 38, 5, 11]
[0, 8, 4, 27, 26, 6, 7, 31, 10, 36, 35, 30, 32, 9, 34, 18, 25, 39, 37, 28, 29, 38, 5, 11]
です。どれが回転群の元か調べたり、この様に回転群の元に気が及ぶとこのプログラムは間違っていることに気が付きます。 即ち、full subgroups は必ず鏡映が入っている部分群しか考えていなかった事に気づきます。ではどの様な生成元の集合を考えるべきか？ すべての部分集合では私のパソコンでは何時答えが出るか分かりません。 https://www2.itc.kansai-u.ac.jp/~wakui/2011sotsuron.pdf を眺めると群論だけでなく、「正多面体とコクセター図形との対応」などを学べば、 多分、解が見つかると思います。効率的なアルゴリズムを探すには、我々凡人は正多面体に関連する色々な事を学ぶ必要があるみたいです。 何を言っているかと言うと、正 P 角形の対称群＝二面体群の構造を調べるプログラムを作った時、兎も角、小さい数値 P に対して正しい答えが出れば差し当たり良いとは 書きましたが、小学生でも理解できることなので、キチンと考えるべきだったと言うことです。 正 P 角形を動かさない合同変換は恒等変換と 2π/ P の角度の回転と線対象（鏡映）と P が偶数の時は点対称（180度の回転）及びそれらの合成があり、 鏡映は1種類で2回続けると元に戻り位数は２ですが、回転は P の値によっては何回続けると元に戻るかが異なり、色々な位数のものがあります。 正 P 角形の合同変換群を求めるには、正 P 角形の合同変換であるすべての回転と鏡映（線対象変換）を一つ一つ追加する方法と生成元を見つける方法が 普通考えられます。 鏡映一個や回転1個では全体を生成できませんが、任意の鏡映2個或いは鏡映1個と回転1個で生成できるか？ p の値によって答えが異なります。簡単な整数論の問題になりますが、簡潔に表現するのは私には難しいですが、答えは良く知られています。 すべての部分群を求めるためには、単純な方法は正 P 角形の合同変換群のすべての部分集合の中で部分群になっているものを見つけることで求めることも 勿論出来ますが、実際問題としてはコンピュータにやらすにしても大変な作業になります。普通は、多分、 適当な生成元達の集合で生成される部分群達を求めることで実現します。上のプログラムの間違いは、立方体の鏡映全体の集合のすべての部分集合を生成元として チェックすれば、すべての部分群が見つかると勘違いしていた事です。これでは回転だけで構成される部分群が求まりません。 各鏡映と恒等変換で群になるので、鏡映一つづつの生成元からなる集合をチェックする生成元の集合に含めなければなりません。 回転だけを含む部分群を求めるには P の値によって異なりますが、P の約数の位数を持つ回転を一つづつ含む集合をチェックする生成元の集合に含めなければなりません。 鏡映と回転と共に含む部分群をすべて求めるには、先ずは「鏡映2個」或いは「鏡映1個と回転1個」からなる集合をチェックする生成元の集合に含めなければなりませんが、 すべての組み合わせを含める必要はありませんが、どれが不要かキチンと調べるのは厄介です。誰か調べて、公表してくれていないか探してみます。 見つけることが出来なければ、自分で考えなければなりませんが、数学者でなければ、見栄を張るのでなければ、パソコンで実験してみて、 多少の無駄には目をつぶり、実用的には、楽で自分が理解できる確実なアルゴリズムで妥協すれば良いです。本来、 「INTERNATIONAL TABLES for CRYSTALLOGRAPHY」を読もうとしていたことを思い出し、 即ち、この本の Examples を理解するためにプログラミングしていることを思い出し、それが出来れば良いので、横道にそれるのはほどほどにします。 例えば、the conjugacy classes of symmetry group 3m of an equilateral triangle は {1},{m10,m01,m11}and{3+,3−} the conjugacy classes of symmetry group 4mm of a square は {1},{2},{m10,m01},{m11,m11―}and{4+,4−} が示せれば良いだけです。この場合は 

    def conjugate_set(self, i):
        h = self.convert_permutation(i)
        S = []
        for g in self.group:
            x = self.perm_product(g, h)
            x = self.perm_product(x, self.inverse(g))
            x = self.permutation2index(x)
            if x not in S:
                S.append(x)
        return S
のような関数が実行出来れば良いです。3m の場合は、軌道(orbit)が 

i= 0  :  [0]
i= 1  :  [1, 2]
i= 2  :  [2, 1]
i= 3  :  [3, 5, 4]
i= 4  :  [4, 3, 5]
i= 5  :  [5, 4, 3]
で、4mm の場合は 

i= 0  :  [0]
i= 1  :  [1, 3]
i= 2  :  [2]
i= 3  :  [3, 1]
i= 4  :  [4, 6]
i= 5  :  [5, 7]
i= 6  :  [6, 4]
i= 7  :  [7, 5]
で、なるほどと納得がいきます。手計算では大変ですが、プログラミングが出来れば、 ポリアさんお勧めの「帰納」によって一般的なプログラムを一度作れば、 様々な P の値に対して、直ちに計算してくれるので、時間の節約（今はやりのタイパ）になります。 但し、手計算をするとこれ以外の情報も手元に残るので、手計算した方が良い場合も勿論あります。 今の例では、それぞれどの元でどの元に移動しているかの情報がこの計算結果では分かりません。 プログラミングでは、最終結果だけでなく、途中の計算過程も表示しないと重要な情報を得ることに失敗する場合も可能性としてはあります。 自分でプログラミング出来れば、思い付いたことに素早く柔軟に対応できます。今の場合、 

    def conjugate_set(self, i):
        h = self.convert_permutation(i)
        S = []
        CE = {}
        for g in self.group:
            x = self.perm_product(g, h)
            x = self.perm_product(x, self.inverse(g))
            x = self.permutation2index(x)
            if x not in S:
                S.append(x)
                CE[(x,)] = [self.permutation2index(g)]
            else:
                v = CE.get((x,))
                v.append(self.permutation2index(g))
                CE[(x,)] = v
        return S, CE
と作り変えると、4mm の場合は 

i= 0  :  ([0], {(0,): [0, 1, 2, 3, 4, 5, 6, 7]})
i= 1  :  ([1, 3], {(1,): [0, 1, 2, 3], (3,): [4, 5, 6, 7]})
i= 2  :  ([2], {(2,): [0, 1, 2, 3, 4, 5, 6, 7]})
i= 3  :  ([3, 1], {(3,): [0, 1, 2, 3], (1,): [4, 5, 6, 7]})
i= 4  :  ([4, 6], {(4,): [0, 2, 4, 6], (6,): [1, 3, 5, 7]})
i= 5  :  ([5, 7], {(5,): [0, 2, 5, 7], (7,): [1, 3, 4, 6]})
i= 6  :  ([6, 4], {(6,): [0, 2, 4, 6], (4,): [1, 3, 5, 7]})
i= 7  :  ([7, 5], {(7,): [0, 2, 5, 7], (5,): [1, 3, 4, 6]})
のような表示を得ることが出来、どの元でどの元に移動しているかが分かるようになります。 同様に、例えば、Orbit-stabilizer theorem の理解でも、我々凡人は定理の証明を論理的に一行一行追うだけでは頭に残りませんから、 具体的に、3m や 4mm のような簡単な群に対して、すべての元の stabilizer を求め、left coset decomposition を求め、定理に述べていることを確かめる 事を虱潰しにやってみます。それだけ時間を費やせば、完璧に理解できるし、記憶に長く残ります。多分。 上の続きで、conjugation による action の場合は 

    def get_stabilizer(self, i):
        STAB = []
        omega = self.convert_permutation(i)
        for g in self.group:
            x = self.perm_product(g, omega)
            x = self.perm_product(x, self.inverse(g))
            x = self.permutation2index(x)
            if x == i and self.permutation2index(g) not in STAB:
              STAB.append(self.permutation2index(g))
        return STAB
のような関数が実行出来れば良いです。3m の場合は、stabilizer は 

i= 0  :  [0, 1, 2, 3, 4, 5]
i= 1  :  [0, 1, 2]
i= 2  :  [0, 1, 2]
i= 3  :  [0, 3]
i= 4  :  [0, 4]
i= 5  :  [0, 5]
で、4mm の場合は 

i= 0  :  [0, 1, 2, 3, 4, 5, 6, 7]
i= 1  :  [0, 1, 2, 3]
i= 2  :  [0, 1, 2, 3, 4, 5, 6, 7]
i= 3  :  [0, 1, 2, 3]
i= 4  :  [0, 2, 4, 6]
i= 5  :  [0, 2, 5, 7]
i= 6  :  [0, 2, 4, 6]
i= 7  :  [0, 2, 5, 7]
です。手作業ではやる気がしないと思いますが、プログラミングは簡単です。 更に、conjugate subgroups や normalizer を求めたいときは 

    def act_on_subgroup(self, H, g):
        S = []
        for h in H:
            x = self.perm_product(g, h)
            x = self.perm_product(x, self.inverse(g))
            x = self.permutation2index(x)
            if x not in S:
                S.append(x)
        S.sort()
        return S
        
    def conjugate_subgroup(self, i):
        H = self.subgroups[i]
        CSG = []
        CE = {}
        for g in self.group:
            S = self.act_on_subgroup(H, g)
            if S not in CSG:
                CSG.append(S)
            key = tuple(S)
            if key in CE:
                v = CE.get(key)
                v.append(self.permutation2index(g))
                CE[key] = v
            else:
                CE[key] = [self.permutation2index(g)]
        return CSG, CE
        
    def normalizer(self, i):
        H = self.subgroups[i]
        HH = self.index_rep_of_subgroup(H)
        N = []
        for g in self.group:
            S = self.act_on_subgroup(H, g)
            if S == HH:
                N.append(self.permutation2index(g))
        return N
のようなプログラムを実行できるようにすれば、 4mm の場合は 

conjugate subgroups of 2: ([[0, 2]], {(0, 2): [0, 1, 2, 3, 4, 5, 6, 7]})
conjugate subgroups of 3 ([[0, 4], [0, 6]], {(0, 4): [0, 2, 4, 6], (0, 6): [1, 3, 5, 7]})
conjugate subgroups of 4 ([[0, 5], [0, 7]], {(0, 5): [0, 2, 5, 7], (0, 7): [1, 3, 4, 6]})
や 

normalizer(2): [0, 1, 2, 3, 4, 5, 6, 7]
normalizer:(3) [0, 2, 4, 6]
normalizer(4): [0, 2, 5, 7]
normalizer(5): [0, 2, 4, 6]
normalizer(6): [0, 2, 5, 7]
と表示させることが出来ます。

プログラミングは何かどうしてもやりたいことがあり、自分で手作業で出来るが時間が掛かりすぎて大変だと言う事柄を コンピュータに代わりにやってもらう技術です。こういうものがあればプログラミングを意欲的に学ぼうと言う気が起きるのではないでしょうか？ やりたい事がまだない小学生に情報教育だと騒ぎ立てる理由が今一つ理解でません。 政治家・官僚にとってここにも利権があり、推進すれば自分の懐が温まるのでしょうか？最近は自分の利益しか考えない人達ばかりになった気がします。 我々凡人が数学を理解するには、頭の中で抽象的に考えるだけでなく、片っ端から具体例で計算してみる必要があります。

更に3次元で例えば正8面体群＝正6面体群は任意の鏡映3個で生成できるか？或いは特別な鏡映3個で生成できるか？鏡映と回転の組み合わせでは どうなるか？立方体の回転は3種類、鏡映は2種類あるので、これらの変換達のの関係、例えば、積で書けるか？共役元か？など。 それらの組み合わせすべてで実験して確かめてみる。更に、全体の部分群や回転だけの群の部分群のすべてを生成するためには、 どの様な生成元の組み合わせが必要か、上のプログラムでいい加減で済ましたことをプログラムを改良してやり直して見ます。 アルゴリズムは必要な計算時間とアルゴリズムの複雑さを比較して、自分の使用に十分であれば、特別な意図がなければ、深追いは止めます。 更には4次元の場合はどうだろう、5次元では？・・・と、 我々凡人は、才能ある優秀な人達の様には頭の中で考えても出来ませんから、 3次元の場合は、例えば、正多面体の模型を眺めながら、コンピュータの力を借りて虱潰しに調べて見る必要があります。 そういう努力をすれば・それだけの時間をかければ、誰でも何をすべきか理解できます。多分。これはどの分野の人たちもやっていることだと思います。 更に、上でやっている様に8次の対称群の部分群として表現するのではなく、 正八面体を使って、6次の対称群の部分群として表現してみるなど、思い付いたことを調べて見れば良いです。 6枚の硬貨で占うと「山火 賁」で、正に、今やっていることは「虎の威を借りる狐」みたいなものですが、 「INTERNATIONAL TABLES for CRYSTALLOGRAPHY」も何とか、コンピュータの力を借りれば、かなりめんどくさい計算も比較的容易に出来て、 一行一行、何を書いているか確かめながら読むことが出来ます。但し、「the geometric element of the rotation 2」など何を意味するか 今の処、理解できないものもあります。3次元の回転の場合は、その回転軸を「the geometric element」と書いています。 2次元でも鏡映に対しては、m10 と m01 は「the geometric element」が共に「lines through the centres of opposite edges of the square」で、 「crystallographically equivarennt」（結晶学的には同値）と書いていて、何を言いたいかは理解できます。 それがどうしても必要な事なら、（rotation 2 は m10 と m01 の合成だからそれらの軸二組の事（即ち、正方形の中心を通る直交する2直線）を 「the geometric element」と考えると辻褄が合いますが）、 後の方まで読んでいけば、多分、分かるようになると思います。群論の応用を考える時には、群論の知識だけでなく、応用したい分野の常識も必要です。 3次元の合同変換群を考えるには、鏡映の組み合わせによる幾何学的イメージを持ちながら、確か６種類（昔勉強した本が行方不明です。 「INTERNATIONAL TABLES for CRYSTALLOGRAPHY」などには「恒等変換」を回転の特別な場合などとせず、8種類と分類しています。）の isometories の 行列表現を駆使する必要があります。この本は空間の結晶学の理解に偏ってはいますが、読んで見ると理解するのに、大学時代に学んだはずの線形代数もうろ覚えで、 時間は掛かり何時終わるか分かりませんが結構面白い本です。大学の線形代数で挫折した人も結晶に興味があれば、読んで見ると良いです。 才能ある優秀な人達はこんな所は一気に駆け抜け、遥か彼方に行っていますが、我々凡人はこんな所を 丁寧に学ばないと先にいけません。多分。この様な3次元ユークリッド空間の変換であれば、現在は、プログラミングが出来さえすれば、 具体的に一つ一つコンピュータ・グラフィックスで確かめながら学ぶことが出来る良い時代になっています。 大学の一般教養で、専門が、多分、中国文学だった（すみません。易の話しか覚えていません。）老教授から、易占いのやり方や 黄 小娥著「黄小娥の易入門」の存在を教えて貰い、時々、占います。「タロットカード」による占いも簡単に出来ます。 これらの参考書（黄さんが道を開いてくれたので、黄さんは業界から締め出されたみたいですが、その後、沢山の易などの参考書が出版されています。）を 丸暗記出来ないので、共に、毎回、本を見ないといけないですが、自分で占えば、他人に付け込まれる事や洗脳される事はありません。 「幾つになっても、知らないと言うことは悲しいこと、知ることは楽しいことです。すべての温泉や観光地、或いは、すべてのアニメの聖地を訊ねて、 インターネットで発信すれば、一躍有名人になりますが、我々庶民には金銭的にも大変ですが、 万障繰り合わせ幾つかの場所を訊ねてみるように、 数学も知られているすべてを知ることは我々凡人には不可能ですが、面白いと思った分野をパソコンを使って調べて見るのも 結構面白い暇つぶし・大してお金の要らない実用的・それなりのリターンもある道楽になります。 例えば、結晶に興味があれば、普通は「物理」や「化学」や「地学」の勉強だと思うと思いますが、結晶を深く研究しようと思うと 結晶群の研究に行きつき、英語の本では「化学」の参考書として結晶(群)の入門書・化学者に対する啓蒙書（即ち、数学的にチャンとは書いてはいませんが） (Donald E. Sands 著「Introduction to Crystallography」)も 洋書は円安で一時の２倍の値段になったとは言え、比較的安価で出版されています。DOVER の本には意外と安価な良書があります。 「INTERNATIONAL TABLES for CRYSTALLOGRAPHY」には、特殊な場合には、与えられた行列がどの様な合同変換であるか判別する方法が証明無しで 解説されています。証明は難しくはないですが、その代わり、その解説を理解するための例が沢山載せてあります。 上の方で、一般の回転の行列 A が与えられた時、その軸と回転角を求める方法を解説しましたが、A が結晶群に出てくるなら、 行列 A が直交行列で det(A)=1 なら回転行列で、トレースの（可換不変性と）相似不変性により、 回転行列 A の tr(A)=1+2cos(α) で回転角αの cos(α) が分かります。 これで A が結晶群に出てくる行列であれば、何乗か（１，２，３，４または６）すれば単位行列になりますが、何乗すれば単位行列になるか分かります。 この数が k の時は u=Y(A)v=(Ak−1+Ak−2+⋯+A+I)v で、v に任意のベクトルで u がゼロベクトルでないものを代入すれば、A の回転の軸 u が求まります。 線形代数も奥が深く、知らないことばかりです。又、多分、線形代数が良く理解できなかった時、同じような参考書を読んでも同じことです。 不思議なことに、行列を列ベクトルや行ベクトルを並べたものと分割して考える柔軟な考え方を教わると我々凡人でも簡単に理解できるようになったりします。 私は「行列プログラマー ―Pythonプログラムで学ぶ線形代数」で、確か、こんなやり方もあるんだと学んだと思います。 更に、ギルバート・ストラング著「ストラング：線形代数イントロダクション」も、持っているだけで、読んではいませんが、同じようなことを 序文に書いてあったと思います。 私達の上の世代の先生が「自分たちは線形代数を教わった」と嬉しそうに話してくださった 意味がやっとこの年になって分かった気がします。

上で保留にしていた立方体の鏡映全体で生成される群のすべての部分群を求める為には 

    def get_full_subgroup(self):
        SG = []
        cand = self.get_all_subset(9)
        for c in cand:
            gen = []
            for n in c:
                gen.append(self.perm_in_ref_perm(n))           
            G = self.ref_generate_subgroup(gen)
            NG = self.arrange(G)
            if NG not in SG:
                SG.append(NG)
        return SG
を 

    def get_full_subgroup(self):
        SG = []
        cand = self.get_subset(48, 3)
        for c in cand:
            gen = []
            for n in c:
                gen.append(self.full_group[n])           
            G = self.ref_generate_subgroup(gen)
            NG = self.arrange(G)
            if NG not in SG:
                SG.append(NG)
        return SG
に変更すれば良いです。cand = self.get_subset(48, 3) の３を2にすると91個の部分群を見つけてくれ、3では98個、4でも98個です。 1では48個、２では1128個増え、3では更に17296個増え、４では更に194580個増え、5では更に1712304個増えた生成元達のチェックになり、 私のパソコンでは5では短時間では答えが出ません。 2時間ぐらい待つと矢張り98個の部分群を見つけてくれます。 ３と４と５で答えが同じなので、絶対正しいとは言えませんが、4個にしても5個にしても増えなかったので、 多分これで良いはずです。暇な時に、立方体の模型を見ながら、 鏡映や回転の2個・3個の積がどの様な合同変換になるか精密な検証をしてみれば良いです。 （2次元の平面の鏡映の積の解析は簡単で解説してくれている英文の参考書があり、私はそれで合同変換群を学びました。 3次元の鏡映の積に関してはそれ程詳しくは書いてなかったように記憶していますが、その参考書が行方不明です。 3次元の空間の鏡映や回転の積はずっと複雑だから一度調べておいた方が良いです。そして、上の98個の部分群がどの様な合同変換から構成されているか 調べて見ます。思い付いたことを何でもしてみます。） 又、回転群のすべての部分群が全部得られているかチェックしてみるとより確からしいと確認できます。 又、立方体の回転群の各元がこの対称群のどの元と対応するかは 

    def index_list_of_rotation_group(self):
        index_list = []
        for k in range(24):
            index_list.append(self.full_group.index(self.v_perm[k]))
        return index_list
と言う関数を追加すれば良いです。 回転群の元 0,1, ... , 23 番目はそれぞれ対称群の元の 

index_list
[0, 15, 10, 12, 13, 11, 16, 22, 18, 20, 27, 26, 32, 31, 25, 28, 30, 29, 21, 17, 19, 14, 23, 24]
番目と対応しています。 継ぎ足し継ぎ足しで何をしているか理解するのが難しいと思いますが、 こいつが作れるんだから俺も作れるはずだと思って、自分でゼロから作ってみると良いです。これが作れるようになれば、 正四面体や正十二面体などのプログラムも簡単に作れるはずです。多分。面白い暇つぶしになります。 更に、合同変換の積を4×４行列のまま計算するプログラム、行列のままで与えた生成元から出来る点群を見つけるプログラム、 各種分子模型の表示とその点群を求めるプログラムを作り、 Donald E. Sands 著「Introduction to Crystallography」の解説を確かめる、 合同変換の4×４行列が8種類のどれか判別する（手掛かりは、主要部分の3×３行列の行列式の符号、固定点が空間全体か平面か直線か一点かそれとも固定点がないか、 及び位数(order)を調べることです。）プログラムなどなど思い付くものを 参考書を読むのと平行して次々作っていけば良いです。簡単に出来るハズです。多分。 まだ分からないことばかりで、作りかけのかなり酷いプログラムで人様に見せるようなものではないですが、参考までに提示すると 

import tkinter as tk
from OpenGL.GL import *
from OpenGL.GLU import *
import numpy as np
from OpenGL import GL
from pyopengltk import OpenGLFrame
import sympy
import re
import copy

class Rotate:
    def rotate(self, n, r, theta):
        n = (1/np.sqrt(np.dot(n, n))) * n
        n_dot = np.dot(r, n)
        n_cross = np.cross(n, r)
        w = np.cos(theta)*r+n_dot*(1-np.cos(theta))*n+np.sin(theta)*n_cross
        return w
    def matrix(self, n, theta):
        t_mtx = []
        m1 = self.rotate(n, np.array([1.0, 0.0, 0.0]), theta)
        m2 = self.rotate(n, np.array([0.0, 1.0, 0.0]), theta)
        m3 = self.rotate(n, np.array([0.0, 0.0, 1.0]), theta)
        t_mtx.extend(m1)
        t_mtx.extend(m2)
        t_mtx.extend(m3)
        mtx = np.array(t_mtx, dtype=float).reshape(3, 3)
        mxt = np.transpose(mtx)
        return mtx

class PointGroup:
    def __init__(self):
        self.Rot = Rotate()
        self.I = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]])
        

    def reflection(self, n):
        p1 = (1/np.sqrt(np.dot(n, n)))*n
        Q = np.array([[p1[0]*p1[0], p1[0]*p1[1], p1[0]*p1[2]], \
                  [p1[1]*p1[0], p1[1]*p1[1], p1[1]*p1[2]], \
                  [p1[2]*p1[0], p1[2]*p1[1], p1[2]*p1[2]]])
        S = self.I - 2*Q
        return S
    
    def rotation(self, n, theta):
        return self.Rot.matrix(n, theta)

    def product(self, M1, M2):
        return np.dot(M1, M2)

    def same_matrix(self, M1, M2):
        for k in range(3):
            for i in range(3):
                if np.abs(M1[k][i]-M2[k][i]) > 0.001:
                    return False
        return True
    
    def foundP(self, g, G):
        for m in G:
            if self.same_matrix(g, m):
                return True
        return False
                
    def generate_subgroup(self, generator):
        flag = True
        G = [self.I]
        NG = copy.deepcopy(G)
        while flag == True:
            flag = False
            for g in generator:
                for h in G:
                    k = self.product(g, h)
                    if self.foundP(k, NG) == False:
                        flag = True
                        NG.append(k)
            G = copy.deepcopy(NG)
        return G

clist = [[1.0, 0.0, 0.0], [0.0, 1.0, 0.0], [0.0, 0.0, 1.0],
        [1.0, 1.0, 0.0], [1.0, 0.0, 1.0], [0.0, 1.0, 1.0],
        [0.5, 0.0, 0.0], [0.0, 0.5, 0.0], [0.0, 0.0, 0.5],
        [0.5, 0.5, 0.0], [0.0, 0.5, 0.5], [0.5, 0.0, 0.5],
        [0.5, 0.7, 0.0], [0.7, 0.5, 0.0], [0.7, 0.0, 0.5],
        [0.5, 0.2, 0.3], [0.2, 0.5, 0.3], [0.3, 0.2, 0.5]]

class Sphere:
    def __init__(self, radius, n_longitude, n_latitude):
        self.radius = radius
        self.n_longitude = n_longitude ## 横の分割数
        self.n_latitude = n_latitude   ## 縦の分割数
    def draw(self, cn):
        glColor(clist[cn][0], clist[cn][1], clist[cn][2], 1.0)        
        end = np.pi
        step_longitude = 2 * np.pi/ self.n_longitude
        step_latitude = np.pi / self.n_latitude
        r = self.radius
        for i in range(self.n_latitude):
            arad1 = i * step_latitude
            arad2 = (i+1) * step_latitude
            for k in range( self.n_longitude):
                brad1 = k * step_longitude
                brad2 = (k+1) * step_longitude               
                x1 = r*np.sin(arad1)*np.cos(brad1)
                y1 = r*np.sin(arad1)*np.sin(brad1)
                z1 = r*np.cos(arad1)                
                x2 = r*np.sin(arad2)*np.cos(brad1)
                y2 = r*np.sin(arad2)*np.sin(brad1)
                z2 = r*np.cos(arad2)
                x3 = r*np.sin(arad2)*np.cos(brad2)
                y3 = r*np.sin(arad2)*np.sin(brad2)
                z3 = r*np.cos(arad2)
                x4 = r*np.sin(arad1)*np.cos(brad2)
                y4 = r*np.sin(arad1)*np.sin(brad2)
                z4 = r*np.cos(arad1)
                glNormal3d(x1, y1, z1)
                glBegin(GL_POLYGON)
                glVertex3d(x1, y1, z1)
                glVertex3d(x2, y2, z2)
                glVertex3d(x3, y3, z3)
                glVertex3d(x4, y4, z4)                
##                glVertex3d(x1, y1, z1)
##                glVertex3d(x4, y4, z4)
##                glVertex3d(x3, y3, z3)
##                glVertex3d(x2, y2, z2)                
                glEnd()
    def draw_wireframe(self, cn):
        glColor(clist[cn][0], clist[cn][1], clist[cn][2], 1.0)        
        end = np.pi
        step_longitude = 2 * np.pi/ self.n_longitude
        step_latitude = np.pi / self.n_latitude
        r = self.radius
        for i in range(self.n_latitude):
            arad1 = i * step_latitude
            arad2 = (i+1) * step_latitude
            for k in range( self.n_longitude):
                brad1 = k * step_longitude
                brad2 = (k+1) * step_longitude               
                x1 = r*np.sin(arad1)*np.cos(brad1)
                y1 = r*np.sin(arad1)*np.sin(brad1)
                z1 = r*np.cos(arad1)                
                x2 = r*np.sin(arad2)*np.cos(brad1)
                y2 = r*np.sin(arad2)*np.sin(brad1)
                z2 = r*np.cos(arad2)
                x3 = r*np.sin(arad2)*np.cos(brad2)
                y3 = r*np.sin(arad2)*np.sin(brad2)
                z3 = r*np.cos(arad2)
                x4 = r*np.sin(arad1)*np.cos(brad2)
                y4 = r*np.sin(arad1)*np.sin(brad2)
                z4 = r*np.cos(arad1)
                glBegin(GL_LINES)
                glVertex3d(x1, y1, z1)
                glVertex3d(x2, y2, z2)
                glVertex3d(x2, y2, z2)
                glVertex3d(x3, y3, z3)
                glVertex3d(x3, y3, z3)
                glVertex3d(x4, y4, z4)                
                glVertex3d(x4, y4, z4)                
                glVertex3d(x1, y1, z1)
                glEnd()


class Line:
    def __init__(self, source, target, dir):
        self.source = source
        self.target = target
        self.dir = dir
    def draw(self, cn):
        glColor(clist[cn][0], clist[cn][1], clist[cn][2], 1.0)        
        glLineWidth(4.0) ## 線の幅
        glBegin(GL_LINES)
        s_vertex = self.source * self.dir
        t_vertex = self.target * self.dir
        glVertex3f(s_vertex[0], s_vertex[1], s_vertex[2])
        glVertex3f(t_vertex[0], t_vertex[1], t_vertex[2])
        glEnd()

class Molecule():
    def __init__(self):
        self.pg = PointGroup()
        self.G = []

    def set_molecule(self, index):
        if index == 0:
            M1 = self.pg.reflection(np.array([0, 0, 1])) 
            M2 = self.pg.reflection(np.array([1, 0, 0]))
            axis = np.array([np.cos(2*np.pi/3), np.sin(2*np.pi/3), 0])
            M3 = self.pg.reflection(axis) 
            self.G = self.pg.generate_subgroup([M1, M2, M3])
            print('index=', index)
            print(len(self.G))
            for i in range(len(self.G)):
                print(self.G[i])
            print()
        elif index == 1:
            M1 = self.pg.reflection(np.array([0, 0, 1])) 
            M2 = self.pg.reflection(np.array([1, 0, 0]))
            axis = np.array([np.cos(np.pi/4), np.sin(np.pi/4), 0])
            M3 = self.pg.reflection(axis) 
            axis = np.array([0, np.cos(np.pi/4), np.sin(np.pi/4)])
            M4 = self.pg.reflection(axis) 
            self.G = self.pg.generate_subgroup([M1, M2, M3, M4])
            print('index=', index)
            print(len(self.G))
            for i in range(len(self.G)):
                print(self.G[i])
            print()
        elif index == 2:
            M2 = self.pg.reflection(np.array([1,0,0]))
            axis = np.array([np.cos(2*np.pi/3), np.sin(2*np.pi/3), 0])
            M3 = self.pg.reflection(axis) 
            self.G = self.pg.generate_subgroup([M2, M3])
            print('index=', index)
            print(len(self.G))
            for i in range(len(self.G)):
                print(self.G[i])
            print()
        
    def draw(self, index):
        if index == 0:
            sphere1 = Sphere(0.5, 10, 10)
            sphere2 = Sphere(0.3, 10, 5)
            sphere1.draw(0)
            sphere1.draw_wireframe(2)
            for i in range(3):
                glPushMatrix()
                ln = Line(0.5, 0.7, np.array([np.cos(2*i*np.pi/3),
                                              np.sin(2*i*np.pi/3), 0.0]))
                ln.draw(5)
                glTranslate(np.cos(2*i*np.pi/3), np.sin(2*i*np.pi/3), 0.0)
                sphere2.draw_wireframe(5)
                glPopMatrix()
            for i in range(2):
                glPushMatrix()
                ln = Line(0.5, 0.7, np.array([0, 0, 2*i-1]))
                ln.draw(5)                          
                glTranslate(0, 0, 2*i-1)
                sphere2.draw_wireframe(5)
                glPopMatrix()
        elif index == 1:
            sphere1 = Sphere(0.5, 10, 10)
            sphere2 = Sphere(0.3, 10, 5)
            sphere1.draw(2)
            sphere1.draw_wireframe(3)
            for i in range(4):
                glPushMatrix()
                ln = Line(0.5, 0.7, np.array([np.cos(2*i*np.pi/4),
                                              np.sin(2*i*np.pi/4), 0.0]))
                ln.draw(6)
                glTranslate(np.cos(2*i*np.pi/4), np.sin(2*i*np.pi/4), 0.0)
                sphere2.draw_wireframe(5)
                glPopMatrix()
            for i in range(2):
                glPushMatrix()
                ln = Line(0.5, 0.7, np.array([0, 0, 2*i-1]))
                ln.draw(6)                          
                glTranslate(0, 0, 2*i-1)
                sphere2.draw_wireframe(5)
                glPopMatrix()
        elif index == 2:
            sphere1 = Sphere(0.3, 10, 10)
            sphere2 = Sphere(0.5, 10, 5)
            sphere3 = Sphere(0.2, 10, 5)
            sphere1.draw(0)
            sphere1.draw_wireframe(2)
            for i in range(3):
                glPushMatrix()
                v = np.array([np.cos(2*i*np.pi/3), np.sin(2*i*np.pi/3), -1.0])
                v = (1/np.sqrt(np.dot(v, v)))*v
                ln = Line(0.3, 0.5, v)
                ln.draw(5)
                glTranslate(v[0], v[1], v[2])
                sphere2.draw_wireframe(5)
                glPopMatrix()
            glPushMatrix()
            ln = Line(0.3, 0.8, np.array([0, 0, 1]))
            ln.draw(5)                          
            glTranslate(0, 0, 1)
            sphere3.draw_wireframe(7)
            glPopMatrix()

index = 1
mol = Molecule()
mol.set_molecule(index)

rotate = 0
scale = 2.0
n_problem = 0


class AppOgl(OpenGLFrame):

    def initgl(self):
        global rotate, cube       
        glViewport(0, 0, self.width, self.height) ## 画面の描画領域       
        glClearColor(1.0, 1.0, 1.0, 1.0) ## 背景色
        self.n_model_list = [0]
        self.n_model = self.n_model_list[0]
        self.old_n_model = -1
        rotate = 0
        self.n_move_list = [0]
        self.n_move = self.n_move_list[0]
           
    def torad(self, deg):
        return deg*(math.pi/180.0)

    def redraw(self):
        global rotate, mtx, mtx2, ex1, scale
        self.n_model = self.n_model_list[0]
        
        glClear(GL_COLOR_BUFFER_BIT)
        
        if self.n_model == 0:
            rotate += 1
            if self.n_model != self.old_n_model:
                self.old_n_model = self.n_model
            glMatrixMode(GL_PROJECTION) ## 投影行列を操作したい
            glLoadIdentity() ## 投影行列を単位行列で初期化する
            glOrtho(-scale, scale, -scale, scale, -scale, scale)
            glMatrixMode(GL_MODELVIEW)
            glLoadIdentity()
            glRotated(rotate, 1.0, 0.0, 1.0)
            mol.draw(index)
                
# メニューから呼び出される関数
def D6h():
    global index
    index = 0
    
def C6():
    global index
    index = 2

def Oh():
    global index
    index = 1

def mtx_mult():
    str_W = text.get("1.0", "end")
    strlist = re.findall('[0-9-.]+', str_W)
    a_W =[]
    for i in range(9):
        a_W.append(float(strlist[i]))
    M1 = np.array([np.array([a_W[0], a_W[1], a_W[2]]),
                     np.array([a_W[3], a_W[4], a_W[5]]),
                     np.array([a_W[6], a_W[7], a_W[8]])])
    str_W = text2.get("1.0", "end")
    strlist = re.findall('[0-9-.]+', str_W)
    a_W =[]
    for i in range(9):
        a_W.append(float(strlist[i]))
    M2 = np.array([np.array([a_W[0], a_W[1], a_W[2]]),
                     np.array([a_W[3], a_W[4], a_W[5]]),
                     np.array([a_W[6], a_W[7], a_W[8]])])
    M3 = np.dot(M1, M2)
    text3.delete("1.0", "end")
    text3.insert( 0., M3 )
    for k in range(3):
        print(M3[k])
    print()
           
def mtx_rot():
    strdata=axis_entry.get()
    strlist = re.findall('[0-9-.]+', strdata)
    axis = np.array([float(strlist[0]), float(strlist[1]), float(strlist[2])])
    angle_str = angle_entry.get()
    angle = float(angle_str)
    M1 = mol.pg.rotation(axis, angle*np.pi/180)
    text3.delete("1.0", "end")
    text3.insert( 0., M1 )
    for k in range(3):
        print(M1[k])
    print()
   
def mtx_ref():
    strdata=normal_entry.get()
    strlist = re.findall('[0-9-.]+', strdata)
    new_w = np.array([float(strlist[0]), float(strlist[1]), float(strlist[2])])
    M2 = mol.pg.reflection(new_w) 
    text3.delete("1.0", "end")
    text3.insert( 0., M2 )
    for k in range(3):
        print(M2[k])
    print()

if __name__ == '__main__':    
    root = tk.Tk()
    root.title('分子の模型の点群表示')
    root.geometry("850x600")
    app = AppOgl(root, width=600, height=600)
    app.place(x=0, y=0)
    app.animate = 1

    matrix_label = tk.Label(text='matrix M1', font = ('MS Gothic', 12),
                     foreground = 'black', background = 'cyan' )
    matrix_label.place(x=620,y=10)
    text = tk.Text(master=root, width=30, height=4)
    text.place(x=620,y=30)
    matrix_label2 = tk.Label(text='matrix M2', font = ('MS Gothic', 12),
                     foreground = 'black', background = 'cyan' )
    matrix_label2.place(x=620,y=90)
    text2 = tk.Text(master=root, width=30, height=4)
    text2.place(x=620,y=110)
    matrix_label3 = tk.Label(text='result matrix', font = ('MS Gothic', 12),
                     foreground = 'black', background = 'cyan' )
    matrix_label3.place(x=620,y=170)
    text3 = tk.Text(master=root, width=30, height=7)
    text3.place(x=620,y=190)
    
    button = tk.Button(root, text='Product',font=("MSゴシック",
                            "15", "bold"), command=mtx_mult)
    button.place(x=620, y=300)    
    axis_label = tk.Label(text='axis', font = ('MS Gothic', 15),
                     foreground = 'black', background = 'cyan' )
    axis_label.place(x=620,y=350)
    axis_entry = tk.Entry(width=20)
    axis_entry.place(x=680,y=350)
    angle_label = tk.Label(text='angle', font = ('MS Gothic', 15),
                     foreground = 'black', background = 'cyan' )
    angle_label.place(x=620,y=390)
    angle_entry = tk.Entry(width=20)
    angle_entry.place(x=680,y=390)
    button2 = tk.Button(root, text='Rotation',font=("MSゴシック",
                            "15", "bold"), command=mtx_rot)
    button2.place(x=620, y=430)
    normal_label = tk.Label(text='normal', font = ('MS Gothic', 15),
                     foreground = 'black', background = 'cyan' )
    normal_label.place(x=620,y=490)
    normal_entry = tk.Entry(width=20)
    normal_entry.place(x=690,y=490)
    
    button3 = tk.Button(root, text='Reflection',font=("MSゴシック",
                            "15", "bold"), command=mtx_ref)
    button3.place(x=620, y=530)

    men = tk.Menu(root) 
    root.config(menu=men) 
    menu_file = tk.Menu(root, tearoff=0) 
    men.add_cascade(label='六方晶系', menu=menu_file) 
    menu_file.add_command(label='D6h', command=D6h) 
    menu_file.add_command(label='C6', command=C6)
    help_menu = tk.Menu(root, tearoff=0) 
    men.add_cascade(label="等軸晶系", menu=help_menu)
    help_menu.add_command(label="Oh", command=Oh)
のようなプログラムなどを作っていけば良いです。


「axis」に回転の軸のベクトルを [0,0,1] の様に、「angle」に60の様にセットし、「Rotation」の ボタンをクリックすれば、回転の行列が「result matrix」に表示され、「normal」に鏡映の mirror plane の normal vector を [0,0,1] の様にセットし、 「Reflection」のボタンをクリックすれば、鏡映の行列が「result matrix」に表示されます。 「matrix M1」と「matrix M2」に「result matrix」に表示される様に [[1,0,0],[0,1,0],[0,0,1]] の様にそれぞれセットし、「Product」の ボタンをクリックすれば、行列の積 M1 M2 が「result matrix」に表示されます。 注意が必要なのは、我々凡人が理解する時、図示したり、この様な数値計算より、手計算でチャンと正確な計算してみた方が良い場合もあります。 例えば、「The order of an N-fold rotoinversion is N for even N and 2N for odd N.」は回転の軸を z 軸とした N-fold rotation の行列と inversion の行列との積を W とする時、W×W, W×W×W を計算してみる方がこの文章が何を言っているか正確かつ容易に分かります。 一方、 2-fold rotoinversion は inversion の中心を通る回転軸に垂直な平面に関する鏡映であることは図を描けばすぐ分かります。 行列で合同変換を表現する時は、座標系を考え、原点が特別な意味を持っています。点対称変換(inversion)は2次元では回転ですが、3次元では handedness を保存しない変換（行列式が -1）で、「回転とinversion の合成」と「回転と鏡映(reflection)の合成」にどの様な関係があるかも調べておく必要があります。 The following equivalences hold:1―=S2,2―=m=S1,3―=S6−1,4―=S4−1 and 6―=S3−1 は、最初の2つは図を描いて、残りは 

import numpy as np

class Rotate:
    def rotate(self, n, r, theta):
        n = (1/np.sqrt(np.dot(n, n))) * n
        n_dot = np.dot(r, n)
        n_cross = np.cross(n, r)
        w = np.cos(theta)*r+n_dot*(1-np.cos(theta))*n+np.sin(theta)*n_cross
        return w
    def matrix(self, n, theta):
        t_mtx = []
        m1 = self.rotate(n, np.array([1.0, 0.0, 0.0]), theta)
        m2 = self.rotate(n, np.array([0.0, 1.0, 0.0]), theta)
        m3 = self.rotate(n, np.array([0.0, 0.0, 1.0]), theta)
        t_mtx.extend(m1)
        t_mtx.extend(m2)
        t_mtx.extend(m3)
        mtx = np.array(t_mtx, dtype=float).reshape(3, 3)
        mxt = np.transpose(mtx)
        return mtx

class Reflect:
    def matrix(self, n):
        I = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]])
        p1 = (1/np.sqrt(np.dot(n, n)))*n
        Q = np.array([[p1[0]*p1[0], p1[0]*p1[1], p1[0]*p1[2]], \
                  [p1[1]*p1[0], p1[1]*p1[1], p1[1]*p1[2]], \
                  [p1[2]*p1[0], p1[2]*p1[1], p1[2]*p1[2]]])
        S = I - 2*Q
        return S

def test():    
    rot = Rotate()
    ref = Reflect()
    n = np.array([0, 0, 1])
    M1 = np.array([[-1, 0, 0],[0, -1, 0], [0, 0, -1]])
    M2 = ref.matrix(n)
    M3 = rot.matrix(n, 2*np.pi/3)
    M4 = rot.matrix(n, 2*np.pi/4)
    M6 = rot.matrix(n, 2*np.pi/6)
    M31 = np.dot(M3, M1)
    M13 = np.dot(M1, M3)
    print('M31=', M31)
    print('M13=', M13)
    M62 = np.dot(M6, M2)
    M26 = np.dot(M2, M6)
    print('M62=', M62)
    print('M26=', M26)
    M162 = np.transpose(M62)
    M126 = np.transpose(M26)
    print('M162=', M162)
    print('M126=', M126)
    print()
    M41 = np.dot(M4, M1)
    M14 = np.dot(M1, M4)
    print('M41=', M41)
    print('M14=', M14)
    M42 = np.dot(M4, M2)
    M24 = np.dot(M2, M4)
    print('M42=', M42)
    print('M24=', M24)
    M142 = np.transpose(M42)
    M124 = np.transpose(M24)
    print('M142=', M142)
    print('M124=', M124)
    print()
    M61 = np.dot(M6, M1)
    M16 = np.dot(M1, M6)
    print('M61=', M61)
    print('M16=', M16)
    M32 = np.dot(M3, M2)
    M23 = np.dot(M2, M3)
    print('M32=', M32)
    print('M23=', M23)
    M132 = np.transpose(M32)
    M123 = np.transpose(M23)
    print('M132=', M132)
    print('M123=', M123)

test()
を実行して 

M31= [[ 0.5       -0.8660254  0.       ]
 [ 0.8660254  0.5        0.       ]
 [ 0.         0.        -1.       ]]
M13= [[ 0.5       -0.8660254  0.       ]
 [ 0.8660254  0.5        0.       ]
 [ 0.         0.        -1.       ]]
M62= [[ 0.5        0.8660254  0.       ]
 [-0.8660254  0.5        0.       ]
 [ 0.         0.        -1.       ]]
M26= [[ 0.5        0.8660254  0.       ]
 [-0.8660254  0.5        0.       ]
 [ 0.         0.        -1.       ]]
M162= [[ 0.5       -0.8660254  0.       ]
 [ 0.8660254  0.5        0.       ]
 [ 0.         0.        -1.       ]]
M126= [[ 0.5       -0.8660254  0.       ]
 [ 0.8660254  0.5        0.       ]
 [ 0.         0.        -1.       ]]

M41= [[-6.123234e-17 -1.000000e+00  0.000000e+00]
 [ 1.000000e+00 -6.123234e-17  0.000000e+00]
 [ 0.000000e+00  0.000000e+00 -1.000000e+00]]
M14= [[-6.123234e-17 -1.000000e+00  0.000000e+00]
 [ 1.000000e+00 -6.123234e-17  0.000000e+00]
 [ 0.000000e+00  0.000000e+00 -1.000000e+00]]
M42= [[ 6.123234e-17  1.000000e+00  0.000000e+00]
 [-1.000000e+00  6.123234e-17  0.000000e+00]
 [ 0.000000e+00  0.000000e+00 -1.000000e+00]]
M24= [[ 6.123234e-17  1.000000e+00  0.000000e+00]
 [-1.000000e+00  6.123234e-17  0.000000e+00]
 [ 0.000000e+00  0.000000e+00 -1.000000e+00]]
M142= [[ 6.123234e-17 -1.000000e+00  0.000000e+00]
 [ 1.000000e+00  6.123234e-17  0.000000e+00]
 [ 0.000000e+00  0.000000e+00 -1.000000e+00]]
M124= [[ 6.123234e-17 -1.000000e+00  0.000000e+00]
 [ 1.000000e+00  6.123234e-17  0.000000e+00]
 [ 0.000000e+00  0.000000e+00 -1.000000e+00]]

M61= [[-0.5       -0.8660254  0.       ]
 [ 0.8660254 -0.5        0.       ]
 [ 0.         0.        -1.       ]]
M16= [[-0.5       -0.8660254  0.       ]
 [ 0.8660254 -0.5        0.       ]
 [ 0.         0.        -1.       ]]
M32= [[-0.5        0.8660254  0.       ]
 [-0.8660254 -0.5        0.       ]
 [ 0.         0.        -1.       ]]
M23= [[-0.5        0.8660254  0.       ]
 [-0.8660254 -0.5        0.       ]
 [ 0.         0.        -1.       ]]
M132= [[-0.5       -0.8660254  0.       ]
 [ 0.8660254 -0.5        0.       ]
 [ 0.         0.        -1.       ]]
M123= [[-0.5       -0.8660254  0.       ]
 [ 0.8660254 -0.5        0.       ]
 [ 0.         0.        -1.       ]]
をチェックしてみれば、納得いきます。2次元の場合と同様に3次元の結晶群では制約があり、面白い法則が成り立ちます。別にこれを暗記する必要はないです。 若くて計算力に自信があれば、勿論こんなことしなくても良いです。 才能ある優秀な人達のようには「1を聞いて10を知る」とはいかず、 我々凡人は今学んでいることが自分にとって本当に必要な事なら「10を聞いて1を知る」で色々やってみる必要があります。 又、毛色の違う関連する2冊の本を交互に読んでいて、先を読むのが嫌になった時、本来読みたかった本の最初の方を読み返すと今まで理解せずに読み飛ばしていた処が どうゆう訳かこれはこうゆうことなのかと凄く良く理解できるようになっていることがあります。 超優秀な有名人が著書で「本は7回読みなさい！」と書いていることと趣旨は多分同じことだと思います。多分、無意識に考え続けているんだと思います。 昨日のプログラム 

def mtx_rot():
    strdata=normal_entry.get()
は 

def mtx_rot():
    strdata=axis_entry.get()
の間違いでした。上のプログラムは修正しています。コピーペーストすると良くこの様な事が起こります。 何をしたかと言うと「Rotation」のボタンの処理で 

def mtx_rot():
    strdata=axis_entry.get()
    strlist = re.findall('[0-9.]+', strdata)
で、チャンと動くと思って、次に「Reflection」のボタンの処理で 

def mtx_ref():
    strdata=normal_entry.get()
    strlist = re.findall('[0-9-.]+', strdata)
と負の数の時も正しく動くように「-」の符号も追加しておくべきだと気が付き、「Rotation」のボタンの処理も修正しなければいけないので、 「-」の符号を追加すれば良いだけなのに、めんどくさいと思って、１行コピーペーストするつもりが、この2行をコピーペーストしてしまい、 その後、削除する行を間違えて、 

def mtx_rot():
    strdata=normal_entry.get()
    strlist = re.findall('[0-9-.]+', strdata)
としてしまい、この様な事をすれば「normal」を「axis」に変更する必要があることを忘れた為に起こりました。 何時も合理的な行動をしている訳ではないみたいです。 メニューから選べば、それぞれの分子の模型の表示とその点群が 計算され打ち出されます。デフォルトは index=1 の立方体の対称群と同型な群になる場合にしています。片っ端から作っていけば良いです。 もし暇で他にすることがなければですが。多分、プログラムは間違ってはいないと思いますが、OpenGL のグラフィックスは複雑で、 どっかで思い違いがあり間違いに気が付いていない見たいで、思い通りに上手く描くことが出来ず、 まだよく理解できていません。遠近感が分かるように if self.n_model == 1: の場合として、透視法射影（透視投影）を使ったものも追加すべきかも？ 勿論、分子の模型もパソコン上の画像・アニメーションではなく、手に取って眺めることが出来る模型が良いのは言うまでもないですが、 多面体の模型を紙で作るのに比べると「市販の綺麗な作成セットにお金が掛る」か「粘土と竹の棒で自作すれば時間が掛り」大変です。 そう言うことが大好きなら問題はないですが？

２０２４年と年が代わったので、前から興味があった４次元正多胞体のグラフィックスをやってみることにします。 やっと高価なワークステーションが自由にメモリーの制限もなく使える恵まれた環境にいるエリートでなくても、 我々貧乏人の安価なパソコンでも無料で使えるオブジェクト指向言語の Python や numpy, sympy, opengl などの python のモジュール充実、 更には探索のアルゴリズムが枯れた技術になり、我々凡人でも自由に使いこなせるように環境が劇的に変化したので、 この様なグラフィックスが我々貧乏人の凡人でも楽しめる時代になりました。 基本的な参考書：一松信「監訳」岡田好一・日野雅之・宮崎興二「訳」H.S.M.コクセター「著」「正多胞体-高次元正多面体原論」丸善出版も最近出版されました。 原著のH.S.M.Coxeter著「REGULAR POLYTOPES」や銀林浩訳・コクセター著「幾何学入門」第二版などH.S.M.Coxeterさんの本は何冊か持っていますが、 読むこともなく本箱で埃を被っていました。 ４次元正多胞体は１９世紀後半にルートヴィッヒ・シェレーフリさんの論文で明らかになったそうで、数学的には解決済みでしょうが、数学やプログラミングの教材としては 面白いものだと思います。n次元正n+1胞体、正2n胞体、正2**n胞体は 図を描いてどの様なものか理解できますが、4次元の正24胞体、正120胞体、正600胞体は我々凡人は図が描けません。 上記の参考書やインターネットの情報で頂点の座標は簡単に知ることが出来るので、パソコンに絵を描いてもらって調べます。 頂点だけ描画しても我々凡人は何を描いているか理解できないので、辺（稜）も描く必要があります。 これは「正多胞体」なので、すべての頂点対に対して、最短距離の頂点対が辺（稜）を構成しているはずですから、パソコンで簡単に見つけることが出来ます。 そのようにして見つけた情報を元に描画しますが、 静止画ではなく、3次元に正射影し、opengl を使い、回転する動画のプログラミングを作りました。 ４次元空間の任意の法線ベクトルで指定する３次元部分空間に３種類の射影変換して描画することが出来るようにしています。 本などに載っている綺麗な図を描くにはどの様にすれば良いか勉強する必要があります。又、上記参考書やインターネットにはこれらの正多胞体について 色々な事が書いてありますが、我々凡人が理解するには、これらのモデルを元に、面を構成する頂点の組みをどの様にすればパソコンに探索させることが 出来るか？、そのアルゴリズムを考える必要があります。例えば、一つの頂点に隣接する2辺で張られる平面上にある頂点達を連立方程式を解くことで見つければ、 その頂点に隣接する正多角形を決定できます。 それが分かれば、今度は正多面体を構成している頂点の組みを見つけるアルゴリズムを考える 必要があります。これも同様の考えで各頂点に隣接する正多面体を決定できます。線形代数の一つの使い方で線形代数の素晴らしい処です。 例えば、正2n多胞体の隣接関係を求めるプログラムは 
import numpy as np
from numpy.linalg import solve
import copy

class GeneralCube:
    def __init__(self, dim):
        self.dim = dim
        self.v =[]
        self.e = []
        self.v, self.e = self.get_single_polytope_inf()
        for k in range(len(self.v)):
            e_list = []
            for i, edge in enumerate(self.e):
                if k in edge:
                    e_list.append(i)
            self.v[k] = [self.v[k],[e_list]]
        self.get_single_polytope_face_inf()
               
    def get_single_cube_vertex(self, t, v):
        if len(t) == self.dim:
            v.append(t)
            return
        for i in range(-1, 2, 2):
            old_t = copy.copy(t)
            t.append(i)
            self.get_single_cube_vertex(t, v)
            t = copy.copy(old_t)

    def get_single_polytope_inf(self):
        v = []
        t = []
        self.get_single_cube_vertex(t, v)
        e = []
        for k in range(len(v)):
            for j in range(k+1, len(v)):
                p = np.array(v[k]) - np.array(v[j])
                if 4 == np.dot(p, np.transpose(p)):
                    e.append([k, j])
        return v, e
    
    def sub_get_combination(self, r, l, s, k):
        if len(s) == k:
            r.append(s)
            return
        new_l = l[:]
        for e in l:
            old_s = s[:]
            s.append(e)
            new_l.remove(e)
            self.sub_get_combination(r, new_l, s, k)
            s = old_s
            
    def get_combination(self, l, k):
        r = []
        self.sub_get_combination(r, l, [], k)
        return r
        
    def same_vectorP(self, v, w):
        for k in range(len(v)):
            if np.abs(v[k]-w[k])>0.0001:
                return False
        return True

    def get_edge_num(self, v1, v2):
        if v1 > v2:
            temp = v1
            v1 = v2
            v2 = temp
        return self.e.index([v1, v2])

    def sub_get_perm(self, r, l, s, k):
        if len(s)==k:
            r.append(s)
            return
        for e in l:
            old_s = s[:]
            s.append(e)
            new_l = l[:]
            new_l.remove(e)
            self.sub_get_perm(r, new_l, s, k)
            s = old_s
    def get_perm(self, l):
        r = []
        n = len(l)
        self.sub_get_perm(r, l, [], n)
        return r

    def new_faceP(self, V):
        pp = self.get_perm(V)
        for k in range(len(self.f)):
            for p in pp:
                if self.f[k][0] == p:
                    return False
        return True
        
    def get_single_polytope_face_inf(self):
        self.f = []
        for k, v_inf in  enumerate(self.v):
            pair = self.get_combination(v_inf[1][0], 2)
            for p in pair:
                a1 = self.v[self.e[p[0]][0]][0]
                a2 = self.v[self.e[p[0]][1]][0]
                b1 = self.v[self.e[p[1]][0]][0]
                b2 = self.v[self.e[p[1]][1]][0]
                if self.same_vectorP(a1, v_inf[0]):
                    e1 = np.array(a2) - np.array(a1)
                    v1 = self.e[p[0]][1]
                else:
                    e1 = np.array(a1) - np.array(a2)
                    v1 = self.e[p[0]][0]
                if self.same_vectorP(b1, v_inf[0]):
                    e2 = np.array(b2) - np.array(b1)
                    v2 = self.e[p[1]][1]
                else:
                    e2 = np.array(b1) - np.array(b2)
                    v2 = self.e[p[1]][0]
                l = [i for i in range(self.dim)]
                pair2 = self.get_combination(l, 2)
                for p2 in pair2:
                    left = np.array([[e1[p2[0]], e2[p2[0]]],
                                     [e1[p2[1]], e2[p2[1]]]])
                    det = np.linalg.det(left)
                    if np.abs(det) > 0.01:
                        ind1 = p2[0]
                        ind2 = p2[1]
                        break
                for i, v_inf2 in  enumerate(self.v):
                    a = v_inf2[0][ind1]-v_inf[0][ind1]
                    b = v_inf2[0][ind2]-v_inf[0][ind2]                
                    right = np.array([a, b])
                    sol = solve(left, right)
                    if np.abs(sol[0])>0.1 and np.abs(sol[1])>0.1:
                        ## 検算
                        L = sol[0]*e1+sol[1]*e2
                        R = np.array(v_inf2[0])-np.array(v_inf[0])
                        if self.same_vectorP(L, R):
                            ## self.v[i] は側面上にある
                            ## ここで面は４角形を仮定している事に注意。他の場合は修正必要
                            e3 = self.get_edge_num(v1, i)
                            e4 = self.get_edge_num(v2, i)
                            if self.new_faceP([k, v1, i, v2]):
                                self.f.append([[k, v1, i, v2], [p[0], e3, e4, p[1]]])
        ## self.v の修正
        for k in range(len(self.v)):
            f_list = []
            for i in range(len(self.f)):
                if k in self.f[i][0]:
                    f_list.append(i)
            self.v[k] = [self.v[k][0], [self.v[k][1][0], f_list]]
        ## self.e の修正
        for k in range(len(self.e)):
            f_list = []
            for i in range(len(self.f)):
                if k in self.f[i][1]:
                    f_list.append(i)
            self.e[k] = [self.e[k], f_list]

cube = GeneralCube(3)
print('cube.v=', cube.v)
print()
print('cube.e=', cube.e)
print()
print('cube.f=', cube.f)
の様なもので良く、プロならもっと良いプログラムを作るはずですが、この様に定義通り忠実に作れば、例えば、立方体の隣接情報は 
cube.v= [[[-1, -1, -1], [[0, 1, 2], [0, 1, 2]]], [[-1, -1, 1], [[0, 3, 4], [0, 1, 3]]], 
[[-1, 1, -1], [[1, 5, 6], [0, 2, 4]]], [[-1, 1, 1], [[3, 5, 7], [0, 3, 4]]], 
[[1, -1, -1], [[2, 8, 9], [1, 2, 5]]], [[1, -1, 1], [[4, 8, 10], [1, 3, 5]]], 
[[1, 1, -1], [[6, 9, 11], [2, 4, 5]]], [[1, 1, 1], [[7, 10, 11], [3, 4, 5]]]]

cube.e= [[[0, 1], [0, 1]], [[0, 2], [0, 2]], [[0, 4], [1, 2]], [[1, 3], [0, 3]], 
[[1, 5], [1, 3]], [[2, 3], [0, 4]], [[2, 6], [2, 4]], [[3, 7], [3, 4]], [[4, 5], 
[1, 5]], [[4, 6], [2, 5]], [[5, 7], [3, 5]], [[6, 7], [4, 5]]]

cube.f= [[[0, 1, 3, 2], [0, 3, 5, 1]], [[0, 1, 5, 4], [0, 4, 8, 2]], 
[[0, 2, 6, 4], [1, 6, 9, 2]], [[1, 3, 7, 5], [3, 7, 10, 4]], 
[[2, 3, 7, 6], [5, 7, 11, 6]], [[4, 5, 7, 6], [8, 10, 11, 9]]]
で、正８胞体の隣接情報は cube.v= [[[-1, -1, -1, -1], [[0, 1, 2, 3], [0, 1, 2, 3, 4, 5]]], [[-1, -1, -1, 1], [[0, 4, 5, 6], [0, 1, 2, 6, 7, 8]]], [[-1, -1, 1, -1], [[1, 7, 8, 9], [0, 3, 4, 9, 10, 11]]], [[-1, -1, 1, 1], [[4, 7, 10, 11], [0, 6, 7, 9, 10, 12]]], [[-1, 1, -1, -1], [[2, 12, 13, 14], [1, 3, 5, 13, 14, 15]]], [[-1, 1, -1, 1], [[5, 12, 15, 16], [1, 6, 8, 13, 14, 16]]], [[-1, 1, 1, -1], [[8, 13, 17, 18], [3, 9, 11, 13, 15, 17]]], [[-1, 1, 1, 1], [[10, 15, 17, 19], [6, 9, 12, 13, 16, 17]]], [[1, -1, -1, -1], [[3, 20, 21, 22], [2, 4, 5, 18, 19, 20]]], [[1, -1, -1, 1], [[6, 20, 23, 24], [2, 7, 8, 18, 19, 21]]], [[1, -1, 1, -1], [[9, 21, 25, 26], [4, 10, 11, 18, 20, 22]]], [[1, -1, 1, 1], [[11, 23, 25, 27], [7, 10, 12, 18, 21, 22]]], [[1, 1, -1, -1], [[14, 22, 28, 29], [5, 14, 15, 19, 20, 23]]], [[1, 1, -1, 1], [[16, 24, 28, 30], [8, 14, 16, 19, 21, 23]]], [[1, 1, 1, -1], [[18, 26, 29, 31], [11, 15, 17, 20, 22, 23]]], [[1, 1, 1, 1], [[19, 27, 30, 31], [12, 16, 17, 21, 22, 23]]]] cube.e= [[[0, 1], [0, 1, 2]], [[0, 2], [0, 3, 4]], [[0, 4], [1, 3, 5]], [[0, 8], [2, 4, 5]], [[1, 3], [0, 6, 7]], [[1, 5], [1, 6, 8]], [[1, 9], [2, 7, 8]], [[2, 3], [0, 9, 10]], [[2, 6], [3, 9, 11]], [[2, 10], [4, 10, 11]], [[3, 7], [6, 9, 12]], [[3, 11], [7, 10, 12]], [[4, 5], [1, 13, 14]], [[4, 6], [3, 13, 15]], [[4, 12], [5, 14, 15]], [[5, 7], [6, 13, 16]], [[5, 13], [8, 14, 16]], [[6, 7], [9, 13, 17]], [[6, 14], [11, 15, 17]], [[7, 15], [12, 16, 17]], [[8, 9], [2, 18, 19]], [[8, 10], [4, 18, 20]], [[8, 12], [5, 19, 20]], [[9, 11], [7, 18, 21]], [[9, 13], [8, 19, 21]], [[10, 11], [10, 18, 22]], [[10, 14], [11, 20, 22]], [[11, 15], [12, 21, 22]], [[12, 13], [14, 19, 23]], [[12, 14], [15, 20, 23]], [[13, 15], [16, 21, 23]], [[14, 15], [17, 22, 23]]] cube.f= [[[0, 1, 3, 2], [0, 4, 7, 1]], [[0, 1, 5, 4], [0, 5, 12, 2]], [[0, 1, 9, 8], [0, 6, 20, 3]], [[0, 2, 6, 4], [1, 8, 13, 2]], [[0, 2, 10, 8], [1, 9, 21, 3]], [[0, 4, 12, 8], [2, 14, 22, 3]], [[1, 3, 7, 5], [4, 10, 15, 5]], [[1, 3, 11, 9], [4, 11, 23, 6]], [[1, 5, 13, 9], [5, 16, 24, 6]], [[2, 3, 7, 6], [7, 10, 17, 8]], [[2, 3, 11, 10], [7, 11, 25, 9]], [[2, 6, 14, 10], [8, 18, 26, 9]], [[3, 7, 15, 11], [10, 19, 27, 11]], [[4, 5, 7, 6], [12, 15, 17, 13]], [[4, 5, 13, 12], [12, 16, 28, 14]], [[4, 6, 14, 12], [13, 18, 29, 14]], [[5, 7, 15, 13], [15, 19, 30, 16]], [[6, 7, 15, 14], [17, 19, 31, 18]], [[8, 9, 11, 10], [20, 23, 25, 21]], [[8, 9, 13, 12], [20, 24, 28, 22]], [[8, 10, 14, 12], [21, 26, 29, 22]], [[9, 11, 15, 13], [23, 27, 30, 24]], [[10, 11, 15, 14], [25, 27, 31, 26]], [[12, 13, 15, 14], [28, 30, 31, 29]]] 
の様に一瞬で与えてくれます。これは

## 各頂点の座標と隣接する辺と面の番号
## 各辺を構成する頂点の番号,隣接する面の番号
## 各面を構成する頂点の番号,辺の番号


を計算しています。
面の情報までしか計算していませんが、胞の情報なども欲しければ簡単に拡張できます。既に使ってきたアルゴリズムを使っているだけです。
だから、昔は大学の一般教養で「線形代数」が開講されていました。「数式ソフト」があるから、直ぐにお金になることを教育しろ、
大学に数学者は必要ないとされましたが、日本の指導者層の短絡的で浅はかな馬鹿げた考えで、
パソコンの性能が向上し、誰でも高性能のパソコンが使えるようになったので、パソコンの有効活用のためには、一般の人達に、益々、数学の理解が必要になっています。
情報産業を支えているのは、新しいアルゴリズムの開発で、それを支えているのは数学の知識・技能です。
勿論、上記の参考書がスラスラ理解できればこんなことしなくても良いです。そんなことして何になると思っている方もいるはずですが、
例えば、「数独」のパズルを解く・或いは作るのが息抜きである人達が沢山いると思いますが、誰でも簡単に「バックトラッキング」のアルゴリズムを
使えば、「数独」を一瞬で解くプログラムを作れるのに、そんなものが何で面白いんだと言うのと同じことです。
多分、中学校で立方体の切断面がどうなるか習う様に、これら正多胞体の切断も面白いみたいだし、更には、5次元超立方格子の断面として
２次元の非周期模様が構成できると言う昔の研究もあるので、それらにも挑戦してみたいです。
（更には、4次元の合同変換は、２次元や３次元の合同変換の様に、具体的な分かりやすい形に分類できるかと言う問題もあります。既に出来ているだろうか？）
これらが我々凡人が出来る「帰納」と「類比」と「パソコンに依る計算・探索」です。「スローガン」が３つだと我々凡人でも覚えることが出来ます。
２・３０年前は高性能で高価なワークステーションでないと
出来なかったことが今では誰でも「線形代数(連立方程式の解法、正規直交基底の作り方、ベクトル・行列・合同変換などの基本的な知識など：
数学者の書いた参考書が理解できても出来なくても、Philip N. Klein著「行列プログラマー　Pythonプログラムで学ぶ線形代数」を読んで見れば良いです。)」や
「群論の基礎知識」や
「Python(list や dictionary や class や再帰呼び出し(かって人工知能と呼ばれ今は誰でも知っている枯れた技術になっている色々な探索のアルゴリズムの理解)や
 numpy や sympy や tkinter や turtle graphics や pyopengl や
高望みかも分かりませんが可能であれば C++ を使った Python の module の作り方（これらは今まで上で書いてきたことですが）などの基本的知識・技能)」が
理解できれば安価なパソコンで確かめることが可能になっています。立方体などの知っていることから、したいことを一つ一つ確かめながら、階段を昇れば良いです。
即ち、我々凡人は良く知っている立方体でまず頂点の情報だけから、辺や面をパソコンに探索させるプログラムや任意の平面で切断した時の断面を描画するプログラムを
作ってみて、正しいプログラムが作れるようになれば、他の３次元多面体や４次元、５次元、６次元、７次元、・・・、の多胞体へと拡張していけば良いです。
20数年ぐらい前に正多面体を平面で切りとる Java の apllet を作りましたが、（Javaの仕様が変更になり動かなくなりましたが）
その時は頂点。辺。面の隣接関係の情報を与えてプログラミングしましたが、
今回は頂点の座標の情報だけでプログラミングする必要があるので、立方体でチャンと出来るかプログラミングしてみます。
「正多胞体の頂点の座標はどうやって求めたんだ」と言う疑問は残りますが、今回はそこのところは目をつぶり過去の数学の天才達の結果を信じて使います。
これなら独学でも出来るはずです。但し、本にはミスプリントが付き物ですから、実際、インターネットの情報ほどではないですが間違っている本もあるので、
一冊の本の「正多胞体の頂点の座標データ」だけでなく、インターネットの情報や複数の本などで比較し正しいデータを使います。
色々な次元の立方格子を切って１次元、２次元、３次元非周期模様が作れることが
１９８９年初版の古い本ですが宮崎興二・石原慶一著「４次元グラフィックス　高次元 CG への道」朝倉書店に載っています。
これも現在は普通のパソコンを使って Python のプログラミングで我々凡人でも確かめることが出来るハズです。
世の中には、将棋や囲碁やチェスや象棋や奇妙な文字を使う外国語だけでなく、大してお金を掛けなくても楽しめる面白いものが一杯あります。
今、贅沢をするために他人を欺くことに必死な人達ばかりが目に付く世の中になりましたが、
こんなお金にもならない暇つぶしをする余裕が持てる平穏で、しかし、質素な生活が何とか送れるのは有難いことです。


「とさのさと」と言う農協の高知県全体のお百姓さん達（農作物だけでなく、手作りの弁当や羊羹やお寿司なども売っていますが）の為の直販所で売っているのを見つけたので、
比べてみると「バイカオウレン」は枯れてしまったみたいで、又、購入しました。小さな可憐な花が咲きました。
どうもお皿に水を張って、小さな盆栽をその中に置いておかないといけなかった見たいです。「とさのさと」では、そうやって販売していました。
プログラミングは集中しないと作れないので、直ぐに植物の世話をすっかり忘れてしまうので、生き物を栽培・飼育するのは止めた方が良いみたいですが、
又、購入してしまいました。困ったもんです。「とさのさと」と「スーパーマーケット」と「免税で買い物ができるドラッグストア」が一ヶ所に並んであり、
週一位で「台湾と高知の直航便」が現在はあるので、台湾人の団体さんが定期的にやって来ます。我々庶民には困りものの「円安」ですが、
外国人には日本に来れば、かっての２倍ぐらい金持ちになったと実感でき、歓迎すべきことみたいです。



「5次元超立方格子の断面として２次元の非周期模様：ペンローズタイリングが構成できる」を理解するのが難しいです。
思い通りの図を描くためには、正確な窓のサイズを数学的に理論通り計算する必要がある
（例えば、１次元の場合は、|sin(θ)|+|cos(θ)|です。上の特殊な3次元の立方格子の場合は参考書に正確な値を書いてくれていますが、
（答えを書いてくれているのでそれを使えば良い。先を急ごう！と言う考えもありますが、どの様にして求めたんだろうと考えることが、
自分で新しいことを思い付く際の思考の糧になります。今はやりの「タイパ」が最善の戦略とは限りません。）
3次元の立方格子の一般の回転の場合や高次元の立方格子の一般の回転の場合の窓のサイズは、自分で計算する必要があります。
今の場合、「5次元超立方体を窓空間内に射影して生ずる立体（菱形20面体）内に存在する頂点のみを2次元に射影する」の意味が理解できない。
何を言っているか、5次元超立方体を3次元空間に射影すれば菱形20面体になるのか、プログラミングして、実験してみる必要があります。







そして、「菱形20面体」の模型を紙で作ってみて、「菱形20面体」や「菱形30面体」や「菱形12面体」を見比べて、どの様な関係があるかも調べて見ます。
「菱形30面体」から帯状の１０枚の面を取り除けば、「菱形20面体」ですが、「菱形30面体」は規則的に菱形の紙片を貼り付ければ出来ますが、
「菱形20面体」はひしゃげた形の多面体なのでどの様な形か正確に認識していないと意外と厄介です。「菱形12面体」は更に８枚面を取り除きます。
小中学生にやらせてみると良いです。小学校の先生が後に解説している「ストローの模型」も自分で作って、教室の棚に並べて展示しておくだけでも良いと思います。
パソコンで菱形を沢山描いた紙を沢山打ち出すだけですから、大してお金はかかりません。
私の様に不器用なものは「菱形12面体」は展開図で作る方が綺麗に作れます。
更には、針金で模型を作ってみると更に良いとは思いますが、私には出来ません。子供の事、近所の若者が鳥かごを針金を半田付けして作っていて、
近所の子供たちが作る様子を見に行っていました。才能があり上手に作れるようになれば、小遣い稼ぎが出来る様になります。
私が子供の頃は、皆、手作業で色々なものを作っていました。その人は次男だったので一時帰郷していただけで直ぐにいなくなりましたが。
骨組みだけの模型も多面体・多胞体を理解するのに役立ちます。
写真で見るプロの作った素人には無理だなと思う「金属の精巧な骨格模型」ではなく、素人でも手軽に作れる模型作成では「ポリドロン」と言う知育玩具が
有名ですがそんなに高額なお金を掛けなくても
世の中には優秀な人が実際は星の数ほどいて、様々な工夫をして、
大してお金を掛けなくても百均やDIYのホームセンターで揃う材料でどんな幾何学的な模型でも作れる方法を発表してくれている人がいます。
例えば、正多面体を「ストロー」で作る動画をアップしている人がいます。
ストロー（色々の色のストローがあります。「竹のストロー」もありますが「目の細かいノコギリ」が必要です。）と
タコ糸とタタミ針（この二つは動画で言っている様にテグスで代用できますが、
やってみるとタコ糸を使った方が作りやすいです。但し、テグスは釣具屋でも購入できますが、当然釣り用でテグスの量が多く結構高価ですが、
ホームセンターの工作用の細いものと異なり、種類が多く、太いものを手に入れることが出来、
これを使うと糸と同様の使い勝手だと思いました。タタミ針はこのタコ糸が使える針はありますかとホームセンターの店員さんに質問して教えて貰ったものですが、
2本組で238円で売っていて大きく長くて不器用な私には使い易いです。勿論、タコ糸が使える針なら何でも良いです。）と
針金（ステンレスの0.55mmが良いと動画では言っていましたが、骨組みの支えになり曲げやすいものなら材質（アルミや銅でも）や太さは何でもいいです）と
ハサミとラジオペンチと定規があれば良いです。任意の大きさのどんな多面体の模型でも作れます。
真似をして、手始めに「菱形20面体」や「菱形30面体」や「菱形12面体」の模型を作ってみれば良いです。動画で解説している様には作らなくても
各面が三角形なら針金は要りませんがそうでなけれな針金を通して動かないようにし、適当に糸を通して固定すれば良いです。
ストローの模型を大量に作ってインテリアとして商品化しインターネットで売りさばこうと考えるなら、タコ糸の使用量を最適化するためにどの様な
順番で通せば良いかが収益を最大化するためにその解決が大問題になり、これは位相幾何学（グラフ理論）の問題になり、
普通はコンピュータで最適解を探すことになりますが、（所謂文科系の人達が役に立たないと思っている現代数学がこんな時にも役に立ちます。）、
個人が幾つか作ってみるのであれば、使用する糸の量など気にせずに適当に固定できたと思うまで糸を通せば良いです。
不器用な私が作っても売り物にはなりませんが、手に取って眺めればが多面体・多胞体の理解が深まります。
「針金をゴム紐」に変えて、小さな子供の為の知的遊具の作り方を紹介している人もいます。
楽に作れる方法は当然、作れる多面体が制限されたり、必要なお金の金額が多くなりますが、「綿棒」で作っている人や「鉄球と棒磁石」で作っている人もいます。
実物を見たことがありませんが「ゾムツール(Zome Tool)」と言うアメリカのゾムツール社が開発した数学的な立体を作る道具もあり、
正600胞体の投影図の模型を作るワークショップが開催されたこともあるそうです。
又、小学校の教員志望の学生さん達に教えていましたが、折り紙で正多面体の紙風船なども作ることも出来ます。正二十面体などは綺麗に作るのは難しいです。
複数の参考書があります。
針金細工の動画もあります。芸術作品作りが主流ですが、私は子供の頃、叔父に教えて貰い、針金で知恵の輪を作り遊んでいました。
才能がないので、教えて貰ったものしか作れませんでしたが。
現在は様々な材料で知恵の輪の作り方を解説した参考書もあります。もう絶版になっているかも分かりませんが。幾つか作ってみましたが、本箱の何処かにあるはずです。
現在は実際に作成している人の処に出かけなくてもやり方をインターネットで教えて貰えます。
コンピュータ・グラフィックスより手に取れる模型の方がより良く理解できるはずです。
「菱形20面体」の「ストローの骨格模型」も美術工芸品にはなりませし、私には正確な形に固定は出来ませんが紙の模型と見比べれば良いです。
お金持ちの子供なら楽に高価な教材・教具を使って勉強できますが、貧乏人の子供でも工夫すれば大してお金を掛けずに学ぶことが出来ますし、得るものが多いはずです。
「紙の模型」が最も手軽ですが、「ストローの模型」も内部が見えるので多面体・多胞体の構造を理解するのに有効です。作るのがめんどくさそうですが。
伝統的な「竹ひごや木片」を接着剤で付付けたり、「針金」を半田付けしたりすれば綺麗な骨格模型が作れ、商品にもなるはずですが、
作る多面体の正確な計量の知識（隣接する辺や面の間の角度や複数の長さの辺を使うのであればそれらの比率、更には接着による影響の補正が必要かも）や接着の技術が必要ですが、
「ストローの模型」はそのようなものは必要なく、辺（稜）の隣接関係（繋がり方：トポロジー）だけ理解していれば良く、組み立てた後で形を整えればよく、
小中学生でも手軽に作れます。最初に思いついた人は誰だか知りませんが、作ろうとする立体に関する細かな知識が無くても誰でも「ストローの模型」なら
作れることです。
沢山作ってみれば上手になります。多分。
私が作った不格好な立方体の骨格模型（更に、場合によっては、糸やテグスを追加して、空間に補助線を作って補えば）でも手に取って眺めると参考書に描かれている図が
どの方向から見たものか、それをコンピューターグラフィックスで描くためには立方体をどのように変換すれば良いか我々凡人にも容易に理解できます。
小説には名人・上手と言う人は材料の石や木を眺めれば、作るべきものが見えると書いていますが、我々凡人は、紙に描いた図形に補助線を引くことで幾何学の
問題が既に理解していることに還元され理解できるように、骨格模型に糸やテグスで空間に補助線を引くことが出来、理解を助けてくれます。






更には、４次元の正８胞体を
$$ \sqrt{1/2} \begin{pmatrix}
   1 & \cos(\pi/4) & \cos(2\pi/4) & \cos(3\pi/4) \\
   0 & \sin(\pi/4) & \sin(2\pi/4 & \sin(3\pi/4)  \\
   1 & \cos(3\pi/4) & \cos(6\pi/4) & \cos(9\pi/4) \\
   0 & \sin(3\pi/4) & \sin(6\pi/4 & \sin(9\pi/4)  \\
\end{pmatrix}
$$
で回転した後、３次元に正射影した図形（４次元の正８胞体の説明に良く使われる図形:4次元の多胞体を直接見ることは出来ないので、色々な方向から３次元空間や
２次元平面に
射影するか３次元の空間や２次元の平面での切断面を調べることにより４次元の多胞体を理解しようとします。
これは、一般の微分多様体に対して微分トポロジー(モース理論)でやられていたことでもあります。
一定の幅を持って切断すると面白い規則的な（非周期的な）模様が浮かび上がることが知られています。）のコンピューターグラフィックスを作り、
それを見ながら「ストローの模型」も作ってみると良いです。
一回目は作るだけでようようですが、２回目からは辺の色分けを工夫するなど
構造が理解しやすい骨格模型を作ることが出来るようになります。多分。
コンピュータ・グラフィックスは学んだ数学の知識がチャンと使えるか・チャンと理解できているか自分で確かめる為に使います。
又、コンピュータが射影などで描いた幾何学模様がどんな構造か探索する子分・助手としてパソコンは我々凡人には必要不可欠です。自分なりの学び方を見つけます。
他の次元の場合も使われている回転の行列や窓の中の取り出すべき頂点の範囲をどの様にして決定しているか理解する必要があります。
「類比」で考えれば良いですが、余次元が1なら射影が線分なので、幅で良いが、
2以上なら幅でなく射影した図形に含まれるかで判断する必要があると多分言っているみたいです。
パソコンが使えるので、プログラミングして図を描いてみて、思い付いたことを片っ端から確かめて、自分なりの理解をすれば良いです。
多分、それが自ら考え・学ぶと言うことです。）ので、
キチンと基本的な参考書：一松信著「高次元の正多面体」や
一松信「監訳」岡田好一・日野雅之・宮崎興二「訳」H.S.M.コクセター「著」「正多胞体-高次元正多面体原論」丸善出版を
読んで、正多胞体や合同変換に関する常識とされていることを自分なりの方法で理解しておく必要があります。正確なことをアウトプットする為には、
大量のインプットが必要です。


キチンと４次元の正多胞体から勉強した方が良いみたいです。
手始めに、中村義作著「四次元の幾何学　不思議な図形の世界をのぞく」BLUE BACKS で解説していることをプログラミングして確かめる必要があります。
色々の事を解説していますが、コンピュータを使って簡単に出来ることでは超立方体の射影と断面図を解説しています。この本の出版が昭和６１年（１９８６年）で、
宮崎興二・石原慶一著「４次元グラフィックス　高次元 CG への道」の出版が１９８９年ですから、４０年近く昔の事です。
当時、恵まれた環境にいたエリート達がやっていたことがやっと我々凡人でも安価なパソコンで楽しめるようになりました。
現在の恵まれた環境にいるエリート達は潤沢な資金でお金になる最先端の研究・商品開発をしているのに、
今更、こんなコンピューターグラフィックスの基本をやってみても仕方がない
だろうと言う話ですが、私も大学を退職して大分経ちますし、もうこれをしなければと言う義務もないし、暇つぶしには格好のテーマです。
「5次元超立方格子の断面として２次元の非周期模様：ペンローズタイリングが構成できる」はすぐには出来そうにないので、
正多胞体の射影と断面図を表示することから始めます。






の様なプログラムを作っています。最初は立方体を回転して断面図を描画するプログラムでしたが、中村義作さんの書いていることを読むと
視点を変化して、立方体を射影する平面を上下運動した方が断面図の変化が
分り易いので機能を増やし、４次元の正８胞体の射影と断面図の描画も出来るように、更には、すべての正多角形や４次元・５次元の正多胞体に拡張したいですが、
上の図のように出鱈目な図を描きます。手計算してみて、何処で間違えたか探すのに我々凡人は凄く時間が掛かります。
具体的には

    n = (1/np.sqrt(np.dot(n,n)))*n


とすべき処を

    n = (1/np.dot(n,n))*n


と間違えていました。「与えられた４次元ベクトル n に対して、n を含む正規直交基底{n, x, y, z}を見つける」計算が正しいか
間違っていそうな処で打ち出した値を使って調べる

import numpy as np

n= [0.25, 0.25, 0.25, 0.25]
x= [ 0.70710678,  0,          0,         -0.70710678]
y= [-0.40824829,  0.81649658,  0,         -0.40824829]
z= [-0.28867513, -0.28867513,  0.8660254,  -0.28867513]


##n= [0.5, 0.5, 0.5, 0.5]
##x= [ 0.70710678,  0,          0,        -0.70710678]
##y= [-0.40824829,  0.81649658,  0,        -0.40824829]
##z= [-0.28867513, -0.28867513,  0.8660254,  -0.28867513]

print('n, n=', np.dot(n, n))
print('x, x=', np.dot(x, x))
print('y, y=', np.dot(y, y))
print('z, z=', np.dot(z, z))

print('n, x=', np.dot(n, x))
print('n, y=', np.dot(n, y))
print('n, z=', np.dot(n, z))

print('x, x=', np.dot(x, y))
print('x, z=', np.dot(x, z))
print('y, z=', np.dot(y, z))


様なプログラムを実行してみて、n が単位ベクトルになっていないので、n を単位ベクトルに変換したつもりの処を調べ、
上の様な間違いをしている処を見つけ、修正して、新たに打ち出されたコメントアウトしているデータに変更すると
チャンと「与えられた４次元ベクトル n に対して、n を含む正規直交基底{n, x, y, z}を見つける」の計算の部分は間違っていないことも
分かるので、更にあるはずの別の間違えている処を探します。
本当は、個々に n を単位ベクトルに変換して、「与えられた４次元ベクトル n に対して、n を含む正規直交基底{n, x, y, z}を見つける」の計算の
関数を呼び出すのではなく、この関数の開始時点で n を単位ベクトルに変換するようにしておけばバグの発生を削減出来ました。
この様な事をバグがなくなったと思えるまで、我々凡人は繰り返す必要があります。
集中してやっても何日も悪戦苦闘する必要があります。一般的な場合は正しく描画するようになりましたが






まだ、特別な配置になるとこの様な図を描画します。これは誤差の処理を怠っていたのが原因でした。






と正しい描画をするようになりました。複雑な場合の例は






です。これで出来ていると思います。切断面の面の情報を計算して陰線処理をするか面を描き、面に色を付けた方が理解しやすいと思います。
これで、中村義作著「四次元の幾何学　不思議な図形の世界をのぞく」BLUE BACKS で解説している切断面が描けるようになったはずです。






これは正8胞体を平面で切った断面図を描画したものです。大きな画像は回転しているので見やすい図が得られませんでした。
やってみれば分かりますが我々凡人はいきなり４次元の多胞体を平面で切断した図を作ることは不可能なので、
（これは誤解を招く表現で、３次元空間の多面体の平面に依る切断面を求める為には、平面は交わるときは一般に平面図形で交わり、
その頂点は辺上の点ですから、多面体の各面に対して、面の周りのすべての辺と平面との交点を求め、見つかった２つの交点を結べば、
切断面の辺を見つけることが出来ますが、４次元の正8胞体を平面で切った断面図を求める為には、
宮崎興二・石原慶一著「４次元グラフィックス　高次元 CG への道」の８ページの図６，図７，図８で図解してくれている様に、
一般に直線との交わりは一点、多角形との交わりは線分、多面体との交わりは多角形ですから、正8胞体の各胞に対して、
その胞の周りの各多面体と平面の交線を求め、切断面の多角形を決定する必要があります。これも「類比」ではありますが、
ここで使った様に２段階で切断面を求める方が頂点と辺の情報から面や胞を決定する関数を作りかけているから良いと判断しました。
簡潔に言えば、前者は辺との交わりを計算すれば良いが、後者の場合は面との交わりを計算しないと切断面の辺が決定できないと言うことです。）
先ず空間で切断し、切断で出来る多面体（今の場合は正八面体）の構造をコンピュータに計算させ、頂点、辺、面の隣接関係を使って、
切断面の多面体を更に平面で切断します。まだ特別な配置の時、バグが顕在化する可能性が残っています。
早速バグが見つかりました。






辺の長さがバラバラだと厄介なので、頂点と辺の情報から面や胞などの情報を得る部分をモジュールにして、
切断面の構造をコンピュータに解析して貰っています。
この解析プログラムにバグがありました。
この様な２次元の図ではどの様になっているか分からないと思いますが、プログラムでは中央の大きな図は回転させているので、
赤い線は正八面体で、太い青い線は正六角形に対角線が引かれていることが見て取れます。この対角線はあってはいけない線です。
考えていたアルゴリズムでは、正八面体の中央の４個の辺で囲まれた正八面体内部の正方形も面として
カウントしていました。この正方形は正八面体の面ではないので取り除かなければなりません。
正八面体は凸ですから、位相幾何学の定理より、（こんな大げさな数学の定理を持ち出さなくても正八面体のストローの模型を眺めれば、
小学生でも気が付くことですが）「正方形の重心から一つ直線を引いて他の二つの面と交われば内部にある」ので、簡単に修正できます。
直線の引き方によっては頂点を通ることもあるので、その場合のチェックも当然必要です。細心の注意がプログラミングには必要で、
我々凡人は只管デバッグの作業を続けなければいけません。しかしこれはいい戦略ではありません。
各頂点に隣接する辺の集合から任意のペアーに対して、その２辺で構成される面を求めたので
この様な結果になりました。最初、立方体・超立方体だけ考えアルゴリズムを考え、
次に正四面体の様な三角形の面にも対応すべきだと気づいてアルゴリズムを修正しましたが、これらは頂点の次数が３の多面体で、
今度は正八面体に対応しなければならなくなり正八面体や正２０面体の様な頂点の次数が４や５の時にも通用するアルゴリズムに
修正することが必要になりました。すべての正多面体の模型を作り、眺めて、アルゴリズムを考えれば、良かったのですが、
我々凡人は適応範囲の狭い単純なアルゴリズムから始め、間違い・適応すべき範囲の拡大の必要性が見つかる度に修正し、
適用範囲の広い完全なアルゴリズムに近づけていくしか方法がありません。






の様に正しく描画されるようになりました。正８胞体は頂点の次数が４ですが一つの頂点の周りに６個の面が隣接しています。
我々凡人は頭の中でイメージすることが出来ないので、「ストローの模型」を作って、眺めながら考えます。
これは「紙の模型」でと言う訳にはいきません。amazon で調べると「ゾムツール(Zome Tool)」も取り扱っていて、
商品の画像を見ると良くできた教材みたいですが結構高価な教材です。George W. Hart 著「Zome Gemetry」2001 と言う参考書もあるそうです。

我々貧乏人は３次元に投影し、それを見ながら「ストローの模型」を作っていけば良いです。
正８胞体の「ストローの模型」はそのようにして作りました。
勿論、宮崎興二・石原慶一著「４次元グラフィックス　高次元 CG への道」の79ページからには各種投影図が掲載されていますが、
これを見て、正１２０胞体、正６００胞体の模型が作れるとも思いませんし、私には作るだけの根性もありません。
（George W. Hart 著「Zome Gemetry」2001 の記述を参考に正１２０面体の模型を作ったと言う人の投稿もあります。
この本を手に入れて、眺めてみると
George W. Hart 著「Zome Gemetry」2001 は基本的には３次元多面体の参考書で、３次元多面体に関しては様々な多面体を解説していますが、
「ゾムツール(Zome Tool)」による各種多面体の模型の作り方を懇切丁寧に解説している参考書ではありませんでした。
普通の多面体の参考書に近い補助教材です。各ユニットの最初に Challenge と題された問題が数個並んでいて、「ゾムツール(Zome Tool)」を
使って実験・実習して自分で解いてみなさいと言う形式になっています。ただ単に、「ゾムツール(Zome Tool)」で工作が出来ればよいと言うのではなく、
その後に、それに関する質問が続き、理解を深めることが出来るように構成されています。一時期、「実験数学」を提唱した人もいましたが、
日本では兎も角所謂偏差値の高い大学に合格させることが初等・中等教育に関わる人達の最大の義務・目標とされているので、普及はしなかったと思います。
しかし、数学を真に理解するためには、この様な訓練が有効だと思います。唯、これは、唯でさえ円安で高価な「ゾムツール(Zome Tool)」を使わなくても、
たいしてお金を掛けずに済む「紙の模型」や「ストローの模型」や「コンピュータグラフィックスのプログラミング」を組合すことで可能だと思います。
昔、LOGO が開発され、LOGO を使った教育が盛んに発信されましたが、いつの間にか消えて、今はその後継の Scratch が流行っている様に、
更には、KSEG や GeoGeba と言うソフトも子供たちが自ら幾何学の法則を発見するとの触れ込みで一時期流行りましたが、これも廃れた様に思いますが、
「ゾムツール(Zome Tool)」と言う教育用機材が開発され、それを使った幾何教育の教育例のサンプルの参考書です。
四次元多胞体に関しては殆ど記述がなく、僅かに正１２０面体の模型に関して２ページ分の記述がある位で、
これだけ読んで１２０面体の模型を作った人は凄く優秀な人だと思います。パット眺めただけでは私には作り方がこれで解説してあるとは思えません。）
作れなければ、「類比」で何とかしなければなりませんが、この様な貧乏くさい方法でも何とかなります。多分。
何を言っているかと言うと、私が今やっている方法だと3次元の射影した図形のデータがパソコン内にあるので、
思い付くプログラムを次々作れば、どの様な図形か解析できるので、
参考書の投影図を眺める以上の情報をプログラミングで取り出すことが出来ます。
才能ある優秀な人達はどの様にしているか知りませんが、我々凡人がいきなり完全なアルゴリズムを作るのは難しいです。
時間は掛かりますがこの様に単純なことから順番にやっていれば我々凡人でもその内出来上がります。多分。
頂点と隣接する辺の間の角度を計算し、どの様な順番で辺が配置しているか、頂点の周りの辺の配置を決定し、
連続する２辺で構成される面だけ求めればこの様な事は起こらなかったはずです。
我々凡人が真っ先に思いつくことは大抵役に立ちません。正八面体のストローの模型を眺めていれば、色々なアイデアが浮かんできます。
頭の中だけで考えるとこの様な見落としが必ずあるので、優秀な人達の真似をしても駄目で、見栄を張らずに、様々なパターンの模型を作って、
模型を見ながら作ればバグを減らせます。分かっていても面倒なのでやらずに、膨大な時間を無駄にします。失敗から全然学んでいません。

この様に、我々凡人の作ったプログラムでは、特殊な配置で必ずと言っても良いほどバグが見つかります。
更に、面に色を付けるなどの改良するなど綺麗な図を描画するにはやることが一杯あります。

かなり複雑な計算をさせているので描画のデータを準備するのに時間が掛かるので、
チャンとうごくPython のプログラムが出来れば、この計算の部分は C++ で作り、Python のモジュールを
作った方が快適だと思います。
最終的には正２４胞体、正１２０胞体、正６００胞体などの胞、面、辺、頂点の隣接関係を頂点の座標の情報だけから計算機に計算させる
アルゴリズムまで作りたいです。その道程は長いですがその内終わるはずです。
この様に計算機の力を借りれば、天才達には見えていただろう世界が我々凡人でも安価なパソコンを使って見ることが現在は出来るようになっています。
昭和の人間なので、バグを潰すのに、ディスプレイを見ることでは考えることが出来ないので、コンピュータが何をしているか調べるのに
大量のコピー用紙が必要です。パソコンが思い通りの結果を描き出すと嬉しいものです。
正8胞体を理解するための道具を作るのも結構大変です。しかも、理解できるようになる事は１９世紀には知られていたことです。
しかし、当時の天才達しか理解できなかったことが現在では、整備された線形代数とコンピュータの力を借りれば、我々凡人でもそれなりの時間を掛ければ理解できます。
才能ある優秀な人達はこの様な事はあっと言う間に理解して、凄いスピードで一気に駆け抜けて、最先端の研究領域に達するはずですが、
共に学ぶ朋友・仲間もいない、我々凡人は自分で必要な道具を一つ一つ手作りし、時間を掛けないと完全には理解できません。
唯、我々貧乏人でも現在は安価なパソコンが結構高性能になってき、高度なライブラリーも使える様になってきたので、
ここでやっている様にそれなりに時間を掛ければ何とか理解することが出来ます。
泥縄式にプログラミングしているので、プログラムがぐちゃぐちゃになってきたので、それぞれの機能別に別のファイルにし、
モジュールの呼び出しで、プログラムを構成しないと生産性が落ちるようになってきました。
更に、一つのプログラムに機能を詰め込みすぎると時が経つと作った本人も使い方が分からなくなるので、
３次元多面体の切断面描画用と４次元多胞体の投影図・切断面描画用に用途を分離した二つのソフトにします。












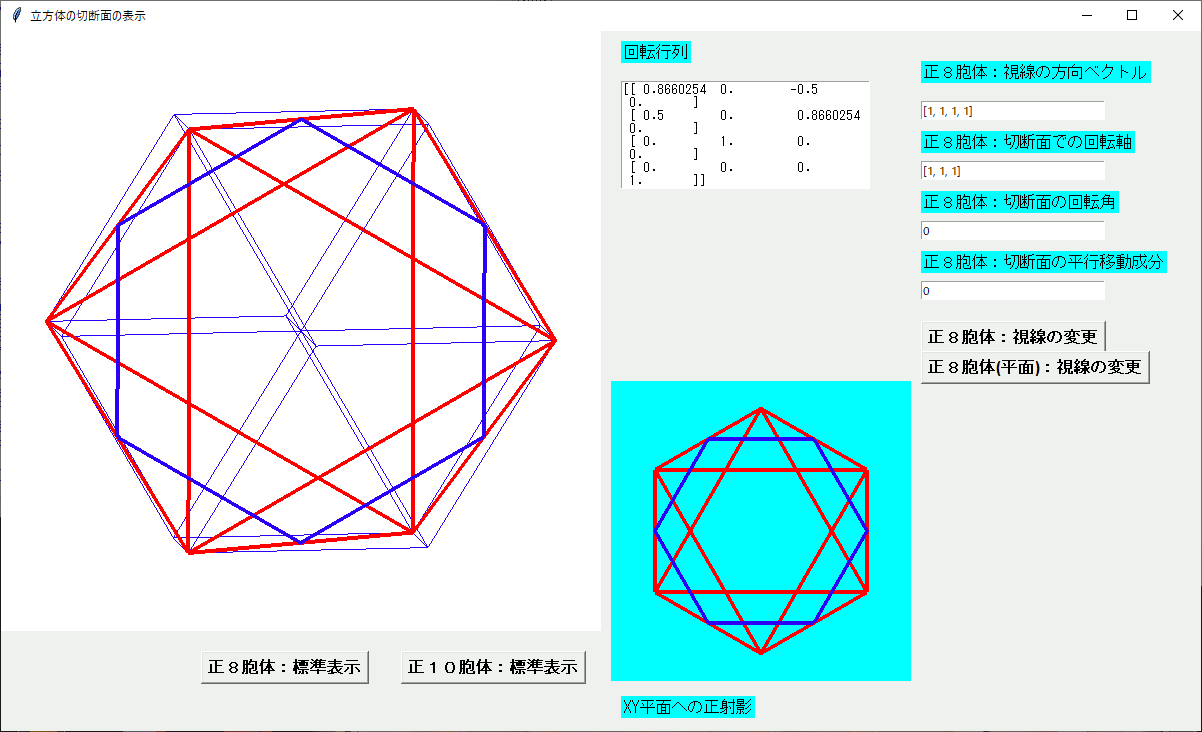
この様にモジュール化すると、例えば、頂点、辺、面、胞の隣接関係を計算するモジュールをデバッグ用と完成版と二通り作り使い分けるなど、
プログラミングが楽になります。
後の他の正多面体や4次元の他の正多胞体や5次元の正多胞体などの投影と切断面の描画も時間さえ掛ければ出来るハズです。
ここまで出来ると「5次元超立方格子の断面として２次元の非周期模様：ペンローズタイリングが構成できる」や
一松信著「高次元の正多面体」や
一松信「監訳」岡田好一・日野雅之・宮崎興二「訳」H.S.M.コクセター「著」「正多胞体-高次元正多面体原論」丸善出版に
挑戦できるんではと思います。これらの参考書の著者達が常識と思っていることを準備するには我々凡人は膨大な時間が必要です。

最近は、日中も何回にも分けて少しづつ寝ますが、起きて集中してやっている時ではなく、寝床でこうしたら良いと思い付きます。
９９パーセントはあそこで間違えているですが。
直前に提示した頂点の情報から辺や面の情報を導くプログラムを一般化し、面が三角形や五角形などでも大丈夫なように改良し、
更に４次元以上では胞の情報も表示するプログラムに作り変えました、


正8胞体の隣接関係は

len(cube.v)= 16 
cube.v= [[[-1, -1, -1, -1], [[0, 1, 2, 3], [0, 1, 2, 3, 4, 5], [0, 1, 2, 3]]], 
[[-1, -1, -1, 1], [[0, 4, 5, 6], [0, 1, 2, 6, 7, 8], [0, 1, 2, 4]]], [[-1, -1, 1, -1], [[1, 7, 8, 9], [0, 3, 4, 9, 10, 11], [0, 1, 3, 5]]], 
[[-1, -1, 1, 1], [[4, 7, 10, 11], [0, 6, 7, 9, 10, 12], [0, 1, 4, 5]]], [[-1, 1, -1, -1],[[2, 12, 13, 14], [1, 3, 5, 13, 14, 15], [0, 2, 3, 6]]], 
[[-1, 1, -1, 1], [[5, 12, 15, 16], [1, 6, 8, 13, 14, 16], [0, 2, 4, 6]]], [[-1, 1, 1, -1], [[8, 13, 17, 18], [3, 9, 11, 13, 15, 17], [0, 3, 5, 6]]], 
[[-1, 1, 1, 1], [[10, 15, 17, 19], [6, 9, 12, 13, 16, 17], [0, 4, 5, 6]]], [[1, -1, -1, -1], [[3, 20, 21, 22], [2, 4, 5, 18, 19, 20], [1, 2, 3, 7]]], 
[[1, -1, -1, 1], [[6, 20, 23, 24], [2, 7, 8, 18, 19, 21], [1, 2, 4, 7]]], [[1, -1, 1, -1], 
[[9, 21, 25, 26], [4, 10, 11, 18, 20, 22], [1, 3, 5, 7]]], [[1, -1, 1, 1], [[11, 23, 25, 27], [7, 10, 12, 18, 21, 22], [1, 4, 5, 7]]], 
[[1, 1, -1, -1], [[14, 22, 28, 29], [5, 14, 15, 19, 20, 23], [2, 3, 6, 7]]], [[1, 1, -1, 1], [[16, 24, 28, 30], [8, 14, 16, 19, 21, 23], [2, 4, 6, 7]]], 
[[1, 1, 1, -1], [[18, 26, 29, 31], [11, 15, 17, 20, 22, 23], [3, 5, 6, 7]]], [[1, 1, 1, 1], [[19, 27, 30, 31], [12, 16, 17, 21, 22, 23], [4, 5, 6, 7]]]]

len(cube.e)= 32 
cube.e= [[[0, 1], [0, 1, 2], [0, 1, 2]], [[0, 2], [0, 3, 4], [0, 1, 3]], [[0, 4], [1, 3, 5], [0, 2, 3]], [[0, 8], [2, 4, 5], [1, 2, 3]], 
[[1, 3], [0, 6, 7], [0, 1, 4]], [[1, 5], [1, 6, 8], [0, 2, 4]], [[1, 9], [2, 7, 8], [1, 2, 4]], [[2, 3], [0, 9, 10], [0, 1, 5]], 
[[2, 6], [3, 9, 11], [0, 3, 5]], [[2, 10], [4, 10, 11], [1, 3, 5]], [[3, 7], [6, 9, 12], [0, 4, 5]], [[3, 11], [7, 10, 12], [1, 4, 5]], 
[[4, 5], [1, 13, 14], [0, 2, 6]], [[4, 6], [3, 13, 15], [0, 3, 6]], [[4, 12], [5, 14, 15], [2, 3, 6]], [[5, 7], [6, 13, 16], [0, 4, 6]], 
[[5, 13], [8, 14, 16], [2, 4, 6]], [[6, 7], [9, 13, 17], [0, 5, 6]], [[6, 14], [11, 15, 17], [3, 5, 6]], [[7, 15], [12, 16, 17], [4, 5, 6]], 
[[8, 9], [2, 18, 19], [1, 2, 7]], [[8, 10], [4, 18, 20], [1, 3, 7]], [[8, 12], [5, 19, 20], [2, 3, 7]], [[9, 11], [7, 18, 21], [1, 4, 7]], 
[[9, 13], [8, 19, 21], [2, 4, 7]], [[10, 11], [10, 18, 22], [1, 5, 7]], [[10, 14], [11, 20, 22], [3, 5, 7]], [[11, 15], [12, 21, 22], [4, 5, 7]], 
[[12, 13], [14, 19, 23], [2, 6, 7]], [[12, 14], [15, 20, 23], [3, 6, 7]], [[13, 15], [16, 21, 23], [4, 6, 7]], [[14, 15], [17, 22, 23], [5, 6, 7]]]

len(cube.f)= 24 
cube.f= [[[0, 1, 3, 2], [0, 4, 7, 1], [0, 1]], [[0, 1, 5, 4], [0, 5, 12, 2], [0, 2]], [[0, 1, 9, 8], [0, 6, 20, 3], [1, 2]], 
[[0, 2, 6, 4], [1, 8, 13, 2], [0, 3]], [[0, 2, 10, 8], [1, 9, 21, 3], [1, 3]], [[0, 4, 12, 8], [2, 14, 22, 3], [2, 3]], 
[[1, 3, 7, 5], [4, 10, 15, 5], [0, 4]], [[1, 3, 11, 9], [4, 11, 23, 6], [1, 4]], [[1, 5, 13, 9], [5, 16, 24, 6], [2, 4]], 
[[2, 3, 7, 6], [7, 10, 17, 8], [0, 5]], [[2, 3, 11, 10], [7, 11, 25, 9], [1, 5]], [[2, 6, 14, 10], [8, 18, 26, 9], [3, 5]], 
[[3, 7, 15, 11], [10, 19, 27, 11], [4, 5]], [[4, 5, 7, 6], [12, 15, 17, 13], [0, 6]], [[4, 5, 13, 12], [12, 16, 28, 14], [2, 6]], 
[[4, 6, 14, 12], [13, 18, 29, 14], [3, 6]], [[5, 7, 15, 13], [15, 19, 30, 16], [4, 6]], [[6, 7, 15, 14], [17, 19, 31, 18], [5, 6]], 
[[8, 9, 11, 10], [20, 23, 25, 21], [1, 7]], [[8, 9, 13, 12], [20, 24, 28, 22], [2, 7]], [[8, 10, 14, 12], [21, 26, 29, 22], [3, 7]], 
[[9, 11, 15, 13], [23, 27, 30, 24], [4, 7]], [[10, 11, 15, 14], [25, 27, 31, 26], [5, 7]], [[12, 13, 15, 14], [28, 30, 31, 29], [6, 7]]]

len(cube.c)= 8 
cube.c= [[[0, 1, 2, 4, 3, 5, 6, 7], [0, 1, 2, 4, 5, 7, 8, 12, 13, 10, 15, 17], [0, 1, 3, 6, 9, 13]], 
[[0, 1, 2, 8, 3, 9, 10, 11], [0, 1, 3, 4, 6, 7, 9, 20, 21, 11, 23, 25], [0, 2, 4, 7, 10, 18]], 
[[0, 1, 4, 8, 5, 9, 12, 13], [0, 2, 3, 5, 6, 12, 14, 20, 22, 16, 24, 28], [1, 2, 5, 8, 14, 19]], 
[[0, 2, 4, 8, 6, 10, 12, 14], [1, 2, 3, 8, 9, 13, 14, 21, 22, 18, 26, 29], [3, 4, 5, 11, 15, 20]], 
[[1, 3, 5, 9, 7, 11, 13, 15], [4, 5, 6, 10, 11, 15, 16, 23, 24, 19, 27, 30], [6, 7, 8, 12, 16, 21]], 
[[2, 3, 6, 10, 7, 11, 14, 15], [7, 8, 9, 10, 11, 17, 18, 25, 26, 19, 27, 31], [9, 10, 11, 12, 17, 22]], 
[[4, 5, 6, 12, 7, 13, 14, 15], [12, 13, 14, 15, 16, 17, 18, 28, 29, 19, 30, 31], [13, 14, 15, 16, 17, 23]], 
[[8, 9, 10, 12, 11, 13, 14, 15], [20, 21, 22, 23, 24, 25, 26, 28, 29, 27, 30, 31], [18, 19, 20, 21, 22, 23]]]


で与えられているはずです。中村義作著「四次元の幾何学　不思議な図形の世界をのぞく」の５４ページの超直方体の頂点、辺。面、胞の個数と
一致しているので多分正しいデータを打ち出しているはずです。確かめるには「ストローの模型」を調べて図を描いて
頂点の座標を使って頂点に番号を振り、隣接関係を調べれば良いですが、
めんどくさいので、この情報を使うプログラムを使って変なことが起これば見直せば良いです。正8胞体でも３次元の多面体の「類比」が
使えないことも多いので、正8胞体以外の「ストローの模型」を作って、アルゴリズムの適応範囲の拡張をする必要があります。
三次元の多面体は「ストローの模型」で正確なものが作れますが、四次元の多胞体を３次元の「ストローの模型」では正確なものを作るのは不可能なので、
「辺の繋がり方という位相幾何学的な情報」だけ正確に保存する模型を作ればいいです。
裕福で潤沢な資金があれば、「ゾムツール(Zome Tool)」の様な商品で、作成手引書とにらめっこして作れば、美しい模型が作れますが、
「ストローの模型」でも、例えば、正８胞体なら２種類の説明図をよく見ますが、それを見ながら兎も角作ってみれば良いです。
最初は失敗作を作ることになると思いますが、それを見て、面の中に辺を通してみたり、辺に応じてストローの長さを変えるなどして、
兎も角「辺の隣接関係は保つ」、自分が美しい（対称性の多い模型）と思う、良くやったと思う模型を作れば良いです。
「ストローの模型」の模型は正四面体の内部に新たな頂点を追加し、正四面体の４個の頂点と結べば綺麗な「ストローの模型」が作れます。
正１６胞体は「ストローの模型」と同様に正８面体の内部に新たな頂点を２個追加し、それぞれ元の正８面体の６個の頂点と結べば良いですが、
最後の２本の辺が既に作った他の辺と重なってしまいますが、「ストローの模型」なので無理やり追加すれば、出来たと言えば出来ます。
内部に作る辺の長さを工夫すれば、辺が重ならない、もっと見やすい模型が作れるはずです。
この失敗作を見ながら辺が重ならない「ストローの模型」を作ります。面が三角形なので、針金は使わなくても作成可能ですが、
それなりに複雑ですから、針金の芯を入れて、固定するようにすれば綺麗な模型が作れるはずです。私は不器用なので駄目ですが。
処で、一松信「監訳」岡田好一・日野雅之・宮崎興二「訳」H.S.M.コクセター「著」「正多胞体-高次元正多面体原論」丸善出版の１２１ページに
掲載されている正８角形の対角線の内、反対側と結ぶ対角線だけを除いたグラフで十分ではないかと言う疑問も湧きますが、
模型を手に取って眺めると正八面体からどの様にして作っているかも分かりますし、模型を眺めると様々な考えが浮かびますし、何より、
私の様な老人には手を動かし細かい作業をすることが老化防止になります。他の正多胞体は作るのは大変で、正２４胞体ぐらいは作ってみたいけど、
プログラムが未完成で準備できていないので、正２４胞体をパソコンに調べさせる事が出来ず、その構造をまだ理解していません。






不器用ですから、不細工な物しか作れませんが、正多胞体がどの様な物かは分かります。残念ながら他の趣味の本を読む時間が取れていません。

正5胞体の隣接関係は

len(cube.v)= 5 
cube.v= [[[0.5, -0.28867513459481287, -0.20412414523193148, -0.15811388300841897], [[0, 1, 2, 3], [0, 1, 2, 3, 4, 5], [0, 1, 2, 3]]], 
[[-0.5, -0.28867513459481287, -0.20412414523193148, -0.15811388300841897], [[0, 4, 5, 6], [0, 1, 2, 6, 7, 8], [0, 1, 2, 4]]], 
[[0, 0.5773502691896257, -0.20412414523193148, -0.15811388300841897], [[1, 4, 7, 8], [0, 3, 4, 6, 7, 9], [0, 1, 3, 4]]], 
[[0, 0, 0.6123724356957945, -0.15811388300841897], [[2, 5, 7, 9], [1, 3, 5, 6, 8, 9], [0, 2, 3, 4]]], 
[[0, 0, 0, 0.6324555320336759], [[3, 6, 8, 9], [2, 4, 5, 7, 8, 9], [1, 2, 3, 4]]]]

len(cube.e)= 10 
cube.e= [[[0, 1], [0, 1, 2], [0, 1, 2]], [[0, 2], [0, 3, 4], [0, 1, 3]], [[0, 3], [1, 3, 5], [0, 2, 3]], 
[[0, 4], [2, 4, 5], [1, 2, 3]], [[1, 2], [0, 6, 7], [0, 1, 4]], [[1, 3], [1, 6, 8], [0, 2, 4]], [[1, 4], [2, 7, 8], [1, 2, 4]], 
[[2, 3], [3, 6, 9], [0, 3, 4]], [[2, 4], [4, 7, 9], [1, 3, 4]], [[3, 4], [5, 8, 9], [2, 3, 4]]]

len(cube.f)= 10 
cube.f= [[[0, 1, 2], [0, 1, 4], [0, 1]], [[0, 1, 3], [0, 2, 5], [0, 2]], [[0, 1, 4], [0, 3, 6], [1, 2]], 
[[0, 2, 3], [1, 2, 7], [0, 3]], [[0, 2, 4], [1, 3, 8], [1, 3]], [[0, 3, 4], [2, 3, 9], [2, 3]], [[1, 2, 3], [4, 5, 7], [0, 4]], 
[[1, 2, 4], [4, 6, 8], [1, 4]], [[1, 3, 4], [5, 6, 9], [2, 4]], [[2, 3, 4], [7, 8, 9], [3, 4]]]

len(cube.c)= 5 
cube.c= [[[0, 1, 2, 3], [0, 1, 2, 4, 5, 7], [0, 1, 3, 6]], [[0, 1, 2, 4], [0, 1, 3, 4, 6, 8], [0, 2, 4, 7]], 
[[0, 1, 3, 4], [0, 2, 3, 5, 6, 9], [1, 2, 5, 8]], [[0, 2, 3, 4], [1, 2, 3, 7, 8, 9], [3, 4, 5, 9]], 
[[1, 2, 3, 4], [4, 5, 6, 7, 8, 9], [6, 7, 8, 9]]]


で与えられます。
又、正16胞体の隣接関係は

len(cube.v)= 8 
cube.v= [[[1, 0, 0, 0], [[0, 1, 2, 3, 4, 5], [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11], [0, 1, 2, 3, 4, 5, 6, 7]]], 
[[-1, 0, 0, 0], [[6, 7, 8, 9, 10, 11], [12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23], [8, 9, 10, 11, 12, 13, 14, 15]]], 
[[0, 1, 0, 0], [[0, 6, 12, 13, 14, 15], [0, 1, 2, 3, 12, 13, 14, 15, 24, 25, 26, 27], [0, 1, 2, 3, 8, 9, 10, 11]]], 
[[0, -1, 0, 0], [[1, 7, 16, 17, 18, 19], [4, 5, 6, 7, 16, 17, 18, 19, 28, 29, 30, 31], [4, 5, 6, 7, 12, 13, 14, 15]]], 
[[0, 0, 1, 0], [[2, 8, 12, 16, 20, 21], [0, 4, 8, 9, 12, 16, 20, 21, 24, 25, 28, 29], [0, 1, 4, 5, 8, 9, 12, 13]]], 
[[0, 0, -1, 0], [[3, 9, 13, 17, 22, 23], [1, 5, 10, 11, 13, 17, 22, 23, 26, 27, 30, 31], [2, 3, 6, 7, 10, 11, 14, 15]]], 
[[0, 0, 0, 1], [[4, 10, 14, 18, 20, 22], [2, 6, 8, 10, 14, 18, 20, 22, 24, 26, 28, 30], [0, 2, 4, 6, 8, 10, 12, 14]]], 
[[0, 0, 0, -1], [[5, 11, 15, 19, 21, 23], [3, 7, 9, 11, 15, 19, 21, 23, 25, 27, 29, 31], [1, 3, 5, 7, 9, 11, 13, 15]]]]

len(cube.e)= 24 
cube.e= [[[0, 2], [0, 1, 2, 3], [0, 1, 2, 3]], [[0, 3], [4, 5, 6, 7], [4, 5, 6, 7]], 
[[0, 4], [0, 4, 8, 9], [0, 1, 4, 5]], [[0, 5], [1, 5, 10, 11], [2, 3, 6, 7]], 
[[0, 6], [2, 6, 8, 10], [0, 2, 4, 6]], [[0, 7], [3, 7, 9, 11], [1, 3, 5, 7]], 
[[1, 2], [12, 13, 14, 15], [8, 9, 10, 11]], [[1, 3], [16, 17, 18, 19], [12, 13, 14, 15]], 
[[1, 4], [12, 16, 20, 21], [8, 9, 12, 13]], [[1, 5], [13, 17, 22, 23], [10, 11, 14, 15]],
 [[1, 6], [14, 18, 20, 22], [8, 10, 12, 14]], [[1, 7], [15, 19, 21, 23], [9, 11, 13, 15]], 
[[2, 4], [0, 12, 24, 25], [0, 1, 8, 9]], [[2, 5], [1, 13, 26, 27], [2, 3, 10, 11]], 
[[2, 6], [2, 14, 24, 26], [0, 2, 8, 10]], [[2, 7], [3, 15, 25, 27], [1, 3, 9, 11]], 
[[3, 4], [4, 16, 28, 29], [4, 5, 12, 13]], [[3, 5], [5, 17, 30, 31], [6, 7, 14, 15]], 
[[3, 6], [6, 18, 28, 30], [4, 6, 12, 14]], [[3, 7], [7, 19, 29, 31], [5, 7, 13, 15]], 
[[4, 6], [8, 20, 24, 28], [0, 4, 8, 12]], [[4, 7], [9, 21, 25, 29], [1, 5, 9, 13]], 
[[5, 6], [10, 22, 26, 30], [2, 6, 10, 14]], [[5, 7], [11, 23, 27, 31], [3, 7, 11, 15]]]

len(cube.f)= 32 
cube.f= [[[0, 2, 4], [0, 2, 12], [0, 1]], [[0, 2, 5], [0, 3, 13], [2, 3]], 
[[0, 2, 6], [0, 4, 14], [0, 2]], [[0, 2, 7], [0, 5, 15], [1, 3]], [[0, 3, 4], [1, 2, 16], [4, 5]], 
[[0, 3, 5], [1, 3, 17], [6, 7]], [[0, 3, 6], [1, 4, 18], [4, 6]], [[0, 3, 7], [1, 5, 19], [5, 7]], 
[[0, 4, 6], [2, 4, 20], [0, 4]], [[0, 4, 7], [2, 5, 21], [1, 5]], [[0, 5, 6], [3, 4, 22], [2, 6]], 
[[0, 5, 7], [3, 5, 23], [3, 7]], [[1, 2, 4], [6, 8, 12], [8, 9]], [[1, 2, 5], [6, 9, 13], [10, 11]], 
[[1, 2, 6], [6, 10, 14], [8, 10]], [[1, 2, 7], [6, 11, 15], [9, 11]], [[1, 3, 4], [7, 8, 16], [12, 13]], 
[[1, 3, 5], [7, 9, 17], [14, 15]], [[1, 3, 6], [7, 10, 18], [12, 14]], [[1, 3, 7], [7, 11, 19], [13, 15]], 
[[1, 4, 6], [8, 10, 20], [8, 12]], [[1, 4, 7], [8, 11, 21], [9, 13]], [[1, 5, 6], [9, 10, 22], [10, 14]], 
[[1, 5, 7], [9, 11, 23], [11, 15]], [[2, 4, 6], [12, 14, 20], [0, 8]], [[2, 4, 7], [12, 15, 21], [1, 9]], 
[[2, 5, 6], [13, 14, 22], [2, 10]], [[2, 5, 7], [13, 15, 23], [3, 11]], [[3, 4, 6], [16, 18, 20], [4, 12]], 
[[3, 4, 7], [16, 19, 21], [5, 13]], [[3, 5, 6], [17, 18, 22], [6, 14]], [[3, 5, 7], [17, 19, 23], [7, 15]]]

len(cube.c)= 16 
cube.c= [[[0, 2, 4, 6], [0, 2, 4, 12, 14, 20], [0, 2, 8, 24]], 
[[0, 2, 4, 7], [0, 2, 5, 12, 15, 21], [0, 3, 9, 25]], [[0, 2, 5, 6], [0, 3, 4, 13, 14, 22], [1, 2, 10, 26]], 
[[0, 2, 5, 7], [0, 3, 5, 13, 15, 23], [1, 3, 11, 27]], [[0, 3, 4, 6], [1, 2, 4, 16, 18, 20], [4, 6, 8, 28]], 
[[0, 3, 4, 7], [1, 2, 5, 16, 19, 21], [4, 7, 9, 29]], [[0, 3, 5, 6], [1, 3, 4, 17, 18, 22], [5, 6, 10, 30]], 
[[0, 3, 5, 7], [1, 3, 5, 17, 19, 23], [5, 7, 11, 31]], [[1, 2, 4, 6], [6, 8, 10, 12, 14, 20], [12, 14, 20, 24]], 
[[1, 2, 4, 7], [6, 8, 11, 12, 15, 21], [12, 15, 21, 25]], [[1, 2, 5, 6], [6, 9, 10, 13, 14, 22], [13, 14, 22, 26]], 
[[1, 2, 5, 7], [6, 9, 11, 13, 15, 23], [13, 15, 23, 27]], [[1, 3, 4, 6], [7, 8, 10, 16, 18, 20], [16, 18, 20, 28]], 
[[1, 3, 4, 7], [7, 8, 11, 16, 19, 21], [16, 19, 21, 29]], [[1, 3, 5, 6], [7, 9, 10, 17, 18, 22], [17, 18, 22, 30]], 
[[1, 3, 5, 7], [7, 9, 11, 17, 19, 23], [17, 19, 23, 31]]]


で与えられているはずです。これは今までの単純なアルゴリズムでは計算できませんでした。
頂点０で

[[1, 0, 0, 0], [[0, 1, 2, 3, 4, 5], [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]]


の情報の頂点０に隣接している辺の集合 [0, 1, 2, 3, 4, 5] の任意の３個の辺を含む胞（多面体）を求めるのでは余計なものも含むので、
余計なものを除く必要があります。
データを打ち出し調べると辺の３組 [e1, e2, e3] の端点で辺で結ばれていない組がある場合には不要な胞（多面体）を見つけ出します。
しかし、正８胞体の場合はすべての辺の３組 [e1, e2, e3] の端点が辺で結ばれていないのでこれで判定するのは正１６胞体にしか通用しません。
正５胞体、正８胞体と矛盾しない判定法は辺の３組 [e1, e2, e3] に対して、同一の面に含まれないペアがある時も不要な胞（多面体）を見つけ出します。
この判定条件を追加し、胞を見つけるアルゴリズムを修正しました。単純なアルゴリズムなのに実装に半日掛かりました。情けないです。
正８面体の場合は、内部に含まれる面を削除する必要がありました。複雑な正多胞体の場合にもそんな事は起こらないでしょうか？
正２４胞体は現在の私のアルゴリズムでは、頂点２４個、辺９６本、正三角形の面９６個の面の情報までは計算してくれますが、
正八面体だと言う胞の情報は計算してくれません。

len(cube.v)= 24 
cube.v= [[array([1, 1, 0, 0]), [[0, 1, 2, 3, 4, 5, 6, 7], [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11], []]], 
[array([ 1, -1,  0,  0]), [[8, 9, 10, 11, 12, 13, 14, 15], [12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23], []]], 
[array([-1,  1,  0,  0]), [[16, 17, 18, 19, 20, 21, 22, 23], [24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35], []]], 
[array([-1, -1,  0,  0]), [[24, 25, 26, 27, 28, 29, 30, 31], [36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47], []]], 
[array([1, 0, 1, 0]), [[0, 8, 32, 33, 34, 35, 36, 37], [0, 1, 2, 12, 13, 14, 48, 49, 50, 51, 52, 53], []]], 
[array([ 1,  0, -1,  0]), [[1, 9, 38, 39, 40, 41, 42, 43], [3, 4, 5, 15, 16, 17, 54, 55, 56, 57, 58, 59], []]], 
[array([-1,  0,  1,  0]), [[16, 24, 44, 45, 46, 47, 48, 49], [24, 25, 26, 36, 37, 38, 60, 61, 62, 63, 64, 65], []]], 
[array([-1,  0, -1,  0]), [[17, 25, 50, 51, 52, 53, 54, 55], [27, 28, 29, 39, 40, 41, 66, 67, 68, 69, 70, 71], []]], 
[array([1, 0, 0, 1]), [[2, 10, 32, 38, 56, 57, 58, 59], [0, 3, 6, 12, 15, 18, 48, 54, 72, 73, 74, 75], []]], 
[array([ 1,  0,  0, -1]), [[3, 11, 33, 39, 60, 61, 62, 63], [1, 4, 7, 13, 16, 19, 49, 55, 76, 77, 78, 79], []]], 
[array([-1,  0,  0,  1]), [[18, 26, 44, 50, 64, 65, 66, 67], [24, 27, 30, 36, 39, 42, 60, 66, 80, 81, 82, 83], []]], 
[array([-1,  0,  0, -1]), [[19, 27, 45, 51, 68, 69, 70, 71], [25, 28, 31, 37, 40, 43, 61, 67, 84, 85, 86, 87], []]], 
[array([0, 1, 1, 0]), [[4, 20, 34, 46, 72, 73, 74, 75], [2, 8, 9, 26, 32, 33, 50, 51, 62, 63, 88, 89], []]], 
[array([ 0,  1, -1,  0]), [[5, 21, 40, 52, 76, 77, 78, 79], [5, 10, 11, 29, 34, 35, 56, 57, 68, 69, 90, 91], []]], 
[array([ 0, -1,  1,  0]), [[12, 28, 35, 47, 80, 81, 82, 83], [14, 20, 21, 38, 44, 45, 52, 53, 64, 65, 92, 93], []]], 
[array([ 0, -1, -1,  0]), [[13, 29, 41, 53, 84, 85, 86, 87], [17, 22, 23, 41, 46, 47, 58, 59, 70, 71, 94, 95], []]], 
[array([0, 1, 0, 1]), [[6, 22, 56, 64, 72, 76, 88, 89], [6, 8, 10, 30, 32, 34, 72, 73, 80, 81, 88, 90], []]], 
[array([ 0,  1,  0, -1]), [[7, 23, 60, 68, 73, 77, 90, 91], [7, 9, 11, 31, 33, 35, 76, 77, 84, 85, 89, 91], []]], 
[array([ 0, -1,  0,  1]), [[14, 30, 57, 65, 80, 84, 92, 93], [18, 20, 22, 42, 44, 46, 74, 75, 82, 83, 92, 94], []]], 
[array([ 0, -1,  0, -1]), [[15, 31, 61, 69, 81, 85, 94, 95], [19, 21, 23, 43, 45, 47, 78, 79, 86, 87, 93, 95], []]], 
[array([0, 0, 1, 1]), [[36, 48, 58, 66, 74, 82, 88, 92], [48, 50, 52, 60, 62, 64, 72, 74, 80, 82, 88, 92], []]], 
[array([ 0,  0,  1, -1]), [[37, 49, 62, 70, 75, 83, 90, 94], [49, 51, 53, 61, 63, 65, 76, 78, 84, 86, 89, 93], []]], 
[array([ 0,  0, -1,  1]), [[42, 54, 59, 67, 78, 86, 89, 93], [54, 56, 58, 66, 68, 70, 73, 75, 81, 83, 90, 94], []]], 
[array([ 0,  0, -1, -1]), [[43, 55, 63, 71, 79, 87, 91, 95], [55, 57, 59, 67, 69, 71, 77, 79, 85, 87, 91, 95], []]]]

len(cube.e)= 96 
cube.e= [[[0, 4], [0, 1, 2], []], [[0, 5], [3, 4, 5], []], [[0, 8], [0, 3, 6], []], [[0, 9], [1, 4, 7], []], 
[[0, 12], [2, 8, 9], []], [[0, 13], [5, 10, 11], []], [[0, 16], [6, 8, 10], []], [[0, 17], [7, 9, 11], []], 
[[1, 4], [12, 13, 14], []], [[1, 5], [15, 16, 17], []], [[1, 8], [12, 15, 18], []], [[1, 9], [13, 16, 19], 
[]], [[1, 14], [14, 20, 21], []], [[1, 15], [17, 22, 23], []], [[1, 18], [18, 20, 22], []], 
[[1, 19], [19, 21, 23], []], [[2, 6], [24, 25, 26], []], [[2, 7], [27, 28, 29], []], [[2, 10], [24, 27, 30], []], 
[[2, 11], [25, 28, 31], []], [[2, 12], [26, 32, 33], []], [[2, 13], [29, 34, 35], []], [[2, 16], [30, 32, 34], []], 
[[2, 17], [31, 33, 35], []], [[3, 6], [36, 37, 38], []], [[3, 7], [39, 40, 41], []], [[3, 10], [36, 39, 42], []], 
[[3, 11], [37, 40, 43], []], [[3, 14], [38, 44, 45], []], [[3, 15], [41, 46, 47], []], [[3, 18], [42, 44, 46], []], 
[[3, 19], [43, 45, 47], []], [[4, 8], [0, 12, 48], []], [[4, 9], [1, 13, 49], []], [[4, 12], [2, 50, 51], []], 
[[4, 14], [14, 52, 53], []], [[4, 20], [48, 50, 52], []], [[4, 21], [49, 51, 53], []], [[5, 8], [3, 15, 54], []], 
[[5, 9], [4, 16, 55], []], [[5, 13], [5, 56, 57], []], [[5, 15], [17, 58, 59], []], [[5, 22], [54, 56, 58], []], 
[[5, 23], [55, 57, 59], []], [[6, 10], [24, 36, 60], []], [[6, 11], [25, 37, 61], []], [[6, 12], [26, 62, 63], []], 
[[6, 14], [38, 64, 65], []], [[6, 20], [60, 62, 64], []], [[6, 21], [61, 63, 65], []], [[7, 10], [27, 39, 66], []], 
[[7, 11], [28, 40, 67], []], [[7, 13], [29, 68, 69], []], [[7, 15], [41, 70, 71], []], [[7, 22], [66, 68, 70], []], [
[7, 23], [67, 69, 71], []], [[8, 16], [6, 72, 73], []], [[8, 18], [18, 74, 75], []], [[8, 20], [48, 72, 74], []], 
[[8, 22], [54, 73, 75], []], [[9, 17], [7, 76, 77], []], [[9, 19], [19, 78, 79], []], [[9, 21], [49, 76, 78], []], 
[[9, 23], [55, 77, 79], []], [[10, 16], [30, 80, 81], []], [[10, 18], [42, 82, 83], []], [[10, 20], [60, 80, 82], []], 
[[10, 22], [66, 81, 83], []], [[11, 17], [31, 84, 85], []], [[11, 19], [43, 86, 87], []], [[11, 21], [61, 84, 86], []], 
[[11, 23], [67, 85, 87], []], [[12, 16], [8, 32, 88], []], [[12, 17], [9, 33, 89], []], [[12, 20], [50, 62, 88], []], 
[[12, 21], [51, 63, 89], []], [[13, 16], [10, 34, 90], []], [[13, 17], [11, 35, 91], []], [[13, 22], [56, 68, 90], []], 
[[13, 23], [57, 69, 91], []], [[14, 18], [20, 44, 92], []], [[14, 19], [21, 45, 93], []], [[14, 20], [52, 64, 92], []], 
[[14, 21], [53, 65, 93], []], [[15, 18], [22, 46, 94], []], [[15, 19], [23, 47, 95], []], [[15, 22], [58, 70, 94], []], 
[[15, 23], [59, 71, 95], []], [[16, 20], [72, 80, 88], []], [[16, 22], [73, 81, 90], []], [[17, 21], [76, 84, 89], []], 
[[17, 23], [77, 85, 91], []], [[18, 20], [74, 82, 92], []], [[18, 22], [75, 83, 94], []], [[19, 21], [78, 86, 93], []], 
[[19, 23], [79, 87, 95], []]]

len(cube.f)= 96 
cube.f= [[[0, 4, 8], [0, 2, 32], []], [[0, 4, 9], [0, 3, 33], []], [[0, 4, 12], [0, 4, 34], []], 
[[0, 5, 8], [1, 2, 38], []], [[0, 5, 9], [1, 3, 39], []], [[0, 5, 13], [1, 5, 40], []], [[0, 8, 16], [2, 6, 56], []], 
[[0, 9, 17], [3, 7, 60], []], [[0, 12, 16], [4, 6, 72], []], [[0, 12, 17], [4, 7, 73], []], [[0, 13, 16], [5, 6, 76], []], 
[[0, 13, 17], [5, 7, 77], []], [[1, 4, 8], [8, 10, 32], []], [[1, 4, 9], [8, 11, 33], []], 
[[1, 4, 14], [8, 12, 35], []], [[1, 5, 8], [9, 10, 38], []], [[1, 5, 9], [9, 11, 39], []], 
[[1, 5, 15], [9, 13, 41], []], [[1, 8, 18], [10, 14, 57], []], [[1, 9, 19], [11, 15, 61], [
]], [[1, 14, 18], [12, 14, 80], []], [[1, 14, 19], [12, 15, 81], []], [[1, 15, 18], [13, 14, 84], []], 
[[1, 15, 19], [13, 15, 85], []], [[2, 6, 10], [16, 18, 44], []], [[2, 6, 11], [16, 19, 45], []], 
[[2, 6, 12], [16, 20, 46], []], [[2, 7, 10], [17, 18, 50], []], [[2, 7, 11], [17, 19, 51], []], 
[[2, 7, 13], [17, 21, 52], []], [[2, 10, 16], [18, 22, 64], []], [[2, 11, 17], [19, 23, 68], []], 
[[2, 12, 16], [20, 22, 72], []], [[2, 12, 17], [20, 23, 73], []], [[2, 13, 16], [21, 22, 76], []], 
[[2, 13, 17], [21, 23, 77], []], [[3, 6, 10], [24, 26, 44], []], [[3, 6, 11], [24, 27, 45], []], 
[[3, 6, 14], [24, 28, 47], []], [[3, 7, 10], [25, 26, 50], []], [[3, 7, 11], [25, 27, 51], []], 
[[3, 7, 15], [25, 29, 53], []], [[3, 10, 18], [26, 30, 65], []], [[3, 11, 19], [27, 31, 69], []], 
[[3, 14, 18], [28, 30, 80], []], [[3, 14, 19], [28, 31, 81], []], [[3, 15, 18], [29, 30, 84], []], 
[[3, 15, 19], [29, 31, 85], []], [[4, 8, 20], [32, 36, 58], []], [[4, 9, 21], [33, 37, 62], []], 
[[4, 12, 20], [34, 36, 74], []], [[4, 12, 21], [34, 37, 75], []], [[4, 14, 20], [35, 36, 82], []], 
[[4, 14, 21], [35, 37, 83], []], [[5, 8, 22], [38, 42, 59], []], [[5, 9, 23], [39, 43, 63], []], 
[[5, 13, 22], [40, 42, 78], []], [[5, 13, 23], [40, 43, 79], []], [[5, 15, 22], [41, 42, 86], []], 
[[5, 15, 23], [41, 43, 87], []], [[6, 10, 20], [44, 48, 66], []], [[6, 11, 21], [45, 49, 70], []], 
[[6, 12, 20], [46, 48, 74], []], [[6, 12, 21], [46, 49, 75], []], [[6, 14, 20], [47, 48, 82], []],
 [[6, 14, 21], [47, 49, 83], []], [[7, 10, 22], [50, 54, 67], []], [[7, 11, 23], [51, 55, 71], []], 
[[7, 13, 22], [52, 54, 78], []], [[7, 13, 23], [52, 55, 79], []], [[7, 15, 22], [53, 54, 86], []], 
[[7, 15, 23], [53, 55, 87], []], [[8, 16, 20], [56, 58, 88], []], [[8, 16, 22], [56, 59, 89], []], 
[[8, 18, 20], [57, 58, 92], []], [[8, 18, 22], [57, 59, 93], []], [[9, 17, 21], [60, 62, 90], []], 
[[9, 17, 23], [60, 63, 91], []], [[9, 19, 21], [61, 62, 94], []], [[9, 19, 23], [61, 63, 95], []], 
[[10, 16, 20], [64, 66, 88], []], [[10, 16, 22], [64, 67, 89], []], [[10, 18, 20], [65, 66, 92], []], 
[[10, 18, 22], [65, 67, 93], []], [[11, 17, 21], [68, 70, 90], []], [[11, 17, 23], [68, 71, 91], []], 
[[11, 19, 21], [69, 70, 94], []], [[11, 19, 23], [69, 71, 95], []], [[12, 16, 20], [72, 74, 88], []], 
[[12, 17, 21], [73, 75, 90], []], [[13, 16, 22], [76, 78, 89], []], [[13, 17, 23], [77, 79, 91], []], 
[[14, 18, 20], [80, 82, 92], []], [[14, 19, 21], [81, 83, 94], []], [[15, 18, 22], [84, 86, 93], []], 
[[15, 19, 23], [85, 87, 95], []]]

len(cube.c)= 0 
cube.c= []


この計算結果を見ると頂点２４個、辺９６個、面９６個なので「正２４胞体の基本的な頂点の座標のデータ」は間違っていない事が分かります。
「立方体のストローの模型」を様々な方向から眺めると形が変わるように、射影図はどの方向から射影するかに依って、全然別の図になります。
よく見る「正２４胞体の標準的な射影図」がどの方向から射影すると得られるか、誰か答えを書いてくれてないか探して見つからなければ、
自分で試行錯誤で実験してみる必要があります。
差し当たって、宮崎興二・石原慶一著「４次元グラフィックス　高次元 CG への道」の１9ページの点心、線心、面心、胞心を確かめてみる必要があります。
更に、それを４次元の回転行列でどの様に表現できるか調べることも勉強になります。
時間は掛かりますが、経験値を上げることが出来ます。今、流行りの「タイパ」が最善とは限りません。
３個の辺で正八面体を見つけようと言うアイデアそのものが間違っています。
３次元の正八面体の模型を眺めて考える必要があります。３次元の空間に含まれる３個づつは一時独立な４個の辺が必要です。
菱形十二面体（３個でも可能な気もします？次数３の他の頂点で見つけることが出来るハズです。）も同様です。
正二十面体や菱形二十面体（３個でも可能な気もします？次数３の他の頂点で見つけることが出来るハズです。）が胞なら
３次元の空間に含まれる３個づつは一時独立な５個の辺が必要です
胞（多面体）が何か分かれば計算できるでは適応範囲が狭く大した意味がないので、
一般的に通用する胞となる多面体を確定・決定するアイデア・アルゴリズムは何か探す必要があります。
昔の才能ある優秀な人達は見つけたから何か方法があるはずです。
例えば、次のようなPythonプログラム

import numpy as np
##from Frame import *
from Icositetrachoron import *

cube = GeneralCube(4)
print('len(cube.v)=', len(cube.frame.v), 'cube.v=', cube.frame.v)
print()
print('len(cube.e)=', len(cube.frame.e), 'cube.e=', cube.frame.e)
print()
print('len(cube.f)=', len(cube.frame.f), 'cube.f=', cube.frame.f)
print()
print('len(cube.c)=', len(cube.frame.c), 'cube.c=', cube.frame.c)

e_list = cube.v[0][1][0]

def sub_get_combination(r, l, s, k):
    if len(s) == k:
        r.append(s)
        return
    new_l = l[:]
    for e in l:
        old_s = s[:]
        s.append(e)
        new_l.remove(e)
        sub_get_combination(r, new_l, s, k)
        s = old_s
            
def get_combination(l, k):
    r = []
    sub_get_combination(r, l, [], k)
    return r

A = get_combination(e_list, 4)
v = np.zeros(4*2*4).reshape(4,2,4)
V = np.zeros(4*4).reshape(4,4)
cnt = 0
cnt2 = 0
candidate = []
for k, M in enumerate(A):
    for i, e in enumerate(M):
        v[i][0] = cube.v[cube.e[e][0][0]][0]
        v[i][1] = cube.v[cube.e[e][0][1]][0]
    for i in range(4):
        if v[i][0][0] == cube.v[0][0][0] and v[i][0][1] == cube.v[0][0][1] and \
           v[i][0][2] == cube.v[0][0][2] and v[i][0][2] == cube.v[0][0][2]:
            V[i] = v[i][1]-v[i][0]
        else:
            V[i] = v[i][0]-v[i][1]
    MV = np.array(V)
    if np.linalg.matrix_rank(MV) == 3:
        ind = [i for i in range(4)]
        flag = True
        r_list = get_combination(ind, 3)
        for r in r_list:
            W = []
            for j in range(3):
                W.append(V[r[j]])
            MW = np.array(W)
            if np.linalg.matrix_rank(MW) < 3:
                flag = False
                break
        if flag == True:
            candidate.append([M, MV])
            cnt2 = cnt2+1
            
    if  np.linalg.det(MV) == 0:
        ind = [i for i in range(4)]
        r_list = get_combination(ind, 3)
        FLAG = True
        for r in r_list:
            c_list = get_combination(ind, 3)
            flag = True
            for c in c_list:
                W = []
                for j in range(3):
                    W.append([V[r[j]][c[0]], V[r[j]][c[1]], V[r[j]][c[2]]])
                MW = np.array(W)
                if  np.linalg.det(MW) != 0:
                    flag = True
                    break
            if flag == False:
                FLAG  = False
                break
        if FLAG == True:
            cnt = cnt+1

print('cnt2=', cnt2)
for k in range(cnt2):
    print('candidate[', k, ']=', candidate[k])

def same_vectorP(v, w):
    for k in range(len(v)):
        if np.abs(v[k]-w[k])>0.0001:
            return False
    return True

def sub_get_perm(r, l, s, k):
    if len(s)==k:
        r.append(s)
        return
    for e in l:
        old_s = s[:]
        s.append(e)
        new_l = l[:]
        new_l.remove(e)
        sub_get_perm(r, new_l, s, k)
        s = old_s
def get_perm(l):
    r = []
    n = len(l)
    sub_get_perm(r, l, [], n)
    return r

def new_c_listP(temp_C, c_list):
    perm = get_perm(c_list)
    for P in perm:
        if P in temp_C:
            return False
    return True

def octahedronP(a, v1, v2, v3, v4, b):
    check_list = [[a,v1],[a,v2],[a,v3],[a,v4],[b,v1],[b,v2],[b,v3],[b,v4]]
    for p in check_list:
        flag = False
        for k in range(len(cube.e)):
            if (p[0]==cube.e[k][0][0] and p[1]==cube.e[k][0][1]) or \
               (p[0]==cube.e[k][0][1] and p[1]==cube.e[k][0][0]):
                flag = True
                break
        if flag == False:
            return False
    check_list2 = [[[v1,v2],[v2,v3],[v3,v4],[v4,v1]],
                   [[v1,v2],[v2,v4],[v4,v3],[v3,v1]],
                   [[v1,v3],[v3,v2],[v2,v4],[v4,v1]]]
    for cycle in check_list2:
        for p in cycle:
            flag = False
            for k in range(len(cube.e)):
                if (p[0]==cube.e[k][0][0] and p[1]==cube.e[k][0][1]) or \
                   (p[0]==cube.e[k][0][1] and p[1]==cube.e[k][0][0]):
                    flag = True
                    break
            if flag == False:
                break
        if flag == True:
            return True
    return False

temp_C = []  
for k in range(len(candidate)):
    FLAG = False
    triple = get_combination(candidate[k][0], 3)
    for p in triple:
        e1 = candidate[k][1][candidate[k][0].index(p[0])]
        e2 = candidate[k][1][candidate[k][0].index(p[1])]
        e3 = candidate[k][1][candidate[k][0].index(p[2])]
        if cube.e[p[0]][0][0] == 0:
            v1 = cube.e[p[0]][0][1]
        else:
            v1 = cube.e[p[0]][0][0]
        if cube.e[p[1]][0][0] == 0:
            v2 = cube.e[p[1]][0][1]
        else:
            v2 = cube.e[p[1]][0][0]
        if cube.e[p[2]][0][0] == 0:
            v3 = cube.e[p[2]][0][1]
        else:
            v3 = cube.e[p[2]][0][0]
        for e in candidate[k][0]:
            if e != p[0] and  e != p[1] and e != p[2]:
                if cube.e[e][0][0] == 0:
                    v4 = cube.e[e][0][1]
                else:
                    v4 = cube.e[e][0][0]
                break
        l = [i for i in range(4)]
        triple2 = get_combination(l, 3)
        for p2 in triple2:
            left = np.array([[e1[p2[0]], e2[p2[0]], e3[p2[0]]],
                            [e1[p2[1]], e2[p2[1]], e3[p2[1]]],
                            [e1[p2[2]], e2[p2[2]], e3[p2[2]]]])
            det = np.linalg.det(left)
            if np.abs(det) > 0.01:
                ind1 = p2[0]
                ind2 = p2[1]
                ind3 = p2[2]
                break
        c_list = []
        ## search vertex
        for i, v_inf2 in enumerate(cube.v):
            a = v_inf2[0][ind1]-cube.v[0][0][ind1]
            b = v_inf2[0][ind2]-cube.v[0][0][ind2]
            c = v_inf2[0][ind3]-cube.v[0][0][ind3]
            right = np.array([a, b, c])
            sol = solve(left, right)
            if sol[0]>-0.01 or sol[1]>-0.01 or sol[2]>-0.01:
                if (np.abs(sol[0])>0.1 and np.abs(sol[1])>0.1) or \
                       (np.abs(sol[1])>0.1 and np.abs(sol[2])>0.1) or \
                       (np.abs(sol[0])>0.1 and np.abs(sol[2])>0.1):
                    ## 検算
                    L = sol[0]*e1+sol[1]*e2+sol[2]*e3
                    R = np.array(v_inf2[0])-np.array(cube.v[0][0])
                    if same_vectorP(L, R):
                        if i==0 or i==v1 or i==v2 or i==v3 or i==v4:
                            continue
                        if octahedronP(0, v1, v2, v3, v4, i):
                            if len(c_list) == 0:
                                c_list.append(0)
                                c_list.append(v1)
                                c_list.append(v2)
                                c_list.append(v3)
                                c_list.append(v4)
                            c_list.append(i)
                            FLAG =True
                            break
        if len(c_list)>0 and new_c_listP(temp_C, c_list):
            temp_C.append(c_list)
        break
        if FLAG == True:
            break
print('temp_C=', temp_C)


を実行してみる。頂点０に隣接する正八面体を全部見つけるプログラムです。前回提示していたプログラムも間違っていました。何度も作り直してやっと出来ました。
行列のランクの計算方法は色々考えられますが、numpy の rank() 関数を使うのが一番楽です。
かなりめんどくさいですが、numpy の det() 関数を使う方法も示しています。自分で手作業でするアルゴリズムを実装するのも勉強になります。

・・・
cnt2= 12
candidate[ 0 ]= [[0, 1, 2, 3], array([[ 0., -1.,  1.,  0.],
       [ 0., -1., -1.,  0.],
       [ 0., -1.,  0.,  1.],
       [ 0., -1.,  0., -1.]])]
candidate[ 1 ]= [[0, 1, 4, 5], array([[ 0., -1.,  1.,  0.],
       [ 0., -1., -1.,  0.],
       [-1.,  0.,  1.,  0.],
       [-1.,  0., -1.,  0.]])]
candidate[ 2 ]= [[0, 2, 4, 6], array([[ 0., -1.,  1.,  0.],
       [ 0., -1.,  0.,  1.],
       [-1.,  0.,  1.,  0.],
       [-1.,  0.,  0.,  1.]])]
candidate[ 3 ]= [[0, 2, 5, 7], array([[ 0., -1.,  1.,  0.],
       [ 0., -1.,  0.,  1.],
       [-1.,  0., -1.,  0.],
       [-1.,  0.,  0., -1.]])]
candidate[ 4 ]= [[0, 3, 4, 7], array([[ 0., -1.,  1.,  0.],
       [ 0., -1.,  0., -1.],
       [-1.,  0.,  1.,  0.],
       [-1.,  0.,  0., -1.]])]
candidate[ 5 ]= [[0, 3, 5, 6], array([[ 0., -1.,  1.,  0.],
       [ 0., -1.,  0., -1.],
       [-1.,  0., -1.,  0.],
       [-1.,  0.,  0.,  1.]])]
candidate[ 6 ]= [[1, 2, 4, 7], array([[ 0., -1., -1.,  0.],
       [ 0., -1.,  0.,  1.],
       [-1.,  0.,  1.,  0.],
       [-1.,  0.,  0., -1.]])]
candidate[ 7 ]= [[1, 2, 5, 6], array([[ 0., -1., -1.,  0.],
       [ 0., -1.,  0.,  1.],
       [-1.,  0., -1.,  0.],
       [-1.,  0.,  0.,  1.]])]
candidate[ 8 ]= [[1, 3, 4, 6], array([[ 0., -1., -1.,  0.],
       [ 0., -1.,  0., -1.],
       [-1.,  0.,  1.,  0.],
       [-1.,  0.,  0.,  1.]])]
candidate[ 9 ]= [[1, 3, 5, 7], array([[ 0., -1., -1.,  0.],
       [ 0., -1.,  0., -1.],
       [-1.,  0., -1.,  0.],
       [-1.,  0.,  0., -1.]])]
candidate[ 10 ]= [[2, 3, 6, 7], array([[ 0., -1.,  0.,  1.],
       [ 0., -1.,  0., -1.],
       [-1.,  0.,  0.,  1.],
       [-1.,  0.,  0., -1.]])]
candidate[ 11 ]= [[4, 5, 6, 7], array([[-1.,  0.,  1.,  0.],
       [-1.,  0., -1.,  0.],
       [-1.,  0.,  0.,  1.],
       [-1.,  0.,  0., -1.]])]
temp_C= [[0, 4, 5, 8, 9, 1], [0, 4, 8, 12, 16, 20], [0, 4, 9, 12, 17, 21], [0, 5, 8, 13, 16, 22], [0, 5, 9, 13, 17, 23], [0, 12, 13, 16, 17, 2]]


の様になります。先頭で、上に示した正２４胞体の頂点、辺、面の隣接情報が表示されます。
困ったことに、candidate[] は12個あります。
一つの頂点に６個の正８面体がくっ付いているはずなのに辺の組み合わせは12個可能だと言っています。
一行一行プログラムが何をしているか print() 関数で打ち出し、大量のコピー用紙を無駄にして、それを見ながら手計算で確かめると正八面体を構成しないものが６個あり、
正２４胞体にしか通用しない、余り上手なアルゴリズムではありませんが、candidate[] の計算部分はそのままにし、見つかった６番目の頂点と合わせた６頂点で、
強引に正八面体を構成しない組み合わせは除くことで、無事、６個の正八面体を見つけることが出来ました。
このアルゴリズムをすべての正２４胞体の頂点に適応すれば、正２４胞体の胞を含む隣接情報を計算できます。
無理やりプログラムをでっち上げましたが

len(cube.v)= 24 
cube.v= [[array([1, 1, 0, 0]), [[0, 1, 2, 3, 4, 5, 6, 7], [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11], [0, 1, 2, 3, 4, 5]]], 
[array([ 1, -1,  0,  0]), [[8, 9, 10, 11, 12, 13, 14, 15], [12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23], [0, 7, 9, 13, 18, 21]]], 
[array([-1,  1,  0,  0]), [[16, 17, 18, 19, 20, 21, 22, 23], [24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35], [5, 6, 10, 14, 19, 22]]], 
[array([-1, -1,  0,  0]), [[24, 25, 26, 27, 28, 29, 30, 31], [36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47], [6, 7, 11, 15, 20, 23]]], 
[array([1, 0, 1, 0]), [[0, 8, 32, 33, 34, 35, 36, 37], [0, 1, 2, 12, 13, 14, 48, 49, 50, 51, 52, 53], [0, 1, 2, 8, 9, 13]]], 
[array([ 1,  0, -1,  0]), [[1, 9, 38, 39, 40, 41, 42, 43], [3, 4, 5, 15, 16, 17, 54, 55, 56, 57, 58, 59], [0, 3, 4, 17, 18, 21]]], 
[array([-1,  0,  1,  0]), [[16, 24, 44, 45, 46, 47, 48, 49], [24, 25, 26, 36, 37, 38, 60, 61, 62, 63, 64, 65], [6, 8, 10, 11, 14, 15]]], 
[array([-1,  0, -1,  0]), [[17, 25, 50, 51, 52, 53, 54, 55], [27, 28, 29, 39, 40, 41, 66, 67, 68, 69, 70, 71], [6, 17, 19, 20, 22, 23]]], 
[array([1, 0, 0, 1]), [[2, 10, 32, 38, 56, 57, 58, 59], [0, 3, 6, 12, 15, 18, 48, 54, 72, 73, 74, 75], [0, 1, 3, 9, 12, 18]]], 
[array([ 1,  0,  0, -1]), [[3, 11, 33, 39, 60, 61, 62, 63], [1, 4, 7, 13, 16, 19, 49, 55, 76, 77, 78, 79], [0, 2, 4, 13, 16, 21]]], 
[array([-1,  0,  0,  1]), [[18, 26, 44, 50, 64, 65, 66, 67], [24, 27, 30, 36, 39, 42, 60, 66, 80, 81, 82, 83], [6, 10, 11, 12, 19, 20]]], 
[array([-1,  0,  0, -1]), [[19, 27, 45, 51, 68, 69, 70, 71], [25, 28, 31, 37, 40, 43, 61, 67, 84, 85, 86, 87], [6, 14, 15, 16, 22, 23]]], 
[array([0, 1, 1, 0]), [[4, 20, 34, 46, 72, 73, 74, 75], [2, 8, 9, 26, 32, 33, 50, 51, 62, 63, 88, 89], [1, 2, 5, 8, 10, 14]]], 
[array([ 0,  1, -1,  0]), [[5, 21, 40, 52, 76, 77, 78, 79], [5, 10, 11, 29, 34, 35, 56, 57, 68, 69, 90, 91], [3, 4, 5, 17, 19, 22]]], 
[array([ 0, -1,  1,  0]), [[12, 28, 35, 47, 80, 81, 82, 83], [14, 20, 21, 38, 44, 45, 52, 53, 64, 65, 92, 93], [7, 8, 9, 11, 13, 15]]], 
[array([ 0, -1, -1,  0]), [[13, 29, 41, 53, 84, 85, 86, 87], [17, 22, 23, 41, 46, 47, 58, 59, 70, 71, 94, 95], [7, 17, 18, 20, 21, 23]]], 
[array([0, 1, 0, 1]), [[6, 22, 56, 64, 72, 76, 88, 89], [6, 8, 10, 30, 32, 34, 72, 73, 80, 81, 88, 90], [1, 3, 5, 10, 12, 19]]], 
[array([ 0,  1,  0, -1]), [[7, 23, 60, 68, 73, 77, 90, 91], [7, 9, 11, 31, 33, 35, 76, 77, 84, 85, 89, 91], [2, 4, 5, 14, 16, 22]]], 
[array([ 0, -1,  0,  1]), [[14, 30, 57, 65, 80, 84, 92, 93], [18, 20, 22, 42, 44, 46, 74, 75, 82, 83, 92, 94], [7, 9, 11, 12, 18, 20]]], 
[array([ 0, -1,  0, -1]), [[15, 31, 61, 69, 81, 85, 94, 95], [19, 21, 23, 43, 45, 47, 78, 79, 86, 87, 93, 95], [7, 13, 15, 16, 21, 23]]], 
[array([0, 0, 1, 1]), [[36, 48, 58, 66, 74, 82, 88, 92], [48, 50, 52, 60, 62, 64, 72, 74, 80, 82, 88, 92], [1, 8, 9, 10, 11, 12]]], 
[array([ 0,  0,  1, -1]), [[37, 49, 62, 70, 75, 83, 90, 94], [49, 51, 53, 61, 63, 65, 76, 78, 84, 86, 89, 93], [2, 8, 13, 14, 15, 16]]], 
[array([ 0,  0, -1,  1]), [[42, 54, 59, 67, 78, 86, 89, 93], [54, 56, 58, 66, 68, 70, 73, 75, 81, 83, 90, 94], [3, 12, 17, 18, 19, 20]]], 
[array([ 0,  0, -1, -1]), [[43, 55, 63, 71, 79, 87, 91, 95], [55, 57, 59, 67, 69, 71, 77, 79, 85, 87, 91, 95], [4, 16, 17, 21, 22, 23]]]]

len(cube.e)= 96 
cube.e= [[[0, 4], [0, 1, 2], [0, 1, 2]], [[0, 5], [3, 4, 5], [0, 3, 4]], [[0, 8], [0, 3, 6], [0, 1, 3]], [[0, 9], [1, 4, 7], [0, 2, 4]], 
[[0, 12], [2, 8, 9], [1, 2, 5]], [[0, 13], [5, 10, 11], [3, 4, 5]], [[0, 16], [6, 8, 10], [1, 3, 5]], [[0, 17], [7, 9, 11], [2, 4, 5]], 
[[1, 4], [12, 13, 14], [0, 9, 13]], [[1, 5], [15, 16, 17], [0, 18, 21]], [[1, 8], [12, 15, 18], [0, 9, 18]], 
[[1, 9], [13, 16, 19], [0, 13, 21]], [[1, 14], [14, 20, 21], [7, 9, 13]], [[1, 15], [17, 22, 23], [7, 18, 21]], 
[[1, 18], [18, 20, 22], [7, 9, 18]], [[1, 19], [19, 21, 23], [7, 13, 21]], [[2, 6], [24, 25, 26], [6, 10, 14]], 
[[2, 7], [27, 28, 29], [6, 19, 22]], [[2, 10], [24, 27, 30], [6, 10, 19]], [[2, 11], [25, 28, 31], [6, 14, 22]], 
[[2, 12], [26, 32, 33], [5, 10, 14]], [[2, 13], [29, 34, 35], [5, 19, 22]], [[2, 16], [30, 32, 34], [5, 10, 19]], 
[[2, 17], [31, 33, 35], [5, 14, 22]], [[3, 6], [36, 37, 38], [6, 11, 15]], [[3, 7], [39, 40, 41], [6, 20, 23]], 
[[3, 10], [36, 39, 42], [6, 11, 20]], [[3, 11], [37, 40, 43], [6, 15, 23]], [[3, 14], [38, 44, 45], [7, 11, 15]], 
[[3, 15], [41, 46, 47], [7, 20, 23]], [[3, 18], [42, 44, 46], [7, 11, 20]], [[3, 19], [43, 45, 47], [7, 15, 23]], 
[[4, 8], [0, 12, 48], [0, 1, 9]], [[4, 9], [1, 13, 49], [0, 2, 13]], [[4, 12], [2, 50, 51], [1, 2, 8]], 
[[4, 14], [14, 52, 53], [8, 9, 13]], [[4, 20], [48, 50, 52], [1, 8, 9]], [[4, 21], [49, 51, 53], [2, 8, 13]], 
[[5, 8], [3, 15, 54], [0, 3, 18]], [[5, 9], [4, 16, 55], [0, 4, 21]], [[5, 13], [5, 56, 57], [3, 4, 17]], 
[[5, 15], [17, 58, 59], [17, 18, 21]], [[5, 22], [54, 56, 58], [3, 17, 18]], [[5, 23], [55, 57, 59], [4, 17, 21]], 
[[6, 10], [24, 36, 60], [6, 10, 11]], [[6, 11], [25, 37, 61], [6, 14, 15]], [[6, 12], [26, 62, 63], [8, 10, 14]], 
[[6, 14], [38, 64, 65], [8, 11, 15]], [[6, 20], [60, 62, 64], [8, 10, 11]], [[6, 21], [61, 63, 65], [8, 14, 15]], 
[[7, 10], [27, 39, 66], [6, 19, 20]], [[7, 11], [28, 40, 67], [6, 22, 23]], [[7, 13], [29, 68, 69], [17, 19, 22]], 
[[7, 15], [41, 70, 71], [17, 20, 23]], [[7, 22], [66, 68, 70], [17, 19, 20]], [[7, 23], [67, 69, 71], [17, 22, 23]], 
[[8, 16], [6, 72, 73], [1, 3, 12]], [[8, 18], [18, 74, 75], [9, 12, 18]], [[8, 20], [48, 72, 74], [1, 9, 12]], 
[[8, 22], [54, 73, 75], [3, 12, 18]], [[9, 17], [7, 76, 77], [2, 4, 16]], [[9, 19], [19, 78, 79], [13, 16, 21]], 
[[9, 21], [49, 76, 78], [2, 13, 16]], [[9, 23], [55, 77, 79], [4, 16, 21]], [[10, 16], [30, 80, 81], [10, 12, 19]], 
[[10, 18], [42, 82, 83], [11, 12, 20]], [[10, 20], [60, 80, 82], [10, 11, 12]], [[10, 22], [66, 81, 83], [12, 19, 20]], 
[[11, 17], [31, 84, 85], [14, 16, 22]], [[11, 19], [43, 86, 87], [15, 16, 23]], [[11, 21], [61, 84, 86], [14, 15, 16]], 
[[11, 23], [67, 85, 87], [16, 22, 23]], [[12, 16], [8, 32, 88], [1, 5, 10]], [[12, 17], [9, 33, 89], [2, 5, 14]], 
[[12, 20], [50, 62, 88], [1, 8, 10]], [[12, 21], [51, 63, 89], [2, 8, 14]], [[13, 16], [10, 34, 90], [3, 5, 19]], 
[[13, 17], [11, 35, 91], [4, 5, 22]], [[13, 22], [56, 68, 90], [3, 17, 19]], [[13, 23], [57, 69, 91], [4, 17, 22]], 
[[14, 18], [20, 44, 92], [7, 9, 11]], [[14, 19], [21, 45, 93], [7, 13, 15]], [[14, 20], [52, 64, 92], [8, 9, 11]], 
[[14, 21], [53, 65, 93], [8, 13, 15]], [[15, 18], [22, 46, 94], [7, 18, 20]], [[15, 19], [23, 47, 95], [7, 21, 23]], 
[[15, 22], [58, 70, 94], [17, 18, 20]], [[15, 23], [59, 71, 95], [17, 21, 23]], [[16, 20], [72, 80, 88], [1, 10, 12]], 
[[16, 22], [73, 81, 90], [3, 12, 19]], [[17, 21], [76, 84, 89], [2, 14, 16]], [[17, 23], [77, 85, 91], [4, 16, 22]], 
[[18, 20], [74, 82, 92], [9, 11, 12]], [[18, 22], [75, 83, 94], [12, 18, 20]], [[19, 21], [78, 86, 93], [13, 15, 16]], 
[[19, 23], [79, 87, 95], [16, 21, 23]]]

len(cube.f)= 96 
cube.f= [[[0, 4, 8], [0, 2, 32], [0, 1]], [[0, 4, 9], [0, 3, 33], [0, 2]], [[0, 4, 12], [0, 4, 34], [1, 2]], 
[[0, 5, 8], [1, 2, 38], [0, 3]], [[0, 5, 9], [1, 3, 39], [0, 4]], [[0, 5, 13], [1, 5, 40], [3, 4]], 
[[0, 8, 16], [2, 6, 56], [1, 3]], [[0, 9, 17], [3, 7, 60], [2, 4]], [[0, 12, 16], [4, 6, 72], [1, 5]], 
[[0, 12, 17], [4, 7, 73], [2, 5]], [[0, 13, 16], [5, 6, 76], [3, 5]], [[0, 13, 17], [5, 7, 77], [4, 5]], 
[[1, 4, 8], [8, 10, 32], [0, 9]], [[1, 4, 9], [8, 11, 33], [0, 13]], [[1, 4, 14], [8, 12, 35], [9, 13]], 
[[1, 5, 8], [9, 10, 38], [0, 18]], [[1, 5, 9], [9, 11, 39], [0, 21]], [[1, 5, 15], [9, 13, 41], [18, 21]], 
[[1, 8, 18], [10, 14, 57], [9, 18]], [[1, 9, 19], [11, 15, 61], [13, 21]], [[1, 14, 18], [12, 14, 80], [7, 9]], 
[[1, 14, 19], [12, 15, 81], [7, 13]], [[1, 15, 18], [13, 14, 84], [7, 18]], [[1, 15, 19], [13, 15, 85], [7, 21]], 
[[2, 6, 10], [16, 18, 44], [6, 10]], [[2, 6, 11], [16, 19, 45], [6, 14]], [[2, 6, 12], [16, 20, 46], [10, 14]], 
[[2, 7, 10], [17, 18, 50], [6, 19]], [[2, 7, 11], [17, 19, 51], [6, 22]], [[2, 7, 13], [17, 21, 52], [19, 22]], 
[[2, 10, 16], [18, 22, 64], [10, 19]], [[2, 11, 17], [19, 23, 68], [14, 22]], [[2, 12, 16], [20, 22, 72], [5, 10]], 
[[2, 12, 17], [20, 23, 73], [5, 14]], [[2, 13, 16], [21, 22, 76], [5, 19]], [[2, 13, 17], [21, 23, 77], [5, 22]], 
[[3, 6, 10], [24, 26, 44], [6, 11]], [[3, 6, 11], [24, 27, 45], [6, 15]], [[3, 6, 14], [24, 28, 47], [11, 15]], 
[[3, 7, 10], [25, 26, 50], [6, 20]], [[3, 7, 11], [25, 27, 51], [6, 23]], [[3, 7, 15], [25, 29, 53], [20, 23]], 
[[3, 10, 18], [26, 30, 65], [11, 20]], [[3, 11, 19], [27, 31, 69], [15, 23]], [[3, 14, 18], [28, 30, 80], [7, 11]], 
[[3, 14, 19], [28, 31, 81], [7, 15]], [[3, 15, 18], [29, 30, 84], [7, 20]], [[3, 15, 19], [29, 31, 85], [7, 23]], 
[[4, 8, 20], [32, 36, 58], [1, 9]], [[4, 9, 21], [33, 37, 62], [2, 13]], [[4, 12, 20], [34, 36, 74], [1, 8]], 
[[4, 12, 21], [34, 37, 75], [2, 8]], [[4, 14, 20], [35, 36, 82], [8, 9]], [[4, 14, 21], [35, 37, 83], [8, 13]], 
[[5, 8, 22], [38, 42, 59], [3, 18]], [[5, 9, 23], [39, 43, 63], [4, 21]], [[5, 13, 22], [40, 42, 78], [3, 17]], 
[[5, 13, 23], [40, 43, 79], [4, 17]], [[5, 15, 22], [41, 42, 86], [17, 18]], [[5, 15, 23], [41, 43, 87], [17, 21]], 
[[6, 10, 20], [44, 48, 66], [10, 11]], [[6, 11, 21], [45, 49, 70], [14, 15]], [[6, 12, 20], [46, 48, 74], [8, 10]], 
[[6, 12, 21], [46, 49, 75], [8, 14]], [[6, 14, 20], [47, 48, 82], [8, 11]], [[6, 14, 21], [47, 49, 83], [8, 15]], 
[[7, 10, 22], [50, 54, 67], [19, 20]], [[7, 11, 23], [51, 55, 71], [22, 23]], [[7, 13, 22], [52, 54, 78], [17, 19]], 
[[7, 13, 23], [52, 55, 79], [17, 22]], [[7, 15, 22], [53, 54, 86], [17, 20]], [[7, 15, 23], [53, 55, 87], [17, 23]], 
[[8, 16, 20], [56, 58, 88], [1, 12]], [[8, 16, 22], [56, 59, 89], [3, 12]], [[8, 18, 20], [57, 58, 92], [9, 12]], 
[[8, 18, 22], [57, 59, 93], [12, 18]], [[9, 17, 21], [60, 62, 90], [2, 16]], [[9, 17, 23], [60, 63, 91], [4, 16]], 
[[9, 19, 21], [61, 62, 94], [13, 16]], [[9, 19, 23], [61, 63, 95], [16, 21]], [[10, 16, 20], [64, 66, 88], [10, 12]], 
[[10, 16, 22], [64, 67, 89], [12, 19]], [[10, 18, 20], [65, 66, 92], [11, 12]], [[10, 18, 22], [65, 67, 93], [12, 20]], 
[[11, 17, 21], [68, 70, 90], [14, 16]], [[11, 17, 23], [68, 71, 91], [16, 22]], [[11, 19, 21], [69, 70, 94], [15, 16]], 
[[11, 19, 23], [69, 71, 95], [16, 23]], [[12, 16, 20], [72, 74, 88], [1, 10]], [[12, 17, 21], [73, 75, 90], [2, 14]], 
[[13, 16, 22], [76, 78, 89], [3, 19]], [[13, 17, 23], [77, 79, 91], [4, 22]], [[14, 18, 20], [80, 82, 92], [9, 11]], 
[[14, 19, 21], [81, 83, 94], [13, 15]], [[15, 18, 22], [84, 86, 93], [18, 20]], [[15, 19, 23], [85, 87, 95], [21, 23]]]

len(cube.c)= 24 
cube.c= [[[0, 4, 5, 8, 9, 1], [0, 1, 2, 3, 32, 33, 8, 38, 39, 9, 10, 11], [0, 1, 3, 4, 12, 13, 15, 16]], 
[[0, 4, 8, 12, 16, 20], [0, 2, 4, 6, 32, 34, 36, 56, 58, 72, 74, 88], [0, 2, 6, 8, 48, 50, 72, 88]], 
[[0, 4, 9, 12, 17, 21], [0, 3, 4, 7, 33, 34, 37, 60, 62, 73, 75, 90], [1, 2, 7, 9, 49, 51, 76, 89]], 
[[0, 5, 8, 13, 16, 22], [1, 2, 5, 6, 38, 40, 42, 56, 59, 76, 78, 89], [3, 5, 6, 10, 54, 56, 73, 90]], 
[[0, 5, 9, 13, 17, 23], [1, 3, 5, 7, 39, 40, 43, 60, 63, 77, 79, 91], [4, 5, 7, 11, 55, 57, 77, 91]], 
[[0, 12, 13, 16, 17, 2], [4, 5, 6, 7, 72, 73, 20, 76, 77, 21, 22, 23], [8, 9, 10, 11, 32, 33, 34, 35]], 
[[10, 2, 3, 6, 7, 11], [18, 26, 44, 50, 16, 17, 19, 24, 25, 27, 45, 51], [24, 27, 36, 39, 25, 28, 37, 40]], 
[[18, 1, 3, 14, 15, 19], [14, 30, 80, 84, 12, 13, 15, 28, 29, 31, 81, 85], [20, 22, 44, 46, 21, 23, 45, 47]], 
[[20, 4, 6, 12, 14, 21], [36, 48, 74, 82, 34, 35, 37, 46, 47, 49, 75, 83], [50, 52, 62, 64, 51, 53, 63, 65]], 
[[20, 4, 8, 14, 18, 1], [36, 58, 82, 92, 32, 35, 8, 57, 10, 80, 12, 14], [48, 52, 74, 92, 12, 14, 18, 20]], 
[[20, 6, 10, 12, 16, 2], [48, 66, 74, 88, 44, 46, 16, 64, 18, 72, 20, 22], [60, 62, 80, 88, 24, 26, 30, 32]], 
[[20, 6, 10, 14, 18, 3], [48, 66, 82, 92, 44, 47, 24, 65, 26, 80, 28, 30], [60, 64, 82, 92, 36, 38, 42, 44]], 
[[20, 8, 10, 16, 18, 22], [58, 66, 88, 92, 56, 57, 59, 64, 65, 67, 89, 93], [72, 74, 80, 82, 73, 75, 81, 83]], 
[[21, 4, 9, 14, 19, 1], [37, 62, 83, 94, 33, 35, 8, 61, 11, 81, 12, 15], [49, 53, 78, 93, 13, 14, 19, 21]], 
[[21, 6, 11, 12, 17, 2], [49, 70, 75, 90, 45, 46, 16, 68, 19, 73, 20, 23], [61, 63, 84, 89, 25, 26, 31, 33]], 
[[21, 6, 11, 14, 19, 3], [49, 70, 83, 94, 45, 47, 24, 69, 27, 81, 28, 31], [61, 65, 86, 93, 37, 38, 43, 45]], 
[[21, 9, 11, 17, 19, 23], [62, 70, 90, 94, 60, 61, 63, 68, 69, 71, 91, 95], [76, 78, 84, 86, 77, 79, 85, 87]], 
[[22, 5, 7, 13, 15, 23], [42, 54, 78, 86, 40, 41, 43, 52, 53, 55, 79, 87], [56, 58, 68, 70, 57, 59, 69, 71]], 
[[22, 5, 8, 15, 18, 1], [42, 59, 86, 93, 38, 41, 9, 57, 10, 84, 13, 14], [54, 58, 75, 94, 15, 17, 18, 22]], 
[[22, 7, 10, 13, 16, 2], [54, 67, 78, 89, 50, 52, 17, 64, 18, 76, 21, 22], [66, 68, 81, 90, 27, 29, 30, 34]], 
[[22, 7, 10, 15, 18, 3], [54, 67, 86, 93, 50, 53, 25, 65, 26, 84, 29, 30], [66, 70, 83, 94, 39, 41, 42, 46]], 
[[23, 5, 9, 15, 19, 1], [43, 63, 87, 95, 39, 41, 9, 61, 11, 85, 13, 15], [55, 59, 79, 95, 16, 17, 19, 23]], 
[[23, 7, 11, 13, 17, 2], [55, 71, 79, 91, 51, 52, 17, 68, 19, 77, 21, 23], [67, 69, 85, 91, 28, 29, 31, 35]], 
[[23, 7, 11, 15, 19, 3], [55, 71, 87, 95, 51, 53, 25, 69, 27, 85, 29, 31], [67, 71, 87, 95, 40, 41, 43, 47]]]


で正２４胞体の頂点、辺、面、胞の隣接関係の情報を得ているはずです。


次に簡単なのは正６００胞体の頂点、辺、面、胞の隣接関係の情報を得ることです。

len(cube.v)= 120 
cube.v= [
[array([1, 1, 1, 1]), 
　[[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11], 
　[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 
　20, 21, 22, 23, 24, 25, 26, 27, 28, 29], 
　[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 
　10, 11, 12, 13, 14, 15, 16, 17, 18, 19]]], 
[array([-1,  1,  1,  1]), 
　[[12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23], 
　[30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 
　47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59], 
　[20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 
　30, 31, 32, 33, 34, 35, 36, 37, 38, 39]]],
 [array([ 1, -1,  1,  1]), 
 　[[24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35], 
 　[60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 
 　77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89], 
 　[40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 
 　50, 51, 52, 53, 54, 55, 56, 57, 58, 59]]], 
[array([-1, -1,  1,  1]), 
　[[36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47], 
　[90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 
　105, 106, 107, 108, 109, 110, 111, 112, 
　113, 114, 115, 116, 117, 118, 119], 
　[60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 
　71, 72, 73, 74, 75, 76, 77, 78, 79]]], 
[array([ 1,  1, -1,  1]), 
　[[48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59], 
　[120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 
　133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149], 
　[80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 
　91, 92, 93, 94, 95, 96, 97, 98, 99]]], 
[array([-1,  1, -1,  1]), [[60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71], 
　[150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 
　163, 164, 165, 166, 167, 168, 169, 170, 171, 172, 
　173, 174, 175, 176, 177, 178, 179], 
　[100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 
　110, 111, 112, 113, 114, 115, 116, 117, 118, 119]]], 
[array([ 1, -1, -1,  1]), [[72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83], 
　[180, 181, 182, 183, 184, 185, 186, 187, 188, 189, 190, 191, 192, 
　193, 194, 195, 196, 197, 198, 199, 200, 201, 202, 
　203, 204, 205, 206, 207, 208, 209], 
　[120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 
　130, 131, 132, 133, 134, 135, 136, 137, 138, 139]]], 
[array([-1, -1, -1,  1]), 
　[[84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95], 
　[210, 211, 212, 213, 214, 215, 216, 217, 218, 219, 220, 221, 222, 
　223, 224, 225, 226, 227, 228, 229, 230, 231, 232, 
　233, 234, 235, 236, 237, 238, 239], 
　[140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 
　150, 151, 152, 153, 154, 155, 156, 157, 158, 159]]], 
[array([ 1,  1,  1, -1]), 
　[[96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107], 
　[240, 241, 242, 243, 244, 245, 246, 247, 248, 249, 250, 251, 252, 
　253, 254, 255, 256, 257, 258, 259, 260, 261, 262, 263, 
　264, 265, 266, 267, 268, 269], 
　[160, 161, 162, 163, 164, 165, 166, 167, 168, 169, 170, 
　171, 172, 173, 174, 175, 176, 177, 178, 179]]], 
[array([-1,  1,  1, -1]), 
　[[108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119], 
　[270, 271, 272, 273, 274, 275, 276, 277, 278, 279, 280, 281, 282, 
　283, 284, 285, 286, 287, 288, 289, 290, 291, 292, 293, 294, 
　295, 296, 297, 298, 299], 
　[180, 181, 182, 183, 184, 185, 186, 187, 188, 189, 190, 191, 
　192, 193, 194, 195, 196, 197, 198, 199]]], 
[array([ 1, -1,  1, -1]), 
　[[120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131], 
　[300, 301, 302, 303, 304, 305, 306, 307, 308, 309, 310, 311, 312, 
　313, 314, 315, 316, 317, 318, 319, 320, 321, 322, 323, 324, 
　325, 326, 327, 328, 329], 
　[200, 201, 202, 203, 204, 205, 206, 207, 208, 209, 210, 211, 212, 
　213, 214, 215, 216, 217, 218, 219]]], 
[array([-1, -1,  1, -1]), [[132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143], 
　[330, 331, 332, 333, 334, 335, 336, 337, 338, 339, 340, 341, 342, 
　343, 344, 345, 346, 347, 348, 349, 350, 351, 352, 353, 354, 355, 356, 357, 358, 359], 
　[220, 221, 222, 223, 224, 225, 226, 227, 228, 229, 230, 231, 232, 233, 234, 235, 236, 237, 238, 239]]], 
[array([ 1,  1, -1, -1]), [[144, 145, 146, 147, 148, 149, 150, 151, 152, 153, 154, 155], 
　[360, 361, 362, 363, 364, 365, 366, 367, 368, 369, 370, 371, 372, 
　373, 374, 375, 376, 377, 378, 379, 380, 381, 382, 383, 384, 385, 386, 387, 388, 389], 
　[240, 241, 242, 243, 244, 245, 246, 247, 248, 249, 250, 251, 252, 253, 254, 255, 256, 257, 258, 259]]], 
[array([-1,  1, -1, -1]), [[156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167], 
　[390, 391, 392, 393, 394, 395, 396, 397, 398, 399, 400, 401, 402, 
　403, 404, 405, 406, 407, 408, 409, 410, 411, 412, 413, 414, 415, 416, 417, 418, 419], 
　[260, 261, 262, 263, 264, 265, 266, 267, 268, 269, 270, 271, 272, 273, 274, 275, 276, 277, 278, 279]]], 
[array([ 1, -1, -1, -1]), [[168, 169, 170, 171, 172, 173, 174, 175, 176, 177, 178, 179], 
　[420, 421, 422, 423, 424, 425, 426, 427, 428, 429, 430, 431, 432, 
　433, 434, 435, 436, 437, 438, 439, 440, 441, 442, 443, 444, 445, 446, 447, 448, 449], 
　[280, 281, 282, 283, 284, 285, 286, 287, 288, 289, 290, 291, 292, 293, 294, 295, 296, 297, 298, 299]]], 
[array([-1, -1, -1, -1]), [[180, 181, 182, 183, 184, 185, 186, 187, 188, 189, 190, 191], 
　[450, 451, 452, 453, 454, 455, 456, 457, 458, 459, 460, 461, 462, 
　463, 464, 465, 466, 467, 468, 469, 470, 471, 472, 473, 474, 475, 476, 477, 478, 479], 
　[300, 301, 302, 303, 304, 305, 306, 307, 308, 309, 310, 311, 312, 313, 314, 315, 316, 317, 318, 319]]], 
[array([2, 0, 0, 0]), [[192, 193, 194, 195, 196, 197, 198, 199, 200, 201, 202, 203], 
　[480, 481, 482, 483, 484, 485, 486, 487, 488, 489, 490, 491, 492, 
　493, 494, 495, 496, 497, 498, 499, 500, 501, 502, 503, 504, 505, 506, 507, 508, 509], 
　[320, 321, 322, 323, 324, 325, 326, 327, 328, 329, 330, 331, 332, 333, 334, 335, 336, 337, 338, 339]]], 
[array([-2,  0,  0,  0]), [[204, 205, 206, 207, 208, 209, 210, 211, 212, 213, 214, 215], 
　[510, 511, 512, 513, 514, 515, 516, 517, 518, 519, 520, 521, 522, 
　523, 524, 525, 526, 527, 528, 529, 530, 531, 532, 533, 534, 535, 536, 537, 538, 539], 
　[340, 341, 342, 343, 344, 345, 346, 347, 348, 349, 350, 351, 352, 353, 354, 355, 356, 357, 358, 359]]], 
[array([0, 2, 0, 0]), [[216, 217, 218, 219, 220, 221, 222, 223, 224, 225, 226, 227], 
　[540, 541, 542, 543, 544, 545, 546, 547, 548, 549, 550, 551, 552, 
　553, 554, 555, 556, 557, 558, 559, 560, 561, 562, 563, 564, 565, 566, 567, 568, 569], 
　[360, 361, 362, 363, 364, 365, 366, 367, 368, 369, 370, 371, 372, 373, 374, 375, 376, 377, 378, 379]]], 
[array([ 0, -2,  0,  0]), [[228, 229, 230, 231, 232, 233, 234, 235, 236, 237, 238, 239], 
　[570, 571, 572, 573, 574, 575, 576, 577, 578, 579, 580, 581, 582, 
　583, 584, 585, 586, 587, 588, 589, 590, 591, 592, 593, 594, 595, 596, 597, 598, 599], 
　[380, 381, 382, 383, 384, 385, 386, 387, 388, 389, 390, 391, 392, 393, 394, 395, 396, 397, 398, 399]]], 
[array([0, 0, 2, 0]), [[240, 241, 242, 243, 244, 245, 246, 247, 248, 249, 250, 251], 
　[600, 601, 602, 603, 604, 605, 606, 607, 608, 609, 610, 611, 612, 
　613, 614, 615, 616, 617, 618, 619, 620, 621, 622, 623, 624, 625, 626, 627, 628, 629], 
　[400, 401, 402, 403, 404, 405, 406, 407, 408, 409, 410, 411, 412, 413, 414, 415, 416, 417, 418, 419]]], 
[array([ 0,  0, -2,  0]), [[252, 253, 254, 255, 256, 257, 258, 259, 260, 261, 262, 263], 
　[630, 631, 632, 633, 634, 635, 636, 637, 638, 639, 640, 641, 642, 
　643, 644, 645, 646, 647, 648, 649, 650, 651, 652, 653, 654, 655, 656, 657, 658, 659], 
　[420, 421, 422, 423, 424, 425, 426, 427, 428, 429, 430, 431, 432, 433, 434, 435, 436, 437, 438, 439]]], 
[array([0, 0, 0, 2]), [[264, 265, 266, 267, 268, 269, 270, 271, 272, 273, 274, 275], 
　[660, 661, 662, 663, 664, 665, 666, 667, 668, 669, 670, 671, 672, 
　673, 674, 675, 676, 677, 678, 679, 680, 681, 682, 683, 684, 685, 686, 687, 688, 689], 
　[440, 441, 442, 443, 444, 445, 446, 447, 448, 449, 450, 451, 452, 453, 454, 455, 456, 457, 458, 459]]], 
[array([ 0,  0,  0, -2]), [[276, 277, 278, 279, 280, 281, 282, 283, 284, 285, 286, 287], 
　[690, 691, 692, 693, 694, 695, 696, 697, 698, 699, 700, 701, 702, 
　703, 704, 705, 706, 707, 708, 709, 710, 711, 712, 713, 714, 715, 716, 717, 718, 719], 
　[460, 461, 462, 463, 464, 465, 466, 467, 468, 469, 470, 471, 472, 473, 474, 475, 476, 477, 478, 479]]], 
[array([0.        , 1.        , 0.61803399, 1.61803399]), [[0, 12, 264, 288, 289, 290, 291, 292, 293, 294, 295, 296], 
　[0, 1, 2, 3, 4, 30, 31, 32, 33, 34, 660, 661, 662, 663, 664, 720, 721, 
　722, 723, 724, 725, 726, 727, 728, 729, 730, 731, 732, 733, 734], 
　[0, 1, 2, 3, 4, 20, 21, 22, 23, 24, 440, 441, 442, 443, 444, 480, 481, 482, 483, 484]]], 
[array([0.        , 0.61803399, 1.61803399, 1.        ]), [[1, 13, 240, 288, 297, 298, 299, 300, 301, 302, 303, 304], 
　[0, 5, 6, 7, 8, 30, 35, 36, 37, 38, 600, 601, 602, 603, 604, 720, 721, 
　722, 735, 736, 737, 738, 739, 740, 741, 742, 743, 744, 745, 746], 
　[0, 1, 5, 6, 7, 20, 21, 25, 26, 27, 400, 401, 402, 403, 404, 480, 485, 486, 487, 488]]], 
[array([0.        , 1.61803399, 1.        , 0.61803399]), [[2, 14, 216, 289, 297, 305, 306, 307, 308, 309, 310, 311], 
　[1, 5, 9, 10, 11, 31, 35, 39, 40, 41, 540, 541, 542, 543, 544, 720, 
　723, 724, 735, 736, 747, 748, 749, 750, 751, 752, 753, 754, 755, 756], 
　[0, 2, 5, 8, 9, 20, 22, 25, 28, 29, 360, 361, 362, 363, 364, 481, 485, 489, 490, 491]]], 
[array([1.        , 0.        , 1.61803399, 0.61803399]), [[3, 24, 241, 298, 312, 313, 314, 315, 316, 317, 318, 319], 
　[6, 12, 13, 14, 15, 60, 61, 62, 63, 64, 600, 605, 606, 607, 608, 737, 
　738, 739, 757, 758, 759, 760, 761, 762, 763, 764, 765, 766, 767, 768], 
　[6, 7, 10, 11, 12, 40, 41, 42, 43, 44, 400, 401, 405, 406, 407, 486, 492, 493, 494, 495]]], 
[array([1.        , 0.61803399, 0.        , 1.61803399]), [[4, 48, 265, 290, 320, 321, 322, 323, 324, 325, 326, 327], 
　[2, 16, 17, 18, 19, 120, 121, 122, 123, 124, 660, 665, 666, 667, 668, 
　725, 726, 727, 769, 770, 771, 772, 773, 774, 775, 776, 777, 778, 779, 780], 
　[3, 4, 13, 14, 15, 80, 81, 82, 83, 84, 440, 441, 445, 446, 447, 482, 496, 497, 498, 499]]], 
[array([1.        , 1.61803399, 0.61803399, 0.        ]), [[5, 96, 217, 305, 328, 329, 330, 331, 332, 333, 334, 335], 
　[9, 20, 21, 22, 23, 240, 241, 242, 243, 244, 540, 545, 546, 547, 548, 
　747, 748, 749, 781, 782, 783, 784, 785, 786, 787, 788, 789, 790, 791, 792], 
　[8, 9, 16, 17, 18, 160, 161, 162, 163, 164, 360, 361, 365, 366, 367, 489, 500, 501, 502, 503]]], 
[array([0.61803399, 0.        , 1.        , 1.61803399]), [[6, 25, 266, 291, 299, 312, 320, 336, 337, 338, 339, 340], 
　[3, 7, 12, 16, 24, 60, 65, 66, 67, 68, 661, 665, 669, 670, 671, 721, 
　725, 728, 737, 740, 741, 757, 758, 769, 770, 793, 794, 795, 796, 797], 
　[1, 3, 6, 10, 13, 40, 41, 45, 46, 47, 440, 442, 445, 448, 449, 480, 486, 487, 496, 504]]], 
[array([0.61803399, 1.        , 1.61803399, 0.        ]), [[7, 97, 242, 300, 306, 313, 328, 341, 342, 343, 344, 345], 
　[8, 10, 13, 20, 25, 240, 245, 246, 247, 248, 601, 605, 609, 610, 
　611, 735, 738, 742, 747, 750, 751, 759, 760, 781, 782, 798, 799, 800, 801, 802], 
　[5, 7, 8, 11, 16, 160, 161, 165, 166, 167, 400, 402, 405, 408, 409, 485, 489, 490, 492, 505]]], 
[array([0.61803399, 1.61803399, 0.        , 1.        ]), [[8, 49, 218, 292, 307, 321, 329, 346, 347, 348, 349, 350], 
　[4, 11, 17, 21, 26, 120, 125, 126, 127, 128, 541, 545, 549, 550, 
　551, 723, 726, 729, 730, 748, 752, 771, 772, 783, 784, 803, 804, 805, 806, 807], 
　[2, 4, 9, 14, 17, 80, 81, 85, 86, 87, 360, 362, 365, 368, 369, 481, 482, 483, 500, 506]]], 
[array([1.61803399, 0.        , 0.61803399, 1.        ]), [[9, 26, 192, 314, 322, 336, 351, 352, 353, 354, 355, 356], 
　[14, 18, 24, 27, 28, 61, 65, 69, 70, 71, 480, 481, 482, 483, 484, 
　757, 761, 762, 769, 773, 774, 775, 793, 808, 809, 810, 811, 812, 813, 814], 
　[10, 12, 13, 15, 19, 40, 42, 45, 48, 49, 320, 321, 322, 323, 324, 493, 496, 497, 498, 507]]], 
[array([1.61803399, 1.        , 0.        , 0.61803399]), [[10, 50, 193, 323, 330, 346, 351, 357, 358, 359, 360, 361], 
　[19, 22, 26, 27, 29, 121, 125, 129, 130, 131, 480, 485, 486, 487, 
　488, 771, 773, 776, 783, 785, 786, 787, 803, 808, 809, 815, 816, 817, 818, 819], 
　[14, 15, 17, 18, 19, 80, 82, 85, 88, 89, 320, 321, 325, 326, 327, 497, 500, 501, 502, 508]]], 
[array([1.61803399, 0.61803399, 1.        , 0.        ]), [[11, 98, 194, 315, 331, 341, 352, 357, 362, 363, 364, 365], 
　[15, 23, 25, 28, 29, 241, 245, 249, 250, 251, 481, 485, 489, 490, 
　491, 759, 761, 763, 764, 781, 785, 788, 798, 808, 810, 815, 820, 821, 822, 823], 
　[11, 12, 16, 18, 19, 160, 162, 165, 168, 169, 320, 322, 325, 328, 329, 492, 493, 494, 501, 509]]], 
[array([ 0.        ,  1.        ,  0.61803399, -1.61803399]), [[99, 108, 276, 366, 367, 368, 369, 370, 371, 372, 373, 374], 
　[252, 253, 254, 255, 256, 270, 271, 272, 273, 274, 690, 691, 692, 
　693, 694, 824, 825, 826, 827, 828, 829, 830, 831, 832, 833, 834, 835, 836, 837, 838], 
　[170, 171, 172, 173, 174, 180, 181, 182, 183, 184, 460, 461, 462, 463, 464, 510, 511, 512, 513, 514]]], 
[array([ 0.        ,  0.61803399,  1.61803399, -1.        ]), [[100, 109, 243, 342, 366, 375, 376, 377, 378, 379, 380, 381], 
　[246, 252, 257, 258, 259, 270, 275, 276, 277, 278, 609, 612, 613, 
　614, 615, 799, 800, 801, 824, 825, 826, 839, 840, 841, 842, 843, 844, 845, 846, 847], 
　[166, 167, 170, 171, 175, 180, 181, 185, 186, 187, 408, 409, 410, 411, 412, 505, 510, 515, 516, 517]]], 
[array([ 0.        ,  1.61803399,  1.        , -0.61803399]), [[101, 110, 219, 308, 332, 343, 367, 375, 382, 383, 384, 385], 
　[242, 247, 253, 257, 260, 271, 275, 279, 280, 281, 542, 546, 552, 
　553, 554, 749, 750, 753, 754, 782, 789, 799, 802, 824, 827, 828, 839, 848, 849, 850], 
　[161, 163, 166, 170, 172, 180, 182, 185, 188, 189, 361, 363, 366, 370, 371, 489, 490, 491, 505, 511]]], 
[array([ 1.        ,  0.        ,  1.61803399, -0.61803399]), [[102, 120, 244, 316, 344, 362, 376, 386, 387, 388, 389, 390], 
　[248, 249, 258, 261, 262, 300, 301, 302, 303, 304, 606, 610, 612, 
　616, 617, 760, 763, 765, 766, 798, 800, 820, 821, 840, 841, 851, 852, 853, 854, 855], 
　[165, 167, 168, 175, 176, 200, 201, 202, 203, 204, 405, 406, 408, 410, 413, 492, 494, 495, 509, 515]]], 
[array([ 1.        ,  0.61803399,  0.        , -1.61803399]), [[103, 144, 277, 368, 391, 392, 393, 394, 395, 396, 397, 398], 
　[254, 263, 264, 265, 266, 360, 361, 362, 363, 364, 690, 695, 696, 
　697, 698, 829, 830, 831, 856, 857, 858, 859, 860, 861, 862, 863, 864, 865, 866, 867], 
　[173, 174, 177, 178, 179, 240, 241, 242, 243, 244, 460, 461, 465, 466, 467, 512, 518, 519, 520, 521]]], 
[array([ 1.        ,  1.61803399, -0.61803399,  0.        ]), [[51, 145, 220, 333, 347, 358, 399, 400, 401, 402, 403, 404], 
　[126, 129, 132, 133, 134, 365, 366, 367, 368, 369, 547, 549, 555, 
　556, 557, 784, 786, 790, 791, 803, 804, 816, 817, 868, 869, 870, 871, 872, 873, 874], 
　[85, 86, 88, 90, 91, 245, 246, 247, 248, 249, 365, 367, 368, 372, 373, 500, 502, 503, 508, 522]]], 
[array([ 0.61803399,  0.        ,  1.        , -1.61803399]), [[104, 121, 278, 369, 377, 386, 391, 405, 406, 407, 408, 409], 
　[255, 259, 261, 263, 267, 300, 305, 306, 307, 308, 691, 695, 699, 
　700, 701, 825, 829, 832, 840, 842, 843, 851, 852, 856, 857, 875, 876, 877, 878, 879], 
　[171, 173, 175, 176, 177, 200, 201, 205, 206, 207, 460, 462, 465, 468, 469, 510, 515, 516, 518, 523]]], 
[array([ 0.61803399,  1.        , -1.61803399,  0.        ]), [[52, 146, 252, 399, 410, 411, 412, 413, 414, 415, 416, 417], 
　[132, 135, 136, 137, 138, 365, 370, 371, 372, 373, 630, 631, 632, 
　633, 634, 868, 869, 870, 880, 881, 882, 883, 884, 885, 886, 887, 888, 889, 890, 891], 
　[90, 91, 92, 93, 94, 245, 246, 250, 251, 252, 420, 421, 422, 423, 424, 522, 524, 525, 526, 527]]], 
[array([ 0.61803399,  1.61803399,  0.        , -1.        ]), [[105, 147, 221, 334, 370, 382, 392, 400, 418, 419, 420, 421], 
　[243, 256, 260, 264, 268, 360, 366, 374, 375, 376, 548, 552, 555, 
　558, 559, 789, 790, 792, 827, 830, 833, 834, 848, 858, 859, 871, 872, 892, 893, 894], 
　[163, 164, 172, 174, 178, 240, 241, 247, 248, 253, 366, 367, 370, 372, 374, 503, 511, 512, 513, 528]]], 
[array([ 1.61803399,  0.        ,  0.61803399, -1.        ]), [[106, 122, 195, 363, 387, 393, 405, 422, 423, 424, 425, 426], 
　[250, 262, 265, 267, 269, 301, 305, 309, 310, 311, 489, 492, 493, 
　494, 495, 820, 822, 823, 851, 853, 856, 860, 861, 862, 875, 895, 896, 897, 898, 899], 
　[168, 169, 176, 177, 179, 200, 202, 205, 208, 209, 328, 329, 330, 331, 332, 509, 518, 519, 520, 529]]], 
[array([ 1.61803399,  1.        ,  0.        , -0.61803399]), [[107, 148, 196, 335, 359, 364, 394, 401, 418, 422, 427, 428], 
　[244, 251, 266, 268, 269, 361, 367, 374, 377, 378, 486, 490, 492, 
　496, 497, 787, 788, 791, 792, 815, 816, 818, 822, 858, 860, 863, 871, 873, 895, 900], 
　[162, 164, 169, 178, 179, 240, 242, 247, 249, 254, 325, 326, 328, 330, 333, 501, 502, 503, 508, 519]]], 
[array([ 1.61803399,  0.61803399, -1.        ,  0.        ]), [[53, 149, 197, 360, 402, 410, 427, 429, 430, 431, 432, 433], 
　[130, 133, 135, 139, 140, 368, 370, 377, 379, 380, 487, 496, 498, 
　499, 500, 817, 818, 819, 868, 873, 880, 881, 900, 901, 902, 903, 904, 905, 906, 907], 
　[88, 89, 90, 92, 95, 245, 249, 250, 254, 255, 326, 327, 333, 334, 335, 508, 524, 530, 531, 532]]], 
[array([ 0.        ,  1.        , -0.61803399,  1.61803399]), [[54, 60, 267, 293, 324, 348, 434, 435, 436, 437, 438, 439], 
　[122, 127, 141, 142, 143, 150, 151, 152, 153, 154, 662, 666, 672, 
　673, 674, 727, 729, 731, 732, 772, 777, 805, 806, 908, 909, 910, 911, 912, 913, 914], 
　[81, 83, 87, 96, 97, 100, 101, 102, 103, 104, 441, 443, 446, 450, 451, 482, 483, 484, 506, 533]]], 
[array([ 0.        ,  0.61803399, -1.61803399,  1.        ]), [[55, 61, 253, 411, 434, 440, 441, 442, 443, 444, 445, 446], 
　[136, 141, 144, 145, 146, 150, 155, 156, 157, 158, 630, 635, 636, 
　637, 638, 882, 883, 884, 908, 909, 910, 915, 916, 917, 918, 919, 920, 921, 922, 923], 
　[93, 94, 96, 97, 98, 100, 101, 105, 106, 107, 420, 421, 425, 426, 427, 525, 533, 534, 535, 536]]], 
[array([ 0.        ,  1.61803399, -1.        ,  0.61803399]), [[56, 62, 222, 349, 403, 412, 435, 440, 447, 448, 449, 450], 
　[128, 134, 137, 142, 144, 151, 155, 159, 160, 161, 550, 556, 560, 
　561, 562, 804, 805, 807, 869, 874, 882, 885, 886, 908, 911, 915, 924, 925, 926, 927], 
　[86, 87, 91, 93, 96, 100, 102, 105, 108, 109, 368, 369, 373, 375, 376, 506, 522, 525, 526, 537]]], 
[array([ 1.        ,  0.        , -1.61803399,  0.61803399]), [[57, 72, 254, 413, 429, 441, 451, 452, 453, 454, 455, 456], 
　[138, 139, 145, 147, 148, 180, 181, 182, 183, 184, 631, 635, 639, 
　640, 641, 880, 883, 887, 901, 902, 903, 916, 917, 928, 929, 930, 931, 932, 933, 934], 
　[92, 94, 95, 98, 99, 120, 121, 122, 123, 124, 420, 422, 425, 428, 429, 524, 530, 531, 534, 538]]], 
[array([ 1.        , -0.61803399,  0.        ,  1.61803399]), [[27, 73, 268, 325, 337, 353, 457, 458, 459, 460, 461, 462], 
　[66, 69, 72, 73, 74, 185, 186, 187, 188, 189, 667, 669, 675, 676, 
　677, 770, 774, 778, 779, 793, 794, 811, 812, 935, 936, 937, 938, 939, 940, 941], 
　[45, 46, 48, 50, 51, 125, 126, 127, 128, 129, 445, 447, 448, 452, 453, 496, 498, 499, 507, 539]]], 
[array([ 1.        , -1.61803399,  0.61803399,  0.        ]), [[28, 123, 228, 463, 464, 465, 466, 467, 468, 469, 470, 471], 
　[75, 76, 77, 78, 79, 312, 313, 314, 315, 316, 570, 571, 572, 573, 
　574, 942, 943, 944, 945, 946, 947, 948, 949, 950, 951, 952, 953, 954, 955, 956], 
　[52, 53, 54, 55, 56, 210, 211, 212, 213, 214, 380, 381, 382, 383, 384, 540, 541, 542, 543, 544]]], 
[array([ 0.61803399,  0.        , -1.        ,  1.61803399]), [[58, 74, 269, 326, 436, 442, 451, 457, 472, 473, 474, 475], 
　[123, 143, 146, 147, 149, 180, 185, 190, 191, 192, 668, 672, 675, 
　678, 679, 777, 778, 780, 909, 912, 916, 918, 919, 928, 929, 935, 936, 957, 958, 959], 
　[83, 84, 97, 98, 99, 120, 121, 125, 126, 130, 446, 447, 450, 452, 454, 499, 533, 534, 535, 545]]], 
[array([ 0.61803399, -1.        ,  1.61803399,  0.        ]), [[29, 124, 245, 317, 388, 463, 476, 477, 478, 479, 480, 481], 
　[62, 75, 80, 81, 82, 302, 312, 317, 318, 319, 607, 616, 618, 619, 
　620, 765, 767, 768, 854, 855, 942, 943, 944, 960, 961, 962, 963, 964, 965, 966], 
　[43, 44, 52, 53, 57, 203, 204, 210, 211, 215, 406, 407, 413, 414, 415, 495, 540, 546, 547, 548]]], 
[array([ 0.61803399, -1.61803399,  0.        ,  1.        ]), [[30, 75, 229, 458, 464, 482, 483, 484, 485, 486, 487, 488], 
　[72, 76, 83, 84, 85, 186, 193, 194, 195, 196, 570, 575, 576, 577, 
　578, 937, 938, 939, 945, 946, 947, 967, 968, 969, 970, 971, 972, 973, 974, 975], 
　[50, 51, 54, 55, 58, 127, 128, 131, 132, 133, 380, 381, 385, 386, 387, 539, 541, 549, 550, 551]]], 
[array([ 1.61803399,  0.        , -0.61803399,  1.        ]), [[59, 76, 198, 327, 354, 361, 430, 452, 459, 472, 489, 490], 
　[124, 131, 140, 148, 149, 181, 187, 190, 197, 198, 482, 488, 498, 
　501, 502, 775, 776, 779, 780, 809, 811, 813, 819, 901, 904, 928, 930, 935, 940, 976], 
　[82, 84, 89, 95, 99, 120, 122, 125, 129, 134, 321, 323, 327, 334, 336, 497, 498, 499, 507, 530]]], 
[array([ 1.61803399, -1.        ,  0.        ,  0.61803399]), [[31, 77, 199, 355, 460, 465, 482, 489, 491, 492, 493, 494], 
　[70, 73, 77, 83, 86, 188, 193, 197, 199, 200, 483, 501, 503, 504, 
　505, 812, 813, 814, 937, 940, 945, 948, 949, 950, 967, 976, 977, 978, 979, 980], 
　[48, 49, 50, 54, 56, 127, 129, 131, 134, 135, 323, 324, 336, 337, 338, 507, 541, 542, 543, 552]]], 
[array([ 1.61803399, -0.61803399,  1.        ,  0.        ]), [[32, 125, 200, 318, 356, 365, 389, 423, 466, 476, 491, 495], 
　[63, 71, 78, 80, 86, 303, 309, 313, 317, 320, 484, 491, 493, 503, 
　506, 762, 764, 766, 767, 810, 814, 821, 823, 853, 854, 896, 942, 948, 951, 977], 
　[42, 43, 49, 52, 56, 202, 203, 208, 210, 212, 322, 324, 329, 331, 337, 493, 494, 495, 509, 542]]], 
[array([ 0.        ,  1.        , -0.61803399, -1.61803399]), [[150, 156, 279, 371, 395, 419, 496, 497, 498, 499, 500, 501], 
　[362, 375, 381, 382, 383, 390, 391, 392, 393, 394, 692, 696, 702, 
　703, 704, 831, 833, 835, 836, 859, 864, 892, 893, 981, 982, 983, 984, 985, 986, 987], 
　[241, 243, 253, 256, 257, 260, 261, 262, 263, 264, 461, 463, 466, 470, 471, 512, 513, 514, 528, 553]]], 
[array([ 0.        ,  0.61803399, -1.61803399, -1.        ]), [[151, 157, 255, 414, 496, 502, 503, 504, 505, 506, 507, 508], 
　[371, 381, 384, 385, 386, 390, 395, 396, 397, 398, 632, 642, 643, 
　644, 645, 888, 889, 890, 981, 982, 983, 988, 989, 990, 991, 992, 993, 994, 995, 996], 
　[251, 252, 256, 257, 258, 260, 261, 265, 266, 267, 423, 424, 430, 431, 432, 527, 553, 554, 555, 556]]], 
[array([ 0.        ,  1.61803399, -1.        , -0.61803399]), [[152, 158, 223, 404, 415, 420, 447, 497, 502, 509, 510, 511], 
　[369, 372, 376, 382, 384, 391, 395, 399, 400, 401, 557, 558, 560, 
　563, 564, 870, 872, 874, 885, 888, 891, 892, 894, 924, 925, 981, 984, 988, 997, 998], 
　[246, 248, 251, 253, 256, 260, 262, 265, 268, 269, 372, 373, 374, 375, 377, 522, 526, 527, 528, 537]]], 
[array([ 1.        ,  0.        , -1.61803399, -0.61803399]), [[153, 168, 256, 416, 431, 453, 503, 512, 513, 514, 515, 516], 
　[373, 379, 385, 387, 388, 420, 421, 422, 423, 424, 633, 639, 642, 
　646, 647, 881, 887, 889, 902, 905, 906, 931, 932, 989, 990, 999, 1000, 1001, 1002, 1003], 
　[250, 252, 255, 258, 259, 280, 281, 282, 283, 284, 422, 423, 428, 430, 433, 524, 531, 532, 538, 554]]], 
[array([ 1.        , -0.61803399,  0.        , -1.61803399]), [[126, 169, 280, 396, 406, 424, 517, 518, 519, 520, 521, 522], 
　[306, 310, 321, 322, 323, 425, 426, 427, 428, 429, 697, 699, 705, 
　706, 707, 857, 861, 865, 866, 875, 876, 897, 898, 1004, 1005, 1006, 1007, 1008, 1009, 1010], 
　[205, 206, 209, 216, 217, 285, 286, 287, 288, 289, 465, 467, 468, 472, 473, 518, 520, 521, 529, 557]]], 
[array([ 1.        , -1.61803399, -0.61803399,  0.        ]), [[78, 170, 230, 467, 483, 492, 523, 524, 525, 526, 527, 528], 
　[194, 199, 201, 202, 203, 430, 431, 432, 433, 434, 571, 575, 579,
　 580, 581, 946, 949, 952, 953, 967, 968, 978, 979, 1011, 1012, 1013, 1014, 1015, 1016, 1017], 
　 [131, 132, 135, 136, 137, 290, 291, 292, 293, 294, 380, 382, 385, 388, 389, 541, 543, 544, 552, 558]]], 
[array([ 0.61803399,  0.        , -1.        , -1.61803399]), [[154, 171, 281, 397, 498, 504, 512, 517, 529, 530, 531, 532], 
　[363, 383, 386, 387, 389, 420, 425, 435, 436, 437, 698, 702, 705, 
　708, 709, 864, 865, 867, 982, 985, 989, 991, 992, 999, 1000, 1004, 1005, 1018, 1019, 1020], 
　[243, 244, 257, 258, 259, 280, 281, 285, 286, 295, 466, 467, 470, 472, 474, 521, 553, 554, 555, 559]]], 
[array([ 0.61803399, -1.        , -1.61803399,  0.        ]), [[79, 172, 257, 454, 513, 523, 533, 534, 535, 536, 537, 538], 
　[182, 201, 204, 205, 206, 421, 430, 438, 439, 440, 640, 646, 648, 
　649, 650, 931, 933, 934, 1001, 1002, 1011, 1012, 1013, 1021, 1022, 1023, 1024, 1025, 1026, 1027], 
　[123, 124, 136, 137, 138, 282, 283, 290, 291, 296, 428, 429, 433, 434, 435, 538, 558, 560, 561, 562]]], 
[array([ 0.61803399, -1.61803399,  0.        , -1.        ]), [[127, 173, 231, 468, 518, 524, 539, 540, 541, 542, 543, 544], 
　[314, 321, 324, 325, 326, 426, 431, 441, 442, 443, 572, 579, 582, 
　583, 584, 952, 954, 955, 1006, 1007, 1008, 1014, 1015, 1028, 1029, 1030, 1031, 1032, 1033, 1034], 
　[213, 214, 216, 217, 218, 287, 288, 292, 293, 297, 382, 383, 388, 390, 391, 544, 557, 563, 564, 565]]], 
[array([ 1.61803399,  0.        , -0.61803399, -1.        ]), [[155, 174, 201, 398, 425, 428, 432, 514, 519, 529, 545, 546], 
　[364, 378, 380, 388, 389, 422, 427, 435, 444, 445, 494, 497, 499, 
　507, 508, 862, 863, 866, 867, 895, 897, 899, 900, 905, 907, 999, 1003, 1004, 1009, 1035], 
　[242, 244, 254, 255, 259, 280, 284, 285, 289, 298, 330, 332, 333, 335, 339, 519, 520, 521, 529, 532]]], 
[array([ 1.61803399, -1.        ,  0.        , -0.61803399]), [[128, 175, 202, 426, 469, 493, 495, 520, 525, 539, 545, 547], 
　[311, 315, 320, 322, 324, 428, 432, 441, 444, 446, 495, 504, 506, 
　507, 509, 896, 898, 899, 950, 951, 953, 954, 977, 978, 980, 1006, 1009, 1014, 1016, 1035], 
　[208, 209, 212, 213, 216, 287, 289, 292, 294, 298, 331, 332, 337, 338, 339, 529, 542, 543, 544, 552]]], 
[array([ 1.61803399, -0.61803399, -1.        ,  0.        ]), [[80, 176, 203, 433, 455, 490, 494, 515, 526, 533, 546, 547], 
　[183, 198, 200, 202, 204, 423, 433, 438, 445, 446, 500, 502, 505, 
　508, 509, 903, 904, 906, 907, 930, 932, 933, 976, 979, 980, 1001, 1003, 1011, 1016, 1035], 
　[122, 123, 134, 135, 136, 282, 284, 290, 294, 298, 334, 335, 336, 338, 339, 530, 531, 532, 538, 552]]], 
[array([ 0.        , -1.        ,  0.61803399,  1.61803399]), [[33, 36, 270, 338, 461, 484, 548, 549, 550, 551, 552, 553], 
　[67, 74, 84, 87, 88, 90, 91, 92, 93, 94, 670, 676, 680, 681, 682, 794, 
　795, 796, 938, 941, 969, 970, 971, 1036, 1037, 1038, 1039, 1040, 1041, 1042], 
　[46, 47, 51, 58, 59, 60, 61, 62, 63, 64, 448, 449, 453, 455, 456, 504, 539, 549, 550, 566]]], 
[array([ 0.        , -0.61803399,  1.61803399,  1.        ]), [[34, 37, 246, 301, 319, 339, 477, 548, 554, 555, 556, 557], 
　[64, 68, 81, 87, 89, 90, 95, 96, 97, 98, 602, 608, 618, 621, 622, 739, 
　740, 743, 744, 758, 768, 795, 797, 960, 961, 1036, 1037, 1043, 1044, 1045], 
　[41, 44, 47, 57, 59, 60, 61, 65, 66, 67, 401, 403, 407, 414, 416, 486, 487, 488, 504, 546]]], 
[array([ 0.        , -1.61803399,  1.        ,  0.61803399]), [[35, 38, 232, 470, 478, 485, 549, 554, 558, 559, 560, 561], 
　[79, 82, 85, 88, 89, 91, 95, 99, 100, 101, 573, 576, 585, 586, 587, 943, 
　947, 956, 960, 962, 963, 969, 972, 1036, 1038, 1043, 1046, 1047, 1048, 1049], 
　[53, 55, 57, 58, 59, 60, 62, 65, 68, 69, 381, 384, 386, 392, 393, 540, 546, 547, 549, 567]]], 
[array([-1.        ,  0.        ,  1.61803399,  0.61803399]), [[15, 39, 247, 302, 555, 562, 563, 564, 565, 566, 567, 568], 
　[36, 42, 43, 44, 45, 96, 102, 103, 104, 105, 603, 621, 623, 624, 625, 743, 
　745, 746, 1044, 1045, 1050, 1051, 1052, 1053, 1054, 1055, 1056, 1057, 1058, 1059], 
　[26, 27, 30, 31, 32, 66, 67, 70, 71, 72, 403, 404, 416, 417, 418, 488, 568, 569, 570, 571]]], 
[array([-1.        ,  0.61803399,  0.        ,  1.61803399]), [[16, 63, 271, 294, 437, 569, 570, 571, 572, 573, 574, 575], 
　[32, 46, 47, 48, 49, 152, 162, 163, 164, 165, 663, 673, 683, 684, 685, 731, 
　733, 734, 913, 914, 1060, 1061, 1062, 1063, 1064, 1065, 1066, 1067, 1068, 1069], 
　[23, 24, 33, 34, 35, 103, 104, 110, 111, 112, 443, 444, 451, 457, 458, 484, 572, 573, 574, 575]]], 
[array([-1.        ,  1.61803399,  0.61803399,  0.        ]), [[17, 111, 224, 309, 383, 576, 577, 578, 579, 580, 581, 582], 
　[39, 50, 51, 52, 53, 279, 282, 283, 284, 285, 543, 553, 565, 566, 567, 753, 
　755, 756, 849, 850, 1070, 1071, 1072, 1073, 1074, 1075, 1076, 1077, 1078, 1079], 
　[28, 29, 36, 37, 38, 188, 189, 190, 191, 192, 363, 364, 371, 378, 379, 491, 576, 577, 578, 579]]], 
[array([-0.61803399,  0.        ,  1.        ,  1.61803399]), [[18, 40, 272, 295, 303, 340, 550, 556, 562, 569, 583, 584], 
　[33, 37, 42, 46, 54, 92, 97, 102, 106, 107, 664, 671, 680, 683, 686, 722, 
　728, 733, 741, 744, 745, 796, 797, 1037, 1039, 1044, 1050, 1060, 1061, 1080], 
　[21, 23, 26, 30, 33, 61, 63, 66, 70, 73, 442, 444, 449, 455, 457, 480, 487, 488, 504, 572]]], 
[array([-0.61803399,  1.        ,  1.61803399,  0.        ]), [[19, 112, 248, 304, 310, 345, 378, 384, 563, 576, 585, 586], 
　[38, 40, 43, 50, 55, 276, 280, 282, 286, 287, 604, 611, 613, 623, 626, 
　736, 742, 746, 751, 754, 755, 801, 802, 839, 844, 849, 1051, 1052, 1070, 1081], 
　[25, 27, 28, 31, 36, 185, 186, 188, 190, 193, 402, 404, 409, 411, 417, 485, 490, 491, 505, 568]]], 
[array([-0.61803399,  1.61803399,  0.        ,  1.        ]), [[20, 64, 225, 296, 311, 350, 438, 448, 570, 577, 587, 588], 
　[34, 41, 47, 51, 56, 153, 159, 162, 166, 167, 544, 551, 561, 565, 568, 
　724, 730, 732, 734, 752, 756, 806, 807, 911, 913, 926, 1062, 1071, 1072, 1082], 
　[22, 24, 29, 34, 37, 102, 103, 108, 110, 113, 362, 364, 369, 376, 378, 481, 483, 484, 506, 576]]], 
[array([-1.61803399,  0.        ,  0.61803399,  1.        ]), [[21, 41, 204, 564, 571, 583, 589, 590, 591, 592, 593, 594], 
　[44, 48, 54, 57, 58, 103, 106, 108, 109, 110, 510, 511, 512, 513, 514, 
　1050, 1053, 1054, 1060, 1063, 1064, 1065, 1080, 1083, 1084, 1085, 1086, 1087, 1088, 1089], 
　[30, 32, 33, 35, 39, 70, 71, 73, 74, 75, 340, 341, 342, 343, 344, 569, 572, 573, 574, 580]]], 
[array([-1.61803399,  1.        ,  0.        ,  0.61803399]), [[22, 65, 205, 572, 578, 587, 589, 595, 596, 597, 598, 599], 
　[49, 52, 56, 57, 59, 163, 166, 168, 169, 170, 510, 515, 516, 517, 518, 
　1062, 1063, 1066, 1071, 1073, 1074, 1075, 1082, 1083, 1084, 1090, 1091, 1092, 1093, 1094], 
　[34, 35, 37, 38, 39, 110, 111, 113, 114, 115, 340, 341, 345, 346, 347, 573, 576, 577, 578, 581]]], 
[array([-1.61803399,  0.61803399,  1.        ,  0.        ]), [[23, 113, 206, 565, 579, 585, 590, 595, 600, 601, 602, 603], 
　[45, 53, 55, 58, 59, 283, 286, 288, 289, 290, 511, 515, 519, 520, 521, 
　1051, 1053, 1055, 1056, 1070, 1073, 1076, 1081, 1083, 1085, 1090, 1095, 1096, 1097, 1098], 
　[31, 32, 36, 38, 39, 190, 191, 193, 194, 195, 340, 342, 345, 348, 349, 568, 569, 570, 577, 582]]], 
[array([ 0.        , -1.        ,  0.61803399, -1.61803399]), [[129, 132, 282, 407, 521, 540, 604, 605, 606, 607, 608, 609], 
　[307, 323, 325, 327, 328, 330, 331, 332, 333, 334, 700, 706, 710, 
　711, 712, 876, 877, 878, 1007, 1010, 1028, 1029, 1030, 1099, 1100, 1101, 1102, 1103, 1104, 1105], 
　[206, 207, 217, 218, 219, 220, 221, 222, 223, 224, 468, 469, 473, 475, 476, 523, 557, 563, 564, 583]]], 
[array([ 0.        , -0.61803399,  1.61803399, -1.        ]), [[130, 133, 249, 379, 390, 408, 479, 604, 610, 611, 612, 613], 
　[304, 308, 318, 327, 329, 330, 335, 336, 337, 338, 614, 617, 619, 
　627, 628, 841, 842, 845, 846, 852, 855, 877, 879, 964, 965, 1099, 1100, 1106, 1107, 1108], 
　[201, 204, 207, 215, 219, 220, 221, 225, 226, 227, 410, 412, 413, 415, 419, 515, 516, 517, 523, 548]]], 
[array([ 0.        , -1.61803399,  1.        , -0.61803399]), [[131, 134, 233, 471, 480, 541, 558, 605, 610, 614, 615, 616], 
　[316, 319, 326, 328, 329, 331, 335, 339, 340, 341, 574, 582, 585, 
　588, 589, 944, 955, 956, 962, 964, 966, 1028, 1031, 1046, 1047, 1099, 1101, 1106, 1109, 1110], 
　[211, 214, 215, 218, 219, 220, 222, 225, 228, 229, 383, 384, 390, 392, 394, 540, 547, 548, 563, 567]]], 
[array([-1.        ,  0.        ,  1.61803399, -0.61803399]), [[114, 135, 250, 380, 566, 586, 600, 611, 617, 618, 619, 620], 
　[277, 287, 288, 291, 292, 336, 342, 343, 344, 345, 615, 624, 626, 
　627, 629, 844, 845, 847, 1052, 1055, 1057, 1058, 1081, 1095, 1096, 1107, 1108, 1111, 1112, 1113], 
　[186, 187, 193, 194, 196, 226, 227, 230, 231, 232, 411, 412, 417, 418, 419, 517, 568, 570, 571, 582]]], 
[array([-1.        ,  0.61803399,  0.        , -1.61803399]), [[115, 159, 283, 372, 499, 621, 622, 623, 624, 625, 626, 627], 
　[272, 293, 294, 295, 296, 392, 402, 403, 404, 405, 693, 703, 713, 
　714, 715, 835, 837, 838, 986, 987, 1114, 1115, 1116, 1117, 1118, 1119, 1120, 1121, 1122, 1123], 
　[183, 184, 197, 198, 199, 263, 264, 270, 271, 272, 463, 464, 471, 477, 478, 514, 584, 585, 586, 587]]], 
[array([-1.        ,  1.61803399, -0.61803399,  0.        ]), [[66, 160, 226, 449, 509, 580, 588, 596, 628, 629, 630, 631], 
　[160, 167, 168, 171, 172, 399, 406, 407, 408, 409, 562, 563, 566, 
　568, 569, 924, 926, 927, 997, 998, 1072, 1074, 1077, 1078, 1082, 1091, 1092, 1124, 1125, 1126], 
　[108, 109, 113, 114, 116, 268, 269, 273, 274, 275, 375, 376, 377, 378, 379, 537, 576, 578, 579, 581]]], 
[array([-0.61803399,  0.        ,  1.        , -1.61803399]), [[116, 136, 284, 373, 381, 409, 606, 612, 617, 621, 632, 633], 
　[273, 278, 291, 293, 297, 332, 337, 342, 346, 347, 694, 701, 710, 
　713, 716, 826, 832, 837, 843, 846, 847, 878, 879, 1100, 1102, 1107, 1111, 1114, 1115, 1127], 
　[181, 183, 187, 196, 197, 221, 223, 226, 230, 233, 462, 464, 469, 475, 477, 510, 516, 517, 523, 584]]], 
[array([-0.61803399,  1.        , -1.61803399,  0.        ]), [[67, 161, 258, 417, 443, 450, 505, 510, 628, 634, 635, 636], 
　[156, 161, 171, 173, 174, 396, 400, 406, 410, 411, 634, 636, 643, 
　651, 652, 884, 886, 890, 891, 915, 920, 925, 927, 988, 993, 997, 1124, 1128, 1129, 1130], 
　[105, 106, 109, 116, 117, 265, 266, 268, 273, 276, 421, 424, 426, 431, 436, 525, 526, 527, 537, 588]]], 
[array([-0.61803399,  1.61803399,  0.        , -1.        ]), [[117, 162, 227, 374, 385, 421, 500, 511, 581, 622, 629, 637], 
　[274, 281, 284, 294, 298, 393, 401, 402, 407, 412, 554, 559, 564, 
　567, 569, 828, 834, 836, 838, 848, 850, 893, 894, 984, 986, 998, 1077, 1079, 1116, 1125], 
　[182, 184, 189, 192, 198, 262, 263, 269, 270, 274, 370, 371, 374, 377, 379, 511, 513, 514, 528, 579]]], 
[array([-1.61803399,  0.        ,  0.61803399, -1.        ]), [[118, 137, 207, 601, 618, 623, 632, 638, 639, 640, 641, 642], 
　[289, 292, 295, 297, 299, 343, 346, 348, 349, 350, 519, 522, 523, 
　524, 525, 1095, 1097, 1098, 1111, 1112, 1114, 1117, 1118, 1119, 1127, 1131, 1132, 1133, 1134, 1135], 
　[194, 195, 196, 197, 199, 230, 231, 233, 234, 235, 348, 349, 350, 351, 352, 582, 584, 585, 586, 589]]], 
[array([-1.61803399,  1.        ,  0.        , -0.61803399]), [[119, 163, 208, 582, 597, 602, 624, 630, 637, 638, 643, 644], 
　[285, 290, 296, 298, 299, 403, 408, 412, 413, 414, 516, 520, 522, 
　526, 527, 1075, 1076, 1078, 1079, 1090, 1091, 1093, 1097, 1116, 1117, 1120, 1125, 1126, 1131, 1136], 
　[191, 192, 195, 198, 199, 270, 271, 274, 275, 277, 345, 346, 348, 350, 353, 577, 578, 579, 581, 585]]], 
[array([-1.61803399,  0.61803399, -1.        ,  0.        ]), [[68, 164, 209, 598, 631, 634, 643, 645, 646, 647, 648, 649], 
　[169, 172, 173, 175, 176, 409, 410, 413, 415, 416, 517, 526, 528, 
　529, 530, 1092, 1093, 1094, 1124, 1126, 1128, 1129, 1136, 1137, 1138, 1139, 1140, 1141, 1142, 1143], 
　[114, 115, 116, 117, 118, 273, 275, 276, 277, 278, 346, 347, 353, 354, 355, 581, 588, 590, 591, 592]]], 
[array([ 0.        , -1.        , -0.61803399,  1.61803399]), [[81, 84, 273, 462, 473, 486, 551, 650, 651, 652, 653, 654], 
　[189, 191, 195, 207, 208, 210, 211, 212, 213, 214, 677, 678, 681, 
　687, 688, 936, 939, 941, 957, 958, 970, 973, 974, 1040, 1041, 1144, 1145, 1146, 1147, 1148], 
　[126, 128, 130, 133, 139, 140, 141, 142, 143, 144, 452, 453, 454, 456, 459, 539, 545, 550, 551, 566]]], 
[array([ 0.        , -0.61803399, -1.61803399,  1.        ]), [[82, 85, 259, 444, 456, 474, 534, 650, 655, 656, 657, 658], 
　[184, 192, 205, 207, 209, 210, 215, 216, 217, 218, 637, 641, 648, 
　653, 654, 917, 918, 921, 922, 929, 934, 957, 959, 1021, 1022, 1144, 1145, 1149, 1150, 1151], 
　[121, 124, 130, 138, 139, 140, 141, 145, 146, 147, 425, 427, 429, 434, 437, 534, 535, 536, 545, 560]]], 
[array([ 0.        , -1.61803399, -1.        ,  0.61803399]), [[83, 86, 234, 487, 527, 535, 651, 655, 659, 660, 661, 662], 
　[196, 203, 206, 208, 209, 211, 215, 219, 220, 221, 577, 580, 590, 
　591, 592, 968, 973, 975, 1012, 1017, 1021, 1023, 1024, 1144, 1146, 1149, 1152, 1153, 1154, 1155], 
　[132, 133, 137, 138, 139, 140, 142, 145, 148, 149, 385, 387, 389, 395, 396, 551, 558, 560, 561, 593]]], 
[array([-1.        ,  0.        , -1.61803399,  0.61803399]), [[69, 87, 260, 445, 635, 645, 656, 663, 664, 665, 666, 667], 
　[157, 174, 175, 177, 178, 216, 222, 223, 224, 225, 638, 651, 653, 
　655, 656, 920, 921, 923, 1128, 1130, 1137, 1138, 1139, 1150, 1151, 1156, 1157, 1158, 1159, 1160], 
　[106, 107, 117, 118, 119, 146, 147, 150, 151, 152, 426, 427, 436, 437, 438, 536, 588, 590, 591, 594]]], 
[array([-1.        , -0.61803399,  0.        ,  1.61803399]), [[42, 88, 274, 552, 573, 584, 591, 652, 668, 669, 670, 671], 
　[93, 107, 108, 111, 112, 212, 226, 227, 228, 229, 682, 684, 686, 
　687, 689, 1039, 1040, 1042, 1061, 1064, 1067, 1068, 1080, 1086, 1087, 1147, 1148, 1161, 1162, 1163], 
　[63, 64, 73, 74, 76, 143, 144, 153, 154, 155, 455, 456, 457, 458, 459, 566, 572, 574, 575, 580]]], 
[array([-1.        , -1.61803399,  0.61803399,  0.        ]), [[43, 138, 235, 559, 614, 672, 673, 674, 675, 676, 677, 678], 
　[99, 113, 114, 115, 116, 339, 351, 352, 353, 354, 586, 588, 593,
　 594, 595, 1046, 1048, 1049, 1109, 1110, 1164, 1165, 1166, 1167, 　 1168, 1169, 1170, 1171, 1172, 1173], 
　 [68, 69, 77, 78, 79, 228, 229, 236, 237, 238, 392, 393, 394, 397, 398, 567, 595, 596, 597, 598]]], 
[array([-0.61803399,  0.        , -1.        ,  1.61803399]), [[70, 89, 275, 439, 446, 475, 574, 653, 657, 663, 668, 679], 
　[154, 158, 164, 177, 179, 213, 217, 222, 226, 230, 674, 679, 685, 
　688, 689, 910, 912, 914, 919, 922, 923, 958, 959, 1067, 1069, 1145, 1147, 1150, 1156, 1161], 
　[101, 104, 107, 112, 119, 141, 143, 146, 150, 153, 450, 451, 454, 458, 459, 533, 535, 536, 545, 575]]], 
[array([-0.61803399, -1.        ,  1.61803399,  0.        ]), [[44, 139, 251, 481, 557, 560, 567, 613, 615, 619, 672, 680], 
　[98, 100, 104, 113, 117, 338, 340, 344, 351, 355, 620, 622, 625, 
　628, 629, 961, 963, 965, 966, 1043, 1045, 1047, 1048, 1057, 1059, 1106, 1108, 1109, 1113, 1164], 
　[65, 67, 68, 72, 77, 225, 227, 228, 232, 236, 414, 415, 416, 418, 419, 546, 547, 548, 567, 571]]], 
[array([-0.61803399, -1.61803399,  0.        ,  1.        ]), [[45, 90, 236, 488, 553, 561, 654, 659, 669, 673, 681, 682], 
　[94, 101, 111, 114, 118, 214, 219, 227, 231, 232, 578, 587, 590, 
　593, 596, 971, 972, 974, 975, 1038, 1041, 1042, 1049, 1146, 1148, 1152, 1162, 1165, 1166, 1174], 
　[62, 64, 69, 76, 78, 142, 144, 148, 154, 156, 386, 387, 393, 395, 397, 549, 550, 551, 566, 595]]], 
[array([-1.61803399,  0.        , -0.61803399,  1.        ]), [[71, 91, 210, 575, 592, 599, 646, 664, 670, 679, 683, 684], 
　[165, 170, 176, 178, 179, 223, 228, 230, 233, 234, 512, 518, 528, 
　531, 532, 1065, 1066, 1068, 1069, 1084, 1086, 1088, 1094, 1137, 1140, 1156, 1157, 1161, 1163, 1175], 
　[111, 112, 115, 118, 119, 150, 151, 153, 155, 157, 341, 343, 347, 354, 356, 573, 574, 575, 580, 590]]], 
[array([-1.61803399, -1.        ,  0.        ,  0.61803399]), [[46, 92, 211, 593, 671, 674, 681, 683, 685, 686, 687, 688], 
　[109, 112, 115, 118, 119, 229, 231, 233, 235, 236, 513, 531, 533, 
　534, 535, 1087, 1088, 1089, 1162, 1163, 1165, 1167, 1168, 1169, 1174, 1175, 1176, 1177, 1178, 1179], 
　[74, 75, 76, 78, 79, 154, 155, 156, 157, 158, 343, 344, 356, 357, 358, 580, 595, 596, 597, 599]]], 
[array([-1.61803399, -0.61803399,  1.        ,  0.        ]), [[47, 140, 212, 568, 594, 603, 620, 639, 675, 680, 685, 689], 
　[105, 110, 116, 117, 119, 345, 348, 352, 355, 356, 514, 521, 523, 
　533, 536, 1054, 1056, 1058, 1059, 1085, 1089, 1096, 1098, 1112, 1113, 1132, 1164, 1167, 1170, 1176], 
　[71, 72, 75, 77, 79, 231, 232, 234, 236, 237, 342, 344, 349, 351, 357, 569, 570, 571, 582, 596]]], 
[array([ 0.        , -1.        , -0.61803399, -1.61803399]), [[177, 180, 285, 522, 530, 542, 607, 690, 691, 692, 693, 694], 
　[429, 436, 442, 447, 448, 450, 451, 452, 453, 454, 707, 708, 711, 
　717, 718, 1005, 1008, 1010, 1018, 1019, 1029, 1032, 1033, 1103, 1104, 1180, 1181, 1182, 1183, 1184], 
　[286, 288, 295, 297, 299, 300, 301, 302, 303, 304, 472, 473, 474, 476, 479, 557, 559, 564, 565, 583]]], 
[array([ 0.        , -0.61803399, -1.61803399, -1.        ]), [[178, 181, 261, 506, 516, 531, 536, 690, 695, 696, 697, 698], 
　[424, 437, 439, 447, 449, 450, 455, 456, 457, 458, 644, 647, 649, 
　657, 658, 990, 991, 994, 995, 1000, 1002, 1018, 1020, 1025, 1026, 1180, 1181, 1185, 1186, 1187], 
　[281, 283, 295, 296, 299, 300, 301, 305, 306, 307, 430, 432, 433, 435, 439, 554, 555, 556, 559, 562]]], 
[array([ 0.        , -1.61803399, -1.        , -0.61803399]), [[179, 182, 237, 528, 537, 543, 660, 691, 695, 699, 700, 701], 
　[434, 440, 443, 448, 449, 451, 455, 459, 460, 461, 581, 583, 591,
　 597, 598, 1013, 1015, 1017, 1023, 1025, 1027, 1032, 1034, 1153, 1154, 1180, 1182, 1185, 1188, 1189], 
　 [291, 293, 296, 297, 299, 300, 302, 305, 308, 309, 388, 389, 391, 396, 399, 558, 561, 562, 565, 593]]], 
[array([-1.        ,  0.        , -1.61803399, -0.61803399]), [[165, 183, 262, 507, 636, 647, 665, 696, 702, 703, 704, 705], 
　[397, 411, 415, 417, 418, 456, 462, 463, 464, 465, 645, 652, 655, 
　657, 659, 993, 994, 996, 1129, 1130, 1138, 1141, 1142, 1158, 1159, 1186, 1187, 1190, 1191, 1192], 
　[266, 267, 276, 278, 279, 306, 307, 310, 311, 312, 431, 432, 436, 438, 439, 556, 588, 591, 592, 594]]], 
[array([-1.        , -0.61803399,  0.        , -1.61803399]), [[141, 184, 286, 608, 625, 633, 640, 692, 706, 707, 708, 709], 
　[333, 347, 349, 357, 358, 452, 466, 467, 468, 469, 712, 714, 716, 
　717, 719, 1102, 1103, 1105, 1115, 1118, 1121, 1122, 1127, 1133, 1134, 1183, 1184, 1193, 1194, 1195], 
　[223, 224, 233, 235, 239, 303, 304, 313, 314, 315, 475, 476, 477, 478, 479, 583, 584, 586, 587, 589]]], 
[array([-1.        , -1.61803399, -0.61803399,  0.        ]), [[93, 185, 238, 661, 676, 682, 686, 699, 710, 711, 712, 713], 
　[220, 232, 235, 237, 238, 459, 470, 471, 472, 473, 592, 594, 596, 
　597, 599, 1152, 1153, 1155, 1166, 1168, 1171, 1172, 1174, 1177, 1178, 1188, 1189, 1196, 1197, 1198], 
　[148, 149, 156, 158, 159, 308, 309, 316, 317, 318, 395, 396, 397, 398, 399, 593, 595, 597, 598, 599]]], 
[array([-0.61803399,  0.        , -1.        , -1.61803399]), [[166, 186, 287, 501, 508, 532, 626, 693, 697, 702, 706, 714], 
　[394, 398, 404, 417, 419, 453, 457, 462, 466, 474, 704, 709, 715, 
　718, 719, 983, 985, 987, 992, 995, 996, 1019, 1020, 1121, 1123, 1181, 1183, 1186, 1190, 1193], 
　[261, 264, 267, 272, 279, 301, 303, 306, 310, 313, 470, 471, 474, 478, 479, 553, 555, 556, 559, 587]]], 
[array([-0.61803399, -1.        , -1.61803399,  0.        ]), [[94, 187, 263, 538, 658, 662, 666, 698, 700, 703, 710, 715], 
　[218, 221, 224, 237, 239, 458, 460, 463, 470, 475, 650, 654, 656, 
　658, 659, 1022, 1024, 1026, 1027, 1149, 1151, 1154, 1155, 1158, 1160, 1185, 1187, 1188, 1191, 1196], 
　[145, 147, 149, 152, 159, 305, 307, 308, 311, 316, 434, 435, 437, 438, 439, 560, 561, 562, 593, 594]]], 
[array([-0.61803399, -1.61803399,  0.        , -1.        ]), [[142, 188, 239, 544, 609, 616, 677, 694, 701, 707, 711, 716], 
　[334, 341, 353, 357, 359, 454, 461, 467, 471, 476, 584, 589, 595, 
　598, 599, 1030, 1031, 1033, 1034, 1101, 1104, 1105, 1110, 1171, 1173, 1182, 1184, 1189, 1194, 1197], 
　[222, 224, 229, 238, 239, 302, 304, 309, 314, 317, 390, 391, 394, 398, 399, 563, 564, 565, 583, 598]]], 
[array([-1.61803399,  0.        , -0.61803399, -1.        ]), [[167, 189, 213, 627, 641, 644, 648, 704, 708, 714, 717, 718], 
　[405, 414, 416, 418, 419, 464, 468, 474, 477, 478, 524, 527, 529, 
　537, 538, 1119, 1120, 1122, 1123, 1131, 1133, 1135, 1136, 1141, 1143, 1190, 1192, 1193, 1195, 1199], 
　[271, 272, 277, 278, 279, 310, 312, 313, 315, 319, 350, 352, 353, 355, 359, 585, 586, 587, 589, 592]]], 
[array([-1.61803399, -1.        ,  0.        , -0.61803399]), [[143, 190, 214, 642, 678, 687, 689, 709, 712, 716, 717, 719], 
　[350, 354, 356, 358, 359, 469, 472, 476, 477, 479, 525, 534, 536, 
　537, 539, 1132, 1134, 1135, 1169, 1170, 1172, 1173, 1176, 1177, 1179, 1194, 1195, 1197, 1198, 1199], 
　[234, 235, 237, 238, 239, 314, 315, 317, 318, 319, 351, 352, 357, 358, 359, 589, 596, 597, 598, 599]]], 
[array([-1.61803399, -0.61803399, -1.        ,  0.        ]), [[95, 191, 215, 649, 667, 684, 688, 705, 713, 715, 718, 719], 
　[225, 234, 236, 238, 239, 465, 473, 475, 478, 479, 530, 532, 535, 
　538, 539, 1139, 1140, 1142, 1143, 1157, 1159, 1160, 1175, 1178, 1179, 1191, 1192, 1196, 1198, 1199], 
　[151, 152, 157, 158, 159, 311, 312, 316, 318, 319, 354, 355, 356, 358, 359, 590, 591, 592, 594, 599]]]
]

len(cube.e)= 720 
cube.e= [
[[0, 24], [0, 1, 2, 3, 4], [0, 1, 2, 3, 4]], 
[[0, 25], [0, 5, 6, 7, 8], [0, 1, 5, 6, 7]], 
[[0, 26], [1, 5, 9, 10, 11], [0, 2, 5, 8, 9]], 
[[0, 27], [6, 12, 13, 14, 15], [6, 7, 10, 11, 12]], 
[[0, 28], [2, 16, 17, 18, 19], [3, 4, 13, 14, 15]], 
[[0, 29], [9, 20, 21, 22, 23], [8, 9, 16, 17, 18]], 
[[0, 30], [3, 7, 12, 16, 24], [1, 3, 6, 10, 13]], 
[[0, 31], [8, 10, 13, 20, 25], [5, 7, 8, 11, 16]], 
[[0, 32], [4, 11, 17, 21, 26], [2, 4, 9, 14, 17]], 
[[0, 33], [14, 18, 24, 27, 28], [10, 12, 13, 15, 19]], 
[[0, 34], [19, 22, 26, 27, 29], [14, 15, 17, 18, 19]], 
[[0, 35], [15, 23, 25, 28, 29], [11, 12, 16, 18, 19]], 
[[1, 24], [30, 31, 32, 33, 34], [20, 21, 22, 23, 24]], 
[[1, 25], [30, 35, 36, 37, 38], [20, 21, 25, 26, 27]], 
[[1, 26], [31, 35, 39, 40, 41], [20, 22, 25, 28, 29]], 
[[1, 75], [36, 42, 43, 44, 45], [26, 27, 30, 31, 32]], 
[[1, 76], [32, 46, 47, 48, 49], [23, 24, 33, 34, 35]], 
[[1, 77], [39, 50, 51, 52, 53], [28, 29, 36, 37, 38]], 
[[1, 78], [33, 37, 42, 46, 54], [21, 23, 26, 30, 33]], 
[[1, 79], [38, 40, 43, 50, 55], [25, 27, 28, 31, 36]], 
[[1, 80], [34, 41, 47, 51, 56], [22, 24, 29, 34, 37]], 
[[1, 81], [44, 48, 54, 57, 58], [30, 32, 33, 35, 39]], 
[[1, 82], [49, 52, 56, 57, 59], [34, 35, 37, 38, 39]], 
[[1, 83], [45, 53, 55, 58, 59], [31, 32, 36, 38, 39]], 
[[2, 27], [60, 61, 62, 63, 64], [40, 41, 42, 43, 44]], 
[[2, 30], [60, 65, 66, 67, 68], [40, 41, 45, 46, 47]], 
[[2, 33], [61, 65, 69, 70, 71], [40, 42, 45, 48, 49]], 
[[2, 52], [66, 69, 72, 73, 74], [45, 46, 48, 50, 51]], 
[[2, 53], [75, 76, 77, 78, 79], [52, 53, 54, 55, 56]], 
[[2, 55], [62, 75, 80, 81, 82], [43, 44, 52, 53, 57]], 
[[2, 56], [72, 76, 83, 84, 85], [50, 51, 54, 55, 58]], 
[[2, 58], [70, 73, 77, 83, 86], [48, 49, 50, 54, 56]], 
[[2, 59], [63, 71, 78, 80, 86], [42, 43, 49, 52, 56]], 
[[2, 72], [67, 74, 84, 87, 88], [46, 47, 51, 58, 59]], 
[[2, 73], [64, 68, 81, 87, 89], [41, 44, 47, 57, 59]], 
[[2, 74], [79, 82, 85, 88, 89], [53, 55, 57, 58, 59]], 
[[3, 72], [90, 91, 92, 93, 94], [60, 61, 62, 63, 64]], 
[[3, 73], [90, 95, 96, 97, 98], [60, 61, 65, 66, 67]], 
[[3, 74], [91, 95, 99, 100, 101], [60, 62, 65, 68, 69]], 
[[3, 75], [96, 102, 103, 104, 105], [66, 67, 70, 71, 72]], 
[[3, 78], [92, 97, 102, 106, 107], [61, 63, 66, 70, 73]], 
[[3, 81], [103, 106, 108, 109, 110], [70, 71, 73, 74, 75]], 
[[3, 100], [93, 107, 108, 111, 112], [63, 64, 73, 74, 76]], 
[[3, 101], [99, 113, 114, 115, 116], [68, 69, 77, 78, 79]], 
[[3, 103], [98, 100, 104, 113, 117], [65, 67, 68, 72, 77]], 
[[3, 104], [94, 101, 111, 114, 118], [62, 64, 69, 76, 78]], 
[[3, 106], [109, 112, 115, 118, 119], [74, 75, 76, 78, 79]], 
[[3, 107], [105, 110, 116, 117, 119], [71, 72, 75, 77, 79]], 
[[4, 28], [120, 121, 122, 123, 124], [80, 81, 82, 83, 84]], 
[[4, 32], [120, 125, 126, 127, 128], [80, 81, 85, 86, 87]], 
[[4, 34], [121, 125, 129, 130, 131], [80, 82, 85, 88, 89]], 
[[4, 41], [126, 129, 132, 133, 134], [85, 86, 88, 90, 91]], 
[[4, 43], [132, 135, 136, 137, 138], [90, 91, 92, 93, 94]], 
[[4, 47], [130, 133, 135, 139, 140], [88, 89, 90, 92, 95]], 
[[4, 48], [122, 127, 141, 142, 143], [81, 83, 87, 96, 97]], 
[[4, 49], [136, 141, 144, 145, 146], [93, 94, 96, 97, 98]], 
[[4, 50], [128, 134, 137, 142, 144], [86, 87, 91, 93, 96]], 
[[4, 51], [138, 139, 145, 147, 148], [92, 94, 95, 98, 99]], 
[[4, 54], [123, 143, 146, 147, 149], [83, 84, 97, 98, 99]], 
[[4, 57], [124, 131, 140, 148, 149], [82, 84, 89, 95, 99]], 
[[5, 48], [150, 151, 152, 153, 154], [100, 101, 102, 103, 104]], 
[[5, 49], [150, 155, 156, 157, 158], [100, 101, 105, 106, 107]], 
[[5, 50], [151, 155, 159, 160, 161], [100, 102, 105, 108, 109]], 
[[5, 76], [152, 162, 163, 164, 165], [103, 104, 110, 111, 112]], 
[[5, 80], [153, 159, 162, 166, 167], [102, 103, 108, 110, 113]], 
[[5, 82], [163, 166, 168, 169, 170], [110, 111, 113, 114, 115]], 
[[5, 89], [160, 167, 168, 171, 172], [108, 109, 113, 114, 116]], 
[[5, 91], [156, 161, 171, 173, 174], [105, 106, 109, 116, 117]], 
[[5, 95], [169, 172, 173, 175, 176], [114, 115, 116, 117, 118]], 
[[5, 99], [157, 174, 175, 177, 178], [106, 107, 117, 118, 119]], 
[[5, 102], [154, 158, 164, 177, 179], [101, 104, 107, 112, 119]], 
[[5, 105], [165, 170, 176, 178, 179], [111, 112, 115, 118, 119]], 
[[6, 51], [180, 181, 182, 183, 184], [120, 121, 122, 123, 124]], 
[[6, 52], [185, 186, 187, 188, 189], [125, 126, 127, 128, 129]], 
[[6, 54], [180, 185, 190, 191, 192], [120, 121, 125, 126, 130]], 
[[6, 56], [186, 193, 194, 195, 196], [127, 128, 131, 132, 133]], 
[[6, 57], [181, 187, 190, 197, 198], [120, 122, 125, 129, 134]], 
[[6, 58], [188, 193, 197, 199, 200], [127, 129, 131, 134, 135]], 
[[6, 65], [194, 199, 201, 202, 203], [131, 132, 135, 136, 137]], 
[[6, 67], [182, 201, 204, 205, 206], [123, 124, 136, 137, 138]], 
[[6, 71], [183, 198, 200, 202, 204], [122, 123, 134, 135, 136]], 
[[6, 96], [189, 191, 195, 207, 208], [126, 128, 130, 133, 139]], 
[[6, 97], [184, 192, 205, 207, 209], [121, 124, 130, 138, 139]], 
[[6, 98], [196, 203, 206, 208, 209], [132, 133, 137, 138, 139]], 
[[7, 96], [210, 211, 212, 213, 214], [140, 141, 142, 143, 144]], 
[[7, 97], [210, 215, 216, 217, 218], [140, 141, 145, 146, 147]], 
[[7, 98], [211, 215, 219, 220, 221], [140, 142, 145, 148, 149]], 
[[7, 99], [216, 222, 223, 224, 225], [146, 147, 150, 151, 152]], 
[[7, 100], [212, 226, 227, 228, 229], [143, 144, 153, 154, 155]], 
[[7, 102], [213, 217, 222, 226, 230], [141, 143, 146, 150, 153]], 
[[7, 104], [214, 219, 227, 231, 232], [142, 144, 148, 154, 156]], 
[[7, 105], [223, 228, 230, 233, 234], [150, 151, 153, 155, 157]], 
[[7, 106], [229, 231, 233, 235, 236], [154, 155, 156, 157, 158]], 
[[7, 113], [220, 232, 235, 237, 238], [148, 149, 156, 158, 159]], 
[[7, 115], [218, 221, 224, 237, 239], [145, 147, 149, 152, 159]], 
[[7, 119], [225, 234, 236, 238, 239], [151, 152, 157, 158, 159]], 
[[8, 29], [240, 241, 242, 243, 244], [160, 161, 162, 163, 164]], 
[[8, 31], [240, 245, 246, 247, 248], [160, 161, 165, 166, 167]], 
[[8, 35], [241, 245, 249, 250, 251], [160, 162, 165, 168, 169]], 
[[8, 36], [252, 253, 254, 255, 256], [170, 171, 172, 173, 174]], 
[[8, 37], [246, 252, 257, 258, 259], [166, 167, 170, 171, 175]], 
[[8, 38], [242, 247, 253, 257, 260], [161, 163, 166, 170, 172]], 
[[8, 39], [248, 249, 258, 261, 262], [165, 167, 168, 175, 176]], 
[[8, 40], [254, 263, 264, 265, 266], [173, 174, 177, 178, 179]], 
[[8, 42], [255, 259, 261, 263, 267], [171, 173, 175, 176, 177]], 
[[8, 44], [243, 256, 260, 264, 268], [163, 164, 172, 174, 178]], 
[[8, 45], [250, 262, 265, 267, 269], [168, 169, 176, 177, 179]], 
[[8, 46], [244, 251, 266, 268, 269], [162, 164, 169, 178, 179]], 
[[9, 36], [270, 271, 272, 273, 274], [180, 181, 182, 183, 184]], 
[[9, 37], [270, 275, 276, 277, 278], [180, 181, 185, 186, 187]], 
[[9, 38], [271, 275, 279, 280, 281], [180, 182, 185, 188, 189]], 
[[9, 77], [279, 282, 283, 284, 285], [188, 189, 190, 191, 192]], 
[[9, 79], [276, 280, 282, 286, 287], [185, 186, 188, 190, 193]], 
[[9, 83], [283, 286, 288, 289, 290], [190, 191, 193, 194, 195]], 
[[9, 87], [277, 287, 288, 291, 292], [186, 187, 193, 194, 196]], 
[[9, 88], [272, 293, 294, 295, 296], [183, 184, 197, 198, 199]], 
[[9, 90], [273, 278, 291, 293, 297], [181, 183, 187, 196, 197]], 
[[9, 92], [274, 281, 284, 294, 298], [182, 184, 189, 192, 198]], 
[[9, 93], [289, 292, 295, 297, 299], [194, 195, 196, 197, 199]], 
[[9, 94], [285, 290, 296, 298, 299], [191, 192, 195, 198, 199]], 
[[10, 39], [300, 301, 302, 303, 304], [200, 201, 202, 203, 204]], 
[[10, 42], [300, 305, 306, 307, 308], [200, 201, 205, 206, 207]], 
[[10, 45], [301, 305, 309, 310, 311], [200, 202, 205, 208, 209]], 
[[10, 53], [312, 313, 314, 315, 316], [210, 211, 212, 213, 214]], 
[[10, 55], [302, 312, 317, 318, 319], [203, 204, 210, 211, 215]], 
[[10, 59], [303, 309, 313, 317, 320], [202, 203, 208, 210, 212]], 
[[10, 64], [306, 310, 321, 322, 323], [205, 206, 209, 216, 217]], 
[[10, 68], [314, 321, 324, 325, 326], [213, 214, 216, 217, 218]], 
[[10, 70], [311, 315, 320, 322, 324], [208, 209, 212, 213, 216]], 
[[10, 84], [307, 323, 325, 327, 328], [206, 207, 217, 218, 219]], 
[[10, 85], [304, 308, 318, 327, 329], [201, 204, 207, 215, 219]], 
[[10, 86], [316, 319, 326, 328, 329], [211, 214, 215, 218, 219]], 
[[11, 84], [330, 331, 332, 333, 334], [220, 221, 222, 223, 224]], 
[[11, 85], [330, 335, 336, 337, 338], [220, 221, 225, 226, 227]], 
[[11, 86], [331, 335, 339, 340, 341], [220, 222, 225, 228, 229]], 
[[11, 87], [336, 342, 343, 344, 345], [226, 227, 230, 231, 232]], 
[[11, 90], [332, 337, 342, 346, 347], [221, 223, 226, 230, 233]], 
[[11, 93], [343, 346, 348, 349, 350], [230, 231, 233, 234, 235]], 
[[11, 101], [339, 351, 352, 353, 354], [228, 229, 236, 237, 238]], 
[[11, 103], [338, 340, 344, 351, 355], [225, 227, 228, 232, 236]], 
[[11, 107], [345, 348, 352, 355, 356], [231, 232, 234, 236, 237]], 
[[11, 112], [333, 347, 349, 357, 358], [223, 224, 233, 235, 239]], 
[[11, 116], [334, 341, 353, 357, 359], [222, 224, 229, 238, 239]], 
[[11, 118], [350, 354, 356, 358, 359], [234, 235, 237, 238, 239]], 
[[12, 40], [360, 361, 362, 363, 364], [240, 241, 242, 243, 244]], 
[[12, 41], [365, 366, 367, 368, 369], [245, 246, 247, 248, 249]], 
[[12, 43], [365, 370, 371, 372, 373], [245, 246, 250, 251, 252]], 
[[12, 44], [360, 366, 374, 375, 376], [240, 241, 247, 248, 253]], 
[[12, 46], [361, 367, 374, 377, 378], [240, 242, 247, 249, 254]], 
[[12, 47], [368, 370, 377, 379, 380], [245, 249, 250, 254, 255]], 
[[12, 60], [362, 375, 381, 382, 383], [241, 243, 253, 256, 257]], 
[[12, 61], [371, 381, 384, 385, 386], [251, 252, 256, 257, 258]], 
[[12, 62], [369, 372, 376, 382, 384], [246, 248, 251, 253, 256]], 
[[12, 63], [373, 379, 385, 387, 388], [250, 252, 255, 258, 259]], 
[[12, 66], [363, 383, 386, 387, 389], [243, 244, 257, 258, 259]], 
[[12, 69], [364, 378, 380, 388, 389], [242, 244, 254, 255, 259]], 
[[13, 60], [390, 391, 392, 393, 394], [260, 261, 262, 263, 264]], 
[[13, 61], [390, 395, 396, 397, 398], [260, 261, 265, 266, 267]], 
[[13, 62], [391, 395, 399, 400, 401], [260, 262, 265, 268, 269]], 
[[13, 88], [392, 402, 403, 404, 405], [263, 264, 270, 271, 272]], 
[[13, 89], [399, 406, 407, 408, 409], [268, 269, 273, 274, 275]], 
[[13, 91], [396, 400, 406, 410, 411], [265, 266, 268, 273, 276]], 
[[13, 92], [393, 401, 402, 407, 412], [262, 263, 269, 270, 274]], 
[[13, 94], [403, 408, 412, 413, 414], [270, 271, 274, 275, 277]], 
[[13, 95], [409, 410, 413, 415, 416], [273, 275, 276, 277, 278]], 
[[13, 111], [397, 411, 415, 417, 418], [266, 267, 276, 278, 279]], 
[[13, 114], [394, 398, 404, 417, 419], [261, 264, 267, 272, 279]], 
[[13, 117], [405, 414, 416, 418, 419], [271, 272, 277, 278, 279]], 
[[14, 63], [420, 421, 422, 423, 424], [280, 281, 282, 283, 284]], 
[[14, 64], [425, 426, 427, 428, 429], [285, 286, 287, 288, 289]], 
[[14, 65], [430, 431, 432, 433, 434], [290, 291, 292, 293, 294]], 
[[14, 66], [420, 425, 435, 436, 437], [280, 281, 285, 286, 295]], 
[[14, 67], [421, 430, 438, 439, 440], [282, 283, 290, 291, 296]], 
[[14, 68], [426, 431, 441, 442, 443], [287, 288, 292, 293, 297]], 
[[14, 69], [422, 427, 435, 444, 445], [280, 284, 285, 289, 298]], 
[[14, 70], [428, 432, 441, 444, 446], [287, 289, 292, 294, 298]], 
[[14, 71], [423, 433, 438, 445, 446], [282, 284, 290, 294, 298]], 
[[14, 108], [429, 436, 442, 447, 448], [286, 288, 295, 297, 299]], 
[[14, 109], [424, 437, 439, 447, 449], [281, 283, 295, 296, 299]], 
[[14, 110], [434, 440, 443, 448, 449], [291, 293, 296, 297, 299]], 
[[15, 108], [450, 451, 452, 453, 454], [300, 301, 302, 303, 304]], 
[[15, 109], [450, 455, 456, 457, 458], [300, 301, 305, 306, 307]], 
[[15, 110], [451, 455, 459, 460, 461], [300, 302, 305, 308, 309]], 
[[15, 111], [456, 462, 463, 464, 465], [306, 307, 310, 311, 312]], 
[[15, 112], [452, 466, 467, 468, 469], [303, 304, 313, 314, 315]], 
[[15, 113], [459, 470, 471, 472, 473], [308, 309, 316, 317, 318]], 
[[15, 114], [453, 457, 462, 466, 474], [301, 303, 306, 310, 313]], 
[[15, 115], [458, 460, 463, 470, 475], [305, 307, 308, 311, 316]], 
[[15, 116], [454, 461, 467, 471, 476], [302, 304, 309, 314, 317]], 
[[15, 117], [464, 468, 474, 477, 478], [310, 312, 313, 315, 319]], 
[[15, 118], [469, 472, 476, 477, 479], [314, 315, 317, 318, 319]], 
[[15, 119], [465, 473, 475, 478, 479], [311, 312, 316, 318, 319]], 
[[16, 33], [480, 481, 482, 483, 484], [320, 321, 322, 323, 324]], 
[[16, 34], [480, 485, 486, 487, 488], [320, 321, 325, 326, 327]], 
[[16, 35], [481, 485, 489, 490, 491], [320, 322, 325, 328, 329]], 
[[16, 45], [489, 492, 493, 494, 495], [328, 329, 330, 331, 332]], 
[[16, 46], [486, 490, 492, 496, 497], [325, 326, 328, 330, 333]], 
[[16, 47], [487, 496, 498, 499, 500], [326, 327, 333, 334, 335]], 
[[16, 57], [482, 488, 498, 501, 502], [321, 323, 327, 334, 336]], 
[[16, 58], [483, 501, 503, 504, 505], [323, 324, 336, 337, 338]], 
[[16, 59], [484, 491, 493, 503, 506], [322, 324, 329, 331, 337]], 
[[16, 69], [494, 497, 499, 507, 508], [330, 332, 333, 335, 339]], 
[[16, 70], [495, 504, 506, 507, 509], [331, 332, 337, 338, 339]], 
[[16, 71], [500, 502, 505, 508, 509], [334, 335, 336, 338, 339]], 
[[17, 81], [510, 511, 512, 513, 514], [340, 341, 342, 343, 344]], 
[[17, 82], [510, 515, 516, 517, 518], [340, 341, 345, 346, 347]], 
[[17, 83], [511, 515, 519, 520, 521], [340, 342, 345, 348, 349]], 
[[17, 93], [519, 522, 523, 524, 525], [348, 349, 350, 351, 352]], 
[[17, 94], [516, 520, 522, 526, 527], [345, 346, 348, 350, 353]], 
[[17, 95], [517, 526, 528, 529, 530], [346, 347, 353, 354, 355]], 
[[17, 105], [512, 518, 528, 531, 532], [341, 343, 347, 354, 356]], 
[[17, 106], [513, 531, 533, 534, 535], [343, 344, 356, 357, 358]], 
[[17, 107], [514, 521, 523, 533, 536], [342, 344, 349, 351, 357]], 
[[17, 117], [524, 527, 529, 537, 538], [350, 352, 353, 355, 359]], 
[[17, 118], [525, 534, 536, 537, 539], [351, 352, 357, 358, 359]], 
[[17, 119], [530, 532, 535, 538, 539], [354, 355, 356, 358, 359]], 
[[18, 26], [540, 541, 542, 543, 544], [360, 361, 362, 363, 364]], 
[[18, 29], [540, 545, 546, 547, 548], [360, 361, 365, 366, 367]], 
[[18, 32], [541, 545, 549, 550, 551], [360, 362, 365, 368, 369]], 
[[18, 38], [542, 546, 552, 553, 554], [361, 363, 366, 370, 371]], 
[[18, 41], [547, 549, 555, 556, 557], [365, 367, 368, 372, 373]], 
[[18, 44], [548, 552, 555, 558, 559], [366, 367, 370, 372, 374]], 
[[18, 50], [550, 556, 560, 561, 562], [368, 369, 373, 375, 376]], 
[[18, 62], [557, 558, 560, 563, 564], [372, 373, 374, 375, 377]], 
[[18, 77], [543, 553, 565, 566, 567], [363, 364, 371, 378, 379]], 
[[18, 80], [544, 551, 561, 565, 568], [362, 364, 369, 376, 378]], 
[[18, 89], [562, 563, 566, 568, 569], [375, 376, 377, 378, 379]], 
[[18, 92], [554, 559, 564, 567, 569], [370, 371, 374, 377, 379]], 
[[19, 53], [570, 571, 572, 573, 574], [380, 381, 382, 383, 384]], 
[[19, 56], [570, 575, 576, 577, 578], [380, 381, 385, 386, 387]], 
[[19, 65], [571, 575, 579, 580, 581], [380, 382, 385, 388, 389]], 
[[19, 68], [572, 579, 582, 583, 584], [382, 383, 388, 390, 391]], 
[[19, 74], [573, 576, 585, 586, 587], [381, 384, 386, 392, 393]], 
[[19, 86], [574, 582, 585, 588, 589], [383, 384, 390, 392, 394]], 
[[19, 98], [577, 580, 590, 591, 592], [385, 387, 389, 395, 396]], 
[[19, 101], [586, 588, 593, 594, 595], [392, 393, 394, 397, 398]], 
[[19, 104], [578, 587, 590, 593, 596], [386, 387, 393, 395, 397]], 
[[19, 110], [581, 583, 591, 597, 598], [388, 389, 391, 396, 399]], 
[[19, 113], [592, 594, 596, 597, 599], [395, 396, 397, 398, 399]], 
[[19, 116], [584, 589, 595, 598, 599], [390, 391, 394, 398, 399]], 
[[20, 25], [600, 601, 602, 603, 604], [400, 401, 402, 403, 404]], 
[[20, 27], [600, 605, 606, 607, 608], [400, 401, 405, 406, 407]], 
[[20, 31], [601, 605, 609, 610, 611], [400, 402, 405, 408, 409]], 
[[20, 37], [609, 612, 613, 614, 615], [408, 409, 410, 411, 412]], 
[[20, 39], [606, 610, 612, 616, 617], [405, 406, 408, 410, 413]], 
[[20, 55], [607, 616, 618, 619, 620], [406, 407, 413, 414, 415]], 
[[20, 73], [602, 608, 618, 621, 622], [401, 403, 407, 414, 416]], 
[[20, 75], [603, 621, 623, 624, 625], [403, 404, 416, 417, 418]], 
[[20, 79], [604, 611, 613, 623, 626], [402, 404, 409, 411, 417]], 
[[20, 85], [614, 617, 619, 627, 628], [410, 412, 413, 415, 419]], 
[[20, 87], [615, 624, 626, 627, 629], [411, 412, 417, 418, 419]], 
[[20, 103], [620, 622, 625, 628, 629], [414, 415, 416, 418, 419]], 
[[21, 43], [630, 631, 632, 633, 634], [420, 421, 422, 423, 424]], 
[[21, 49], [630, 635, 636, 637, 638], [420, 421, 425, 426, 427]], 
[[21, 51], [631, 635, 639, 640, 641], [420, 422, 425, 428, 429]], 
[[21, 61], [632, 642, 643, 644, 645], [423, 424, 430, 431, 432]], 
[[21, 63], [633, 639, 642, 646, 647], [422, 423, 428, 430, 433]], 
[[21, 67], [640, 646, 648, 649, 650], [428, 429, 433, 434, 435]], 
[[21, 91], [634, 636, 643, 651, 652], [421, 424, 426, 431, 436]], 
[[21, 97], [637, 641, 648, 653, 654], [425, 427, 429, 434, 437]], 
[[21, 99], [638, 651, 653, 655, 656], [426, 427, 436, 437, 438]], 
[[21, 109], [644, 647, 649, 657, 658], [430, 432, 433, 435, 439]], 
[[21, 111], [645, 652, 655, 657, 659], [431, 432, 436, 438, 439]], 
[[21, 115], [650, 654, 656, 658, 659], [434, 435, 437, 438, 439]], 
[[22, 24], [660, 661, 662, 663, 664], [440, 441, 442, 443, 444]], 
[[22, 28], [660, 665, 666, 667, 668], [440, 441, 445, 446, 447]], 
[[22, 30], [661, 665, 669, 670, 671], [440, 442, 445, 448, 449]], 
[[22, 48], [662, 666, 672, 673, 674], [441, 443, 446, 450, 451]], 
[[22, 52], [667, 669, 675, 676, 677], [445, 447, 448, 452, 453]], 
[[22, 54], [668, 672, 675, 678, 679], [446, 447, 450, 452, 454]], 
[[22, 72], [670, 676, 680, 681, 682], [448, 449, 453, 455, 456]], 
[[22, 76], [663, 673, 683, 684, 685], [443, 444, 451, 457, 458]], 
[[22, 78], [664, 671, 680, 683, 686], [442, 444, 449, 455, 457]], 
[[22, 96], [677, 678, 681, 687, 688], [452, 453, 454, 456, 459]], 
[[22, 100], [682, 684, 686, 687, 689], [455, 456, 457, 458, 459]], 
[[22, 102], [674, 679, 685, 688, 689], [450, 451, 454, 458, 459]], 
[[23, 36], [690, 691, 692, 693, 694], [460, 461, 462, 463, 464]], 
[[23, 40], [690, 695, 696, 697, 698], [460, 461, 465, 466, 467]], 
[[23, 42], [691, 695, 699, 700, 701], [460, 462, 465, 468, 469]], 
[[23, 60], [692, 696, 702, 703, 704], [461, 463, 466, 470, 471]], 
[[23, 64], [697, 699, 705, 706, 707], [465, 467, 468, 472, 473]], 
[[23, 66], [698, 702, 705, 708, 709], [466, 467, 470, 472, 474]], 
[[23, 84], [700, 706, 710, 711, 712], [468, 469, 473, 475, 476]], 
[[23, 88], [693, 703, 713, 714, 715], [463, 464, 471, 477, 478]], 
[[23, 90], [694, 701, 710, 713, 716], [462, 464, 469, 475, 477]], 
[[23, 108], [707, 708, 711, 717, 718], [472, 473, 474, 476, 479]], 
[[23, 112], [712, 714, 716, 717, 719], [475, 476, 477, 478, 479]], 
[[23, 114], [704, 709, 715, 718, 719], [470, 471, 474, 478, 479]], 
[[24, 25], [0, 30, 720, 721, 722], [0, 1, 20, 21, 480]], 
[[24, 26], [1, 31, 720, 723, 724], [0, 2, 20, 22, 481]], 
[[24, 28], [2, 660, 725, 726, 727], [3, 4, 440, 441, 482]], 
[[24, 30], [3, 661, 721, 725, 728], [1, 3, 440, 442, 480]], 
[[24, 32], [4, 723, 726, 729, 730], [2, 4, 481, 482, 483]], 
[[24, 48], [662, 727, 729, 731, 732], [441, 443, 482, 483, 484]], 
[[24, 76], [32, 663, 731, 733, 734], [23, 24, 443, 444, 484]], 
[[24, 78], [33, 664, 722, 728, 733], [21, 23, 442, 444, 480]], 
[[24, 80], [34, 724, 730, 732, 734], [22, 24, 481, 483, 484]], 
[[25, 26], [5, 35, 720, 735, 736], [0, 5, 20, 25, 485]], 
[[25, 27], [6, 600, 737, 738, 739], [6, 7, 400, 401, 486]], 
[[25, 30], [7, 721, 737, 740, 741], [1, 6, 480, 486, 487]], 
[[25, 31], [8, 601, 735, 738, 742], [5, 7, 400, 402, 485]], 
[[25, 73], [602, 739, 740, 743, 744], [401, 403, 486, 487, 488]], 
[[25, 75], [36, 603, 743, 745, 746], [26, 27, 403, 404, 488]], 
[[25, 78], [37, 722, 741, 744, 745], [21, 26, 480, 487, 488]], 
[[25, 79], [38, 604, 736, 742, 746], [25, 27, 402, 404, 485]], 
[[26, 29], [9, 540, 747, 748, 749], [8, 9, 360, 361, 489]], 
[[26, 31], [10, 735, 747, 750, 751], [5, 8, 485, 489, 490]], 
[[26, 32], [11, 541, 723, 748, 752], [2, 9, 360, 362, 481]], 
[[26, 38], [542, 749, 750, 753, 754], [361, 363, 489, 490, 491]], 
[[26, 77], [39, 543, 753, 755, 756], [28, 29, 363, 364, 491]], 
[[26, 79], [40, 736, 751, 754, 755], [25, 28, 485, 490, 491]], 
[[26, 80], [41, 544, 724, 752, 756], [22, 29, 362, 364, 481]], 
[[27, 30], [12, 60, 737, 757, 758], [6, 10, 40, 41, 486]], 
[[27, 31], [13, 605, 738, 759, 760], [7, 11, 400, 405, 492]], 
[[27, 33], [14, 61, 757, 761, 762], [10, 12, 40, 42, 493]], 
[[27, 35], [15, 759, 761, 763, 764], [11, 12, 492, 493, 494]], 
[[27, 39], [606, 760, 763, 765, 766], [405, 406, 492, 494, 495]], 
[[27, 55], [62, 607, 765, 767, 768], [43, 44, 406, 407, 495]], 
[[27, 59], [63, 762, 764, 766, 767], [42, 43, 493, 494, 495]], 
[[27, 73], [64, 608, 739, 758, 768], [41, 44, 401, 407, 486]], 
[[28, 30], [16, 665, 725, 769, 770], [3, 13, 440, 445, 496]], 
[[28, 32], [17, 120, 726, 771, 772], [4, 14, 80, 81, 482]], 
[[28, 33], [18, 769, 773, 774, 775], [13, 15, 496, 497, 498]], 
[[28, 34], [19, 121, 771, 773, 776], [14, 15, 80, 82, 497]], 
[[28, 48], [122, 666, 727, 772, 777], [81, 83, 441, 446, 482]], 
[[28, 52], [667, 770, 774, 778, 779], [445, 447, 496, 498, 499]], 
[[28, 54], [123, 668, 777, 778, 780], [83, 84, 446, 447, 499]], 
[[28, 57], [124, 775, 776, 779, 780], [82, 84, 497, 498, 499]], 
[[29, 31], [20, 240, 747, 781, 782], [8, 16, 160, 161, 489]], 
[[29, 32], [21, 545, 748, 783, 784], [9, 17, 360, 365, 500]], 
[[29, 34], [22, 783, 785, 786, 787], [17, 18, 500, 501, 502]], 
[[29, 35], [23, 241, 781, 785, 788], [16, 18, 160, 162, 501]], 
[[29, 38], [242, 546, 749, 782, 789], [161, 163, 361, 366, 489]], 
[[29, 41], [547, 784, 786, 790, 791], [365, 367, 500, 502, 503]], 
[[29, 44], [243, 548, 789, 790, 792], [163, 164, 366, 367, 503]], 
[[29, 46], [244, 787, 788, 791, 792], [162, 164, 501, 502, 503]], 
[[30, 33], [24, 65, 757, 769, 793], [10, 13, 40, 45, 496]], 
[[30, 52], [66, 669, 770, 793, 794], [45, 46, 445, 448, 496]], 
[[30, 72], [67, 670, 794, 795, 796], [46, 47, 448, 449, 504]], 
[[30, 73], [68, 740, 758, 795, 797], [41, 47, 486, 487, 504]], 
[[30, 78], [671, 728, 741, 796, 797], [442, 449, 480, 487, 504]], 
[[31, 35], [25, 245, 759, 781, 798], [11, 16, 160, 165, 492]], 
[[31, 37], [246, 609, 799, 800, 801], [166, 167, 408, 409, 505]], 
[[31, 38], [247, 750, 782, 799, 802], [161, 166, 489, 490, 505]], 
[[31, 39], [248, 610, 760, 798, 800], [165, 167, 405, 408, 492]], 
[[31, 79], [611, 742, 751, 801, 802], [402, 409, 485, 490, 505]], 
[[32, 34], [26, 125, 771, 783, 803], [14, 17, 80, 85, 500]], 
[[32, 41], [126, 549, 784, 803, 804], [85, 86, 365, 368, 500]], 
[[32, 48], [127, 729, 772, 805, 806], [81, 87, 482, 483, 506]], 
[[32, 50], [128, 550, 804, 805, 807], [86, 87, 368, 369, 506]], 
[[32, 80], [551, 730, 752, 806, 807], [362, 369, 481, 483, 506]], 
[[33, 34], [27, 480, 773, 808, 809], [15, 19, 320, 321, 497]], 
[[33, 35], [28, 481, 761, 808, 810], [12, 19, 320, 322, 493]], 
[[33, 52], [69, 774, 793, 811, 812], [45, 48, 496, 498, 507]], 
[[33, 57], [482, 775, 809, 811, 813], [321, 323, 497, 498, 507]], 
[[33, 58], [70, 483, 812, 813, 814], [48, 49, 323, 324, 507]], 
[[33, 59], [71, 484, 762, 810, 814], [42, 49, 322, 324, 493]], 
[[34, 35], [29, 485, 785, 808, 815], [18, 19, 320, 325, 501]], 
[[34, 41], [129, 786, 803, 816, 817], [85, 88, 500, 502, 508]], 
[[34, 46], [486, 787, 815, 816, 818], [325, 326, 501, 502, 508]], 
[[34, 47], [130, 487, 817, 818, 819], [88, 89, 326, 327, 508]], 
[[34, 57], [131, 488, 776, 809, 819], [82, 89, 321, 327, 497]], 
[[35, 39], [249, 763, 798, 820, 821], [165, 168, 492, 494, 509]], 
[[35, 45], [250, 489, 820, 822, 823], [168, 169, 328, 329, 509]], 
[[35, 46], [251, 490, 788, 815, 822], [162, 169, 325, 328, 501]], 
[[35, 59], [491, 764, 810, 821, 823], [322, 329, 493, 494, 509]], 
[[36, 37], [252, 270, 824, 825, 826], [170, 171, 180, 181, 510]], 
[[36, 38], [253, 271, 824, 827, 828], [170, 172, 180, 182, 511]], 
[[36, 40], [254, 690, 829, 830, 831], [173, 174, 460, 461, 512]], 
[[36, 42], [255, 691, 825, 829, 832], [171, 173, 460, 462, 510]], 
[[36, 44], [256, 827, 830, 833, 834], [172, 174, 511, 512, 513]], 
[[36, 60], [692, 831, 833, 835, 836], [461, 463, 512, 513, 514]], 
[[36, 88], [272, 693, 835, 837, 838], [183, 184, 463, 464, 514]], 
[[36, 90], [273, 694, 826, 832, 837], [181, 183, 462, 464, 510]], 
[[36, 92], [274, 828, 834, 836, 838], [182, 184, 511, 513, 514]], 
[[37, 38], [257, 275, 799, 824, 839], [166, 170, 180, 185, 505]], 
[[37, 39], [258, 612, 800, 840, 841], [167, 175, 408, 410, 515]], 
[[37, 42], [259, 825, 840, 842, 843], [171, 175, 510, 515, 516]], 
[[37, 79], [276, 613, 801, 839, 844], [185, 186, 409, 411, 505]], 
[[37, 85], [614, 841, 842, 845, 846], [410, 412, 515, 516, 517]], 
[[37, 87], [277, 615, 844, 845, 847], [186, 187, 411, 412, 517]], 
[[37, 90], [278, 826, 843, 846, 847], [181, 187, 510, 516, 517]], 
[[38, 44], [260, 552, 789, 827, 848], [163, 172, 366, 370, 511]], 
[[38, 77], [279, 553, 753, 849, 850], [188, 189, 363, 371, 491]], 
[[38, 79], [280, 754, 802, 839, 849], [185, 188, 490, 491, 505]], 
[[38, 92], [281, 554, 828, 848, 850], [182, 189, 370, 371, 511]], 
[[39, 42], [261, 300, 840, 851, 852], [175, 176, 200, 201, 515]], 
[[39, 45], [262, 301, 820, 851, 853], [168, 176, 200, 202, 509]], 
[[39, 55], [302, 616, 765, 854, 855], [203, 204, 406, 413, 495]], 
[[39, 59], [303, 766, 821, 853, 854], [202, 203, 494, 495, 509]], 
[[39, 85], [304, 617, 841, 852, 855], [201, 204, 410, 413, 515]], 
[[40, 42], [263, 695, 829, 856, 857], [173, 177, 460, 465, 518]], 
[[40, 44], [264, 360, 830, 858, 859], [174, 178, 240, 241, 512]], 
[[40, 45], [265, 856, 860, 861, 862], [177, 179, 518, 519, 520]], 
[[40, 46], [266, 361, 858, 860, 863], [178, 179, 240, 242, 519]], 
[[40, 60], [362, 696, 831, 859, 864], [241, 243, 461, 466, 512]], 
[[40, 64], [697, 857, 861, 865, 866], [465, 467, 518, 520, 521]], 
[[40, 66], [363, 698, 864, 865, 867], [243, 244, 466, 467, 521]], 
[[40, 69], [364, 862, 863, 866, 867], [242, 244, 519, 520, 521]], 
[[41, 43], [132, 365, 868, 869, 870], [90, 91, 245, 246, 522]], 
[[41, 44], [366, 555, 790, 871, 872], [247, 248, 367, 372, 503]], 
[[41, 46], [367, 791, 816, 871, 873], [247, 249, 502, 503, 508]], 
[[41, 47], [133, 368, 817, 868, 873], [88, 90, 245, 249, 508]], 
[[41, 50], [134, 556, 804, 869, 874], [86, 91, 368, 373, 522]], 
[[41, 62], [369, 557, 870, 872, 874], [246, 248, 372, 373, 522]], 
[[42, 45], [267, 305, 851, 856, 875], [176, 177, 200, 205, 518]], 
[[42, 64], [306, 699, 857, 875, 876], [205, 206, 465, 468, 518]], 
[[42, 84], [307, 700, 876, 877, 878], [206, 207, 468, 469, 523]], 
[[42, 85], [308, 842, 852, 877, 879], [201, 207, 515, 516, 523]], 
[[42, 90], [701, 832, 843, 878, 879], [462, 469, 510, 516, 523]], 
[[43, 47], [135, 370, 868, 880, 881], [90, 92, 245, 250, 524]], 
[[43, 49], [136, 630, 882, 883, 884], [93, 94, 420, 421, 525]], 
[[43, 50], [137, 869, 882, 885, 886], [91, 93, 522, 525, 526]], 
[[43, 51], [138, 631, 880, 883, 887], [92, 94, 420, 422, 524]], 
[[43, 61], [371, 632, 888, 889, 890], [251, 252, 423, 424, 527]], 
[[43, 62], [372, 870, 885, 888, 891], [246, 251, 522, 526, 527]], 
[[43, 63], [373, 633, 881, 887, 889], [250, 252, 422, 423, 524]], 
[[43, 91], [634, 884, 886, 890, 891], [421, 424, 525, 526, 527]], 
[[44, 46], [268, 374, 792, 858, 871], [164, 178, 240, 247, 503]], 
[[44, 60], [375, 833, 859, 892, 893], [241, 253, 512, 513, 528]], 
[[44, 62], [376, 558, 872, 892, 894], [248, 253, 372, 374, 528]], 
[[44, 92], [559, 834, 848, 893, 894], [370, 374, 511, 513, 528]], 
[[45, 46], [269, 492, 822, 860, 895], [169, 179, 328, 330, 519]], 
[[45, 59], [309, 493, 823, 853, 896], [202, 208, 329, 331, 509]], 
[[45, 64], [310, 861, 875, 897, 898], [205, 209, 518, 520, 529]], 
[[45, 69], [494, 862, 895, 897, 899], [330, 332, 519, 520, 529]], 
[[45, 70], [311, 495, 896, 898, 899], [208, 209, 331, 332, 529]], 
[[46, 47], [377, 496, 818, 873, 900], [249, 254, 326, 333, 508]], 
[[46, 69], [378, 497, 863, 895, 900], [242, 254, 330, 333, 519]], 
[[47, 51], [139, 880, 901, 902, 903], [92, 95, 524, 530, 531]], 
[[47, 57], [140, 498, 819, 901, 904], [89, 95, 327, 334, 530]], 
[[47, 63], [379, 881, 902, 905, 906], [250, 255, 524, 531, 532]], 
[[47, 69], [380, 499, 900, 905, 907], [254, 255, 333, 335, 532]], 
[[47, 71], [500, 903, 904, 906, 907], [334, 335, 530, 531, 532]], 
[[48, 49], [141, 150, 908, 909, 910], [96, 97, 100, 101, 533]], 
[[48, 50], [142, 151, 805, 908, 911], [87, 96, 100, 102, 506]], 
[[48, 54], [143, 672, 777, 909, 912], [83, 97, 446, 450, 533]], 
[[48, 76], [152, 673, 731, 913, 914], [103, 104, 443, 451, 484]], 
[[48, 80], [153, 732, 806, 911, 913], [102, 103, 483, 484, 506]], 
[[48, 102], [154, 674, 910, 912, 914], [101, 104, 450, 451, 533]], 
[[49, 50], [144, 155, 882, 908, 915], [93, 96, 100, 105, 525]], 
[[49, 51], [145, 635, 883, 916, 917], [94, 98, 420, 425, 534]], 
[[49, 54], [146, 909, 916, 918, 919], [97, 98, 533, 534, 535]], 
[[49, 91], [156, 636, 884, 915, 920], [105, 106, 421, 426, 525]], 
[[49, 97], [637, 917, 918, 921, 922], [425, 427, 534, 535, 536]], 
[[49, 99], [157, 638, 920, 921, 923], [106, 107, 426, 427, 536]], 
[[49, 102], [158, 910, 919, 922, 923], [101, 107, 533, 535, 536]], 
[[50, 62], [560, 874, 885, 924, 925], [373, 375, 522, 526, 537]], 
[[50, 80], [159, 561, 807, 911, 926], [102, 108, 369, 376, 506]], 
[[50, 89], [160, 562, 924, 926, 927], [108, 109, 375, 376, 537]], 
[[50, 91], [161, 886, 915, 925, 927], [105, 109, 525, 526, 537]], 
[[51, 54], [147, 180, 916, 928, 929], [98, 99, 120, 121, 534]], 
[[51, 57], [148, 181, 901, 928, 930], [95, 99, 120, 122, 530]], 
[[51, 63], [639, 887, 902, 931, 932], [422, 428, 524, 531, 538]], 
[[51, 67], [182, 640, 931, 933, 934], [123, 124, 428, 429, 538]], 
[[51, 71], [183, 903, 930, 932, 933], [122, 123, 530, 531, 538]], 
[[51, 97], [184, 641, 917, 929, 934], [121, 124, 425, 429, 534]], 
[[52, 54], [185, 675, 778, 935, 936], [125, 126, 447, 452, 499]], 
[[52, 56], [72, 186, 937, 938, 939], [50, 51, 127, 128, 539]], 
[[52, 57], [187, 779, 811, 935, 940], [125, 129, 498, 499, 507]], 
[[52, 58], [73, 188, 812, 937, 940], [48, 50, 127, 129, 507]], 
[[52, 72], [74, 676, 794, 938, 941], [46, 51, 448, 453, 539]], 
[[52, 96], [189, 677, 936, 939, 941], [126, 128, 452, 453, 539]], 
[[53, 55], [75, 312, 942, 943, 944], [52, 53, 210, 211, 540]], 
[[53, 56], [76, 570, 945, 946, 947], [54, 55, 380, 381, 541]], 
[[53, 58], [77, 945, 948, 949, 950], [54, 56, 541, 542, 543]], 
[[53, 59], [78, 313, 942, 948, 951], [52, 56, 210, 212, 542]], 
[[53, 65], [571, 946, 949, 952, 953], [380, 382, 541, 543, 544]], 
[[53, 68], [314, 572, 952, 954, 955], [213, 214, 382, 383, 544]], 
[[53, 70], [315, 950, 951, 953, 954], [212, 213, 542, 543, 544]], 
[[53, 74], [79, 573, 943, 947, 956], [53, 55, 381, 384, 540]], 
[[53, 86], [316, 574, 944, 955, 956], [211, 214, 383, 384, 540]], 
[[54, 57], [149, 190, 780, 928, 935], [84, 99, 120, 125, 499]], 
[[54, 96], [191, 678, 936, 957, 958], [126, 130, 452, 454, 545]], 
[[54, 97], [192, 918, 929, 957, 959], [121, 130, 534, 535, 545]], 
[[54, 102], [679, 912, 919, 958, 959], [450, 454, 533, 535, 545]], 
[[55, 59], [80, 317, 767, 854, 942], [43, 52, 203, 210, 495]], 
[[55, 73], [81, 618, 768, 960, 961], [44, 57, 407, 414, 546]], 
[[55, 74], [82, 943, 960, 962, 963], [53, 57, 540, 546, 547]], 
[[55, 85], [318, 619, 855, 964, 965], [204, 215, 413, 415, 548]], 
[[55, 86], [319, 944, 962, 964, 966], [211, 215, 540, 547, 548]], 
[[55, 103], [620, 961, 963, 965, 966], [414, 415, 546, 547, 548]], 
[[56, 58], [83, 193, 937, 945, 967], [50, 54, 127, 131, 541]], 
[[56, 65], [194, 575, 946, 967, 968], [131, 132, 380, 385, 541]], 
[[56, 72], [84, 938, 969, 970, 971], [51, 58, 539, 549, 550]], 
[[56, 74], [85, 576, 947, 969, 972], [55, 58, 381, 386, 549]], 
[[56, 96], [195, 939, 970, 973, 974], [128, 133, 539, 550, 551]], 
[[56, 98], [196, 577, 968, 973, 975], [132, 133, 385, 387, 551]], 
[[56, 104], [578, 971, 972, 974, 975], [386, 387, 549, 550, 551]], 
[[57, 58], [197, 501, 813, 940, 976], [129, 134, 323, 336, 507]], 
[[57, 71], [198, 502, 904, 930, 976], [122, 134, 334, 336, 530]], 
[[58, 59], [86, 503, 814, 948, 977], [49, 56, 324, 337, 542]], 
[[58, 65], [199, 949, 967, 978, 979], [131, 135, 541, 543, 552]], 
[[58, 70], [504, 950, 977, 978, 980], [337, 338, 542, 543, 552]], 
[[58, 71], [200, 505, 976, 979, 980], [134, 135, 336, 338, 552]], 
[[59, 70], [320, 506, 896, 951, 977], [208, 212, 331, 337, 542]], 
[[60, 61], [381, 390, 981, 982, 983], [256, 257, 260, 261, 553]], 
[[60, 62], [382, 391, 892, 981, 984], [253, 256, 260, 262, 528]], 
[[60, 66], [383, 702, 864, 982, 985], [243, 257, 466, 470, 553]], 
[[60, 88], [392, 703, 835, 986, 987], [263, 264, 463, 471, 514]], 
[[60, 92], [393, 836, 893, 984, 986], [262, 263, 513, 514, 528]], 
[[60, 114], [394, 704, 983, 985, 987], [261, 264, 470, 471, 553]], 
[[61, 62], [384, 395, 888, 981, 988], [251, 256, 260, 265, 527]], 
[[61, 63], [385, 642, 889, 989, 990], [252, 258, 423, 430, 554]], 
[[61, 66], [386, 982, 989, 991, 992], [257, 258, 553, 554, 555]], 
[[61, 91], [396, 643, 890, 988, 993], [265, 266, 424, 431, 527]], 
[[61, 109], [644, 990, 991, 994, 995], [430, 432, 554, 555, 556]], 
[[61, 111], [397, 645, 993, 994, 996], [266, 267, 431, 432, 556]], 
[[61, 114], [398, 983, 992, 995, 996], [261, 267, 553, 555, 556]], 
[[62, 89], [399, 563, 924, 997, 998], [268, 269, 375, 377, 537]], 
[[62, 91], [400, 891, 925, 988, 997], [265, 268, 526, 527, 537]], 
[[62, 92], [401, 564, 894, 984, 998], [262, 269, 374, 377, 528]], 
[[63, 66], [387, 420, 989, 999, 1000], [258, 259, 280, 281, 554]], 
[[63, 67], [421, 646, 931, 1001, 1002], [282, 283, 428, 433, 538]], 
[[63, 69], [388, 422, 905, 999, 1003], [255, 259, 280, 284, 532]], 
[[63, 71], [423, 906, 932, 1001, 1003], [282, 284, 531, 532, 538]], 
[[63, 109], [424, 647, 990, 1000, 1002], [281, 283, 430, 433, 554]], 
[[64, 66], [425, 705, 865, 1004, 1005], [285, 286, 467, 472, 521]], 
[[64, 68], [321, 426, 1006, 1007, 1008], [216, 217, 287, 288, 557]], 
[[64, 69], [427, 866, 897, 1004, 1009], [285, 289, 520, 521, 529]], 
[[64, 70], [322, 428, 898, 1006, 1009], [209, 216, 287, 289, 529]], 
[[64, 84], [323, 706, 876, 1007, 1010], [206, 217, 468, 473, 557]], 
[[64, 108], [429, 707, 1005, 1008, 1010], [286, 288, 472, 473, 557]], 
[[65, 67], [201, 430, 1011, 1012, 1013], [136, 137, 290, 291, 558]], 
[[65, 68], [431, 579, 952, 1014, 1015], [292, 293, 382, 388, 544]], 
[[65, 70], [432, 953, 978, 1014, 1016], [292, 294, 543, 544, 552]], 
[[65, 71], [202, 433, 979, 1011, 1016], [135, 136, 290, 294, 552]], 
[[65, 98], [203, 580, 968, 1012, 1017], [132, 137, 385, 389, 558]], 
[[65, 110], [434, 581, 1013, 1015, 1017], [291, 293, 388, 389, 558]], 
[[66, 69], [389, 435, 867, 999, 1004], [244, 259, 280, 285, 521]], 
[[66, 108], [436, 708, 1005, 1018, 1019], [286, 295, 472, 474, 559]], 
[[66, 109], [437, 991, 1000, 1018, 1020], [281, 295, 554, 555, 559]], 
[[66, 114], [709, 985, 992, 1019, 1020], [470, 474, 553, 555, 559]], 
[[67, 71], [204, 438, 933, 1001, 1011], [123, 136, 282, 290, 538]], 
[[67, 97], [205, 648, 934, 1021, 1022], [124, 138, 429, 434, 560]], 
[[67, 98], [206, 1012, 1021, 1023, 1024], [137, 138, 558, 560, 561]], 
[[67, 109], [439, 649, 1002, 1025, 1026], [283, 296, 433, 435, 562]], 
[[67, 110], [440, 1013, 1023, 1025, 1027], [291, 296, 558, 561, 562]], 
[[67, 115], [650, 1022, 1024, 1026, 1027], [434, 435, 560, 561, 562]], 
[[68, 70], [324, 441, 954, 1006, 1014], [213, 216, 287, 292, 544]], 
[[68, 84], [325, 1007, 1028, 1029, 1030], [217, 218, 557, 563, 564]], 
[[68, 86], [326, 582, 955, 1028, 1031], [214, 218, 383, 390, 563]], 
[[68, 108], [442, 1008, 1029, 1032, 1033], [288, 297, 557, 564, 565]], 
[[68, 110], [443, 583, 1015, 1032, 1034], [293, 297, 388, 391, 565]], 
[[68, 116], [584, 1030, 1031, 1033, 1034], [390, 391, 563, 564, 565]], 
[[69, 70], [444, 507, 899, 1009, 1035], [289, 298, 332, 339, 529]], 
[[69, 71], [445, 508, 907, 1003, 1035], [284, 298, 335, 339, 532]], 
[[70, 71], [446, 509, 980, 1016, 1035], [294, 298, 338, 339, 552]], 
[[72, 73], [87, 90, 795, 1036, 1037], [47, 59, 60, 61, 504]], 
[[72, 74], [88, 91, 969, 1036, 1038], [58, 59, 60, 62, 549]], 
[[72, 78], [92, 680, 796, 1037, 1039], [61, 63, 449, 455, 504]], 
[[72, 96], [681, 941, 970, 1040, 1041], [453, 456, 539, 550, 566]], 
[[72, 100], [93, 682, 1039, 1040, 1042], [63, 64, 455, 456, 566]], 
[[72, 104], [94, 971, 1038, 1041, 1042], [62, 64, 549, 550, 566]], 
[[73, 74], [89, 95, 960, 1036, 1043], [57, 59, 60, 65, 546]], 
[[73, 75], [96, 621, 743, 1044, 1045], [66, 67, 403, 416, 488]], 
[[73, 78], [97, 744, 797, 1037, 1044], [61, 66, 487, 488, 504]], 
[[73, 103], [98, 622, 961, 1043, 1045], [65, 67, 414, 416, 546]], 
[[74, 86], [585, 956, 962, 1046, 1047], [384, 392, 540, 547, 567]], 
[[74, 101], [99, 586, 1046, 1048, 1049], [68, 69, 392, 393, 567]], 
[[74, 103], [100, 963, 1043, 1047, 1048], [65, 68, 546, 547, 567]], 
[[74, 104], [101, 587, 972, 1038, 1049], [62, 69, 386, 393, 549]], 
[[75, 78], [42, 102, 745, 1044, 1050], [26, 30, 66, 70, 488]], 
[[75, 79], [43, 623, 746, 1051, 1052], [27, 31, 404, 417, 568]], 
[[75, 81], [44, 103, 1050, 1053, 1054], [30, 32, 70, 71, 569]], 
[[75, 83], [45, 1051, 1053, 1055, 1056], [31, 32, 568, 569, 570]], 
[[75, 87], [624, 1052, 1055, 1057, 1058], [417, 418, 568, 570, 571]], 
[[75, 103], [104, 625, 1045, 1057, 1059], [67, 72, 416, 418, 571]], 
[[75, 107], [105, 1054, 1056, 1058, 1059], [71, 72, 569, 570, 571]], 
[[76, 78], [46, 683, 733, 1060, 1061], [23, 33, 444, 457, 572]], 
[[76, 80], [47, 162, 734, 913, 1062], [24, 34, 103, 110, 484]], 
[[76, 81], [48, 1060, 1063, 1064, 1065], [33, 35, 572, 573, 574]], 
[[76, 82], [49, 163, 1062, 1063, 1066], [34, 35, 110, 111, 573]], 
[[76, 100], [684, 1061, 1064, 1067, 1068], [457, 458, 572, 574, 575]], 
[[76, 102], [164, 685, 914, 1067, 1069], [104, 112, 451, 458, 575]], 
[[76, 105], [165, 1065, 1066, 1068, 1069], [111, 112, 573, 574, 575]], 
[[77, 79], [50, 282, 755, 849, 1070], [28, 36, 188, 190, 491]], 
[[77, 80], [51, 565, 756, 1071, 1072], [29, 37, 364, 378, 576]], 
[[77, 82], [52, 1071, 1073, 1074, 1075], [37, 38, 576, 577, 578]], 
[[77, 83], [53, 283, 1070, 1073, 1076], [36, 38, 190, 191, 577]], 
[[77, 89], [566, 1072, 1074, 1077, 1078], [378, 379, 576, 578, 579]], 
[[77, 92], [284, 567, 850, 1077, 1079], [189, 192, 371, 379, 579]], 
[[77, 94], [285, 1075, 1076, 1078, 1079], [191, 192, 577, 578, 579]], 
[[78, 81], [54, 106, 1050, 1060, 1080], [30, 33, 70, 73, 572]], 
[[78, 100], [107, 686, 1039, 1061, 1080], [63, 73, 455, 457, 572]], 
[[79, 83], [55, 286, 1051, 1070, 1081], [31, 36, 190, 193, 568]], 
[[79, 87], [287, 626, 844, 1052, 1081], [186, 193, 411, 417, 568]], 
[[80, 82], [56, 166, 1062, 1071, 1082], [34, 37, 110, 113, 576]], 
[[80, 89], [167, 568, 926, 1072, 1082], [108, 113, 376, 378, 576]], 
[[81, 82], [57, 510, 1063, 1083, 1084], [35, 39, 340, 341, 573]], 
[[81, 83], [58, 511, 1053, 1083, 1085], [32, 39, 340, 342, 569]], 
[[81, 100], [108, 1064, 1080, 1086, 1087], [73, 74, 572, 574, 580]], 
[[81, 105], [512, 1065, 1084, 1086, 1088], [341, 343, 573, 574, 580]], 
[[81, 106], [109, 513, 1087, 1088, 1089], [74, 75, 343, 344, 580]], 
[[81, 107], [110, 514, 1054, 1085, 1089], [71, 75, 342, 344, 569]], 
[[82, 83], [59, 515, 1073, 1083, 1090], [38, 39, 340, 345, 577]], 
[[82, 89], [168, 1074, 1082, 1091, 1092], [113, 114, 576, 578, 581]], 
[[82, 94], [516, 1075, 1090, 1091, 1093], [345, 346, 577, 578, 581]], 
[[82, 95], [169, 517, 1092, 1093, 1094], [114, 115, 346, 347, 581]], 
[[82, 105], [170, 518, 1066, 1084, 1094], [111, 115, 341, 347, 573]], 
[[83, 87], [288, 1055, 1081, 1095, 1096], [193, 194, 568, 570, 582]], 
[[83, 93], [289, 519, 1095, 1097, 1098], [194, 195, 348, 349, 582]], 
[[83, 94], [290, 520, 1076, 1090, 1097], [191, 195, 345, 348, 577]], 
[[83, 107], [521, 1056, 1085, 1096, 1098], [342, 349, 569, 570, 582]], 
[[84, 85], [327, 330, 877, 1099, 1100], [207, 219, 220, 221, 523]], 
[[84, 86], [328, 331, 1028, 1099, 1101], [218, 219, 220, 222, 563]], 
[[84, 90], [332, 710, 878, 1100, 1102], [221, 223, 469, 475, 523]], 
[[84, 108], [711, 1010, 1029, 1103, 1104], [473, 476, 557, 564, 583]], 
[[84, 112], [333, 712, 1102, 1103, 1105], [223, 224, 475, 476, 583]], 
[[84, 116], [334, 1030, 1101, 1104, 1105], [222, 224, 563, 564, 583]], 
[[85, 86], [329, 335, 964, 1099, 1106], [215, 219, 220, 225, 548]], 
[[85, 87], [336, 627, 845, 1107, 1108], [226, 227, 412, 419, 517]], 
[[85, 90], [337, 846, 879, 1100, 1107], [221, 226, 516, 517, 523]], 
[[85, 103], [338, 628, 965, 1106, 1108], [225, 227, 415, 419, 548]], 
[[86, 101], [339, 588, 1046, 1109, 1110], [228, 229, 392, 394, 567]], 
[[86, 103], [340, 966, 1047, 1106, 1109], [225, 228, 547, 548, 567]], 
[[86, 116], [341, 589, 1031, 1101, 1110], [222, 229, 390, 394, 563]], 
[[87, 90], [291, 342, 847, 1107, 1111], [187, 196, 226, 230, 517]], 
[[87, 93], [292, 343, 1095, 1111, 1112], [194, 196, 230, 231, 582]], 
[[87, 103], [344, 629, 1057, 1108, 1113], [227, 232, 418, 419, 571]], 
[[87, 107], [345, 1058, 1096, 1112, 1113], [231, 232, 570, 571, 582]], 
[[88, 90], [293, 713, 837, 1114, 1115], [183, 197, 464, 477, 584]], 
[[88, 92], [294, 402, 838, 986, 1116], [184, 198, 263, 270, 514]], 
[[88, 93], [295, 1114, 1117, 1118, 1119], [197, 199, 584, 585, 586]], 
[[88, 94], [296, 403, 1116, 1117, 1120], [198, 199, 270, 271, 585]], 
[[88, 112], [714, 1115, 1118, 1121, 1122], [477, 478, 584, 586, 587]], 
[[88, 114], [404, 715, 987, 1121, 1123], [264, 272, 471, 478, 587]], 
[[88, 117], [405, 1119, 1120, 1122, 1123], [271, 272, 585, 586, 587]], 
[[89, 91], [171, 406, 927, 997, 1124], [109, 116, 268, 273, 537]], 
[[89, 92], [407, 569, 998, 1077, 1125], [269, 274, 377, 379, 579]], 
[[89, 94], [408, 1078, 1091, 1125, 1126], [274, 275, 578, 579, 581]], 
[[89, 95], [172, 409, 1092, 1124, 1126], [114, 116, 273, 275, 581]], 
[[90, 93], [297, 346, 1111, 1114, 1127], [196, 197, 230, 233, 584]], 
[[90, 112], [347, 716, 1102, 1115, 1127], [223, 233, 475, 477, 584]], 
[[91, 95], [173, 410, 1124, 1128, 1129], [116, 117, 273, 276, 588]], 
[[91, 99], [174, 651, 920, 1128, 1130], [106, 117, 426, 436, 588]], 
[[91, 111], [411, 652, 993, 1129, 1130], [266, 276, 431, 436, 588]], 
[[92, 94], [298, 412, 1079, 1116, 1125], [192, 198, 270, 274, 579]], 
[[93, 94], [299, 522, 1097, 1117, 1131], [195, 199, 348, 350, 585]], 
[[93, 107], [348, 523, 1098, 1112, 1132], [231, 234, 349, 351, 582]], 
[[93, 112], [349, 1118, 1127, 1133, 1134], [233, 235, 584, 586, 589]], 
[[93, 117], [524, 1119, 1131, 1133, 1135], [350, 352, 585, 586, 589]], 
[[93, 118], [350, 525, 1132, 1134, 1135], [234, 235, 351, 352, 589]], 
[[94, 95], [413, 526, 1093, 1126, 1136], [275, 277, 346, 353, 581]], 
[[94, 117], [414, 527, 1120, 1131, 1136], [271, 277, 350, 353, 585]], 
[[95, 99], [175, 1128, 1137, 1138, 1139], [117, 118, 588, 590, 591]], 
[[95, 105], [176, 528, 1094, 1137, 1140], [115, 118, 347, 354, 590]], 
[[95, 111], [415, 1129, 1138, 1141, 1142], [276, 278, 588, 591, 592]], 
[[95, 117], [416, 529, 1136, 1141, 1143], [277, 278, 353, 355, 592]], 
[[95, 119], [530, 1139, 1140, 1142, 1143], [354, 355, 590, 591, 592]], 
[[96, 97], [207, 210, 957, 1144, 1145], [130, 139, 140, 141, 545]], 
[[96, 98], [208, 211, 973, 1144, 1146], [133, 139, 140, 142, 551]], 
[[96, 100], [212, 687, 1040, 1147, 1148], [143, 144, 456, 459, 566]], 
[[96, 102], [213, 688, 958, 1145, 1147], [141, 143, 454, 459, 545]], 
[[96, 104], [214, 974, 1041, 1146, 1148], [142, 144, 550, 551, 566]], 
[[97, 98], [209, 215, 1021, 1144, 1149], [138, 139, 140, 145, 560]], 
[[97, 99], [216, 653, 921, 1150, 1151], [146, 147, 427, 437, 536]], 
[[97, 102], [217, 922, 959, 1145, 1150], [141, 146, 535, 536, 545]], 
[[97, 115], [218, 654, 1022, 1149, 1151], [145, 147, 434, 437, 560]], 
[[98, 104], [219, 590, 975, 1146, 1152], [142, 148, 387, 395, 551]], 
[[98, 110], [591, 1017, 1023, 1153, 1154], [389, 396, 558, 561, 593]], 
[[98, 113], [220, 592, 1152, 1153, 1155], [148, 149, 395, 396, 593]], 
[[98, 115], [221, 1024, 1149, 1154, 1155], [145, 149, 560, 561, 593]], 
[[99, 102], [177, 222, 923, 1150, 1156], [107, 119, 146, 150, 536]], 
[[99, 105], [178, 223, 1137, 1156, 1157], [118, 119, 150, 151, 590]], 
[[99, 111], [655, 1130, 1138, 1158, 1159], [436, 438, 588, 591, 594]], 
[[99, 115], [224, 656, 1151, 1158, 1160], [147, 152, 437, 438, 594]], 
[[99, 119], [225, 1139, 1157, 1159, 1160], [151, 152, 590, 591, 594]], 
[[100, 102], [226, 689, 1067, 1147, 1161], [143, 153, 458, 459, 575]], 
[[100, 104], [111, 227, 1042, 1148, 1162], [64, 76, 144, 154, 566]], 
[[100, 105], [228, 1068, 1086, 1161, 1163], [153, 155, 574, 575, 580]], 
[[100, 106], [112, 229, 1087, 1162, 1163], [74, 76, 154, 155, 580]], 
[[101, 103], [113, 351, 1048, 1109, 1164], [68, 77, 228, 236, 567]], 
[[101, 104], [114, 593, 1049, 1165, 1166], [69, 78, 393, 397, 595]], 
[[101, 106], [115, 1165, 1167, 1168, 1169], [78, 79, 595, 596, 597]], 
[[101, 107], [116, 352, 1164, 1167, 1170], [77, 79, 236, 237, 596]], 
[[101, 113], [594, 1166, 1168, 1171, 1172], [397, 398, 595, 597, 598]], 
[[101, 116], [353, 595, 1110, 1171, 1173], [229, 238, 394, 398, 598]], 
[[101, 118], [354, 1169, 1170, 1172, 1173], [237, 238, 596, 597, 598]], 
[[102, 105], [179, 230, 1069, 1156, 1161], [112, 119, 150, 153, 575]], 
[[103, 107], [117, 355, 1059, 1113, 1164], [72, 77, 232, 236, 571]], 
[[104, 106], [118, 231, 1162, 1165, 1174], [76, 78, 154, 156, 595]], 
[[104, 113], [232, 596, 1152, 1166, 1174], [148, 156, 395, 397, 595]], 
[[105, 106], [233, 531, 1088, 1163, 1175], [155, 157, 343, 356, 580]], 
[[105, 119], [234, 532, 1140, 1157, 1175], [151, 157, 354, 356, 590]], 
[[106, 107], [119, 533, 1089, 1167, 1176], [75, 79, 344, 357, 596]], 
[[106, 113], [235, 1168, 1174, 1177, 1178], [156, 158, 595, 597, 599]], 
[[106, 118], [534, 1169, 1176, 1177, 1179], [357, 358, 596, 597, 599]], 
[[106, 119], [236, 535, 1175, 1178, 1179], [157, 158, 356, 358, 599]], 
[[107, 118], [356, 536, 1132, 1170, 1176], [234, 237, 351, 357, 596]], 
[[108, 109], [447, 450, 1018, 1180, 1181], [295, 299, 300, 301, 559]], 
[[108, 110], [448, 451, 1032, 1180, 1182], [297, 299, 300, 302, 565]], 
[[108, 112], [452, 717, 1103, 1183, 1184], [303, 304, 476, 479, 583]], 
[[108, 114], [453, 718, 1019, 1181, 1183], [301, 303, 474, 479, 559]], 
[[108, 116], [454, 1033, 1104, 1182, 1184], [302, 304, 564, 565, 583]], 
[[109, 110], [449, 455, 1025, 1180, 1185], [296, 299, 300, 305, 562]], 
[[109, 111], [456, 657, 994, 1186, 1187], [306, 307, 432, 439, 556]], 
[[109, 114], [457, 995, 1020, 1181, 1186], [301, 306, 555, 556, 559]], 
[[109, 115], [458, 658, 1026, 1185, 1187], [305, 307, 435, 439, 562]], 
[[110, 113], [459, 597, 1153, 1188, 1189], [308, 309, 396, 399, 593]], 
[[110, 115], [460, 1027, 1154, 1185, 1188], [305, 308, 561, 562, 593]], 
[[110, 116], [461, 598, 1034, 1182, 1189], [302, 309, 391, 399, 565]], 
[[111, 114], [417, 462, 996, 1186, 1190], [267, 279, 306, 310, 556]], 
[[111, 115], [463, 659, 1158, 1187, 1191], [307, 311, 438, 439, 594]], 
[[111, 117], [418, 464, 1141, 1190, 1192], [278, 279, 310, 312, 592]], 
[[111, 119], [465, 1142, 1159, 1191, 1192], [311, 312, 591, 592, 594]], 
[[112, 114], [466, 719, 1121, 1183, 1193], [303, 313, 478, 479, 587]], 
[[112, 116], [357, 467, 1105, 1184, 1194], [224, 239, 304, 314, 583]], 
[[112, 117], [468, 1122, 1133, 1193, 1195], [313, 315, 586, 587, 589]], 
[[112, 118], [358, 469, 1134, 1194, 1195], [235, 239, 314, 315, 589]], 
[[113, 115], [237, 470, 1155, 1188, 1196], [149, 159, 308, 316, 593]], 
[[113, 116], [471, 599, 1171, 1189, 1197], [309, 317, 398, 399, 598]], 
[[113, 118], [472, 1172, 1177, 1197, 1198], [317, 318, 597, 598, 599]], 
[[113, 119], [238, 473, 1178, 1196, 1198], [158, 159, 316, 318, 599]], 
[[114, 117], [419, 474, 1123, 1190, 1193], [272, 279, 310, 313, 587]], 
[[115, 119], [239, 475, 1160, 1191, 1196], [152, 159, 311, 316, 594]], 
[[116, 118], [359, 476, 1173, 1194, 1197], [238, 239, 314, 317, 598]], 
[[117, 118], [477, 537, 1135, 1195, 1199], [315, 319, 352, 359, 589]], 
[[117, 119], [478, 538, 1143, 1192, 1199], [312, 319, 355, 359, 592]], 
[[118, 119], [479, 539, 1179, 1198, 1199], [318, 319, 358, 359, 599]]
]

len(cube.f)= 1200 
cube.f= [
[[0, 24, 25], [0, 1, 288], [0, 1]], [[0, 24, 26], [0, 2, 289], [0, 2]], 
[[0, 24, 28], [0, 4, 290], [3, 4]], [[0, 24, 30], [0, 6, 291], [1, 3]], 
[[0, 24, 32], [0, 8, 292], [2, 4]], [[0, 25, 26], [1, 2, 297], [0, 5]], 
[[0, 25, 27], [1, 3, 298], [6, 7]], [[0, 25, 30], [1, 6, 299], [1, 6]], 
[[0, 25, 31], [1, 7, 300], [5, 7]], [[0, 26, 29], [2, 5, 305], [8, 9]], 
[[0, 26, 31], [2, 7, 306], [5, 8]], [[0, 26, 32], [2, 8, 307], [2, 9]], 
[[0, 27, 30], [3, 6, 312], [6, 10]], [[0, 27, 31], [3, 7, 313], [7, 11]], 
[[0, 27, 33], [3, 9, 314], [10, 12]], [[0, 27, 35], [3, 11, 315], [11, 12]], 
[[0, 28, 30], [4, 6, 320], [3, 13]], [[0, 28, 32], [4, 8, 321], [4, 14]], 
[[0, 28, 33], [4, 9, 322], [13, 15]], [[0, 28, 34], [4, 10, 323], [14, 15]], 
[[0, 29, 31], [5, 7, 328], [8, 16]], [[0, 29, 32], [5, 8, 329], [9, 17]], 
[[0, 29, 34], [5, 10, 330], [17, 18]], [[0, 29, 35], [5, 11, 331], [16, 18]], 
[[0, 30, 33], [6, 9, 336], [10, 13]], [[0, 31, 35], [7, 11, 341], [11, 16]], 
[[0, 32, 34], [8, 10, 346], [14, 17]], [[0, 33, 34], [9, 10, 351], [15, 19]], 
[[0, 33, 35], [9, 11, 352], [12, 19]], [[0, 34, 35], [10, 11, 357], [18, 19]], 
[[1, 24, 25], [12, 13, 288], [20, 21]], [[1, 24, 26], [12, 14, 289], [20, 22]], 
[[1, 24, 76], [12, 16, 294], [23, 24]], [[1, 24, 78], [12, 18, 295], [21, 23]], 
[[1, 24, 80], [12, 20, 296], [22, 24]], [[1, 25, 26], [13, 14, 297], [20, 25]], 
[[1, 25, 75], [13, 15, 302], [26, 27]], [[1, 25, 78], [13, 18, 303], [21, 26]], 
[[1, 25, 79], [13, 19, 304], [25, 27]], [[1, 26, 77], [14, 17, 309], [28, 29]], 
[[1, 26, 79], [14, 19, 310], [25, 28]], [[1, 26, 80], [14, 20, 311], [22, 29]], 
[[1, 75, 78], [15, 18, 562], [26, 30]], [[1, 75, 79], [15, 19, 563], [27, 31]], 
[[1, 75, 81], [15, 21, 564], [30, 32]], [[1, 75, 83], [15, 23, 565], [31, 32]], 
[[1, 76, 78], [16, 18, 569], [23, 33]], [[1, 76, 80], [16, 20, 570], [24, 34]], 
[[1, 76, 81], [16, 21, 571], [33, 35]], [[1, 76, 82], [16, 22, 572], [34, 35]], 
[[1, 77, 79], [17, 19, 576], [28, 36]], [[1, 77, 80], [17, 20, 577], [29, 37]], 
[[1, 77, 82], [17, 22, 578], [37, 38]], [[1, 77, 83], [17, 23, 579], [36, 38]], 
[[1, 78, 81], [18, 21, 583], [30, 33]], [[1, 79, 83], [19, 23, 585], [31, 36]], 
[[1, 80, 82], [20, 22, 587], [34, 37]], [[1, 81, 82], [21, 22, 589], [35, 39]], 
[[1, 81, 83], [21, 23, 590], [32, 39]], [[1, 82, 83], [22, 23, 595], [38, 39]], 
[[2, 27, 30], [24, 25, 312], [40, 41]], [[2, 27, 33], [24, 26, 314], [40, 42]], 
[[2, 27, 55], [24, 29, 317], [43, 44]], [[2, 27, 59], [24, 32, 318], [42, 43]], 
[[2, 27, 73], [24, 34, 319], [41, 44]], [[2, 30, 33], [25, 26, 336], [40, 45]], 
[[2, 30, 52], [25, 27, 337], [45, 46]], [[2, 30, 72], [25, 33, 338], [46, 47]], 
[[2, 30, 73], [25, 34, 339], [41, 47]], [[2, 33, 52], [26, 27, 353], [45, 48]], 
[[2, 33, 58], [26, 31, 355], [48, 49]], [[2, 33, 59], [26, 32, 356], [42, 49]], 
[[2, 52, 56], [27, 30, 458], [50, 51]], [[2, 52, 58], [27, 31, 460], [48, 50]], 
[[2, 52, 72], [27, 33, 461], [46, 51]], [[2, 53, 55], [28, 29, 463], [52, 53]], 
[[2, 53, 56], [28, 30, 464], [54, 55]], [[2, 53, 58], [28, 31, 465], [54, 56]], 
[[2, 53, 59], [28, 32, 466], [52, 56]], [[2, 53, 74], [28, 35, 470], [53, 55]], 
[[2, 55, 59], [29, 32, 476], [43, 52]], [[2, 55, 73], [29, 34, 477], [44, 57]], 
[[2, 55, 74], [29, 35, 478], [53, 57]], [[2, 56, 58], [30, 31, 482], [50, 54]], 
[[2, 56, 72], [30, 33, 484], [51, 58]], [[2, 56, 74], [30, 35, 485], [55, 58]], 
[[2, 58, 59], [31, 32, 491], [49, 56]], [[2, 72, 73], [33, 34, 548], [47, 59]], 
[[2, 72, 74], [33, 35, 549], [58, 59]], [[2, 73, 74], [34, 35, 554], [57, 59]], 
[[3, 72, 73], [36, 37, 548], [60, 61]], [[3, 72, 74], [36, 38, 549], [60, 62]], 
[[3, 72, 78], [36, 40, 550], [61, 63]], [[3, 72, 100], [36, 42, 552], [63, 64]], 
[[3, 72, 104], [36, 45, 553], [62, 64]], [[3, 73, 74], [37, 38, 554], [60, 65]], 
[[3, 73, 75], [37, 39, 555], [66, 67]], [[3, 73, 78], [37, 40, 556], [61, 66]], 
[[3, 73, 103], [37, 44, 557], [65, 67]], [[3, 74, 101], [38, 43, 559], [68, 69]], 
[[3, 74, 103], [38, 44, 560], [65, 68]], [[3, 74, 104], [38, 45, 561], [62, 69]], 
[[3, 75, 78], [39, 40, 562], [66, 70]], [[3, 75, 81], [39, 41, 564], [70, 71]], 
[[3, 75, 103], [39, 44, 567], [67, 72]], [[3, 75, 107], [39, 47, 568], [71, 72]], 
[[3, 78, 81], [40, 41, 583], [70, 73]], [[3, 78, 100], [40, 42, 584], [63, 73]], 
[[3, 81, 100], [41, 42, 591], [73, 74]], [[3, 81, 106], [41, 46, 593], [74, 75]], 
[[3, 81, 107], [41, 47, 594], [71, 75]], [[3, 100, 104], [42, 45, 669], [64, 76]], 
[[3, 100, 106], [42, 46, 671], [74, 76]], [[3, 101, 103], [43, 44, 672], [68, 77]], 
[[3, 101, 104], [43, 45, 673], [69, 78]], [[3, 101, 106], [43, 46, 674], [78, 79]], 
[[3, 101, 107], [43, 47, 675], [77, 79]], [[3, 103, 107], [44, 47, 680], [72, 77]], 
[[3, 104, 106], [45, 46, 681], [76, 78]], [[3, 106, 107], [46, 47, 685], [75, 79]], 
[[4, 28, 32], [48, 49, 321], [80, 81]], [[4, 28, 34], [48, 50, 323], [80, 82]], 
[[4, 28, 48], [48, 54, 324], [81, 83]], [[4, 28, 54], [48, 58, 326], [83, 84]], 
[[4, 28, 57], [48, 59, 327], [82, 84]], [[4, 32, 34], [49, 50, 346], [80, 85]], 
[[4, 32, 41], [49, 51, 347], [85, 86]], [[4, 32, 48], [49, 54, 348], [81, 87]], 
[[4, 32, 50], [49, 56, 349], [86, 87]], [[4, 34, 41], [50, 51, 358], [85, 88]], 
[[4, 34, 47], [50, 53, 360], [88, 89]], [[4, 34, 57], [50, 59, 361], [82, 89]], 
[[4, 41, 43], [51, 52, 399], [90, 91]], [[4, 41, 47], [51, 53, 402], [88, 90]], 
[[4, 41, 50], [51, 56, 403], [86, 91]], [[4, 43, 47], [52, 53, 410], [90, 92]], 
[[4, 43, 49], [52, 55, 411], [93, 94]], [[4, 43, 50], [52, 56, 412], [91, 93]], 
[[4, 43, 51], [52, 57, 413], [92, 94]], [[4, 47, 51], [53, 57, 429], [92, 95]], 
[[4, 47, 57], [53, 59, 430], [89, 95]], [[4, 48, 49], [54, 55, 434], [96, 97]], 
[[4, 48, 50], [54, 56, 435], [87, 96]], [[4, 48, 54], [54, 58, 436], [83, 97]], 
[[4, 49, 50], [55, 56, 440], [93, 96]], [[4, 49, 51], [55, 57, 441], [94, 98]], 
[[4, 49, 54], [55, 58, 442], [97, 98]], [[4, 51, 54], [57, 58, 451], [98, 99]], 
[[4, 51, 57], [57, 59, 452], [95, 99]], [[4, 54, 57], [58, 59, 472], [84, 99]], 
[[5, 48, 49], [60, 61, 434], [100, 101]], [[5, 48, 50], [60, 62, 435], [100, 102]], 
[[5, 48, 76], [60, 63, 437], [103, 104]], [[5, 48, 80], [60, 64, 438], [102, 103]], 
[[5, 48, 102], [60, 70, 439], [101, 104]], [[5, 49, 50], [61, 62, 440], [100, 105]], 
[[5, 49, 91], [61, 67, 443], [105, 106]], [[5, 49, 99], [61, 69, 445], [106, 107]], 
[[5, 49, 102], [61, 70, 446], [101, 107]], [[5, 50, 80], [62, 64, 448], [102, 108]], 
[[5, 50, 89], [62, 66, 449], [108, 109]], [[5, 50, 91], [62, 67, 450], [105, 109]], 
[[5, 76, 80], [63, 64, 570], [103, 110]], [[5, 76, 82], [63, 65, 572], [110, 111]], 
[[5, 76, 102], [63, 70, 574], [104, 112]], [[5, 76, 105], [63, 71, 575], [111, 112]], 
[[5, 80, 82], [64, 65, 587], [110, 113]], [[5, 80, 89], [64, 66, 588], [108, 113]], 
[[5, 82, 89], [65, 66, 596], [113, 114]], [[5, 82, 95], [65, 68, 598], [114, 115]], 
[[5, 82, 105], [65, 71, 599], [111, 115]], [[5, 89, 91], [66, 67, 628], [109, 116]], 
[[5, 89, 95], [66, 68, 631], [114, 116]], [[5, 91, 95], [67, 68, 634], [116, 117]], 
[[5, 91, 99], [67, 69, 635], [106, 117]], [[5, 95, 99], [68, 69, 645], [117, 118]], 
[[5, 95, 105], [68, 71, 646], [115, 118]], [[5, 99, 102], [69, 70, 663], [107, 119]], 
[[5, 99, 105], [69, 71, 664], [118, 119]], [[5, 102, 105], [70, 71, 679], [112, 119]], 
[[6, 51, 54], [72, 74, 451], [120, 121]], [[6, 51, 57], [72, 76, 452], [120, 122]], 
[[6, 51, 67], [72, 79, 454], [123, 124]], [[6, 51, 71], [72, 80, 455], [122, 123]], 
[[6, 51, 97], [72, 82, 456], [121, 124]], [[6, 52, 54], [73, 74, 457], [125, 126]], 
[[6, 52, 56], [73, 75, 458], [127, 128]], [[6, 52, 57], [73, 76, 459], [125, 129]], 
[[6, 52, 58], [73, 77, 460], [127, 129]], [[6, 52, 96], [73, 81, 462], [126, 128]], 
[[6, 54, 57], [74, 76, 472], [120, 125]], [[6, 54, 96], [74, 81, 473], [126, 130]], 
[[6, 54, 97], [74, 82, 474], [121, 130]], [[6, 56, 58], [75, 77, 482], [127, 131]], 
[[6, 56, 65], [75, 78, 483], [131, 132]], [[6, 56, 96], [75, 81, 486], [128, 133]], 
[[6, 56, 98], [75, 83, 487], [132, 133]], [[6, 57, 58], [76, 77, 489], [129, 134]], 
[[6, 57, 71], [76, 80, 490], [122, 134]], [[6, 58, 65], [77, 78, 492], [131, 135]], 
[[6, 58, 71], [77, 80, 494], [134, 135]], [[6, 65, 67], [78, 79, 523], [136, 137]], 
[[6, 65, 71], [78, 80, 526], [135, 136]], [[6, 65, 98], [78, 83, 527], [132, 137]], 
[[6, 67, 71], [79, 80, 533], [123, 136]], [[6, 67, 97], [79, 82, 534], [124, 138]], 
[[6, 67, 98], [79, 83, 535], [137, 138]], [[6, 96, 97], [81, 82, 650], [130, 139]], 
[[6, 96, 98], [81, 83, 651], [133, 139]], [[6, 97, 98], [82, 83, 655], [138, 139]], 
[[7, 96, 97], [84, 85, 650], [140, 141]], [[7, 96, 98], [84, 86, 651], [140, 142]], 
[[7, 96, 100], [84, 88, 652], [143, 144]], [[7, 96, 102], [84, 89, 653], [141, 143]], 
[[7, 96, 104], [84, 90, 654], [142, 144]], [[7, 97, 98], [85, 86, 655], [140, 145]], 
[[7, 97, 99], [85, 87, 656], [146, 147]], [[7, 97, 102], [85, 89, 657], [141, 146]], 
[[7, 97, 115], [85, 94, 658], [145, 147]], [[7, 98, 104], [86, 90, 659], [142, 148]], 
[[7, 98, 113], [86, 93, 661], [148, 149]], [[7, 98, 115], [86, 94, 662], [145, 149]], 
[[7, 99, 102], [87, 89, 663], [146, 150]], [[7, 99, 105], [87, 91, 664], [150, 151]], 
[[7, 99, 115], [87, 94, 666], [147, 152]], [[7, 99, 119], [87, 95, 667], [151, 152]], 
[[7, 100, 102], [88, 89, 668], [143, 153]], [[7, 100, 104], [88, 90, 669], [144, 154]], 
[[7, 100, 105], [88, 91, 670], [153, 155]], [[7, 100, 106], [88, 92, 671], [154, 155]], 
[[7, 102, 105], [89, 91, 679], [150, 153]], [[7, 104, 106], [90, 92, 681], [154, 156]], 
[[7, 104, 113], [90, 93, 682], [148, 156]], [[7, 105, 106], [91, 92, 683], [155, 157]], 
[[7, 105, 119], [91, 95, 684], [151, 157]], [[7, 106, 113], [92, 93, 686], [156, 158]], 
[[7, 106, 119], [92, 95, 688], [157, 158]], [[7, 113, 115], [93, 94, 710], [149, 159]], 
[[7, 113, 119], [93, 95, 713], [158, 159]], [[7, 115, 119], [94, 95, 715], [152, 159]], 
[[8, 29, 31], [96, 97, 328], [160, 161]], [[8, 29, 35], [96, 98, 331], [160, 162]], 
[[8, 29, 38], [96, 101, 332], [161, 163]], [[8, 29, 44], [96, 105, 334], [163, 164]], 
[[8, 29, 46], [96, 107, 335], [162, 164]], [[8, 31, 35], [97, 98, 341], [160, 165]], 
[[8, 31, 37], [97, 100, 342], [166, 167]], [[8, 31, 38], [97, 101, 343], [161, 166]], 
[[8, 31, 39], [97, 102, 344], [165, 167]], [[8, 35, 39], [98, 102, 362], [165, 168]], 
[[8, 35, 45], [98, 106, 363], [168, 169]], [[8, 35, 46], [98, 107, 364], [162, 169]], 
[[8, 36, 37], [99, 100, 366], [170, 171]], [[8, 36, 38], [99, 101, 367], [170, 172]], 
[[8, 36, 40], [99, 103, 368], [173, 174]], [[8, 36, 42], [99, 104, 369], [171, 173]], 
[[8, 36, 44], [99, 105, 370], [172, 174]], [[8, 37, 38], [100, 101, 375], [166, 170]], 
[[8, 37, 39], [100, 102, 376], [167, 175]], [[8, 37, 42], [100, 104, 377], [171, 175]], 
[[8, 38, 44], [101, 105, 382], [163, 172]], [[8, 39, 42], [102, 104, 386], [175, 176]], 
[[8, 39, 45], [102, 106, 387], [168, 176]], [[8, 40, 42], [103, 104, 391], [173, 177]], 
[[8, 40, 44], [103, 105, 392], [174, 178]], [[8, 40, 45], [103, 106, 393], [177, 179]], 
[[8, 40, 46], [103, 107, 394], [178, 179]], [[8, 42, 45], [104, 106, 405], [176, 177]], 
[[8, 44, 46], [105, 107, 418], [164, 178]], [[8, 45, 46], [106, 107, 422], [169, 179]], 
[[9, 36, 37], [108, 109, 366], [180, 181]], [[9, 36, 38], [108, 110, 367], [180, 182]], 
[[9, 36, 88], [108, 115, 372], [183, 184]], [[9, 36, 90], [108, 116, 373], [181, 183]], 
[[9, 36, 92], [108, 117, 374], [182, 184]], [[9, 37, 38], [109, 110, 375], [180, 185]], 
[[9, 37, 79], [109, 112, 378], [185, 186]], [[9, 37, 87], [109, 114, 380], [186, 187]], 
[[9, 37, 90], [109, 116, 381], [181, 187]], [[9, 38, 77], [110, 111, 383], [188, 189]], 
[[9, 38, 79], [110, 112, 384], [185, 188]], [[9, 38, 92], [110, 117, 385], [182, 189]], 
[[9, 77, 79], [111, 112, 576], [188, 190]], [[9, 77, 83], [111, 113, 579], [190, 191]], 
[[9, 77, 92], [111, 117, 581], [189, 192]], [[9, 77, 94], [111, 119, 582], [191, 192]], 
[[9, 79, 83], [112, 113, 585], [190, 193]], [[9, 79, 87], [112, 114, 586], [186, 193]], 
[[9, 83, 87], [113, 114, 600], [193, 194]], [[9, 83, 93], [113, 118, 601], [194, 195]], 
[[9, 83, 94], [113, 119, 602], [191, 195]], [[9, 87, 90], [114, 116, 617], [187, 196]], 
[[9, 87, 93], [114, 118, 618], [194, 196]], [[9, 88, 90], [115, 116, 621], [183, 197]], 
[[9, 88, 92], [115, 117, 622], [184, 198]], [[9, 88, 93], [115, 118, 623], [197, 199]], 
[[9, 88, 94], [115, 119, 624], [198, 199]], [[9, 90, 93], [116, 118, 632], [196, 197]], 
[[9, 92, 94], [117, 119, 637], [192, 198]], [[9, 93, 94], [118, 119, 638], [195, 199]], 
[[10, 39, 42], [120, 121, 386], [200, 201]], [[10, 39, 45], [120, 122, 387], [200, 202]], 
[[10, 39, 55], [120, 124, 388], [203, 204]], [[10, 39, 59], [120, 125, 389], [202, 203]], 
[[10, 39, 85], [120, 130, 390], [201, 204]], [[10, 42, 45], [121, 122, 405], [200, 205]], 
[[10, 42, 64], [121, 126, 406], [205, 206]], [[10, 42, 84], [121, 129, 407], [206, 207]], 
[[10, 42, 85], [121, 130, 408], [201, 207]], [[10, 45, 59], [122, 125, 423], [202, 208]], 
[[10, 45, 64], [122, 126, 424], [205, 209]], [[10, 45, 70], [122, 128, 426], [208, 209]], 
[[10, 53, 55], [123, 124, 463], [210, 211]], [[10, 53, 59], [123, 125, 466], [210, 212]], 
[[10, 53, 68], [123, 127, 468], [213, 214]], [[10, 53, 70], [123, 128, 469], [212, 213]], 
[[10, 53, 86], [123, 131, 471], [211, 214]], [[10, 55, 59], [124, 125, 476], [203, 210]], 
[[10, 55, 85], [124, 130, 479], [204, 215]], [[10, 55, 86], [124, 131, 480], [211, 215]], 
[[10, 59, 70], [125, 128, 495], [208, 212]], [[10, 64, 68], [126, 127, 518], [216, 217]], 
[[10, 64, 70], [126, 128, 520], [209, 216]], [[10, 64, 84], [126, 129, 521], [206, 217]], 
[[10, 68, 70], [127, 128, 539], [213, 216]], [[10, 68, 84], [127, 129, 540], [217, 218]], 
[[10, 68, 86], [127, 131, 541], [214, 218]], [[10, 84, 85], [129, 130, 604], [207, 219]], 
[[10, 84, 86], [129, 131, 605], [218, 219]], [[10, 85, 86], [130, 131, 610], [215, 219]], 
[[11, 84, 85], [132, 133, 604], [220, 221]], [[11, 84, 86], [132, 134, 605], [220, 222]], 
[[11, 84, 90], [132, 136, 606], [221, 223]], [[11, 84, 112], [132, 141, 608], [223, 224]], 
[[11, 84, 116], [132, 142, 609], [222, 224]], [[11, 85, 86], [133, 134, 610], [220, 225]], 
[[11, 85, 87], [133, 135, 611], [226, 227]], [[11, 85, 90], [133, 136, 612], [221, 226]], 
[[11, 85, 103], [133, 139, 613], [225, 227]], [[11, 86, 101], [134, 138, 614], [228, 229]], 
[[11, 86, 103], [134, 139, 615], [225, 228]], [[11, 86, 116], [134, 142, 616], [222, 229]], 
[[11, 87, 90], [135, 136, 617], [226, 230]], [[11, 87, 93], [135, 137, 618], [230, 231]], 
[[11, 87, 103], [135, 139, 619], [227, 232]], [[11, 87, 107], [135, 140, 620], [231, 232]], 
[[11, 90, 93], [136, 137, 632], [230, 233]], [[11, 90, 112], [136, 141, 633], [223, 233]], 
[[11, 93, 107], [137, 140, 639], [231, 234]], [[11, 93, 112], [137, 141, 640], [233, 235]], 
[[11, 93, 118], [137, 143, 642], [234, 235]], [[11, 101, 103], [138, 139, 672], [228, 236]], 
[[11, 101, 107], [138, 140, 675], [236, 237]], [[11, 101, 116], [138, 142, 677], [229, 238]], 
[[11, 101, 118], [138, 143, 678], [237, 238]], [[11, 103, 107], [139, 140, 680], [232, 236]], 
[[11, 107, 118], [140, 143, 689], [234, 237]], [[11, 112, 116], [141, 142, 707], [224, 239]], 
[[11, 112, 118], [141, 143, 709], [235, 239]], [[11, 116, 118], [142, 143, 716], [238, 239]], 
[[12, 40, 44], [144, 147, 392], [240, 241]], [[12, 40, 46], [144, 148, 394], [240, 242]], 
[[12, 40, 60], [144, 150, 395], [241, 243]], [[12, 40, 66], [144, 154, 397], [243, 244]], 
[[12, 40, 69], [144, 155, 398], [242, 244]], [[12, 41, 43], [145, 146, 399], [245, 246]], 
[[12, 41, 44], [145, 147, 400], [247, 248]], [[12, 41, 46], [145, 148, 401], [247, 249]], 
[[12, 41, 47], [145, 149, 402], [245, 249]], [[12, 41, 62], [145, 152, 404], [246, 248]], 
[[12, 43, 47], [146, 149, 410], [245, 250]], [[12, 43, 61], [146, 151, 414], [251, 252]], 
[[12, 43, 62], [146, 152, 415], [246, 251]], [[12, 43, 63], [146, 153, 416], [250, 252]], 
[[12, 44, 46], [147, 148, 418], [240, 247]], [[12, 44, 60], [147, 150, 419], [241, 253]], 
[[12, 44, 62], [147, 152, 420], [248, 253]], [[12, 46, 47], [148, 149, 427], [249, 254]], 
[[12, 46, 69], [148, 155, 428], [242, 254]], [[12, 47, 63], [149, 153, 431], [250, 255]], 
[[12, 47, 69], [149, 155, 432], [254, 255]], [[12, 60, 61], [150, 151, 496], [256, 257]], 
[[12, 60, 62], [150, 152, 497], [253, 256]], [[12, 60, 66], [150, 154, 498], [243, 257]], 
[[12, 61, 62], [151, 152, 502], [251, 256]], [[12, 61, 63], [151, 153, 503], [252, 258]], 
[[12, 61, 66], [151, 154, 504], [257, 258]], [[12, 63, 66], [153, 154, 512], [258, 259]], 
[[12, 63, 69], [153, 155, 514], [255, 259]], [[12, 66, 69], [154, 155, 529], [244, 259]], 
[[13, 60, 61], [156, 157, 496], [260, 261]], [[13, 60, 62], [156, 158, 497], [260, 262]], 
[[13, 60, 88], [156, 159, 499], [263, 264]], [[13, 60, 92], [156, 162, 500], [262, 263]], 
[[13, 60, 114], [156, 166, 501], [261, 264]], [[13, 61, 62], [157, 158, 502], [260, 265]], 
[[13, 61, 91], [157, 161, 505], [265, 266]], [[13, 61, 111], [157, 165, 507], [266, 267]], 
[[13, 61, 114], [157, 166, 508], [261, 267]], [[13, 62, 89], [158, 160, 509], [268, 269]], 
[[13, 62, 91], [158, 161, 510], [265, 268]], [[13, 62, 92], [158, 162, 511], [262, 269]], 
[[13, 88, 92], [159, 162, 622], [263, 270]], [[13, 88, 94], [159, 163, 624], [270, 271]], 
[[13, 88, 114], [159, 166, 626], [264, 272]], [[13, 88, 117], [159, 167, 627], [271, 272]], 
[[13, 89, 91], [160, 161, 628], [268, 273]], [[13, 89, 92], [160, 162, 629], [269, 274]], 
[[13, 89, 94], [160, 163, 630], [274, 275]], [[13, 89, 95], [160, 164, 631], [273, 275]], 
[[13, 91, 95], [161, 164, 634], [273, 276]], [[13, 91, 111], [161, 165, 636], [266, 276]], 
[[13, 92, 94], [162, 163, 637], [270, 274]], [[13, 94, 95], [163, 164, 643], [275, 277]], 
[[13, 94, 117], [163, 167, 644], [271, 277]], [[13, 95, 111], [164, 165, 647], [276, 278]], 
[[13, 95, 117], [164, 167, 648], [277, 278]], [[13, 111, 114], [165, 166, 702], [267, 279]], 
[[13, 111, 117], [165, 167, 704], [278, 279]], [[13, 114, 117], [166, 167, 714], [272, 279]], 
[[14, 63, 66], [168, 171, 512], [280, 281]], [[14, 63, 67], [168, 172, 513], [282, 283]], 
[[14, 63, 69], [168, 174, 514], [280, 284]], [[14, 63, 71], [168, 176, 515], [282, 284]], 
[[14, 63, 109], [168, 178, 516], [281, 283]], [[14, 64, 66], [169, 171, 517], [285, 286]], 
[[14, 64, 68], [169, 173, 518], [287, 288]], [[14, 64, 69], [169, 174, 519], [285, 289]], 
[[14, 64, 70], [169, 175, 520], [287, 289]], [[14, 64, 108], [169, 177, 522], [286, 288]], 
[[14, 65, 67], [170, 172, 523], [290, 291]], [[14, 65, 68], [170, 173, 524], [292, 293]], 
[[14, 65, 70], [170, 175, 525], [292, 294]], [[14, 65, 71], [170, 176, 526], [290, 294]], 
[[14, 65, 110], [170, 179, 528], [291, 293]], [[14, 66, 69], [171, 174, 529], [280, 285]], 
[[14, 66, 108], [171, 177, 530], [286, 295]], [[14, 66, 109], [171, 178, 531], [281, 295]], 
[[14, 67, 71], [172, 176, 533], [282, 290]], [[14, 67, 109], [172, 178, 536], [283, 296]], 
[[14, 67, 110], [172, 179, 537], [291, 296]], [[14, 68, 70], [173, 175, 539], [287, 292]], 
[[14, 68, 108], [173, 177, 542], [288, 297]], [[14, 68, 110], [173, 179, 543], [293, 297]], 
[[14, 69, 70], [174, 175, 545], [289, 298]], [[14, 69, 71], [174, 176, 546], [284, 298]], 
[[14, 70, 71], [175, 176, 547], [294, 298]], [[14, 108, 109], [177, 178, 690], [295, 299]], 
[[14, 108, 110], [177, 179, 691], [297, 299]], [[14, 109, 110], [178, 179, 695], [296, 299]], 
[[15, 108, 109], [180, 181, 690], [300, 301]], [[15, 108, 110], [180, 182, 691], [300, 302]], 
[[15, 108, 112], [180, 184, 692], [303, 304]], [[15, 108, 114], [180, 186, 693], [301, 303]], 
[[15, 108, 116], [180, 188, 694], [302, 304]], [[15, 109, 110], [181, 182, 695], [300, 305]], 
[[15, 109, 111], [181, 183, 696], [306, 307]], [[15, 109, 114], [181, 186, 697], [301, 306]], 
[[15, 109, 115], [181, 187, 698], [305, 307]], [[15, 110, 113], [182, 185, 699], [308, 309]], 
[[15, 110, 115], [182, 187, 700], [305, 308]], [[15, 110, 116], [182, 188, 701], [302, 309]], 
[[15, 111, 114], [183, 186, 702], [306, 310]], [[15, 111, 115], [183, 187, 703], [307, 311]], 
[[15, 111, 117], [183, 189, 704], [310, 312]], [[15, 111, 119], [183, 191, 705], [311, 312]], 
[[15, 112, 114], [184, 186, 706], [303, 313]], [[15, 112, 116], [184, 188, 707], [304, 314]], 
[[15, 112, 117], [184, 189, 708], [313, 315]], [[15, 112, 118], [184, 190, 709], [314, 315]], 
[[15, 113, 115], [185, 187, 710], [308, 316]], [[15, 113, 116], [185, 188, 711], [309, 317]], 
[[15, 113, 118], [185, 190, 712], [317, 318]], [[15, 113, 119], [185, 191, 713], [316, 318]], 
[[15, 114, 117], [186, 189, 714], [310, 313]], [[15, 115, 119], [187, 191, 715], [311, 316]], 
[[15, 116, 118], [188, 190, 716], [314, 317]], [[15, 117, 118], [189, 190, 717], [315, 319]], 
[[15, 117, 119], [189, 191, 718], [312, 319]], [[15, 118, 119], [190, 191, 719], [318, 319]], 
[[16, 33, 34], [192, 193, 351], [320, 321]], [[16, 33, 35], [192, 194, 352], [320, 322]], 
[[16, 33, 57], [192, 198, 354], [321, 323]], [[16, 33, 58], [192, 199, 355], [323, 324]], 
[[16, 33, 59], [192, 200, 356], [322, 324]], [[16, 34, 35], [193, 194, 357], [320, 325]], 
[[16, 34, 46], [193, 196, 359], [325, 326]], [[16, 34, 47], [193, 197, 360], [326, 327]], 
[[16, 34, 57], [193, 198, 361], [321, 327]], [[16, 35, 45], [194, 195, 363], [328, 329]], 
[[16, 35, 46], [194, 196, 364], [325, 328]], [[16, 35, 59], [194, 200, 365], [322, 329]], 
[[16, 45, 46], [195, 196, 422], [328, 330]], [[16, 45, 59], [195, 200, 423], [329, 331]], 
[[16, 45, 69], [195, 201, 425], [330, 332]], [[16, 45, 70], [195, 202, 426], [331, 332]], 
[[16, 46, 47], [196, 197, 427], [326, 333]], [[16, 46, 69], [196, 201, 428], [330, 333]], 
[[16, 47, 57], [197, 198, 430], [327, 334]], [[16, 47, 69], [197, 201, 432], [333, 335]], 
[[16, 47, 71], [197, 203, 433], [334, 335]], [[16, 57, 58], [198, 199, 489], [323, 336]], 
[[16, 57, 71], [198, 203, 490], [334, 336]], [[16, 58, 59], [199, 200, 491], [324, 337]], 
[[16, 58, 70], [199, 202, 493], [337, 338]], [[16, 58, 71], [199, 203, 494], [336, 338]], 
[[16, 59, 70], [200, 202, 495], [331, 337]], [[16, 69, 70], [201, 202, 545], [332, 339]], 
[[16, 69, 71], [201, 203, 546], [335, 339]], [[16, 70, 71], [202, 203, 547], [338, 339]], 
[[17, 81, 82], [204, 205, 589], [340, 341]], [[17, 81, 83], [204, 206, 590], [340, 342]], 
[[17, 81, 105], [204, 210, 592], [341, 343]], [[17, 81, 106], [204, 211, 593], [343, 344]], 
[[17, 81, 107], [204, 212, 594], [342, 344]], [[17, 82, 83], [205, 206, 595], [340, 345]], 
[[17, 82, 94], [205, 208, 597], [345, 346]], [[17, 82, 95], [205, 209, 598], [346, 347]], 
[[17, 82, 105], [205, 210, 599], [341, 347]], [[17, 83, 93], [206, 207, 601], [348, 349]], 
[[17, 83, 94], [206, 208, 602], [345, 348]], [[17, 83, 107], [206, 212, 603], [342, 349]], 
[[17, 93, 94], [207, 208, 638], [348, 350]], [[17, 93, 107], [207, 212, 639], [349, 351]], 
[[17, 93, 117], [207, 213, 641], [350, 352]], [[17, 93, 118], [207, 214, 642], [351, 352]], 
[[17, 94, 95], [208, 209, 643], [346, 353]], [[17, 94, 117], [208, 213, 644], [350, 353]], 
[[17, 95, 105], [209, 210, 646], [347, 354]], [[17, 95, 117], [209, 213, 648], [353, 355]], 
[[17, 95, 119], [209, 215, 649], [354, 355]], [[17, 105, 106], [210, 211, 683], [343, 356]], 
[[17, 105, 119], [210, 215, 684], [354, 356]], [[17, 106, 107], [211, 212, 685], [344, 357]], 
[[17, 106, 118], [211, 214, 687], [357, 358]], [[17, 106, 119], [211, 215, 688], [356, 358]], 
[[17, 107, 118], [212, 214, 689], [351, 357]], [[17, 117, 118], [213, 214, 717], [352, 359]], 
[[17, 117, 119], [213, 215, 718], [355, 359]], [[17, 118, 119], [214, 215, 719], [358, 359]], 
[[18, 26, 29], [216, 217, 305], [360, 361]], [[18, 26, 32], [216, 218, 307], [360, 362]], 
[[18, 26, 38], [216, 219, 308], [361, 363]], [[18, 26, 77], [216, 224, 309], [363, 364]], 
[[18, 26, 80], [216, 225, 311], [362, 364]], [[18, 29, 32], [217, 218, 329], [360, 365]], 
[[18, 29, 38], [217, 219, 332], [361, 366]], [[18, 29, 41], [217, 220, 333], [365, 367]], 
[[18, 29, 44], [217, 221, 334], [366, 367]], [[18, 32, 41], [218, 220, 347], [365, 368]], 
[[18, 32, 50], [218, 222, 349], [368, 369]], [[18, 32, 80], [218, 225, 350], [362, 369]], 
[[18, 38, 44], [219, 221, 382], [366, 370]], [[18, 38, 77], [219, 224, 383], [363, 371]], 
[[18, 38, 92], [219, 227, 385], [370, 371]], [[18, 41, 44], [220, 221, 400], [367, 372]], 
[[18, 41, 50], [220, 222, 403], [368, 373]], [[18, 41, 62], [220, 223, 404], [372, 373]], 
[[18, 44, 62], [221, 223, 420], [372, 374]], [[18, 44, 92], [221, 227, 421], [370, 374]], 
[[18, 50, 62], [222, 223, 447], [373, 375]], [[18, 50, 80], [222, 225, 448], [369, 376]], 
[[18, 50, 89], [222, 226, 449], [375, 376]], [[18, 62, 89], [223, 226, 509], [375, 377]], 
[[18, 62, 92], [223, 227, 511], [374, 377]], [[18, 77, 80], [224, 225, 577], [364, 378]], 
[[18, 77, 89], [224, 226, 580], [378, 379]], [[18, 77, 92], [224, 227, 581], [371, 379]], 
[[18, 80, 89], [225, 226, 588], [376, 378]], [[18, 89, 92], [226, 227, 629], [377, 379]], 
[[19, 53, 56], [228, 229, 464], [380, 381]], [[19, 53, 65], [228, 230, 467], [380, 382]], 
[[19, 53, 68], [228, 231, 468], [382, 383]], [[19, 53, 74], [228, 232, 470], [381, 384]], 
[[19, 53, 86], [228, 233, 471], [383, 384]], [[19, 56, 65], [229, 230, 483], [380, 385]], 
[[19, 56, 74], [229, 232, 485], [381, 386]], [[19, 56, 98], [229, 234, 487], [385, 387]], 
[[19, 56, 104], [229, 236, 488], [386, 387]], [[19, 65, 68], [230, 231, 524], [382, 388]], 
[[19, 65, 98], [230, 234, 527], [385, 389]], [[19, 65, 110], [230, 237, 528], [388, 389]], 
[[19, 68, 86], [231, 233, 541], [383, 390]], [[19, 68, 110], [231, 237, 543], [388, 391]], 
[[19, 68, 116], [231, 239, 544], [390, 391]], [[19, 74, 86], [232, 233, 558], [384, 392]], 
[[19, 74, 101], [232, 235, 559], [392, 393]], [[19, 74, 104], [232, 236, 561], [386, 393]], 
[[19, 86, 101], [233, 235, 614], [392, 394]], [[19, 86, 116], [233, 239, 616], [390, 394]],
 [[19, 98, 104], [234, 236, 659], [387, 395]], [[19, 98, 110], [234, 237, 660], [389, 396]], 
 [[19, 98, 113], [234, 238, 661], [395, 396]], [[19, 101, 104], [235, 236, 673], [393, 397]], 
 [[19, 101, 113], [235, 238, 676], [397, 398]], [[19, 101, 116], [235, 239, 677], [394, 398]], 
 [[19, 104, 113], [236, 238, 682], [395, 397]], [[19, 110, 113], [237, 238, 699], [396, 399]], 
 [[19, 110, 116], [237, 239, 701], [391, 399]], [[19, 113, 116], [238, 239, 711], [398, 399]], 
 [[20, 25, 27], [240, 241, 298], [400, 401]], [[20, 25, 31], [240, 242, 300], [400, 402]], 
 [[20, 25, 73], [240, 246, 301], [401, 403]], [[20, 25, 75], [240, 247, 302], [403, 404]], 
 [[20, 25, 79], [240, 248, 304], [402, 404]], [[20, 27, 31], [241, 242, 313], [400, 405]], 
 [[20, 27, 39], [241, 244, 316], [405, 406]], [[20, 27, 55], [241, 245, 317], [406, 407]], 
 [[20, 27, 73], [241, 246, 319], [401, 407]], [[20, 31, 37], [242, 243, 342], [408, 409]], 
 [[20, 31, 39], [242, 244, 344], [405, 408]], [[20, 31, 79], [242, 248, 345], [402, 409]], 
 [[20, 37, 39], [243, 244, 376], [408, 410]], [[20, 37, 79], [243, 248, 378], [409, 411]], 
 [[20, 37, 85], [243, 249, 379], [410, 412]], [[20, 37, 87], [243, 250, 380], [411, 412]], 
 [[20, 39, 55], [244, 245, 388], [406, 413]], [[20, 39, 85], [244, 249, 390], [410, 413]], 
 [[20, 55, 73], [245, 246, 477], [407, 414]], [[20, 55, 85], [245, 249, 479], [413, 415]], 
 [[20, 55, 103], [245, 251, 481], [414, 415]], [[20, 73, 75], [246, 247, 555], [403, 416]], 
 [[20, 73, 103], [246, 251, 557], [414, 416]], [[20, 75, 79], [247, 248, 563], [404, 417]], 
 [[20, 75, 87], [247, 250, 566], [417, 418]], [[20, 75, 103], [247, 251, 567], [416, 418]], 
 [[20, 79, 87], [248, 250, 586], [411, 417]], [[20, 85, 87], [249, 250, 611], [412, 419]], 
 [[20, 85, 103], [249, 251, 613], [415, 419]], [[20, 87, 103], [250, 251, 619], [418, 419]], 
 [[21, 43, 49], [252, 253, 411], [420, 421]], [[21, 43, 51], [252, 254, 413], [420, 422]], 
 [[21, 43, 61], [252, 255, 414], [423, 424]], [[21, 43, 63], [252, 256, 416], [422, 423]], 
 [[21, 43, 91], [252, 258, 417], [421, 424]], [[21, 49, 51], [253, 254, 441], [420, 425]], 
 [[21, 49, 91], [253, 258, 443], [421, 426]], [[21, 49, 97], [253, 259, 444], [425, 427]], 
 [[21, 49, 99], [253, 260, 445], [426, 427]], [[21, 51, 63], [254, 256, 453], [422, 428]], 
 [[21, 51, 67], [254, 257, 454], [428, 429]], [[21, 51, 97], [254, 259, 456], [425, 429]], 
 [[21, 61, 63], [255, 256, 503], [423, 430]], [[21, 61, 91], [255, 258, 505], [424, 431]], 
 [[21, 61, 109], [255, 261, 506], [430, 432]], [[21, 61, 111], [255, 262, 507], [431, 432]], 
 [[21, 63, 67], [256, 257, 513], [428, 433]], [[21, 63, 109], [256, 261, 516], [430, 433]], 
 [[21, 67, 97], [257, 259, 534], [429, 434]], [[21, 67, 109], [257, 261, 536], [433, 435]], 
 [[21, 67, 115], [257, 263, 538], [434, 435]], [[21, 91, 99], [258, 260, 635], [426, 436]], 
 [[21, 91, 111], [258, 262, 636], [431, 436]], [[21, 97, 99], [259, 260, 656], [427, 437]], 
 [[21, 97, 115], [259, 263, 658], [434, 437]], [[21, 99, 111], [260, 262, 665], [436, 438]], 
 [[21, 99, 115], [260, 263, 666], [437, 438]], [[21, 109, 111], [261, 262, 696], [432, 439]], 
 [[21, 109, 115], [261, 263, 698], [435, 439]], [[21, 111, 115], [262, 263, 703], [438, 439]], 
 [[22, 24, 28], [264, 265, 290], [440, 441]], [[22, 24, 30], [264, 266, 291], [440, 442]], 
 [[22, 24, 48], [264, 267, 293], [441, 443]], [[22, 24, 76], [264, 271, 294], [443, 444]], 
 [[22, 24, 78], [264, 272, 295], [442, 444]], [[22, 28, 30], [265, 266, 320], [440, 445]], 
 [[22, 28, 48], [265, 267, 324], [441, 446]], [[22, 28, 52], [265, 268, 325], [445, 447]], 
 [[22, 28, 54], [265, 269, 326], [446, 447]], [[22, 30, 52], [266, 268, 337], [445, 448]], 
 [[22, 30, 72], [266, 270, 338], [448, 449]], [[22, 30, 78], [266, 272, 340], [442, 449]], 
 [[22, 48, 54], [267, 269, 436], [446, 450]], [[22, 48, 76], [267, 271, 437], [443, 451]], 
 [[22, 48, 102], [267, 275, 439], [450, 451]], [[22, 52, 54], [268, 269, 457], [447, 452]], 
 [[22, 52, 72], [268, 270, 461], [448, 453]], [[22, 52, 96], [268, 273, 462], [452, 453]], 
 [[22, 54, 96], [269, 273, 473], [452, 454]], [[22, 54, 102], [269, 275, 475], [450, 454]], 
 [[22, 72, 78], [270, 272, 550], [449, 455]], [[22, 72, 96], [270, 273, 551], [453, 456]], 
 [[22, 72, 100], [270, 274, 552], [455, 456]], [[22, 76, 78], [271, 272, 569], [444, 457]], 
 [[22, 76, 100], [271, 274, 573], [457, 458]], [[22, 76, 102], [271, 275, 574], [451, 458]], 
 [[22, 78, 100], [272, 274, 584], [455, 457]], [[22, 96, 100], [273, 274, 652], [456, 459]], 
 [[22, 96, 102], [273, 275, 653], [454, 459]], [[22, 100, 102], [274, 275, 668], [458, 459]], 
 [[23, 36, 40], [276, 277, 368], [460, 461]], [[23, 36, 42], [276, 278, 369], [460, 462]], 
 [[23, 36, 60], [276, 279, 371], [461, 463]], [[23, 36, 88], [276, 283, 372], [463, 464]], 
 [[23, 36, 90], [276, 284, 373], [462, 464]], [[23, 40, 42], [277, 278, 391], [460, 465]], 
 [[23, 40, 60], [277, 279, 395], [461, 466]], [[23, 40, 64], [277, 280, 396], [465, 467]], 
 [[23, 40, 66], [277, 281, 397], [466, 467]], [[23, 42, 64], [278, 280, 406], [465, 468]], 
 [[23, 42, 84], [278, 282, 407], [468, 469]], [[23, 42, 90], [278, 284, 409], [462, 469]], 
 [[23, 60, 66], [279, 281, 498], [466, 470]], [[23, 60, 88], [279, 283, 499], [463, 471]], 
 [[23, 60, 114], [279, 287, 501], [470, 471]], [[23, 64, 66], [280, 281, 517], [467, 472]], 
 [[23, 64, 84], [280, 282, 521], [468, 473]], [[23, 64, 108], [280, 285, 522], [472, 473]], 
 [[23, 66, 108], [281, 285, 530], [472, 474]], [[23, 66, 114], [281, 287, 532], [470, 474]], 
 [[23, 84, 90], [282, 284, 606], [469, 475]], [[23, 84, 108], [282, 285, 607], [473, 476]], 
 [[23, 84, 112], [282, 286, 608], [475, 476]], [[23, 88, 90], [283, 284, 621], [464, 477]], 
 [[23, 88, 112], [283, 286, 625], [477, 478]], [[23, 88, 114], [283, 287, 626], [471, 478]], 
 [[23, 90, 112], [284, 286, 633], [475, 477]], [[23, 108, 112], [285, 286, 692], [476, 479]], 
 [[23, 108, 114], [285, 287, 693], [474, 479]], [[23, 112, 114], [286, 287, 706], [478, 479]], 
 [[24, 25, 26], [288, 289, 297], [0, 20]], [[24, 25, 30], [288, 291, 299], [1, 480]], 
 [[24, 25, 78], [288, 295, 303], [21, 480]], [[24, 26, 32], [289, 292, 307], [2, 481]], 
 [[24, 26, 80], [289, 296, 311], [22, 481]], [[24, 28, 30], [290, 291, 320], [3, 440]], 
 [[24, 28, 32], [290, 292, 321], [4, 482]], [[24, 28, 48], [290, 293, 324], [441, 482]], 
 [[24, 30, 78], [291, 295, 340], [442, 480]], [[24, 32, 48], [292, 293, 348], [482, 483]], 
 [[24, 32, 80], [292, 296, 350], [481, 483]], [[24, 48, 76], [293, 294, 437], [443, 484]], 
 [[24, 48, 80], [293, 296, 438], [483, 484]], [[24, 76, 78], [294, 295, 569], [23, 444]], 
 [[24, 76, 80], [294, 296, 570], [24, 484]], [[25, 26, 31], [297, 300, 306], [5, 485]], 
 [[25, 26, 79], [297, 304, 310], [25, 485]], [[25, 27, 30], [298, 299, 312], [6, 486]], 
 [[25, 27, 31], [298, 300, 313], [7, 400]], [[25, 27, 73], [298, 301, 319], [401, 486]], 
 [[25, 30, 73], [299, 301, 339], [486, 487]], [[25, 30, 78], [299, 303, 340], [480, 487]], 
 [[25, 31, 79], [300, 304, 345], [402, 485]], [[25, 73, 75], [301, 302, 555], [403, 488]], 
 [[25, 73, 78], [301, 303, 556], [487, 488]], [[25, 75, 78], [302, 303, 562], [26, 488]], 
 [[25, 75, 79], [302, 304, 563], [27, 404]], [[26, 29, 31], [305, 306, 328], [8, 489]], 
 [[26, 29, 32], [305, 307, 329], [9, 360]], [[26, 29, 38], [305, 308, 332], [361, 489]], 
 [[26, 31, 38], [306, 308, 343], [489, 490]], [[26, 31, 79], [306, 310, 345], [485, 490]], 
 [[26, 32, 80], [307, 311, 350], [362, 481]], [[26, 38, 77], [308, 309, 383], [363, 491]], 
 [[26, 38, 79], [308, 310, 384], [490, 491]], [[26, 77, 79], [309, 310, 576], [28, 491]], 
 [[26, 77, 80], [309, 311, 577], [29, 364]], [[27, 30, 33], [312, 314, 336], [10, 40]], 
 [[27, 30, 73], [312, 319, 339], [41, 486]], [[27, 31, 35], [313, 315, 341], [11, 492]], 
 [[27, 31, 39], [313, 316, 344], [405, 492]], [[27, 33, 35], [314, 315, 352], [12, 493]], 
 [[27, 33, 59], [314, 318, 356], [42, 493]], [[27, 35, 39], [315, 316, 362], [492, 494]], 
 [[27, 35, 59], [315, 318, 365], [493, 494]], [[27, 39, 55], [316, 317, 388], [406, 495]], 
 [[27, 39, 59], [316, 318, 389], [494, 495]], [[27, 55, 59], [317, 318, 476], [43, 495]], 
 [[27, 55, 73], [317, 319, 477], [44, 407]], [[28, 30, 33], [320, 322, 336], [13, 496]], 
 [[28, 30, 52], [320, 325, 337], [445, 496]], [[28, 32, 34], [321, 323, 346], [14, 80]], 
 [[28, 32, 48], [321, 324, 348], [81, 482]], [[28, 33, 34], [322, 323, 351], [15, 497]], 
 [[28, 33, 52], [322, 325, 353], [496, 498]], [[28, 33, 57], [322, 327, 354], [497, 498]], 
 [[28, 34, 57], [323, 327, 361], [82, 497]], [[28, 48, 54], [324, 326, 436], [83, 446]], 
 [[28, 52, 54], [325, 326, 457], [447, 499]], [[28, 52, 57], [325, 327, 459], [498, 499]], 
 [[28, 54, 57], [326, 327, 472], [84, 499]], [[29, 31, 35], [328, 331, 341], [16, 160]], 
 [[29, 31, 38], [328, 332, 343], [161, 489]], [[29, 32, 34], [329, 330, 346], [17, 500]], 
 [[29, 32, 41], [329, 333, 347], [365, 500]], [[29, 34, 35], [330, 331, 357], [18, 501]], 
 [[29, 34, 41], [330, 333, 358], [500, 502]], [[29, 34, 46], [330, 335, 359], [501, 502]], 
 [[29, 35, 46], [331, 335, 364], [162, 501]], [[29, 38, 44], [332, 334, 382], [163, 366]], 
 [[29, 41, 44], [333, 334, 400], [367, 503]], [[29, 41, 46], [333, 335, 401], [502, 503]], 
 [[29, 44, 46], [334, 335, 418], [164, 503]], [[30, 33, 52], [336, 337, 353], [45, 496]], 
 [[30, 52, 72], [337, 338, 461], [46, 448]], [[30, 72, 73], [338, 339, 548], [47, 504]], 
 [[30, 72, 78], [338, 340, 550], [449, 504]], [[30, 73, 78], [339, 340, 556], [487, 504]], 
 [[31, 35, 39], [341, 344, 362], [165, 492]], [[31, 37, 38], [342, 343, 375], [166, 505]], 
 [[31, 37, 39], [342, 344, 376], [167, 408]], [[31, 37, 79], [342, 345, 378], [409, 505]], 
 [[31, 38, 79], [343, 345, 384], [490, 505]], [[32, 34, 41], [346, 347, 358], [85, 500]], 
 [[32, 41, 50], [347, 349, 403], [86, 368]], [[32, 48, 50], [348, 349, 435], [87, 506]], 
 [[32, 48, 80], [348, 350, 438], [483, 506]], [[32, 50, 80], [349, 350, 448], [369, 506]], 
 [[33, 34, 35], [351, 352, 357], [19, 320]], [[33, 34, 57], [351, 354, 361], [321, 497]], 
 [[33, 35, 59], [352, 356, 365], [322, 493]], [[33, 52, 57], [353, 354, 459], [498, 507]], 
 [[33, 52, 58], [353, 355, 460], [48, 507]], [[33, 57, 58], [354, 355, 489], [323, 507]], 
 [[33, 58, 59], [355, 356, 491], [49, 324]], [[34, 35, 46], [357, 359, 364], [325, 501]], 
 [[34, 41, 46], [358, 359, 401], [502, 508]], [[34, 41, 47], [358, 360, 402], [88, 508]], 
 [[34, 46, 47], [359, 360, 427], [326, 508]], [[34, 47, 57], [360, 361, 430], [89, 327]], 
 [[35, 39, 45], [362, 363, 387], [168, 509]], [[35, 39, 59], [362, 365, 389], [494, 509]], 
 [[35, 45, 46], [363, 364, 422], [169, 328]], [[35, 45, 59], [363, 365, 423], [329, 509]], 
 [[36, 37, 38], [366, 367, 375], [170, 180]], [[36, 37, 42], [366, 369, 377], [171, 510]], 
 [[36, 37, 90], [366, 373, 381], [181, 510]], [[36, 38, 44], [367, 370, 382], [172, 511]], 
 [[36, 38, 92], [367, 374, 385], [182, 511]], [[36, 40, 42], [368, 369, 391], [173, 460]], 
 [[36, 40, 44], [368, 370, 392], [174, 512]], [[36, 40, 60], [368, 371, 395], [461, 512]], 
 [[36, 42, 90], [369, 373, 409], [462, 510]], [[36, 44, 60], [370, 371, 419], [512, 513]], 
 [[36, 44, 92], [370, 374, 421], [511, 513]], [[36, 60, 88], [371, 372, 499], [463, 514]], 
 [[36, 60, 92], [371, 374, 500], [513, 514]], [[36, 88, 90], [372, 373, 621], [183, 464]], 
 [[36, 88, 92], [372, 374, 622], [184, 514]], [[37, 38, 79], [375, 378, 384], [185, 505]], 
 [[37, 39, 42], [376, 377, 386], [175, 515]], [[37, 39, 85], [376, 379, 390], [410, 515]], 
 [[37, 42, 85], [377, 379, 408], [515, 516]], [[37, 42, 90], [377, 381, 409], [510, 516]], 
 [[37, 79, 87], [378, 380, 586], [186, 411]], [[37, 85, 87], [379, 380, 611], [412, 517]], 
 [[37, 85, 90], [379, 381, 612], [516, 517]], [[37, 87, 90], [380, 381, 617], [187, 517]], 
 [[38, 44, 92], [382, 385, 421], [370, 511]], [[38, 77, 79], [383, 384, 576], [188, 491]], 
 [[38, 77, 92], [383, 385, 581], [189, 371]], [[39, 42, 45], [386, 387, 405], [176, 200]], 
 [[39, 42, 85], [386, 390, 408], [201, 515]], [[39, 45, 59], [387, 389, 423], [202, 509]], 
 [[39, 55, 59], [388, 389, 476], [203, 495]], [[39, 55, 85], [388, 390, 479], [204, 413]], 
 [[40, 42, 45], [391, 393, 405], [177, 518]], [[40, 42, 64], [391, 396, 406], [465, 518]], 
 [[40, 44, 46], [392, 394, 418], [178, 240]], [[40, 44, 60], [392, 395, 419], [241, 512]], 
 [[40, 45, 46], [393, 394, 422], [179, 519]], [[40, 45, 64], [393, 396, 424], [518, 520]], 
 [[40, 45, 69], [393, 398, 425], [519, 520]], [[40, 46, 69], [394, 398, 428], [242, 519]], 
 [[40, 60, 66], [395, 397, 498], [243, 466]], [[40, 64, 66], [396, 397, 517], [467, 521]], 
 [[40, 64, 69], [396, 398, 519], [520, 521]], [[40, 66, 69], [397, 398, 529], [244, 521]], 
 [[41, 43, 47], [399, 402, 410], [90, 245]], [[41, 43, 50], [399, 403, 412], [91, 522]], 
 [[41, 43, 62], [399, 404, 415], [246, 522]], [[41, 44, 46], [400, 401, 418], [247, 503]], 
 [[41, 44, 62], [400, 404, 420], [248, 372]], [[41, 46, 47], [401, 402, 427], [249, 508]], 
 [[41, 50, 62], [403, 404, 447], [373, 522]], [[42, 45, 64], [405, 406, 424], [205, 518]], 
 [[42, 64, 84], [406, 407, 521], [206, 468]], [[42, 84, 85], [407, 408, 604], [207, 523]], 
 [[42, 84, 90], [407, 409, 606], [469, 523]], [[42, 85, 90], [408, 409, 612], [516, 523]], 
 [[43, 47, 51], [410, 413, 429], [92, 524]], [[43, 47, 63], [410, 416, 431], [250, 524]], 
 [[43, 49, 50], [411, 412, 440], [93, 525]], [[43, 49, 51], [411, 413, 441], [94, 420]], 
 [[43, 49, 91], [411, 417, 443], [421, 525]], [[43, 50, 62], [412, 415, 447], [522, 526]], 
 [[43, 50, 91], [412, 417, 450], [525, 526]], [[43, 51, 63], [413, 416, 453], [422, 524]], 
 [[43, 61, 62], [414, 415, 502], [251, 527]], [[43, 61, 63], [414, 416, 503], [252, 423]], 
 [[43, 61, 91], [414, 417, 505], [424, 527]], [[43, 62, 91], [415, 417, 510], [526, 527]], 
 [[44, 60, 62], [419, 420, 497], [253, 528]], [[44, 60, 92], [419, 421, 500], [513, 528]], 
 [[44, 62, 92], [420, 421, 511], [374, 528]], [[45, 46, 69], [422, 425, 428], [330, 519]], 
 [[45, 59, 70], [423, 426, 495], [208, 331]], [[45, 64, 69], [424, 425, 519], [520, 529]], 
 [[45, 64, 70], [424, 426, 520], [209, 529]], [[45, 69, 70], [425, 426, 545], [332, 529]], 
 [[46, 47, 69], [427, 428, 432], [254, 333]], [[47, 51, 57], [429, 430, 452], [95, 530]], 
 [[47, 51, 63], [429, 431, 453], [524, 531]], [[47, 51, 71], [429, 433, 455], [530, 531]], 
 [[47, 57, 71], [430, 433, 490], [334, 530]], [[47, 63, 69], [431, 432, 514], [255, 532]], 
 [[47, 63, 71], [431, 433, 515], [531, 532]], [[47, 69, 71], [432, 433, 546], [335, 532]], 
 [[48, 49, 50], [434, 435, 440], [96, 100]], [[48, 49, 54], [434, 436, 442], [97, 533]], 
 [[48, 49, 102], [434, 439, 446], [101, 533]], [[48, 50, 80], [435, 438, 448], [102, 506]], 
 [[48, 54, 102], [436, 439, 475], [450, 533]], [[48, 76, 80], [437, 438, 570], [103, 484]], 
 [[48, 76, 102], [437, 439, 574], [104, 451]], [[49, 50, 91], [440, 443, 450], [105, 525]], 
 [[49, 51, 54], [441, 442, 451], [98, 534]], [[49, 51, 97], [441, 444, 456], [425, 534]], 
 [[49, 54, 97], [442, 444, 474], [534, 535]], [[49, 54, 102], [442, 446, 475], [533, 535]], 
 [[49, 91, 99], [443, 445, 635], [106, 426]], [[49, 97, 99], [444, 445, 656], [427, 536]], 
 [[49, 97, 102], [444, 446, 657], [535, 536]], [[49, 99, 102], [445, 446, 663], [107, 536]], 
 [[50, 62, 89], [447, 449, 509], [375, 537]], [[50, 62, 91], [447, 450, 510], [526, 537]], 
 [[50, 80, 89], [448, 449, 588], [108, 376]], [[50, 89, 91], [449, 450, 628], [109, 537]], 
 [[51, 54, 57], [451, 452, 472], [99, 120]], [[51, 54, 97], [451, 456, 474], [121, 534]], 
 [[51, 57, 71], [452, 455, 490], [122, 530]], [[51, 63, 67], [453, 454, 513], [428, 538]], 
 [[51, 63, 71], [453, 455, 515], [531, 538]], [[51, 67, 71], [454, 455, 533], [123, 538]], 
 [[51, 67, 97], [454, 456, 534], [124, 429]], [[52, 54, 57], [457, 459, 472], [125, 499]], 
 [[52, 54, 96], [457, 462, 473], [126, 452]], [[52, 56, 58], [458, 460, 482], [50, 127]], 
 [[52, 56, 72], [458, 461, 484], [51, 539]], [[52, 56, 96], [458, 462, 486], [128, 539]], 
 [[52, 57, 58], [459, 460, 489], [129, 507]], [[52, 72, 96], [461, 462, 551], [453, 539]], 
 [[53, 55, 59], [463, 466, 476], [52, 210]], [[53, 55, 74], [463, 470, 478], [53, 540]], 
 [[53, 55, 86], [463, 471, 480], [211, 540]], [[53, 56, 58], [464, 465, 482], [54, 541]], 
 [[53, 56, 65], [464, 467, 483], [380, 541]], [[53, 56, 74], [464, 470, 485], [55, 381]], 
 [[53, 58, 59], [465, 466, 491], [56, 542]], [[53, 58, 65], [465, 467, 492], [541, 543]], 
 [[53, 58, 70], [465, 469, 493], [542, 543]], [[53, 59, 70], [466, 469, 495], [212, 542]], 
 [[53, 65, 68], [467, 468, 524], [382, 544]], [[53, 65, 70], [467, 469, 525], [543, 544]], 
 [[53, 68, 70], [468, 469, 539], [213, 544]], [[53, 68, 86], [468, 471, 541], [214, 383]], 
 [[53, 74, 86], [470, 471, 558], [384, 540]], [[54, 96, 97], [473, 474, 650], [130, 545]], 
 [[54, 96, 102], [473, 475, 653], [454, 545]], [[54, 97, 102], [474, 475, 657], [535, 545]], 
 [[55, 73, 74], [477, 478, 554], [57, 546]], [[55, 73, 103], [477, 481, 557], [414, 546]], 
 [[55, 74, 86], [478, 480, 558], [540, 547]], [[55, 74, 103], [478, 481, 560], [546, 547]], 
 [[55, 85, 86], [479, 480, 610], [215, 548]], [[55, 85, 103], [479, 481, 613], [415, 548]], 
 [[55, 86, 103], [480, 481, 615], [547, 548]], [[56, 58, 65], [482, 483, 492], [131, 541]], 
 [[56, 65, 98], [483, 487, 527], [132, 385]], [[56, 72, 74], [484, 485, 549], [58, 549]], 
 [[56, 72, 96], [484, 486, 551], [539, 550]], [[56, 72, 104], [484, 488, 553], [549, 550]], 
 [[56, 74, 104], [485, 488, 561], [386, 549]], [[56, 96, 98], [486, 487, 651], [133, 551]], 
 [[56, 96, 104], [486, 488, 654], [550, 551]], [[56, 98, 104], [487, 488, 659], [387, 551]], 
 [[57, 58, 71], [489, 490, 494], [134, 336]], [[58, 59, 70], [491, 493, 495], [337, 542]], 
 [[58, 65, 70], [492, 493, 525], [543, 552]], [[58, 65, 71], [492, 494, 526], [135, 552]], 
 [[58, 70, 71], [493, 494, 547], [338, 552]], [[60, 61, 62], [496, 497, 502], [256, 260]], 
 [[60, 61, 66], [496, 498, 504], [257, 553]], [[60, 61, 114], [496, 501, 508], [261, 553]], 
 [[60, 62, 92], [497, 500, 511], [262, 528]], [[60, 66, 114], [498, 501, 532], [470, 553]], 
 [[60, 88, 92], [499, 500, 622], [263, 514]], [[60, 88, 114], [499, 501, 626], [264, 471]], 
 [[61, 62, 91], [502, 505, 510], [265, 527]], [[61, 63, 66], [503, 504, 512], [258, 554]], 
 [[61, 63, 109], [503, 506, 516], [430, 554]], [[61, 66, 109], [504, 506, 531], [554, 555]], 
 [[61, 66, 114], [504, 508, 532], [553, 555]], [[61, 91, 111], [505, 507, 636], [266, 431]], 
 [[61, 109, 111], [506, 507, 696], [432, 556]], [[61, 109, 114], [506, 508, 697], [555, 556]], 
 [[61, 111, 114], [507, 508, 702], [267, 556]], [[62, 89, 91], [509, 510, 628], [268, 537]], 
 [[62, 89, 92], [509, 511, 629], [269, 377]], [[63, 66, 69], [512, 514, 529], [259, 280]], 
 [[63, 66, 109], [512, 516, 531], [281, 554]], [[63, 67, 71], [513, 515, 533], [282, 538]], 
 [[63, 67, 109], [513, 516, 536], [283, 433]], [[63, 69, 71], [514, 515, 546], [284, 532]], 
 [[64, 66, 69], [517, 519, 529], [285, 521]], [[64, 66, 108], [517, 522, 530], [286, 472]], 
 [[64, 68, 70], [518, 520, 539], [216, 287]], [[64, 68, 84], [518, 521, 540], [217, 557]], 
 [[64, 68, 108], [518, 522, 542], [288, 557]], [[64, 69, 70], [519, 520, 545], [289, 529]], 
 [[64, 84, 108], [521, 522, 607], [473, 557]], [[65, 67, 71], [523, 526, 533], [136, 290]], 
 [[65, 67, 98], [523, 527, 535], [137, 558]], [[65, 67, 110], [523, 528, 537], [291, 558]], 
 [[65, 68, 70], [524, 525, 539], [292, 544]], [[65, 68, 110], [524, 528, 543], [293, 388]], 
 [[65, 70, 71], [525, 526, 547], [294, 552]], [[65, 98, 110], [527, 528, 660], [389, 558]], 
 [[66, 108, 109], [530, 531, 690], [295, 559]], [[66, 108, 114], [530, 532, 693], [474, 559]], 
 [[66, 109, 114], [531, 532, 697], [555, 559]], [[67, 97, 98], [534, 535, 655], [138, 560]], 
 [[67, 97, 115], [534, 538, 658], [434, 560]], [[67, 98, 110], [535, 537, 660], [558, 561]], 
 [[67, 98, 115], [535, 538, 662], [560, 561]], [[67, 109, 110], [536, 537, 695], [296, 562]], 
 [[67, 109, 115], [536, 538, 698], [435, 562]], [[67, 110, 115], [537, 538, 700], [561, 562]], 
 [[68, 84, 86], [540, 541, 605], [218, 563]], [[68, 84, 108], [540, 542, 607], [557, 564]], 
 [[68, 84, 116], [540, 544, 609], [563, 564]], [[68, 86, 116], [541, 544, 616], [390, 563]], 
 [[68, 108, 110], [542, 543, 691], [297, 565]], [[68, 108, 116], [542, 544, 694], [564, 565]], 
 [[68, 110, 116], [543, 544, 701], [391, 565]], [[69, 70, 71], [545, 546, 547], [298, 339]], 
 [[72, 73, 74], [548, 549, 554], [59, 60]], [[72, 73, 78], [548, 550, 556], [61, 504]], 
 [[72, 74, 104], [549, 553, 561], [62, 549]], [[72, 78, 100], [550, 552, 584], [63, 455]], 
 [[72, 96, 100], [551, 552, 652], [456, 566]], [[72, 96, 104], [551, 553, 654], [550, 566]], 
 [[72, 100, 104], [552, 553, 669], [64, 566]], [[73, 74, 103], [554, 557, 560], [65, 546]], 
 [[73, 75, 78], [555, 556, 562], [66, 488]], [[73, 75, 103], [555, 557, 567], [67, 416]], 
 [[74, 86, 101], [558, 559, 614], [392, 567]], [[74, 86, 103], [558, 560, 615], [547, 567]], 
 [[74, 101, 103], [559, 560, 672], [68, 567]], [[74, 101, 104], [559, 561, 673], [69, 393]], 
 [[75, 78, 81], [562, 564, 583], [30, 70]], [[75, 79, 83], [563, 565, 585], [31, 568]], 
 [[75, 79, 87], [563, 566, 586], [417, 568]], [[75, 81, 83], [564, 565, 590], [32, 569]], 
 [[75, 81, 107], [564, 568, 594], [71, 569]], [[75, 83, 87], [565, 566, 600], [568, 570]], 
 [[75, 83, 107], [565, 568, 603], [569, 570]], [[75, 87, 103], [566, 567, 619], [418, 571]], 
 [[75, 87, 107], [566, 568, 620], [570, 571]], [[75, 103, 107], [567, 568, 680], [72, 571]], 
 [[76, 78, 81], [569, 571, 583], [33, 572]], [[76, 78, 100], [569, 573, 584], [457, 572]], 
 [[76, 80, 82], [570, 572, 587], [34, 110]], [[76, 81, 82], [571, 572, 589], [35, 573]], 
 [[76, 81, 100], [571, 573, 591], [572, 574]], [[76, 81, 105], [571, 575, 592], [573, 574]], 
 [[76, 82, 105], [572, 575, 599], [111, 573]], [[76, 100, 102], [573, 574, 668], [458, 575]], 
 [[76, 100, 105], [573, 575, 670], [574, 575]], [[76, 102, 105], [574, 575, 679], [112, 575]], 
 [[77, 79, 83], [576, 579, 585], [36, 190]], [[77, 80, 82], [577, 578, 587], [37, 576]], 
 [[77, 80, 89], [577, 580, 588], [378, 576]], [[77, 82, 83], [578, 579, 595], [38, 577]], 
 [[77, 82, 89], [578, 580, 596], [576, 578]], [[77, 82, 94], [578, 582, 597], [577, 578]], 
 [[77, 83, 94], [579, 582, 602], [191, 577]], [[77, 89, 92], [580, 581, 629], [379, 579]], 
 [[77, 89, 94], [580, 582, 630], [578, 579]], [[77, 92, 94], [581, 582, 637], [192, 579]], 
 [[78, 81, 100], [583, 584, 591], [73, 572]], [[79, 83, 87], [585, 586, 600], [193, 568]], 
 [[80, 82, 89], [587, 588, 596], [113, 576]], [[81, 82, 83], [589, 590, 595], [39, 340]], 
 [[81, 82, 105], [589, 592, 599], [341, 573]], [[81, 83, 107], [590, 594, 603], [342, 569]], 
 [[81, 100, 105], [591, 592, 670], [574, 580]], [[81, 100, 106], [591, 593, 671], [74, 580]], 
 [[81, 105, 106], [592, 593, 683], [343, 580]], [[81, 106, 107], [593, 594, 685], [75, 344]], 
 [[82, 83, 94], [595, 597, 602], [345, 577]], [[82, 89, 94], [596, 597, 630], [578, 581]], 
 [[82, 89, 95], [596, 598, 631], [114, 581]], [[82, 94, 95], [597, 598, 643], [346, 581]], 
 [[82, 95, 105], [598, 599, 646], [115, 347]], [[83, 87, 93], [600, 601, 618], [194, 582]], 
 [[83, 87, 107], [600, 603, 620], [570, 582]], [[83, 93, 94], [601, 602, 638], [195, 348]], 
 [[83, 93, 107], [601, 603, 639], [349, 582]], [[84, 85, 86], [604, 605, 610], [219, 220]], 
 [[84, 85, 90], [604, 606, 612], [221, 523]], [[84, 86, 116], [605, 609, 616], [222, 563]], 
 [[84, 90, 112], [606, 608, 633], [223, 475]], [[84, 108, 112], [607, 608, 692], [476, 583]], 
 [[84, 108, 116], [607, 609, 694], [564, 583]], [[84, 112, 116], [608, 609, 707], [224, 583]], 
 [[85, 86, 103], [610, 613, 615], [225, 548]], [[85, 87, 90], [611, 612, 617], [226, 517]], 
 [[85, 87, 103], [611, 613, 619], [227, 419]], [[86, 101, 103], [614, 615, 672], [228, 567]], 
 [[86, 101, 116], [614, 616, 677], [229, 394]], [[87, 90, 93], [617, 618, 632], [196, 230]], 
 [[87, 93, 107], [618, 620, 639], [231, 582]], [[87, 103, 107], [619, 620, 680], [232, 571]], 
 [[88, 90, 93], [621, 623, 632], [197, 584]], [[88, 90, 112], [621, 625, 633], [477, 584]], 
 [[88, 92, 94], [622, 624, 637], [198, 270]], [[88, 93, 94], [623, 624, 638], [199, 585]], 
 [[88, 93, 112], [623, 625, 640], [584, 586]], [[88, 93, 117], [623, 627, 641], [585, 586]], 
 [[88, 94, 117], [624, 627, 644], [271, 585]], [[88, 112, 114], [625, 626, 706], [478, 587]], 
 [[88, 112, 117], [625, 627, 708], [586, 587]], [[88, 114, 117], [626, 627, 714], [272, 587]], 
 [[89, 91, 95], [628, 631, 634], [116, 273]], [[89, 92, 94], [629, 630, 637], [274, 579]], 
 [[89, 94, 95], [630, 631, 643], [275, 581]], [[90, 93, 112], [632, 633, 640], [233, 584]], 
 [[91, 95, 99], [634, 635, 645], [117, 588]], [[91, 95, 111], [634, 636, 647], [276, 588]], 
 [[91, 99, 111], [635, 636, 665], [436, 588]], [[93, 94, 117], [638, 641, 644], [350, 585]], 
 [[93, 107, 118], [639, 642, 689], [234, 351]], [[93, 112, 117], [640, 641, 708], [586, 589]], 
 [[93, 112, 118], [640, 642, 709], [235, 589]], [[93, 117, 118], [641, 642, 717], [352, 589]], 
 [[94, 95, 117], [643, 644, 648], [277, 353]], [[95, 99, 105], [645, 646, 664], [118, 590]], 
 [[95, 99, 111], [645, 647, 665], [588, 591]], [[95, 99, 119], [645, 649, 667], [590, 591]], 
 [[95, 105, 119], [646, 649, 684], [354, 590]], [[95, 111, 117], [647, 648, 704], [278, 592]], 
 [[95, 111, 119], [647, 649, 705], [591, 592]], [[95, 117, 119], [648, 649, 718], [355, 592]], 
 [[96, 97, 98], [650, 651, 655], [139, 140]], [[96, 97, 102], [650, 653, 657], [141, 545]], 
 [[96, 98, 104], [651, 654, 659], [142, 551]], [[96, 100, 102], [652, 653, 668], [143, 459]], 
 [[96, 100, 104], [652, 654, 669], [144, 566]], [[97, 98, 115], [655, 658, 662], [145, 560]], 
 [[97, 99, 102], [656, 657, 663], [146, 536]], [[97, 99, 115], [656, 658, 666], [147, 437]], 
 [[98, 104, 113], [659, 661, 682], [148, 395]], [[98, 110, 113], [660, 661, 699], [396, 593]], 
 [[98, 110, 115], [660, 662, 700], [561, 593]], [[98, 113, 115], [661, 662, 710], [149, 593]], 
 [[99, 102, 105], [663, 664, 679], [119, 150]], [[99, 105, 119], [664, 667, 684], [151, 590]], 
 [[99, 111, 115], [665, 666, 703], [438, 594]], [[99, 111, 119], [665, 667, 705], [591, 594]], 
 [[99, 115, 119], [666, 667, 715], [152, 594]], [[100, 102, 105], [668, 670, 679], [153, 575]], 
 [[100, 104, 106], [669, 671, 681], [76, 154]], [[100, 105, 106], [670, 671, 683], [155, 580]], 
 [[101, 103, 107], [672, 675, 680], [77, 236]], [[101, 104, 106], [673, 674, 681], [78, 595]], 
 [[101, 104, 113], [673, 676, 682], [397, 595]], [[101, 106, 107], [674, 675, 685], [79, 596]], 
 [[101, 106, 113], [674, 676, 686], [595, 597]], [[101, 106, 118], [674, 678, 687], [596, 597]], 
 [[101, 107, 118], [675, 678, 689], [237, 596]], [[101, 113, 116], [676, 677, 711], [398, 598]], 
 [[101, 113, 118], [676, 678, 712], [597, 598]], [[101, 116, 118], [677, 678, 716], [238, 598]], 
 [[104, 106, 113], [681, 682, 686], [156, 595]], [[105, 106, 119], [683, 684, 688], [157, 356]], 
 [[106, 107, 118], [685, 687, 689], [357, 596]], [[106, 113, 118], [686, 687, 712], [597, 599]], 
 [[106, 113, 119], [686, 688, 713], [158, 599]], [[106, 118, 119], [687, 688, 719], [358, 599]], 
 [[108, 109, 110], [690, 691, 695], [299, 300]], [[108, 109, 114], [690, 693, 697], [301, 559]], 
 [[108, 110, 116], [691, 694, 701], [302, 565]], [[108, 112, 114], [692, 693, 706], [303, 479]], 
 [[108, 112, 116], [692, 694, 707], [304, 583]], [[109, 110, 115], [695, 698, 700], [305, 562]], 
 [[109, 111, 114], [696, 697, 702], [306, 556]], [[109, 111, 115], [696, 698, 703], [307, 439]], 
 [[110, 113, 115], [699, 700, 710], [308, 593]], [[110, 113, 116], [699, 701, 711], [309, 399]], 
 [[111, 114, 117], [702, 704, 714], [279, 310]], [[111, 115, 119], [703, 705, 715], [311, 594]], 
 [[111, 117, 119], [704, 705, 718], [312, 592]], [[112, 114, 117], [706, 708, 714], [313, 587]], 
 [[112, 116, 118], [707, 709, 716], [239, 314]], [[112, 117, 118], [708, 709, 717], [315, 589]], 
 [[113, 115, 119], [710, 713, 715], [159, 316]], [[113, 116, 118], [711, 712, 716], [317, 598]], 
 [[113, 118, 119], [712, 713, 719], [318, 599]], [[117, 118, 119], [717, 718, 719], [319, 359]]
 ]

len(cube.c)= 600 
cube.c= [
[[0, 24, 25, 26], [0, 1, 2, 288, 289, 297], [0, 1, 5, 720]], 
[[0, 24, 25, 30], [0, 1, 6, 288, 291, 299], [0, 3, 7, 721]], 
[[0, 24, 26, 32], [0, 2, 8, 289, 292, 307], [1, 4, 11, 723]], 
[[0, 24, 28, 30], [0, 4, 6, 290, 291, 320], [2, 3, 16, 725]], 
[[0, 24, 28, 32], [0, 4, 8, 290, 292, 321], [2, 4, 17, 726]], 
[[0, 25, 26, 31], [1, 2, 7, 297, 300, 306], [5, 8, 10, 735]], 
[[0, 25, 27, 30], [1, 3, 6, 298, 299, 312], [6, 7, 12, 737]], 
[[0, 25, 27, 31], [1, 3, 7, 298, 300, 313], [6, 8, 13, 738]], 
[[0, 26, 29, 31], [2, 5, 7, 305, 306, 328], [9, 10, 20, 747]], 
[[0, 26, 29, 32], [2, 5, 8, 305, 307, 329], [9, 11, 21, 748]], 
[[0, 27, 30, 33], [3, 6, 9, 312, 314, 336], [12, 14, 24, 757]], 
[[0, 27, 31, 35], [3, 7, 11, 313, 315, 341], [13, 15, 25, 759]], 
[[0, 27, 33, 35], [3, 9, 11, 314, 315, 352], [14, 15, 28, 761]], 
[[0, 28, 30, 33], [4, 6, 9, 320, 322, 336], [16, 18, 24, 769]], 
[[0, 28, 32, 34], [4, 8, 10, 321, 323, 346], [17, 19, 26, 771]], 
[[0, 28, 33, 34], [4, 9, 10, 322, 323, 351], [18, 19, 27, 773]], 
[[0, 29, 31, 35], [5, 7, 11, 328, 331, 341], [20, 23, 25, 781]], 
[[0, 29, 32, 34], [5, 8, 10, 329, 330, 346], [21, 22, 26, 783]], 
[[0, 29, 34, 35], [5, 10, 11, 330, 331, 357], [22, 23, 29, 785]], 
[[0, 33, 34, 35], [9, 10, 11, 351, 352, 357], [27, 28, 29, 808]], 
[[1, 24, 25, 26], [12, 13, 14, 288, 289, 297], [30, 31, 35, 720]], 
[[1, 24, 25, 78], [12, 13, 18, 288, 295, 303], [30, 33, 37, 722]], 
[[1, 24, 26, 80], [12, 14, 20, 289, 296, 311], [31, 34, 41, 724]], 
[[1, 24, 76, 78], [12, 16, 18, 294, 295, 569], [32, 33, 46, 733]], 
[[1, 24, 76, 80], [12, 16, 20, 294, 296, 570], [32, 34, 47, 734]], 
[[1, 25, 26, 79], [13, 14, 19, 297, 304, 310], [35, 38, 40, 736]], 
[[1, 25, 75, 78], [13, 15, 18, 302, 303, 562], [36, 37, 42, 745]], 
[[1, 25, 75, 79], [13, 15, 19, 302, 304, 563], [36, 38, 43, 746]], 
[[1, 26, 77, 79], [14, 17, 19, 309, 310, 576], [39, 40, 50, 755]], 
[[1, 26, 77, 80], [14, 17, 20, 309, 311, 577], [39, 41, 51, 756]], 
[[1, 75, 78, 81], [15, 18, 21, 562, 564, 583], [42, 44, 54, 1050]], 
[[1, 75, 79, 83], [15, 19, 23, 563, 565, 585], [43, 45, 55, 1051]], 
[[1, 75, 81, 83], [15, 21, 23, 564, 565, 590], [44, 45, 58, 1053]], 
[[1, 76, 78, 81], [16, 18, 21, 569, 571, 583], [46, 48, 54, 1060]], 
[[1, 76, 80, 82], [16, 20, 22, 570, 572, 587], [47, 49, 56, 1062]], 
[[1, 76, 81, 82], [16, 21, 22, 571, 572, 589], [48, 49, 57, 1063]], 
[[1, 77, 79, 83], [17, 19, 23, 576, 579, 585], [50, 53, 55, 1070]], 
[[1, 77, 80, 82], [17, 20, 22, 577, 578, 587], [51, 52, 56, 1071]], 
[[1, 77, 82, 83], [17, 22, 23, 578, 579, 595], [52, 53, 59, 1073]], 
[[1, 81, 82, 83], [21, 22, 23, 589, 590, 595], [57, 58, 59, 1083]], 
[[2, 27, 30, 33], [24, 25, 26, 312, 314, 336], [60, 61, 65, 757]], 
[[2, 27, 30, 73], [24, 25, 34, 312, 319, 339], [60, 64, 68, 758]], 
[[2, 27, 33, 59], [24, 26, 32, 314, 318, 356], [61, 63, 71, 762]], 
[[2, 27, 55, 59], [24, 29, 32, 317, 318, 476], [62, 63, 80, 767]], 
[[2, 27, 55, 73], [24, 29, 34, 317, 319, 477], [62, 64, 81, 768]], 
[[2, 30, 33, 52], [25, 26, 27, 336, 337, 353], [65, 66, 69, 793]], 
[[2, 30, 52, 72], [25, 27, 33, 337, 338, 461], [66, 67, 74, 794]], 
[[2, 30, 72, 73], [25, 33, 34, 338, 339, 548], [67, 68, 87, 795]], 
[[2, 33, 52, 58], [26, 27, 31, 353, 355, 460], [69, 70, 73, 812]], 
[[2, 33, 58, 59], [26, 31, 32, 355, 356, 491], [70, 71, 86, 814]], 
[[2, 52, 56, 58], [27, 30, 31, 458, 460, 482], [72, 73, 83, 937]], 
[[2, 52, 56, 72], [27, 30, 33, 458, 461, 484], [72, 74, 84, 938]], 
[[2, 53, 55, 59], [28, 29, 32, 463, 466, 476], [75, 78, 80, 942]], 
[[2, 53, 55, 74], [28, 29, 35, 463, 470, 478], [75, 79, 82, 943]], 
[[2, 53, 56, 58], [28, 30, 31, 464, 465, 482], [76, 77, 83, 945]], 
[[2, 53, 56, 74], [28, 30, 35, 464, 470, 485], [76, 79, 85, 947]], 
[[2, 53, 58, 59], [28, 31, 32, 465, 466, 491], [77, 78, 86, 948]], 
[[2, 55, 73, 74], [29, 34, 35, 477, 478, 554], [81, 82, 89, 960]], 
[[2, 56, 72, 74], [30, 33, 35, 484, 485, 549], [84, 85, 88, 969]], 
[[2, 72, 73, 74], [33, 34, 35, 548, 549, 554], [87, 88, 89, 1036]], 
[[3, 72, 73, 74], [36, 37, 38, 548, 549, 554], [90, 91, 95, 1036]], 
[[3, 72, 73, 78], [36, 37, 40, 548, 550, 556], [90, 92, 97, 1037]], 
[[3, 72, 74, 104], [36, 38, 45, 549, 553, 561], [91, 94, 101, 1038]], 
[[3, 72, 78, 100], [36, 40, 42, 550, 552, 584], [92, 93, 107, 1039]],
 [[3, 72, 100, 104], [36, 42, 45, 552, 553, 669], [93, 94, 111, 1042]], 
 [[3, 73, 74, 103], [37, 38, 44, 554, 557, 560], [95, 98, 100, 1043]], 
 [[3, 73, 75, 78], [37, 39, 40, 555, 556, 562], [96, 97, 102, 1044]], 
 [[3, 73, 75, 103], [37, 39, 44, 555, 557, 567], [96, 98, 104, 1045]], 
 [[3, 74, 101, 103], [38, 43, 44, 559, 560, 672], [99, 100, 113, 1048]], 
 [[3, 74, 101, 104], [38, 43, 45, 559, 561, 673], [99, 101, 114, 1049]], 
 [[3, 75, 78, 81], [39, 40, 41, 562, 564, 583], [102, 103, 106, 1050]], 
 [[3, 75, 81, 107], [39, 41, 47, 564, 568, 594], [103, 105, 110, 1054]], 
 [[3, 75, 103, 107], [39, 44, 47, 567, 568, 680], [104, 105, 117, 1059]], 
 [[3, 78, 81, 100], [40, 41, 42, 583, 584, 591], [106, 107, 108, 1080]], 
 [[3, 81, 100, 106], [41, 42, 46, 591, 593, 671], [108, 109, 112, 1087]], 
 [[3, 81, 106, 107], [41, 46, 47, 593, 594, 685], [109, 110, 119, 1089]], 
 [[3, 100, 104, 106], [42, 45, 46, 669, 671, 681], [111, 112, 118, 1162]], 
 [[3, 101, 103, 107], [43, 44, 47, 672, 675, 680], [113, 116, 117, 1164]], 
 [[3, 101, 104, 106], [43, 45, 46, 673, 674, 681], [114, 115, 118, 1165]], 
 [[3, 101, 106, 107], [43, 46, 47, 674, 675, 685], [115, 116, 119, 1167]], 
 [[4, 28, 32, 34], [48, 49, 50, 321, 323, 346], [120, 121, 125, 771]], 
 [[4, 28, 32, 48], [48, 49, 54, 321, 324, 348], [120, 122, 127, 772]], 
 [[4, 28, 34, 57], [48, 50, 59, 323, 327, 361], [121, 124, 131, 776]], 
 [[4, 28, 48, 54], [48, 54, 58, 324, 326, 436], [122, 123, 143, 777]], 
 [[4, 28, 54, 57], [48, 58, 59, 326, 327, 472], [123, 124, 149, 780]], 
 [[4, 32, 34, 41], [49, 50, 51, 346, 347, 358], [125, 126, 129, 803]], 
 [[4, 32, 41, 50], [49, 51, 56, 347, 349, 403], [126, 128, 134, 804]], 
 [[4, 32, 48, 50], [49, 54, 56, 348, 349, 435], [127, 128, 142, 805]], 
 [[4, 34, 41, 47], [50, 51, 53, 358, 360, 402], [129, 130, 133, 817]], 
 [[4, 34, 47, 57], [50, 53, 59, 360, 361, 430], [130, 131, 140, 819]], 
 [[4, 41, 43, 47], [51, 52, 53, 399, 402, 410], [132, 133, 135, 868]], 
 [[4, 41, 43, 50], [51, 52, 56, 399, 403, 412], [132, 134, 137, 869]], 
 [[4, 43, 47, 51], [52, 53, 57, 410, 413, 429], [135, 138, 139, 880]], 
 [[4, 43, 49, 50], [52, 55, 56, 411, 412, 440], [136, 137, 144, 882]], 
 [[4, 43, 49, 51], [52, 55, 57, 411, 413, 441], [136, 138, 145, 883]], 
 [[4, 47, 51, 57], [53, 57, 59, 429, 430, 452], [139, 140, 148, 901]], 
 [[4, 48, 49, 50], [54, 55, 56, 434, 435, 440], [141, 142, 144, 908]], 
 [[4, 48, 49, 54], [54, 55, 58, 434, 436, 442], [141, 143, 146, 909]], 
 [[4, 49, 51, 54], [55, 57, 58, 441, 442, 451], [145, 146, 147, 916]], 
 [[4, 51, 54, 57], [57, 58, 59, 451, 452, 472], [147, 148, 149, 928]], 
 [[5, 48, 49, 50], [60, 61, 62, 434, 435, 440], [150, 151, 155, 908]], 
 [[5, 48, 49, 102], [60, 61, 70, 434, 439, 446], [150, 154, 158, 910]], 
 [[5, 48, 50, 80], [60, 62, 64, 435, 438, 448], [151, 153, 159, 911]], 
 [[5, 48, 76, 80], [60, 63, 64, 437, 438, 570], [152, 153, 162, 913]], 
 [[5, 48, 76, 102], [60, 63, 70, 437, 439, 574], [152, 154, 164, 914]], 
 [[5, 49, 50, 91], [61, 62, 67, 440, 443, 450], [155, 156, 161, 915]], 
 [[5, 49, 91, 99], [61, 67, 69, 443, 445, 635], [156, 157, 174, 920]], 
 [[5, 49, 99, 102], [61, 69, 70, 445, 446, 663], [157, 158, 177, 923]], 
 [[5, 50, 80, 89], [62, 64, 66, 448, 449, 588], [159, 160, 167, 926]], 
 [[5, 50, 89, 91], [62, 66, 67, 449, 450, 628], [160, 161, 171, 927]], 
 [[5, 76, 80, 82], [63, 64, 65, 570, 572, 587], [162, 163, 166, 1062]], 
 [[5, 76, 82, 105], [63, 65, 71, 572, 575, 599], [163, 165, 170, 1066]], 
 [[5, 76, 102, 105], [63, 70, 71, 574, 575, 679], [164, 165, 179, 1069]], 
 [[5, 80, 82, 89], [64, 65, 66, 587, 588, 596], [166, 167, 168, 1082]], 
 [[5, 82, 89, 95], [65, 66, 68, 596, 598, 631], [168, 169, 172, 1092]], 
 [[5, 82, 95, 105], [65, 68, 71, 598, 599, 646], [169, 170, 176, 1094]], 
 [[5, 89, 91, 95], [66, 67, 68, 628, 631, 634], [171, 172, 173, 1124]], 
 [[5, 91, 95, 99], [67, 68, 69, 634, 635, 645], [173, 174, 175, 1128]], 
 [[5, 95, 99, 105], [68, 69, 71, 645, 646, 664], [175, 176, 178, 1137]], 
 [[5, 99, 102, 105], [69, 70, 71, 663, 664, 679], [177, 178, 179, 1156]], 
 [[6, 51, 54, 57], [72, 74, 76, 451, 452, 472], [180, 181, 190, 928]], 
 [[6, 51, 54, 97], [72, 74, 82, 451, 456, 474], [180, 184, 192, 929]], 
 [[6, 51, 57, 71], [72, 76, 80, 452, 455, 490], [181, 183, 198, 930]], 
 [[6, 51, 67, 71], [72, 79, 80, 454, 455, 533], [182, 183, 204, 933]], 
 [[6, 51, 67, 97], [72, 79, 82, 454, 456, 534], [182, 184, 205, 934]], 
 [[6, 52, 54, 57], [73, 74, 76, 457, 459, 472], [185, 187, 190, 935]], 
 [[6, 52, 54, 96], [73, 74, 81, 457, 462, 473], [185, 189, 191, 936]], 
 [[6, 52, 56, 58], [73, 75, 77, 458, 460, 482], [186, 188, 193, 937]], 
 [[6, 52, 56, 96], [73, 75, 81, 458, 462, 486], [186, 189, 195, 939]], 
 [[6, 52, 57, 58], [73, 76, 77, 459, 460, 489], [187, 188, 197, 940]], 
 [[6, 54, 96, 97], [74, 81, 82, 473, 474, 650], [191, 192, 207, 957]], 
 [[6, 56, 58, 65], [75, 77, 78, 482, 483, 492], [193, 194, 199, 967]], 
 [[6, 56, 65, 98], [75, 78, 83, 483, 487, 527], [194, 196, 203, 968]], 
 [[6, 56, 96, 98], [75, 81, 83, 486, 487, 651], [195, 196, 208, 973]], 
 [[6, 57, 58, 71], [76, 77, 80, 489, 490, 494], [197, 198, 200, 976]], 
 [[6, 58, 65, 71], [77, 78, 80, 492, 494, 526], [199, 200, 202, 979]], 
 [[6, 65, 67, 71], [78, 79, 80, 523, 526, 533], [201, 202, 204, 1011]], 
 [[6, 65, 67, 98], [78, 79, 83, 523, 527, 535], [201, 203, 206, 1012]], 
 [[6, 67, 97, 98], [79, 82, 83, 534, 535, 655], [205, 206, 209, 1021]], 
 [[6, 96, 97, 98], [81, 82, 83, 650, 651, 655], [207, 208, 209, 1144]], 
 [[7, 96, 97, 98], [84, 85, 86, 650, 651, 655], [210, 211, 215, 1144]], 
 [[7, 96, 97, 102], [84, 85, 89, 650, 653, 657], [210, 213, 217, 1145]], 
 [[7, 96, 98, 104], [84, 86, 90, 651, 654, 659], [211, 214, 219, 1146]], 
 [[7, 96, 100, 102], [84, 88, 89, 652, 653, 668], [212, 213, 226, 1147]], 
 [[7, 96, 100, 104], [84, 88, 90, 652, 654, 669], [212, 214, 227, 1148]], 
 [[7, 97, 98, 115], [85, 86, 94, 655, 658, 662], [215, 218, 221, 1149]], 
 [[7, 97, 99, 102], [85, 87, 89, 656, 657, 663], [216, 217, 222, 1150]], 
 [[7, 97, 99, 115], [85, 87, 94, 656, 658, 666], [216, 218, 224, 1151]], 
 [[7, 98, 104, 113], [86, 90, 93, 659, 661, 682], [219, 220, 232, 1152]], 
 [[7, 98, 113, 115], [86, 93, 94, 661, 662, 710], [220, 221, 237, 1155]], 
 [[7, 99, 102, 105], [87, 89, 91, 663, 664, 679], [222, 223, 230, 1156]], 
 [[7, 99, 105, 119], [87, 91, 95, 664, 667, 684], [223, 225, 234, 1157]], 
 [[7, 99, 115, 119], [87, 94, 95, 666, 667, 715], [224, 225, 239, 1160]], 
 [[7, 100, 102, 105], [88, 89, 91, 668, 670, 679], [226, 228, 230, 1161]], 
 [[7, 100, 104, 106], [88, 90, 92, 669, 671, 681], [227, 229, 231, 1162]], 
 [[7, 100, 105, 106], [88, 91, 92, 670, 671, 683], [228, 229, 233, 1163]], 
 [[7, 104, 106, 113], [90, 92, 93, 681, 682, 686], [231, 232, 235, 1174]], 
 [[7, 105, 106, 119], [91, 92, 95, 683, 684, 688], [233, 234, 236, 1175]], 
 [[7, 106, 113, 119], [92, 93, 95, 686, 688, 713], [235, 236, 238, 1178]], 
 [[7, 113, 115, 119], [93, 94, 95, 710, 713, 715], [237, 238, 239, 1196]], 
 [[8, 29, 31, 35], [96, 97, 98, 328, 331, 341], [240, 241, 245, 781]], 
 [[8, 29, 31, 38], [96, 97, 101, 328, 332, 343], [240, 242, 247, 782]], 
 [[8, 29, 35, 46], [96, 98, 107, 331, 335, 364], [241, 244, 251, 788]], 
 [[8, 29, 38, 44], [96, 101, 105, 332, 334, 382], [242, 243, 260, 789]], 
 [[8, 29, 44, 46], [96, 105, 107, 334, 335, 418], [243, 244, 268, 792]], 
 [[8, 31, 35, 39], [97, 98, 102, 341, 344, 362], [245, 248, 249, 798]], 
 [[8, 31, 37, 38], [97, 100, 101, 342, 343, 375], [246, 247, 257, 799]], 
 [[8, 31, 37, 39], [97, 100, 102, 342, 344, 376], [246, 248, 258, 800]], 
 [[8, 35, 39, 45], [98, 102, 106, 362, 363, 387], [249, 250, 262, 820]], 
 [[8, 35, 45, 46], [98, 106, 107, 363, 364, 422], [250, 251, 269, 822]], 
 [[8, 36, 37, 38], [99, 100, 101, 366, 367, 375], [252, 253, 257, 824]], 
 [[8, 36, 37, 42], [99, 100, 104, 366, 369, 377], [252, 255, 259, 825]], 
 [[8, 36, 38, 44], [99, 101, 105, 367, 370, 382], [253, 256, 260, 827]], 
 [[8, 36, 40, 42], [99, 103, 104, 368, 369, 391], [254, 255, 263, 829]], 
 [[8, 36, 40, 44], [99, 103, 105, 368, 370, 392], [254, 256, 264, 830]], 
 [[8, 37, 39, 42], [100, 102, 104, 376, 377, 386], [258, 259, 261, 840]], 
 [[8, 39, 42, 45], [102, 104, 106, 386, 387, 405], [261, 262, 267, 851]], 
 [[8, 40, 42, 45], [103, 104, 106, 391, 393, 405], [263, 265, 267, 856]], 
 [[8, 40, 44, 46], [103, 105, 107, 392, 394, 418], [264, 266, 268, 858]], 
 [[8, 40, 45, 46], [103, 106, 107, 393, 394, 422], [265, 266, 269, 860]], 
 [[9, 36, 37, 38], [108, 109, 110, 366, 367, 375], [270, 271, 275, 824]], 
 [[9, 36, 37, 90], [108, 109, 116, 366, 373, 381], [270, 273, 278, 826]], 
 [[9, 36, 38, 92], [108, 110, 117, 367, 374, 385], [271, 274, 281, 828]], 
 [[9, 36, 88, 90], [108, 115, 116, 372, 373, 621], [272, 273, 293, 837]], 
 [[9, 36, 88, 92], [108, 115, 117, 372, 374, 622], [272, 274, 294, 838]], 
 [[9, 37, 38, 79], [109, 110, 112, 375, 378, 384], [275, 276, 280, 839]], 
 [[9, 37, 79, 87], [109, 112, 114, 378, 380, 586], [276, 277, 287, 844]], 
 [[9, 37, 87, 90], [109, 114, 116, 380, 381, 617], [277, 278, 291, 847]], 
 [[9, 38, 77, 79], [110, 111, 112, 383, 384, 576], [279, 280, 282, 849]], 
 [[9, 38, 77, 92], [110, 111, 117, 383, 385, 581], [279, 281, 284, 850]], 
 [[9, 77, 79, 83], [111, 112, 113, 576, 579, 585], [282, 283, 286, 1070]], 
 [[9, 77, 83, 94], [111, 113, 119, 579, 582, 602], [283, 285, 290, 1076]], 
 [[9, 77, 92, 94], [111, 117, 119, 581, 582, 637], [284, 285, 298, 1079]], 
 [[9, 79, 83, 87], [112, 113, 114, 585, 586, 600], [286, 287, 288, 1081]], 
 [[9, 83, 87, 93], [113, 114, 118, 600, 601, 618], [288, 289, 292, 1095]], 
 [[9, 83, 93, 94], [113, 118, 119, 601, 602, 638], [289, 290, 299, 1097]], 
 [[9, 87, 90, 93], [114, 116, 118, 617, 618, 632], [291, 292, 297, 1111]], 
 [[9, 88, 90, 93], [115, 116, 118, 621, 623, 632], [293, 295, 297, 1114]], 
 [[9, 88, 92, 94], [115, 117, 119, 622, 624, 637], [294, 296, 298, 1116]], 
 [[9, 88, 93, 94], [115, 118, 119, 623, 624, 638], [295, 296, 299, 1117]], 
 [[10, 39, 42, 45], [120, 121, 122, 386, 387, 405], [300, 301, 305, 851]], 
 [[10, 39, 42, 85], [120, 121, 130, 386, 390, 408], [300, 304, 308, 852]], 
 [[10, 39, 45, 59], [120, 122, 125, 387, 389, 423], [301, 303, 309, 853]], 
 [[10, 39, 55, 59], [120, 124, 125, 388, 389, 476], [302, 303, 317, 854]], 
 [[10, 39, 55, 85], [120, 124, 130, 388, 390, 479], [302, 304, 318, 855]], 
 [[10, 42, 45, 64], [121, 122, 126, 405, 406, 424], [305, 306, 310, 875]], 
 [[10, 42, 64, 84], [121, 126, 129, 406, 407, 521], [306, 307, 323, 876]], 
 [[10, 42, 84, 85], [121, 129, 130, 407, 408, 604], [307, 308, 327, 877]], 
 [[10, 45, 59, 70], [122, 125, 128, 423, 426, 495], [309, 311, 320, 896]], 
 [[10, 45, 64, 70], [122, 126, 128, 424, 426, 520], [310, 311, 322, 898]], 
 [[10, 53, 55, 59], [123, 124, 125, 463, 466, 476], [312, 313, 317, 942]], 
 [[10, 53, 55, 86], [123, 124, 131, 463, 471, 480], [312, 316, 319, 944]], 
 [[10, 53, 59, 70], [123, 125, 128, 466, 469, 495], [313, 315, 320, 951]], 
 [[10, 53, 68, 70], [123, 127, 128, 468, 469, 539], [314, 315, 324, 954]], 
 [[10, 53, 68, 86], [123, 127, 131, 468, 471, 541], [314, 316, 326, 955]], 
 [[10, 55, 85, 86], [124, 130, 131, 479, 480, 610], [318, 319, 329, 964]], 
 [[10, 64, 68, 70], [126, 127, 128, 518, 520, 539], [321, 322, 324, 1006]], 
 [[10, 64, 68, 84], [126, 127, 129, 518, 521, 540], [321, 323, 325, 1007]], 
 [[10, 68, 84, 86], [127, 129, 131, 540, 541, 605], [325, 326, 328, 1028]], 
 [[10, 84, 85, 86], [129, 130, 131, 604, 605, 610], [327, 328, 329, 1099]], 
 [[11, 84, 85, 86], [132, 133, 134, 604, 605, 610], [330, 331, 335, 1099]], 
 [[11, 84, 85, 90], [132, 133, 136, 604, 606, 612], [330, 332, 337, 1100]], 
 [[11, 84, 86, 116], [132, 134, 142, 605, 609, 616], [331, 334, 341, 1101]], 
 [[11, 84, 90, 112], [132, 136, 141, 606, 608, 633], [332, 333, 347, 1102]], 
 [[11, 84, 112, 116], [132, 141, 142, 608, 609, 707], [333, 334, 357, 1105]], 
 [[11, 85, 86, 103], [133, 134, 139, 610, 613, 615], [335, 338, 340, 1106]], 
 [[11, 85, 87, 90], [133, 135, 136, 611, 612, 617], [336, 337, 342, 1107]], 
 [[11, 85, 87, 103], [133, 135, 139, 611, 613, 619], [336, 338, 344, 1108]], 
 [[11, 86, 101, 103], [134, 138, 139, 614, 615, 672], [339, 340, 351, 1109]], 
 [[11, 86, 101, 116], [134, 138, 142, 614, 616, 677], [339, 341, 353, 1110]], 
 [[11, 87, 90, 93], [135, 136, 137, 617, 618, 632], [342, 343, 346, 1111]], 
 [[11, 87, 93, 107], [135, 137, 140, 618, 620, 639], [343, 345, 348, 1112]], 
 [[11, 87, 103, 107], [135, 139, 140, 619, 620, 680], [344, 345, 355, 1113]], 
 [[11, 90, 93, 112], [136, 137, 141, 632, 633, 640], [346, 347, 349, 1127]], 
 [[11, 93, 107, 118], [137, 140, 143, 639, 642, 689], [348, 350, 356, 1132]], 
 [[11, 93, 112, 118], [137, 141, 143, 640, 642, 709], [349, 350, 358, 1134]], 
 [[11, 101, 103, 107], [138, 139, 140, 672, 675, 680], [351, 352, 355, 1164]], 
 [[11, 101, 107, 118], [138, 140, 143, 675, 678, 689], [352, 354, 356, 1170]], 
 [[11, 101, 116, 118], [138, 142, 143, 677, 678, 716], [353, 354, 359, 1173]], 
 [[11, 112, 116, 118], [141, 142, 143, 707, 709, 716], [357, 358, 359, 1194]], 
 [[12, 40, 44, 46], [144, 147, 148, 392, 394, 418], [360, 361, 374, 858]], 
 [[12, 40, 44, 60], [144, 147, 150, 392, 395, 419], [360, 362, 375, 859]], 
 [[12, 40, 46, 69], [144, 148, 155, 394, 398, 428], [361, 364, 378, 863]], 
 [[12, 40, 60, 66], [144, 150, 154, 395, 397, 498], [362, 363, 383, 864]], 
 [[12, 40, 66, 69], [144, 154, 155, 397, 398, 529], [363, 364, 389, 867]], 
 [[12, 41, 43, 47], [145, 146, 149, 399, 402, 410], [365, 368, 370, 868]], 
 [[12, 41, 43, 62], [145, 146, 152, 399, 404, 415], [365, 369, 372, 870]], 
 [[12, 41, 44, 46], [145, 147, 148, 400, 401, 418], [366, 367, 374, 871]], 
 [[12, 41, 44, 62], [145, 147, 152, 400, 404, 420], [366, 369, 376, 872]], 
 [[12, 41, 46, 47], [145, 148, 149, 401, 402, 427], [367, 368, 377, 873]], 
 [[12, 43, 47, 63], [146, 149, 153, 410, 416, 431], [370, 373, 379, 881]], 
 [[12, 43, 61, 62], [146, 151, 152, 414, 415, 502], [371, 372, 384, 888]], 
 [[12, 43, 61, 63], [146, 151, 153, 414, 416, 503], [371, 373, 385, 889]], 
 [[12, 44, 60, 62], [147, 150, 152, 419, 420, 497], [375, 376, 382, 892]], 
 [[12, 46, 47, 69], [148, 149, 155, 427, 428, 432], [377, 378, 380, 900]], 
 [[12, 47, 63, 69], [149, 153, 155, 431, 432, 514], [379, 380, 388, 905]], 
 [[12, 60, 61, 62], [150, 151, 152, 496, 497, 502], [381, 382, 384, 981]], 
 [[12, 60, 61, 66], [150, 151, 154, 496, 498, 504], [381, 383, 386, 982]], 
 [[12, 61, 63, 66], [151, 153, 154, 503, 504, 512], [385, 386, 387, 989]], 
 [[12, 63, 66, 69], [153, 154, 155, 512, 514, 529], [387, 388, 389, 999]], 
 [[13, 60, 61, 62], [156, 157, 158, 496, 497, 502], [390, 391, 395, 981]], 
 [[13, 60, 61, 114], [156, 157, 166, 496, 501, 508], [390, 394, 398, 983]], 
 [[13, 60, 62, 92], [156, 158, 162, 497, 500, 511], [391, 393, 401, 984]], 
 [[13, 60, 88, 92], [156, 159, 162, 499, 500, 622], [392, 393, 402, 986]], 
 [[13, 60, 88, 114], [156, 159, 166, 499, 501, 626], [392, 394, 404, 987]], 
 [[13, 61, 62, 91], [157, 158, 161, 502, 505, 510], [395, 396, 400, 988]], 
 [[13, 61, 91, 111], [157, 161, 165, 505, 507, 636], [396, 397, 411, 993]], 
 [[13, 61, 111, 114], [157, 165, 166, 507, 508, 702], [397, 398, 417, 996]], 
 [[13, 62, 89, 91], [158, 160, 161, 509, 510, 628], [399, 400, 406, 997]], 
 [[13, 62, 89, 92], [158, 160, 162, 509, 511, 629], [399, 401, 407, 998]], 
 [[13, 88, 92, 94], [159, 162, 163, 622, 624, 637], [402, 403, 412, 1116]], 
 [[13, 88, 94, 117], [159, 163, 167, 624, 627, 644], [403, 405, 414, 1120]], 
 [[13, 88, 114, 117], [159, 166, 167, 626, 627, 714], [404, 405, 419, 1123]], 
 [[13, 89, 91, 95], [160, 161, 164, 628, 631, 634], [406, 409, 410, 1124]], 
 [[13, 89, 92, 94], [160, 162, 163, 629, 630, 637], [407, 408, 412, 1125]], 
 [[13, 89, 94, 95], [160, 163, 164, 630, 631, 643], [408, 409, 413, 1126]], 
 [[13, 91, 95, 111], [161, 164, 165, 634, 636, 647], [410, 411, 415, 1129]], 
 [[13, 94, 95, 117], [163, 164, 167, 643, 644, 648], [413, 414, 416, 1136]], 
 [[13, 95, 111, 117], [164, 165, 167, 647, 648, 704], [415, 416, 418, 1141]], 
 [[13, 111, 114, 117], [165, 166, 167, 702, 704, 714], [417, 418, 419, 1190]], 
 [[14, 63, 66, 69], [168, 171, 174, 512, 514, 529], [420, 422, 435, 999]], 
 [[14, 63, 66, 109], [168, 171, 178, 512, 516, 531], [420, 424, 437, 1000]], 
 [[14, 63, 67, 71], [168, 172, 176, 513, 515, 533], [421, 423, 438, 1001]], 
 [[14, 63, 67, 109], [168, 172, 178, 513, 516, 536], [421, 424, 439, 1002]], 
 [[14, 63, 69, 71], [168, 174, 176, 514, 515, 546], [422, 423, 445, 1003]], 
 [[14, 64, 66, 69], [169, 171, 174, 517, 519, 529], [425, 427, 435, 1004]], 
 [[14, 64, 66, 108], [169, 171, 177, 517, 522, 530], [425, 429, 436, 1005]], 
 [[14, 64, 68, 70], [169, 173, 175, 518, 520, 539], [426, 428, 441, 1006]], 
 [[14, 64, 68, 108], [169, 173, 177, 518, 522, 542], [426, 429, 442, 1008]], 
 [[14, 64, 69, 70], [169, 174, 175, 519, 520, 545], [427, 428, 444, 1009]], 
 [[14, 65, 67, 71], [170, 172, 176, 523, 526, 533], [430, 433, 438, 1011]], 
 [[14, 65, 67, 110], [170, 172, 179, 523, 528, 537], [430, 434, 440, 1013]], 
 [[14, 65, 68, 70], [170, 173, 175, 524, 525, 539], [431, 432, 441, 1014]], 
 [[14, 65, 68, 110], [170, 173, 179, 524, 528, 543], [431, 434, 443, 1015]], 
 [[14, 65, 70, 71], [170, 175, 176, 525, 526, 547], [432, 433, 446, 1016]], 
 [[14, 66, 108, 109], [171, 177, 178, 530, 531, 690], [436, 437, 447, 1018]], 
 [[14, 67, 109, 110], [172, 178, 179, 536, 537, 695], [439, 440, 449, 1025]], 
 [[14, 68, 108, 110], [173, 177, 179, 542, 543, 691], [442, 443, 448, 1032]], 
 [[14, 69, 70, 71], [174, 175, 176, 545, 546, 547], [444, 445, 446, 1035]], 
 [[14, 108, 109, 110], [177, 178, 179, 690, 691, 695], [447, 448, 449, 1180]], 
 [[15, 108, 109, 110], [180, 181, 182, 690, 691, 695], [450, 451, 455, 1180]], 
 [[15, 108, 109, 114], [180, 181, 186, 690, 693, 697], [450, 453, 457, 1181]], 
 [[15, 108, 110, 116], [180, 182, 188, 691, 694, 701], [451, 454, 461, 1182]], 
 [[15, 108, 112, 114], [180, 184, 186, 692, 693, 706], [452, 453, 466, 1183]], 
 [[15, 108, 112, 116], [180, 184, 188, 692, 694, 707], [452, 454, 467, 1184]], 
 [[15, 109, 110, 115], [181, 182, 187, 695, 698, 700], [455, 458, 460, 1185]], 
 [[15, 109, 111, 114], [181, 183, 186, 696, 697, 702], [456, 457, 462, 1186]], 
 [[15, 109, 111, 115], [181, 183, 187, 696, 698, 703], [456, 458, 463, 1187]], 
 [[15, 110, 113, 115], [182, 185, 187, 699, 700, 710], [459, 460, 470, 1188]], 
 [[15, 110, 113, 116], [182, 185, 188, 699, 701, 711], [459, 461, 471, 1189]], 
 [[15, 111, 114, 117], [183, 186, 189, 702, 704, 714], [462, 464, 474, 1190]], 
 [[15, 111, 115, 119], [183, 187, 191, 703, 705, 715], [463, 465, 475, 1191]], 
 [[15, 111, 117, 119], [183, 189, 191, 704, 705, 718], [464, 465, 478, 1192]], 
 [[15, 112, 114, 117], [184, 186, 189, 706, 708, 714], [466, 468, 474, 1193]], 
 [[15, 112, 116, 118], [184, 188, 190, 707, 709, 716], [467, 469, 476, 1194]], 
 [[15, 112, 117, 118], [184, 189, 190, 708, 709, 717], [468, 469, 477, 1195]], 
 [[15, 113, 115, 119], [185, 187, 191, 710, 713, 715], [470, 473, 475, 1196]], 
 [[15, 113, 116, 118], [185, 188, 190, 711, 712, 716], [471, 472, 476, 1197]], 
 [[15, 113, 118, 119], [185, 190, 191, 712, 713, 719], [472, 473, 479, 1198]], 
 [[15, 117, 118, 119], [189, 190, 191, 717, 718, 719], [477, 478, 479, 1199]], 
 [[16, 33, 34, 35], [192, 193, 194, 351, 352, 357], [480, 481, 485, 808]], 
 [[16, 33, 34, 57], [192, 193, 198, 351, 354, 361], [480, 482, 488, 809]], 
 [[16, 33, 35, 59], [192, 194, 200, 352, 356, 365], [481, 484, 491, 810]], 
 [[16, 33, 57, 58], [192, 198, 199, 354, 355, 489], [482, 483, 501, 813]], 
 [[16, 33, 58, 59], [192, 199, 200, 355, 356, 491], [483, 484, 503, 814]], 
 [[16, 34, 35, 46], [193, 194, 196, 357, 359, 364], [485, 486, 490, 815]], 
 [[16, 34, 46, 47], [193, 196, 197, 359, 360, 427], [486, 487, 496, 818]], 
 [[16, 34, 47, 57], [193, 197, 198, 360, 361, 430], [487, 488, 498, 819]], 
 [[16, 35, 45, 46], [194, 195, 196, 363, 364, 422], [489, 490, 492, 822]], 
 [[16, 35, 45, 59], [194, 195, 200, 363, 365, 423], [489, 491, 493, 823]], 
 [[16, 45, 46, 69], [195, 196, 201, 422, 425, 428], [492, 494, 497, 895]], 
 [[16, 45, 59, 70], [195, 200, 202, 423, 426, 495], [493, 495, 506, 896]], 
 [[16, 45, 69, 70], [195, 201, 202, 425, 426, 545], [494, 495, 507, 899]], 
 [[16, 46, 47, 69], [196, 197, 201, 427, 428, 432], [496, 497, 499, 900]], 
 [[16, 47, 57, 71], [197, 198, 203, 430, 433, 490], [498, 500, 502, 904]], 
 [[16, 47, 69, 71], [197, 201, 203, 432, 433, 546], [499, 500, 508, 907]], 
 [[16, 57, 58, 71], [198, 199, 203, 489, 490, 494], [501, 502, 505, 976]], 
 [[16, 58, 59, 70], [199, 200, 202, 491, 493, 495], [503, 504, 506, 977]], 
 [[16, 58, 70, 71], [199, 202, 203, 493, 494, 547], [504, 505, 509, 980]], 
 [[16, 69, 70, 71], [201, 202, 203, 545, 546, 547], [507, 508, 509, 1035]], 
 [[17, 81, 82, 83], [204, 205, 206, 589, 590, 595], [510, 511, 515, 1083]], 
 [[17, 81, 82, 105], [204, 205, 210, 589, 592, 599], [510, 512, 518, 1084]], 
 [[17, 81, 83, 107], [204, 206, 212, 590, 594, 603], [511, 514, 521, 1085]], 
 [[17, 81, 105, 106], [204, 210, 211, 592, 593, 683], [512, 513, 531, 1088]], 
 [[17, 81, 106, 107], [204, 211, 212, 593, 594, 685], [513, 514, 533, 1089]], 
 [[17, 82, 83, 94], [205, 206, 208, 595, 597, 602], [515, 516, 520, 1090]], 
 [[17, 82, 94, 95], [205, 208, 209, 597, 598, 643], [516, 517, 526, 1093]], 
 [[17, 82, 95, 105], [205, 209, 210, 598, 599, 646], [517, 518, 528, 1094]], 
 [[17, 83, 93, 94], [206, 207, 208, 601, 602, 638], [519, 520, 522, 1097]], 
 [[17, 83, 93, 107], [206, 207, 212, 601, 603, 639], [519, 521, 523, 1098]], 
 [[17, 93, 94, 117], [207, 208, 213, 638, 641, 644], [522, 524, 527, 1131]], 
 [[17, 93, 107, 118], [207, 212, 214, 639, 642, 689], [523, 525, 536, 1132]], 
 [[17, 93, 117, 118], [207, 213, 214, 641, 642, 717], [524, 525, 537, 1135]], 
 [[17, 94, 95, 117], [208, 209, 213, 643, 644, 648], [526, 527, 529, 1136]], 
 [[17, 95, 105, 119], [209, 210, 215, 646, 649, 684], [528, 530, 532, 1140]], 
 [[17, 95, 117, 119], [209, 213, 215, 648, 649, 718], [529, 530, 538, 1143]], 
 [[17, 105, 106, 119], [210, 211, 215, 683, 684, 688], [531, 532, 535, 1175]], 
 [[17, 106, 107, 118], [211, 212, 214, 685, 687, 689], [533, 534, 536, 1176]], 
 [[17, 106, 118, 119], [211, 214, 215, 687, 688, 719], [534, 535, 539, 1179]], 
 [[17, 117, 118, 119], [213, 214, 215, 717, 718, 719], [537, 538, 539, 1199]], 
 [[18, 26, 29, 32], [216, 217, 218, 305, 307, 329], [540, 541, 545, 748]], 
 [[18, 26, 29, 38], [216, 217, 219, 305, 308, 332], [540, 542, 546, 749]], 
 [[18, 26, 32, 80], [216, 218, 225, 307, 311, 350], [541, 544, 551, 752]], 
 [[18, 26, 38, 77], [216, 219, 224, 308, 309, 383], [542, 543, 553, 753]], 
 [[18, 26, 77, 80], [216, 224, 225, 309, 311, 577], [543, 544, 565, 756]], 
 [[18, 29, 32, 41], [217, 218, 220, 329, 333, 347], [545, 547, 549, 784]], 
 [[18, 29, 38, 44], [217, 219, 221, 332, 334, 382], [546, 548, 552, 789]], 
 [[18, 29, 41, 44], [217, 220, 221, 333, 334, 400], [547, 548, 555, 790]], 
 [[18, 32, 41, 50], [218, 220, 222, 347, 349, 403], [549, 550, 556, 804]], 
 [[18, 32, 50, 80], [218, 222, 225, 349, 350, 448], [550, 551, 561, 807]], 
 [[18, 38, 44, 92], [219, 221, 227, 382, 385, 421], [552, 554, 559, 848]], 
 [[18, 38, 77, 92], [219, 224, 227, 383, 385, 581], [553, 554, 567, 850]], 
 [[18, 41, 44, 62], [220, 221, 223, 400, 404, 420], [555, 557, 558, 872]], 
 [[18, 41, 50, 62], [220, 222, 223, 403, 404, 447], [556, 557, 560, 874]], 
 [[18, 44, 62, 92], [221, 223, 227, 420, 421, 511], [558, 559, 564, 894]], 
 [[18, 50, 62, 89], [222, 223, 226, 447, 449, 509], [560, 562, 563, 924]], 
 [[18, 50, 80, 89], [222, 225, 226, 448, 449, 588], [561, 562, 568, 926]], 
 [[18, 62, 89, 92], [223, 226, 227, 509, 511, 629], [563, 564, 569, 998]], 
 [[18, 77, 80, 89], [224, 225, 226, 577, 580, 588], [565, 566, 568, 1072]], 
 [[18, 77, 89, 92], [224, 226, 227, 580, 581, 629], [566, 567, 569, 1077]], 
 [[19, 53, 56, 65], [228, 229, 230, 464, 467, 483], [570, 571, 575, 946]], 
 [[19, 53, 56, 74], [228, 229, 232, 464, 470, 485], [570, 573, 576, 947]], 
 [[19, 53, 65, 68], [228, 230, 231, 467, 468, 524], [571, 572, 579, 952]], 
 [[19, 53, 68, 86], [228, 231, 233, 468, 471, 541], [572, 574, 582, 955]], 
 [[19, 53, 74, 86], [228, 232, 233, 470, 471, 558], [573, 574, 585, 956]], 
 [[19, 56, 65, 98], [229, 230, 234, 483, 487, 527], [575, 577, 580, 968]], 
 [[19, 56, 74, 104], [229, 232, 236, 485, 488, 561], [576, 578, 587, 972]], 
 [[19, 56, 98, 104], [229, 234, 236, 487, 488, 659], [577, 578, 590, 975]], 
 [[19, 65, 68, 110], [230, 231, 237, 524, 528, 543], [579, 581, 583, 1015]], 
 [[19, 65, 98, 110], [230, 234, 237, 527, 528, 660], [580, 581, 591, 1017]], 
 [[19, 68, 86, 116], [231, 233, 239, 541, 544, 616], [582, 584, 589, 1031]], 
 [[19, 68, 110, 116], [231, 237, 239, 543, 544, 701], [583, 584, 598, 1034]], 
 [[19, 74, 86, 101], [232, 233, 235, 558, 559, 614], [585, 586, 588, 1046]], 
 [[19, 74, 101, 104], [232, 235, 236, 559, 561, 673], [586, 587, 593, 1049]], 
 [[19, 86, 101, 116], [233, 235, 239, 614, 616, 677], [588, 589, 595, 1110]], 
 [[19, 98, 104, 113], [234, 236, 238, 659, 661, 682], [590, 592, 596, 1152]], 
 [[19, 98, 110, 113], [234, 237, 238, 660, 661, 699], [591, 592, 597, 1153]], 
 [[19, 101, 104, 113], [235, 236, 238, 673, 676, 682], [593, 594, 596, 1166]], 
 [[19, 101, 113, 116], [235, 238, 239, 676, 677, 711], [594, 595, 599, 1171]], 
 [[19, 110, 113, 116], [237, 238, 239, 699, 701, 711], [597, 598, 599, 1189]], 
 [[20, 25, 27, 31], [240, 241, 242, 298, 300, 313], [600, 601, 605, 738]], 
 [[20, 25, 27, 73], [240, 241, 246, 298, 301, 319], [600, 602, 608, 739]], 
 [[20, 25, 31, 79], [240, 242, 248, 300, 304, 345], [601, 604, 611, 742]], 
 [[20, 25, 73, 75], [240, 246, 247, 301, 302, 555], [602, 603, 621, 743]], 
 [[20, 25, 75, 79], [240, 247, 248, 302, 304, 563], [603, 604, 623, 746]], 
 [[20, 27, 31, 39], [241, 242, 244, 313, 316, 344], [605, 606, 610, 760]], 
 [[20, 27, 39, 55], [241, 244, 245, 316, 317, 388], [606, 607, 616, 765]], 
 [[20, 27, 55, 73], [241, 245, 246, 317, 319, 477], [607, 608, 618, 768]], 
 [[20, 31, 37, 39], [242, 243, 244, 342, 344, 376], [609, 610, 612, 800]], 
 [[20, 31, 37, 79], [242, 243, 248, 342, 345, 378], [609, 611, 613, 801]], 
 [[20, 37, 39, 85], [243, 244, 249, 376, 379, 390], [612, 614, 617, 841]], 
 [[20, 37, 79, 87], [243, 248, 250, 378, 380, 586], [613, 615, 626, 844]], 
 [[20, 37, 85, 87], [243, 249, 250, 379, 380, 611], [614, 615, 627, 845]], 
 [[20, 39, 55, 85], [244, 245, 249, 388, 390, 479], [616, 617, 619, 855]], 
 [[20, 55, 73, 103], [245, 246, 251, 477, 481, 557], [618, 620, 622, 961]], 
 [[20, 55, 85, 103], [245, 249, 251, 479, 481, 613], [619, 620, 628, 965]], 
 [[20, 73, 75, 103], [246, 247, 251, 555, 557, 567], [621, 622, 625, 1045]], 
 [[20, 75, 79, 87], [247, 248, 250, 563, 566, 586], [623, 624, 626, 1052]], 
 [[20, 75, 87, 103], [247, 250, 251, 566, 567, 619], [624, 625, 629, 1057]], 
 [[20, 85, 87, 103], [249, 250, 251, 611, 613, 619], [627, 628, 629, 1108]], 
 [[21, 43, 49, 51], [252, 253, 254, 411, 413, 441], [630, 631, 635, 883]], 
 [[21, 43, 49, 91], [252, 253, 258, 411, 417, 443], [630, 634, 636, 884]], 
 [[21, 43, 51, 63], [252, 254, 256, 413, 416, 453], [631, 633, 639, 887]], 
 [[21, 43, 61, 63], [252, 255, 256, 414, 416, 503], [632, 633, 642, 889]], 
 [[21, 43, 61, 91], [252, 255, 258, 414, 417, 505], [632, 634, 643, 890]], 
 [[21, 49, 51, 97], [253, 254, 259, 441, 444, 456], [635, 637, 641, 917]], 
 [[21, 49, 91, 99], [253, 258, 260, 443, 445, 635], [636, 638, 651, 920]], 
 [[21, 49, 97, 99], [253, 259, 260, 444, 445, 656], [637, 638, 653, 921]], 
 [[21, 51, 63, 67], [254, 256, 257, 453, 454, 513], [639, 640, 646, 931]], 
 [[21, 51, 67, 97], [254, 257, 259, 454, 456, 534], [640, 641, 648, 934]], 
 [[21, 61, 63, 109], [255, 256, 261, 503, 506, 516], [642, 644, 647, 990]], 
 [[21, 61, 91, 111], [255, 258, 262, 505, 507, 636], [643, 645, 652, 993]], 
 [[21, 61, 109, 111], [255, 261, 262, 506, 507, 696], [644, 645, 657, 994]], 
 [[21, 63, 67, 109], [256, 257, 261, 513, 516, 536], [646, 647, 649, 1002]], 
 [[21, 67, 97, 115], [257, 259, 263, 534, 538, 658], [648, 650, 654, 1022]], 
 [[21, 67, 109, 115], [257, 261, 263, 536, 538, 698], [649, 650, 658, 1026]], 
 [[21, 91, 99, 111], [258, 260, 262, 635, 636, 665], [651, 652, 655, 1130]], 
 [[21, 97, 99, 115], [259, 260, 263, 656, 658, 666], [653, 654, 656, 1151]], 
 [[21, 99, 111, 115], [260, 262, 263, 665, 666, 703], [655, 656, 659, 1158]], 
 [[21, 109, 111, 115], [261, 262, 263, 696, 698, 703], [657, 658, 659, 1187]], 
 [[22, 24, 28, 30], [264, 265, 266, 290, 291, 320], [660, 661, 665, 725]], 
 [[22, 24, 28, 48], [264, 265, 267, 290, 293, 324], [660, 662, 666, 727]], 
 [[22, 24, 30, 78], [264, 266, 272, 291, 295, 340], [661, 664, 671, 728]], 
 [[22, 24, 48, 76], [264, 267, 271, 293, 294, 437], [662, 663, 673, 731]], 
 [[22, 24, 76, 78], [264, 271, 272, 294, 295, 569], [663, 664, 683, 733]], 
 [[22, 28, 30, 52], [265, 266, 268, 320, 325, 337], [665, 667, 669, 770]], 
 [[22, 28, 48, 54], [265, 267, 269, 324, 326, 436], [666, 668, 672, 777]], 
 [[22, 28, 52, 54], [265, 268, 269, 325, 326, 457], [667, 668, 675, 778]], 
 [[22, 30, 52, 72], [266, 268, 270, 337, 338, 461], [669, 670, 676, 794]], 
 [[22, 30, 72, 78], [266, 270, 272, 338, 340, 550], [670, 671, 680, 796]], 
 [[22, 48, 54, 102], [267, 269, 275, 436, 439, 475], [672, 674, 679, 912]], 
 [[22, 48, 76, 102], [267, 271, 275, 437, 439, 574], [673, 674, 685, 914]], 
 [[22, 52, 54, 96], [268, 269, 273, 457, 462, 473], [675, 677, 678, 936]], 
 [[22, 52, 72, 96], [268, 270, 273, 461, 462, 551], [676, 677, 681, 941]], 
 [[22, 54, 96, 102], [269, 273, 275, 473, 475, 653], [678, 679, 688, 958]], 
 [[22, 72, 78, 100], [270, 272, 274, 550, 552, 584], [680, 682, 686, 1039]], 
 [[22, 72, 96, 100], [270, 273, 274, 551, 552, 652], [681, 682, 687, 1040]], 
 [[22, 76, 78, 100], [271, 272, 274, 569, 573, 584], [683, 684, 686, 1061]], 
 [[22, 76, 100, 102], [271, 274, 275, 573, 574, 668], [684, 685, 689, 1067]], 
 [[22, 96, 100, 102], [273, 274, 275, 652, 653, 668], [687, 688, 689, 1147]], 
 [[23, 36, 40, 42], [276, 277, 278, 368, 369, 391], [690, 691, 695, 829]], 
 [[23, 36, 40, 60], [276, 277, 279, 368, 371, 395], [690, 692, 696, 831]], 
 [[23, 36, 42, 90], [276, 278, 284, 369, 373, 409], [691, 694, 701, 832]], 
 [[23, 36, 60, 88], [276, 279, 283, 371, 372, 499], [692, 693, 703, 835]], 
 [[23, 36, 88, 90], [276, 283, 284, 372, 373, 621], [693, 694, 713, 837]], 
 [[23, 40, 42, 64], [277, 278, 280, 391, 396, 406], [695, 697, 699, 857]], 
 [[23, 40, 60, 66], [277, 279, 281, 395, 397, 498], [696, 698, 702, 864]], 
 [[23, 40, 64, 66], [277, 280, 281, 396, 397, 517], [697, 698, 705, 865]], 
 [[23, 42, 64, 84], [278, 280, 282, 406, 407, 521], [699, 700, 706, 876]], 
 [[23, 42, 84, 90], [278, 282, 284, 407, 409, 606], [700, 701, 710, 878]], 
 [[23, 60, 66, 114], [279, 281, 287, 498, 501, 532], [702, 704, 709, 985]], 
 [[23, 60, 88, 114], [279, 283, 287, 499, 501, 626], [703, 704, 715, 987]], 
 [[23, 64, 66, 108], [280, 281, 285, 517, 522, 530], [705, 707, 708, 1005]], 
 [[23, 64, 84, 108], [280, 282, 285, 521, 522, 607], [706, 707, 711, 1010]], 
 [[23, 66, 108, 114], [281, 285, 287, 530, 532, 693], [708, 709, 718, 1019]], 
 [[23, 84, 90, 112], [282, 284, 286, 606, 608, 633], [710, 712, 716, 1102]], 
 [[23, 84, 108, 112], [282, 285, 286, 607, 608, 692], [711, 712, 717, 1103]], 
 [[23, 88, 90, 112], [283, 284, 286, 621, 625, 633], [713, 714, 716, 1115]], 
 [[23, 88, 112, 114], [283, 286, 287, 625, 626, 706], [714, 715, 719, 1121]], 
 [[23, 108, 112, 114], [285, 286, 287, 692, 693, 706], [717, 718, 719, 1183]], 
 [[24, 25, 30, 78], [288, 291, 295, 299, 303, 340], [721, 722, 728, 741]], 
 [[24, 26, 32, 80], [289, 292, 296, 307, 311, 350], [723, 724, 730, 752]], 
 [[24, 28, 32, 48], [290, 292, 293, 321, 324, 348], [726, 727, 729, 772]], 
 [[24, 32, 48, 80], [292, 293, 296, 348, 350, 438], [729, 730, 732, 806]], 
 [[24, 48, 76, 80], [293, 294, 296, 437, 438, 570], [731, 732, 734, 913]], 
 [[25, 26, 31, 79], [297, 300, 304, 306, 310, 345], [735, 736, 742, 751]], 
 [[25, 27, 30, 73], [298, 299, 301, 312, 319, 339], [737, 739, 740, 758]], 
 [[25, 30, 73, 78], [299, 301, 303, 339, 340, 556], [740, 741, 744, 797]], 
 [[25, 73, 75, 78], [301, 302, 303, 555, 556, 562], [743, 744, 745, 1044]], 
 [[26, 29, 31, 38], [305, 306, 308, 328, 332, 343], [747, 749, 750, 782]], 
 [[26, 31, 38, 79], [306, 308, 310, 343, 345, 384], [750, 751, 754, 802]], 
 [[26, 38, 77, 79], [308, 309, 310, 383, 384, 576], [753, 754, 755, 849]], 
 [[27, 31, 35, 39], [313, 315, 316, 341, 344, 362], [759, 760, 763, 798]], 
 [[27, 33, 35, 59], [314, 315, 318, 352, 356, 365], [761, 762, 764, 810]], 
 [[27, 35, 39, 59], [315, 316, 318, 362, 365, 389], [763, 764, 766, 821]], 
 [[27, 39, 55, 59], [316, 317, 318, 388, 389, 476], [765, 766, 767, 854]], 
 [[28, 30, 33, 52], [320, 322, 325, 336, 337, 353], [769, 770, 774, 793]],
  [[28, 33, 34, 57], [322, 323, 327, 351, 354, 361], [773, 775, 776, 809]], 
  [[28, 33, 52, 57], [322, 325, 327, 353, 354, 459], [774, 775, 779, 811]], 
  [[28, 52, 54, 57], [325, 326, 327, 457, 459, 472], [778, 779, 780, 935]], 
  [[29, 32, 34, 41], [329, 330, 333, 346, 347, 358], [783, 784, 786, 803]], 
  [[29, 34, 35, 46], [330, 331, 335, 357, 359, 364], [785, 787, 788, 815]], 
  [[29, 34, 41, 46], [330, 333, 335, 358, 359, 401], [786, 787, 791, 816]], 
  [[29, 41, 44, 46], [333, 334, 335, 400, 401, 418], [790, 791, 792, 871]], 
  [[30, 72, 73, 78], [338, 339, 340, 548, 550, 556], [795, 796, 797, 1037]], 
  [[31, 37, 38, 79], [342, 343, 345, 375, 378, 384], [799, 801, 802, 839]], 
  [[32, 48, 50, 80], [348, 349, 350, 435, 438, 448], [805, 806, 807, 911]], 
  [[33, 52, 57, 58], [353, 354, 355, 459, 460, 489], [811, 812, 813, 940]], 
  [[34, 41, 46, 47], [358, 359, 360, 401, 402, 427], [816, 817, 818, 873]], 
  [[35, 39, 45, 59], [362, 363, 365, 387, 389, 423], [820, 821, 823, 853]], 
  [[36, 37, 42, 90], [366, 369, 373, 377, 381, 409], [825, 826, 832, 843]], 
  [[36, 38, 44, 92], [367, 370, 374, 382, 385, 421], [827, 828, 834, 848]], 
  [[36, 40, 44, 60], [368, 370, 371, 392, 395, 419], [830, 831, 833, 859]], 
  [[36, 44, 60, 92], [370, 371, 374, 419, 421, 500], [833, 834, 836, 893]], 
  [[36, 60, 88, 92], [371, 372, 374, 499, 500, 622], [835, 836, 838, 986]], 
  [[37, 39, 42, 85], [376, 377, 379, 386, 390, 408], [840, 841, 842, 852]], 
  [[37, 42, 85, 90], [377, 379, 381, 408, 409, 612], [842, 843, 846, 879]], 
  [[37, 85, 87, 90], [379, 380, 381, 611, 612, 617], [845, 846, 847, 1107]], 
  [[40, 42, 45, 64], [391, 393, 396, 405, 406, 424], [856, 857, 861, 875]], 
  [[40, 45, 46, 69], [393, 394, 398, 422, 425, 428], [860, 862, 863, 895]], 
  [[40, 45, 64, 69], [393, 396, 398, 424, 425, 519], [861, 862, 866, 897]], 
  [[40, 64, 66, 69], [396, 397, 398, 517, 519, 529], [865, 866, 867, 1004]], 
  [[41, 43, 50, 62], [399, 403, 404, 412, 415, 447], [869, 870, 874, 885]], 
  [[42, 84, 85, 90], [407, 408, 409, 604, 606, 612], [877, 878, 879, 1100]], 
  [[43, 47, 51, 63], [410, 413, 416, 429, 431, 453], [880, 881, 887, 902]], 
  [[43, 49, 50, 91], [411, 412, 417, 440, 443, 450], [882, 884, 886, 915]], 
  [[43, 50, 62, 91], [412, 415, 417, 447, 450, 510], [885, 886, 891, 925]], 
  [[43, 61, 62, 91], [414, 415, 417, 502, 505, 510], [888, 890, 891, 988]], 
  [[44, 60, 62, 92], [419, 420, 421, 497, 500, 511], [892, 893, 894, 984]], 
  [[45, 64, 69, 70], [424, 425, 426, 519, 520, 545], [897, 898, 899, 1009]], 
  [[47, 51, 57, 71], [429, 430, 433, 452, 455, 490], [901, 903, 904, 930]], 
  [[47, 51, 63, 71], [429, 431, 433, 453, 455, 515], [902, 903, 906, 932]], 
  [[47, 63, 69, 71], [431, 432, 433, 514, 515, 546], [905, 906, 907, 1003]], 
  [[48, 49, 54, 102], [434, 436, 439, 442, 446, 475], [909, 910, 912, 919]], 
  [[49, 51, 54, 97], [441, 442, 444, 451, 456, 474], [916, 917, 918, 929]], 
  [[49, 54, 97, 102], [442, 444, 446, 474, 475, 657], [918, 919, 922, 959]], 
  [[49, 97, 99, 102], [444, 445, 446, 656, 657, 663], [921, 922, 923, 1150]], 
  [[50, 62, 89, 91], [447, 449, 450, 509, 510, 628], [924, 925, 927, 997]], 
  [[51, 63, 67, 71], [453, 454, 455, 513, 515, 533], [931, 932, 933, 1001]], 
  [[52, 56, 72, 96], [458, 461, 462, 484, 486, 551], [938, 939, 941, 970]], 
  [[53, 55, 74, 86], [463, 470, 471, 478, 480, 558], [943, 944, 956, 962]], 
  [[53, 56, 58, 65], [464, 465, 467, 482, 483, 492], [945, 946, 949, 967]], 
  [[53, 58, 59, 70], [465, 466, 469, 491, 493, 495], [948, 950, 951, 977]], 
  [[53, 58, 65, 70], [465, 467, 469, 492, 493, 525], [949, 950, 953, 978]], 
  [[53, 65, 68, 70], [467, 468, 469, 524, 525, 539], [952, 953, 954, 1014]], 
  [[54, 96, 97, 102], [473, 474, 475, 650, 653, 657], [957, 958, 959, 1145]], 
  [[55, 73, 74, 103], [477, 478, 481, 554, 557, 560], [960, 961, 963, 1043]], 
  [[55, 74, 86, 103], [478, 480, 481, 558, 560, 615], [962, 963, 966, 1047]], 
  [[55, 85, 86, 103], [479, 480, 481, 610, 613, 615], [964, 965, 966, 1106]], 
  [[56, 72, 74, 104], [484, 485, 488, 549, 553, 561], [969, 971, 972, 1038]], 
  [[56, 72, 96, 104], [484, 486, 488, 551, 553, 654], [970, 971, 974, 1041]], 
  [[56, 96, 98, 104], [486, 487, 488, 651, 654, 659], [973, 974, 975, 1146]], 
  [[58, 65, 70, 71], [492, 493, 494, 525, 526, 547], [978, 979, 980, 1016]], 
  [[60, 61, 66, 114], [496, 498, 501, 504, 508, 532], [982, 983, 985, 992]], 
  [[61, 63, 66, 109], [503, 504, 506, 512, 516, 531], [989, 990, 991, 1000]], 
  [[61, 66, 109, 114], [504, 506, 508, 531, 532, 697], [991, 992, 995, 1020]], 
  [[61, 109, 111, 114], [506, 507, 508, 696, 697, 702], [994, 995, 996, 1186]], 
  [[64, 68, 84, 108], [518, 521, 522, 540, 542, 607], [1007, 1008, 1010, 1029]], 
  [[65, 67, 98, 110], [523, 527, 528, 535, 537, 660], [1012, 1013, 1017, 1023]], 
  [[66, 108, 109, 114], [530, 531, 532, 690, 693, 697], [1018, 1019, 1020, 1181]], 
  [[67, 97, 98, 115], [534, 535, 538, 655, 658, 662], [1021, 1022, 1024, 1149]], 
  [[67, 98, 110, 115], [535, 537, 538, 660, 662, 700], [1023, 1024, 1027, 1154]], 
  [[67, 109, 110, 115], [536, 537, 538, 695, 698, 700], [1025, 1026, 1027, 1185]], 
  [[68, 84, 86, 116], [540, 541, 544, 605, 609, 616], [1028, 1030, 1031, 1101]], 
  [[68, 84, 108, 116], [540, 542, 544, 607, 609, 694], [1029, 1030, 1033, 1104]], 
  [[68, 108, 110, 116], [542, 543, 544, 691, 694, 701], [1032, 1033, 1034, 1182]], 
  [[72, 96, 100, 104], [551, 552, 553, 652, 654, 669], [1040, 1041, 1042, 1148]], 
  [[74, 86, 101, 103], [558, 559, 560, 614, 615, 672], [1046, 1047, 1048, 1109]], 
  [[75, 79, 83, 87], [563, 565, 566, 585, 586, 600], [1051, 1052, 1055, 1081]], 
  [[75, 81, 83, 107], [564, 565, 568, 590, 594, 603], [1053, 1054, 1056, 1085]], 
  [[75, 83, 87, 107], [565, 566, 568, 600, 603, 620], [1055, 1056, 1058, 1096]], 
  [[75, 87, 103, 107], [566, 567, 568, 619, 620, 680], [1057, 1058, 1059, 1113]], 
  [[76, 78, 81, 100], [569, 571, 573, 583, 584, 591], [1060, 1061, 1064, 1080]],
   [[76, 81, 82, 105], [571, 572, 575, 589, 592, 599], [1063, 1065, 1066, 1084]], 
   [[76, 81, 100, 105], [571, 573, 575, 591, 592, 670], [1064, 1065, 1068, 1086]], 
   [[76, 100, 102, 105], [573, 574, 575, 668, 670, 679], [1067, 1068, 1069, 1161]], 
   [[77, 80, 82, 89], [577, 578, 580, 587, 588, 596], [1071, 1072, 1074, 1082]], 
   [[77, 82, 83, 94], [578, 579, 582, 595, 597, 602], [1073, 1075, 1076, 1090]], 
   [[77, 82, 89, 94], [578, 580, 582, 596, 597, 630], [1074, 1075, 1078, 1091]], 
   [[77, 89, 92, 94], [580, 581, 582, 629, 630, 637], [1077, 1078, 1079, 1125]], 
   [[81, 100, 105, 106], [591, 592, 593, 670, 671, 683], [1086, 1087, 1088, 1163]], 
   [[82, 89, 94, 95], [596, 597, 598, 630, 631, 643], [1091, 1092, 1093, 1126]], 
   [[83, 87, 93, 107], [600, 601, 603, 618, 620, 639], [1095, 1096, 1098, 1112]], 
   [[84, 108, 112, 116], [607, 608, 609, 692, 694, 707], [1103, 1104, 1105, 1184]], 
   [[88, 90, 93, 112], [621, 623, 625, 632, 633, 640], [1114, 1115, 1118, 1127]], 
   [[88, 93, 94, 117], [623, 624, 627, 638, 641, 644], [1117, 1119, 1120, 1131]], 
   [[88, 93, 112, 117], [623, 625, 627, 640, 641, 708], [1118, 1119, 1122, 1133]], 
   [[88, 112, 114, 117], [625, 626, 627, 706, 708, 714], [1121, 1122, 1123, 1193]], 
   [[91, 95, 99, 111], [634, 635, 636, 645, 647, 665], [1128, 1129, 1130, 1138]], 
   [[93, 112, 117, 118], [640, 641, 642, 708, 709, 717], [1133, 1134, 1135, 1195]], 
   [[95, 99, 105, 119], [645, 646, 649, 664, 667, 684], [1137, 1139, 1140, 1157]], 
   [[95, 99, 111, 119], [645, 647, 649, 665, 667, 705], [1138, 1139, 1142, 1159]], 
   [[95, 111, 117, 119], [647, 648, 649, 704, 705, 718], [1141, 1142, 1143, 1192]], 
   [[98, 110, 113, 115], [660, 661, 662, 699, 700, 710], [1153, 1154, 1155, 1188]], 
   [[99, 111, 115, 119], [665, 666, 667, 703, 705, 715], [1158, 1159, 1160, 1191]], 
   [[101, 104, 106, 113], [673, 674, 676, 681, 682, 686], [1165, 1166, 1168, 1174]], 
   [[101, 106, 107, 118], [674, 675, 678, 685, 687, 689], [1167, 1169, 1170, 1176]], 
   [[101, 106, 113, 118], [674, 676, 678, 686, 687, 712], [1168, 1169, 1172, 1177]], 
   [[101, 113, 116, 118], [676, 677, 678, 711, 712, 716], [1171, 1172, 1173, 1197]], 
   [[106, 113, 118, 119], [686, 687, 688, 712, 713, 719], [1177, 1178, 1179, 1198]]
   ]


の様になります。
頂点の個数：１２０個、辺の個数：７２０本、面（正三角形）の個数：１２００枚、胞（正四面体）の個数：６００個が合っているので多分正しいです。
一松信著「高次元の正多面体」の正６００胞体の構造の難解な解説もこのデータがあれば、何とか理解できるかも。
残りの４次元の正多胞体は正１２０胞体ですが、一松信さんは「正百二十胞体の構成は最も厄介です。最も早いのは上記の正六百胞体の双対として、
すなわちその各胞の中心をとるものです。」と書いてあり、上の情報でこれが可能になりましたが、プログラミングの練習の為には、
直接与えられている座標

$$ (\pm 2, \pm 2, 0, 0) の置換　6 \times 4 = 24 個 $$
$$ (\pm \sqrt{5}, \pm 1, \pm 1, \pm1) の置換　4 \times 16 = 64 個 $$
$$ (\pm \tau, \pm \tau, \pm \tau, \pm \tau^{-2}) の置換　4 \times 16 = 64 個 $$
$$ (\pm \tau ^2, \pm \tau^{-1}, \pm \tau^{-1}, \pm \tau^{-1}) の置換　4 \times 16 = 64 個 $$
$$ (\pm \tau ^2, \pm \tau^{-2}, \pm 1, 0) の偶置換　12 \times 8 = 96 個 $$
$$ (\pm \sqrt{5}, \pm \tau^{-1}, \pm \tau, 0) の偶置換　12 \times 8 = 96 個  $$
$$ (\pm 2, \pm 1, \pm \tau, \pm \tau^{-1}) の偶置換　12 \times 16 = 192 個  $$

を使って、プログラミングしてみると良いと思います。我々凡人がプログラミングすると必ず間違え、完成まで何日も掛かりますが。
上の4つは置換ですので、数値の順番はどうでも良いですが、後の３個は偶置換なので、数値の順番を勝手に変えると正しい答えは得られません。
手計算で、置換や偶置換を書き並べることが出来るなら、即ち、アルゴリズムが理解できる・作れるなら楽にプログラミング出来ます。
どの様なプログラムを作っているかによって話は当然違ってきますが、プログラミングが出来るようになる為に本質的に必要な素養は
基本的な数学的素養があるか、即ち、数学を公式の丸暗記ではなく、本当に基本から理解しているかだと思います。
正１２０胞体の胞（正１２面体）を見つけるプログラムが一番計算時間が掛かり、素人とプロで大きな差が出ると思います。
誰も知らないことを見つけようとする数学研究ではなく

正１２０胞体(Regular hecatonicosachoron)
胞：正１２面体１２０個
面：７２０枚の各正五角形に正１２面体２個が集まる
辺：１２００本の各辺に正五角形３枚、正１２面体３個が集まる
頂点：６００個の各頂点に辺４本、正五角形６枚、正１２面体４個が集まる
双対：正６００胞体
シュレーフリの記号｛５，３，３｝


と言う情報が多分、１９世紀後半には知られていたので、それを使えば楽にプログラミング出来ます。
私はつぎの様に考えて計算しました。一度に全部やろうとするとデバッグにも時間が掛かりますから、０番目の頂点に隣接する正１２面体４個を
見つけるプログラムを先ず作ります。０番目の頂点に隣接する辺は４本で既に求めています。正１２面体は０番目の頂点とそれに隣接する３本の辺で
完全に決まります。隣接する辺が４本なので４個の辺から３本の辺を選ぶ組み合わせ４個の一つ一つに正１２面体が一つ張り付いているはずです。
０番目の頂点と３本の辺から決まる３個のベクトルで張られる３次元部分空間に含まれる頂点を連立方程式を解いて求めます。
全６００個の頂点について、この３次元部分空間に含まれる頂点は丁度一つ分の正１２面体を構成する頂点だけだと言うことが分かります。
従って、最大６００×４個の連立方程式を解けば４個の正１２面体を決定できます。こう言う事実が分かれば、正１２面体を構成する頂点が
得られた時点で探索を打ち切れば、計算時間を短縮することが出来ます。更に、素早く探索できるように探索する６００個の頂点を前もって
０番目の頂点から距離が小さい順に並べておけば、素早く見つけることが出来ます。この場合、６００個の頂点すべてをソートする必要はなく、
確実に見つかる範囲に頂点だけ集めれば良いです。
或いは「正１２面体のストローの模型」を眺めていれば誰でも気が付くことですが、「正１２面体の頂点対の最大距離」より遠い頂点は連立方程式を
解くまでもなく無視できるので、連立方程式を解く前にずっと簡単な距離を計算すれば計算時間が短縮できるハズです。
但し、これをする為にも時間が掛かるので、実際に計算時間が短縮されるかは実験してみる必要があります。
これが出来れば、全体の胞：正１２面体１２０個を求めれば良いです。これも１２０個求まった時点で探索を止めれば計算時間を短縮出来ます。
０番目の頂点に隣接する正１２面体４個を見つけるのに１分かかれば、単純なプログラムでは１０時間かかりますが、一度計算すれば、
結果をファイルに保存して、必要になればファイルから読み込んで使えば良いので、計算時間はそれほど重要でないかも？寝ている間に計算できます。
容量がなくなっているので新しい記述をする度にどっかの図とプログラムを削除して、容量を確保しています。もう限界だし、
正多胞体以前のプログラムが理解でき、大学の一般教養程度の数学を理解していれば、自力でプログラミング出来るハズですから、プログラムは載せません。
計算結果は

len(cube.v)= 600 
cube.v= [[array([2, 2, 0, 0]), [[0, 1, 2, 3], [0, 1, 2, 3, 4, 5], [0, 49, 72, 75]]], 
[array([ 2, -2,  0,  0]), [[4, 5, 6, 7], [6, 7, 8, 9, 10, 11], [1, 55, 84, 99]]], 
[array([-2,  2,  0,  0]), [[8, 9, 10, 11], [12, 13, 14, 15, 16, 17], [2, 60, 87, 96]]], 
[array([-2, -2,  0,  0]), [[12, 13, 14, 15], [18, 19, 20, 21, 22, 23], [3, 67, 108, 111]]], 
[array([2, 0, 2, 0]), [[16, 17, 18, 19], [24, 25, 26, 27, 28, 29], [4, 48, 74, 76]]], 
[array([ 2,  0, -2,  0]), [[20, 21, 22, 23], [30, 31, 32, 33, 34, 35], [5, 54, 86, 100]]], 
[array([-2,  0,  2,  0]), [[24, 25, 26, 27], [36, 37, 38, 39, 40, 41], [6, 62, 88, 98]]], 
[array([-2,  0, -2,  0]), [[28, 29, 30, 31], [42, 43, 44, 45, 46, 47], [7, 66, 110, 112]]], 
[array([2, 0, 0, 2]), [[32, 33, 34, 35], [48, 49, 50, 51, 52, 53], [8, 50, 73, 77]]], 
[array([ 2,  0,  0, -2]), [[36, 37, 38, 39], [54, 55, 56, 57, 58, 59], [9, 56, 85, 101]]], 
[array([-2,  0,  0,  2]), [[40, 41, 42, 43], [60, 61, 62, 63, 64, 65], [10, 61, 89, 97]]], 
[array([-2,  0,  0, -2]), [[44, 45, 46, 47], [66, 67, 68, 69, 70, 71], [11, 68, 109, 113]]], 
[array([0, 2, 2, 0]), [[48, 49, 50, 51], [72, 73, 74, 75, 76, 77], [12, 52, 78, 82]]], 
[array([ 0,  2, -2,  0]), [[52, 53, 54, 55], [78, 79, 80, 81, 82, 83], [13, 63, 90, 106]]], 
[array([ 0, -2,  2,  0]), [[56, 57, 58, 59], [84, 85, 86, 87, 88, 89], [14, 58, 94, 102]]], 
[array([ 0, -2, -2,  0]), [[60, 61, 62, 63], [90, 91, 92, 93, 94, 95], [15, 70, 114, 118]]], 
[array([0, 2, 0, 2]), [[64, 65, 66, 67], [96, 97, 98, 99, 100, 101], [16, 51, 79, 81]]], 
[array([ 0,  2,  0, -2]), [[68, 69, 70, 71], [102, 103, 104, 105, 106, 107], [17, 57, 93, 103]]], 
[array([ 0, -2,  0,  2]), [[72, 73, 74, 75], [108, 109, 110, 111, 112, 113], [18, 65, 91, 105]]], 
[array([ 0, -2,  0, -2]), [[76, 77, 78, 79], [114, 115, 116, 117, 118, 119], [19, 69, 115, 117]]], 
[array([0, 0, 2, 2]), [[80, 81, 82, 83], [120, 121, 122, 123, 124, 125], [20, 53, 80, 83]]], 
[array([ 0,  0,  2, -2]), [[84, 85, 86, 87], [126, 127, 128, 129, 130, 131], [21, 64, 92, 107]]], 
[array([ 0,  0, -2,  2]), [[88, 89, 90, 91], [132, 133, 134, 135, 136, 137], [22, 59, 95, 104]]], 
[array([ 0,  0, -2, -2]), [[92, 93, 94, 95], [138, 139, 140, 141, 142, 143], [23, 71, 116, 119]]], 
[array([2.23606798, 1.        , 1.        , 1.        ]), [[96, 97, 98, 99], [144, 145, 146, 147, 148, 149], [24, 72, 73, 74]]], 
[array([-2.23606798,  1.        ,  1.        ,  1.        ]), [[100, 101, 102, 103], [150, 151, 152, 153, 154, 155], [25, 96, 97, 98]]], 
[array([1.        , 2.23606798, 1.        , 1.        ]), [[104, 105, 106, 107], [156, 157, 158, 159, 160, 161], [24, 75, 78, 81]]], 
[array([ 1.        , -2.23606798,  1.        ,  1.        ]), [[108, 109, 110, 111], [162, 163, 164, 165, 166, 167], [26, 99, 102, 105]]], 
[array([1.        , 1.        , 2.23606798, 1.        ]), [[112, 113, 114, 115], [168, 169, 170, 171, 172, 173], [24, 76, 80, 82]]], 
[array([ 1.        ,  1.        , -2.23606798,  1.        ]), [[116, 117, 118, 119], [174, 175, 176, 177, 178, 179], [27, 100, 104, 106]]], 
[array([1.        , 1.        , 1.        , 2.23606798]), [[120, 121, 122, 123], [180, 181, 182, 183, 184, 185], [24, 77, 79, 83]]], 
[array([ 1.        ,  1.        ,  1.        , -2.23606798]), [[124, 125, 126, 127], [186, 187, 188, 189, 190, 191], [28, 101, 103, 107]]], 
[array([ 2.23606798,  1.        ,  1.        , -1.        ]), [[128, 129, 130, 131], [192, 193, 194, 195, 196, 197], [28, 48, 72, 85]]], 
[array([-2.23606798,  1.        ,  1.        , -1.        ]), [[132, 133, 134, 135], [198, 199, 200, 201, 202, 203], [6, 29, 96, 109]]], 
[array([ 1.        ,  2.23606798,  1.        , -1.        ]), [[136, 137, 138, 139], [204, 205, 206, 207, 208, 209], [0, 28, 78, 93]]], 
[array([ 1.        , -2.23606798,  1.        , -1.        ]), [[140, 141, 142, 143], [210, 211, 212, 213, 214, 215], [1, 30, 102, 117]]], 
[array([ 1.        ,  1.        ,  2.23606798, -1.        ]), [[144, 145, 146, 147], [216, 217, 218, 219, 220, 221], [28, 52, 76, 92]]], 
[array([ 1.        ,  1.        , -2.23606798, -1.        ]), [[148, 149, 150, 151], [222, 223, 224, 225, 226, 227], [13, 31, 100, 116]]], 
[array([ 1.        ,  1.        , -1.        ,  2.23606798]), [[152, 153, 154, 155], [228, 229, 230, 231, 232, 233], [8, 27, 79, 95]]], 
[array([ 1.        ,  1.        , -1.        , -2.23606798]), [[156, 157, 158, 159], [234, 235, 236, 237, 238, 239], [9, 31, 103, 119]]], 
[array([ 2.23606798,  1.        , -1.        ,  1.        ]), [[160, 161, 162, 163], [240, 241, 242, 243, 244, 245], [27, 49, 73, 86]]], 
[array([-2.23606798,  1.        , -1.        ,  1.        ]), [[164, 165, 166, 167], [246, 247, 248, 249, 250, 251], [2, 32, 97, 110]]], 
[array([ 1.        ,  2.23606798, -1.        ,  1.        ]), [[168, 169, 170, 171], [252, 253, 254, 255, 256, 257], [27, 51, 75, 90]]], 
[array([ 1.        , -2.23606798, -1.        ,  1.        ]), [[172, 173, 174, 175], [258, 259, 260, 261, 262, 263], [18, 33, 99, 114]]], 
[array([ 1.        , -1.        ,  2.23606798,  1.        ]), [[176, 177, 178, 179], [264, 265, 266, 267, 268, 269], [4, 26, 80, 94]]], 
[array([ 1.        , -1.        , -2.23606798,  1.        ]), [[180, 181, 182, 183], [270, 271, 272, 273, 274, 275], [5, 33, 104, 118]]], 
[array([ 1.        , -1.        ,  1.        ,  2.23606798]), [[184, 185, 186, 187], [276, 277, 278, 279, 280, 281], [26, 53, 77, 91]]], 
[array([ 1.        , -1.        ,  1.        , -2.23606798]), [[188, 189, 190, 191], [282, 283, 284, 285, 286, 287], [21, 30, 101, 115]]], 
[array([ 2.23606798,  1.        , -1.        , -1.        ]), [[192, 193, 194, 195], [288, 289, 290, 291, 292, 293], [31, 49, 54, 85]]], 
[array([-2.23606798,  1.        , -1.        , -1.        ]), [[196, 197, 198, 199], [294, 295, 296, 297, 298, 299], [2, 34, 66, 109]]], 
[array([ 1.        ,  2.23606798, -1.        , -1.        ]), [[200, 201, 202, 203], [300, 301, 302, 303, 304, 305], [0, 31, 57, 90]]], 
[array([ 1.        , -2.23606798, -1.        , -1.        ]), [[204, 205, 206, 207], [306, 307, 308, 309, 310, 311], [1, 35, 69, 114]]], 
[array([ 1.        , -1.        ,  2.23606798, -1.        ]), [[208, 209, 210, 211], [312, 313, 314, 315, 316, 317], [4, 30, 58, 92]]], 
[array([ 1.        , -1.        , -2.23606798, -1.        ]), [[212, 213, 214, 215], [318, 319, 320, 321, 322, 323], [5, 35, 70, 116]]], 
[array([ 1.        , -1.        , -1.        ,  2.23606798]), [[216, 217, 218, 219], [324, 325, 326, 327, 328, 329], [8, 33, 59, 91]]], 
[array([ 1.        , -1.        , -1.        , -2.23606798]), [[220, 221, 222, 223], [330, 331, 332, 333, 334, 335], [9, 35, 71, 115]]], 
[array([ 2.23606798, -1.        ,  1.        ,  1.        ]), [[224, 225, 226, 227], [336, 337, 338, 339, 340, 341], [26, 50, 74, 84]]], 
[array([-2.23606798, -1.        ,  1.        ,  1.        ]), [[228, 229, 230, 231], [342, 343, 344, 345, 346, 347], [10, 36, 98, 108]]], 
[array([-1.        ,  2.23606798,  1.        ,  1.        ]), [[232, 233, 234, 235], [348, 349, 350, 351, 352, 353], [12, 25, 81, 87]]], 
[array([-1.        , -2.23606798,  1.        ,  1.        ]), [[236, 237, 238, 239], [354, 355, 356, 357, 358, 359], [14, 36, 105, 111]]], 
[array([-1.        ,  1.        ,  2.23606798,  1.        ]), [[240, 241, 242, 243], [360, 361, 362, 363, 364, 365], [20, 25, 82, 88]]], 
[array([-1.        ,  1.        , -2.23606798,  1.        ]), [[244, 245, 246, 247], [366, 367, 368, 369, 370, 371], [22, 32, 106, 112]]], 
[array([-1.        ,  1.        ,  1.        ,  2.23606798]), [[248, 249, 250, 251], [372, 373, 374, 375, 376, 377], [16, 25, 83, 89]]], 
[array([-1.        ,  1.        ,  1.        , -2.23606798]), [[252, 253, 254, 255], [378, 379, 380, 381, 382, 383], [17, 29, 107, 113]]], 
[array([ 2.23606798, -1.        ,  1.        , -1.        ]), [[256, 257, 258, 259], [384, 385, 386, 387, 388, 389], [30, 48, 56, 84]]], 
[array([-2.23606798, -1.        ,  1.        , -1.        ]), [[260, 261, 262, 263], [390, 391, 392, 393, 394, 395], [6, 37, 68, 108]]], 
[array([-1.        ,  2.23606798,  1.        , -1.        ]), [[264, 265, 266, 267], [396, 397, 398, 399, 400, 401], [12, 29, 60, 93]]], 
[array([-1.        , -2.23606798,  1.        , -1.        ]), [[268, 269, 270, 271], [402, 403, 404, 405, 406, 407], [3, 14, 37, 117]]], 
[array([-1.        ,  1.        ,  2.23606798, -1.        ]), [[272, 273, 274, 275], [408, 409, 410, 411, 412, 413], [29, 52, 64, 88]]], 
[array([-1.        ,  1.        , -2.23606798, -1.        ]), [[276, 277, 278, 279], [414, 415, 416, 417, 418, 419], [13, 23, 34, 112]]], 
[array([-1.        ,  1.        , -1.        ,  2.23606798]), [[280, 281, 282, 283], [420, 421, 422, 423, 424, 425], [16, 32, 61, 95]]], 
[array([-1.        ,  1.        , -1.        , -2.23606798]), [[284, 285, 286, 287], [426, 427, 428, 429, 430, 431], [11, 17, 34, 119]]], 
[array([ 2.23606798, -1.        , -1.        ,  1.        ]), [[288, 289, 290, 291], [432, 433, 434, 435, 436, 437], [33, 50, 55, 86]]], 
[array([-2.23606798, -1.        , -1.        ,  1.        ]), [[292, 293, 294, 295], [438, 439, 440, 441, 442, 443], [10, 38, 67, 110]]], 
[array([-1.        ,  2.23606798, -1.        ,  1.        ]), [[296, 297, 298, 299], [444, 445, 446, 447, 448, 449], [32, 51, 63, 87]]], 
[array([-1.        , -2.23606798, -1.        ,  1.        ]), [[300, 301, 302, 303], [450, 451, 452, 453, 454, 455], [15, 18, 38, 111]]], 
[array([-1.        , -1.        ,  2.23606798,  1.        ]), [[304, 305, 306, 307], [456, 457, 458, 459, 460, 461], [20, 36, 62, 94]]], 
[array([-1.        , -1.        , -2.23606798,  1.        ]), [[308, 309, 310, 311], [462, 463, 464, 465, 466, 467], [7, 22, 38, 118]]], 
[array([-1.        , -1.        ,  1.        ,  2.23606798]), [[312, 313, 314, 315], [468, 469, 470, 471, 472, 473], [36, 53, 65, 89]]], 
[array([-1.        , -1.        ,  1.        , -2.23606798]), [[316, 317, 318, 319], [474, 475, 476, 477, 478, 479], [19, 21, 37, 113]]], 
[array([ 2.23606798, -1.        , -1.        , -1.        ]), [[320, 321, 322, 323], [480, 481, 482, 483, 484, 485], [35, 54, 55, 56]]], 
[array([-2.23606798, -1.        , -1.        , -1.        ]), [[324, 325, 326, 327], [486, 487, 488, 489, 490, 491], [39, 66, 67, 68]]], 
[array([-1.        ,  2.23606798, -1.        , -1.        ]), [[328, 329, 330, 331], [492, 493, 494, 495, 496, 497], [34, 57, 60, 63]]], 
[array([-1.        , -2.23606798, -1.        , -1.        ]), [[332, 333, 334, 335], [498, 499, 500, 501, 502, 503], [3, 15, 39, 69]]], 
[array([-1.        , -1.        ,  2.23606798, -1.        ]), [[336, 337, 338, 339], [504, 505, 506, 507, 508, 509], [37, 58, 62, 64]]], 
[array([-1.        , -1.        , -2.23606798, -1.        ]), [[340, 341, 342, 343], [510, 511, 512, 513, 514, 515], [7, 23, 39, 70]]], 
[array([-1.        , -1.        , -1.        ,  2.23606798]), [[344, 345, 346, 347], [516, 517, 518, 519, 520, 521], [38, 59, 61, 65]]], 
[array([-1.        , -1.        , -1.        , -2.23606798]), [[348, 349, 350, 351], [522, 523, 524, 525, 526, 527], [11, 19, 39, 71]]], 
[array([0.38196601, 1.61803399, 1.61803399, 1.61803399]), [[352, 353, 354, 355], [160, 172, 184, 528, 529, 530], [24, 81, 82, 83]]], 
[array([-0.38196601,  1.61803399,  1.61803399,  1.61803399]), [[352, 356, 357, 358], [352, 364, 376, 528, 529, 530], [25, 81, 82, 83]]], 
[array([1.61803399, 0.38196601, 1.61803399, 1.61803399]), [[359, 360, 361, 362], [148, 173, 183, 531, 532, 533], [24, 74, 77, 80]]], 
[array([ 1.61803399, -0.38196601,  1.61803399,  1.61803399]), [[359, 363, 364, 365], [268, 280, 340, 531, 532, 533], [26, 74, 77, 80]]], 
[array([1.61803399, 1.61803399, 0.38196601, 1.61803399]), [[366, 367, 368, 369], [149, 159, 185, 534, 535, 536], [24, 73, 75, 79]]], 
[array([ 1.61803399,  1.61803399, -0.38196601,  1.61803399]), [[366, 370, 371, 372], [232, 244, 256, 534, 535, 536], [27, 73, 75, 79]]], 
[array([1.61803399, 1.61803399, 1.61803399, 0.38196601]), [[373, 374, 375, 376], [147, 161, 171, 537, 538, 539], [24, 72, 76, 78]]], 
[array([ 1.61803399,  1.61803399,  1.61803399, -0.38196601]), [[373, 377, 378, 379], [196, 208, 220, 537, 538, 539], [28, 72, 76, 78]]], 
[array([ 0.38196601,  1.61803399,  1.61803399, -1.61803399]), [[380, 381, 382, 383], [190, 209, 219, 540, 541, 542], [28, 52, 93, 107]]], 
[array([-0.38196601,  1.61803399,  1.61803399, -1.61803399]), [[380, 384, 385, 386], [382, 401, 411, 540, 541, 542], [29, 52, 93, 107]]], 
[array([ 1.61803399,  0.38196601,  1.61803399, -1.61803399]), [[387, 388, 389, 390], [189, 195, 221, 543, 544, 545], [28, 48, 92, 101]]], 
[array([ 1.61803399, -0.38196601,  1.61803399, -1.61803399]), [[387, 391, 392, 393], [286, 317, 387, 543, 544, 545], [30, 48, 92, 101]]], 
[array([ 1.61803399,  1.61803399,  0.38196601, -1.61803399]), [[394, 395, 396, 397], [191, 197, 207, 546, 547, 548], [0, 28, 85, 103]]], 
[array([ 1.61803399,  1.61803399, -0.38196601, -1.61803399]), [[394, 398, 399, 400], [238, 293, 303, 546, 547, 548], [0, 31, 85, 103]]], 
[array([ 1.61803399,  1.61803399, -1.61803399,  0.38196601]), [[401, 402, 403, 404], [177, 243, 257, 549, 550, 551], [27, 49, 90, 100]]], 
[array([ 1.61803399,  1.61803399, -1.61803399, -0.38196601]), [[401, 405, 406, 407], [226, 291, 305, 549, 550, 551], [31, 49, 90, 100]]], 
[array([ 0.38196601,  1.61803399, -1.61803399,  1.61803399]), [[408, 409, 410, 411], [178, 233, 255, 552, 553, 554], [27, 51, 95, 106]]], 
[array([-0.38196601,  1.61803399, -1.61803399,  1.61803399]), [[408, 412, 413, 414], [370, 425, 447, 552, 553, 554], [32, 51, 95, 106]]], 
[array([ 1.61803399,  0.38196601, -1.61803399,  1.61803399]), [[415, 416, 417, 418], [179, 231, 245, 555, 556, 557], [8, 27, 86, 104]]], 
[array([ 1.61803399, -0.38196601, -1.61803399,  1.61803399]), [[415, 419, 420, 421], [274, 327, 437, 555, 556, 557], [8, 33, 86, 104]]], 
[array([ 1.61803399, -1.61803399,  0.38196601,  1.61803399]), [[422, 423, 424, 425], [165, 281, 339, 558, 559, 560], [26, 50, 91, 99]]], 
[array([ 1.61803399, -1.61803399, -0.38196601,  1.61803399]), [[422, 426, 427, 428], [262, 329, 435, 558, 559, 560], [33, 50, 91, 99]]], 
[array([ 1.61803399, -1.61803399,  1.61803399,  0.38196601]), [[429, 430, 431, 432], [167, 267, 341, 561, 562, 563], [4, 26, 84, 102]]], 
[array([ 1.61803399, -1.61803399,  1.61803399, -0.38196601]), [[429, 433, 434, 435], [214, 315, 389, 561, 562, 563], [4, 30, 84, 102]]], 
[array([ 0.38196601,  1.61803399, -1.61803399, -1.61803399]), [[436, 437, 438, 439], [225, 239, 304, 564, 565, 566], [13, 31, 57, 119]]], 
[array([-0.38196601,  1.61803399, -1.61803399, -1.61803399]), [[436, 440, 441, 442], [417, 431, 496, 564, 565, 566], [13, 34, 57, 119]]], 
[array([ 1.61803399,  0.38196601, -1.61803399, -1.61803399]), [[443, 444, 445, 446], [227, 237, 292, 567, 568, 569], [9, 31, 54, 116]]], 
[array([ 1.61803399, -0.38196601, -1.61803399, -1.61803399]), [[443, 447, 448, 449], [323, 333, 484, 567, 568, 569], [9, 35, 54, 116]]], 
[array([ 1.61803399, -1.61803399,  0.38196601, -1.61803399]), [[450, 451, 452, 453], [213, 287, 388, 570, 571, 572], [1, 30, 56, 115]]], 
[array([ 1.61803399, -1.61803399, -0.38196601, -1.61803399]), [[450, 454, 455, 456], [309, 335, 485, 570, 571, 572], [1, 35, 56, 115]]], 
[array([ 1.61803399, -1.61803399, -1.61803399,  0.38196601]), [[457, 458, 459, 460], [263, 273, 436, 573, 574, 575], [5, 33, 55, 114]]], 
[array([ 1.61803399, -1.61803399, -1.61803399, -0.38196601]), [[457, 461, 462, 463], [311, 321, 483, 573, 574, 575], [5, 35, 55, 114]]], 
[array([ 0.38196601, -1.61803399,  1.61803399,  1.61803399]), [[464, 465, 466, 467], [166, 269, 279, 576, 577, 578], [26, 53, 94, 105]]], 
[array([-0.38196601, -1.61803399,  1.61803399,  1.61803399]), [[464, 468, 469, 470], [358, 461, 471, 576, 577, 578], [36, 53, 94, 105]]], 
[array([-1.61803399,  0.38196601,  1.61803399,  1.61803399]), [[471, 472, 473, 474], [154, 363, 377, 579, 580, 581], [20, 25, 89, 98]]], 
[array([-1.61803399, -0.38196601,  1.61803399,  1.61803399]), [[471, 475, 476, 477], [346, 459, 473, 579, 580, 581], [20, 36, 89, 98]]], 
[array([-1.61803399,  1.61803399,  0.38196601,  1.61803399]), [[478, 479, 480, 481], [155, 353, 375, 582, 583, 584], [16, 25, 87, 97]]], 
[array([-1.61803399,  1.61803399, -0.38196601,  1.61803399]), [[478, 482, 483, 484], [250, 423, 449, 582, 583, 584], [16, 32, 87, 97]]], 
[array([-1.61803399,  1.61803399,  1.61803399,  0.38196601]), [[485, 486, 487, 488], [153, 351, 365, 585, 586, 587], [12, 25, 88, 96]]], 
[array([-1.61803399,  1.61803399,  1.61803399, -0.38196601]), [[485, 489, 490, 491], [202, 399, 413, 585, 586, 587], [12, 29, 88, 96]]], 
[array([ 0.38196601, -1.61803399,  1.61803399, -1.61803399]), [[492, 493, 494, 495], [215, 285, 316, 588, 589, 590], [21, 30, 58, 117]]], 
[array([-0.38196601, -1.61803399,  1.61803399, -1.61803399]), [[492, 496, 497, 498], [407, 477, 508, 588, 589, 590], [21, 37, 58, 117]]], 
[array([-1.61803399,  0.38196601,  1.61803399, -1.61803399]), [[499, 500, 501, 502], [201, 383, 412, 591, 592, 593], [6, 29, 64, 113]]], 
[array([-1.61803399, -0.38196601,  1.61803399, -1.61803399]), [[499, 503, 504, 505], [393, 479, 509, 591, 592, 593], [6, 37, 64, 113]]], 
[array([-1.61803399,  1.61803399,  0.38196601, -1.61803399]), [[506, 507, 508, 509], [203, 381, 400, 594, 595, 596], [17, 29, 60, 109]]], 
[array([-1.61803399,  1.61803399, -0.38196601, -1.61803399]), [[506, 510, 511, 512], [299, 429, 495, 594, 595, 596], [17, 34, 60, 109]]], 
[array([-1.61803399,  1.61803399, -1.61803399,  0.38196601]), [[513, 514, 515, 516], [249, 371, 448, 597, 598, 599], [2, 32, 63, 112]]], 
[array([-1.61803399,  1.61803399, -1.61803399, -0.38196601]), [[513, 517, 518, 519], [297, 419, 497, 597, 598, 599], [2, 34, 63, 112]]], 
[array([ 0.38196601, -1.61803399, -1.61803399,  1.61803399]), [[520, 521, 522, 523], [261, 275, 328, 600, 601, 602], [18, 33, 59, 118]]], 
[array([-0.38196601, -1.61803399, -1.61803399,  1.61803399]), [[520, 524, 525, 526], [453, 467, 520, 600, 601, 602], [18, 38, 59, 118]]], 
[array([-1.61803399,  0.38196601, -1.61803399,  1.61803399]), [[527, 528, 529, 530], [251, 369, 424, 603, 604, 605], [22, 32, 61, 110]]], 
[array([-1.61803399, -0.38196601, -1.61803399,  1.61803399]), [[527, 531, 532, 533], [443, 465, 519, 603, 604, 605], [22, 38, 61, 110]]], 
[array([-1.61803399, -1.61803399,  0.38196601,  1.61803399]), [[534, 535, 536, 537], [345, 359, 472, 606, 607, 608], [10, 36, 65, 111]]], 
[array([-1.61803399, -1.61803399, -0.38196601,  1.61803399]), [[534, 538, 539, 540], [441, 455, 521, 606, 607, 608], [10, 38, 65, 111]]], 
[array([-1.61803399, -1.61803399,  1.61803399,  0.38196601]), [[541, 542, 543, 544], [347, 357, 460, 609, 610, 611], [14, 36, 62, 108]]], 
[array([-1.61803399, -1.61803399,  1.61803399, -0.38196601]), [[541, 545, 546, 547], [395, 405, 507, 609, 610, 611], [14, 37, 62, 108]]], 
[array([ 0.38196601, -1.61803399, -1.61803399, -1.61803399]), [[548, 549, 550, 551], [310, 322, 334, 612, 613, 614], [35, 69, 70, 71]]], 
[array([-0.38196601, -1.61803399, -1.61803399, -1.61803399]), [[548, 552, 553, 554], [502, 514, 526, 612, 613, 614], [39, 69, 70, 71]]], 
[array([-1.61803399,  0.38196601, -1.61803399, -1.61803399]), [[555, 556, 557, 558], [298, 418, 430, 615, 616, 617], [11, 23, 34, 66]]], 
[array([-1.61803399, -0.38196601, -1.61803399, -1.61803399]), [[555, 559, 560, 561], [490, 515, 525, 615, 616, 617], [11, 23, 39, 66]]], 
[array([-1.61803399, -1.61803399,  0.38196601, -1.61803399]), [[562, 563, 564, 565], [394, 406, 478, 618, 619, 620], [3, 19, 37, 68]]], 
[array([-1.61803399, -1.61803399, -0.38196601, -1.61803399]), [[562, 566, 567, 568], [491, 501, 527, 618, 619, 620], [3, 19, 39, 68]]], 
[array([-1.61803399, -1.61803399, -1.61803399,  0.38196601]), [[569, 570, 571, 572], [442, 454, 466, 621, 622, 623], [7, 15, 38, 67]]], 
[array([-1.61803399, -1.61803399, -1.61803399, -0.38196601]), [[569, 573, 574, 575], [489, 503, 513, 621, 622, 623], [7, 15, 39, 67]]], 
[array([2.61803399, 0.61803399, 0.61803399, 0.61803399]), [[96, 576, 577, 578], [144, 145, 146, 624, 625, 626], [40, 72, 73, 74]]], 
[array([-2.61803399,  0.61803399,  0.61803399,  0.61803399]), [[100, 579, 580, 581], [150, 151, 152, 627, 628, 629], [41, 96, 97, 98]]], 
[array([0.61803399, 2.61803399, 0.61803399, 0.61803399]), [[104, 582, 583, 584], [156, 157, 158, 630, 631, 632], [42, 75, 78, 81]]], 
[array([ 0.61803399, -2.61803399,  0.61803399,  0.61803399]), [[108, 585, 586, 587], [162, 163, 164, 633, 634, 635], [43, 99, 102, 105]]], 
[array([0.61803399, 0.61803399, 2.61803399, 0.61803399]), [[112, 588, 589, 590], [168, 169, 170, 636, 637, 638], [44, 76, 80, 82]]], 
[array([ 0.61803399,  0.61803399, -2.61803399,  0.61803399]), [[116, 591, 592, 593], [174, 175, 176, 639, 640, 641], [45, 100, 104, 106]]], 
[array([0.61803399, 0.61803399, 0.61803399, 2.61803399]), [[120, 594, 595, 596], [180, 181, 182, 642, 643, 644], [46, 77, 79, 83]]], 
[array([ 0.61803399,  0.61803399,  0.61803399, -2.61803399]), [[124, 597, 598, 599], [186, 187, 188, 645, 646, 647], [47, 101, 103, 107]]], 
[array([ 2.61803399,  0.61803399,  0.61803399, -0.61803399]), [[128, 600, 601, 602], [192, 193, 194, 624, 648, 649], [40, 48, 72, 85]]], 
[array([-2.61803399,  0.61803399,  0.61803399, -0.61803399]), [[132, 603, 604, 605], [198, 199, 200, 627, 650, 651], [6, 41, 96, 109]]], 
[array([ 0.61803399,  2.61803399,  0.61803399, -0.61803399]), [[136, 606, 607, 608], [204, 205, 206, 632, 652, 653], [0, 42, 78, 93]]], 
[array([ 0.61803399, -2.61803399,  0.61803399, -0.61803399]), [[140, 609, 610, 611], [210, 211, 212, 635, 654, 655], [1, 43, 102, 117]]], 
[array([ 0.61803399,  0.61803399,  2.61803399, -0.61803399]), [[144, 612, 613, 614], [216, 217, 218, 636, 656, 657], [44, 52, 76, 92]]], 
[array([ 0.61803399,  0.61803399, -2.61803399, -0.61803399]), [[148, 615, 616, 617], [222, 223, 224, 639, 658, 659], [13, 45, 100, 116]]], 
[array([ 0.61803399,  0.61803399, -0.61803399,  2.61803399]), [[152, 618, 619, 620], [228, 229, 230, 644, 660, 661], [8, 46, 79, 95]]], 
[array([ 0.61803399,  0.61803399, -0.61803399, -2.61803399]), [[156, 621, 622, 623], [234, 235, 236, 647, 662, 663], [9, 47, 103, 119]]], 
[array([ 2.61803399,  0.61803399, -0.61803399,  0.61803399]), [[160, 624, 625, 626], [240, 241, 242, 626, 664, 665], [40, 49, 73, 86]]], 
[array([-2.61803399,  0.61803399, -0.61803399,  0.61803399]), [[164, 627, 628, 629], [246, 247, 248, 629, 666, 667], [2, 41, 97, 110]]], 
[array([ 0.61803399,  2.61803399, -0.61803399,  0.61803399]), [[168, 630, 631, 632], [252, 253, 254, 630, 668, 669], [42, 51, 75, 90]]], 
[array([ 0.61803399, -2.61803399, -0.61803399,  0.61803399]), [[172, 633, 634, 635], [258, 259, 260, 633, 670, 671], [18, 43, 99, 114]]], 
[array([ 0.61803399, -0.61803399,  2.61803399,  0.61803399]), [[176, 636, 637, 638], [264, 265, 266, 638, 672, 673], [4, 44, 80, 94]]], 
[array([ 0.61803399, -0.61803399, -2.61803399,  0.61803399]), [[180, 639, 640, 641], [270, 271, 272, 641, 674, 675], [5, 45, 104, 118]]],
 [array([ 0.61803399, -0.61803399,  0.61803399,  2.61803399]), [[184, 642, 643, 644], [276, 277, 278, 642, 676, 677], [46, 53, 77, 91]]], 
[array([ 0.61803399, -0.61803399,  0.61803399, -2.61803399]), [[188, 645, 646, 647], [282, 283, 284, 645, 678, 679], [21, 47, 101, 115]]], 
[array([ 2.61803399,  0.61803399, -0.61803399, -0.61803399]), [[192, 648, 649, 650], [288, 289, 290, 649, 664, 680], [40, 49, 54, 85]]], 
[array([-2.61803399,  0.61803399, -0.61803399, -0.61803399]), [[196, 651, 652, 653], [294, 295, 296, 651, 666, 681], [2, 41, 66, 109]]], 
[array([ 0.61803399,  2.61803399, -0.61803399, -0.61803399]), [[200, 654, 655, 656], [300, 301, 302, 652, 669, 682], [0, 42, 57, 90]]],
 [array([ 0.61803399, -2.61803399, -0.61803399, -0.61803399]), [[204, 657, 658, 659], [306, 307, 308, 654, 671, 683], [1, 43, 69, 114]]], 
[array([ 0.61803399, -0.61803399,  2.61803399, -0.61803399]), [[208, 660, 661, 662], [312, 313, 314, 657, 672, 684], [4, 44, 58, 92]]], 
[array([ 0.61803399, -0.61803399, -2.61803399, -0.61803399]), [[212, 663, 664, 665], [318, 319, 320, 659, 674, 685], [5, 45, 70, 116]]], 
[array([ 0.61803399, -0.61803399, -0.61803399,  2.61803399]), [[216, 666, 667, 668], [324, 325, 326, 660, 677, 686], [8, 46, 59, 91]]], 
[array([ 0.61803399, -0.61803399, -0.61803399, -2.61803399]), [[220, 669, 670, 671], [330, 331, 332, 662, 679, 687], [9, 47, 71, 115]]], 
[array([ 2.61803399, -0.61803399,  0.61803399,  0.61803399]), [[224, 672, 673, 674], [336, 337, 338, 625, 688, 689], [40, 50, 74, 84]]], 
[array([-2.61803399, -0.61803399,  0.61803399,  0.61803399]), [[228, 675, 676, 677], [342, 343, 344, 628, 690, 691], [10, 41, 98, 108]]], 
[array([-0.61803399,  2.61803399,  0.61803399,  0.61803399]), [[232, 678, 679, 680], [348, 349, 350, 631, 692, 693], [12, 42, 81, 87]]], 
[array([-0.61803399, -2.61803399,  0.61803399,  0.61803399]), [[236, 681, 682, 683], [354, 355, 356, 634, 694, 695], [14, 43, 105, 111]]], 
[array([-0.61803399,  0.61803399,  2.61803399,  0.61803399]), [[240, 684, 685, 686], [360, 361, 362, 637, 696, 697], [20, 44, 82, 88]]], 
[array([-0.61803399,  0.61803399, -2.61803399,  0.61803399]), [[244, 687, 688, 689], [366, 367, 368, 640, 698, 699], [22, 45, 106, 112]]], 
[array([-0.61803399,  0.61803399,  0.61803399,  2.61803399]), [[248, 690, 691, 692], [372, 373, 374, 643, 700, 701], [16, 46, 83, 89]]], 
[array([-0.61803399,  0.61803399,  0.61803399, -2.61803399]), [[252, 693, 694, 695], [378, 379, 380, 646, 702, 703], [17, 47, 107, 113]]], 
[array([ 2.61803399, -0.61803399,  0.61803399, -0.61803399]), [[256, 696, 697, 698], [384, 385, 386, 648, 689, 704], [40, 48, 56, 84]]], 
[array([-2.61803399, -0.61803399,  0.61803399, -0.61803399]), [[260, 699, 700, 701], [390, 391, 392, 650, 691, 705], [6, 41, 68, 108]]], 
[array([-0.61803399,  2.61803399,  0.61803399, -0.61803399]), [[264, 702, 703, 704], [396, 397, 398, 653, 692, 706], [12, 42, 60, 93]]], 
[array([-0.61803399, -2.61803399,  0.61803399, -0.61803399]), [[268, 705, 706, 707], [402, 403, 404, 655, 694, 707], [3, 14, 43, 117]]], 
[array([-0.61803399,  0.61803399,  2.61803399, -0.61803399]), [[272, 708, 709, 710], [408, 409, 410, 656, 697, 708], [44, 52, 64, 88]]], 
[array([-0.61803399,  0.61803399, -2.61803399, -0.61803399]), [[276, 711, 712, 713], [414, 415, 416, 658, 699, 709], [13, 23, 45, 112]]], 
[array([-0.61803399,  0.61803399, -0.61803399,  2.61803399]), [[280, 714, 715, 716], [420, 421, 422, 661, 700, 710], [16, 46, 61, 95]]], 
[array([-0.61803399,  0.61803399, -0.61803399, -2.61803399]), [[284, 717, 718, 719], [426, 427, 428, 663, 702, 711], [11, 17, 47, 119]]], 
[array([ 2.61803399, -0.61803399, -0.61803399,  0.61803399]), [[288, 720, 721, 722], [432, 433, 434, 665, 688, 712], [40, 50, 55, 86]]], 
[array([-2.61803399, -0.61803399, -0.61803399,  0.61803399]), [[292, 723, 724, 725], [438, 439, 440, 667, 690, 713], [10, 41, 67, 110]]], 
[array([-0.61803399,  2.61803399, -0.61803399,  0.61803399]), [[296, 726, 727, 728], [444, 445, 446, 668, 693, 714], [42, 51, 63, 87]]], 
[array([-0.61803399, -2.61803399, -0.61803399,  0.61803399]), [[300, 729, 730, 731], [450, 451, 452, 670, 695, 715], [15, 18, 43, 111]]], 
[array([-0.61803399, -0.61803399,  2.61803399,  0.61803399]), [[304, 732, 733, 734], [456, 457, 458, 673, 696, 716], [20, 44, 62, 94]]], 
[array([-0.61803399, -0.61803399, -2.61803399,  0.61803399]), [[308, 735, 736, 737], [462, 463, 464, 675, 698, 717], [7, 22, 45, 118]]], 
[array([-0.61803399, -0.61803399,  0.61803399,  2.61803399]), [[312, 738, 739, 740], [468, 469, 470, 676, 701, 718], [46, 53, 65, 89]]], 
[array([-0.61803399, -0.61803399,  0.61803399, -2.61803399]), [[316, 741, 742, 743], [474, 475, 476, 678, 703, 719], [19, 21, 47, 113]]], 
[array([ 2.61803399, -0.61803399, -0.61803399, -0.61803399]), [[320, 744, 745, 746], [480, 481, 482, 680, 704, 712], [40, 54, 55, 56]]], 
[array([-2.61803399, -0.61803399, -0.61803399, -0.61803399]), [[324, 747, 748, 749], [486, 487, 488, 681, 705, 713], [41, 66, 67, 68]]], 
[array([-0.61803399,  2.61803399, -0.61803399, -0.61803399]), [[328, 750, 751, 752], [492, 493, 494, 682, 706, 714], [42, 57, 60, 63]]], 
[array([-0.61803399, -2.61803399, -0.61803399, -0.61803399]), [[332, 753, 754, 755], [498, 499, 500, 683, 707, 715], [3, 15, 43, 69]]], 
[array([-0.61803399, -0.61803399,  2.61803399, -0.61803399]), [[336, 756, 757, 758], [504, 505, 506, 684, 708, 716], [44, 58, 62, 64]]],
 [array([-0.61803399, -0.61803399, -2.61803399, -0.61803399]), [[340, 759, 760, 761], [510, 511, 512, 685, 709, 717], [7, 23, 45, 70]]], 
[array([-0.61803399, -0.61803399, -0.61803399,  2.61803399]), [[344, 762, 763, 764], [516, 517, 518, 686, 710, 718], [46, 59, 61, 65]]], 
[array([-0.61803399, -0.61803399, -0.61803399, -2.61803399]), [[348, 765, 766, 767], [522, 523, 524, 687, 711, 719], [11, 19, 47, 71]]], 
[array([2.61803399, 0.38196601, 1.        , 0.        ]), [[576, 600, 768, 769], [25, 144, 192, 624, 625, 648], [40, 48, 72, 74]]], 
[array([2.61803399, 1.        , 0.        , 0.38196601]), [[577, 624, 770, 771], [1, 145, 240, 624, 626, 664], [40, 49, 72, 73]]], 
[array([2.61803399, 0.        , 0.38196601, 1.        ]), [[578, 672, 772, 773], [49, 146, 336, 625, 626, 688], [40, 50, 73, 74]]], 
[array([0.38196601, 2.61803399, 0.        , 1.        ]), [[582, 630, 774, 775], [97, 156, 252, 630, 631, 668], [42, 51, 75, 81]]], 
[array([0.38196601, 1.        , 2.61803399, 0.        ]), [[588, 612, 776, 777], [73, 168, 216, 636, 637, 656], [44, 52, 76, 82]]], 
[array([0.38196601, 0.        , 1.        , 2.61803399]), [[594, 642, 778, 779], [121, 180, 276, 642, 643, 676], [46, 53, 77, 83]]], 
[array([1.        , 2.61803399, 0.38196601, 0.        ]), [[583, 606, 780, 781], [4, 157, 204, 630, 632, 652], [0, 42, 75, 78]]], 
[array([1.        , 0.38196601, 0.        , 2.61803399]), [[595, 618, 782, 783], [52, 181, 228, 642, 644, 660], [8, 46, 77, 79]]], 
[array([1.        , 0.        , 2.61803399, 0.38196601]), [[589, 636, 784, 785], [28, 169, 264, 636, 638, 672], [4, 44, 76, 80]]], 
[array([0.        , 2.61803399, 1.        , 0.38196601]), [[584, 678, 786, 787], [76, 158, 348, 631, 632, 692], [12, 42, 78, 81]]], 
[array([0.        , 0.38196601, 2.61803399, 1.        ]), [[590, 684, 788, 789], [124, 170, 360, 637, 638, 696], [20, 44, 80, 82]]], 
[array([0.        , 1.        , 0.38196601, 2.61803399]), [[596, 690, 790, 791], [100, 182, 372, 643, 644, 700], [16, 46, 79, 83]]], 
[array([ 2.61803399,  0.38196601, -1.        ,  0.        ]), [[625, 648, 792, 793], [30, 241, 288, 664, 665, 680], [40, 49, 54, 86]]], 
[array([ 2.61803399, -1.        ,  0.        ,  0.38196601]), [[673, 720, 794, 795], [6, 337, 432, 688, 689, 712], [40, 50, 55, 84]]], 
[array([ 2.61803399,  0.        ,  0.38196601, -1.        ]), [[601, 696, 796, 797], [54, 193, 384, 648, 649, 704], [40, 48, 56, 85]]], 
[array([ 0.38196601,  2.61803399,  0.        , -1.        ]), [[607, 654, 798, 799], [102, 205, 300, 652, 653, 682], [0, 42, 57, 93]]], 
[array([ 0.38196601, -1.        ,  2.61803399,  0.        ]), [[637, 660, 800, 801], [84, 265, 312, 672, 673, 684], [4, 44, 58, 94]]], 
[array([ 0.38196601,  0.        , -1.        ,  2.61803399]), [[619, 666, 802, 803], [132, 229, 324, 660, 661, 686], [8, 46, 59, 95]]], 
[array([-1.        ,  2.61803399,  0.38196601,  0.        ]), [[679, 702, 804, 805], [12, 349, 396, 692, 693, 706], [12, 42, 60, 87]]], 
[array([-1.        ,  0.38196601,  0.        ,  2.61803399]), [[691, 714, 806, 807], [60, 373, 420, 700, 701, 710], [16, 46, 61, 89]]], 
[array([-1.        ,  0.        ,  2.61803399,  0.38196601]), [[685, 732, 808, 809], [36, 361, 456, 696, 697, 716], [20, 44, 62, 88]]], 
[array([ 0.        ,  2.61803399, -1.        ,  0.38196601]), [[631, 726, 810, 811], [78, 253, 444, 668, 669, 714], [42, 51, 63, 90]]], 
[array([ 0.        ,  0.38196601,  2.61803399, -1.        ]), [[613, 708, 812, 813], [126, 217, 408, 656, 657, 708], [44, 52, 64, 92]]], 
[array([ 0.        , -1.        ,  0.38196601,  2.61803399]), [[643, 738, 814, 815], [108, 277, 468, 676, 677, 718], [46, 53, 65, 91]]], 
[array([ 2.61803399, -0.38196601,  1.        ,  0.        ]), [[674, 697, 768, 816], [25, 338, 385, 625, 648, 689], [40, 48, 74, 84]]], 
[array([ 2.61803399,  1.        ,  0.        , -0.38196601]), [[602, 649, 770, 817], [1, 194, 289, 624, 649, 664], [40, 49, 72, 85]]], 
[array([ 2.61803399,  0.        , -0.38196601,  1.        ]), [[626, 721, 772, 818], [49, 242, 433, 626, 665, 688], [40, 50, 73, 86]]], 
[array([-0.38196601,  2.61803399,  0.        ,  1.        ]), [[680, 727, 774, 819], [97, 350, 445, 631, 668, 693], [42, 51, 81, 87]]], 
[array([-0.38196601,  1.        ,  2.61803399,  0.        ]), [[686, 709, 776, 820], [73, 362, 409, 637, 656, 697], [44, 52, 82, 88]]], 
[array([-0.38196601,  0.        ,  1.        ,  2.61803399]), [[692, 739, 778, 821], [121, 374, 469, 643, 676, 701], [46, 53, 83, 89]]], 
[array([ 1.        ,  2.61803399, -0.38196601,  0.        ]), [[632, 655, 780, 822], [4, 254, 301, 630, 652, 669], [0, 42, 75, 90]]], 
[array([ 1.        , -0.38196601,  0.        ,  2.61803399]), [[644, 667, 782, 823], [52, 278, 325, 642, 660, 677], [8, 46, 77, 91]]], 
[array([ 1.        ,  0.        ,  2.61803399, -0.38196601]), [[614, 661, 784, 824], [28, 218, 313, 636, 657, 672], [4, 44, 76, 92]]], 
[array([ 0.        ,  2.61803399,  1.        , -0.38196601]), [[608, 703, 786, 825], [76, 206, 397, 632, 653, 692], [12, 42, 78, 93]]], 
[array([ 0.        , -0.38196601,  2.61803399,  1.        ]), [[638, 733, 788, 826], [124, 266, 457, 638, 673, 696], [20, 44, 80, 94]]], 
[array([ 0.        ,  1.        , -0.38196601,  2.61803399]), [[620, 715, 790, 827], [100, 230, 421, 644, 661, 700], [16, 46, 79, 95]]], 
[array([ 2.61803399, -0.38196601, -1.        ,  0.        ]), [[722, 744, 792, 828], [30, 434, 480, 665, 680, 712], [40, 54, 55, 86]]], 
[array([ 2.61803399, -1.        ,  0.        , -0.38196601]), [[698, 745, 794, 829], [6, 386, 481, 689, 704, 712], [40, 55, 56, 84]]], 
[array([ 2.61803399,  0.        , -0.38196601, -1.        ]), [[650, 746, 796, 830], [54, 290, 482, 649, 680, 704], [40, 54, 56, 85]]], 
[array([-0.38196601,  2.61803399,  0.        , -1.        ]), [[704, 750, 798, 831], [102, 398, 492, 653, 682, 706], [42, 57, 60, 93]]], 
[array([-0.38196601, -1.        ,  2.61803399,  0.        ]), [[734, 756, 800, 832], [84, 458, 504, 673, 684, 716], [44, 58, 62, 94]]], 
[array([-0.38196601,  0.        , -1.        ,  2.61803399]), [[716, 762, 802, 833], [132, 422, 516, 661, 686, 710], [46, 59, 61, 95]]], 
[array([-1.        ,  2.61803399, -0.38196601,  0.        ]), [[728, 751, 804, 834], [12, 446, 493, 693, 706, 714], [42, 60, 63, 87]]], 
[array([-1.        , -0.38196601,  0.        ,  2.61803399]), [[740, 763, 806, 835], [60, 470, 517, 701, 710, 718], [46, 61, 65, 89]]], 
[array([-1.        ,  0.        ,  2.61803399, -0.38196601]), [[710, 757, 808, 836], [36, 410, 505, 697, 708, 716], [44, 62, 64, 88]]], 
[array([ 0.        ,  2.61803399, -1.        , -0.38196601]), [[656, 752, 810, 837], [78, 302, 494, 669, 682, 714], [42, 57, 63, 90]]], 
[array([ 0.        , -0.38196601,  2.61803399, -1.        ]), [[662, 758, 812, 838], [126, 314, 506, 657, 684, 708], [44, 58, 64, 92]]], 
[array([ 0.        , -1.        , -0.38196601,  2.61803399]), [[668, 764, 814, 839], [108, 326, 518, 677, 686, 718], [46, 59, 65, 91]]], 
[array([-2.61803399,  0.38196601,  1.        ,  0.        ]), [[579, 603, 840, 841], [41, 150, 198, 627, 628, 650], [6, 41, 96, 98]]], 
[array([-2.61803399,  1.        ,  0.        ,  0.38196601]), [[580, 627, 842, 843], [17, 151, 246, 627, 629, 666], [2, 41, 96, 97]]], 
[array([-2.61803399,  0.        ,  0.38196601,  1.        ]), [[581, 675, 844, 845], [65, 152, 342, 628, 629, 690], [10, 41, 97, 98]]], 
[array([ 0.38196601, -2.61803399,  0.        ,  1.        ]), [[585, 633, 846, 847], [113, 162, 258, 633, 634, 670], [18, 43, 99, 105]]], 
[array([ 0.38196601,  1.        , -2.61803399,  0.        ]), [[591, 615, 848, 849], [83, 174, 222, 639, 640, 658], [13, 45, 100, 106]]], 
[array([ 0.38196601,  0.        ,  1.        , -2.61803399]), [[597, 645, 850, 851], [131, 186, 282, 645, 646, 678], [21, 47, 101, 107]]], 
[array([ 1.        , -2.61803399,  0.38196601,  0.        ]), [[586, 609, 852, 853], [11, 163, 210, 633, 635, 654], [1, 43, 99, 102]]], 
[array([ 1.        ,  0.38196601,  0.        , -2.61803399]), [[598, 621, 854, 855], [59, 187, 234, 645, 647, 662], [9, 47, 101, 103]]], 
[array([ 1.        ,  0.        , -2.61803399,  0.38196601]), [[592, 639, 856, 857], [35, 175, 270, 639, 641, 674], [5, 45, 100, 104]]], 
[array([ 0.        , -2.61803399,  1.        ,  0.38196601]), [[587, 681, 858, 859], [89, 164, 354, 634, 635, 694], [14, 43, 102, 105]]], 
[array([ 0.        ,  0.38196601, -2.61803399,  1.        ]), [[593, 687, 860, 861], [137, 176, 366, 640, 641, 698], [22, 45, 104, 106]]], 
[array([ 0.        ,  1.        ,  0.38196601, -2.61803399]), [[599, 693, 862, 863], [107, 188, 378, 646, 647, 702], [17, 47, 103, 107]]], 
[array([-2.61803399,  0.38196601, -1.        ,  0.        ]), [[628, 651, 864, 865], [43, 247, 294, 666, 667, 681], [2, 41, 66, 110]]], 
[array([-2.61803399, -1.        ,  0.        ,  0.38196601]), [[676, 723, 866, 867], [19, 343, 438, 690, 691, 713], [10, 41, 67, 108]]], 
[array([-2.61803399,  0.        ,  0.38196601, -1.        ]), [[604, 699, 868, 869], [67, 199, 390, 650, 651, 705], [6, 41, 68, 109]]], 
[array([ 0.38196601, -2.61803399,  0.        , -1.        ]), [[610, 657, 870, 871], [115, 211, 306, 654, 655, 683], [1, 43, 69, 117]]], 
[array([ 0.38196601, -1.        , -2.61803399,  0.        ]), [[640, 663, 872, 873], [91, 271, 318, 674, 675, 685], [5, 45, 70, 118]]], 
[array([ 0.38196601,  0.        , -1.        , -2.61803399]), [[622, 669, 874, 875], [139, 235, 330, 662, 663, 687], [9, 47, 71, 119]]], 
[array([-1.        , -2.61803399,  0.38196601,  0.        ]), [[682, 705, 876, 877], [22, 355, 402, 694, 695, 707], [3, 14, 43, 111]]], 
[array([-1.        ,  0.38196601,  0.        , -2.61803399]), [[694, 717, 878, 879], [70, 379, 426, 702, 703, 711], [11, 17, 47, 113]]], 
[array([-1.        ,  0.        , -2.61803399,  0.38196601]), [[688, 735, 880, 881], [46, 367, 462, 698, 699, 717], [7, 22, 45, 112]]], 
[array([ 0.        , -2.61803399, -1.        ,  0.38196601]), [[634, 729, 882, 883], [94, 259, 450, 670, 671, 715], [15, 18, 43, 114]]], 
[array([ 0.        ,  0.38196601, -2.61803399, -1.        ]), [[616, 711, 884, 885], [142, 223, 414, 658, 659, 709], [13, 23, 45, 116]]], 
[array([ 0.        , -1.        ,  0.38196601, -2.61803399]), [[646, 741, 886, 887], [118, 283, 474, 678, 679, 719], [19, 21, 47, 115]]], 
[array([-2.61803399, -0.38196601,  1.        ,  0.        ]), [[677, 700, 840, 888], [41, 344, 391, 628, 650, 691], [6, 41, 98, 108]]], 
[array([-2.61803399,  1.        ,  0.        , -0.38196601]), [[605, 652, 842, 889], [17, 200, 295, 627, 651, 666], [2, 41, 96, 109]]], 
[array([-2.61803399,  0.        , -0.38196601,  1.        ]), [[629, 724, 844, 890], [65, 248, 439, 629, 667, 690], [10, 41, 97, 110]]], 
[array([-0.38196601, -2.61803399,  0.        ,  1.        ]), [[683, 730, 846, 891], [113, 356, 451, 634, 670, 695], [18, 43, 105, 111]]], 
[array([-0.38196601,  1.        , -2.61803399,  0.        ]), [[689, 712, 848, 892], [83, 368, 415, 640, 658, 699], [13, 45, 106, 112]]], 
[array([-0.38196601,  0.        ,  1.        , -2.61803399]), [[695, 742, 850, 893], [131, 380, 475, 646, 678, 703], [21, 47, 107, 113]]], 
[array([ 1.        , -2.61803399, -0.38196601,  0.        ]), [[635, 658, 852, 894], [11, 260, 307, 633, 654, 671], [1, 43, 99, 114]]], 
[array([ 1.        , -0.38196601,  0.        , -2.61803399]), [[647, 670, 854, 895], [59, 284, 331, 645, 662, 679], [9, 47, 101, 115]]], 
[array([ 1.        ,  0.        , -2.61803399, -0.38196601]), [[617, 664, 856, 896], [35, 224, 319, 639, 659, 674], [5, 45, 100, 116]]], 
[array([ 0.        , -2.61803399,  1.        , -0.38196601]), [[611, 706, 858, 897], [89, 212, 403, 635, 655, 694], [14, 43, 102, 117]]], 
[array([ 0.        , -0.38196601, -2.61803399,  1.        ]), [[641, 736, 860, 898], [137, 272, 463, 641, 675, 698], [22, 45, 104, 118]]], 
[array([ 0.        ,  1.        , -0.38196601, -2.61803399]), [[623, 718, 862, 899], [107, 236, 427, 647, 663, 702], [17, 47, 103, 119]]], 
[array([-2.61803399, -0.38196601, -1.        ,  0.        ]), [[725, 747, 864, 900], [43, 440, 486, 667, 681, 713], [41, 66, 67, 110]]], 
[array([-2.61803399, -1.        ,  0.        , -0.38196601]), [[701, 748, 866, 901], [19, 392, 487, 691, 705, 713], [41, 67, 68, 108]]], 
[array([-2.61803399,  0.        , -0.38196601, -1.        ]), [[653, 749, 868, 902], [67, 296, 488, 651, 681, 705], [41, 66, 68, 109]]], 
[array([-0.38196601, -2.61803399,  0.        , -1.        ]), [[707, 753, 870, 903], [115, 404, 498, 655, 683, 707], [3, 43, 69, 117]]], 
[array([-0.38196601, -1.        , -2.61803399,  0.        ]), [[737, 759, 872, 904], [91, 464, 510, 675, 685, 717], [7, 45, 70, 118]]], 
[array([-0.38196601,  0.        , -1.        , -2.61803399]), [[719, 765, 874, 905], [139, 428, 522, 663, 687, 711], [11, 47, 71, 119]]], 
[array([-1.        , -2.61803399, -0.38196601,  0.        ]), [[731, 754, 876, 906], [22, 452, 499, 695, 707, 715], [3, 15, 43, 111]]], 
[array([-1.        , -0.38196601,  0.        , -2.61803399]), [[743, 766, 878, 907], [70, 476, 523, 703, 711, 719], [11, 19, 47, 113]]], 
[array([-1.        ,  0.        , -2.61803399, -0.38196601]), [[713, 760, 880, 908], [46, 416, 511, 699, 709, 717], [7, 23, 45, 112]]], 
[array([ 0.        , -2.61803399, -1.        , -0.38196601]), [[659, 755, 882, 909], [94, 308, 500, 671, 683, 715], [15, 43, 69, 114]]], 
[array([ 0.        , -0.38196601, -2.61803399, -1.        ]), [[665, 761, 884, 910], [142, 320, 512, 659, 685, 709], [23, 45, 70, 116]]], 
[array([ 0.        , -1.        , -0.38196601, -2.61803399]), [[671, 767, 886, 911], [118, 332, 524, 679, 687, 719], [19, 47, 71, 115]]], 
[array([2.23606798, 0.61803399, 1.61803399, 0.        ]), [[16, 769, 912, 913], [24, 25, 26, 144, 192, 537], [48, 72, 74, 76]]], 
[array([2.23606798, 1.61803399, 0.        , 0.61803399]), [[0, 771, 914, 915], [0, 1, 2, 145, 240, 534], [49, 72, 73, 75]]], 
[array([2.23606798, 0.        , 0.61803399, 1.61803399]), [[32, 773, 916, 917], [48, 49, 50, 146, 336, 531], [50, 73, 74, 77]]], 
[array([0.61803399, 2.23606798, 0.        , 1.61803399]), [[64, 775, 918, 919], [96, 97, 98, 156, 252, 535], [51, 75, 79, 81]]], 
[array([0.61803399, 1.61803399, 2.23606798, 0.        ]), [[48, 777, 920, 921], [72, 73, 74, 168, 216, 538], [52, 76, 78, 82]]], 
[array([0.61803399, 0.        , 1.61803399, 2.23606798]), [[80, 779, 922, 923], [120, 121, 122, 180, 276, 532], [53, 77, 80, 83]]], 
[array([1.61803399, 2.23606798, 0.61803399, 0.        ]), [[1, 781, 924, 925], [0, 3, 4, 157, 204, 539], [0, 72, 75, 78]]], 
[array([1.61803399, 0.61803399, 0.        , 2.23606798]), [[33, 783, 926, 927], [48, 51, 52, 181, 228, 536], [8, 73, 77, 79]]], 
[array([1.61803399, 0.        , 2.23606798, 0.61803399]), [[17, 785, 928, 929], [24, 27, 28, 169, 264, 533], [4, 74, 76, 80]]], 
[array([0.        , 2.23606798, 1.61803399, 0.61803399]), [[49, 787, 930, 931], [72, 75, 76, 158, 348, 528], [12, 78, 81, 82]]], 
[array([0.        , 0.61803399, 2.23606798, 1.61803399]), [[81, 789, 932, 933], [120, 123, 124, 170, 360, 529], [20, 80, 82, 83]]], 
[array([0.        , 1.61803399, 0.61803399, 2.23606798]), [[65, 791, 934, 935], [96, 99, 100, 182, 372, 530], [16, 79, 81, 83]]], 
[array([ 2.23606798,  0.61803399, -1.61803399,  0.        ]), [[20, 793, 936, 937], [30, 31, 32, 241, 288, 549], [49, 54, 86, 100]]], 
[array([ 2.23606798, -1.61803399,  0.        ,  0.61803399]), [[4, 795, 938, 939], [6, 7, 8, 337, 432, 558], [50, 55, 84, 99]]], 
[array([ 2.23606798,  0.        ,  0.61803399, -1.61803399]), [[36, 797, 940, 941], [54, 55, 56, 193, 384, 543], [48, 56, 85, 101]]], 
[array([ 0.61803399,  2.23606798,  0.        , -1.61803399]), [[68, 799, 942, 943], [102, 103, 104, 205, 300, 546], [0, 57, 93, 103]]], 
[array([ 0.61803399, -1.61803399,  2.23606798,  0.        ]), [[56, 801, 944, 945], [84, 85, 86, 265, 312, 561], [4, 58, 94, 102]]], 
[array([ 0.61803399,  0.        , -1.61803399,  2.23606798]), [[88, 803, 946, 947], [132, 133, 134, 229, 324, 555], [8, 59, 95, 104]]], 
[array([-1.61803399,  2.23606798,  0.61803399,  0.        ]), [[8, 805, 948, 949], [12, 13, 14, 349, 396, 585], [12, 60, 87, 96]]], 
[array([-1.61803399,  0.61803399,  0.        ,  2.23606798]), [[40, 807, 950, 951], [60, 61, 62, 373, 420, 582], [16, 61, 89, 97]]], 
[array([-1.61803399,  0.        ,  2.23606798,  0.61803399]), [[24, 809, 952, 953], [36, 37, 38, 361, 456, 579], [20, 62, 88, 98]]], 
[array([ 0.        ,  2.23606798, -1.61803399,  0.61803399]), [[52, 811, 954, 955], [78, 79, 80, 253, 444, 552], [51, 63, 90, 106]]], 
[array([ 0.        ,  0.61803399,  2.23606798, -1.61803399]), [[84, 813, 956, 957], [126, 127, 128, 217, 408, 540], [52, 64, 92, 107]]], 
[array([ 0.        , -1.61803399,  0.61803399,  2.23606798]), [[72, 815, 958, 959], [108, 109, 110, 277, 468, 576], [53, 65, 91, 105]]], 
[array([ 2.23606798, -0.61803399,  1.61803399,  0.        ]), [[18, 816, 960, 961], [25, 27, 29, 338, 385, 562], [4, 48, 74, 84]]], 
[array([ 2.23606798,  1.61803399,  0.        , -0.61803399]), [[2, 817, 962, 963], [1, 3, 5, 194, 289, 547], [0, 49, 72, 85]]], 
[array([ 2.23606798,  0.        , -0.61803399,  1.61803399]), [[34, 818, 964, 965], [49, 51, 53, 242, 433, 556], [8, 50, 73, 86]]], 
[array([-0.61803399,  2.23606798,  0.        ,  1.61803399]), [[66, 819, 966, 967], [97, 99, 101, 350, 445, 583], [16, 51, 81, 87]]], 
[array([-0.61803399,  1.61803399,  2.23606798,  0.        ]), [[50, 820, 968, 969], [73, 75, 77, 362, 409, 586], [12, 52, 82, 88]]], 
[array([-0.61803399,  0.        ,  1.61803399,  2.23606798]), [[82, 821, 970, 971], [121, 123, 125, 374, 469, 580], [20, 53, 83, 89]]], 
[array([ 1.61803399,  2.23606798, -0.61803399,  0.        ]), [[3, 822, 972, 973], [2, 4, 5, 254, 301, 550], [0, 49, 75, 90]]], 
[array([ 1.61803399, -0.61803399,  0.        ,  2.23606798]), [[35, 823, 974, 975], [50, 52, 53, 278, 325, 559], [8, 50, 77, 91]]], 
[array([ 1.61803399,  0.        ,  2.23606798, -0.61803399]), [[19, 824, 976, 977], [26, 28, 29, 218, 313, 544], [4, 48, 76, 92]]], 
[array([ 0.        ,  2.23606798,  1.61803399, -0.61803399]), [[51, 825, 978, 979], [74, 76, 77, 206, 397, 541], [12, 52, 78, 93]]], 
[array([ 0.        , -0.61803399,  2.23606798,  1.61803399]), [[83, 826, 980, 981], [122, 124, 125, 266, 457, 577], [20, 53, 80, 94]]], 
[array([ 0.        ,  1.61803399, -0.61803399,  2.23606798]), [[67, 827, 982, 983], [98, 100, 101, 230, 421, 553], [16, 51, 79, 95]]], 
[array([ 2.23606798, -0.61803399, -1.61803399,  0.        ]), [[21, 828, 984, 985], [30, 33, 34, 434, 480, 573], [5, 54, 55, 86]]], 
[array([ 2.23606798, -1.61803399,  0.        , -0.61803399]), [[5, 829, 986, 987], [6, 9, 10, 386, 481, 570], [1, 55, 56, 84]]], 
[array([ 2.23606798,  0.        , -0.61803399, -1.61803399]), [[37, 830, 988, 989], [54, 57, 58, 290, 482, 567], [9, 54, 56, 85]]], 
[array([-0.61803399,  2.23606798,  0.        , -1.61803399]), [[69, 831, 990, 991], [102, 105, 106, 398, 492, 594], [17, 57, 60, 93]]], 
[array([-0.61803399, -1.61803399,  2.23606798,  0.        ]), [[57, 832, 992, 993], [84, 87, 88, 458, 504, 609], [14, 58, 62, 94]]], 
[array([-0.61803399,  0.        , -1.61803399,  2.23606798]), [[89, 833, 994, 995], [132, 135, 136, 422, 516, 603], [22, 59, 61, 95]]], 
[array([-1.61803399,  2.23606798, -0.61803399,  0.        ]), [[9, 834, 996, 997], [12, 15, 16, 446, 493, 597], [2, 60, 63, 87]]], 
[array([-1.61803399, -0.61803399,  0.        ,  2.23606798]), [[41, 835, 998, 999], [60, 63, 64, 470, 517, 606], [10, 61, 65, 89]]], 
[array([-1.61803399,  0.        ,  2.23606798, -0.61803399]), [[25, 836, 1000, 1001], [36, 39, 40, 410, 505, 591], [6, 62, 64, 88]]], 
[array([ 0.        ,  2.23606798, -1.61803399, -0.61803399]), [[53, 837, 1002, 1003], [78, 81, 82, 302, 494, 564], [13, 57, 63, 90]]], 
[array([ 0.        , -0.61803399,  2.23606798, -1.61803399]), [[85, 838, 1004, 1005], [126, 129, 130, 314, 506, 588], [21, 58, 64, 92]]], 
[array([ 0.        , -1.61803399, -0.61803399,  2.23606798]), [[73, 839, 1006, 1007], [108, 111, 112, 326, 518, 600], [18, 59, 65, 91]]], 
[array([-2.23606798,  0.61803399,  1.61803399,  0.        ]), [[26, 841, 1008, 1009], [37, 39, 41, 150, 198, 587], [6, 88, 96, 98]]], 
[array([-2.23606798,  1.61803399,  0.        ,  0.61803399]), [[10, 843, 1010, 1011], [13, 15, 17, 151, 246, 584], [2, 87, 96, 97]]], 
[array([-2.23606798,  0.        ,  0.61803399,  1.61803399]), [[42, 845, 1012, 1013], [61, 63, 65, 152, 342, 581], [10, 89, 97, 98]]], 
[array([ 0.61803399, -2.23606798,  0.        ,  1.61803399]), [[74, 847, 1014, 1015], [109, 111, 113, 162, 258, 560], [18, 91, 99, 105]]], 
[array([ 0.61803399,  1.61803399, -2.23606798,  0.        ]), [[54, 849, 1016, 1017], [79, 81, 83, 174, 222, 551], [13, 90, 100, 106]]], 
[array([ 0.61803399,  0.        ,  1.61803399, -2.23606798]), [[86, 851, 1018, 1019], [127, 129, 131, 186, 282, 545], [21, 92, 101, 107]]], 
[array([ 1.61803399, -2.23606798,  0.61803399,  0.        ]), [[6, 853, 1020, 1021], [7, 9, 11, 163, 210, 563], [1, 84, 99, 102]]], 
[array([ 1.61803399,  0.61803399,  0.        , -2.23606798]), [[38, 855, 1022, 1023], [55, 57, 59, 187, 234, 548], [9, 85, 101, 103]]], 
[array([ 1.61803399,  0.        , -2.23606798,  0.61803399]), [[22, 857, 1024, 1025], [31, 33, 35, 175, 270, 557], [5, 86, 100, 104]]], 
[array([ 0.        , -2.23606798,  1.61803399,  0.61803399]), [[58, 859, 1026, 1027], [85, 87, 89, 164, 354, 578], [14, 94, 102, 105]]], 
[array([ 0.        ,  0.61803399, -2.23606798,  1.61803399]), [[90, 861, 1028, 1029], [133, 135, 137, 176, 366, 554], [22, 95, 104, 106]]], 
[array([ 0.        ,  1.61803399,  0.61803399, -2.23606798]), [[70, 863, 1030, 1031], [103, 105, 107, 188, 378, 542], [17, 93, 103, 107]]], 
[array([-2.23606798,  0.61803399, -1.61803399,  0.        ]), [[28, 865, 1032, 1033], [42, 43, 44, 247, 294, 598], [2, 66, 110, 112]]], 
[array([-2.23606798, -1.61803399,  0.        ,  0.61803399]), [[12, 867, 1034, 1035], [18, 19, 20, 343, 438, 607], [10, 67, 108, 111]]], 
[array([-2.23606798,  0.        ,  0.61803399, -1.61803399]), [[44, 869, 1036, 1037], [66, 67, 68, 199, 390, 592], [6, 68, 109, 113]]], 
[array([ 0.61803399, -2.23606798,  0.        , -1.61803399]), [[76, 871, 1038, 1039], [114, 115, 116, 211, 306, 571], [1, 69, 115, 117]]], 
[array([ 0.61803399, -1.61803399, -2.23606798,  0.        ]), [[60, 873, 1040, 1041], [90, 91, 92, 271, 318, 574], [5, 70, 114, 118]]], 
[array([ 0.61803399,  0.        , -1.61803399, -2.23606798]), [[92, 875, 1042, 1043], [138, 139, 140, 235, 330, 568], [9, 71, 116, 119]]], 
[array([-1.61803399, -2.23606798,  0.61803399,  0.        ]), [[13, 877, 1044, 1045], [18, 21, 22, 355, 402, 610], [3, 14, 108, 111]]], 
[array([-1.61803399,  0.61803399,  0.        , -2.23606798]), [[45, 879, 1046, 1047], [66, 69, 70, 379, 426, 595], [11, 17, 109, 113]]], 
[array([-1.61803399,  0.        , -2.23606798,  0.61803399]), [[29, 881, 1048, 1049], [42, 45, 46, 367, 462, 604], [7, 22, 110, 112]]], 
[array([ 0.        , -2.23606798, -1.61803399,  0.61803399]), [[61, 883, 1050, 1051], [90, 93, 94, 259, 450, 601], [15, 18, 114, 118]]], 
[array([ 0.        ,  0.61803399, -2.23606798, -1.61803399]), [[93, 885, 1052, 1053], [138, 141, 142, 223, 414, 565], [13, 23, 116, 119]]], 
[array([ 0.        , -1.61803399,  0.61803399, -2.23606798]), [[77, 887, 1054, 1055], [114, 117, 118, 283, 474, 589], [19, 21, 115, 117]]], 
[array([-2.23606798, -0.61803399,  1.61803399,  0.        ]), [[27, 888, 1056, 1057], [38, 40, 41, 344, 391, 611], [6, 62, 98, 108]]], 
[array([-2.23606798,  1.61803399,  0.        , -0.61803399]), [[11, 889, 1058, 1059], [14, 16, 17, 200, 295, 596], [2, 60, 96, 109]]], 
[array([-2.23606798,  0.        , -0.61803399,  1.61803399]), [[43, 890, 1060, 1061], [62, 64, 65, 248, 439, 605], [10, 61, 97, 110]]], 
[array([-0.61803399, -2.23606798,  0.        ,  1.61803399]), [[75, 891, 1062, 1063], [110, 112, 113, 356, 451, 608], [18, 65, 105, 111]]], 
[array([-0.61803399,  1.61803399, -2.23606798,  0.        ]), [[55, 892, 1064, 1065], [80, 82, 83, 368, 415, 599], [13, 63, 106, 112]]], 
[array([-0.61803399,  0.        ,  1.61803399, -2.23606798]), [[87, 893, 1066, 1067], [128, 130, 131, 380, 475, 593], [21, 64, 107, 113]]], 
[array([ 1.61803399, -2.23606798, -0.61803399,  0.        ]), [[7, 894, 1068, 1069], [8, 10, 11, 260, 307, 575], [1, 55, 99, 114]]], 
[array([ 1.61803399, -0.61803399,  0.        , -2.23606798]), [[39, 895, 1070, 1071], [56, 58, 59, 284, 331, 572], [9, 56, 101, 115]]], 
[array([ 1.61803399,  0.        , -2.23606798, -0.61803399]), [[23, 896, 1072, 1073], [32, 34, 35, 224, 319, 569], [5, 54, 100, 116]]], 
[array([ 0.        , -2.23606798,  1.61803399, -0.61803399]), [[59, 897, 1074, 1075], [86, 88, 89, 212, 403, 590], [14, 58, 102, 117]]], 
[array([ 0.        , -0.61803399, -2.23606798,  1.61803399]), [[91, 898, 1076, 1077], [134, 136, 137, 272, 463, 602], [22, 59, 104, 118]]], 
[array([ 0.        ,  1.61803399, -0.61803399, -2.23606798]), [[71, 899, 1078, 1079], [104, 106, 107, 236, 427, 566], [17, 57, 103, 119]]], 
[array([-2.23606798, -0.61803399, -1.61803399,  0.        ]), [[30, 900, 1080, 1081], [43, 45, 47, 440, 486, 621], [7, 66, 67, 110]]], 
[array([-2.23606798, -1.61803399,  0.        , -0.61803399]), [[14, 901, 1082, 1083], [19, 21, 23, 392, 487, 618], [3, 67, 68, 108]]], 
[array([-2.23606798,  0.        , -0.61803399, -1.61803399]), [[46, 902, 1084, 1085], [67, 69, 71, 296, 488, 615], [11, 66, 68, 109]]], 
[array([-0.61803399, -2.23606798,  0.        , -1.61803399]), [[78, 903, 1086, 1087], [115, 117, 119, 404, 498, 619], [3, 19, 69, 117]]], 
[array([-0.61803399, -1.61803399, -2.23606798,  0.        ]), [[62, 904, 1088, 1089], [91, 93, 95, 464, 510, 622], [7, 15, 70, 118]]], 
[array([-0.61803399,  0.        , -1.61803399, -2.23606798]), [[94, 905, 1090, 1091], [139, 141, 143, 428, 522, 616], [11, 23, 71, 119]]],
 [array([-1.61803399, -2.23606798, -0.61803399,  0.        ]), [[15, 906, 1092, 1093], [20, 22, 23, 452, 499, 623], [3, 15, 67, 111]]], 
[array([-1.61803399, -0.61803399,  0.        , -2.23606798]), [[47, 907, 1094, 1095], [68, 70, 71, 476, 523, 620], [11, 19, 68, 113]]], 
[array([-1.61803399,  0.        , -2.23606798, -0.61803399]), [[31, 908, 1096, 1097], [44, 46, 47, 416, 511, 617], [7, 23, 66, 112]]], 
[array([ 0.        , -2.23606798, -1.61803399, -0.61803399]), [[63, 909, 1098, 1099], [92, 94, 95, 308, 500, 612], [15, 69, 70, 114]]], 
[array([ 0.        , -0.61803399, -2.23606798, -1.61803399]), [[95, 910, 1100, 1101], [140, 142, 143, 320, 512, 613], [23, 70, 71, 116]]], 
[array([ 0.        , -1.61803399, -0.61803399, -2.23606798]), [[79, 911, 1102, 1103], [116, 118, 119, 332, 524, 614], [19, 69, 71, 115]]], 
[array([2.        , 1.        , 1.61803399, 0.61803399]), [[97, 374, 912, 1104], [24, 144, 147, 148, 171, 537], [24, 72, 74, 76]]], 
[array([2.        , 1.61803399, 0.61803399, 1.        ]), [[98, 367, 914, 1105], [0, 145, 147, 149, 159, 534], [24, 72, 73, 75]]], 
[array([2.        , 0.61803399, 1.        , 1.61803399]), [[99, 360, 916, 1106], [48, 146, 148, 149, 183, 531], [24, 73, 74, 77]]], 
[array([1.        , 2.        , 0.61803399, 1.61803399]), [[105, 368, 918, 1107], [96, 156, 159, 160, 185, 535], [24, 75, 79, 81]]], 
[array([1.        , 1.61803399, 2.        , 0.61803399]), [[113, 375, 920, 1108], [72, 161, 168, 171, 172, 538], [24, 76, 78, 82]]], 
[array([1.        , 0.61803399, 1.61803399, 2.        ]), [[121, 361, 922, 1109], [120, 173, 180, 183, 184, 532], [24, 77, 80, 83]]], 
[array([1.61803399, 2.        , 1.        , 0.61803399]), [[106, 376, 924, 1105], [0, 147, 157, 159, 161, 539], [24, 72, 75, 78]]], 
[array([1.61803399, 1.        , 0.61803399, 2.        ]), [[122, 369, 926, 1106], [48, 149, 181, 183, 185, 536], [24, 73, 77, 79]]], 
[array([1.61803399, 0.61803399, 2.        , 1.        ]), [[114, 362, 928, 1104], [24, 148, 169, 171, 173, 533], [24, 74, 76, 80]]], 
[array([0.61803399, 2.        , 1.61803399, 1.        ]), [[107, 353, 930, 1108], [72, 158, 160, 161, 172, 528], [24, 78, 81, 82]]], 
[array([0.61803399, 1.        , 2.        , 1.61803399]), [[115, 354, 932, 1109], [120, 170, 172, 173, 184, 529], [24, 80, 82, 83]]], 
[array([0.61803399, 1.61803399, 1.        , 2.        ]), [[123, 355, 934, 1107], [96, 160, 182, 184, 185, 530], [24, 79, 81, 83]]], 
[array([ 2.        ,  1.        ,  1.61803399, -0.61803399]), [[129, 377, 913, 1110], [26, 192, 195, 196, 220, 537], [28, 48, 72, 76]]], 
[array([ 2.        ,  1.61803399, -0.61803399,  1.        ]), [[161, 370, 915, 1111], [2, 240, 243, 244, 256, 534], [27, 49, 73, 75]]], 
[array([ 2.        , -0.61803399,  1.        ,  1.61803399]), [[225, 363, 917, 1112], [50, 280, 336, 339, 340, 531], [26, 50, 74, 77]]], 
[array([ 1.        ,  2.        , -0.61803399,  1.61803399]), [[169, 371, 919, 1113], [98, 232, 252, 255, 256, 535], [27, 51, 75, 79]]], 
[array([ 1.        ,  1.61803399,  2.        , -0.61803399]), [[145, 378, 921, 1114], [74, 208, 216, 219, 220, 538], [28, 52, 76, 78]]], 
[array([ 1.        , -0.61803399,  1.61803399,  2.        ]), [[185, 364, 923, 1115], [122, 268, 276, 279, 280, 532], [26, 53, 77, 80]]], 
[array([ 1.61803399,  2.        ,  1.        , -0.61803399]), [[137, 379, 925, 1116], [3, 196, 204, 207, 208, 539], [0, 28, 72, 78]]], 
[array([ 1.61803399,  1.        , -0.61803399,  2.        ]), [[153, 372, 927, 1117], [51, 228, 231, 232, 244, 536], [8, 27, 73, 79]]], 
[array([ 1.61803399, -0.61803399,  2.        ,  1.        ]), [[177, 365, 929, 1118], [27, 264, 267, 268, 340, 533], [4, 26, 74, 80]]], 
[array([-0.61803399,  2.        ,  1.61803399,  1.        ]), [[233, 356, 931, 1119], [75, 348, 351, 352, 364, 528], [12, 25, 81, 82]]], 
[array([-0.61803399,  1.        ,  2.        ,  1.61803399]), [[241, 357, 933, 1120], [123, 360, 363, 364, 376, 529], [20, 25, 82, 83]]], 
[array([-0.61803399,  1.61803399,  1.        ,  2.        ]), [[249, 358, 935, 1121], [99, 352, 372, 375, 376, 530], [16, 25, 81, 83]]], 
[array([ 2.        ,  1.        , -1.61803399,  0.61803399]), [[162, 402, 936, 1122], [31, 177, 241, 243, 245, 549], [27, 49, 86, 100]]], 
[array([ 2.        , -1.61803399,  0.61803399,  1.        ]), [[226, 423, 938, 1123], [7, 165, 337, 339, 341, 558], [26, 50, 84, 99]]], 
[array([ 2.        ,  0.61803399,  1.        , -1.61803399]), [[130, 388, 940, 1124], [55, 189, 193, 195, 197, 543], [28, 48, 85, 101]]], 
[array([ 1.        ,  2.        ,  0.61803399, -1.61803399]), [[138, 395, 942, 1125], [103, 191, 205, 207, 209, 546], [0, 28, 93, 103]]], 
[array([ 1.        , -1.61803399,  2.        ,  0.61803399]), [[178, 430, 944, 1126], [85, 167, 265, 267, 269, 561], [4, 26, 94, 102]]], 
[array([ 1.        ,  0.61803399, -1.61803399,  2.        ]), [[154, 416, 946, 1127], [133, 179, 229, 231, 233, 555], [8, 27, 95, 104]]], 
[array([-1.61803399,  2.        ,  1.        ,  0.61803399]), [[234, 486, 948, 1128], [13, 153, 349, 351, 353, 585], [12, 25, 87, 96]]], 
[array([-1.61803399,  1.        ,  0.61803399,  2.        ]), [[250, 479, 950, 1129], [61, 155, 373, 375, 377, 582], [16, 25, 89, 97]]], 
[array([-1.61803399,  0.61803399,  2.        ,  1.        ]), [[242, 472, 952, 1130], [37, 154, 361, 363, 365, 579], [20, 25, 88, 98]]], 
[array([ 0.61803399,  2.        , -1.61803399,  1.        ]), [[170, 409, 954, 1131], [79, 178, 253, 255, 257, 552], [27, 51, 90, 106]]], 
[array([ 0.61803399,  1.        ,  2.        , -1.61803399]), [[146, 381, 956, 1132], [127, 190, 217, 219, 221, 540], [28, 52, 92, 107]]], 
[array([ 0.61803399, -1.61803399,  1.        ,  2.        ]), [[186, 465, 958, 1133], [109, 166, 277, 279, 281, 576], [26, 53, 91, 105]]], 
[array([ 2.        ,  1.        , -1.61803399, -0.61803399]), [[193, 405, 937, 1134], [32, 226, 288, 291, 292, 549], [31, 49, 54, 100]]],
 [array([ 2.        , -1.61803399, -0.61803399,  1.        ]), [[289, 426, 939, 1135], [8, 262, 432, 435, 436, 558], [33, 50, 55, 99]]], 
[array([ 2.        , -0.61803399,  1.        , -1.61803399]), [[257, 391, 941, 1136], [56, 286, 384, 387, 388, 543], [30, 48, 56, 101]]], 
[array([ 1.        ,  2.        , -0.61803399, -1.61803399]), [[201, 398, 943, 1137], [104, 238, 300, 303, 304, 546], [0, 31, 57, 103]]], 
[array([ 1.        , -1.61803399,  2.        , -0.61803399]), [[209, 433, 945, 1138], [86, 214, 312, 315, 316, 561], [4, 30, 58, 102]]], 
[array([ 1.        , -0.61803399, -1.61803399,  2.        ]), [[217, 419, 947, 1139], [134, 274, 324, 327, 328, 555], [8, 33, 59, 104]]], 
[array([-1.61803399,  2.        ,  1.        , -0.61803399]), [[265, 489, 949, 1140], [14, 202, 396, 399, 400, 585], [12, 29, 60, 96]]], 
[array([-1.61803399,  1.        , -0.61803399,  2.        ]), [[281, 482, 951, 1141], [62, 250, 420, 423, 424, 582], [16, 32, 61, 97]]], 
[array([-1.61803399, -0.61803399,  2.        ,  1.        ]), [[305, 475, 953, 1142], [38, 346, 456, 459, 460, 579], [20, 36, 62, 98]]], 
[array([-0.61803399,  2.        , -1.61803399,  1.        ]), [[297, 412, 955, 1143], [80, 370, 444, 447, 448, 552], [32, 51, 63, 106]]], 
[array([-0.61803399,  1.        ,  2.        , -1.61803399]), [[273, 384, 957, 1144], [128, 382, 408, 411, 412, 540], [29, 52, 64, 107]]], 
[array([-0.61803399, -1.61803399,  1.        ,  2.        ]), [[313, 468, 959, 1145], [110, 358, 468, 471, 472, 576], [36, 53, 65, 105]]], 
[array([ 2.        , -1.        ,  1.61803399,  0.61803399]), [[227, 431, 960, 1118], [27, 267, 338, 340, 341, 562], [4, 26, 74, 84]]], 
[array([ 2.        ,  1.61803399,  0.61803399, -1.        ]), [[131, 396, 962, 1116], [3, 194, 196, 197, 207, 547], [0, 28, 72, 85]]], 
[array([ 2.        ,  0.61803399, -1.        ,  1.61803399]), [[163, 417, 964, 1117], [51, 231, 242, 244, 245, 556], [8, 27, 73, 86]]], 
[array([-1.        ,  2.        ,  0.61803399,  1.61803399]), [[235, 480, 966, 1121], [99, 350, 352, 353, 375, 583], [16, 25, 81, 87]]], 
[array([-1.        ,  1.61803399,  2.        ,  0.61803399]), [[243, 487, 968, 1119], [75, 351, 362, 364, 365, 586], [12, 25, 82, 88]]], 
[array([-1.        ,  0.61803399,  1.61803399,  2.        ]), [[251, 473, 970, 1120], [123, 363, 374, 376, 377, 580], [20, 25, 83, 89]]], 
[array([ 1.61803399,  2.        , -1.        ,  0.61803399]), [[171, 403, 972, 1111], [2, 243, 254, 256, 257, 550], [27, 49, 75, 90]]], 
[array([ 1.61803399, -1.        ,  0.61803399,  2.        ]), [[187, 424, 974, 1112], [50, 278, 280, 281, 339, 559], [26, 50, 77, 91]]], 
[array([ 1.61803399,  0.61803399,  2.        , -1.        ]), [[147, 389, 976, 1110], [26, 195, 218, 220, 221, 544], [28, 48, 76, 92]]], 
[array([ 0.61803399,  2.        ,  1.61803399, -1.        ]), [[139, 382, 978, 1114], [74, 206, 208, 209, 219, 541], [28, 52, 78, 93]]], 
[array([ 0.61803399, -1.        ,  2.        ,  1.61803399]), [[179, 466, 980, 1115], [122, 266, 268, 269, 279, 577], [26, 53, 80, 94]]], 
[array([ 0.61803399,  1.61803399, -1.        ,  2.        ]), [[155, 410, 982, 1113], [98, 230, 232, 233, 255, 553], [27, 51, 79, 95]]], 
[array([ 2.        , -1.        ,  1.61803399, -0.61803399]), [[258, 434, 961, 1146], [29, 315, 385, 387, 389, 562], [4, 30, 48, 84]]], 
[array([ 2.        ,  1.61803399, -0.61803399, -1.        ]), [[194, 399, 963, 1147], [5, 289, 291, 293, 303, 547], [0, 31, 49, 85]]], 
[array([ 2.        , -0.61803399, -1.        ,  1.61803399]), [[290, 420, 965, 1148], [53, 327, 433, 435, 437, 556], [8, 33, 50, 86]]], 
[array([-1.        ,  2.        , -0.61803399,  1.61803399]), [[298, 483, 967, 1149], [101, 423, 445, 447, 449, 583], [16, 32, 51, 87]]], 
[array([-1.        ,  1.61803399,  2.        , -0.61803399]), [[274, 490, 969, 1150], [77, 399, 409, 411, 413, 586], [12, 29, 52, 88]]], 
[array([-1.        , -0.61803399,  1.61803399,  2.        ]), [[314, 476, 971, 1151], [125, 459, 469, 471, 473, 580], [20, 36, 53, 89]]], 
[array([ 1.61803399,  2.        , -1.        , -0.61803399]), [[202, 406, 973, 1147], [5, 291, 301, 303, 305, 550], [0, 31, 49, 90]]], 
[array([ 1.61803399, -1.        , -0.61803399,  2.        ]), [[218, 427, 975, 1148], [53, 325, 327, 329, 435, 559], [8, 33, 50, 91]]], 
[array([ 1.61803399, -0.61803399,  2.        , -1.        ]), [[210, 392, 977, 1146], [29, 313, 315, 317, 387, 544], [4, 30, 48, 92]]], 
[array([-0.61803399,  2.        ,  1.61803399, -1.        ]), [[266, 385, 979, 1150], [77, 397, 399, 401, 411, 541], [12, 29, 52, 93]]], 
[array([-0.61803399, -1.        ,  2.        ,  1.61803399]), [[306, 469, 981, 1151], [125, 457, 459, 461, 471, 577], [20, 36, 53, 94]]], 
[array([-0.61803399,  1.61803399, -1.        ,  2.        ]), [[282, 413, 983, 1149], [101, 421, 423, 425, 447, 553], [16, 32, 51, 95]]], 
[array([ 2.        , -1.        , -1.61803399,  0.61803399]), [[291, 458, 984, 1152], [33, 273, 434, 436, 437, 573], [5, 33, 55, 86]]], 
[array([ 2.        , -1.61803399,  0.61803399, -1.        ]), [[259, 451, 986, 1153], [9, 213, 386, 388, 389, 570], [1, 30, 56, 84]]], 
[array([ 2.        ,  0.61803399, -1.        , -1.61803399]), [[195, 444, 988, 1154], [57, 237, 290, 292, 293, 567], [9, 31, 54, 85]]], 
[array([-1.        ,  2.        ,  0.61803399, -1.61803399]), [[267, 507, 990, 1155], [105, 381, 398, 400, 401, 594], [17, 29, 60, 93]]],
 [array([-1.        , -1.61803399,  2.        ,  0.61803399]), [[307, 542, 992, 1156], [87, 357, 458, 460, 461, 609], [14, 36, 62, 94]]], 
[array([-1.        ,  0.61803399, -1.61803399,  2.        ]), [[283, 528, 994, 1157], [135, 369, 422, 424, 425, 603], [22, 32, 61, 95]]], 
[array([-1.61803399,  2.        , -1.        ,  0.61803399]), [[299, 514, 996, 1158], [15, 249, 446, 448, 449, 597], [2, 32, 63, 87]]], 
[array([-1.61803399, -1.        ,  0.61803399,  2.        ]), [[315, 535, 998, 1159], [63, 345, 470, 472, 473, 606], [10, 36, 65, 89]]], 
[array([-1.61803399,  0.61803399,  2.        , -1.        ]), [[275, 500, 1000, 1160], [39, 201, 410, 412, 413, 591], [6, 29, 64, 88]]],
 [array([ 0.61803399,  2.        , -1.61803399, -1.        ]), [[203, 437, 1002, 1161], [81, 225, 302, 304, 305, 564], [13, 31, 57, 90]]], 
[array([ 0.61803399, -1.        ,  2.        , -1.61803399]), [[211, 493, 1004, 1162], [129, 285, 314, 316, 317, 588], [21, 30, 58, 92]]], 
[array([ 0.61803399, -1.61803399, -1.        ,  2.        ]), [[219, 521, 1006, 1163], [111, 261, 326, 328, 329, 600], [18, 33, 59, 91]]],
 [array([ 2.        , -1.        , -1.61803399, -0.61803399]), [[321, 461, 985, 1164], [34, 321, 480, 483, 484, 573], [5, 35, 54, 55]]],
 [array([ 2.        , -1.61803399, -0.61803399, -1.        ]), [[322, 454, 987, 1165], [10, 309, 481, 483, 485, 570], [1, 35, 55, 56]]], 
[array([ 2.        , -0.61803399, -1.        , -1.61803399]), [[323, 447, 989, 1166], [58, 333, 482, 484, 485, 567], [9, 35, 54, 56]]], 
[array([-1.        ,  2.        , -0.61803399, -1.61803399]), [[329, 510, 991, 1167], [106, 429, 492, 495, 496, 594], [17, 34, 57, 60]]],
 [array([-1.        , -1.61803399,  2.        , -0.61803399]), [[337, 545, 993, 1168], [88, 405, 504, 507, 508, 609], [14, 37, 58, 62]]], 
[array([-1.        , -0.61803399, -1.61803399,  2.        ]), [[345, 531, 995, 1169], [136, 465, 516, 519, 520, 603], [22, 38, 59, 61]]], 
[array([-1.61803399,  2.        , -1.        , -0.61803399]), [[330, 517, 997, 1170], [16, 297, 493, 495, 497, 597], [2, 34, 60, 63]]], 
[array([-1.61803399, -1.        , -0.61803399,  2.        ]), [[346, 538, 999, 1171], [64, 441, 517, 519, 521, 606], [10, 38, 61, 65]]],
 [array([-1.61803399, -0.61803399,  2.        , -1.        ]), [[338, 503, 1001, 1172], [40, 393, 505, 507, 509, 591], [6, 37, 62, 64]]], 
[array([-0.61803399,  2.        , -1.61803399, -1.        ]), [[331, 440, 1003, 1173], [82, 417, 494, 496, 497, 564], [13, 34, 57, 63]]], 
[array([-0.61803399, -1.        ,  2.        , -1.61803399]), [[339, 496, 1005, 1174], [130, 477, 506, 508, 509, 588], [21, 37, 58, 64]]],
 [array([-0.61803399, -1.61803399, -1.        ,  2.        ]), [[347, 524, 1007, 1175], [112, 453, 518, 520, 521, 600], [18, 38, 59, 65]]], 
[array([-2.        ,  1.        ,  1.61803399,  0.61803399]), [[101, 488, 1008, 1130], [37, 150, 153, 154, 365, 587], [25, 88, 96, 98]]], 
[array([-2.        ,  1.61803399,  0.61803399,  1.        ]), [[102, 481, 1010, 1128], [13, 151, 153, 155, 353, 584], [25, 87, 96, 97]]], 
[array([-2.        ,  0.61803399,  1.        ,  1.61803399]), [[103, 474, 1012, 1129], [61, 152, 154, 155, 377, 581], [25, 89, 97, 98]]], 
[array([ 1.        , -2.        ,  0.61803399,  1.61803399]), [[109, 425, 1014, 1133], [109, 162, 165, 166, 281, 560], [26, 91, 99, 105]]], 
[array([ 1.        ,  1.61803399, -2.        ,  0.61803399]), [[117, 404, 1016, 1131], [79, 174, 177, 178, 257, 551], [27, 90, 100, 106]]], 
[array([ 1.        ,  0.61803399,  1.61803399, -2.        ]), [[125, 390, 1018, 1132], [127, 186, 189, 190, 221, 545], [28, 92, 101, 107]]], 
[array([ 1.61803399, -2.        ,  1.        ,  0.61803399]), [[110, 432, 1020, 1123], [7, 163, 165, 167, 341, 563], [26, 84, 99, 102]]], 
[array([ 1.61803399,  1.        ,  0.61803399, -2.        ]), [[126, 397, 1022, 1124], [55, 187, 189, 191, 197, 548], [28, 85, 101, 103]]], 
[array([ 1.61803399,  0.61803399, -2.        ,  1.        ]), [[118, 418, 1024, 1122], [31, 175, 177, 179, 245, 557], [27, 86, 100, 104]]], 
[array([ 0.61803399, -2.        ,  1.61803399,  1.        ]), [[111, 467, 1026, 1126], [85, 164, 166, 167, 269, 578], [26, 94, 102, 105]]], 
[array([ 0.61803399,  1.        , -2.        ,  1.61803399]), [[119, 411, 1028, 1127], [133, 176, 178, 179, 233, 554], [27, 95, 104, 106]]],
 [array([ 0.61803399,  1.61803399,  1.        , -2.        ]), [[127, 383, 1030, 1125], [103, 188, 190, 191, 209, 542], [28, 93, 103, 107]]], 
[array([-2.        ,  1.        ,  1.61803399, -0.61803399]), [[133, 491, 1009, 1160], [39, 198, 201, 202, 413, 587], [6, 29, 88, 96]]], 
[array([-2.        ,  1.61803399, -0.61803399,  1.        ]), [[165, 484, 1011, 1158], [15, 246, 249, 250, 449, 584], [2, 32, 87, 97]]], 
[array([-2.        , -0.61803399,  1.        ,  1.61803399]), [[229, 477, 1013, 1159], [63, 342, 345, 346, 473, 581], [10, 36, 89, 98]]], 
[array([ 1.        , -2.        , -0.61803399,  1.61803399]), [[173, 428, 1015, 1163], [111, 258, 261, 262, 329, 560], [18, 33, 91, 99]]], 
[array([ 1.        ,  1.61803399, -2.        , -0.61803399]), [[149, 407, 1017, 1161], [81, 222, 225, 226, 305, 551], [13, 31, 90, 100]]], 
[array([ 1.        , -0.61803399,  1.61803399, -2.        ]), [[189, 393, 1019, 1162], [129, 282, 285, 286, 317, 545], [21, 30, 92, 101]]],
 [array([ 1.61803399, -2.        ,  1.        , -0.61803399]), [[141, 435, 1021, 1153], [9, 210, 213, 214, 389, 563], [1, 30, 84, 102]]], 
[array([ 1.61803399,  1.        , -0.61803399, -2.        ]), [[157, 400, 1023, 1154], [57, 234, 237, 238, 293, 548], [9, 31, 85, 103]]], 
[array([ 1.61803399, -0.61803399, -2.        ,  1.        ]), [[181, 421, 1025, 1152], [33, 270, 273, 274, 437, 557], [5, 33, 86, 104]]],
 [array([-0.61803399, -2.        ,  1.61803399,  1.        ]), [[237, 470, 1027, 1156], [87, 354, 357, 358, 461, 578], [14, 36, 94, 105]]],
 [array([-0.61803399,  1.        , -2.        ,  1.61803399]), [[245, 414, 1029, 1157], [135, 366, 369, 370, 425, 554], [22, 32, 95, 106]]],
 [array([-0.61803399,  1.61803399,  1.        , -2.        ]), [[253, 386, 1031, 1155], [105, 378, 381, 382, 401, 542], [17, 29, 93, 107]]],
 [array([-2.        ,  1.        , -1.61803399,  0.61803399]), [[166, 515, 1032, 1176], [42, 247, 249, 251, 371, 598], [2, 32, 110, 112]]],
 [array([-2.        , -1.61803399,  0.61803399,  1.        ]), [[230, 536, 1034, 1177], [18, 343, 345, 347, 359, 607], [10, 36, 108, 111]]],
 [array([-2.        ,  0.61803399,  1.        , -1.61803399]), [[134, 501, 1036, 1178], [66, 199, 201, 203, 383, 592], [6, 29, 109, 113]]],
 [array([ 1.        , -2.        ,  0.61803399, -1.61803399]), [[142, 452, 1038, 1179], [114, 211, 213, 215, 287, 571], [1, 30, 115, 117]]], 
[array([ 1.        , -1.61803399, -2.        ,  0.61803399]), [[182, 459, 1040, 1180], [90, 263, 271, 273, 275, 574], [5, 33, 114, 118]]],
 [array([ 1.        ,  0.61803399, -1.61803399, -2.        ]), [[158, 445, 1042, 1181], [138, 227, 235, 237, 239, 568], [9, 31, 116, 119]]], 
[array([-1.61803399, -2.        ,  1.        ,  0.61803399]), [[238, 543, 1044, 1177], [18, 347, 355, 357, 359, 610], [14, 36, 108, 111]]], 
[array([-1.61803399,  1.        ,  0.61803399, -2.        ]), [[254, 508, 1046, 1178], [66, 203, 379, 381, 383, 595], [17, 29, 109, 113]]], 
[array([-1.61803399,  0.61803399, -2.        ,  1.        ]), [[246, 529, 1048, 1176], [42, 251, 367, 369, 371, 604], [22, 32, 110, 112]]],
 [array([ 0.61803399, -2.        , -1.61803399,  1.        ]), [[174, 522, 1050, 1180], [90, 259, 261, 263, 275, 601], [18, 33, 114, 118]]], 
[array([ 0.61803399,  1.        , -2.        , -1.61803399]), [[150, 438, 1052, 1181], [138, 223, 225, 227, 239, 565], [13, 31, 116, 119]]],
 [array([ 0.61803399, -1.61803399,  1.        , -2.        ]), [[190, 494, 1054, 1179], [114, 215, 283, 285, 287, 589], [21, 30, 115, 117]]], 
[array([-2.        ,  1.        , -1.61803399, -0.61803399]), [[197, 518, 1033, 1182], [44, 294, 297, 298, 419, 598], [2, 34, 66, 112]]], 
[array([-2.        , -1.61803399, -0.61803399,  1.        ]), [[293, 539, 1035, 1183], [20, 438, 441, 442, 455, 607], [10, 38, 67, 111]]], 
[array([-2.        , -0.61803399,  1.        , -1.61803399]), [[261, 504, 1037, 1184], [68, 390, 393, 394, 479, 592], [6, 37, 68, 113]]], 
[array([ 1.        , -2.        , -0.61803399, -1.61803399]), [[205, 455, 1039, 1185], [116, 306, 309, 310, 335, 571], [1, 35, 69, 115]]], 
[array([ 1.        , -1.61803399, -2.        , -0.61803399]), [[213, 462, 1041, 1186], [92, 311, 318, 321, 322, 574], [5, 35, 70, 114]]], 
[array([ 1.        , -0.61803399, -1.61803399, -2.        ]), [[221, 448, 1043, 1187], [140, 323, 330, 333, 334, 568], [9, 35, 71, 116]]], 
[array([-1.61803399, -2.        ,  1.        , -0.61803399]), [[269, 546, 1045, 1188], [21, 395, 402, 405, 406, 610], [3, 14, 37, 108]]],
 [array([-1.61803399,  1.        , -0.61803399, -2.        ]), [[285, 511, 1047, 1189], [69, 299, 426, 429, 430, 595], [11, 17, 34, 109]]], 
[array([-1.61803399, -0.61803399, -2.        ,  1.        ]), [[309, 532, 1049, 1190], [45, 443, 462, 465, 466, 604], [7, 22, 38, 110]]],
 [array([-0.61803399, -2.        , -1.61803399,  1.        ]), [[301, 525, 1051, 1191], [93, 450, 453, 454, 467, 601], [15, 18, 38, 118]]],
 [array([-0.61803399,  1.        , -2.        , -1.61803399]), [[277, 441, 1053, 1192], [141, 414, 417, 418, 431, 565], [13, 23, 34, 119]]],
 [array([-0.61803399, -1.61803399,  1.        , -2.        ]), [[317, 497, 1055, 1193], [117, 407, 474, 477, 478, 589], [19, 21, 37, 117]]],
 [array([-2.        , -1.        ,  1.61803399,  0.61803399]), [[231, 544, 1056, 1142], [38, 344, 346, 347, 460, 611], [36, 62, 98, 108]]], 
[array([-2.        ,  1.61803399,  0.61803399, -1.        ]), [[135, 509, 1058, 1140], [14, 200, 202, 203, 400, 596], [29, 60, 96, 109]]],
 [array([-2.        ,  0.61803399, -1.        ,  1.61803399]), [[167, 530, 1060, 1141], [62, 248, 250, 251, 424, 605], [32, 61, 97, 110]]],
 [array([-1.        , -2.        ,  0.61803399,  1.61803399]), [[239, 537, 1062, 1145], [110, 356, 358, 359, 472, 608], [36, 65, 105, 111]]], 
[array([-1.        ,  1.61803399, -2.        ,  0.61803399]), [[247, 516, 1064, 1143], [80, 368, 370, 371, 448, 599], [32, 63, 106, 112]]], 
[array([-1.        ,  0.61803399,  1.61803399, -2.        ]), [[255, 502, 1066, 1144], [128, 380, 382, 383, 412, 593], [29, 64, 107, 113]]], 
[array([ 1.61803399, -2.        , -1.        ,  0.61803399]), [[175, 460, 1068, 1135], [8, 260, 262, 263, 436, 575], [33, 55, 99, 114]]],
 [array([ 1.61803399, -1.        ,  0.61803399, -2.        ]), [[191, 453, 1070, 1136], [56, 284, 286, 287, 388, 572], [30, 56, 101, 115]]], 
[array([ 1.61803399,  0.61803399, -2.        , -1.        ]), [[151, 446, 1072, 1134], [32, 224, 226, 227, 292, 569], [31, 54, 100, 116]]], 
[array([ 0.61803399, -2.        ,  1.61803399, -1.        ]), [[143, 495, 1074, 1138], [86, 212, 214, 215, 316, 590], [30, 58, 102, 117]]], 
[array([ 0.61803399, -1.        , -2.        ,  1.61803399]), [[183, 523, 1076, 1139], [134, 272, 274, 275, 328, 602], [33, 59, 104, 118]]], 
[array([ 0.61803399,  1.61803399, -1.        , -2.        ]), [[159, 439, 1078, 1137], [104, 236, 238, 239, 304, 566], [31, 57, 103, 119]]], 
[array([-2.        , -1.        ,  1.61803399, -0.61803399]), [[262, 547, 1057, 1172], [40, 391, 393, 395, 507, 611], [6, 37, 62, 108]]],
 [array([-2.        ,  1.61803399, -0.61803399, -1.        ]), [[198, 512, 1059, 1170], [16, 295, 297, 299, 495, 596], [2, 34, 60, 109]]],
 [array([-2.        , -0.61803399, -1.        ,  1.61803399]), [[294, 533, 1061, 1171], [64, 439, 441, 443, 519, 605], [10, 38, 61, 110]]],
 [array([-1.        , -2.        , -0.61803399,  1.61803399]), [[302, 540, 1063, 1175], [112, 451, 453, 455, 521, 608], [18, 38, 65, 111]]], 
[array([-1.        ,  1.61803399, -2.        , -0.61803399]), [[278, 519, 1065, 1173], [82, 415, 417, 419, 497, 599], [13, 34, 63, 112]]],
 [array([-1.        , -0.61803399,  1.61803399, -2.        ]), [[318, 505, 1067, 1174], [130, 475, 477, 479, 509, 593], [21, 37, 64, 113]]],
 [array([ 1.61803399, -2.        , -1.        , -0.61803399]), [[206, 463, 1069, 1165], [10, 307, 309, 311, 483, 575], [1, 35, 55, 114]]], 
[array([ 1.61803399, -1.        , -0.61803399, -2.        ]), [[222, 456, 1071, 1166], [58, 331, 333, 335, 485, 572], [9, 35, 56, 115]]], 
[array([ 1.61803399, -0.61803399, -2.        , -1.        ]), [[214, 449, 1073, 1164], [34, 319, 321, 323, 484, 569], [5, 35, 54, 116]]], 
[array([-0.61803399, -2.        ,  1.61803399, -1.        ]), [[270, 498, 1075, 1168], [88, 403, 405, 407, 508, 590], [14, 37, 58, 117]]],
 [array([-0.61803399, -1.        , -2.        ,  1.61803399]), [[310, 526, 1077, 1169], [136, 463, 465, 467, 520, 602], [22, 38, 59, 118]]],
 [array([-0.61803399,  1.61803399, -1.        , -2.        ]), [[286, 442, 1079, 1167], [106, 427, 429, 431, 496, 566], [17, 34, 57, 119]]],
 [array([-2.        , -1.        , -1.61803399,  0.61803399]), [[295, 570, 1080, 1190], [45, 440, 442, 443, 466, 621], [7, 38, 67, 110]]], 
[array([-2.        , -1.61803399,  0.61803399, -1.        ]), [[263, 563, 1082, 1188], [21, 392, 394, 395, 406, 618], [3, 37, 68, 108]]], 
[array([-2.        ,  0.61803399, -1.        , -1.61803399]), [[199, 556, 1084, 1189], [69, 296, 298, 299, 430, 615], [11, 34, 66, 109]]], 
[array([-1.        , -2.        ,  0.61803399, -1.61803399]), [[271, 564, 1086, 1193], [117, 404, 406, 407, 478, 619], [3, 19, 37, 117]]], 
[array([-1.        , -1.61803399, -2.        ,  0.61803399]), [[311, 571, 1088, 1191], [93, 454, 464, 466, 467, 622], [7, 15, 38, 118]]], 
[array([-1.        ,  0.61803399, -1.61803399, -2.        ]), [[287, 557, 1090, 1192], [141, 418, 428, 430, 431, 616], [11, 23, 34, 119]]],
 [array([-1.61803399, -2.        , -1.        ,  0.61803399]), [[303, 572, 1092, 1183], [20, 442, 452, 454, 455, 623], [15, 38, 67, 111]]], 
[array([-1.61803399, -1.        ,  0.61803399, -2.        ]), [[319, 565, 1094, 1184], [68, 394, 476, 478, 479, 620], [19, 37, 68, 113]]],
 [array([-1.61803399,  0.61803399, -2.        , -1.        ]), [[279, 558, 1096, 1182], [44, 298, 416, 418, 419, 617], [23, 34, 66, 112]]],
 [array([ 0.61803399, -2.        , -1.61803399, -1.        ]), [[207, 549, 1098, 1186], [92, 308, 310, 311, 322, 612], [35, 69, 70, 114]]], 
[array([ 0.61803399, -1.        , -2.        , -1.61803399]), [[215, 550, 1100, 1187], [140, 320, 322, 323, 334, 613], [35, 70, 71, 116]]],
 [array([ 0.61803399, -1.61803399, -1.        , -2.        ]), [[223, 551, 1102, 1185], [116, 310, 332, 334, 335, 614], [35, 69, 71, 115]]],
 [array([-2.        , -1.        , -1.61803399, -0.61803399]), [[325, 573, 1081, 1194], [47, 486, 489, 490, 513, 621], [7, 39, 66, 67]]], 
[array([-2.        , -1.61803399, -0.61803399, -1.        ]), [[326, 566, 1083, 1195], [23, 487, 489, 491, 501, 618], [3, 39, 67, 68]]],
 [array([-2.        , -0.61803399, -1.        , -1.61803399]), [[327, 559, 1085, 1196], [71, 488, 490, 491, 525, 615], [11, 39, 66, 68]]], 
[array([-1.        , -2.        , -0.61803399, -1.61803399]), [[333, 567, 1087, 1197], [119, 498, 501, 502, 527, 619], [3, 19, 39, 69]]],
 [array([-1.        , -1.61803399, -2.        , -0.61803399]), [[341, 574, 1089, 1198], [95, 503, 510, 513, 514, 622], [7, 15, 39, 70]]], 
[array([-1.        , -0.61803399, -1.61803399, -2.        ]), [[349, 560, 1091, 1199], [143, 515, 522, 525, 526, 616], [11, 23, 39, 71]]], 
[array([-1.61803399, -2.        , -1.        , -0.61803399]), [[334, 575, 1093, 1195], [23, 489, 499, 501, 503, 623], [3, 15, 39, 67]]], 
[array([-1.61803399, -1.        , -0.61803399, -2.        ]), [[350, 568, 1095, 1196], [71, 491, 523, 525, 527, 620], [11, 19, 39, 68]]],
 [array([-1.61803399, -0.61803399, -2.        , -1.        ]), [[342, 561, 1097, 1194], [47, 490, 511, 513, 515, 617], [7, 23, 39, 66]]], 
[array([-0.61803399, -2.        , -1.61803399, -1.        ]), [[335, 552, 1099, 1198], [95, 500, 502, 503, 514, 612], [15, 39, 69, 70]]],
 [array([-0.61803399, -1.        , -2.        , -1.61803399]), [[343, 553, 1101, 1199], [143, 512, 514, 515, 526, 613], [23, 39, 70, 71]]],
 [array([-0.61803399, -1.61803399, -1.        , -2.        ]), [[351, 554, 1103, 1197], [119, 502, 524, 526, 527, 614], [19, 39, 69, 71]]]]


len(cube.e)= 1200 
cube.e= [[[0, 313], [0, 1, 2], [49, 72, 75]], [[0, 318], [0, 3, 4], [0, 72, 75]], [[0, 337], [1, 3, 5], [0, 49, 72]], 
[[0, 342], [2, 4, 5], [0, 49, 75]], [[1, 325], [6, 7, 8], [55, 84, 99]], [[1, 349], [6, 9, 10], [1, 55, 84]], 
[[1, 366], [7, 9, 11], [1, 84, 99]], [[1, 390], [8, 10, 11], [1, 55, 99]], [[2, 330], [12, 13, 14], [60, 87, 96]], 
[[2, 354], [12, 15, 16], [2, 60, 87]], [[2, 361], [13, 15, 17], [2, 87, 96]], [[2, 385], [14, 16, 17], [2, 60, 96]], 
[[3, 373], [18, 19, 20], [67, 108, 111]], [[3, 378], [18, 21, 22], [3, 108, 111]], [[3, 397], [19, 21, 23], [3, 67, 108]],
 [[3, 402], [20, 22, 23], [3, 67, 111]], [[4, 312], [24, 25, 26], [48, 74, 76]], [[4, 320], [24, 27, 28], [4, 74, 76]], 
[[4, 336], [25, 27, 29], [4, 48, 74]], [[4, 344], [26, 28, 29], [4, 48, 76]], [[5, 324], [30, 31, 32], [54, 86, 100]], 
[[5, 348], [30, 33, 34], [5, 54, 86]], [[5, 368], [31, 33, 35], [5, 86, 100]], [[5, 392], [32, 34, 35], [5, 54, 100]],
 [[6, 332], [36, 37, 38], [62, 88, 98]], [[6, 356], [36, 39, 40], [6, 62, 88]], [[6, 360], [37, 39, 41], [6, 88, 98]],
 [[6, 384], [38, 40, 41], [6, 62, 98]], [[7, 372], [42, 43, 44], [66, 110, 112]], [[7, 380], [42, 45, 46], [7, 110, 112]], 
[[7, 396], [43, 45, 47], [7, 66, 110]], [[7, 404], [44, 46, 47], [7, 66, 112]], [[8, 314], [48, 49, 50], [50, 73, 77]],
 [[8, 319], [48, 51, 52], [8, 73, 77]], [[8, 338], [49, 51, 53], [8, 50, 73]], [[8, 343], [50, 52, 53], [8, 50, 77]],
 [[9, 326], [54, 55, 56], [56, 85, 101]], [[9, 350], [54, 57, 58], [9, 56, 85]], [[9, 367], [55, 57, 59], [9, 85, 101]],
 [[9, 391], [56, 58, 59], [9, 56, 101]], [[10, 331], [60, 61, 62], [61, 89, 97]], [[10, 355], [60, 63, 64], [10, 61, 89]],
 [[10, 362], [61, 63, 65], [10, 89, 97]], [[10, 386], [62, 64, 65], [10, 61, 97]], [[11, 374], [66, 67, 68], [68, 109, 113]], 
[[11, 379], [66, 69, 70], [11, 109, 113]], [[11, 398], [67, 69, 71], [11, 68, 109]], [[11, 403], [68, 70, 71], [11, 68, 113]], 
[[12, 316], [72, 73, 74], [52, 78, 82]], [[12, 321], [72, 75, 76], [12, 78, 82]], [[12, 340], [73, 75, 77], [12, 52, 82]],
 [[12, 345], [74, 76, 77], [12, 52, 78]], [[13, 333], [78, 79, 80], [63, 90, 106]], [[13, 357], [78, 81, 82], [13, 63, 90]],
 [[13, 364], [79, 81, 83], [13, 90, 106]], [[13, 388], [80, 82, 83], [13, 63, 106]], [[14, 328], [84, 85, 86], [58, 94, 102]], 
[[14, 352], [84, 87, 88], [14, 58, 94]], [[14, 369], [85, 87, 89], [14, 94, 102]], [[14, 393], [86, 88, 89], [14, 58, 102]],
 [[15, 376], [90, 91, 92], [70, 114, 118]], [[15, 381], [90, 93, 94], [15, 114, 118]], [[15, 400], [91, 93, 95], [15, 70, 118]],
 [[15, 405], [92, 94, 95], [15, 70, 114]], [[16, 315], [96, 97, 98], [51, 79, 81]], [[16, 323], [96, 99, 100], [16, 79, 81]], 
[[16, 339], [97, 99, 101], [16, 51, 81]], [[16, 347], [98, 100, 101], [16, 51, 79]], [[17, 327], [102, 103, 104], [57, 93, 103]], 
[[17, 351], [102, 105, 106], [17, 57, 93]], [[17, 371], [103, 105, 107], [17, 93, 103]], [[17, 395], [104, 106, 107], [17, 57, 103]],
 [[18, 335], [108, 109, 110], [65, 91, 105]], [[18, 359], [108, 111, 112], [18, 65, 91]], [[18, 363], [109, 111, 113], [18, 91, 105]],
 [[18, 387], [110, 112, 113], [18, 65, 105]], [[19, 375], [114, 115, 116], [69, 115, 117]], [[19, 383], [114, 117, 118], [19, 115, 117]],
 [[19, 399], [115, 117, 119], [19, 69, 117]], [[19, 407], [116, 118, 119], [19, 69, 115]], [[20, 317], [120, 121, 122], [53, 80, 83]],
 [[20, 322], [120, 123, 124], [20, 80, 83]], [[20, 341], [121, 123, 125], [20, 53, 83]], [[20, 346], [122, 124, 125], [20, 53, 80]], 
[[21, 334], [126, 127, 128], [64, 92, 107]], [[21, 358], [126, 129, 130], [21, 64, 92]], [[21, 365], [127, 129, 131], [21, 92, 107]],
 [[21, 389], [128, 130, 131], [21, 64, 107]], [[22, 329], [132, 133, 134], [59, 95, 104]], [[22, 353], [132, 135, 136], [22, 59, 95]],
 [[22, 370], [133, 135, 137], [22, 95, 104]], [[22, 394], [134, 136, 137], [22, 59, 104]], [[23, 377], [138, 139, 140], [71, 116, 119]],
 [[23, 382], [138, 141, 142], [23, 116, 119]], [[23, 401], [139, 141, 143], [23, 71, 119]], [[23, 406], [140, 142, 143], [23, 71, 116]],
 [[24, 152], [144, 145, 146], [72, 73, 74]], [[24, 408], [144, 147, 148], [24, 72, 74]], [[24, 409], [145, 147, 149], [24, 72, 73]],
 [[24, 410], [146, 148, 149], [24, 73, 74]], [[25, 153], [150, 151, 152], [96, 97, 98]], [[25, 504], [150, 153, 154], [25, 96, 98]], 
[[25, 505], [151, 153, 155], [25, 96, 97]], [[25, 506], [152, 154, 155], [25, 97, 98]], [[26, 154], [156, 157, 158], [75, 78, 81]],
 [[26, 411], [156, 159, 160], [24, 75, 81]], [[26, 414], [157, 159, 161], [24, 75, 78]], [[26, 417], [158, 160, 161], [24, 78, 81]], 
[[27, 155], [162, 163, 164], [99, 102, 105]], [[27, 507], [162, 165, 166], [26, 99, 105]], [[27, 510], [163, 165, 167], [26, 99, 102]], 
[[27, 513], [164, 166, 167], [26, 102, 105]], [[28, 156], [168, 169, 170], [76, 80, 82]], [[28, 412], [168, 171, 172], [24, 76, 82]],
 [[28, 416], [169, 171, 173], [24, 76, 80]], [[28, 418], [170, 172, 173], [24, 80, 82]], [[29, 157], [174, 175, 176], [100, 104, 106]], 
[[29, 508], [174, 177, 178], [27, 100, 106]], [[29, 512], [175, 177, 179], [27, 100, 104]], [[29, 514], [176, 178, 179], [27, 104, 106]],
 [[30, 158], [180, 181, 182], [77, 79, 83]], [[30, 413], [180, 183, 184], [24, 77, 83]], [[30, 415], [181, 183, 185], [24, 77, 79]],
 [[30, 419], [182, 184, 185], [24, 79, 83]], [[31, 159], [186, 187, 188], [101, 103, 107]], [[31, 509], [186, 189, 190], [28, 101, 107]],
 [[31, 511], [187, 189, 191], [28, 101, 103]], [[31, 515], [188, 190, 191], [28, 103, 107]], [[32, 160], [192, 193, 194], [48, 72, 85]],
 [[32, 420], [192, 195, 196], [28, 48, 72]], [[32, 434], [193, 195, 197], [28, 48, 85]], [[32, 457], [194, 196, 197], [28, 72, 85]], 
[[33, 161], [198, 199, 200], [6, 96, 109]], [[33, 516], [198, 201, 202], [6, 29, 96]], [[33, 530], [199, 201, 203], [6, 29, 109]], 
[[33, 553], [200, 202, 203], [29, 96, 109]], [[34, 162], [204, 205, 206], [0, 78, 93]], [[34, 426], [204, 207, 208], [0, 28, 78]], 
[[34, 435], [205, 207, 209], [0, 28, 93]], [[34, 465], [206, 208, 209], [28, 78, 93]], [[35, 163], [210, 211, 212], [1, 102, 117]],
 [[35, 522], [210, 213, 214], [1, 30, 102]], [[35, 531], [211, 213, 215], [1, 30, 117]], [[35, 561], [212, 214, 215], [30, 102, 117]], 
[[36, 164], [216, 217, 218], [52, 76, 92]], [[36, 424], [216, 219, 220], [28, 52, 76]], [[36, 442], [217, 219, 221], [28, 52, 92]],
 [[36, 464], [218, 220, 221], [28, 76, 92]], [[37, 165], [222, 223, 224], [13, 100, 116]], [[37, 520], [222, 225, 226], [13, 31, 100]],
 [[37, 538], [223, 225, 227], [13, 31, 116]], [[37, 560], [224, 226, 227], [31, 100, 116]], [[38, 166], [228, 229, 230], [8, 79, 95]], 
[[38, 427], [228, 231, 232], [8, 27, 79]], [[38, 437], [229, 231, 233], [8, 27, 95]], [[38, 467], [230, 232, 233], [27, 79, 95]],
 [[39, 167], [234, 235, 236], [9, 103, 119]], [[39, 523], [234, 237, 238], [9, 31, 103]], [[39, 533], [235, 237, 239], [9, 31, 119]], 
[[39, 563], [236, 238, 239], [31, 103, 119]], [[40, 168], [240, 241, 242], [49, 73, 86]], [[40, 421], [240, 243, 244], [27, 49, 73]],
 [[40, 432], [241, 243, 245], [27, 49, 86]], [[40, 458], [242, 244, 245], [27, 73, 86]], [[41, 169], [246, 247, 248], [2, 97, 110]],
 [[41, 517], [246, 249, 250], [2, 32, 97]], [[41, 528], [247, 249, 251], [2, 32, 110]], [[41, 554], [248, 250, 251], [32, 97, 110]], 
[[42, 170], [252, 253, 254], [51, 75, 90]], [[42, 423], [252, 255, 256], [27, 51, 75]], [[42, 441], [253, 255, 257], [27, 51, 90]], 
[[42, 462], [254, 256, 257], [27, 75, 90]], [[43, 171], [258, 259, 260], [18, 99, 114]], [[43, 519], [258, 261, 262], [18, 33, 99]], 
[[43, 537], [259, 261, 263], [18, 33, 114]], [[43, 558], [260, 262, 263], [33, 99, 114]], [[44, 172], [264, 265, 266], [4, 80, 94]],
 [[44, 428], [264, 267, 268], [4, 26, 80]], [[44, 436], [265, 267, 269], [4, 26, 94]], [[44, 466], [266, 268, 269], [26, 80, 94]], 
[[45, 173], [270, 271, 272], [5, 104, 118]], [[45, 524], [270, 273, 274], [5, 33, 104]], [[45, 532], [271, 273, 275], [5, 33, 118]],
 [[45, 562], [272, 274, 275], [33, 104, 118]], [[46, 174], [276, 277, 278], [53, 77, 91]], [[46, 425], [276, 279, 280], [26, 53, 77]], 
[[46, 443], [277, 279, 281], [26, 53, 91]], [[46, 463], [278, 280, 281], [26, 77, 91]], [[47, 175], [282, 283, 284], [21, 101, 115]],
 [[47, 521], [282, 285, 286], [21, 30, 101]], [[47, 539], [283, 285, 287], [21, 30, 115]], [[47, 559], [284, 286, 287], [30, 101, 115]],
 [[48, 176], [288, 289, 290], [49, 54, 85]], [[48, 444], [288, 291, 292], [31, 49, 54]], [[48, 469], [289, 291, 293], [31, 49, 85]], 
[[48, 482], [290, 292, 293], [31, 54, 85]], [[49, 177], [294, 295, 296], [2, 66, 109]], [[49, 540], [294, 297, 298], [2, 34, 66]], 
[[49, 565], [295, 297, 299], [2, 34, 109]], [[49, 578], [296, 298, 299], [34, 66, 109]], [[50, 178], [300, 301, 302], [0, 57, 90]], 
[[50, 447], [300, 303, 304], [0, 31, 57]], [[50, 474], [301, 303, 305], [0, 31, 90]], [[50, 489], [302, 304, 305], [31, 57, 90]], 
[[51, 179], [306, 307, 308], [1, 69, 114]], [[51, 543], [306, 309, 310], [1, 35, 69]], [[51, 570], [307, 309, 311], [1, 35, 114]], 
[[51, 585], [308, 310, 311], [35, 69, 114]], [[52, 180], [312, 313, 314], [4, 58, 92]], [[52, 448], [312, 315, 316], [4, 30, 58]], 
[[52, 476], [313, 315, 317], [4, 30, 92]], [[52, 490], [314, 316, 317], [30, 58, 92]], [[53, 181], [318, 319, 320], [5, 70, 116]],
 [[53, 544], [318, 321, 322], [5, 35, 70]], [[53, 572], [319, 321, 323], [5, 35, 116]], [[53, 586], [320, 322, 323], [35, 70, 116]],
 [[54, 182], [324, 325, 326], [8, 59, 91]], [[54, 449], [324, 327, 328], [8, 33, 59]], [[54, 475], [325, 327, 329], [8, 33, 91]],
 [[54, 491], [326, 328, 329], [33, 59, 91]], [[55, 183], [330, 331, 332], [9, 71, 115]], [[55, 545], [330, 333, 334], [9, 35, 71]],
 [[55, 571], [331, 333, 335], [9, 35, 115]], [[55, 587], [332, 334, 335], [35, 71, 115]], [[56, 184], [336, 337, 338], [50, 74, 84]],
 [[56, 422], [336, 339, 340], [26, 50, 74]], [[56, 433], [337, 339, 341], [26, 50, 84]], [[56, 456], [338, 340, 341], [26, 74, 84]],
 [[57, 185], [342, 343, 344], [10, 98, 108]], [[57, 518], [342, 345, 346], [10, 36, 98]], [[57, 529], [343, 345, 347], [10, 36, 108]],
 [[57, 552], [344, 346, 347], [36, 98, 108]], [[58, 186], [348, 349, 350], [12, 81, 87]], [[58, 429], [348, 351, 352], [12, 25, 81]],
 [[58, 438], [349, 351, 353], [12, 25, 87]], [[58, 459], [350, 352, 353], [25, 81, 87]], [[59, 187], [354, 355, 356], [14, 105, 111]], 
[[59, 525], [354, 357, 358], [14, 36, 105]], [[59, 534], [355, 357, 359], [14, 36, 111]], [[59, 555], [356, 358, 359], [36, 105, 111]],
 [[60, 188], [360, 361, 362], [20, 82, 88]], [[60, 430], [360, 363, 364], [20, 25, 82]], [[60, 440], [361, 363, 365], [20, 25, 88]],
 [[60, 460], [362, 364, 365], [25, 82, 88]], [[61, 189], [366, 367, 368], [22, 106, 112]], [[61, 526], [366, 369, 370], [22, 32, 106]],
 [[61, 536], [367, 369, 371], [22, 32, 112]], [[61, 556], [368, 370, 371], [32, 106, 112]], [[62, 190], [372, 373, 374], [16, 83, 89]],
 [[62, 431], [372, 375, 376], [16, 25, 83]], [[62, 439], [373, 375, 377], [16, 25, 89]], [[62, 461], [374, 376, 377], [25, 83, 89]],
 [[63, 191], [378, 379, 380], [17, 107, 113]], [[63, 527], [378, 381, 382], [17, 29, 107]], [[63, 535], [379, 381, 383], [17, 29, 113]], 
[[63, 557], [380, 382, 383], [29, 107, 113]], [[64, 192], [384, 385, 386], [48, 56, 84]], [[64, 446], [384, 387, 388], [30, 48, 56]], 
[[64, 468], [385, 387, 389], [30, 48, 84]], [[64, 481], [386, 388, 389], [30, 56, 84]], [[65, 193], [390, 391, 392], [6, 68, 108]], 
[[65, 542], [390, 393, 394], [6, 37, 68]], [[65, 564], [391, 393, 395], [6, 37, 108]], [[65, 577], [392, 394, 395], [37, 68, 108]], 
[[66, 194], [396, 397, 398], [12, 60, 93]], [[66, 450], [396, 399, 400], [12, 29, 60]], [[66, 477], [397, 399, 401], [12, 29, 93]], 
[[66, 483], [398, 400, 401], [29, 60, 93]], [[67, 195], [402, 403, 404], [3, 14, 117]], [[67, 546], [402, 405, 406], [3, 14, 37]], 
[[67, 573], [403, 405, 407], [14, 37, 117]], [[67, 579], [404, 406, 407], [3, 37, 117]], [[68, 196], [408, 409, 410], [52, 64, 88]],
 [[68, 454], [408, 411, 412], [29, 52, 64]], [[68, 472], [409, 411, 413], [29, 52, 88]], [[68, 488], [410, 412, 413], [29, 64, 88]],
 [[69, 197], [414, 415, 416], [13, 23, 112]], [[69, 550], [414, 417, 418], [13, 23, 34]], [[69, 568], [415, 417, 419], [13, 34, 112]], 
[[69, 584], [416, 418, 419], [23, 34, 112]], [[70, 198], [420, 421, 422], [16, 61, 95]], [[70, 451], [420, 423, 424], [16, 32, 61]],
 [[70, 479], [421, 423, 425], [16, 32, 95]], [[70, 485], [422, 424, 425], [32, 61, 95]], [[71, 199], [426, 427, 428], [11, 17, 119]],
 [[71, 547], [426, 429, 430], [11, 17, 34]], [[71, 575], [427, 429, 431], [17, 34, 119]], [[71, 581], [428, 430, 431], [11, 34, 119]],
 [[72, 200], [432, 433, 434], [50, 55, 86]], [[72, 445], [432, 435, 436], [33, 50, 55]], [[72, 470], [433, 435, 437], [33, 50, 86]], 
[[72, 480], [434, 436, 437], [33, 55, 86]], [[73, 201], [438, 439, 440], [10, 67, 110]], [[73, 541], [438, 441, 442], [10, 38, 67]],
 [[73, 566], [439, 441, 443], [10, 38, 110]], [[73, 576], [440, 442, 443], [38, 67, 110]], [[74, 202], [444, 445, 446], [51, 63, 87]],
 [[74, 453], [444, 447, 448], [32, 51, 63]], [[74, 471], [445, 447, 449], [32, 51, 87]], [[74, 486], [446, 448, 449], [32, 63, 87]],
 [[75, 203], [450, 451, 452], [15, 18, 111]], [[75, 549], [450, 453, 454], [15, 18, 38]], [[75, 567], [451, 453, 455], [18, 38, 111]],
 [[75, 582], [452, 454, 455], [15, 38, 111]], [[76, 204], [456, 457, 458], [20, 62, 94]], [[76, 452], [456, 459, 460], [20, 36, 62]], 
[[76, 478], [457, 459, 461], [20, 36, 94]], [[76, 484], [458, 460, 461], [36, 62, 94]], [[77, 205], [462, 463, 464], [7, 22, 118]],
 [[77, 548], [462, 465, 466], [7, 22, 38]], [[77, 574], [463, 465, 467], [22, 38, 118]], [[77, 580], [464, 466, 467], [7, 38, 118]], 
[[78, 206], [468, 469, 470], [53, 65, 89]], [[78, 455], [468, 471, 472], [36, 53, 65]], [[78, 473], [469, 471, 473], [36, 53, 89]],
 [[78, 487], [470, 472, 473], [36, 65, 89]], [[79, 207], [474, 475, 476], [19, 21, 113]], [[79, 551], [474, 477, 478], [19, 21, 37]],
 [[79, 569], [475, 477, 479], [21, 37, 113]], [[79, 583], [476, 478, 479], [19, 37, 113]], [[80, 208], [480, 481, 482], [54, 55, 56]], 
[[80, 492], [480, 483, 484], [35, 54, 55]], [[80, 493], [481, 483, 485], [35, 55, 56]], [[80, 494], [482, 484, 485], [35, 54, 56]], 
[[81, 209], [486, 487, 488], [66, 67, 68]], [[81, 588], [486, 489, 490], [39, 66, 67]], [[81, 589], [487, 489, 491], [39, 67, 68]], 
[[81, 590], [488, 490, 491], [39, 66, 68]], [[82, 210], [492, 493, 494], [57, 60, 63]], [[82, 495], [492, 495, 496], [34, 57, 60]],
 [[82, 498], [493, 495, 497], [34, 60, 63]], [[82, 501], [494, 496, 497], [34, 57, 63]], [[83, 211], [498, 499, 500], [3, 15, 69]], 
[[83, 591], [498, 501, 502], [3, 39, 69]], [[83, 594], [499, 501, 503], [3, 15, 39]], [[83, 597], [500, 502, 503], [15, 39, 69]],
 [[84, 212], [504, 505, 506], [58, 62, 64]], [[84, 496], [504, 507, 508], [37, 58, 62]], [[84, 500], [505, 507, 509], [37, 62, 64]], 
[[84, 502], [506, 508, 509], [37, 58, 64]], [[85, 213], [510, 511, 512], [7, 23, 70]], [[85, 592], [510, 513, 514], [7, 39, 70]], 
[[85, 596], [511, 513, 515], [7, 23, 39]], [[85, 598], [512, 514, 515], [23, 39, 70]], [[86, 214], [516, 517, 518], [59, 61, 65]], 
[[86, 497], [516, 519, 520], [38, 59, 61]], [[86, 499], [517, 519, 521], [38, 61, 65]], [[86, 503], [518, 520, 521], [38, 59, 65]],
 [[87, 215], [522, 523, 524], [11, 19, 71]], [[87, 593], [522, 525, 526], [11, 39, 71]], [[87, 595], [523, 525, 527], [11, 19, 39]],
 [[87, 599], [524, 526, 527], [19, 39, 71]], [[88, 89], [528, 529, 530], [81, 82, 83]], [[88, 417], [160, 172, 528], [24, 81, 82]], 
[[88, 418], [172, 184, 529], [24, 82, 83]], [[88, 419], [160, 184, 530], [24, 81, 83]], [[89, 429], [352, 364, 528], [25, 81, 82]], 
[[89, 430], [364, 376, 529], [25, 82, 83]], [[89, 431], [352, 376, 530], [25, 81, 83]], [[90, 91], [531, 532, 533], [74, 77, 80]], 
[[90, 410], [148, 183, 531], [24, 74, 77]], [[90, 413], [173, 183, 532], [24, 77, 80]], [[90, 416], [148, 173, 533], [24, 74, 80]],
 [[91, 422], [280, 340, 531], [26, 74, 77]], [[91, 425], [268, 280, 532], [26, 77, 80]], [[91, 428], [268, 340, 533], [26, 74, 80]], 
[[92, 93], [534, 535, 536], [73, 75, 79]], [[92, 409], [149, 159, 534], [24, 73, 75]], [[92, 411], [159, 185, 535], [24, 75, 79]],
 [[92, 415], [149, 185, 536], [24, 73, 79]], [[93, 421], [244, 256, 534], [27, 73, 75]], [[93, 423], [232, 256, 535], [27, 75, 79]], 
[[93, 427], [232, 244, 536], [27, 73, 79]], [[94, 95], [537, 538, 539], [72, 76, 78]], [[94, 408], [147, 171, 537], [24, 72, 76]],
 [[94, 412], [161, 171, 538], [24, 76, 78]], [[94, 414], [147, 161, 539], [24, 72, 78]], [[95, 420], [196, 220, 537], [28, 72, 76]], 
[[95, 424], [208, 220, 538], [28, 76, 78]], [[95, 426], [196, 208, 539], [28, 72, 78]], [[96, 97], [540, 541, 542], [52, 93, 107]], 
[[96, 442], [190, 219, 540], [28, 52, 107]], [[96, 465], [209, 219, 541], [28, 52, 93]], [[96, 515], [190, 209, 542], [28, 93, 107]],
 [[97, 454], [382, 411, 540], [29, 52, 107]], [[97, 477], [401, 411, 541], [29, 52, 93]], [[97, 527], [382, 401, 542], [29, 93, 107]],
 [[98, 99], [543, 544, 545], [48, 92, 101]], [[98, 434], [189, 195, 543], [28, 48, 101]], [[98, 464], [195, 221, 544], [28, 48, 92]],
 [[98, 509], [189, 221, 545], [28, 92, 101]], [[99, 446], [286, 387, 543], [30, 48, 101]], [[99, 476], [317, 387, 544], [30, 48, 92]], 
[[99, 521], [286, 317, 545], [30, 92, 101]], [[100, 101], [546, 547, 548], [0, 85, 103]], [[100, 435], [191, 207, 546], [0, 28, 103]], 
[[100, 457], [197, 207, 547], [0, 28, 85]], [[100, 511], [191, 197, 548], [28, 85, 103]], [[101, 447], [238, 303, 546], [0, 31, 103]], 
[[101, 469], [293, 303, 547], [0, 31, 85]], [[101, 523], [238, 293, 548], [31, 85, 103]], [[102, 103], [549, 550, 551], [49, 90, 100]], 
[[102, 432], [177, 243, 549], [27, 49, 100]], [[102, 462], [243, 257, 550], [27, 49, 90]], [[102, 508], [177, 257, 551], [27, 90, 100]],
 [[103, 444], [226, 291, 549], [31, 49, 100]], [[103, 474], [291, 305, 550], [31, 49, 90]], [[103, 520], [226, 305, 551], [31, 90, 100]], 
[[104, 105], [552, 553, 554], [51, 95, 106]], [[104, 441], [178, 255, 552], [27, 51, 106]], [[104, 467], [233, 255, 553], [27, 51, 95]],
 [[104, 514], [178, 233, 554], [27, 95, 106]], [[105, 453], [370, 447, 552], [32, 51, 106]], [[105, 479], [425, 447, 553], [32, 51, 95]],
 [[105, 526], [370, 425, 554], [32, 95, 106]], [[106, 107], [555, 556, 557], [8, 86, 104]], [[106, 437], [179, 231, 555], [8, 27, 104]],
 [[106, 458], [231, 245, 556], [8, 27, 86]], [[106, 512], [179, 245, 557], [27, 86, 104]], [[107, 449], [274, 327, 555], [8, 33, 104]], 
[[107, 470], [327, 437, 556], [8, 33, 86]], [[107, 524], [274, 437, 557], [33, 86, 104]], [[108, 109], [558, 559, 560], [50, 91, 99]],
 [[108, 433], [165, 339, 558], [26, 50, 99]], [[108, 463], [281, 339, 559], [26, 50, 91]], [[108, 507], [165, 281, 560], [26, 91, 99]],
 [[109, 445], [262, 435, 558], [33, 50, 99]], [[109, 475], [329, 435, 559], [33, 50, 91]], [[109, 519], [262, 329, 560], [33, 91, 99]], 
[[110, 111], [561, 562, 563], [4, 84, 102]], [[110, 436], [167, 267, 561], [4, 26, 102]], [[110, 456], [267, 341, 562], [4, 26, 84]],
 [[110, 510], [167, 341, 563], [26, 84, 102]], [[111, 448], [214, 315, 561], [4, 30, 102]], [[111, 468], [315, 389, 562], [4, 30, 84]],
 [[111, 522], [214, 389, 563], [30, 84, 102]], [[112, 113], [564, 565, 566], [13, 57, 119]], [[112, 489], [225, 304, 564], [13, 31, 57]], 
[[112, 538], [225, 239, 565], [13, 31, 119]], [[112, 563], [239, 304, 566], [31, 57, 119]], [[113, 501], [417, 496, 564], [13, 34, 57]], 
[[113, 550], [417, 431, 565], [13, 34, 119]], [[113, 575], [431, 496, 566], [34, 57, 119]], [[114, 115], [567, 568, 569], [9, 54, 116]],
 [[114, 482], [237, 292, 567], [9, 31, 54]], [[114, 533], [227, 237, 568], [9, 31, 116]], [[114, 560], [227, 292, 569], [31, 54, 116]], 
[[115, 494], [333, 484, 567], [9, 35, 54]], [[115, 545], [323, 333, 568], [9, 35, 116]], [[115, 572], [323, 484, 569], [35, 54, 116]], 
[[116, 117], [570, 571, 572], [1, 56, 115]], [[116, 481], [213, 388, 570], [1, 30, 56]], [[116, 531], [213, 287, 571], [1, 30, 115]],
 [[116, 559], [287, 388, 572], [30, 56, 115]], [[117, 493], [309, 485, 570], [1, 35, 56]], [[117, 543], [309, 335, 571], [1, 35, 115]], 
[[117, 571], [335, 485, 572], [35, 56, 115]], [[118, 119], [573, 574, 575], [5, 55, 114]], [[118, 480], [273, 436, 573], [5, 33, 55]],
 [[118, 532], [263, 273, 574], [5, 33, 114]], [[118, 558], [263, 436, 575], [33, 55, 114]], [[119, 492], [321, 483, 573], [5, 35, 55]], 
[[119, 544], [311, 321, 574], [5, 35, 114]], [[119, 570], [311, 483, 575], [35, 55, 114]], [[120, 121], [576, 577, 578], [53, 94, 105]], 
[[120, 443], [166, 279, 576], [26, 53, 105]], [[120, 466], [269, 279, 577], [26, 53, 94]], [[120, 513], [166, 269, 578], [26, 94, 105]],
 [[121, 455], [358, 471, 576], [36, 53, 105]], [[121, 478], [461, 471, 577], [36, 53, 94]], [[121, 525], [358, 461, 578], [36, 94, 105]],
 [[122, 123], [579, 580, 581], [20, 89, 98]], [[122, 440], [154, 363, 579], [20, 25, 98]], [[122, 461], [363, 377, 580], [20, 25, 89]],
 [[122, 506], [154, 377, 581], [25, 89, 98]], [[123, 452], [346, 459, 579], [20, 36, 98]], [[123, 473], [459, 473, 580], [20, 36, 89]],
 [[123, 518], [346, 473, 581], [36, 89, 98]], [[124, 125], [582, 583, 584], [16, 87, 97]], [[124, 439], [155, 375, 582], [16, 25, 97]], 
[[124, 459], [353, 375, 583], [16, 25, 87]], [[124, 505], [155, 353, 584], [25, 87, 97]], [[125, 451], [250, 423, 582], [16, 32, 97]],
 [[125, 471], [423, 449, 583], [16, 32, 87]], [[125, 517], [250, 449, 584], [32, 87, 97]], [[126, 127], [585, 586, 587], [12, 88, 96]],
 [[126, 438], [153, 351, 585], [12, 25, 96]], [[126, 460], [351, 365, 586], [12, 25, 88]], [[126, 504], [153, 365, 587], [25, 88, 96]],
 [[127, 450], [202, 399, 585], [12, 29, 96]], [[127, 472], [399, 413, 586], [12, 29, 88]], [[127, 516], [202, 413, 587], [29, 88, 96]],
 [[128, 129], [588, 589, 590], [21, 58, 117]], [[128, 490], [285, 316, 588], [21, 30, 58]], [[128, 539], [215, 285, 589], [21, 30, 117]],
 [[128, 561], [215, 316, 590], [30, 58, 117]], [[129, 502], [477, 508, 588], [21, 37, 58]], [[129, 551], [407, 477, 589], [21, 37, 117]], 
[[129, 573], [407, 508, 590], [37, 58, 117]], [[130, 131], [591, 592, 593], [6, 64, 113]], [[130, 488], [201, 412, 591], [6, 29, 64]], 
[[130, 530], [201, 383, 592], [6, 29, 113]], [[130, 557], [383, 412, 593], [29, 64, 113]], [[131, 500], [393, 509, 591], [6, 37, 64]],
 [[131, 542], [393, 479, 592], [6, 37, 113]], [[131, 569], [479, 509, 593], [37, 64, 113]], [[132, 133], [594, 595, 596], [17, 60, 109]],
 [[132, 483], [381, 400, 594], [17, 29, 60]], [[132, 535], [203, 381, 595], [17, 29, 109]], [[132, 553], [203, 400, 596], [29, 60, 109]],
 [[133, 495], [429, 495, 594], [17, 34, 60]], [[133, 547], [299, 429, 595], [17, 34, 109]], [[133, 565], [299, 495, 596], [34, 60, 109]],
 [[134, 135], [597, 598, 599], [2, 63, 112]], [[134, 486], [249, 448, 597], [2, 32, 63]], [[134, 528], [249, 371, 598], [2, 32, 112]],
 [[134, 556], [371, 448, 599], [32, 63, 112]], [[135, 498], [297, 497, 597], [2, 34, 63]], [[135, 540], [297, 419, 598], [2, 34, 112]],
 [[135, 568], [419, 497, 599], [34, 63, 112]], [[136, 137], [600, 601, 602], [18, 59, 118]], [[136, 491], [261, 328, 600], [18, 33, 59]],
 [[136, 537], [261, 275, 601], [18, 33, 118]], [[136, 562], [275, 328, 602], [33, 59, 118]], [[137, 503], [453, 520, 600], [18, 38, 59]], 
[[137, 549], [453, 467, 601], [18, 38, 118]], [[137, 574], [467, 520, 602], [38, 59, 118]], [[138, 139], [603, 604, 605], [22, 61, 110]], 
[[138, 485], [369, 424, 603], [22, 32, 61]], [[138, 536], [251, 369, 604], [22, 32, 110]], [[138, 554], [251, 424, 605], [32, 61, 110]], 
[[139, 497], [465, 519, 603], [22, 38, 61]], [[139, 548], [443, 465, 604], [22, 38, 110]], [[139, 566], [443, 519, 605], [38, 61, 110]],
 [[140, 141], [606, 607, 608], [10, 65, 111]], [[140, 487], [345, 472, 606], [10, 36, 65]], [[140, 529], [345, 359, 607], [10, 36, 111]], 
[[140, 555], [359, 472, 608], [36, 65, 111]], [[141, 499], [441, 521, 606], [10, 38, 65]], [[141, 541], [441, 455, 607], [10, 38, 111]],
 [[141, 567], [455, 521, 608], [38, 65, 111]], [[142, 143], [609, 610, 611], [14, 62, 108]], [[142, 484], [357, 460, 609], [14, 36, 62]], 
[[142, 534], [347, 357, 610], [14, 36, 108]], [[142, 552], [347, 460, 611], [36, 62, 108]], [[143, 496], [405, 507, 609], [14, 37, 62]], 
[[143, 546], [395, 405, 610], [14, 37, 108]], [[143, 564], [395, 507, 611], [37, 62, 108]], [[144, 145], [612, 613, 614], [69, 70, 71]],
 [[144, 585], [310, 322, 612], [35, 69, 70]], [[144, 586], [322, 334, 613], [35, 70, 71]], [[144, 587], [310, 334, 614], [35, 69, 71]],
 [[145, 597], [502, 514, 612], [39, 69, 70]], [[145, 598], [514, 526, 613], [39, 70, 71]], [[145, 599], [502, 526, 614], [39, 69, 71]],
 [[146, 147], [615, 616, 617], [11, 23, 66]], [[146, 578], [298, 430, 615], [11, 34, 66]], [[146, 581], [418, 430, 616], [11, 23, 34]],
 [[146, 584], [298, 418, 617], [23, 34, 66]], [[147, 590], [490, 525, 615], [11, 39, 66]], [[147, 593], [515, 525, 616], [11, 23, 39]], 
[[147, 596], [490, 515, 617], [23, 39, 66]], [[148, 149], [618, 619, 620], [3, 19, 68]], [[148, 577], [394, 406, 618], [3, 37, 68]], 
[[148, 579], [406, 478, 619], [3, 19, 37]], [[148, 583], [394, 478, 620], [19, 37, 68]], [[149, 589], [491, 501, 618], [3, 39, 68]],
 [[149, 591], [501, 527, 619], [3, 19, 39]], [[149, 595], [491, 527, 620], [19, 39, 68]], [[150, 151], [621, 622, 623], [7, 15, 67]],
 [[150, 576], [442, 466, 621], [7, 38, 67]], [[150, 580], [454, 466, 622], [7, 15, 38]], [[150, 582], [442, 454, 623], [15, 38, 67]], 
[[151, 588], [489, 513, 621], [7, 39, 67]], [[151, 592], [503, 513, 622], [7, 15, 39]], [[151, 594], [489, 503, 623], [15, 39, 67]], 
[[152, 216], [144, 624, 625], [40, 72, 74]], [[152, 217], [145, 624, 626], [40, 72, 73]], [[152, 218], [146, 625, 626], [40, 73, 74]],
 [[153, 264], [150, 627, 628], [41, 96, 98]], [[153, 265], [151, 627, 629], [41, 96, 97]], [[153, 266], [152, 628, 629], [41, 97, 98]], 
[[154, 219], [156, 630, 631], [42, 75, 81]], [[154, 222], [157, 630, 632], [42, 75, 78]], [[154, 225], [158, 631, 632], [42, 78, 81]], 
[[155, 267], [162, 633, 634], [43, 99, 105]], [[155, 270], [163, 633, 635], [43, 99, 102]], [[155, 273], [164, 634, 635], [43, 102, 105]],
 [[156, 220], [168, 636, 637], [44, 76, 82]], [[156, 224], [169, 636, 638], [44, 76, 80]], [[156, 226], [170, 637, 638], [44, 80, 82]], 
[[157, 268], [174, 639, 640], [45, 100, 106]], [[157, 272], [175, 639, 641], [45, 100, 104]], [[157, 274], [176, 640, 641], [45, 104, 106]],
 [[158, 221], [180, 642, 643], [46, 77, 83]], [[158, 223], [181, 642, 644], [46, 77, 79]], [[158, 227], [182, 643, 644], [46, 79, 83]], 
[[159, 269], [186, 645, 646], [47, 101, 107]], [[159, 271], [187, 645, 647], [47, 101, 103]], [[159, 275], [188, 646, 647], [47, 103, 107]], 
[[160, 216], [192, 624, 648], [40, 48, 72]], [[160, 230], [193, 648, 649], [40, 48, 85]], [[160, 241], [194, 624, 649], [40, 72, 85]], 
[[161, 264], [198, 627, 650], [6, 41, 96]], [[161, 278], [199, 650, 651], [6, 41, 109]], [[161, 289], [200, 627, 651], [41, 96, 109]],
 [[162, 222], [204, 632, 652], [0, 42, 78]], [[162, 231], [205, 652, 653], [0, 42, 93]], [[162, 249], [206, 632, 653], [42, 78, 93]], 
[[163, 270], [210, 635, 654], [1, 43, 102]], [[163, 279], [211, 654, 655], [1, 43, 117]], [[163, 297], [212, 635, 655], [43, 102, 117]], 
[[164, 220], [216, 636, 656], [44, 52, 76]], [[164, 238], [217, 656, 657], [44, 52, 92]], [[164, 248], [218, 636, 657], [44, 76, 92]],
 [[165, 268], [222, 639, 658], [13, 45, 100]], [[165, 286], [223, 658, 659], [13, 45, 116]], [[165, 296], [224, 639, 659], [45, 100, 116]], 
[[166, 223], [228, 644, 660], [8, 46, 79]], [[166, 233], [229, 660, 661], [8, 46, 95]], [[166, 251], [230, 644, 661], [46, 79, 95]],
 [[167, 271], [234, 647, 662], [9, 47, 103]], [[167, 281], [235, 662, 663], [9, 47, 119]], [[167, 299], [236, 647, 663], [47, 103, 119]],
 [[168, 217], [240, 626, 664], [40, 49, 73]], [[168, 228], [241, 664, 665], [40, 49, 86]], [[168, 242], [242, 626, 665], [40, 73, 86]],
 [[169, 265], [246, 629, 666], [2, 41, 97]], [[169, 276], [247, 666, 667], [2, 41, 110]], [[169, 290], [248, 629, 667], [41, 97, 110]],
 [[170, 219], [252, 630, 668], [42, 51, 75]], [[170, 237], [253, 668, 669], [42, 51, 90]], [[170, 246], [254, 630, 669], [42, 75, 90]],
 [[171, 267], [258, 633, 670], [18, 43, 99]], [[171, 285], [259, 670, 671], [18, 43, 114]], [[171, 294], [260, 633, 671], [43, 99, 114]],
 [[172, 224], [264, 638, 672], [4, 44, 80]], [[172, 232], [265, 672, 673], [4, 44, 94]], [[172, 250], [266, 638, 673], [44, 80, 94]], 
[[173, 272], [270, 641, 674], [5, 45, 104]], [[173, 280], [271, 674, 675], [5, 45, 118]], [[173, 298], [272, 641, 675], [45, 104, 118]],
 [[174, 221], [276, 642, 676], [46, 53, 77]], [[174, 239], [277, 676, 677], [46, 53, 91]], [[174, 247], [278, 642, 677], 
[46, 77, 91]], [[175, 269], [282, 645, 678], [21, 47, 101]], [[175, 287], [283, 678, 679], [21, 47, 115]], 
[[175, 295], [284, 645, 679], [47, 101, 115]], [[176, 228], [288, 664, 680], [40, 49, 54]], [[176, 241], [289, 649, 664], [40, 49, 85]],
 [[176, 254], [290, 649, 680], [40, 54, 85]], [[177, 276], [294, 666, 681], [2, 41, 66]], [[177, 289], [295, 651, 666], [2, 41, 109]], 
[[177, 302], [296, 651, 681], [41, 66, 109]], [[178, 231], [300, 652, 682], [0, 42, 57]], [[178, 246], [301, 652, 669], [0, 42, 90]],
 [[178, 261], [302, 669, 682], [42, 57, 90]], [[179, 279], [306, 654, 683], [1, 43, 69]], [[179, 294], [307, 654, 671], [1, 43, 114]], 
[[179, 309], [308, 671, 683], [43, 69, 114]], [[180, 232], [312, 672, 684], [4, 44, 58]], [[180, 248], [313, 657, 672], [4, 44, 92]], 
[[180, 262], [314, 657, 684], [44, 58, 92]], [[181, 280], [318, 674, 685], [5, 45, 70]], [[181, 296], [319, 659, 674], [5, 45, 116]],
 [[181, 310], [320, 659, 685], [45, 70, 116]], [[182, 233], [324, 660, 686], [8, 46, 59]], [[182, 247], [325, 660, 677], [8, 46, 91]], 
[[182, 263], [326, 677, 686], [46, 59, 91]], [[183, 281], [330, 662, 687], [9, 47, 71]], [[183, 295], [331, 662, 679], [9, 47, 115]],
 [[183, 311], [332, 679, 687], [47, 71, 115]], [[184, 218], [336, 625, 688], [40, 50, 74]], [[184, 229], [337, 688, 689], [40, 50, 84]], 
[[184, 240], [338, 625, 689], [40, 74, 84]], [[185, 266], [342, 628, 690], [10, 41, 98]], [[185, 277], [343, 690, 691], [10, 41, 108]], 
[[185, 288], [344, 628, 691], [41, 98, 108]], [[186, 225], [348, 631, 692], [12, 42, 81]], [[186, 234], [349, 692, 693], [12, 42, 87]],
 [[186, 243], [350, 631, 693], [42, 81, 87]], [[187, 273], [354, 634, 694], [14, 43, 105]], [[187, 282], [355, 694, 695], [14, 43, 111]],
 [[187, 291], [356, 634, 695], [43, 105, 111]], [[188, 226], [360, 637, 696], [20, 44, 82]], [[188, 236], [361, 696, 697], [20, 44, 88]],
 [[188, 244], [362, 637, 697], [44, 82, 88]], [[189, 274], [366, 640, 698], [22, 45, 106]], [[189, 284], [367, 698, 699], [22, 45, 112]],
 [[189, 292], [368, 640, 699], [45, 106, 112]], [[190, 227], [372, 643, 700], [16, 46, 83]], [[190, 235], [373, 700, 701], [16, 46, 89]],
 [[190, 245], [374, 643, 701], [46, 83, 89]], [[191, 275], [378, 646, 702], [17, 47, 107]], [[191, 283], [379, 702, 703], [17, 47, 113]],
 [[191, 293], [380, 646, 703], [47, 107, 113]], [[192, 230], [384, 648, 704], [40, 48, 56]], [[192, 240], [385, 648, 689], [40, 48, 84]],
 [[192, 253], [386, 689, 704], [40, 56, 84]], [[193, 278], [390, 650, 705], [6, 41, 68]], [[193, 288], [391, 650, 691], [6, 41, 108]],
 [[193, 301], [392, 691, 705], [41, 68, 108]], [[194, 234], [396, 692, 706], [12, 42, 60]], [[194, 249], [397, 653, 692], [12, 42, 93]],
 [[194, 255], [398, 653, 706], [42, 60, 93]], [[195, 282], [402, 694, 707], [3, 14, 43]], [[195, 297], [403, 655, 694], [14, 43, 117]],
 [[195, 303], [404, 655, 707], [3, 43, 117]], [[196, 238], [408, 656, 708], [44, 52, 64]], [[196, 244], [409, 656, 697], [44, 52, 88]],
 [[196, 260], [410, 697, 708], [44, 64, 88]], [[197, 286], [414, 658, 709], [13, 23, 45]], [[197, 292], [415, 658, 699], [13, 45, 112]],
 [[197, 308], [416, 699, 709], [23, 45, 112]], [[198, 235], [420, 700, 710], [16, 46, 61]], [[198, 251], [421, 661, 700], [16, 46, 95]],
 [[198, 257], [422, 661, 710], [46, 61, 95]], [[199, 283], [426, 702, 711], [11, 17, 47]], [[199, 299], [427, 663, 702], [17, 47, 119]], 
[[199, 305], [428, 663, 711], [11, 47, 119]], [[200, 229], [432, 688, 712], [40, 50, 55]], [[200, 242], [433, 665, 688], [40, 50, 86]], 
[[200, 252], [434, 665, 712], [40, 55, 86]], [[201, 277], [438, 690, 713], [10, 41, 67]], [[201, 290], [439, 667, 690], [10, 41, 110]],
 [[201, 300], [440, 667, 713], [41, 67, 110]], [[202, 237], [444, 668, 714], [42, 51, 63]], [[202, 243], [445, 668, 693], [42, 51, 87]],
 [[202, 258], [446, 693, 714], [42, 63, 87]], [[203, 285], [450, 670, 715], [15, 18, 43]], [[203, 291], [451, 670, 695], [18, 43, 111]], 
[[203, 306], [452, 695, 715], [15, 43, 111]], [[204, 236], [456, 696, 716], [20, 44, 62]], [[204, 250], [457, 673, 696], [20, 44, 94]], 
[[204, 256], [458, 673, 716], [44, 62, 94]], [[205, 284], [462, 698, 717], [7, 22, 45]], [[205, 298], [463, 675, 698], [22, 45, 118]],
 [[205, 304], [464, 675, 717], [7, 45, 118]], [[206, 239], [468, 676, 718], [46, 53, 65]], [[206, 245], [469, 676, 701], [46, 53, 89]],
 [[206, 259], [470, 701, 718], [46, 65, 89]], [[207, 287], [474, 678, 719], [19, 21, 47]], [[207, 293], [475, 678, 703], [21, 47, 113]], 
[[207, 307], [476, 703, 719], [19, 47, 113]], [[208, 252], [480, 680, 712], [40, 54, 55]], [[208, 253], [481, 704, 712], [40, 55, 56]], 
[[208, 254], [482, 680, 704], [40, 54, 56]], [[209, 300], [486, 681, 713], [41, 66, 67]], [[209, 301], [487, 705, 713], [41, 67, 68]],
 [[209, 302], [488, 681, 705], [41, 66, 68]], [[210, 255], [492, 682, 706], [42, 57, 60]], [[210, 258], [493, 706, 714], [42, 60, 63]],
 [[210, 261], [494, 682, 714], [42, 57, 63]], [[211, 303], [498, 683, 707], [3, 43, 69]], [[211, 306], [499, 707, 715], [3, 15, 43]], 
[[211, 309], [500, 683, 715], [15, 43, 69]], [[212, 256], [504, 684, 716], [44, 58, 62]], [[212, 260], [505, 708, 716], [44, 62, 64]],
 [[212, 262], [506, 684, 708], [44, 58, 64]], [[213, 304], [510, 685, 717], [7, 45, 70]], [[213, 308], [511, 709, 717], [7, 23, 45]],
 [[213, 310], [512, 685, 709], [23, 45, 70]], [[214, 257], [516, 686, 710], [46, 59, 61]], [[214, 259], [517, 710, 718], [46, 61, 65]],
 [[214, 263], [518, 686, 718], [46, 59, 65]], [[215, 305], [522, 687, 711], [11, 47, 71]], [[215, 307], [523, 711, 719], [11, 19, 47]], 
[[215, 311], [524, 687, 719], [19, 47, 71]], [[216, 240], [25, 625, 648], [40, 48, 74]], [[216, 312], [25, 144, 192], [48, 72, 74]],
 [[217, 241], [1, 624, 664], [40, 49, 72]], [[217, 313], [1, 145, 240], [49, 72, 73]], [[218, 242], [49, 626, 688], [40, 50, 73]],
 [[218, 314], [49, 146, 336], [50, 73, 74]], [[219, 243], [97, 631, 668], [42, 51, 81]], [[219, 315], [97, 156, 252], [51, 75, 81]],
 [[220, 244], [73, 637, 656], [44, 52, 82]], [[220, 316], [73, 168, 216], [52, 76, 82]], [[221, 245], [121, 643, 676], [46, 53, 83]],
 [[221, 317], [121, 180, 276], [53, 77, 83]], [[222, 246], [4, 630, 652], [0, 42, 75]], [[222, 318], [4, 157, 204], [0, 75, 78]],
 [[223, 247], [52, 642, 660], [8, 46, 77]], [[223, 319], [52, 181, 228], [8, 77, 79]], [[224, 248], [28, 636, 672], [4, 44, 76]],
 [[224, 320], [28, 169, 264], [4, 76, 80]], [[225, 249], [76, 632, 692], [12, 42, 78]], [[225, 321], [76, 158, 348], [12, 78, 81]],
 [[226, 250], [124, 638, 696], [20, 44, 80]], [[226, 322], [124, 170, 360], [20, 80, 82]], [[227, 251], [100, 644, 700], [16, 46, 79]], 
[[227, 323], [100, 182, 372], [16, 79, 83]], [[228, 252], [30, 665, 680], [40, 54, 86]], [[228, 324], [30, 241, 288], [49, 54, 86]],
 [[229, 253], [6, 689, 712], [40, 55, 84]], [[229, 325], [6, 337, 432], [50, 55, 84]], [[230, 254], [54, 649, 704], [40, 56, 85]],
 [[230, 326], [54, 193, 384], [48, 56, 85]], [[231, 255], [102, 653, 682], [42, 57, 93]], [[231, 327], [102, 205, 300], [0, 57, 93]],
 [[232, 256], [84, 673, 684], [44, 58, 94]], [[232, 328], [84, 265, 312], [4, 58, 94]], [[233, 257], [132, 661, 686], [46, 59, 95]],
 [[233, 329], [132, 229, 324], [8, 59, 95]], [[234, 258], [12, 693, 706], [42, 60, 87]], [[234, 330], [12, 349, 396], [12, 60, 87]],
 [[235, 259], [60, 701, 710], [46, 61, 89]], [[235, 331], [60, 373, 420], [16, 61, 89]], [[236, 260], [36, 697, 716], [44, 62, 88]],
 [[236, 332], [36, 361, 456], [20, 62, 88]], [[237, 261], [78, 669, 714], [42, 63, 90]], [[237, 333], [78, 253, 444], [51, 63, 90]],
 [[238, 262], [126, 657, 708], [44, 64, 92]], [[238, 334], [126, 217, 408], [52, 64, 92]], [[239, 263], [108, 677, 718], [46, 65, 91]],
 [[239, 335], [108, 277, 468], [53, 65, 91]], [[240, 336], [25, 338, 385], [48, 74, 84]], [[241, 337], [1, 194, 289], [49, 72, 85]], 
[[242, 338], [49, 242, 433], [50, 73, 86]], [[243, 339], [97, 350, 445], [51, 81, 87]], [[244, 340], [73, 362, 409], [52, 82, 88]],
 [[245, 341], [121, 374, 469], [53, 83, 89]], [[246, 342], [4, 254, 301], [0, 75, 90]], [[247, 343], [52, 278, 325], [8, 77, 91]],
 [[248, 344], [28, 218, 313], [4, 76, 92]], [[249, 345], [76, 206, 397], [12, 78, 93]], [[250, 346], [124, 266, 457], [20, 80, 94]],
 [[251, 347], [100, 230, 421], [16, 79, 95]], [[252, 348], [30, 434, 480], [54, 55, 86]], [[253, 349], [6, 386, 481], [55, 56, 84]], 
[[254, 350], [54, 290, 482], [54, 56, 85]], [[255, 351], [102, 398, 492], [57, 60, 93]], [[256, 352], [84, 458, 504], [58, 62, 94]],
 [[257, 353], [132, 422, 516], [59, 61, 95]], [[258, 354], [12, 446, 493], [60, 63, 87]], [[259, 355], [60, 470, 517], [61, 65, 89]],
 [[260, 356], [36, 410, 505], [62, 64, 88]], [[261, 357], [78, 302, 494], [57, 63, 90]], [[262, 358], [126, 314, 506], [58, 64, 92]], 
[[263, 359], [108, 326, 518], [59, 65, 91]], [[264, 288], [41, 628, 650], [6, 41, 98]], [[264, 360], [41, 150, 198], [6, 96, 98]], 
[[265, 289], [17, 627, 666], [2, 41, 96]], [[265, 361], [17, 151, 246], [2, 96, 97]], [[266, 290], [65, 629, 690], [10, 41, 97]],
 [[266, 362], [65, 152, 342], [10, 97, 98]], [[267, 291], [113, 634, 670], [18, 43, 105]], [[267, 363], [113, 162, 258], [18, 99, 105]],
 [[268, 292], [83, 640, 658], [13, 45, 106]], [[268, 364], [83, 174, 222], [13, 100, 106]], [[269, 293], [131, 646, 678], [21, 47, 107]], 
[[269, 365], [131, 186, 282], [21, 101, 107]], [[270, 294], [11, 633, 654], [1, 43, 99]], [[270, 366], [11, 163, 210], [1, 99, 102]],
 [[271, 295], [59, 645, 662], [9, 47, 101]], [[271, 367], [59, 187, 234], [9, 101, 103]], [[272, 296], [35, 639, 674], [5, 45, 100]], 
[[272, 368], [35, 175, 270], [5, 100, 104]], [[273, 297], [89, 635, 694], [14, 43, 102]], [[273, 369], [89, 164, 354], [14, 102, 105]],
 [[274, 298], [137, 641, 698], [22, 45, 104]], [[274, 370], [137, 176, 366], [22, 104, 106]], [[275, 299], [107, 647, 702], [17, 47, 103]], 
[[275, 371], [107, 188, 378], [17, 103, 107]], [[276, 300], [43, 667, 681], [41, 66, 110]], [[276, 372], [43, 247, 294], [2, 66, 110]],
 [[277, 301], [19, 691, 713], [41, 67, 108]], [[277, 373], [19, 343, 438], [10, 67, 108]], [[278, 302], [67, 651, 705], [41, 68, 109]],
 [[278, 374], [67, 199, 390], [6, 68, 109]], [[279, 303], [115, 655, 683], [43, 69, 117]], [[279, 375], [115, 211, 306], [1, 69, 117]],
 [[280, 304], [91, 675, 685], [45, 70, 118]], [[280, 376], [91, 271, 318], [5, 70, 118]], [[281, 305], [139, 663, 687], [47, 71, 119]],
 [[281, 377], [139, 235, 330], [9, 71, 119]], [[282, 306], [22, 695, 707], [3, 43, 111]], [[282, 378], [22, 355, 402], [3, 14, 111]],
 [[283, 307], [70, 703, 711], [11, 47, 113]], [[283, 379], [70, 379, 426], [11, 17, 113]], [[284, 308], [46, 699, 717], [7, 45, 112]],
 [[284, 380], [46, 367, 462], [7, 22, 112]], [[285, 309], [94, 671, 715], [15, 43, 114]], [[285, 381], [94, 259, 450], [15, 18, 114]],
 [[286, 310], [142, 659, 709], [23, 45, 116]], [[286, 382], [142, 223, 414], [13, 23, 116]], [[287, 311], [118, 679, 719], [19, 47, 115]],
 [[287, 383], [118, 283, 474], [19, 21, 115]], [[288, 384], [41, 344, 391], [6, 98, 108]], [[289, 385], [17, 200, 295], [2, 96, 109]],
 [[290, 386], [65, 248, 439], [10, 97, 110]], [[291, 387], [113, 356, 451], [18, 105, 111]], [[292, 388], [83, 368, 415], [13, 106, 112]], 
[[293, 389], [131, 380, 475], [21, 107, 113]], [[294, 390], [11, 260, 307], [1, 99, 114]], [[295, 391], [59, 284, 331], [9, 101, 115]],
 [[296, 392], [35, 224, 319], [5, 100, 116]], [[297, 393], [89, 212, 403], [14, 102, 117]], [[298, 394], [137, 272, 463], [22, 104, 118]],
 [[299, 395], [107, 236, 427], [17, 103, 119]], [[300, 396], [43, 440, 486], [66, 67, 110]], [[301, 397], [19, 392, 487], [67, 68, 108]],
 [[302, 398], [67, 296, 488], [66, 68, 109]], [[303, 399], [115, 404, 498], [3, 69, 117]], [[304, 400], [91, 464, 510], [7, 70, 118]], 
[[305, 401], [139, 428, 522], [11, 71, 119]], [[306, 402], [22, 452, 499], [3, 15, 111]], [[307, 403], [70, 476, 523], [11, 19, 113]],
 [[308, 404], [46, 416, 511], [7, 23, 112]], [[309, 405], [94, 308, 500], [15, 69, 114]], [[310, 406], [142, 320, 512], [23, 70, 116]],
 [[311, 407], [118, 332, 524], [19, 71, 115]], [[312, 408], [24, 144, 537], [72, 74, 76]], [[312, 420], [26, 192, 537], [48, 72, 76]], 
[[313, 409], [0, 145, 534], [72, 73, 75]], [[313, 421], [2, 240, 534], [49, 73, 75]], [[314, 410], [48, 146, 531], [73, 74, 77]],
 [[314, 422], [50, 336, 531], [50, 74, 77]], [[315, 411], [96, 156, 535], [75, 79, 81]], [[315, 423], [98, 252, 535], [51, 75, 79]],
 [[316, 412], [72, 168, 538], [76, 78, 82]], [[316, 424], [74, 216, 538], [52, 76, 78]], [[317, 413], [120, 180, 532], [77, 80, 83]],
 [[317, 425], [122, 276, 532], [53, 77, 80]], [[318, 414], [0, 157, 539], [72, 75, 78]], [[318, 426], [3, 204, 539], [0, 72, 78]],
 [[319, 415], [48, 181, 536], [73, 77, 79]], [[319, 427], [51, 228, 536], [8, 73, 79]], [[320, 416], [24, 169, 533], [74, 76, 80]],
 [[320, 428], [27, 264, 533], [4, 74, 80]], [[321, 417], [72, 158, 528], [78, 81, 82]], [[321, 429], [75, 348, 528], [12, 81, 82]], 
[[322, 418], [120, 170, 529], [80, 82, 83]], [[322, 430], [123, 360, 529], [20, 82, 83]], [[323, 419], [96, 182, 530], [79, 81, 83]], 
[[323, 431], [99, 372, 530], [16, 81, 83]], [[324, 432], [31, 241, 549], [49, 86, 100]], [[324, 444], [32, 288, 549], [49, 54, 100]], 
[[325, 433], [7, 337, 558], [50, 84, 99]], [[325, 445], [8, 432, 558], [50, 55, 99]], [[326, 434], [55, 193, 543], [48, 85, 101]],
 [[326, 446], [56, 384, 543], [48, 56, 101]], [[327, 435], [103, 205, 546], [0, 93, 103]], [[327, 447], [104, 300, 546], [0, 57, 103]],
 [[328, 436], [85, 265, 561], [4, 94, 102]], [[328, 448], [86, 312, 561], [4, 58, 102]], [[329, 437], [133, 229, 555], [8, 95, 104]], 
[[329, 449], [134, 324, 555], [8, 59, 104]], [[330, 438], [13, 349, 585], [12, 87, 96]], [[330, 450], [14, 396, 585], [12, 60, 96]],
 [[331, 439], [61, 373, 582], [16, 89, 97]], [[331, 451], [62, 420, 582], [16, 61, 97]], [[332, 440], [37, 361, 579], [20, 88, 98]],
 [[332, 452], [38, 456, 579], [20, 62, 98]], [[333, 441], [79, 253, 552], [51, 90, 106]], [[333, 453], [80, 444, 552], [51, 63, 106]], 
[[334, 442], [127, 217, 540], [52, 92, 107]], [[334, 454], [128, 408, 540], [52, 64, 107]], [[335, 443], [109, 277, 576], [53, 91, 105]], 
[[335, 455], [110, 468, 576], [53, 65, 105]], [[336, 456], [27, 338, 562], [4, 74, 84]], [[336, 468], [29, 385, 562], [4, 48, 84]],
 [[337, 457], [3, 194, 547], [0, 72, 85]], [[337, 469], [5, 289, 547], [0, 49, 85]], [[338, 458], [51, 242, 556], [8, 73, 86]],
 [[338, 470], [53, 433, 556], [8, 50, 86]], [[339, 459], [99, 350, 583], [16, 81, 87]], [[339, 471], [101, 445, 583], [16, 51, 87]],
 [[340, 460], [75, 362, 586], [12, 82, 88]], [[340, 472], [77, 409, 586], [12, 52, 88]], [[341, 461], [123, 374, 580], [20, 83, 89]], 
[[341, 473], [125, 469, 580], [20, 53, 89]], [[342, 462], [2, 254, 550], [49, 75, 90]], [[342, 474], [5, 301, 550], [0, 49, 90]],
 [[343, 463], [50, 278, 559], [50, 77, 91]], [[343, 475], [53, 325, 559], [8, 50, 91]], [[344, 464], [26, 218, 544], [48, 76, 92]],
 [[344, 476], [29, 313, 544], [4, 48, 92]], [[345, 465], [74, 206, 541], [52, 78, 93]], [[345, 477], [77, 397, 541], [12, 52, 93]], 
[[346, 466], [122, 266, 577], [53, 80, 94]], [[346, 478], [125, 457, 577], [20, 53, 94]], [[347, 467], [98, 230, 553], [51, 79, 95]], 
[[347, 479], [101, 421, 553], [16, 51, 95]], [[348, 480], [33, 434, 573], [5, 55, 86]], [[348, 492], [34, 480, 573], [5, 54, 55]], 
[[349, 481], [9, 386, 570], [1, 56, 84]], [[349, 493], [10, 481, 570], [1, 55, 56]], [[350, 482], [57, 290, 567], [9, 54, 85]], 
[[350, 494], [58, 482, 567], [9, 54, 56]], [[351, 483], [105, 398, 594], [17, 60, 93]], [[351, 495], [106, 492, 594], [17, 57, 60]],
 [[352, 484], [87, 458, 609], [14, 62, 94]], [[352, 496], [88, 504, 609], [14, 58, 62]], [[353, 485], [135, 422, 603], [22, 61, 95]], 
[[353, 497], [136, 516, 603], [22, 59, 61]], [[354, 486], [15, 446, 597], [2, 63, 87]], [[354, 498], [16, 493, 597], [2, 60, 63]], 
[[355, 487], [63, 470, 606], [10, 65, 89]], [[355, 499], [64, 517, 606], [10, 61, 65]], [[356, 488], [39, 410, 591], [6, 64, 88]],
 [[356, 500], [40, 505, 591], [6, 62, 64]], [[357, 489], [81, 302, 564], [13, 57, 90]], [[357, 501], [82, 494, 564], [13, 57, 63]], 
[[358, 490], [129, 314, 588], [21, 58, 92]], [[358, 502], [130, 506, 588], [21, 58, 64]], [[359, 491], [111, 326, 600], [18, 59, 91]],
 [[359, 503], [112, 518, 600], [18, 59, 65]], [[360, 504], [37, 150, 587], [88, 96, 98]], [[360, 516], [39, 198, 587], [6, 88, 96]],
 [[361, 505], [13, 151, 584], [87, 96, 97]], [[361, 517], [15, 246, 584], [2, 87, 97]], [[362, 506], [61, 152, 581], [89, 97, 98]],
 [[362, 518], [63, 342, 581], [10, 89, 98]], [[363, 507], [109, 162, 560], [91, 99, 105]], [[363, 519], [111, 258, 560], [18, 91, 99]],
 [[364, 508], [79, 174, 551], [90, 100, 106]], [[364, 520], [81, 222, 551], [13, 90, 100]], [[365, 509], [127, 186, 545], [92, 101, 107]],
 [[365, 521], [129, 282, 545], [21, 92, 101]], [[366, 510], [7, 163, 563], [84, 99, 102]], [[366, 522], [9, 210, 563], [1, 84, 102]],
 [[367, 511], [55, 187, 548], [85, 101, 103]], [[367, 523], [57, 234, 548], [9, 85, 103]], [[368, 512], [31, 175, 557], [86, 100, 104]],
 [[368, 524], [33, 270, 557], [5, 86, 104]], [[369, 513], [85, 164, 578], [94, 102, 105]], [[369, 525], [87, 354, 578], [14, 94, 105]],
 [[370, 514], [133, 176, 554], [95, 104, 106]], [[370, 526], [135, 366, 554], [22, 95, 106]], 
[[371, 515], [103, 188, 542], [93, 103, 107]], [[371, 527], [105, 378, 542], [17, 93, 107]], 
[[372, 528], [42, 247, 598], [2, 110, 112]], [[372, 540], [44, 294, 598], [2, 66, 112]], 
[[373, 529], [18, 343, 607], [10, 108, 111]], [[373, 541], [20, 438, 607], [10, 67, 111]],
 [[374, 530], [66, 199, 592], [6, 109, 113]], [[374, 542], [68, 390, 592], [6, 68, 113]],
 [[375, 531], [114, 211, 571], [1, 115, 117]], [[375, 543], [116, 306, 571], [1, 69, 115]],
 [[376, 532], [90, 271, 574], [5, 114, 118]], [[376, 544], [92, 318, 574], [5, 70, 114]],
 [[377, 533], [138, 235, 568], [9, 116, 119]], [[377, 545], [140, 330, 568], [9, 71, 116]],
 [[378, 534], [18, 355, 610], [14, 108, 111]], [[378, 546], [21, 402, 610], [3, 14, 108]],
 [[379, 535], [66, 379, 595], [17, 109, 113]], [[379, 547], [69, 426, 595], [11, 17, 109]], 
[[380, 536], [42, 367, 604], [22, 110, 112]], [[380, 548], [45, 462, 604], [7, 22, 110]], 
[[381, 537], [90, 259, 601], [18, 114, 118]], [[381, 549], [93, 450, 601], [15, 18, 118]],
 [[382, 538], [138, 223, 565], [13, 116, 119]], [[382, 550], [141, 414, 565], [13, 23, 119]], 
[[383, 539], [114, 283, 589], [21, 115, 117]], [[383, 551], [117, 474, 589], [19, 21, 117]], 
[[384, 552], [38, 344, 611], [62, 98, 108]], [[384, 564], [40, 391, 611], [6, 62, 108]],
 [[385, 553], [14, 200, 596], [60, 96, 109]], [[385, 565], [16, 295, 596], [2, 60, 109]],
 [[386, 554], [62, 248, 605], [61, 97, 110]], [[386, 566], [64, 439, 605], [10, 61, 110]],
 [[387, 555], [110, 356, 608], [65, 105, 111]], [[387, 567], [112, 451, 608], [18, 65, 111]], 
[[388, 556], [80, 368, 599], [63, 106, 112]], [[388, 568], [82, 415, 599], [13, 63, 112]],
 [[389, 557], [128, 380, 593], [64, 107, 113]], [[389, 569], [130, 475, 593], [21, 64, 113]],
 [[390, 558], [8, 260, 575], [55, 99, 114]], [[390, 570], [10, 307, 575], [1, 55, 114]],
 [[391, 559], [56, 284, 572], [56, 101, 115]], [[391, 571], [58, 331, 572], [9, 56, 115]], 
[[392, 560], [32, 224, 569], [54, 100, 116]], [[392, 572], [34, 319, 569], [5, 54, 116]],
 [[393, 561], [86, 212, 590], [58, 102, 117]], [[393, 573], [88, 403, 590], [14, 58, 117]],
 [[394, 562], [134, 272, 602], [59, 104, 118]], [[394, 574], [136, 463, 602], [22, 59, 118]],
 [[395, 563], [104, 236, 566], [57, 103, 119]], [[395, 575], [106, 427, 566], [17, 57, 119]], 
[[396, 576], [45, 440, 621], [7, 67, 110]], [[396, 588], [47, 486, 621], [7, 66, 67]],
 [[397, 577], [21, 392, 618], [3, 68, 108]], [[397, 589], [23, 487, 618], [3, 67, 68]],
 [[398, 578], [69, 296, 615], [11, 66, 109]], [[398, 590], [71, 488, 615], [11, 66, 68]],
 [[399, 579], [117, 404, 619], [3, 19, 117]], [[399, 591], [119, 498, 619], [3, 19, 69]], 
[[400, 580], [93, 464, 622], [7, 15, 118]], [[400, 592], [95, 510, 622], [7, 15, 70]],
 [[401, 581], [141, 428, 616], [11, 23, 119]], [[401, 593], [143, 522, 616], [11, 23, 71]],
 [[402, 582], [20, 452, 623], [15, 67, 111]], [[402, 594], [23, 499, 623], [3, 15, 67]],
 [[403, 583], [68, 476, 620], [19, 68, 113]], [[403, 595], [71, 523, 620], [11, 19, 68]],
 [[404, 584], [44, 416, 617], [23, 66, 112]], [[404, 596], [47, 511, 617], [7, 23, 66]],
 [[405, 585], [92, 308, 612], [69, 70, 114]], [[405, 597], [95, 500, 612], [15, 69, 70]], 
[[406, 586], [140, 320, 613], [70, 71, 116]], [[406, 598], [143, 512, 613], [23, 70, 71]],
 [[407, 587], [116, 332, 614], [69, 71, 115]], [[407, 599], [119, 524, 614], [19, 69, 71]],
 [[408, 416], [24, 148, 171], [24, 74, 76]], [[409, 414], [0, 147, 159], [24, 72, 75]],
 [[410, 415], [48, 149, 183], [24, 73, 77]], [[411, 419], [96, 160, 185], [24, 79, 81]],
 [[412, 417], [72, 161, 172], [24, 78, 82]], [[413, 418], [120, 173, 184], [24, 80, 83]],
 [[420, 464], [26, 195, 220], [28, 48, 76]], [[421, 462], [2, 243, 256], [27, 49, 75]],
 [[422, 463], [50, 280, 339], [26, 50, 77]], [[423, 467], [98, 232, 255], [27, 51, 79]],
 [[424, 465], [74, 208, 219], [28, 52, 78]], [[425, 466], [122, 268, 279],
 [26, 53, 80]], [[426, 457], [3, 196, 207], [0, 28, 72]],
 [[427, 458], [51, 231, 244], [8, 27, 73]], [[428, 456], [27, 267, 340], [4, 26, 74]],
 [[429, 460], [75, 351, 364], [12, 25, 82]], [[430, 461], [123, 363, 376], [20, 25, 83]],
 [[431, 459], [99, 352, 375], [16, 25, 81]], [[432, 512], [31, 177, 245], [27, 86, 100]],
 [[433, 510], [7, 165, 341], [26, 84, 99]], [[434, 511], [55, 189, 197], [28, 85, 101]],
 [[435, 515], [103, 191, 209], [28, 93, 103]], [[436, 513], [85, 167, 269], [26, 94, 102]],
 [[437, 514], [133, 179, 233], [27, 95, 104]], [[438, 505], [13, 153, 353], [25, 87, 96]],
 [[439, 506], [61, 155, 377], [25, 89, 97]], [[440, 504], [37, 154, 365], [25, 88, 98]],
 [[441, 508], [79, 178, 257], [27, 90, 106]], [[442, 509], [127, 190, 221], [28, 92, 107]],
 [[443, 507], [109, 166, 281], [26, 91, 105]], [[444, 560], [32, 226, 292], [31, 54, 100]], 
[[445, 558], [8, 262, 436], [33, 55, 99]], [[446, 559], [56, 286, 388], [30, 56, 101]], 
[[447, 563], [104, 238, 304], [31, 57, 103]], [[448, 561], [86, 214, 316], [30, 58, 102]],
 [[449, 562], [134, 274, 328], [33, 59, 104]], [[450, 553], [14, 202, 400], [29, 60, 96]],
 [[451, 554], [62, 250, 424], [32, 61, 97]], [[452, 552], [38, 346, 460], [36, 62, 98]],
 [[453, 556], [80, 370, 448], [32, 63, 106]], [[454, 557], [128, 382, 412], [29, 64, 107]],
 [[455, 555], [110, 358, 472], [36, 65, 105]], [[468, 476], [29, 315, 387], [4, 30, 48]],
 [[469, 474], [5, 291, 303], [0, 31, 49]], [[470, 475], [53, 327, 435], [8, 33, 50]],
 [[471, 479], [101, 423, 447], [16, 32, 51]], [[472, 477], [77, 399, 411], [12, 29, 52]],
 [[473, 478], [125, 459, 471], [20, 36, 53]], [[480, 524], [33, 273, 437], [5, 33, 86]],
 [[481, 522], [9, 213, 389], [1, 30, 84]], [[482, 523], [57, 237, 293], [9, 31, 85]],
 [[483, 527], [105, 381, 401], [17, 29, 93]], [[484, 525], [87, 357, 461], [14, 36, 94]],
 [[485, 526], [135, 369, 425], [22, 32, 95]], [[486, 517], [15, 249, 449], [2, 32, 87]],
 [[487, 518], [63, 345, 473], [10, 36, 89]], [[488, 516], [39, 201, 413], [6, 29, 88]],
 [[489, 520], [81, 225, 305], [13, 31, 90]], [[490, 521], [129, 285, 317], [21, 30, 92]],
 [[491, 519], [111, 261, 329], [18, 33, 91]], [[492, 572], [34, 321, 484], [5, 35, 54]],
 [[493, 570], [10, 309, 483], [1, 35, 55]], [[494, 571], [58, 333, 485], [9, 35, 56]],
 [[495, 575], [106, 429, 496], [17, 34, 57]], [[496, 573], [88, 405, 508], [14, 37, 58]],
 [[497, 574], [136, 465, 520], [22, 38, 59]], [[498, 565], [16, 297, 495], [2, 34, 60]],
 [[499, 566], [64, 441, 519], [10, 38, 61]], [[500, 564], [40, 393, 507], [6, 37, 62]],
 [[501, 568], [82, 417, 497], [13, 34, 63]], [[502, 569], [130, 477, 509], [21, 37, 64]],
 [[503, 567], [112, 453, 521], [18, 38, 65]], [[528, 536], [42, 251, 371], [32, 110, 112]],
 [[529, 534], [18, 347, 359], [36, 108, 111]], [[530, 535], [66, 203, 383], [29, 109, 113]],
 [[531, 539], [114, 215, 287], [30, 115, 117]], [[532, 537], [90, 263, 275], [33, 114, 118]],
 [[533, 538], [138, 227, 239], [31, 116, 119]], [[540, 584], [44, 298, 419], [34, 66, 112]],
 [[541, 582], [20, 442, 455], [38, 67, 111]], [[542, 583], [68, 394, 479], [37, 68, 113]],
 [[543, 587], [116, 310, 335], [35, 69, 115]], [[544, 585], [92, 311, 322], [35, 70, 114]],
 [[545, 586], [140, 323, 334], [35, 71, 116]], [[546, 577], [21, 395, 406], [3, 37, 108]],
 [[547, 578], [69, 299, 430], [11, 34, 109]], [[548, 576], [45, 443, 466], [7, 38, 110]], 
[[549, 580], [93, 454, 467], [15, 38, 118]], [[550, 581], [141, 418, 431], [23, 34, 119]],
 [[551, 579], [117, 407, 478], [19, 37, 117]], [[588, 596], [47, 490, 513], [7, 39, 66]], 
[[589, 594], [23, 489, 501], [3, 39, 67]], [[590, 595], [71, 491, 525], [11, 39, 68]],
 [[591, 599], [119, 502, 527], [19, 39, 69]], [[592, 597], [95, 503, 514], [15, 39, 70]],
 [[593, 598], [143, 515, 526], [23, 39, 71]]]

len(cube.f)= 720 
cube.f= [[[0, 313, 409, 414, 318], [0, 914, 1105, 924, 1], [72, 75]], [[0, 313, 217, 241, 337], [0, 771, 770, 817, 2], [49, 72]],
 [[0, 313, 421, 462, 342], [0, 915, 1111, 972, 3], [49, 75]], [[0, 318, 426, 457, 337], [1, 925, 1116, 962, 2], [0, 72]],
 [[0, 318, 222, 246, 342], [1, 781, 780, 822, 3], [0, 75]], [[0, 337, 469, 474, 342], [2, 963, 1147, 973, 3], [0, 49]],
 [[1, 325, 229, 253, 349], [4, 795, 794, 829, 5], [55, 84]], [[1, 325, 433, 510, 366], [4, 938, 1123, 1020, 6], [84, 99]],
 [[1, 325, 445, 558, 390], [4, 939, 1135, 1068, 7], [55, 99]], [[1, 349, 481, 522, 366], [5, 986, 1153, 1021, 6], [1, 84]],
 [[1, 349, 493, 570, 390], [5, 987, 1165, 1069, 7], [1, 55]], [[1, 366, 270, 294, 390], [6, 853, 852, 894, 7], [1, 99]],
 [[2, 330, 234, 258, 354], [8, 805, 804, 834, 9], [60, 87]], [[2, 330, 438, 505, 361], [8, 948, 1128, 1010, 10], [87, 96]],
 [[2, 330, 450, 553, 385], [8, 949, 1140, 1058, 11], [60, 96]], [[2, 354, 486, 517, 361], [9, 996, 1158, 1011, 10], [2, 87]],
 [[2, 354, 498, 565, 385], [9, 997, 1170, 1059, 11], [2, 60]], [[2, 361, 265, 289, 385], [10, 843, 842, 889, 11], [2, 96]],
 [[3, 373, 529, 534, 378], [12, 1034, 1177, 1044, 13], [108, 111]], [[3, 373, 277, 301, 397], [12, 867, 866, 901, 14], [67, 108]],
 [[3, 373, 541, 582, 402], [12, 1035, 1183, 1092, 15], [67, 111]], [[3, 378, 546, 577, 397], [13, 1045, 1188, 1082, 14], [3, 108]],
 [[3, 378, 282, 306, 402], [13, 877, 876, 906, 15], [3, 111]], [[3, 397, 589, 594, 402], [14, 1083, 1195, 1093, 15], [3, 67]],
 [[4, 312, 408, 416, 320], [16, 912, 1104, 928, 17], [74, 76]], [[4, 312, 216, 240, 336], [16, 769, 768, 816, 18], [48, 74]],
 [[4, 312, 420, 464, 344], [16, 913, 1110, 976, 19], [48, 76]], [[4, 320, 428, 456, 336], [17, 929, 1118, 960, 18], [4, 74]],
 [[4, 320, 224, 248, 344], [17, 785, 784, 824, 19], [4, 76]], [[4, 336, 468, 476, 344], [18, 961, 1146, 977, 19], [4, 48]],
 [[5, 324, 228, 252, 348], [20, 793, 792, 828, 21], [54, 86]], [[5, 324, 432, 512, 368], [20, 936, 1122, 1024, 22], [86, 100]],
 [[5, 324, 444, 560, 392], [20, 937, 1134, 1072, 23], [54, 100]], [[5, 348, 480, 524, 368], [21, 984, 1152, 1025, 22], [5, 86]],
 [[5, 348, 492, 572, 392], [21, 985, 1164, 1073, 23], [5, 54]], [[5, 368, 272, 296, 392], [22, 857, 856, 896, 23], [5, 100]],
 [[6, 332, 236, 260, 356], [24, 809, 808, 836, 25], [62, 88]], [[6, 332, 440, 504, 360], [24, 952, 1130, 1008, 26], [88, 98]],
 [[6, 332, 452, 552, 384], [24, 953, 1142, 1056, 27], [62, 98]], [[6, 356, 488, 516, 360], [25, 1000, 1160, 1009, 26], [6, 88]],
 [[6, 356, 500, 564, 384], [25, 1001, 1172, 1057, 27], [6, 62]], [[6, 360, 264, 288, 384], [26, 841, 840, 888, 27], [6, 98]],
 [[7, 372, 528, 536, 380], [28, 1032, 1176, 1048, 29], [110, 112]], [[7, 372, 276, 300, 396], [28, 865, 864, 900, 30], [66, 110]],
 [[7, 372, 540, 584, 404], [28, 1033, 1182, 1096, 31], [66, 112]], [[7, 380, 548, 576, 396], [29, 1049, 1190, 1080, 30], [7, 110]],
 [[7, 380, 284, 308, 404], [29, 881, 880, 908, 31], [7, 112]], [[7, 396, 588, 596, 404], [30, 1081, 1194, 1097, 31], [7, 66]],
 [[8, 314, 410, 415, 319], [32, 916, 1106, 926, 33], [73, 77]], [[8, 314, 218, 242, 338], [32, 773, 772, 818, 34], [50, 73]],
 [[8, 314, 422, 463, 343], [32, 917, 1112, 974, 35], [50, 77]], [[8, 319, 427, 458, 338], [33, 927, 1117, 964, 34], [8, 73]], 
[[8, 319, 223, 247, 343], [33, 783, 782, 823, 35], [8, 77]], [[8, 338, 470, 475, 343], [34, 965, 1148, 975, 35], [8, 50]],
 [[9, 326, 230, 254, 350], [36, 797, 796, 830, 37], [56, 85]], [[9, 326, 434, 511, 367], [36, 940, 1124, 1022, 38], [85, 101]], 
[[9, 326, 446, 559, 391], [36, 941, 1136, 1070, 39], [56, 101]], [[9, 350, 482, 523, 367], [37, 988, 1154, 1023, 38], [9, 85]],
 [[9, 350, 494, 571, 391], [37, 989, 1166, 1071, 39], [9, 56]], [[9, 367, 271, 295, 391], [38, 855, 854, 895, 39], [9, 101]], 
[[10, 331, 235, 259, 355], [40, 807, 806, 835, 41], [61, 89]], [[10, 331, 439, 506, 362], [40, 950, 1129, 1012, 42], [89, 97]],
 [[10, 331, 451, 554, 386], [40, 951, 1141, 1060, 43], [61, 97]], [[10, 355, 487, 518, 362], [41, 998, 1159, 1013, 42], [10, 89]],
 [[10, 355, 499, 566, 386], [41, 999, 1171, 1061, 43], [10, 61]], [[10, 362, 266, 290, 386], [42, 845, 844, 890, 43], [10, 97]], 
[[11, 374, 530, 535, 379], [44, 1036, 1178, 1046, 45], [109, 113]], [[11, 374, 278, 302, 398], [44, 869, 868, 902, 46], [68, 109]],
 [[11, 374, 542, 583, 403], [44, 1037, 1184, 1094, 47], [68, 113]], [[11, 379, 547, 578, 398], [45, 1047, 1189, 1084, 46], [11, 109]],
 [[11, 379, 283, 307, 403], [45, 879, 878, 907, 47], [11, 113]], [[11, 398, 590, 595, 403], [46, 1085, 1196, 1095, 47], [11, 68]],
 [[12, 316, 412, 417, 321], [48, 920, 1108, 930, 49], [78, 82]], [[12, 316, 220, 244, 340], [48, 777, 776, 820, 50], [52, 82]], 
[[12, 316, 424, 465, 345], [48, 921, 1114, 978, 51], [52, 78]], [[12, 321, 429, 460, 340], [49, 931, 1119, 968, 50], [12, 82]], 
[[12, 321, 225, 249, 345], [49, 787, 786, 825, 51], [12, 78]], [[12, 340, 472, 477, 345], [50, 969, 1150, 979, 51], [12, 52]],
 [[13, 333, 237, 261, 357], [52, 811, 810, 837, 53], [63, 90]], [[13, 333, 441, 508, 364], [52, 954, 1131, 1016, 54], [90, 106]],
 [[13, 333, 453, 556, 388], [52, 955, 1143, 1064, 55], [63, 106]], [[13, 357, 489, 520, 364], [53, 1002, 1161, 1017, 54], [13, 90]], 
[[13, 357, 501, 568, 388], [53, 1003, 1173, 1065, 55], [13, 63]], [[13, 364, 268, 292, 388], [54, 849, 848, 892, 55], [13, 106]],
 [[14, 328, 232, 256, 352], [56, 801, 800, 832, 57], [58, 94]], [[14, 328, 436, 513, 369], [56, 944, 1126, 1026, 58], [94, 102]], 
[[14, 328, 448, 561, 393], [56, 945, 1138, 1074, 59], [58, 102]], [[14, 352, 484, 525, 369], [57, 992, 1156, 1027, 58], [14, 94]], 
[[14, 352, 496, 573, 393], [57, 993, 1168, 1075, 59], [14, 58]], [[14, 369, 273, 297, 393], [58, 859, 858, 897, 59], [14, 102]], 
[[15, 376, 532, 537, 381], [60, 1040, 1180, 1050, 61], [114, 118]], [[15, 376, 280, 304, 400], [60, 873, 872, 904, 62], [70, 118]], 
[[15, 376, 544, 585, 405], [60, 1041, 1186, 1098, 63], [70, 114]], [[15, 381, 549, 580, 400], [61, 1051, 1191, 1088, 62], [15, 118]],
 [[15, 381, 285, 309, 405], [61, 883, 882, 909, 63], [15, 114]], [[15, 400, 592, 597, 405], [62, 1089, 1198, 1099, 63], [15, 70]],
 [[16, 315, 411, 419, 323], [64, 918, 1107, 934, 65], [79, 81]], [[16, 315, 219, 243, 339], [64, 775, 774, 819, 66], [51, 81]],
 [[16, 315, 423, 467, 347], [64, 919, 1113, 982, 67], [51, 79]], [[16, 323, 431, 459, 339], [65, 935, 1121, 966, 66], [16, 81]],
 [[16, 323, 227, 251, 347], [65, 791, 790, 827, 67], [16, 79]], [[16, 339, 471, 479, 347], [66, 967, 1149, 983, 67], [16, 51]], 
[[17, 327, 231, 255, 351], [68, 799, 798, 831, 69], [57, 93]], [[17, 327, 435, 515, 371], [68, 942, 1125, 1030, 70], [93, 103]],
 [[17, 327, 447, 563, 395], [68, 943, 1137, 1078, 71], [57, 103]], [[17, 351, 483, 527, 371], [69, 990, 1155, 1031, 70], [17, 93]],
 [[17, 351, 495, 575, 395], [69, 991, 1167, 1079, 71], [17, 57]], [[17, 371, 275, 299, 395], [70, 863, 862, 899, 71], [17, 103]], 
[[18, 335, 239, 263, 359], [72, 815, 814, 839, 73], [65, 91]], [[18, 335, 443, 507, 363], [72, 958, 1133, 1014, 74], [91, 105]],

 [[18, 335, 455, 555, 387], [72, 959, 1145, 1062, 75], [65, 105]], [[18, 359, 491, 519, 363], [73, 1006, 1163, 1015, 74], [18, 91]],
 [[18, 359, 503, 567, 387], [73, 1007, 1175, 1063, 75], [18, 65]], [[18, 363, 267, 291, 387], [74, 847, 846, 891, 75], [18, 105]], 
[[19, 375, 531, 539, 383], [76, 1038, 1179, 1054, 77], [115, 117]], [[19, 375, 279, 303, 399], [76, 871, 870, 903, 78], [69, 117]], 
[[19, 375, 543, 587, 407], [76, 1039, 1185, 1102, 79], [69, 115]], [[19, 383, 551, 579, 399], [77, 1055, 1193, 1086, 78], [19, 117]],
 [[19, 383, 287, 311, 407], [77, 887, 886, 911, 79], [19, 115]], [[19, 399, 591, 599, 407], [78, 1087, 1197, 1103, 79], [19, 69]],
 [[20, 317, 413, 418, 322], [80, 922, 1109, 932, 81], [80, 83]], [[20, 317, 221, 245, 341], [80, 779, 778, 821, 82], [53, 83]],
 [[20, 317, 425, 466, 346], [80, 923, 1115, 980, 83], [53, 80]], [[20, 322, 430, 461, 341], [81, 933, 1120, 970, 82], [20, 83]], 
[[20, 322, 226, 250, 346], [81, 789, 788, 826, 83], [20, 80]], [[20, 341, 473, 478, 346], [82, 971, 1151, 981, 83], [20, 53]],
 [[21, 334, 238, 262, 358], [84, 813, 812, 838, 85], [64, 92]], [[21, 334, 442, 509, 365], [84, 956, 1132, 1018, 86], [92, 107]],
 [[21, 334, 454, 557, 389], [84, 957, 1144, 1066, 87], [64, 107]], [[21, 358, 490, 521, 365], [85, 1004, 1162, 1019, 86], [21, 92]], 
[[21, 358, 502, 569, 389], [85, 1005, 1174, 1067, 87], [21, 64]], [[21, 365, 269, 293, 389], [86, 851, 850, 893, 87], [21, 107]],
 [[22, 329, 233, 257, 353], [88, 803, 802, 833, 89], [59, 95]], [[22, 329, 437, 514, 370], [88, 946, 1127, 1028, 90], [95, 104]], 
[[22, 329, 449, 562, 394], [88, 947, 1139, 1076, 91], [59, 104]], [[22, 353, 485, 526, 370], [89, 994, 1157, 1029, 90], [22, 95]], 
[[22, 353, 497, 574, 394], [89, 995, 1169, 1077, 91], [22, 59]], [[22, 370, 274, 298, 394], [90, 861, 860, 898, 91], [22, 104]], 
[[23, 377, 533, 538, 382], [92, 1042, 1181, 1052, 93], [116, 119]], [[23, 377, 281, 305, 401], [92, 875, 874, 905, 94], [71, 119]], 
[[23, 377, 545, 586, 406], [92, 1043, 1187, 1100, 95], [71, 116]], [[23, 382, 550, 581, 401], [93, 1053, 1192, 1090, 94], [23, 119]],
 [[23, 382, 286, 310, 406], [93, 885, 884, 910, 95], [23, 116]], [[23, 401, 593, 598, 406], [94, 1091, 1199, 1101, 95], [23, 71]],
 [[24, 152, 216, 312, 408], [96, 576, 769, 912, 97], [72, 74]], [[24, 152, 217, 313, 409], [96, 577, 771, 914, 98], [72, 73]],
 [[24, 152, 218, 314, 410], [96, 578, 773, 916, 99], [73, 74]], [[24, 408, 94, 414, 409], [97, 374, 376, 1105, 98], [24, 72]], 
[[24, 408, 416, 90, 410], [97, 1104, 362, 360, 99], [24, 74]], [[24, 409, 92, 415, 410], [98, 367, 369, 1106, 99], [24, 73]],
 [[25, 153, 264, 360, 504], [100, 579, 841, 1008, 101], [96, 98]], [[25, 153, 265, 361, 505], [100, 580, 843, 1010, 102], [96, 97]],
 [[25, 153, 266, 362, 506], [100, 581, 845, 1012, 103], [97, 98]], [[25, 504, 126, 438, 505], [101, 488, 486, 1128, 102], [25, 96]],
 [[25, 504, 440, 122, 506], [101, 1130, 472, 474, 103], [25, 98]], [[25, 505, 124, 439, 506], [102, 481, 479, 1129, 103], [25, 97]],
 [[26, 154, 219, 315, 411], [104, 582, 775, 918, 105], [75, 81]], [[26, 154, 222, 318, 414], [104, 583, 781, 924, 106], [75, 78]],
 [[26, 154, 225, 321, 417], [104, 584, 787, 930, 107], [78, 81]], [[26, 411, 92, 409, 414], [105, 368, 367, 1105, 106], [24, 75]],
 [[26, 411, 419, 88, 417], [105, 1107, 355, 353, 107], [24, 81]], [[26, 414, 94, 412, 417], [106, 376, 375, 1108, 107], [24, 78]], 
[[27, 155, 267, 363, 507], [108, 585, 847, 1014, 109], [99, 105]], [[27, 155, 270, 366, 510], [108, 586, 853, 1020, 110], [99, 102]],
 [[27, 155, 273, 369, 513], [108, 587, 859, 1026, 111], [102, 105]], [[27, 507, 108, 433, 510], [109, 425, 423, 1123, 110], [26, 99]],
 [[27, 507, 443, 120, 513], [109, 1133, 465, 467, 111], [26, 105]], [[27, 510, 110, 436, 513], [110, 432, 430, 1126, 111], [26, 102]],
 [[28, 156, 220, 316, 412], [112, 588, 777, 920, 113], [76, 82]], [[28, 156, 224, 320, 416], [112, 589, 785, 928, 114], [76, 80]],
 [[28, 156, 226, 322, 418], [112, 590, 789, 932, 115], [80, 82]], [[28, 412, 94, 408, 416], [113, 375, 374, 1104, 114], [24, 76]], 
[[28, 412, 417, 88, 418], [113, 1108, 353, 354, 115], [24, 82]], [[28, 416, 90, 413, 418], [114, 362, 361, 1109, 115], [24, 80]], 
[[29, 157, 268, 364, 508], [116, 591, 849, 1016, 117], [100, 106]], [[29, 157, 272, 368, 512], [116, 592, 857, 1024, 118], [100, 104]],
 [[29, 157, 274, 370, 514], [116, 593, 861, 1028, 119], [104, 106]], [[29, 508, 102, 432, 512], [117, 404, 402, 1122, 118], [27, 100]],
 [[29, 508, 441, 104, 514], [117, 1131, 409, 411, 119], [27, 106]], [[29, 512, 106, 437, 514], [118, 418, 416, 1127, 119], [27, 104]], 
[[30, 158, 221, 317, 413], [120, 594, 779, 922, 121], [77, 83]], [[30, 158, 223, 319, 415], [120, 595, 783, 926, 122], [77, 79]],
 [[30, 158, 227, 323, 419], [120, 596, 791, 934, 123], [79, 83]], [[30, 413, 90, 410, 415], [121, 361, 360, 1106, 122], [24, 77]],
 [[30, 413, 418, 88, 419], [121, 1109, 354, 355, 123], [24, 83]], [[30, 415, 92, 411, 419], [122, 369, 368, 1107, 123], [24, 79]],
 [[31, 159, 269, 365, 509], [124, 597, 851, 1018, 125], [101, 107]], [[31, 159, 271, 367, 511], [124, 598, 855, 1022, 126], [101, 103]],
 [[31, 159, 275, 371, 515], [124, 599, 863, 1030, 127], [103, 107]], [[31, 509, 98, 434, 511], [125, 390, 388, 1124, 126], [28, 101]], 
[[31, 509, 442, 96, 515], [125, 1132, 381, 383, 127], [28, 107]], [[31, 511, 100, 435, 515], [126, 397, 395, 1125, 127], [28, 103]],
 [[32, 160, 216, 312, 420], [128, 600, 769, 913, 129], [48, 72]], [[32, 160, 230, 326, 434], [128, 601, 797, 940, 130], [48, 85]],
 [[32, 160, 241, 337, 457], [128, 602, 817, 962, 131], [72, 85]], [[32, 420, 464, 98, 434], [129, 1110, 389, 388, 130], [28, 48]], 
[[32, 420, 95, 426, 457], [129, 377, 379, 1116, 131], [28, 72]], [[32, 434, 511, 100, 457], [130, 1124, 397, 396, 131], [28, 85]],
 [[33, 161, 264, 360, 516], [132, 603, 841, 1009, 133], [6, 96]], [[33, 161, 278, 374, 530], [132, 604, 869, 1036, 134], [6, 109]],
 [[33, 161, 289, 385, 553], [132, 605, 889, 1058, 135], [96, 109]], [[33, 516, 488, 130, 530], [133, 1160, 500, 501, 134], [6, 29]], 
[[33, 516, 127, 450, 553], [133, 491, 489, 1140, 135], [29, 96]], [[33, 530, 535, 132, 553], [134, 1178, 508, 509, 135], [29, 109]], 
[[34, 162, 222, 318, 426], [136, 606, 781, 925, 137], [0, 78]], [[34, 162, 231, 327, 435], [136, 607, 799, 942, 138], [0, 93]],
 [[34, 162, 249, 345, 465], [136, 608, 825, 978, 139], [78, 93]], [[34, 426, 457, 100, 435], [137, 1116, 396, 395, 138], [0, 28]], 
[[34, 426, 95, 424, 465], [137, 379, 378, 1114, 139], [28, 78]], [[34, 435, 515, 96, 465], [138, 1125, 383, 382, 139], [28, 93]], 
[[35, 163, 270, 366, 522], [140, 609, 853, 1021, 141], [1, 102]], [[35, 163, 279, 375, 531], [140, 610, 871, 1038, 142], [1, 117]], 
[[35, 163, 297, 393, 561], [140, 611, 897, 1074, 143], [102, 117]], [[35, 522, 481, 116, 531], [141, 1153, 451, 452, 142], [1, 30]],
 [[35, 522, 111, 448, 561], [141, 435, 433, 1138, 143], [30, 102]], [[35, 531, 539, 128, 561], [142, 1179, 494, 495, 143], [30, 117]], 
[[36, 164, 220, 316, 424], [144, 612, 777, 921, 145], [52, 76]], [[36, 164, 238, 334, 442], [144, 613, 813, 956, 146], [52, 92]],
 [[36, 164, 248, 344, 464], [144, 614, 824, 976, 147], [76, 92]], [[36, 424, 465, 96, 442], [145, 1114, 382, 381, 146], [28, 52]],
 [[36, 424, 95, 420, 464], [145, 378, 377, 1110, 147], [28, 76]], [[36, 442, 509, 98, 464], [146, 1132, 390, 389, 147], [28, 92]],
 [[37, 165, 268, 364, 520], [148, 615, 849, 1017, 149], [13, 100]], [[37, 165, 286, 382, 538], [148, 616, 885, 1052, 150], [13, 116]], 
[[37, 165, 296, 392, 560], [148, 617, 896, 1072, 151], [100, 116]], [[37, 520, 489, 112, 538], [149, 1161, 437, 438, 150], [13, 31]],
 [[37, 520, 103, 444, 560], [149, 407, 405, 1134, 151], [31, 100]], [[37, 538, 533, 114, 560], [150, 1181, 445, 446, 151], [31, 116]],
 [[38, 166, 223, 319, 427], [152, 618, 783, 927, 153], [8, 79]], [[38, 166, 233, 329, 437], [152, 619, 803, 946, 154], [8, 95]],
 [[38, 166, 251, 347, 467], [152, 620, 827, 982, 155], [79, 95]], [[38, 427, 458, 106, 437], [153, 1117, 417, 416, 154], [8, 27]], 
[[38, 427, 93, 423, 467], [153, 372, 371, 1113, 155], [27, 79]], [[38, 437, 514, 104, 467], [154, 1127, 411, 410, 155], [27, 95]],
 [[39, 167, 271, 367, 523], [156, 621, 855, 1023, 157], [9, 103]], [[39, 167, 281, 377, 533], [156, 622, 875, 1042, 158], [9, 119]],
 [[39, 167, 299, 395, 563], [156, 623, 899, 1078, 159], [103, 119]], [[39, 523, 482, 114, 533], [157, 1154, 444, 445, 158], [9, 31]],
 [[39, 523, 101, 447, 563], [157, 400, 398, 1137, 159], [31, 103]], [[39, 533, 538, 112, 563], [158, 1181, 438, 439, 159], [31, 119]],
 [[40, 168, 217, 313, 421], [160, 624, 771, 915, 161], [49, 73]], [[40, 168, 228, 324, 432], [160, 625, 793, 936, 162], [49, 86]],
 [[40, 168, 242, 338, 458], [160, 626, 818, 964, 163], [73, 86]], [[40, 421, 462, 102, 432], [161, 1111, 403, 402, 162], [27, 49]],
 [[40, 421, 93, 427, 458], [161, 370, 372, 1117, 163], [27, 73]], [[40, 432, 512, 106, 458], [162, 1122, 418, 417, 163], [27, 86]],
 [[41, 169, 265, 361, 517], [164, 627, 843, 1011, 165], [2, 97]], [[41, 169, 276, 372, 528], [164, 628, 865, 1032, 166], [2, 110]], 
[[41, 169, 290, 386, 554], [164, 629, 890, 1060, 167], [97, 110]], [[41, 517, 486, 134, 528], [165, 1158, 514, 515, 166], [2, 32]],
 [[41, 517, 125, 451, 554], [165, 484, 482, 1141, 167], [32, 97]], [[41, 528, 536, 138, 554], [166, 1176, 529, 530, 167], [32, 110]], 
[[42, 170, 219, 315, 423], [168, 630, 775, 919, 169], [51, 75]], [[42, 170, 237, 333, 441], [168, 631, 811, 954, 170], [51, 90]],
 [[42, 170, 246, 342, 462], [168, 632, 822, 972, 171], [75, 90]], [[42, 423, 467, 104, 441], [169, 1113, 410, 409, 170], [27, 51]], 
[[42, 423, 93, 421, 462], [169, 371, 370, 1111, 171], [27, 75]], [[42, 441, 508, 102, 462], [170, 1131, 404, 403, 171], [27, 90]],
 [[43, 171, 267, 363, 519], [172, 633, 847, 1015, 173], [18, 99]], [[43, 171, 285, 381, 537], [172, 634, 883, 1050, 174], [18, 114]],
 [[43, 171, 294, 390, 558], [172, 635, 894, 1068, 175], [99, 114]], [[43, 519, 491, 136, 537], [173, 1163, 521, 522, 174], [18, 33]], 
[[43, 519, 109, 445, 558], [173, 428, 426, 1135, 175], [33, 99]], [[43, 537, 532, 118, 558], [174, 1180, 459, 460, 175], [33, 114]],
 [[44, 172, 224, 320, 428], [176, 636, 785, 929, 177], [4, 80]], [[44, 172, 232, 328, 436], [176, 637, 801, 944, 178], [4, 94]],
 [[44, 172, 250, 346, 466], [176, 638, 826, 980, 179], [80, 94]], [[44, 428, 456, 110, 436], [177, 1118, 431, 430, 178], [4, 26]],
 [[44, 428, 91, 425, 466], [177, 365, 364, 1115, 179], [26, 80]], [[44, 436, 513, 120, 466], [178, 1126, 467, 466, 179], [26, 94]], 
[[45, 173, 272, 368, 524], [180, 639, 857, 1025, 181], [5, 104]], [[45, 173, 280, 376, 532], [180, 640, 873, 1040, 182], [5, 118]],
 [[45, 173, 298, 394, 562], [180, 641, 898, 1076, 183], [104, 118]], [[45, 524, 480, 118, 532], [181, 1152, 458, 459, 182], [5, 33]],
 [[45, 524, 107, 449, 562], [181, 421, 419, 1139, 183], [33, 104]], [[45, 532, 537, 136, 562], [182, 1180, 522, 523, 183], [33, 118]],
 [[46, 174, 221, 317, 425], [184, 642, 779, 923, 185], [53, 77]], [[46, 174, 239, 335, 443], [184, 643, 815, 958, 186], [53, 91]],
 [[46, 174, 247, 343, 463], [184, 644, 823, 974, 187], [77, 91]], [[46, 425, 466, 120, 443], [185, 1115, 466, 465, 186], [26, 53]], 
[[46, 425, 91, 422, 463], [185, 364, 363, 1112, 187], [26, 77]], [[46, 443, 507, 108, 463], [186, 1133, 425, 424, 187], [26, 91]],
 [[47, 175, 269, 365, 521], [188, 645, 851, 1019, 189], [21, 101]], [[47, 175, 287, 383, 539], [188, 646, 887, 1054, 190], [21, 115]],
 [[47, 175, 295, 391, 559], [188, 647, 895, 1070, 191], [101, 115]], [[47, 521, 490, 128, 539], [189, 1162, 493, 494, 190], [21, 30]],
 [[47, 521, 99, 446, 559], [189, 393, 391, 1136, 191], [30, 101]], [[47, 539, 531, 116, 559], [190, 1179, 452, 453, 191], [30, 115]],
 [[48, 176, 228, 324, 444], [192, 648, 793, 937, 193], [49, 54]], [[48, 176, 241, 337, 469], [192, 649, 817, 963, 194], [49, 85]],
 [[48, 176, 254, 350, 482], [192, 650, 830, 988, 195], [54, 85]], [[48, 444, 103, 474, 469], [193, 405, 406, 1147, 194], [31, 49]],
 [[48, 444, 560, 114, 482], [193, 1134, 446, 444, 195], [31, 54]], [[48, 469, 101, 523, 482], [194, 399, 400, 1154, 195], [31, 85]], 
[[49, 177, 276, 372, 540], [196, 651, 865, 1033, 197], [2, 66]], [[49, 177, 289, 385, 565], [196, 652, 889, 1059, 198], [2, 109]],
 [[49, 177, 302, 398, 578], [196, 653, 902, 1084, 199], [66, 109]], [[49, 540, 135, 498, 565], [197, 518, 517, 1170, 198], [2, 34]],
 [[49, 540, 584, 146, 578], [197, 1182, 558, 556, 199], [34, 66]], [[49, 565, 133, 547, 578], [198, 512, 511, 1189, 199], [34, 109]],
 [[50, 178, 231, 327, 447], [200, 654, 799, 943, 201], [0, 57]], [[50, 178, 246, 342, 474], [200, 655, 822, 973, 202], [0, 90]],
 [[50, 178, 261, 357, 489], [200, 656, 837, 1002, 203], [57, 90]], [[50, 447, 101, 469, 474], [201, 398, 399, 1147, 202], [0, 31]],
 [[50, 447, 563, 112, 489], [201, 1137, 439, 437, 203], [31, 57]], [[50, 474, 103, 520, 489], [202, 406, 407, 1161, 203], [31, 90]],
 [[51, 179, 279, 375, 543], [204, 657, 871, 1039, 205], [1, 69]], [[51, 179, 294, 390, 570], [204, 658, 894, 1069, 206], [1, 114]],
 [[51, 179, 309, 405, 585], [204, 659, 909, 1098, 207], [69, 114]], [[51, 543, 117, 493, 570], [205, 455, 454, 1165, 206], [1, 35]],
 [[51, 543, 587, 144, 585], [205, 1185, 551, 549, 207], [35, 69]], [[51, 570, 119, 544, 585], [206, 463, 462, 1186, 207], [35, 114]],
 [[52, 180, 232, 328, 448], [208, 660, 801, 945, 209], [4, 58]], [[52, 180, 248, 344, 476], [208, 661, 824, 977, 210], [4, 92]], 
[[52, 180, 262, 358, 490], [208, 662, 838, 1004, 211], [58, 92]], [[52, 448, 111, 468, 476], [209, 433, 434, 1146, 210], [4, 30]],
 [[52, 448, 561, 128, 490], [209, 1138, 495, 493, 211], [30, 58]], [[52, 476, 99, 521, 490], [210, 392, 393, 1162, 211], [30, 92]],
 [[53, 181, 280, 376, 544], [212, 663, 873, 1041, 213], [5, 70]], [[53, 181, 296, 392, 572], [212, 664, 896, 1073, 214], [5, 116]],
 [[53, 181, 310, 406, 586], [212, 665, 910, 1100, 215], [70, 116]], [[53, 544, 119, 492, 572], [213, 462, 461, 1164, 214], [5, 35]],
 [[53, 544, 585, 144, 586], [213, 1186, 549, 550, 215], [35, 70]], [[53, 572, 115, 545, 586], [214, 449, 448, 1187, 215], [35, 116]],
 [[54, 182, 233, 329, 449], [216, 666, 803, 947, 217], [8, 59]], [[54, 182, 247, 343, 475], [216, 667, 823, 975, 218], [8, 91]], 
[[54, 182, 263, 359, 491], [216, 668, 839, 1006, 219], [59, 91]], [[54, 449, 107, 470, 475], [217, 419, 420, 1148, 218], [8, 33]], 
[[54, 449, 562, 136, 491], [217, 1139, 523, 521, 219], [33, 59]], [[54, 475, 109, 519, 491], [218, 427, 428, 1163, 219], [33, 91]], 
[[55, 183, 281, 377, 545], [220, 669, 875, 1043, 221], [9, 71]], [[55, 183, 295, 391, 571], [220, 670, 895, 1071, 222], [9, 115]],
 [[55, 183, 311, 407, 587], [220, 671, 911, 1102, 223], [71, 115]], [[55, 545, 115, 494, 571], [221, 448, 447, 1166, 222], [9, 35]], 
[[55, 545, 586, 144, 587], [221, 1187, 550, 551, 223], [35, 71]], [[55, 571, 117, 543, 587], [222, 456, 455, 1185, 223], [35, 115]],
 [[56, 184, 218, 314, 422], [224, 672, 773, 917, 225], [50, 74]], [[56, 184, 229, 325, 433], [224, 673, 795, 938, 226], [50, 84]], 
[[56, 184, 240, 336, 456], [224, 674, 816, 960, 227], [74, 84]], [[56, 422, 463, 108, 433], [225, 1112, 424, 423, 226], [26, 50]],
 [[56, 422, 91, 428, 456], [225, 363, 365, 1118, 227], [26, 74]], [[56, 433, 510, 110, 456], [226, 1123, 432, 431, 227], [26, 84]],
 [[57, 185, 266, 362, 518], [228, 675, 845, 1013, 229], [10, 98]], [[57, 185, 277, 373, 529], [228, 676, 867, 1034, 230], [10, 108]],
 [[57, 185, 288, 384, 552], [228, 677, 888, 1056, 231], [98, 108]], [[57, 518, 487, 140, 529], [229, 1159, 535, 536, 230], [10, 36]],
 [[57, 518, 123, 452, 552], [229, 477, 475, 1142, 231], [36, 98]], [[57, 529, 534, 142, 552], [230, 1177, 543, 544, 231], [36, 108]],
 [[58, 186, 225, 321, 429], [232, 678, 787, 931, 233], [12, 81]], [[58, 186, 234, 330, 438], [232, 679, 805, 948, 234], [12, 87]],
 [[58, 186, 243, 339, 459], [232, 680, 819, 966, 235], [81, 87]], [[58, 429, 460, 126, 438], [233, 1119, 487, 486, 234], [12, 25]],
 [[58, 429, 89, 431, 459], [233, 356, 358, 1121, 235], [25, 81]], [[58, 438, 505, 124, 459], [234, 1128, 481, 480, 235], [25, 87]],
 [[59, 187, 273, 369, 525], [236, 681, 859, 1027, 237], [14, 105]], [[59, 187, 282, 378, 534], [236, 682, 877, 1044, 238], [14, 111]], 
[[59, 187, 291, 387, 555], [236, 683, 891, 1062, 239], [105, 111]], [[59, 525, 484, 142, 534], [237, 1156, 542, 543, 238], [14, 36]],
 [[59, 525, 121, 455, 555], [237, 470, 468, 1145, 239], [36, 105]], [[59, 534, 529, 140, 555], [238, 1177, 536, 537, 239], [36, 111]], 
[[60, 188, 226, 322, 430], [240, 684, 789, 933, 241], [20, 82]], [[60, 188, 236, 332, 440], [240, 685, 809, 952, 242], [20, 88]],
 [[60, 188, 244, 340, 460], [240, 686, 820, 968, 243], [82, 88]], [[60, 430, 461, 122, 440], [241, 1120, 473, 472, 242], [20, 25]],
 [[60, 430, 89, 429, 460], [241, 357, 356, 1119, 243], [25, 82]], [[60, 440, 504, 126, 460], [242, 1130, 488, 487, 243], [25, 88]], 
[[61, 189, 274, 370, 526], [244, 687, 861, 1029, 245], [22, 106]], [[61, 189, 284, 380, 536], [244, 688, 881, 1048, 246], [22, 112]], 
[[61, 189, 292, 388, 556], [244, 689, 892, 1064, 247], [106, 112]], [[61, 526, 485, 138, 536], [245, 1157, 528, 529, 246], [22, 32]],
 [[61, 526, 105, 453, 556], [245, 414, 412, 1143, 247], [32, 106]], [[61, 536, 528, 134, 556], [246, 1176, 515, 516, 247], [32, 112]],
 [[62, 190, 227, 323, 431], [248, 690, 791, 935, 249], [16, 83]], [[62, 190, 235, 331, 439], [248, 691, 807, 950, 250], [16, 89]],
 [[62, 190, 245, 341, 461], [248, 692, 821, 970, 251], [83, 89]], [[62, 431, 459, 124, 439], [249, 1121, 480, 479, 250], [16, 25]], 
[[62, 431, 89, 430, 461], [249, 358, 357, 1120, 251], [25, 83]], [[62, 439, 506, 122, 461], [250, 1129, 474, 473, 251], [25, 89]], 
[[63, 191, 275, 371, 527], [252, 693, 863, 1031, 253], [17, 107]], [[63, 191, 283, 379, 535], [252, 694, 879, 1046, 254], [17, 113]], 
[[63, 191, 293, 389, 557], [252, 695, 893, 1066, 255], [107, 113]], [[63, 527, 483, 132, 535], [253, 1155, 507, 508, 254], [17, 29]],
 [[63, 527, 97, 454, 557], [253, 386, 384, 1144, 255], [29, 107]], [[63, 535, 530, 130, 557], [254, 1178, 501, 502, 255], [29, 113]],
 [[64, 192, 230, 326, 446], [256, 696, 797, 941, 257], [48, 56]], [[64, 192, 240, 336, 468], [256, 697, 816, 961, 258], [48, 84]], 
[[64, 192, 253, 349, 481], [256, 698, 829, 986, 259], [56, 84]], [[64, 446, 99, 476, 468], [257, 391, 392, 1146, 258], [30, 48]],
 [[64, 446, 559, 116, 481], [257, 1136, 453, 451, 259], [30, 56]], [[64, 468, 111, 522, 481], [258, 434, 435, 1153, 259], [30, 84]],
 [[65, 193, 278, 374, 542], [260, 699, 869, 1037, 261], [6, 68]], [[65, 193, 288, 384, 564], [260, 700, 888, 1057, 262], [6, 108]], 
[[65, 193, 301, 397, 577], [260, 701, 901, 1082, 263], [68, 108]], [[65, 542, 131, 500, 564], [261, 504, 503, 1172, 262], [6, 37]], 
[[65, 542, 583, 148, 577], [261, 1184, 565, 563, 263], [37, 68]], [[65, 564, 143, 546, 577], [262, 547, 546, 1188, 263], [37, 108]],
 [[66, 194, 234, 330, 450], [264, 702, 805, 949, 265], [12, 60]], [[66, 194, 249, 345, 477], [264, 703, 825, 979, 266], [12, 93]],
 [[66, 194, 255, 351, 483], [264, 704, 831, 990, 267], [60, 93]], [[66, 450, 127, 472, 477], [265, 489, 490, 1150, 266], [12, 29]], 
[[66, 450, 553, 132, 483], [265, 1140, 509, 507, 267], [29, 60]], [[66, 477, 97, 527, 483], [266, 385, 386, 1155, 267], [29, 93]],
 [[67, 195, 282, 378, 546], [268, 705, 877, 1045, 269], [3, 14]], [[67, 195, 297, 393, 573], [268, 706, 897, 1075, 270], [14, 117]], 
[[67, 195, 303, 399, 579], [268, 707, 903, 1086, 271], [3, 117]], [[67, 546, 143, 496, 573], [269, 546, 545, 1168, 270], [14, 37]], 
[[67, 546, 577, 148, 579], [269, 1188, 563, 564, 271], [3, 37]], [[67, 573, 129, 551, 579], [270, 498, 497, 1193, 271], [37, 117]], 
[[68, 196, 238, 334, 454], [272, 708, 813, 957, 273], [52, 64]], [[68, 196, 244, 340, 472], [272, 709, 820, 969, 274], [52, 88]],
 [[68, 196, 260, 356, 488], [272, 710, 836, 1000, 275], [64, 88]], [[68, 454, 97, 477, 472], [273, 384, 385, 1150, 274], [29, 52]], 
[[68, 454, 557, 130, 488], [273, 1144, 502, 500, 275], [29, 64]], [[68, 472, 127, 516, 488], [274, 490, 491, 1160, 275], [29, 88]],
 [[69, 197, 286, 382, 550], [276, 711, 885, 1053, 277], [13, 23]], [[69, 197, 292, 388, 568], [276, 712, 892, 1065, 278], [13, 112]],
 [[69, 197, 308, 404, 584], [276, 713, 908, 1096, 279], [23, 112]], [[69, 550, 113, 501, 568], [277, 441, 440, 1173, 278], [13, 34]], 
[[69, 550, 581, 146, 584], [277, 1192, 557, 558, 279], [23, 34]], [[69, 568, 135, 540, 584], [278, 519, 518, 1182, 279], [34, 112]], 
[[70, 198, 235, 331, 451], [280, 714, 807, 951, 281], [16, 61]], [[70, 198, 251, 347, 479], [280, 715, 827, 983, 282], [16, 95]], 
[[70, 198, 257, 353, 485], [280, 716, 833, 994, 283], [61, 95]], [[70, 451, 125, 471, 479], [281, 482, 483, 1149, 282], [16, 32]], 
[[70, 451, 554, 138, 485], [281, 1141, 530, 528, 283], [32, 61]], [[70, 479, 105, 526, 485], [282, 413, 414, 1157, 283], [32, 95]],
 [[71, 199, 283, 379, 547], [284, 717, 879, 1047, 285], [11, 17]], [[71, 199, 299, 395, 575], [284, 718, 899, 1079, 286], [17, 119]], 
[[71, 199, 305, 401, 581], [284, 719, 905, 1090, 287], [11, 119]], [[71, 547, 133, 495, 575], [285, 511, 510, 1167, 286], [17, 34]],
 [[71, 547, 578, 146, 581], [285, 1189, 556, 557, 287], [11, 34]], [[71, 575, 113, 550, 581], [286, 442, 441, 1192, 287], [34, 119]],
 [[72, 200, 229, 325, 445], [288, 720, 795, 939, 289], [50, 55]], [[72, 200, 242, 338, 470], [288, 721, 818, 965, 290], [50, 86]], 
[[72, 200, 252, 348, 480], [288, 722, 828, 984, 291], [55, 86]], [[72, 445, 109, 475, 470], [289, 426, 427, 1148, 290], [33, 50]],
 [[72, 445, 558, 118, 480], [289, 1135, 460, 458, 291], [33, 55]], [[72, 470, 107, 524, 480], [290, 420, 421, 1152, 291], [33, 86]],
 [[73, 201, 277, 373, 541], [292, 723, 867, 1035, 293], [10, 67]], [[73, 201, 290, 386, 566], [292, 724, 890, 1061, 294], [10, 110]],
 [[73, 201, 300, 396, 576], [292, 725, 900, 1080, 295], [67, 110]], [[73, 541, 141, 499, 566], [293, 539, 538, 1171, 294], [10, 38]], 
[[73, 541, 582, 150, 576], [293, 1183, 572, 570, 295], [38, 67]], [[73, 566, 139, 548, 576], [294, 533, 532, 1190, 295], [38, 110]],
 [[74, 202, 237, 333, 453], [296, 726, 811, 955, 297], [51, 63]], [[74, 202, 243, 339, 471], [296, 727, 819, 967, 298], [51, 87]],
 [[74, 202, 258, 354, 486], [296, 728, 834, 996, 299], [63, 87]], [[74, 453, 105, 479, 471], [297, 412, 413, 1149, 298], [32, 51]],
 [[74, 453, 556, 134, 486], [297, 1143, 516, 514, 299], [32, 63]], [[74, 471, 125, 517, 486], [298, 483, 484, 1158, 299], [32, 87]], 
[[75, 203, 285, 381, 549], [300, 729, 883, 1051, 301], [15, 18]], [[75, 203, 291, 387, 567], [300, 730, 891, 1063, 302], [18, 111]],
 [[75, 203, 306, 402, 582], [300, 731, 906, 1092, 303], [15, 111]], [[75, 549, 137, 503, 567], [301, 525, 524, 1175, 302], [18, 38]],
 [[75, 549, 580, 150, 582], [301, 1191, 571, 572, 303], [15, 38]], [[75, 567, 141, 541, 582], [302, 540, 539, 1183, 303], [38, 111]],
 [[76, 204, 236, 332, 452], [304, 732, 809, 953, 305], [20, 62]], [[76, 204, 250, 346, 478], [304, 733, 826, 981, 306], [20, 94]],
 [[76, 204, 256, 352, 484], [304, 734, 832, 992, 307], [62, 94]], [[76, 452, 123, 473, 478], [305, 475, 476, 1151, 306], [20, 36]],
 [[76, 452, 552, 142, 484], [305, 1142, 544, 542, 307], [36, 62]], [[76, 478, 121, 525, 484], [306, 469, 470, 1156, 307], [36, 94]],
 [[77, 205, 284, 380, 548], [308, 735, 881, 1049, 309], [7, 22]], [[77, 205, 298, 394, 574], [308, 736, 898, 1077, 310], [22, 118]],
 [[77, 205, 304, 400, 580], [308, 737, 904, 1088, 311], [7, 118]], [[77, 548, 139, 497, 574], [309, 532, 531, 1169, 310], [22, 38]], 
[[77, 548, 576, 150, 580], [309, 1190, 570, 571, 311], [7, 38]], [[77, 574, 137, 549, 580], [310, 526, 525, 1191, 311], [38, 118]],
 [[78, 206, 239, 335, 455], [312, 738, 815, 959, 313], [53, 65]], [[78, 206, 245, 341, 473], [312, 739, 821, 971, 314], [53, 89]],
 [[78, 206, 259, 355, 487], [312, 740, 835, 998, 315], [65, 89]], [[78, 455, 121, 478, 473], [313, 468, 469, 1151, 314], [36, 53]],
 [[78, 455, 555, 140, 487], [313, 1145, 537, 535, 315], [36, 65]], [[78, 473, 123, 518, 487], [314, 476, 477, 1159, 315], [36, 89]], 
[[79, 207, 287, 383, 551], [316, 741, 887, 1055, 317], [19, 21]], [[79, 207, 293, 389, 569], [316, 742, 893, 1067, 318], [21, 113]],
 [[79, 207, 307, 403, 583], [316, 743, 907, 1094, 319], [19, 113]], [[79, 551, 129, 502, 569], [317, 497, 496, 1174, 318], [21, 37]],
 [[79, 551, 579, 148, 583], [317, 1193, 564, 565, 319], [19, 37]], [[79, 569, 131, 542, 583], [318, 505, 504, 1184, 319], [37, 113]], 
[[80, 208, 252, 348, 492], [320, 744, 828, 985, 321], [54, 55]], [[80, 208, 253, 349, 493], [320, 745, 829, 987, 322], [55, 56]],
 [[80, 208, 254, 350, 494], [320, 746, 830, 989, 323], [54, 56]], [[80, 492, 119, 570, 493], [321, 461, 463, 1165, 322], [35, 55]],
 [[80, 492, 572, 115, 494], [321, 1164, 449, 447, 323], [35, 54]], [[80, 493, 117, 571, 494], [322, 454, 456, 1166, 323], [35, 56]],
 [[81, 209, 300, 396, 588], [324, 747, 900, 1081, 325], [66, 67]], [[81, 209, 301, 397, 589], [324, 748, 901, 1083, 326], [67, 68]],
 [[81, 209, 302, 398, 590], [324, 749, 902, 1085, 327], [66, 68]], [[81, 588, 151, 594, 589], [325, 573, 575, 1195, 326], [39, 67]], 
[[81, 588, 596, 147, 590], [325, 1194, 561, 559, 327], [39, 66]], [[81, 589, 149, 595, 590], [326, 566, 568, 1196, 327], [39, 68]],
 [[82, 210, 255, 351, 495], [328, 750, 831, 991, 329], [57, 60]], [[82, 210, 258, 354, 498], [328, 751, 834, 997, 330], [60, 63]],
 [[82, 210, 261, 357, 501], [328, 752, 837, 1003, 331], [57, 63]], [[82, 495, 133, 565, 498], [329, 510, 512, 1170, 330], [34, 60]],
 [[82, 495, 575, 113, 501], [329, 1167, 442, 440, 331], [34, 57]], [[82, 498, 135, 568, 501], [330, 517, 519, 1173, 331], [34, 63]],
 [[83, 211, 303, 399, 591], [332, 753, 903, 1087, 333], [3, 69]], [[83, 211, 306, 402, 594], [332, 754, 906, 1093, 334], [3, 15]],
 [[83, 211, 309, 405, 597], [332, 755, 909, 1099, 335], [15, 69]], [[83, 591, 149, 589, 594], [333, 567, 566, 1195, 334], [3, 39]],
 [[83, 591, 599, 145, 597], [333, 1197, 554, 552, 335], [39, 69]], [[83, 594, 151, 592, 597], [334, 575, 574, 1198, 335], [15, 39]],
 [[84, 212, 256, 352, 496], [336, 756, 832, 993, 337], [58, 62]], [[84, 212, 260, 356, 500], [336, 757, 836, 1001, 338], [62, 64]],
 [[84, 212, 262, 358, 502], [336, 758, 838, 1005, 339], [58, 64]], [[84, 496, 143, 564, 500], [337, 545, 547, 1172, 338], [37, 62]],
 [[84, 496, 573, 129, 502], [337, 1168, 498, 496, 339], [37, 58]], [[84, 500, 131, 569, 502], [338, 503, 505, 1174, 339], [37, 64]],
 [[85, 213, 304, 400, 592], [340, 759, 904, 1089, 341], [7, 70]], [[85, 213, 308, 404, 596], [340, 760, 908, 1097, 342], [7, 23]],
 [[85, 213, 310, 406, 598], [340, 761, 910, 1101, 343], [23, 70]], [[85, 592, 151, 588, 596], [341, 574, 573, 1194, 342], [7, 39]],
 [[85, 592, 597, 145, 598], [341, 1198, 552, 553, 343], [39, 70]], [[85, 596, 147, 593, 598], [342, 561, 560, 1199, 343], [23, 39]], 
[[86, 214, 257, 353, 497], [344, 762, 833, 995, 345], [59, 61]], [[86, 214, 259, 355, 499], [344, 763, 835, 999, 346], [61, 65]],
 [[86, 214, 263, 359, 503], [344, 764, 839, 1007, 347], [59, 65]], [[86, 497, 139, 566, 499], [345, 531, 533, 1171, 346], [38, 61]],
 [[86, 497, 574, 137, 503], [345, 1169, 526, 524, 347], [38, 59]], [[86, 499, 141, 567, 503], [346, 538, 540, 1175, 347], [38, 65]],
 [[87, 215, 305, 401, 593], [348, 765, 905, 1091, 349], [11, 71]], [[87, 215, 307, 403, 595], [348, 766, 907, 1095, 350], [11, 19]],
 [[87, 215, 311, 407, 599], [348, 767, 911, 1103, 351], [19, 71]], [[87, 593, 147, 590, 595], [349, 560, 559, 1196, 350], [11, 39]], 
[[87, 593, 598, 145, 599], [349, 1199, 553, 554, 351], [39, 71]], [[87, 595, 149, 591, 599], [350, 568, 567, 1197, 351], [19, 39]],
 [[88, 89, 429, 321, 417], [352, 356, 931, 930, 353], [81, 82]], [[88, 89, 430, 322, 418], [352, 357, 933, 932, 354], [82, 83]],
 [[88, 89, 431, 323, 419], [352, 358, 935, 934, 355], [81, 83]], [[90, 91, 422, 314, 410], [359, 363, 917, 916, 360], [74, 77]], 
[[90, 91, 425, 317, 413], [359, 364, 923, 922, 361], [77, 80]], [[90, 91, 428, 320, 416], [359, 365, 929, 928, 362], [74, 80]],
 [[92, 93, 421, 313, 409], [366, 370, 915, 914, 367], [73, 75]], [[92, 93, 423, 315, 411], [366, 371, 919, 918, 368], [75, 79]],
 [[92, 93, 427, 319, 415], [366, 372, 927, 926, 369], [73, 79]], [[94, 95, 420, 312, 408], [373, 377, 913, 912, 374], [72, 76]],
 [[94, 95, 424, 316, 412], [373, 378, 921, 920, 375], [76, 78]], [[94, 95, 426, 318, 414], [373, 379, 925, 924, 376], [72, 78]],
 [[96, 97, 454, 334, 442], [380, 384, 957, 956, 381], [52, 107]], [[96, 97, 477, 345, 465], [380, 385, 979, 978, 382], [52, 93]],
 [[96, 97, 527, 371, 515], [380, 386, 1031, 1030, 383], [93, 107]], [[98, 99, 446, 326, 434], [387, 391, 941, 940, 388], [48, 101]],
 [[98, 99, 476, 344, 464], [387, 392, 977, 976, 389], [48, 92]], [[98, 99, 521, 365, 509], [387, 393, 1019, 1018, 390], [92, 101]], 
[[100, 101, 447, 327, 435], [394, 398, 943, 942, 395], [0, 103]], [[100, 101, 469, 337, 457], [394, 399, 963, 962, 396], [0, 85]],
 [[100, 101, 523, 367, 511], [394, 400, 1023, 1022, 397], [85, 103]], [[102, 103, 444, 324, 432], [401, 405, 937, 936, 402], [49, 100]], 
[[102, 103, 474, 342, 462], [401, 406, 973, 972, 403], [49, 90]], [[102, 103, 520, 364, 508], [401, 407, 1017, 1016, 404], [90, 100]],
 [[104, 105, 453, 333, 441], [408, 412, 955, 954, 409], [51, 106]], [[104, 105, 479, 347, 467], [408, 413, 983, 982, 410], [51, 95]],
 [[104, 105, 526, 370, 514], [408, 414, 1029, 1028, 411], [95, 106]], [[106, 107, 449, 329, 437], [415, 419, 947, 946, 416], [8, 104]],
 [[106, 107, 470, 338, 458], [415, 420, 965, 964, 417], [8, 86]], [[106, 107, 524, 368, 512], [415, 421, 1025, 1024, 418], [86, 104]],
 [[108, 109, 445, 325, 433], [422, 426, 939, 938, 423], [50, 99]], [[108, 109, 475, 343, 463], [422, 427, 975, 974, 424], [50, 91]], 
[[108, 109, 519, 363, 507], [422, 428, 1015, 1014, 425], [91, 99]], [[110, 111, 448, 328, 436], [429, 433, 945, 944, 430], [4, 102]], 
[[110, 111, 468, 336, 456], [429, 434, 961, 960, 431], [4, 84]], [[110, 111, 522, 366, 510], [429, 435, 1021, 1020, 432], [84, 102]], 
[[112, 113, 501, 357, 489], [436, 440, 1003, 1002, 437], [13, 57]], [[112, 113, 550, 382, 538], [436, 441, 1053, 1052, 438], [13, 119]],
 [[112, 113, 575, 395, 563], [436, 442, 1079, 1078, 439], [57, 119]], [[114, 115, 494, 350, 482], [443, 447, 989, 988, 444], [9, 54]],
 [[114, 115, 545, 377, 533], [443, 448, 1043, 1042, 445], [9, 116]], [[114, 115, 572, 392, 560], [443, 449, 1073, 1072, 446], [54, 116]],
 [[116, 117, 493, 349, 481], [450, 454, 987, 986, 451], [1, 56]], [[116, 117, 543, 375, 531], [450, 455, 1039, 1038, 452], [1, 115]], 
[[116, 117, 571, 391, 559], [450, 456, 1071, 1070, 453], [56, 115]], [[118, 119, 492, 348, 480], [457, 461, 985, 984, 458], [5, 55]],
 [[118, 119, 544, 376, 532], [457, 462, 1041, 1040, 459], [5, 114]], [[118, 119, 570, 390, 558], [457, 463, 1069, 1068, 460], [55, 114]],
 [[120, 121, 455, 335, 443], [464, 468, 959, 958, 465], [53, 105]], [[120, 121, 478, 346, 466], [464, 469, 981, 980, 466], [53, 94]],
 [[120, 121, 525, 369, 513], [464, 470, 1027, 1026, 467], [94, 105]], [[122, 123, 452, 332, 440], [471, 475, 953, 952, 472], [20, 98]], 
[[122, 123, 473, 341, 461], [471, 476, 971, 970, 473], [20, 89]], [[122, 123, 518, 362, 506], [471, 477, 1013, 1012, 474], [89, 98]],
 [[124, 125, 451, 331, 439], [478, 482, 951, 950, 479], [16, 97]], [[124, 125, 471, 339, 459], [478, 483, 967, 966, 480], [16, 87]],
 [[124, 125, 517, 361, 505], [478, 484, 1011, 1010, 481], [87, 97]], [[126, 127, 450, 330, 438], [485, 489, 949, 948, 486], [12, 96]],
 [[126, 127, 472, 340, 460], [485, 490, 969, 968, 487], [12, 88]], [[126, 127, 516, 360, 504], [485, 491, 1009, 1008, 488], [88, 96]],
 [[128, 129, 502, 358, 490], [492, 496, 1005, 1004, 493], [21, 58]], [[128, 129, 551, 383, 539], [492, 497, 1055, 1054, 494], [21, 117]],
 [[128, 129, 573, 393, 561], [492, 498, 1075, 1074, 495], [58, 117]], [[130, 131, 500, 356, 488], [499, 503, 1001, 1000, 500], [6, 64]],
 [[130, 131, 542, 374, 530], [499, 504, 1037, 1036, 501], [6, 113]], [[130, 131, 569, 389, 557], [499, 505, 1067, 1066, 502], [64, 113]],
 [[132, 133, 495, 351, 483], [506, 510, 991, 990, 507], [17, 60]], [[132, 133, 547, 379, 535], [506, 511, 1047, 1046, 508], [17, 109]], 
[[132, 133, 565, 385, 553], [506, 512, 1059, 1058, 509], [60, 109]], [[134, 135, 498, 354, 486], [513, 517, 997, 996, 514], [2, 63]],
 [[134, 135, 540, 372, 528], [513, 518, 1033, 1032, 515], [2, 112]], [[134, 135, 568, 388, 556], [513, 519, 1065, 1064, 516], [63, 112]], 
[[136, 137, 503, 359, 491], [520, 524, 1007, 1006, 521], [18, 59]], [[136, 137, 549, 381, 537], [520, 525, 1051, 1050, 522], [18, 118]],
 [[136, 137, 574, 394, 562], [520, 526, 1077, 1076, 523], [59, 118]], [[138, 139, 497, 353, 485], [527, 531, 995, 994, 528], [22, 61]],
 [[138, 139, 548, 380, 536], [527, 532, 1049, 1048, 529], [22, 110]], [[138, 139, 566, 386, 554], [527, 533, 1061, 1060, 530], [61, 110]],
 [[140, 141, 499, 355, 487], [534, 538, 999, 998, 535], [10, 65]], [[140, 141, 541, 373, 529], [534, 539, 1035, 1034, 536], [10, 111]],
 [[140, 141, 567, 387, 555], [534, 540, 1063, 1062, 537], [65, 111]], [[142, 143, 496, 352, 484], [541, 545, 993, 992, 542], [14, 62]],
 [[142, 143, 546, 378, 534], [541, 546, 1045, 1044, 543], [14, 108]], [[142, 143, 564, 384, 552], [541, 547, 1057, 1056, 544], [62, 108]],
 [[144, 145, 597, 405, 585], [548, 552, 1099, 1098, 549], [69, 70]], [[144, 145, 598, 406, 586], [548, 553, 1101, 1100, 550], [70, 71]],
 [[144, 145, 599, 407, 587], [548, 554, 1103, 1102, 551], [69, 71]], [[146, 147, 590, 398, 578], [555, 559, 1085, 1084, 556], [11, 66]],
 [[146, 147, 593, 401, 581], [555, 560, 1091, 1090, 557], [11, 23]], [[146, 147, 596, 404, 584], [555, 561, 1097, 1096, 558], [23, 66]],
 [[148, 149, 589, 397, 577], [562, 566, 1083, 1082, 563], [3, 68]], [[148, 149, 591, 399, 579], [562, 567, 1087, 1086, 564], [3, 19]],
 [[148, 149, 595, 403, 583], [562, 568, 1095, 1094, 565], [19, 68]], [[150, 151, 588, 396, 576], [569, 573, 1081, 1080, 570], [7, 67]],
 [[150, 151, 592, 400, 580], [569, 574, 1089, 1088, 571], [7, 15]], [[150, 151, 594, 402, 582], [569, 575, 1093, 1092, 572], [15, 67]], 
[[152, 216, 160, 241, 217], [576, 600, 602, 770, 577], [40, 72]], [[152, 216, 240, 184, 218], [576, 768, 674, 672, 578], [40, 74]],
 [[152, 217, 168, 242, 218], [577, 624, 626, 772, 578], [40, 73]], [[153, 264, 161, 289, 265], [579, 603, 605, 842, 580], [41, 96]],
 [[153, 264, 288, 185, 266], [579, 840, 677, 675, 581], [41, 98]], [[153, 265, 169, 290, 266], [580, 627, 629, 844, 581], [41, 97]],
 [[154, 219, 170, 246, 222], [582, 630, 632, 780, 583], [42, 75]], [[154, 219, 243, 186, 225], [582, 774, 680, 678, 584], [42, 81]],
 [[154, 222, 162, 249, 225], [583, 606, 608, 786, 584], [42, 78]], [[155, 267, 171, 294, 270], [585, 633, 635, 852, 586], [43, 99]],
 [[155, 267, 291, 187, 273], [585, 846, 683, 681, 587], [43, 105]], [[155, 270, 163, 297, 273], [586, 609, 611, 858, 587], [43, 102]],
 [[156, 220, 164, 248, 224], [588, 612, 614, 784, 589], [44, 76]], [[156, 220, 244, 188, 226], [588, 776, 686, 684, 590], [44, 82]],
 [[156, 224, 172, 250, 226], [589, 636, 638, 788, 590], [44, 80]], [[157, 268, 165, 296, 272], [591, 615, 617, 856, 592], [45, 100]],
 [[157, 268, 292, 189, 274], [591, 848, 689, 687, 593], [45, 106]], [[157, 272, 173, 298, 274], [592, 639, 641, 860, 593], [45, 104]], 
[[158, 221, 174, 247, 223], [594, 642, 644, 782, 595], [46, 77]], [[158, 221, 245, 190, 227], [594, 778, 692, 690, 596], [46, 83]],
 [[158, 223, 166, 251, 227], [595, 618, 620, 790, 596], [46, 79]], [[159, 269, 175, 295, 271], [597, 645, 647, 854, 598], [47, 101]],
 [[159, 269, 293, 191, 275], [597, 850, 695, 693, 599], [47, 107]], [[159, 271, 167, 299, 275], [598, 621, 623, 862, 599], [47, 103]],
 [[160, 216, 240, 192, 230], [600, 768, 697, 696, 601], [40, 48]], [[160, 230, 254, 176, 241], [601, 796, 650, 649, 602], [40, 85]],
 [[161, 264, 288, 193, 278], [603, 840, 700, 699, 604], [6, 41]], [[161, 278, 302, 177, 289], [604, 868, 653, 652, 605], [41, 109]],
 [[162, 222, 246, 178, 231], [606, 780, 655, 654, 607], [0, 42]], [[162, 231, 255, 194, 249], [607, 798, 704, 703, 608], [42, 93]],
 [[163, 270, 294, 179, 279], [609, 852, 658, 657, 610], [1, 43]], [[163, 279, 303, 195, 297], [610, 870, 707, 706, 611], [43, 117]],
 [[164, 220, 244, 196, 238], [612, 776, 709, 708, 613], [44, 52]], [[164, 238, 262, 180, 248], [613, 812, 662, 661, 614], [44, 92]],
 [[165, 268, 292, 197, 286], [615, 848, 712, 711, 616], [13, 45]], [[165, 286, 310, 181, 296], [616, 884, 665, 664, 617], [45, 116]],
 [[166, 223, 247, 182, 233], [618, 782, 667, 666, 619], [8, 46]], [[166, 233, 257, 198, 251], [619, 802, 716, 715, 620], [46, 95]], 
[[167, 271, 295, 183, 281], [621, 854, 670, 669, 622], [9, 47]], [[167, 281, 305, 199, 299], [622, 874, 719, 718, 623], [47, 119]], 
[[168, 217, 241, 176, 228], [624, 770, 649, 648, 625], [40, 49]], [[168, 228, 252, 200, 242], [625, 792, 722, 721, 626], [40, 86]],
 [[169, 265, 289, 177, 276], [627, 842, 652, 651, 628], [2, 41]], [[169, 276, 300, 201, 290], [628, 864, 725, 724, 629], [41, 110]],
 [[170, 219, 243, 202, 237], [630, 774, 727, 726, 631], [42, 51]], [[170, 237, 261, 178, 246], [631, 810, 656, 655, 632], [42, 90]],
 [[171, 267, 291, 203, 285], [633, 846, 730, 729, 634], [18, 43]], [[171, 285, 309, 179, 294], [634, 882, 659, 658, 635], [43, 114]], 
[[172, 224, 248, 180, 232], [636, 784, 661, 660, 637], [4, 44]], [[172, 232, 256, 204, 250], [637, 800, 734, 733, 638], [44, 94]],
 [[173, 272, 296, 181, 280], [639, 856, 664, 663, 640], [5, 45]], [[173, 280, 304, 205, 298], [640, 872, 737, 736, 641], [45, 118]],
 [[174, 221, 245, 206, 239], [642, 778, 739, 738, 643], [46, 53]], [[174, 239, 263, 182, 247], [643, 814, 668, 667, 644], [46, 91]],
 [[175, 269, 293, 207, 287], [645, 850, 742, 741, 646], [21, 47]], [[175, 287, 311, 183, 295], [646, 886, 671, 670, 647], [47, 115]],
 [[176, 228, 252, 208, 254], [648, 792, 744, 746, 650], [40, 54]], [[177, 276, 300, 209, 302], [651, 864, 747, 749, 653], [41, 66]],
 [[178, 231, 255, 210, 261], [654, 798, 750, 752, 656], [42, 57]], [[179, 279, 303, 211, 309], [657, 870, 753, 755, 659], [43, 69]],
 [[180, 232, 256, 212, 262], [660, 800, 756, 758, 662], [44, 58]], [[181, 280, 304, 213, 310], [663, 872, 759, 761, 665], [45, 70]],
 [[182, 233, 257, 214, 263], [666, 802, 762, 764, 668], [46, 59]], [[183, 281, 305, 215, 311], [669, 874, 765, 767, 671], [47, 71]],
 [[184, 218, 242, 200, 229], [672, 772, 721, 720, 673], [40, 50]], [[184, 229, 253, 192, 240], [673, 794, 698, 697, 674], [40, 84]],
 [[185, 266, 290, 201, 277], [675, 844, 724, 723, 676], [10, 41]], [[185, 277, 301, 193, 288], [676, 866, 701, 700, 677], [41, 108]],
 [[186, 225, 249, 194, 234], [678, 786, 703, 702, 679], [12, 42]], [[186, 234, 258, 202, 243], [679, 804, 728, 727, 680], [42, 87]],
 [[187, 273, 297, 195, 282], [681, 858, 706, 705, 682], [14, 43]], [[187, 282, 306, 203, 291], [682, 876, 731, 730, 683], [43, 111]],
 [[188, 226, 250, 204, 236], [684, 788, 733, 732, 685], [20, 44]], [[188, 236, 260, 196, 244], [685, 808, 710, 709, 686], [44, 88]],
 [[189, 274, 298, 205, 284], [687, 860, 736, 735, 688], [22, 45]], [[189, 284, 308, 197, 292], [688, 880, 713, 712, 689], [45, 112]],
 [[190, 227, 251, 198, 235], [690, 790, 715, 714, 691], [16, 46]], [[190, 235, 259, 206, 245], [691, 806, 740, 739, 692], [46, 89]],
 [[191, 275, 299, 199, 283], [693, 862, 718, 717, 694], [17, 47]], [[191, 283, 307, 207, 293], [694, 878, 743, 742, 695], [47, 113]],
 [[192, 230, 254, 208, 253], [696, 796, 746, 745, 698], [40, 56]], [[193, 278, 302, 209, 301], [699, 868, 749, 748, 701], [41, 68]],
 [[194, 234, 258, 210, 255], [702, 804, 751, 750, 704], [42, 60]], [[195, 282, 306, 211, 303], [705, 876, 754, 753, 707], [3, 43]],
 [[196, 238, 262, 212, 260], [708, 812, 758, 757, 710], [44, 64]], [[197, 286, 310, 213, 308], [711, 884, 761, 760, 713], [23, 45]],
 [[198, 235, 259, 214, 257], [714, 806, 763, 762, 716], [46, 61]], [[199, 283, 307, 215, 305], [717, 878, 766, 765, 719], [11, 47]],
 [[200, 229, 253, 208, 252], [720, 794, 745, 744, 722], [40, 55]], [[201, 277, 301, 209, 300], [723, 866, 748, 747, 725], [41, 67]],
 [[202, 237, 261, 210, 258], [726, 810, 752, 751, 728], [42, 63]], [[203, 285, 309, 211, 306], [729, 882, 755, 754, 731], [15, 43]],
 [[204, 236, 260, 212, 256], [732, 808, 757, 756, 734], [44, 62]], [[205, 284, 308, 213, 304], [735, 880, 760, 759, 737], [7, 45]],
 [[206, 239, 263, 214, 259], [738, 814, 764, 763, 740], [46, 65]], [[207, 287, 311, 215, 307], [741, 886, 767, 766, 743], [19, 47]]]

len(cube.c)= 120 
cube.c= [[[0, 34, 50, 100, 101, 162, 178, 222, 231, 246, 318, 327, 337, 342, 426, 435, 447, 457, 469, 474], 
[1, 2, 3, 136, 137, 138, 200, 201, 202, 394, 395, 396, 398, 399, 606, 607, 654, 655, 780, 781, 799, 822, 925, 942, 943, 962, 963, 973, 1116, 1147], 
[4, 3, 5, 207, 204, 205, 303, 300, 301, 546, 547, 652]], [[1, 35, 51, 116, 117, 163, 179, 270, 279, 294, 349, 366, 375, 390, 481, 493, 522, 531, 543, 570],
 [5, 6, 7, 140, 141, 142, 204, 205, 206, 450, 451, 452, 454, 455, 609, 610, 657, 658, 852, 853, 871, 894, 986, 987, 1021, 1038, 1039, 1069, 1153, 1165], 
[11, 9, 10, 213, 210, 211, 309, 306, 307, 570, 571, 654]], [[2, 41, 49, 134, 135, 169, 177, 265, 276, 289, 354, 361, 372, 385, 486, 498, 517, 528, 540, 565],
 [9, 10, 11, 164, 165, 166, 196, 197, 198, 513, 514, 515, 517, 518, 627, 628, 651, 652, 842, 843, 865, 889, 996, 997, 1011, 1032, 1033, 1059, 1158, 1170],
 [17, 15, 16, 249, 246, 247, 297, 294, 295, 597, 598, 666]],
 [[3, 67, 83, 148, 149, 195, 211, 282, 303, 306, 378, 397, 399, 402, 546, 577, 579, 589, 591, 594],
 [13, 14, 15, 268, 269, 271, 332, 333, 334, 562, 563, 564, 566, 567, 705, 707, 753, 754, 876, 877, 903, 906, 1045, 1082, 1083, 1086, 1087, 1093, 1188, 1195], 
[22, 21, 23, 406, 402, 404, 501, 498, 499, 618, 619, 707]], [[4, 44, 52, 110, 111, 172, 180, 224, 232, 248, 320, 328, 336, 344, 428, 436, 448, 456, 468, 476],
 [17, 18, 19, 176, 177, 178, 208, 209, 210, 429, 430, 431, 433, 434, 636, 637, 660, 661, 784, 785, 801, 824, 929, 944, 945, 960, 961, 977, 1118, 1146],
 [28, 27, 29, 267, 264, 265, 315, 312, 313, 561, 562, 672]],
 [[5, 45, 53, 118, 119, 173, 181, 272, 280, 296, 348, 368, 376, 392, 480, 492, 524, 532, 544, 572], 
[21, 22, 23, 180, 181, 182, 212, 213, 214, 457, 458, 459, 461, 462, 639, 640, 663, 664, 856, 857, 873, 896, 984, 985, 1025, 1040, 1041, 1073, 1152, 1164],
 [35, 33, 34, 273, 270, 271, 321, 318, 319, 573, 574, 674]], [[6, 33, 65, 130, 131, 161, 193, 264, 278, 288, 356, 360, 374, 384, 488, 500, 516, 530, 542, 564],
 [25, 26, 27, 132, 133, 134, 260, 261, 262, 499, 500, 501, 503, 504, 603, 604, 699, 700, 840, 841, 869, 888, 1000, 1001, 1009, 1036, 1037, 1057, 1160, 1172],
 [41, 39, 40, 201, 198, 199, 393, 390, 391, 591, 592, 650]], [[7, 77, 85, 150, 151, 205, 213, 284, 304, 308, 380, 396, 400, 404, 548, 576, 580, 588, 592, 596],
 [29, 30, 31, 308, 309, 311, 340, 341, 342, 569, 570, 571, 573, 574, 735, 737, 759, 760, 880, 881, 904, 908, 1049, 1080, 1081, 1088, 1089, 1097, 1190, 1194],
 [46, 45, 47, 466, 462, 464, 513, 510, 511, 621, 622, 717]],
 [[8, 38, 54, 106, 107, 166, 182, 223, 233, 247, 319, 329, 338, 343, 427, 437, 449, 458, 470, 475], 
[33, 34, 35, 152, 153, 154, 216, 217, 218, 415, 416, 417, 419, 420, 618, 619, 666, 667, 782, 783, 803, 823, 927, 946, 947, 964, 965, 975, 1117, 1148], 
[52, 51, 53, 231, 228, 229, 327, 324, 325, 555, 556, 660]],
 [[9, 39, 55, 114, 115, 167, 183, 271, 281, 295, 350, 367, 377, 391, 482, 494, 523, 533, 545, 571],
 [37, 38, 39, 156, 157, 158, 220, 221, 222, 443, 444, 445, 447, 448, 621, 622, 669, 670, 854, 855, 875, 895, 988, 989, 1023, 1042, 1043, 1071, 1154, 1166],
 [59, 57, 58, 237, 234, 235, 333, 330, 331, 567, 568, 662]],
 [[10, 57, 73, 140, 141, 185, 201, 266, 277, 290, 355, 362, 373, 386, 487, 499, 518, 529, 541, 566],
 [41, 42, 43, 228, 229, 230, 292, 293, 294, 534, 535, 536, 538, 539, 675, 676, 723, 724, 844, 845, 867, 890, 998, 999, 1013, 1034, 1035, 1061, 1159, 1171],
 [65, 63, 64, 345, 342, 343, 441, 438, 439, 606, 607, 690]],
 [[11, 71, 87, 146, 147, 199, 215, 283, 305, 307, 379, 398, 401, 403, 547, 578, 581, 590, 593, 595],
 [45, 46, 47, 284, 285, 287, 348, 349, 350, 555, 556, 557, 559, 560, 717, 719, 765, 766, 878, 879, 905, 907, 1047, 1084, 1085, 1090, 1091, 1095, 1189, 1196],
 [70, 69, 71, 430, 426, 428, 525, 522, 523, 615, 616, 711]],
 [[12, 58, 66, 126, 127, 186, 194, 225, 234, 249, 321, 330, 340, 345, 429, 438, 450, 460, 472, 477],
 [49, 50, 51, 232, 233, 234, 264, 265, 266, 485, 486, 487, 489, 490, 678, 679, 702, 703, 786, 787, 805, 825, 931, 948, 949, 968, 969, 979, 1119, 1150],
 [76, 75, 77, 351, 348, 349, 399, 396, 397, 585, 586, 692]],
 [[13, 37, 69, 112, 113, 165, 197, 268, 286, 292, 357, 364, 382, 388, 489, 501, 520, 538, 550, 568],
 [53, 54, 55, 148, 149, 150, 276, 277, 278, 436, 437, 438, 440, 441, 615, 616, 711, 712, 848, 849, 885, 892, 1002, 1003, 1017, 1052, 1053, 1065, 1161, 1173],
 [83, 81, 82, 225, 222, 223, 417, 414, 415, 564, 565, 658]],
 [[14, 59, 67, 142, 143, 187, 195, 273, 282, 297, 352, 369, 378, 393, 484, 496, 525, 534, 546, 573],
 [57, 58, 59, 236, 237, 238, 268, 269, 270, 541, 542, 543, 545, 546, 681, 682, 705, 706, 858, 859, 877, 897, 992, 993, 1027, 1044, 1045, 1075, 1156, 1168], 
[89, 87, 88, 357, 354, 355, 405, 402, 403, 609, 610, 694]],
 [[15, 75, 83, 150, 151, 203, 211, 285, 306, 309, 381, 400, 402, 405, 549, 580, 582, 592, 594, 597],
 [61, 62, 63, 300, 301, 303, 332, 334, 335, 569, 571, 572, 574, 575, 729, 731, 754, 755, 882, 883, 906, 909, 1051, 1088, 1089, 1092, 1093, 1099, 1191, 1198],
 [94, 93, 95, 454, 450, 452, 503, 499, 500, 622, 623, 715]], [[16, 62, 70, 124, 125, 190, 198, 227, 235, 251, 323, 331, 339, 347, 431, 439, 451, 459, 471, 479],
 [65, 66, 67, 248, 249, 250, 280, 281, 282, 478, 479, 480, 482, 483, 690, 691, 714, 715, 790, 791, 807, 827, 935, 950, 951, 966, 967, 983, 1121, 1149], 
[100, 99, 101, 375, 372, 373, 423, 420, 421, 582, 583, 700]], 
[[17, 63, 71, 132, 133, 191, 199, 275, 283, 299, 351, 371, 379, 395, 483, 495, 527, 535, 547, 575],
 [69, 70, 71, 252, 253, 254, 284, 285, 286, 506, 507, 508, 510, 511, 693, 694, 717, 718, 862, 863, 879, 899, 990, 991, 1031, 1046, 1047, 1079, 1155, 1167], 
[107, 105, 106, 381, 378, 379, 429, 426, 427, 594, 595, 702]],
 [[18, 43, 75, 136, 137, 171, 203, 267, 285, 291, 359, 363, 381, 387, 491, 503, 519, 537, 549, 567],
 [73, 74, 75, 172, 173, 174, 300, 301, 302, 520, 521, 522, 524, 525, 633, 634, 729, 730, 846, 847, 883, 891, 1006, 1007, 1015, 1050, 1051, 1063, 1163, 1175],
 [113, 111, 112, 261, 258, 259, 453, 450, 451, 600, 601, 670]],
 [[19, 79, 87, 148, 149, 207, 215, 287, 307, 311, 383, 399, 403, 407, 551, 579, 583, 591, 595, 599],
 [77, 78, 79, 316, 317, 319, 348, 350, 351, 562, 564, 565, 567, 568, 741, 743, 766, 767, 886, 887, 907, 911, 1055, 1086, 1087, 1094, 1095, 1103, 1193, 1197],
 [118, 117, 119, 478, 474, 476, 527, 523, 524, 619, 620, 719]],
 [[20, 60, 76, 122, 123, 188, 204, 226, 236, 250, 322, 332, 341, 346, 430, 440, 452, 461, 473, 478],
 [81, 82, 83, 240, 241, 242, 304, 305, 306, 471, 472, 473, 475, 476, 684, 685, 732, 733, 788, 789, 809, 826, 933, 952, 953, 970, 971, 981, 1120, 1151],
 [124, 123, 125, 363, 360, 361, 459, 456, 457, 579, 580, 696]],
 [[21, 47, 79, 128, 129, 175, 207, 269, 287, 293, 358, 365, 383, 389, 490, 502, 521, 539, 551, 569], 
[85, 86, 87, 188, 189, 190, 316, 317, 318, 492, 493, 494, 496, 497, 645, 646, 741, 742, 850, 851, 887, 893, 1004, 1005, 1019, 1054, 1055, 1067, 1162, 1174],
 [131, 129, 130, 285, 282, 283, 477, 474, 475, 588, 589, 678]], 
[[22, 61, 77, 138, 139, 189, 205, 274, 284, 298, 353, 370, 380, 394, 485, 497, 526, 536, 548, 574], 
[89, 90, 91, 244, 245, 246, 308, 309, 310, 527, 528, 529, 531, 532, 687, 688, 735, 736, 860, 861, 881, 898, 994, 995, 1029, 1048, 1049, 1077, 1157, 1169],
 [137, 135, 136, 369, 366, 367, 465, 462, 463, 603, 604, 698]],
 [[23, 69, 85, 146, 147, 197, 213, 286, 308, 310, 382, 401, 404, 406, 550, 581, 584, 593, 596, 598], 
[93, 94, 95, 276, 277, 279, 340, 342, 343, 555, 557, 558, 560, 561, 711, 713, 760, 761, 884, 885, 908, 910, 1053, 1090, 1091, 1096, 1097, 1101, 1192, 1199], 
[142, 141, 143, 418, 414, 416, 515, 511, 512, 616, 617, 709]],
 [[24, 26, 28, 30, 88, 90, 92, 94, 408, 409, 410, 411, 412, 413, 414, 415, 416, 417, 418, 419],
 [97, 98, 99, 105, 106, 107, 113, 114, 115, 121, 122, 123, 353, 354, 355, 360, 361, 362, 367, 368, 369, 374, 375, 376, 1104, 1105, 1106, 1107, 1108, 1109],
 [148, 149, 147, 160, 159, 161, 172, 173, 171, 184, 183, 185]],
 [[25, 58, 60, 62, 89, 122, 124, 126, 429, 430, 431, 438, 439, 440, 459, 460, 461, 504, 505, 506],
 [101, 102, 103, 233, 234, 235, 241, 242, 243, 249, 250, 251, 356, 357, 358, 472, 473, 474, 479, 480, 481, 486, 487, 488, 1119, 1120, 1121, 1128, 1129, 1130],
 [154, 155, 153, 352, 353, 351, 364, 363, 365, 376, 377, 375]],
 [[27, 44, 46, 56, 91, 108, 110, 120, 422, 425, 428, 433, 436, 443, 456, 463, 466, 507, 510, 513],
 [109, 110, 111, 177, 178, 179, 185, 186, 187, 225, 226, 227, 363, 364, 365, 423, 424, 425, 430, 431, 432, 465, 466, 467, 1112, 1115, 1118, 1123, 1126, 1133], 
[165, 167, 166, 268, 267, 269, 280, 281, 279, 340, 339, 341]],
 [[29, 38, 40, 42, 93, 102, 104, 106, 421, 423, 427, 432, 437, 441, 458, 462, 467, 508, 512, 514],
 [117, 118, 119, 153, 154, 155, 161, 162, 163, 169, 170, 171, 370, 371, 372, 402, 403, 404, 409, 410, 411, 416, 417, 418, 1111, 1113, 1117, 1122, 1127, 1131],
 [177, 178, 179, 232, 233, 231, 244, 243, 245, 256, 257, 255]],
 [[31, 32, 34, 36, 95, 96, 98, 100, 420, 424, 426, 434, 435, 442, 457, 464, 465, 509, 511, 515], 
[125, 126, 127, 129, 130, 131, 137, 138, 139, 145, 146, 147, 377, 378, 379, 381, 382, 383, 388, 389, 390, 395, 396, 397, 1110, 1114, 1116, 1124, 1125, 1132], 
[190, 189, 191, 196, 195, 197, 208, 209, 207, 220, 219, 221]], 
[[33, 63, 66, 68, 97, 127, 130, 132, 450, 454, 472, 477, 483, 488, 516, 527, 530, 535, 553, 557],
 [133, 134, 135, 253, 254, 255, 265, 266, 267, 273, 274, 275, 384, 385, 386, 489, 490, 491, 500, 501, 502, 507, 508, 509, 1140, 1144, 1150, 1155, 1160, 1178],
 [202, 201, 203, 382, 383, 381, 401, 399, 400, 411, 413, 412]], 
[[35, 47, 52, 64, 99, 111, 116, 128, 446, 448, 468, 476, 481, 490, 521, 522, 531, 539, 559, 561],
 [141, 142, 143, 189, 190, 191, 209, 210, 211, 257, 258, 259, 391, 392, 393, 433, 434, 435, 451, 452, 453, 493, 494, 495, 1136, 1138, 1146, 1153, 1162, 1179],
 [214, 213, 215, 286, 287, 285, 317, 315, 316, 387, 389, 388]], 
[[37, 39, 48, 50, 101, 103, 112, 114, 444, 447, 469, 474, 482, 489, 520, 523, 533, 538, 560, 563],
 [149, 150, 151, 157, 158, 159, 193, 194, 195, 201, 202, 203, 398, 399, 400, 405, 406, 407, 437, 438, 439, 444, 445, 446, 1134, 1137, 1147, 1154, 1161, 1181],
 [226, 225, 227, 238, 239, 237, 293, 291, 292, 303, 305, 304]],
 [[41, 61, 70, 74, 105, 125, 134, 138, 451, 453, 471, 479, 485, 486, 517, 526, 528, 536, 554, 556], 
[165, 166, 167, 245, 246, 247, 281, 282, 283, 297, 298, 299, 412, 413, 414, 482, 483, 484, 514, 515, 516, 528, 529, 530, 1141, 1143, 1149, 1157, 1158, 1176],
 [250, 249, 251, 370, 371, 369, 425, 423, 424, 447, 449, 448]], 
[[43, 45, 54, 72, 107, 109, 118, 136, 445, 449, 470, 475, 480, 491, 519, 524, 532, 537, 558, 562], 
[173, 174, 175, 181, 182, 183, 217, 218, 219, 289, 290, 291, 419, 420, 421, 426, 427, 428, 458, 459, 460, 521, 522, 523, 1135, 1139, 1148, 1152, 1163, 1180],
 [262, 263, 261, 274, 273, 275, 327, 329, 328, 437, 435, 436]],
 [[49, 69, 71, 82, 113, 133, 135, 146, 495, 498, 501, 540, 547, 550, 565, 568, 575, 578, 581, 584], 
[197, 198, 199, 277, 278, 279, 285, 286, 287, 329, 330, 331, 440, 441, 442, 510, 511, 512, 517, 518, 519, 556, 557, 558, 1167, 1170, 1173, 1182, 1189, 1192],
 [299, 297, 298, 417, 419, 418, 431, 429, 430, 496, 495, 497]],
 [[51, 53, 55, 80, 115, 117, 119, 144, 492, 493, 494, 543, 544, 545, 570, 571, 572, 585, 586, 587], 
[205, 206, 207, 213, 214, 215, 221, 222, 223, 321, 322, 323, 447, 448, 449, 454, 455, 456, 461, 462, 463, 549, 550, 551, 1164, 1165, 1166, 1185, 1186, 1187],
 [309, 311, 310, 323, 321, 322, 333, 335, 334, 484, 485, 483]],
 [[57, 59, 76, 78, 121, 123, 140, 142, 452, 455, 473, 478, 484, 487, 518, 525, 529, 534, 552, 555],
 [229, 230, 231, 237, 238, 239, 305, 306, 307, 313, 314, 315, 468, 469, 470, 475, 476, 477, 535, 536, 537, 542, 543, 544, 1142, 1145, 1151, 1156, 1159, 1177],
 [346, 345, 347, 358, 359, 357, 461, 459, 460, 471, 473, 472]],
 [[65, 67, 79, 84, 129, 131, 143, 148, 496, 500, 502, 542, 546, 551, 564, 569, 573, 577, 579, 583],
 [261, 262, 263, 269, 270, 271, 317, 318, 319, 337, 338, 339, 496, 497, 498, 503, 504, 505, 545, 546, 547, 563, 564, 565, 1168, 1172, 1174, 1184, 1188, 1193],
 [393, 395, 394, 407, 405, 406, 477, 479, 478, 508, 509, 507]],
 [[73, 75, 77, 86, 137, 139, 141, 150, 497, 499, 503, 541, 548, 549, 566, 567, 574, 576, 580, 582],
 [293, 294, 295, 301, 302, 303, 309, 310, 311, 345, 346, 347, 524, 525, 526, 531, 532, 533, 538, 539, 540, 570, 571, 572, 1169, 1171, 1175, 1183, 1190, 1191],
 [443, 441, 442, 453, 455, 454, 467, 465, 466, 520, 519, 521]],
 [[81, 83, 85, 87, 145, 147, 149, 151, 588, 589, 590, 591, 592, 593, 594, 595, 596, 597, 598, 599],
 [325, 326, 327, 333, 334, 335, 341, 342, 343, 349, 350, 351, 552, 553, 554, 559, 560, 561, 566, 567, 568, 573, 574, 575, 1194, 1195, 1196, 1197, 1198, 1199],
 [490, 491, 489, 502, 501, 503, 514, 515, 513, 526, 525, 527]],
 [[152, 160, 168, 176, 184, 192, 200, 208, 216, 217, 218, 228, 229, 230, 240, 241, 242, 252, 253, 254],
 [576, 577, 578, 600, 601, 602, 624, 625, 626, 648, 649, 650, 672, 673, 674, 696, 697, 698, 720, 721, 722, 744, 745, 746, 768, 770, 772, 792, 794, 796],
 [624, 626, 625, 649, 648, 664, 665, 680, 689, 688, 704, 712]],
 [[153, 161, 169, 177, 185, 193, 201, 209, 264, 265, 266, 276, 277, 278, 288, 289, 290, 300, 301, 302],
 [579, 580, 581, 603, 604, 605, 627, 628, 629, 651, 652, 653, 675, 676, 677, 699, 700, 701, 723, 724, 725, 747, 748, 749, 840, 842, 844, 864, 866, 868],
 [627, 629, 628, 651, 650, 666, 667, 681, 691, 690, 705, 713]],
 [[154, 162, 170, 178, 186, 194, 202, 210, 219, 222, 225, 231, 234, 237, 243, 246, 249, 255, 258, 261],
 [582, 583, 584, 606, 607, 608, 630, 631, 632, 654, 655, 656, 678, 679, 680, 702, 703, 704, 726, 727, 728, 750, 751, 752, 774, 780, 786, 798, 804, 810],
 [632, 630, 631, 652, 653, 669, 668, 682, 692, 693, 706, 714]],
 [[155, 163, 171, 179, 187, 195, 203, 211, 267, 270, 273, 279, 282, 285, 291, 294, 297, 303, 306, 309],
 [585, 586, 587, 609, 610, 611, 633, 634, 635, 657, 658, 659, 681, 682, 683, 705, 706, 707, 729, 730, 731, 753, 754, 755, 846, 852, 858, 870, 876, 882],
 [635, 633, 634, 654, 655, 671, 670, 683, 694, 695, 707, 715]],
 [[156, 164, 172, 180, 188, 196, 204, 212, 220, 224, 226, 232, 236, 238, 244, 248, 250, 256, 260, 262],
 [588, 589, 590, 612, 613, 614, 636, 637, 638, 660, 661, 662, 684, 685, 686, 708, 709, 710, 732, 733, 734, 756, 757, 758, 776, 784, 788, 800, 808, 812],
 [636, 638, 637, 657, 656, 672, 673, 684, 697, 696, 708, 716]],
 [[157, 165, 173, 181, 189, 197, 205, 213, 268, 272, 274, 280, 284, 286, 292, 296, 298, 304, 308, 310],
 [591, 592, 593, 615, 616, 617, 639, 640, 641, 663, 664, 665, 687, 688, 689, 711, 712, 713, 735, 736, 737, 759, 760, 761, 848, 856, 860, 872, 880, 884],
 [639, 641, 640, 659, 658, 674, 675, 685, 699, 698, 709, 717]],
 [[158, 166, 174, 182, 190, 198, 206, 214, 221, 223, 227, 233, 235, 239, 245, 247, 251, 257, 259, 263],
 [594, 595, 596, 618, 619, 620, 642, 643, 644, 666, 667, 668, 690, 691, 692, 714, 715, 716, 738, 739, 740, 762, 763, 764, 778, 782, 790, 802, 806, 814],
 [644, 642, 643, 660, 661, 677, 676, 686, 700, 701, 710, 718]],
 [[159, 167, 175, 183, 191, 199, 207, 215, 269, 271, 275, 281, 283, 287, 293, 295, 299, 305, 307, 311],
 [597, 598, 599, 621, 622, 623, 645, 646, 647, 669, 670, 671, 693, 694, 695, 717, 718, 719, 741, 742, 743, 765, 766, 767, 850, 854, 862, 874, 878, 886], 
[647, 645, 646, 662, 663, 679, 678, 687, 702, 703, 711, 719]],
 [[4, 32, 64, 98, 99, 160, 192, 216, 230, 240, 312, 326, 336, 344, 420, 434, 446, 464, 468, 476],
 [16, 18, 19, 128, 129, 130, 256, 257, 258, 387, 388, 389, 391, 392, 600, 601, 696, 697, 768, 769, 797, 816, 913, 940, 941, 961, 976, 977, 1110, 1146],
 [25, 26, 29, 195, 192, 193, 387, 384, 385, 543, 544, 648]], [[0, 40, 48, 102, 103, 168, 176, 217, 228, 241, 313, 324, 337, 342, 421, 432, 444, 462, 469, 474],
 [0, 2, 3, 160, 161, 162, 192, 193, 194, 401, 402, 403, 405, 406, 624, 625, 648, 649, 770, 771, 793, 817, 915, 936, 937, 963, 972, 973, 1111, 1147], 
[1, 2, 5, 243, 240, 241, 291, 288, 289, 549, 550, 664]],
 [[8, 56, 72, 108, 109, 184, 200, 218, 229, 242, 314, 325, 338, 343, 422, 433, 445, 463, 470, 475],
 [32, 34, 35, 224, 225, 226, 288, 289, 290, 422, 423, 424, 426, 427, 672, 673, 720, 721, 772, 773, 795, 818, 917, 938, 939, 965, 974, 975, 1112, 1148],
 [49, 50, 53, 339, 336, 337, 435, 432, 433, 558, 559, 688]],
 [[16, 42, 74, 104, 105, 170, 202, 219, 237, 243, 315, 333, 339, 347, 423, 441, 453, 467, 471, 479],
 [64, 66, 67, 168, 169, 170, 296, 297, 298, 408, 409, 410, 412, 413, 630, 631, 726, 727, 774, 775, 811, 819, 919, 954, 955, 967, 982, 983, 1113, 1149],
 [97, 98, 101, 255, 252, 253, 447, 444, 445, 552, 553, 668]], 
[[12, 36, 68, 96, 97, 164, 196, 220, 238, 244, 316, 334, 340, 345, 424, 442, 454, 465, 472, 477],
 [48, 50, 51, 144, 145, 146, 272, 273, 274, 380, 381, 382, 384, 385, 612, 613, 708, 709, 776, 777, 813, 820, 921, 956, 957, 969, 978, 979, 1114, 1150],
 [73, 74, 77, 219, 216, 217, 411, 408, 409, 540, 541, 656]],
 [[20, 46, 78, 120, 121, 174, 206, 221, 239, 245, 317, 335, 341, 346, 425, 443, 455, 466, 473, 478],
 [80, 82, 83, 184, 185, 186, 312, 313, 314, 464, 465, 466, 468, 469, 642, 643, 738, 739, 778, 779, 815, 821, 923, 958, 959, 971, 980, 981, 1115, 1151],
 [121, 122, 125, 279, 276, 277, 471, 468, 469, 576, 577, 676]],
 [[5, 48, 80, 114, 115, 176, 208, 228, 252, 254, 324, 348, 350, 392, 444, 482, 492, 494, 560, 572],
 [20, 21, 23, 192, 193, 195, 320, 321, 323, 443, 444, 446, 447, 449, 648, 650, 744, 746, 792, 793, 828, 830, 937, 985, 988, 989, 1072, 1073, 1134, 1164],
 [30, 32, 34, 292, 288, 290, 484, 480, 482, 567, 569, 680]],
 [[1, 72, 80, 118, 119, 200, 208, 229, 252, 253, 325, 348, 349, 390, 445, 480, 492, 493, 558, 570],
 [4, 5, 7, 288, 289, 291, 320, 321, 322, 457, 458, 460, 461, 463, 720, 722, 744, 745, 794, 795, 828, 829, 939, 984, 985, 987, 1068, 1069, 1135, 1165],
 [6, 8, 10, 436, 432, 434, 483, 480, 481, 573, 575, 712]],
 [[9, 64, 80, 116, 117, 192, 208, 230, 253, 254, 326, 349, 350, 391, 446, 481, 493, 494, 559, 571],
 [36, 37, 39, 256, 257, 259, 320, 322, 323, 450, 451, 453, 454, 456, 696, 698, 745, 746, 796, 797, 829, 830, 941, 986, 987, 989, 1070, 1071, 1136, 1166],
 [54, 56, 58, 388, 384, 386, 485, 481, 482, 570, 572, 704]],
 [[17, 50, 82, 112, 113, 178, 210, 231, 255, 261, 327, 351, 357, 395, 447, 489, 495, 501, 563, 575],
 [68, 69, 71, 200, 201, 203, 328, 329, 331, 436, 437, 439, 440, 442, 654, 656, 750, 752, 798, 799, 831, 837, 943, 991, 1002, 1003, 1078, 1079, 1137, 1167],
 [102, 104, 106, 304, 300, 302, 496, 492, 494, 564, 566, 682]],
 [[14, 52, 84, 128, 129, 180, 212, 232, 256, 262, 328, 352, 358, 393, 448, 490, 496, 502, 561, 573], 
[56, 57, 59, 208, 209, 211, 336, 337, 339, 492, 493, 495, 496, 498, 660, 662, 756, 758, 800, 801, 832, 838, 945, 993, 1004, 1005, 1074, 1075, 1138, 1168],
 [84, 86, 88, 316, 312, 314, 508, 504, 506, 588, 590, 684]], 
[[22, 54, 86, 136, 137, 182, 214, 233, 257, 263, 329, 353, 359, 394, 449, 491, 497, 503, 562, 574],
 [88, 89, 91, 216, 217, 219, 344, 345, 347, 520, 521, 523, 524, 526, 666, 668, 762, 764, 802, 803, 833, 839, 947, 995, 1006, 1007, 1076, 1077, 1139, 1169],
 [132, 134, 136, 328, 324, 326, 520, 516, 518, 600, 602, 686]],
 [[2, 66, 82, 132, 133, 194, 210, 234, 255, 258, 330, 351, 354, 385, 450, 483, 495, 498, 553, 565],
 [8, 9, 11, 264, 265, 267, 328, 329, 330, 506, 507, 509, 510, 512, 702, 704, 750, 751, 804, 805, 831, 834, 949, 990, 991, 997, 1058, 1059, 1140, 1170],
 [12, 14, 16, 400, 396, 398, 495, 492, 493, 594, 596, 706]],
 [[10, 70, 86, 138, 139, 198, 214, 235, 257, 259, 331, 353, 355, 386, 451, 485, 497, 499, 554, 566],
 [40, 41, 43, 280, 281, 283, 344, 345, 346, 527, 528, 530, 531, 533, 714, 716, 762, 763, 806, 807, 833, 835, 951, 994, 995, 999, 1060, 1061, 1141, 1171],
 [60, 62, 64, 424, 420, 422, 519, 516, 517, 603, 605, 710]],
 [[6, 76, 84, 142, 143, 204, 212, 236, 256, 260, 332, 352, 356, 384, 452, 484, 496, 500, 552, 564],
 [24, 25, 27, 304, 305, 307, 336, 337, 338, 541, 542, 544, 545, 547, 732, 734, 756, 757, 808, 809, 832, 836, 953, 992, 993, 1001, 1056, 1057, 1142, 1172], 
[36, 38, 40, 460, 456, 458, 507, 504, 505, 609, 611, 716]],
 [[13, 74, 82, 134, 135, 202, 210, 237, 258, 261, 333, 354, 357, 388, 453, 486, 498, 501, 556, 568],
 [52, 53, 55, 296, 297, 299, 328, 330, 331, 513, 514, 516, 517, 519, 726, 728, 751, 752, 810, 811, 834, 837, 955, 996, 997, 1003, 1064, 1065, 1143, 1173],
 [78, 80, 82, 448, 444, 446, 497, 493, 494, 597, 599, 714]],
 [[21, 68, 84, 130, 131, 196, 212, 238, 260, 262, 334, 356, 358, 389, 454, 488, 500, 502, 557, 569],
 [84, 85, 87, 272, 273, 275, 336, 338, 339, 499, 500, 502, 503, 505, 708, 710, 757, 758, 812, 813, 836, 838, 957, 1000, 1001, 1005, 1066, 1067, 1144, 1174],
 [126, 128, 130, 412, 408, 410, 509, 505, 506, 591, 593, 708]],
 [[18, 78, 86, 140, 141, 206, 214, 239, 259, 263, 335, 355, 359, 387, 455, 487, 499, 503, 555, 567],
 [72, 73, 75, 312, 313, 315, 344, 346, 347, 534, 535, 537, 538, 540, 738, 740, 763, 764, 814, 815, 835, 839, 959, 998, 999, 1007, 1062, 1063, 1145, 1175], 
[108, 110, 112, 472, 468, 470, 521, 517, 518, 606, 608, 718]],
 [[7, 49, 81, 146, 147, 177, 209, 276, 300, 302, 372, 396, 398, 404, 540, 578, 584, 588, 590, 596],
 [28, 30, 31, 196, 197, 199, 324, 325, 327, 555, 556, 558, 559, 561, 651, 653, 747, 749, 864, 865, 900, 902, 1033, 1081, 1084, 1085, 1096, 1097, 1182, 1194],
 [43, 44, 47, 298, 294, 296, 490, 486, 488, 615, 617, 681]],
 [[3, 73, 81, 150, 151, 201, 209, 277, 300, 301, 373, 396, 397, 402, 541, 576, 582, 588, 589, 594],
 [12, 14, 15, 292, 293, 295, 324, 325, 326, 569, 570, 572, 573, 575, 723, 725, 747, 748, 866, 867, 900, 901, 1035, 1080, 1081, 1083, 1092, 1093, 1183, 1195],
 [19, 20, 23, 442, 438, 440, 489, 486, 487, 621, 623, 713]],
 [[11, 65, 81, 148, 149, 193, 209, 278, 301, 302, 374, 397, 398, 403, 542, 577, 583, 589, 590, 595],
 [44, 46, 47, 260, 261, 263, 324, 326, 327, 562, 563, 565, 566, 568, 699, 701, 748, 749, 868, 869, 901, 902, 1037, 1082, 1083, 1085, 1094, 1095, 1184, 1196],
 [67, 68, 71, 394, 390, 392, 491, 487, 488, 618, 620, 705]],
 [[19, 51, 83, 144, 145, 179, 211, 279, 303, 309, 375, 399, 405, 407, 543, 585, 587, 591, 597, 599],
 [76, 78, 79, 204, 205, 207, 332, 333, 335, 548, 549, 551, 552, 554, 657, 659, 753, 755, 870, 871, 903, 909, 1039, 1087, 1098, 1099, 1102, 1103, 1185, 1197],
 [115, 116, 119, 310, 306, 308, 502, 498, 500, 612, 614, 683]],
 [[15, 53, 85, 144, 145, 181, 213, 280, 304, 310, 376, 400, 405, 406, 544, 585, 586, 592, 597, 598], 
[60, 62, 63, 212, 213, 215, 340, 341, 343, 548, 549, 550, 552, 553, 663, 665, 759, 761, 872, 873, 904, 910, 1041, 1089, 1098, 1099, 1100, 1101, 1186, 1198],
 [91, 92, 95, 322, 318, 320, 514, 510, 512, 612, 613, 685]], 
[[23, 55, 87, 144, 145, 183, 215, 281, 305, 311, 377, 401, 406, 407, 545, 586, 587, 593, 598, 599],
 [92, 94, 95, 220, 221, 223, 348, 349, 351, 548, 550, 551, 553, 554, 669, 671, 765, 767, 874, 875, 905, 911, 1043, 1091, 1100, 1101, 1102, 1103, 1187, 1199],
 [139, 140, 143, 334, 330, 332, 526, 522, 524, 613, 614, 687]],
 [[0, 24, 32, 94, 95, 152, 160, 216, 217, 241, 312, 313, 318, 337, 408, 409, 414, 420, 426, 457],
 [0, 1, 2, 96, 97, 98, 128, 129, 131, 373, 374, 376, 377, 379, 576, 577, 600, 602, 769, 770, 771, 817, 912, 913, 914, 924, 925, 962, 1105, 1116],
 [1, 0, 3, 147, 144, 145, 196, 192, 194, 537, 539, 624]],
 [[8, 24, 40, 92, 93, 152, 168, 217, 218, 242, 313, 314, 319, 338, 409, 410, 415, 421, 427, 458],
 [32, 33, 34, 96, 98, 99, 160, 161, 163, 366, 367, 369, 370, 372, 577, 578, 624, 626, 771, 772, 773, 818, 914, 915, 916, 926, 927, 964, 1106, 1117],
 [49, 48, 51, 149, 145, 146, 244, 240, 242, 534, 536, 626]],
 [[4, 24, 56, 90, 91, 152, 184, 216, 218, 240, 312, 314, 320, 336, 408, 410, 416, 422, 428, 456],
 [16, 17, 18, 96, 97, 99, 224, 225, 227, 359, 360, 362, 363, 365, 576, 578, 672, 674, 768, 769, 773, 816, 912, 916, 917, 928, 929, 960, 1104, 1118],
 [25, 24, 27, 148, 144, 146, 340, 336, 338, 531, 533, 625]], [[0, 26, 42, 92, 93, 154, 170, 219, 222, 246, 313, 315, 318, 342, 409, 411, 414, 421, 423, 462],
 [0, 1, 3, 104, 105, 106, 168, 169, 171, 366, 367, 368, 370, 371, 582, 583, 630, 632, 775, 780, 781, 822, 914, 915, 918, 919, 924, 972, 1105, 1111], 
[4, 0, 2, 159, 156, 157, 256, 252, 254, 534, 535, 630]],
 [[4, 28, 36, 94, 95, 156, 164, 220, 224, 248, 312, 316, 320, 344, 408, 412, 416, 420, 424, 464],
 [16, 17, 19, 112, 113, 114, 144, 145, 147, 373, 374, 375, 377, 378, 588, 589, 612, 614, 777, 784, 785, 824, 912, 913, 920, 921, 928, 976, 1104, 1110],
 [28, 24, 26, 171, 168, 169, 220, 216, 218, 537, 538, 636]],
 [[8, 30, 46, 90, 91, 158, 174, 221, 223, 247, 314, 317, 319, 343, 410, 413, 415, 422, 425, 463],
 [32, 33, 35, 120, 121, 122, 184, 185, 187, 359, 360, 361, 363, 364, 594, 595, 642, 644, 779, 782, 783, 823, 916, 917, 922, 923, 926, 974, 1106, 1112],
 [52, 48, 50, 183, 180, 181, 280, 276, 278, 531, 532, 642]],
 [[12, 26, 34, 94, 95, 154, 162, 222, 225, 249, 316, 318, 321, 345, 412, 414, 417, 424, 426, 465],
 [48, 49, 51, 104, 106, 107, 136, 137, 139, 373, 375, 376, 378, 379, 583, 584, 606, 608, 781, 786, 787, 825, 920, 921, 924, 925, 930, 978, 1108, 1114],
 [76, 72, 74, 161, 157, 158, 208, 204, 206, 538, 539, 632]], [[16, 30, 38, 92, 93, 158, 166, 223, 227, 251, 315, 319, 323, 347, 411, 415, 419, 423, 427, 467],
 [64, 65, 67, 120, 122, 123, 152, 153, 155, 366, 368, 369, 371, 372, 595, 596, 618, 620, 783, 790, 791, 827, 918, 919, 926, 927, 934, 982, 1107, 1113],
 [100, 96, 98, 185, 181, 182, 232, 228, 230, 535, 536, 644]], 
[[20, 28, 44, 90, 91, 156, 172, 224, 226, 250, 317, 320, 322, 346, 413, 416, 418, 425, 428, 466],
 [80, 81, 83, 112, 114, 115, 176, 177, 179, 359, 361, 362, 364, 365, 589, 590, 636, 638, 785, 788, 789, 826, 922, 923, 928, 929, 932, 980, 1109, 1115],
 [124, 120, 122, 173, 169, 170, 268, 264, 266, 532, 533, 638]],
 [[16, 26, 58, 88, 89, 154, 186, 219, 225, 243, 315, 321, 323, 339, 411, 417, 419, 429, 431, 459], 
[64, 65, 66, 104, 105, 107, 232, 233, 235, 352, 353, 355, 356, 358, 582, 584, 678, 680, 774, 775, 787, 819, 918, 930, 931, 934, 935, 966, 1107, 1121],
 [97, 96, 99, 160, 156, 158, 352, 348, 350, 528, 530, 631]],
 [[12, 28, 60, 88, 89, 156, 188, 220, 226, 244, 316, 321, 322, 340, 412, 417, 418, 429, 430, 460], 
[48, 49, 50, 112, 113, 115, 240, 241, 243, 352, 353, 354, 356, 357, 588, 590, 684, 686, 776, 777, 789, 820, 920, 930, 931, 932, 933, 968, 1108, 1119],
 [73, 72, 75, 172, 168, 170, 364, 360, 362, 528, 529, 637]],
 [[20, 30, 62, 88, 89, 158, 190, 221, 227, 245, 317, 322, 323, 341, 413, 418, 419, 430, 431, 461],
 [80, 81, 82, 120, 121, 123, 248, 249, 251, 352, 354, 355, 357, 358, 594, 596, 690, 692, 778, 779, 791, 821, 922, 932, 933, 934, 935, 970, 1109, 1120],
 [121, 120, 123, 184, 180, 182, 376, 372, 374, 529, 530, 643]], 
[[1, 56, 64, 110, 111, 184, 192, 229, 240, 253, 325, 336, 349, 366, 433, 456, 468, 481, 510, 522],
 [4, 5, 6, 224, 226, 227, 256, 258, 259, 429, 431, 432, 434, 435, 673, 674, 697, 698, 794, 795, 816, 829, 938, 960, 961, 986, 1020, 1021, 1123, 1153],
 [6, 7, 9, 341, 337, 338, 389, 385, 386, 562, 563, 689]],
 [[9, 32, 48, 100, 101, 160, 176, 230, 241, 254, 326, 337, 350, 367, 434, 457, 469, 482, 511, 523],
 [36, 37, 38, 128, 130, 131, 192, 194, 195, 394, 396, 397, 399, 400, 601, 602, 649, 650, 796, 797, 817, 830, 940, 962, 963, 988, 1022, 1023, 1124, 1154],
 [54, 55, 57, 197, 193, 194, 293, 289, 290, 547, 548, 649]],
 [[5, 40, 72, 106, 107, 168, 200, 228, 242, 252, 324, 338, 348, 368, 432, 458, 470, 480, 512, 524],
 [20, 21, 22, 160, 162, 163, 288, 290, 291, 415, 417, 418, 420, 421, 625, 626, 721, 722, 792, 793, 818, 828, 936, 964, 965, 984, 1024, 1025, 1122, 1152],
 [30, 31, 33, 245, 241, 242, 437, 433, 434, 556, 557, 665]],
 [[2, 58, 74, 124, 125, 186, 202, 234, 243, 258, 330, 339, 354, 361, 438, 459, 471, 486, 505, 517],
 [8, 9, 10, 232, 234, 235, 296, 298, 299, 478, 480, 481, 483, 484, 679, 680, 727, 728, 804, 805, 819, 834, 948, 966, 967, 996, 1010, 1011, 1128, 1158],
 [12, 13, 15, 353, 349, 350, 449, 445, 446, 583, 584, 693]],
 [[6, 60, 68, 126, 127, 188, 196, 236, 244, 260, 332, 340, 356, 360, 440, 460, 472, 488, 504, 516],
 [24, 25, 26, 240, 242, 243, 272, 274, 275, 485, 487, 488, 490, 491, 685, 686, 709, 710, 808, 809, 820, 836, 952, 968, 969, 1000, 1008, 1009, 1130, 1160],
 [36, 37, 39, 365, 361, 362, 413, 409, 410, 586, 587, 697]],
 [[10, 62, 78, 122, 123, 190, 206, 235, 245, 259, 331, 341, 355, 362, 439, 461, 473, 487, 506, 518],
 [40, 41, 42, 248, 250, 251, 312, 314, 315, 471, 473, 474, 476, 477, 691, 692, 739, 740, 806, 807, 821, 835, 950, 970, 971, 998, 1012, 1013, 1129, 1159], 
[60, 61, 63, 377, 373, 374, 473, 469, 470, 580, 581, 701]], 
[[13, 42, 50, 102, 103, 170, 178, 237, 246, 261, 333, 342, 357, 364, 441, 462, 474, 489, 508, 520],
 [52, 53, 54, 168, 170, 171, 200, 202, 203, 401, 403, 404, 406, 407, 631, 632, 655, 656, 810, 811, 822, 837, 954, 972, 973, 1002, 1016, 1017, 1131, 1161],
 [78, 79, 81, 257, 253, 254, 305, 301, 302, 550, 551, 669]],
 [[18, 46, 54, 108, 109, 174, 182, 239, 247, 263, 335, 343, 359, 363, 443, 463, 475, 491, 507, 519],
 [72, 73, 74, 184, 186, 187, 216, 218, 219, 422, 424, 425, 427, 428, 643, 644, 667, 668, 814, 815, 823, 839, 958, 974, 975, 1006, 1014, 1015, 1133, 1163],
 [108, 109, 111, 281, 277, 278, 329, 325, 326, 559, 560, 677]],
 [[21, 36, 52, 98, 99, 164, 180, 238, 248, 262, 334, 344, 358, 365, 442, 464, 476, 490, 509, 521],
 [84, 85, 86, 144, 146, 147, 208, 210, 211, 387, 389, 390, 392, 393, 613, 614, 661, 662, 812, 813, 824, 838, 956, 976, 977, 1004, 1018, 1019, 1132, 1162],
 [126, 127, 129, 221, 217, 218, 317, 313, 314, 544, 545, 657]],
 [[17, 34, 66, 96, 97, 162, 194, 231, 249, 255, 327, 345, 351, 371, 435, 465, 477, 483, 515, 527],
 [68, 69, 70, 136, 138, 139, 264, 266, 267, 380, 382, 383, 385, 386, 607, 608, 703, 704, 798, 799, 825, 831, 942, 978, 979, 990, 1030, 1031, 1125, 1155],
 [102, 103, 105, 209, 205, 206, 401, 397, 398, 541, 542, 653]], 
[[14, 44, 76, 120, 121, 172, 204, 232, 250, 256, 328, 346, 352, 369, 436, 466, 478, 484, 513, 525],
 [56, 57, 58, 176, 178, 179, 304, 306, 307, 464, 466, 467, 469, 470, 637, 638, 733, 734, 800, 801, 826, 832, 944, 980, 981, 992, 1026, 1027, 1126, 1156],
 [84, 85, 87, 269, 265, 266, 461, 457, 458, 577, 578, 673]], 
[[22, 38, 70, 104, 105, 166, 198, 233, 251, 257, 329, 347, 353, 370, 437, 467, 479, 485, 514, 526], 
[88, 89, 90, 152, 154, 155, 280, 282, 283, 408, 410, 411, 413, 414, 619, 620, 715, 716, 802, 803, 827, 833, 946, 982, 983, 994, 1028, 1029, 1127, 1157],
 [132, 133, 135, 233, 229, 230, 425, 421, 422, 553, 554, 661]],
 [[2, 25, 33, 126, 127, 153, 161, 264, 265, 289, 330, 360, 361, 385, 438, 450, 504, 505, 516, 553],
 [8, 10, 11, 100, 101, 102, 132, 133, 135, 485, 486, 488, 489, 491, 579, 580, 603, 605, 841, 842, 843, 889, 948, 949, 1008, 1009, 1010, 1058, 1128, 1140],
 [17, 13, 14, 153, 150, 151, 202, 198, 200, 585, 587, 627]],
 [[10, 25, 41, 124, 125, 153, 169, 265, 266, 290, 331, 361, 362, 386, 439, 451, 505, 506, 517, 554], 
[40, 42, 43, 100, 102, 103, 164, 165, 167, 478, 479, 481, 482, 484, 580, 581, 627, 629, 843, 844, 845, 890, 950, 951, 1010, 1011, 1012, 1060, 1129, 1141],
 [65, 61, 62, 155, 151, 152, 250, 246, 248, 582, 584, 629]],
 [[6, 25, 57, 122, 123, 153, 185, 264, 266, 288, 332, 360, 362, 384, 440, 452, 504, 506, 518, 552],
 [24, 26, 27, 100, 101, 103, 228, 229, 231, 471, 472, 474, 475, 477, 579, 581, 675, 677, 840, 841, 845, 888, 952, 953, 1008, 1012, 1013, 1056, 1130, 1142],
 [41, 37, 38, 154, 150, 152, 346, 342, 344, 579, 581, 628]],
 [[1, 27, 43, 108, 109, 155, 171, 267, 270, 294, 325, 363, 366, 390, 433, 445, 507, 510, 519, 558],
 [4, 6, 7, 108, 109, 110, 172, 173, 175, 422, 423, 425, 426, 428, 585, 586, 633, 635, 847, 852, 853, 894, 938, 939, 1014, 1015, 1020, 1068, 1123, 1135],
 [11, 7, 8, 165, 162, 163, 262, 258, 260, 558, 560, 633]],
 [[5, 29, 37, 102, 103, 157, 165, 268, 272, 296, 324, 364, 368, 392, 432, 444, 508, 512, 520, 560],
 [20, 22, 23, 116, 117, 118, 148, 149, 151, 401, 402, 404, 405, 407, 591, 592, 615, 617, 849, 856, 857, 896, 936, 937, 1016, 1017, 1024, 1072, 1122, 1134],
 [35, 31, 32, 177, 174, 175, 226, 222, 224, 549, 551, 639]], 
[[9, 31, 47, 98, 99, 159, 175, 269, 271, 295, 326, 365, 367, 391, 434, 446, 509, 511, 521, 559],
 [36, 38, 39, 124, 125, 126, 188, 189, 191, 387, 388, 390, 391, 393, 597, 598, 645, 647, 851, 854, 855, 895, 940, 941, 1018, 1019, 1022, 1070, 1124, 1136],
 [59, 55, 56, 189, 186, 187, 286, 282, 284, 543, 545, 645]],
 [[14, 27, 35, 110, 111, 155, 163, 270, 273, 297, 328, 366, 369, 393, 436, 448, 510, 513, 522, 561],
 [56, 58, 59, 108, 110, 111, 140, 141, 143, 429, 430, 432, 433, 435, 586, 587, 609, 611, 853, 858, 859, 897, 944, 945, 1020, 1021, 1026, 1074, 1126, 1138],
 [89, 85, 86, 167, 163, 164, 214, 210, 212, 561, 563, 635]], 
[[17, 31, 39, 100, 101, 159, 167, 271, 275, 299, 327, 367, 371, 395, 435, 447, 511, 515, 523, 563],
 [68, 70, 71, 124, 126, 127, 156, 157, 159, 394, 395, 397, 398, 400, 598, 599, 621, 623, 855, 862, 863, 899, 942, 943, 1022, 1023, 1030, 1078, 1125, 1137],
 [107, 103, 104, 191, 187, 188, 238, 234, 236, 546, 548, 647]],
 [[22, 29, 45, 106, 107, 157, 173, 272, 274, 298, 329, 368, 370, 394, 437, 449, 512, 514, 524, 562],
 [88, 90, 91, 116, 118, 119, 180, 181, 183, 415, 416, 418, 419, 421, 592, 593, 639, 641, 857, 860, 861, 898, 946, 947, 1024, 1025, 1028, 1076, 1127, 1139],
 [137, 133, 134, 179, 175, 176, 274, 270, 272, 555, 557, 641]], 
[[18, 27, 59, 120, 121, 155, 187, 267, 273, 291, 335, 363, 369, 387, 443, 455, 507, 513, 525, 555], 
[72, 74, 75, 108, 109, 111, 236, 237, 239, 464, 465, 467, 468, 470, 585, 587, 681, 683, 846, 847, 859, 891, 958, 959, 1014, 1026, 1027, 1062, 1133, 1145],
 [113, 109, 110, 166, 162, 164, 358, 354, 356, 576, 578, 634]],
 [[13, 29, 61, 104, 105, 157, 189, 268, 274, 292, 333, 364, 370, 388, 441, 453, 508, 514, 526, 556],
 [52, 54, 55, 116, 117, 119, 244, 245, 247, 408, 409, 411, 412, 414, 591, 593, 687, 689, 848, 849, 861, 892, 954, 955, 1016, 1028, 1029, 1064, 1131, 1143],
 [83, 79, 80, 178, 174, 176, 370, 366, 368, 552, 554, 640]],
 [[21, 31, 63, 96, 97, 159, 191, 269, 275, 293, 334, 365, 371, 389, 442, 454, 509, 515, 527, 557],
 [84, 86, 87, 124, 125, 127, 252, 253, 255, 380, 381, 383, 384, 386, 597, 599, 693, 695, 850, 851, 863, 893, 956, 957, 1018, 1030, 1031, 1066, 1132, 1144],
 [131, 127, 128, 190, 186, 188, 382, 378, 380, 540, 542, 646]],
 [[3, 57, 65, 142, 143, 185, 193, 277, 288, 301, 373, 378, 384, 397, 529, 534, 546, 552, 564, 577], 
[12, 13, 14, 228, 230, 231, 260, 262, 263, 541, 543, 544, 546, 547, 676, 677, 700, 701, 866, 867, 888, 901, 1034, 1044, 1045, 1056, 1057, 1082, 1177, 1188],
 [19, 18, 21, 347, 343, 344, 395, 391, 392, 610, 611, 691]], 
[[11, 33, 49, 132, 133, 161, 177, 278, 289, 302, 374, 379, 385, 398, 530, 535, 547, 553, 565, 578],
 [44, 45, 46, 132, 134, 135, 196, 198, 199, 506, 508, 509, 511, 512, 604, 605, 652, 653, 868, 869, 889, 902, 1036, 1046, 1047, 1058, 1059, 1084, 1178, 1189],
 [67, 66, 69, 203, 199, 200, 299, 295, 296, 595, 596, 651]],
 [[7, 41, 73, 138, 139, 169, 201, 276, 290, 300, 372, 380, 386, 396, 528, 536, 548, 554, 566, 576],
 [28, 29, 30, 164, 166, 167, 292, 294, 295, 527, 529, 530, 532, 533, 628, 629, 724, 725, 864, 865, 890, 900, 1032, 1048, 1049, 1060, 1061, 1080, 1176, 1190],
 [43, 42, 45, 251, 247, 248, 443, 439, 440, 604, 605, 667]],
 [[3, 59, 75, 140, 141, 187, 203, 282, 291, 306, 373, 378, 387, 402, 529, 534, 541, 555, 567, 582],
 [12, 13, 15, 236, 238, 239, 300, 302, 303, 534, 536, 537, 539, 540, 682, 683, 730, 731, 876, 877, 891, 906, 1034, 1035, 1044, 1062, 1063, 1092, 1177, 1183],
 [22, 18, 20, 359, 355, 356, 455, 451, 452, 607, 608, 695]],
 [[7, 61, 69, 134, 135, 189, 197, 284, 292, 308, 372, 380, 388, 404, 528, 536, 540, 556, 568, 584],
 [28, 29, 31, 244, 246, 247, 276, 278, 279, 513, 515, 516, 518, 519, 688, 689, 712, 713, 880, 881, 892, 908, 1032, 1033, 1048, 1064, 1065, 1096, 1176, 1182],
 [46, 42, 44, 371, 367, 368, 419, 415, 416, 598, 599, 699]],
 [[11, 63, 79, 130, 131, 191, 207, 283, 293, 307, 374, 379, 389, 403, 530, 535, 542, 557, 569, 583],
 [44, 45, 47, 252, 254, 255, 316, 318, 319, 499, 501, 502, 504, 505, 694, 695, 742, 743, 878, 879, 893, 907, 1036, 1037, 1046, 1066, 1067, 1094, 1178, 1184],
 [70, 66, 68, 383, 379, 380, 479, 475, 476, 592, 593, 703]], 
[[15, 43, 51, 118, 119, 171, 179, 285, 294, 309, 376, 381, 390, 405, 532, 537, 544, 558, 570, 585],
 [60, 61, 63, 172, 174, 175, 204, 206, 207, 457, 459, 460, 462, 463, 634, 635, 658, 659, 882, 883, 894, 909, 1040, 1041, 1050, 1068, 1069, 1098, 1180, 1186],
 [94, 90, 92, 263, 259, 260, 311, 307, 308, 574, 575, 671]], 
[[19, 47, 55, 116, 117, 175, 183, 287, 295, 311, 375, 383, 391, 407, 531, 539, 543, 559, 571, 587],
 [76, 77, 79, 188, 190, 191, 220, 222, 223, 450, 452, 453, 455, 456, 646, 647, 670, 671, 886, 887, 895, 911, 1038, 1039, 1054, 1070, 1071, 1102, 1179, 1185],
 [118, 114, 116, 287, 283, 284, 335, 331, 332, 571, 572, 679]],
 [[23, 37, 53, 114, 115, 165, 181, 286, 296, 310, 377, 382, 392, 406, 533, 538, 545, 560, 572, 586],
 [92, 93, 95, 148, 150, 151, 212, 214, 215, 443, 445, 446, 448, 449, 616, 617, 664, 665, 884, 885, 896, 910, 1042, 1043, 1052, 1072, 1073, 1100, 1181, 1187],
 [142, 138, 140, 227, 223, 224, 323, 319, 320, 568, 569, 659]],
 [[19, 35, 67, 128, 129, 163, 195, 279, 297, 303, 375, 383, 393, 399, 531, 539, 551, 561, 573, 579], 
[76, 77, 78, 140, 142, 143, 268, 270, 271, 492, 494, 495, 497, 498, 610, 611, 706, 707, 870, 871, 897, 903, 1038, 1054, 1055, 1074, 1075, 1086, 1179, 1193],
 [115, 114, 117, 215, 211, 212, 407, 403, 404, 589, 590, 655]], 
[[15, 45, 77, 136, 137, 173, 205, 280, 298, 304, 376, 381, 394, 400, 532, 537, 549, 562, 574, 580],
 [60, 61, 62, 180, 182, 183, 308, 310, 311, 520, 522, 523, 525, 526, 640, 641, 736, 737, 872, 873, 898, 904, 1040, 1050, 1051, 1076, 1077, 1088, 1180, 1191],
 [91, 90, 93, 275, 271, 272, 467, 463, 464, 601, 602, 675]],
 [[23, 39, 71, 112, 113, 167, 199, 281, 299, 305, 377, 382, 395, 401, 533, 538, 550, 563, 575, 581],
 [92, 93, 94, 156, 158, 159, 284, 286, 287, 436, 438, 439, 441, 442, 622, 623, 718, 719, 874, 875, 899, 905, 1042, 1052, 1053, 1078, 1079, 1090, 1181, 1192],
 [139, 138, 141, 239, 235, 236, 431, 427, 428, 565, 566, 663]]]
 

です。間違ってはいないと思います。これでやっと直投影の点心、線心、面心、胞心のベクトルが計算できる様になりましたし、
買い集めた４次元正多胞体の参考書達をよむ準備が整いました。
インターネットで見かける投影図を得るためには、直投影（正投影・平行投影）だけでなく、中心投影（透視図）も描けるプログラムを作る必要があります。






























切断面の図も多様ですが投影図も多様です。中村義作著「四次元の幾何学　不思議な図形の世界をのぞく」BLUE BACKS や
宮崎興二・石原慶一著「４次元グラフィックス　高次元 CG への道」が出版されてから既に40年近く経ち、
我々貧乏人でもこの様な事がやっと出来るようになりましたが、
この様な我々凡人でも出来ることは、既に誰かがやって公開しているかも知れませんがすべてのパターンを調べて見るのも面白い幾何学的なパズルです。
更に、tkinter と pyopengl を同時に使う時のプログラミングに何か問題があるみたいで、結果オーライでやって来ましたが、複雑な処理をすると
奇妙な振る舞いをするので、対策を講じる必要があります。兎も角、基本的な準備は出来たので後はボチボチ他の趣味の本も読みながらやっていきます。
処で、本来学びたかった高次元タイリングの射影から作られるタイリングは大分前に購入した Michael Baake and Uwe Grimm 著「APERIODIC ORDER」に
詳しい解説があるので、
（「As early as 1982, and independently and independently of the experimental discovery, Peter Kramer from Tubingen constructed a cell model 
with icosahedral symmetry [Kra82] based on ideas from group theory and projections from cells in higher dimensions. 
This was followed by a projection model from 6-space in 1984, developed jointly with his student Roberto Nevi [KN84].」
また、本の裏には
「Quasicrystals are non-periodic solids that were discovered in 1982 by Dan Shechtman, Nobel Prize Laureate in Chemistry 2011.
The underlying mathematics, known as the theory of Aperiodic Order, is the subject of this comprehensive multi-vplume series.
This first volume provides a graduate-level introduction to the many facets of this relatively new area of mathematics.
Special attention is given to methods from algebra, discrete geometry and harmonic analysis, while the main focus is on topics 
motivated by physics and crystallography. In particular, the authors provide a systematic exposition of the mathematical theory 
of kinematic diffraction.」
と書いているので、４０年ぐらい前の事みたいです。宮崎興二・石原慶一著「４次元グラフィックス　高次元 CG への道」が出版されたのが
１９８９年ですからそれからすぐに出版されています。）
矢張り、キチンと理解するには詳しい解説のあるこの本を読む必要があります。
一様、数学の本にみたいですが、勉強したことの無い数学の基本的な知識がないと歯がたたない分野みたいで、
それも解説してくれている唯一持っているこの本（２０１３年出版で、
高次元のセルのタイリングを cut and project （切断と投影：単体に対する基本的なプログラムは上で作りました）に依る Penrose tiling に代表される
２次元や３次元の aperiodic tiling 作成の技法や関連する科学技術とそれを理解するために必要な数学の基礎知識を整理してくれています）
を読む必要があります。厚い英語の本２冊なのでじっくり時間を掛けて読む必要があります。
魅惑的な図が沢山載っていますがキチンと理解するには、暫くは、プログラミングではなく、基礎になっている数学そのものの勉強が必要です。
Volume I : A Mathematical Ivitation のしょぱなからスラスラ読めなければ、もう消しましたが、E. ハイラー/ G. ワナー著　蟹江幸博訳「解析教程上下」を
解析の歴史をパソコンで一つ一つ確かめながら読んで見ると良いです。基本から順番に学べば、本当に理解したければ、
時間は掛かりますが、数学は誰でも理解できます。そうは言っても大学院レベルのこの本は行ったり来たり何度も読み返さないと理解できそうにありません。

又、人間は具体的な例によって理解します。例えば、
$$ A point set \Lambda \subset R^d has finite local complexity (FLC) with respect to translations when the collection 
\{ (t+K) \cap \Lambda | t \in R^d \}, for any given compact K \subset R^d, contains only finitely many cluster up to translations. $$
の様な抽象的な定義の記述では我々凡人は何を言っているのか理解するのは難しいです。
理解するには、この後に書いている1次元の例
$$ \Lambda = - N \cap \{0\} \cap \sqrt{2} N $$
を調べれば、段々何を言っているか・何をやろうとしているか理解できるようになります。少し先まで読んで見れば理解できることもあります。
又、キチンとチェックしておかないとモヤモヤが残るので、例えば、
$$ \Lambda - \Lambda = \{ m + n \sqrt{2} | m, n \in Z and mn \geq 0 \} $$
の証明はどの様にすれば良いかと言った基本的なことは繰り返しやって身につけている必要があります。
この本の定義や定理が実際に必要になるまで兎も角字面だけ読んでいき、tiling の理解に必要になれば最初から読み直せば何とかなるのではと思います。
私には非常に難解な本です。即ち、何の為に必要か不明な定義や定理が続きますが、多分、年を取ったせいで何も考えず只管根を詰めて読んでいくのが辛くなり、
読むだけは読んでおいて、それらが必要な具体的な例が現れてから読み返します。我慢しt読んでいくと抽象的な話でなく Voronoi 図や正多面体の対称群などの
良く知っている具体的な話になります。壁紙群の様な整然とした理論から外れた概念を解説しようとしているので、単純な群論の知識だけでなく、
Coxeter group など学んだことの無い色々な知識が必要になり、それらを拡張するために必要な抽象的な概念を始めに先ず解説していますが、
年を取ると何でそんなことがいるのかとか余計なことを考えますが、適当に読んでいくと段々具体的な話になってきて、
すぐに理解できる話が多くなります。それらを拡張する話で初めの方に解説していることが必要になれば、始めの方の抽象的な定義や定理を読み直せば良いです。
最も若い人達は何も考えずに最初から読んでいけると思います。古い知識が新しいことを学ぶ障害になる事もあります。多分。

しかし、老人も「読むだけは読んでおいて、それらが必要な具体的な例が現れてから読み返します。」では、読むのが辛くなり止めてしまいます。

FLC の具体的な例： $$ \Lambda = - N \cap \{0\} \cap \sqrt{2} N $$ 
（この場合は、１とルート２の移動と言う二つの平行移動（併進）を考えれば良い）だけでなく、FLC の定義の直後に

Later, we will also consider FLC up to Euclidean motions, which is useful for systems such as the pinwheel tiling of Figure 6.33.

と書いているので、CHAPTER 6 Inflation Tilings の図を眺め、6.6 Pinwheel tilings の前半に書いていることと Figure 6.33.を少しを調べれば、
段々何を言っているか・何をやろうとしているか理解できるようになります。この様に飛ばして、少し先を読んで見れば理解できることもあります。
何でも知っている先生がいなくて、しかも、小説や映画では良くあるそれぞれ専門分野・能力の異なる３人が協力して危機を乗り切る事が出来るような
共に学ぶ朋友もいなくて、（数学は個人経営の家内手工業・零細企業みたいな側面が多いので）、一人、独学で数学の参考書を読むときは、この様に、
工夫が必要ですが、基本的には、最初から一行一行、行間を埋めながら読むことが結局、早道です。多分。

また、２２ページからの 2.3. Groups の様なサラーと書いてあるような解説はチャンと理解しようと思えばパソコンを使えば出来るハズですし、
参考文献の H.S.M.コクセター著「正多胞体」(これは高価ですが、H.S.M.Coxeter著「Regular Polytopes」は Dover 本だから円安の今でも翻訳の3分の１で購入できます。)
は持っているので時間を掛けて理解するようにしないと本当に訳が分からなくなります。
例えば、一松信著「高次元の正多面体」に書いてある






の様な正多面体の包含関係も現在は我々貧乏人の安価なパソコンでも簡単に確かめることが出来るので一つ一つプログラミングして確かめます。
更に、 H.S.M.コクセター著「正多胞体」の第３節　準正多面体より
























は「立方体の中接球」と「同じ中接球を持つ正4面体と正4面体の内部に出来る正８面体」と「同じ中接球を持つ立方体と正8面体の内部に出来る立方８面体」と
「同じ中接球を持つ正12面体と正20面体の内部に出来る12・20面体」を描画しています。思い通りの図が回転しだすと嬉しいものです。
色々やってみると今までのプログラムでは立方８面体の面を求める事が出来ないことが分かり、プログラムの改良が必要になり、勉強になります。
最終的には、下手糞なプログラムですが

    def firstP(self, e1, e2):
        if (e1[0] >= 0 and e1[1] >= 0):
            if (e2[0] >= 0 and e2[1] >= 0):
                if e1[0] > e2[0]:
                    return True
                else:
                    return False
            else:
                return True
        elif (e1[0] < 0 and e1[1] >= 0):
            if (e2[0] >= 0 and e2[1] >= 0):
                return False
            elif (e2[0] < 0 and e2[1] >= 0):
                if e1[0] > e2[0]:
                    return True
                else:
                    return False
            else:
                return True
        elif (e1[0] < 0 and e1[1] < 0):
            if (e2[0] >= 0 and e2[1] >= 0):
                return False
            elif (e2[0] < 0 and e2[1] >= 0):
                return False
            elif (e2[0] < 0 and e2[1] < 0):
                if e1[0] < e2[0]:
                    return True
                else:
                    return False
            else:
                return True
        else:
            if (e2[0] >= 0 and e2[1] >= 0):
                return False
            elif (e2[0] < 0 and e2[1] >= 0):
                return False
            elif (e2[0] < 0 and e2[1] < 0):
                return False
            else:
                if e1[0] < e2[0]:
                    return True
                else:
                    return False

    def get_cyclic_pair(self, e_list, v):
        print('### e_list=', e_list)
        print('v=', v)
        
        a1 = self.v[self.e[e_list[0]][0]][0]
        a2 = self.v[self.e[e_list[0]][1]][0]
        b1 = self.v[self.e[e_list[1]][0]][0]
        b2 = self.v[self.e[e_list[1]][1]][0]
        if self.same_vectorP(a1, v):
            e1 = np.array(a2) - np.array(a1)
        else:
            e1 = np.array(a1) - np.array(a2)
        if self.same_vectorP(b1, v):
            e2 = np.array(b2) - np.array(b1)
        else:
            e2 = np.array(b1) - np.array(b2)
        cross = np.cross(e1, e2)
        n = (1/np.sqrt(np.dot(cross, cross))) * cross
        space = Space(self.dim, n)
        x = space.x
        y = space.y
        v_list = []
        ind = 0
        for e in e_list:
            a1 = self.v[self.e[e][0]][0]
            a2 = self.v[self.e[e][1]][0]
            if self.same_vectorP(a1, v):
                e1 = np.array(a2) - np.array(a1)
            else:
                e1 = np.array(a1) - np.array(a2)
            V = np.array([np.dot(x, e1), np.dot(y, e1)])
            V = (1/np.sqrt(np.dot(V, V)))*V
            v_list.append([e_list[ind], V])
            ind = ind+1
        print('#### len(v_list)=', len(v_list))
        print('v_list=', v_list)
        for k in range(len(v_list)):
            for i in range(k+1, len(v_list)):
                if self.firstP(v_list[i][1], v_list[k][1]):
                    temp = v_list[k]
                    v_list[k] = v_list[i]
                    v_list[i] = temp
        result2 = []
        for k in range(len(v_list)):
            if k < len(v_list)-1:
                if v_list[k][0] < v_list[k+1][0]:
                    result2.append([v_list[k][0], v_list[k+1][0]])
                else:
                    result2.append([v_list[k+1][0], v_list[k][0]])
            else:
                if v_list[k][0] < v_list[0][0]:
                    result2.append([v_list[k][0], v_list[0][0]])
                else:
                    result2.append([v_list[0][0], v_list[k][0]])
        return result2


とすることで、一般的に３次元の凸多面体に関して、どの辺のペアに対して、面を調べるべきかを決定することが出来るアルゴリズムを見つけることが出来ました。

更に、昔から私が使っていたものと異なり、一松信著「高次元の正多面体」の２～３ページで与えている正多面体の座標達を使ってこれらのプログラムを
書いてみたので、それらがどの様なものか理解できます。

更に、その後、「これまでに出てきた正８面体、立方８面体、１２・２０面体の模型を観察すれば、それぞれにおいて、何枚かづつの正方形、正６角形、
正１０角形状の赤道多角形(equatorial polygon)で構成されることがわかる。これらの多角形は各多面体の中心を通る平面上にあり、
外接球面上の大円に内接する。」とコクセターさんが書いてあるので、我々凡人は「ストローの模型」を作り、観察し、
赤道多角形達を描くコンピュータグラフィックスをプログラミングしてみます。






優秀な人は例えば一松信著「正多面体を解く」の４９ページの図を眺めると理解すると思いますが我々凡人はコクセターさんが書いている様に
正８面体、立方８面体、１２・２０面体の模型を作り、くるくる回転しながら観察すれば次の図が誰でも見えてきます。
（大事なのは一松信さんはこの図をどうやって描いたのだろうと考えることです。）


















回転している動画で見ると綺麗ですが、静止画ではどうの様な図か残念ながら分かりにくいです。
赤道多角形を opengl の GL_POLYGON で描画するには頂点を綺麗に循環的に並べる必要がありますが、「ストローの模型」を眺めると誰でも分かるように
正８面体、立方８面体、１２・２０面体の隣接関係の情報をパソコンに計算させておけば容易に出来ますが、上に述べたアルゴリズムを使う事も出来ます。
暇ならこの赤道多角形を組み合わせた紙の模型も作ってみると良いです。
この後の2.33及び2.34の公式は理解できますが、図2.3Bの解説が我々凡人には難解です。
一松信著「正多面体を解く」の「ペトリー多角形」ページ４４～４９も併せて読んで見ると良いです。
まだ、このグラフの具体的な式は何だろう（1.72, 2.33, 2.34 から h, N1 を消去した式を求めるだけですが。
二つに分岐すると書いてあります。これは簡単だろうか？どちらの本にも何で答えを書いていないんだろう？）と言う疑問・モヤモヤは残りますが。
解析が苦手なので、直ぐには分かりませんが、我々凡人には、コンピュータで数値計算してグラフを描いてみるしか手はないみたいです。大変です。

本は特別な目的がなければ、皆が読んでいるからでなく、読んで楽しいものを読めばいいです。例えば、ラテン語さん著「世界はラテン語でできている」を
読んで、ラテン語に興味を持ったら、或いは、辞書に載っている英語の語源のラテン語をチャンと知りたいと思ったら、ラテン語の参考書は沢山ありますが、
有田潤著「初級ラテン語入門」の様な薄い簡単な事だけ書いてあるパズル感覚で読める本から
読み始めると私の様な飽きっぽい人間でも暫くは読むことが出来ます。最後まで読み終えることが出来るかどうかは分かりませんが、今の処、面白いです。
辞書は持ってなくても巻末に単語集がありますが、Pocket Oxfprd Latin Dictionary なら円安の今でも「羅和辞典」より遥かに安価で購入できます。
ラテン語は一般に難しいとされていますが、どの外国語も難しく、特に、思い出したら勉強しているロシア語やアラビア語もラテン語同様私には難しいです。
山下太郎著「しっかり学ぶ初級ラテン語」には「本書が想定するラテン語の学習法を述べます。
それは、教科書を広げ、(1)変化表を暗記し、(2)例文の文法的説明を理解し、(3)日本語訳から元の例文が再現できるまで練習を繰り返すことです。」
と書いてありますが、具体的にどの様にすれば暗記できるか書いていないと思いますが、
最近見つけた茂木健一郎さんの「鶴の恩返し勉強法」が具体的な暗記法を解説してくれていて面白いです。実行はやっぱり私の様なずぼらら人間には難しいですが。

エヌビディアの時価２兆ドルを超えたとかで、株価の急騰が続いていますが、生成人工知能（将棋や囲碁などの人工知能全般も同様です）を勉強するには
エヌビディアの主力製品の画像処理半導体(GPU)を備えたコンピューターが必要で、（文部省は地方国立大学ではそのような研究を困難にしたいのか、
自由に使える大学交付金を大幅に削減し続けて、東京と地方の大学間格差の拡大に躍起になっているいます。多分、それが自分の出世と天下りに必要なのでしょう）、
私は GPU 付きのパソコンを持っていませんが、
かなり高額ですが、東京育ちばかりの政府・政治家・官僚が完全無視している地方在住の若い人達でも何とか工面・工夫して最先端を目指すべきです。多分。


頑張って正２４胞体の「ストローの模型」を作ってみようか？正２４胞体の投影図を見ながら、正８面体を探して、やってみます。
途中まで作り訳が分からなくなり、ばらして作り直しています。今度は少しは賢くなって、工夫して
投影図の次に取り付ける正８面体を色鉛筆やカラー水性ペンで塗分け、「ストローの模型」の取り付ける正三角形などに針金を目印に通して、
少し小さい「ストローの模型」の正８面体をあてがってどの様に稜（辺）を作って行けば良いか慎重に調べて作っていきます。
どの稜（辺）の長さが一定で良いのか、どの稜（辺）の長さを変えるべきか、も分かりませんが、作成マニュアルを持っていないので試行錯誤で作っていきすま。
出来上がると良いですが。やったことの無いことをしているので、神経を使い結構難解な幾何学的なパズルです。
先ずは幾何学的に美しい模型でなくとも良いので位相幾何学的に正しい模型を目指します。
しかし、正８面体を5個取り付けた処で挫折しました。紙に印刷した射影図から作った作りかけの模型がイメージ出来ません。
この方法で正２４胞体の「ストローの模型」を作ることは私には出来そうにありません。
しかし、固定した同じ長さのストローの正8面体で作れるところまで作ってみる価値はありそうです。何個まで取り付けることが出来るか？
それを元に「正２４胞体の展開図」の「ストローの模型」を作る事ができるかも？
横道に逸れて、先ず、「正５胞体、正８胞体、正１６胞体の展開図」の「ストローの模型」を作ってみます。「立方体の展開図」の見つけ方の「類比」ですが、
（何を言っているかと言うと「立方体の各面の周りの辺に番号を振り、面をバラバラにし、平面上で辺の番号が一致するように面をくっ付ければ展開図が作れます」が、
同様に「正８胞体の各胞の周りの正方形に番号を振り、胞をバラバラにし、３次元空間で元の様に番号の同じ正方形を一致させ胞をつっ付けていけば展開図が作れます」）、
中村義作著「四次元の幾何学　不思議な図形の世界をのぞく」BLUE BACKS で「超直方体」と「超４面体」の「展開図」を解説してくれています。
更に、「興味ある読者は、超直方体や超４面体の展開図を数え上げてみるとよい。これによって、４次元図形のイメージがかなりつかめるようになることは
疑いない。」と書いています。これは、「立方体の展開図」をすべて数え上げるプログラムと同様なプログラムを作る事により可能で難しくはないはずです。
「立方体の展開図」をすべて数え上げることは、「やり方・考え方を教えれば」、小学生でも手作業で全部見つけ出します。
ここまで書いてきて気が付いたことですが、凡人は凡人らしく、正２４胞体の「ストローの模型」も見栄を張らず、正８面体の紙の模型を２４個作り、
それぞれの面と辺と頂点に、正２４胞体の投影図を見ながら一連の番号を振り（上で正２４胞体の頂点、辺、面、胞の隣接関係の情報を得たので、
それを使えば、正２４胞体の投影図を見ながらより正確に・確実に正８面体の紙の模型２４個それぞれの面と辺と頂点に一連番号を振ることが出来ます）、
紙の模型を番号に合わせて貼り付けながら、「ストローの模型」も作っていくべきでした。そうすれば正２４胞体の模型と展開図を我々凡人でも自力で作れるはずです。
バッハの演奏で有名な女流ピアニストも子供の頃、複雑なバッハの楽譜の旋律ごとに色鉛筆で塗分け、勉強したとテレビで話していました。
才能ある優秀な人達も工夫して学んでいるので、我々凡人は尚更、見栄を張らず、才能ある優秀な人達の様にじっと眺めていてもどうすれば良いか分かりませんから、






正5胞体、正８胞体、正１６胞体、正２４胞体の展開図を上に提示している「頂点、辺、面、胞の隣接関係の表」を見ながら、正多面体の紙の模型の各面に
頂点、辺、面の番号を書き込み、紙の模型の同じ番号の面を張り合わせて作ったものです。張り合わせる面には、「時計回り」と「反時計回り」の
対になるように番号を振らなければ上手くいきません。
何を言っているかと言うと「立方体」の展開図を作る時に、「立方体」の紙の模型で、頂点、辺、面の一連番号を各面に振って、面をバラバラにし、
平面上で面を貼り付ければ、立方体の展開図が得られるように、「正多胞体」の各正多面体に頂点、辺、面、多面体の一連番号を各多面体に振って、
多面体ををバラバラにし、それらの多面体を番号が一致するように張り合わせれば正多胞体の展開図が出来上がります。これが「類比」です。
その時、張り合わせる面には、「時計回り」と「反時計回り」の対になるように番号が振られているハズです。
カメラをパソコンに何日も繋ぎぱなっしにしていて、レンズが駄目になり、
v1 は製造中止なので修理できないと言われました。なんかのひょうしに１，２枚撮影することが出来ますが大失態で大損です。
幸い中古のレンズを手に入れる事が出来ました。中国製のホワイトのレンズで大丈夫かと思いましたがチャンと撮影できます
本体から買い替えるのは年金生活者には負担が大きく、助かりました。現役の時購入した大きい一眼レフカメラも幾つか持っていますし、
多分、まだ使えるコンパクトカメラも色々な種類のが沢山ありますが、
ちょこちょここの様なものを撮影するには小さいミラーレス一眼カメラの方が手軽で高性能で便利です。スマホのカメラは使っていません。
手作業でやったことを整理してパソコンに教えることが出来れば、すべての展開図を求めることや残りの正１２０胞体、正６００胞体の展開図を求めることも
可能になります。但し、正４面体や正８面体や正１２面体は空間充しん形ではないので、
部分展開図などが合同かどうか判定する上手いアルゴリズムを考える必要があります。
又、正８胞体と正２４胞体の展開図を手作業で作るときも各多面体の各面に頂点、辺、面の番号を振る時にやり方を変えました。
実際にやってみないと分からないことが一杯あります。
正６００胞体と正１２０胞体の展開図も頂点、辺、面、多面体の隣接関係を上で計算したので、芸術家の様な根気があれば作れます。
多人数で分担するには、各胞の面の頂点の並びを「時計回り」と「反時計回り」の対にする必要があり、仕事の振り分けが厄介です。
これは、上の頂点、辺、面、多面体の隣接関係のデータから、各多面体の頂点、辺、面の番号を取り出すようにプログラミングすれば、
問題は解決します。何を言っているかと言うと面や多面体を構成する頂点、辺、面達を「単なる集合」としてではなく、
「それぞれの繋がり方も考慮した構造」を計算して表示するようにプログラミングすれば、楽に正多胞体の展開図を作ることが出来ます。
直ぐに駄目だと結論を出さずに少し時間をおいて考えてみれば良いです。良い考えが浮かぶこともあります。
兎も角、手作業で一度やってみれば、何をしなければいけないか理解できます。我々凡人が頭の中だけで考えても時間の無駄です。
時間と手間が掛かりますが、基本に忠実に確実な方法で理解しようとしないと駄目です。
又、上でリストのリスト temp_F にリスト f_list が含まれているかを調べるのに

    def new_f_listP(self, temp_F, f_list):
        perm = self.get_perm(f_list)
        for P in perm:
            if P in temp_F:
                return False
        return True


を使いましたが、リスト f_list の要素数が多いと順列の個数は指数関数的に増大するので時間が掛かります。
次の様にリストのリスト temp_F にリスト f_list をソート（要素を小さい順に並び変えた）したものを保存して置けば、

    def new_f_listP(self, temp_F, f_list):
        C = sorted(c_list)
        if C in temp_C:
                return False
        return True


で素早く判定できます。しかし、例えば、正８面体の頂点たちを見つけた順に、上の頂点、中間の頂点４個、下の頂点の順に並べておけば、
上の展開図を作る時に素早く番号を振ることが出来ます。まあ、後で正８面体の頂点たちを並べ替えるプログラムを作れば良いだけですが。
データを使うまで、何が必要になるか前もって我々凡人には分かりませんが。


一方、正２４胞体の２４個の胞：正八面体を見つける特別なプログラムを作り、３次元の射影を回転させながら、それぞれの胞：正八面体が
どの様に配置されているか目で見えるようにしないと私には正２４胞体の「ストローの模型」は作れそうにありません。時間が掛かります。
正１２０胞体・正６００胞体は更に複雑で、この４次元の分野もそんなに甘い世界ではありません。


上の展開図は４次元では残りの面の対を張り合わすことが出来て、元の正多胞体になりますが、我々３次元に住んでいる人間にはそんなことは
出来ません。しかし、材料が紙でなく、伸び縮みする材料で出来ていれば３次元空間で強引に残りの面の対を張り合わすことで元の正多胞体の
３次元の模型を作れるはずです。写真で見るような模型はどの様にして作ったか知りませんが、暇なら挑戦してみて下さい。
「ストローの模型」をストローの長さを変えながら作り変えていけば、大変困難な作業だとは思いますが、多分、出来ると思います。



中途半端な理解でなく、ちゃんと理解するために、中村義作著「四次元の幾何学　不思議な図形の世界をのぞく」BLUE BACKS で解説されている
単純な多胞体から順番に胞がどの様に配置しているか、我々凡人でも理解できる描画をしてくれるプログラムを作ってみる必要があります。
即ち、上のパソコンの打ち出すデータを分り易く図解してくれるプログラムが私にも作れるなら作ってみたいです。
出来るかどうか分かりませんが。書籍では、２次元の射影図（遠近図法と言う技術もありますが）しか描画出来ませんが、
又、「3D ホログラム」と言う技術も開発されていますが、そんな高価な機器を使うものでなくても、
安価なパソコンで、３次元の座標のデータがあれば、射影図を回転する事で３次元の姿が我々凡人にも見えるように出来る可能性があります。
更に、参考書に載っている２重対称軸、３重対称軸、５重対称軸は具体的にどのベクトルの方向か調べる必要があります。
これらと直投影の点心、線心、面心、胞心との関係は何か？知らないことだらけなので、実験して、調べなければならないことが一杯あります。
「数学」と「プログラミング」は遺伝に関係なく、優れた参考書を時間を掛けて、暗記ではなく、この様に順番に理解していけば、誰でも出来ます。
勿論、これは時間が限られている大学受験などの準備には通用しない主張だと思いますが、大学受験だけで人生が決まる訳ではなく、
それからの人生が長いです。独学でも大学受験の失敗を取り返している人達が世の中には星の数ほどいます。
（但し、これは以外に厄介で、面の情報の改良と胞の情報を得るまで、Knuth さんはプロは一日に５００行のプログラムを作ると言うのに
コンピュータが何をしているか知るための最終的には不要な print 関数がある僅か３９１行のこのプログラムを作るのに２日強掛かりました。
夜中の３時までやって、バグは無いと思いますが？
今、イギリスで富士通の子会社が提供したソフトを巡って、英国史上最大の冤罪事件が起きたと大問題になっていますが、プログラミングは結構大変です。）、
経営者が言うように「コードを書くことは単純作業である」とは到底思えません。コスト削減の為に、非正規の派遣社員に低賃金で働かせば良いと思っています。
ある政治家も「国民全員を食べらすことは出来ないから、低賃金で我慢してもらう国民も必要だ」と受け取れる発言を国会質疑で発言していました。
お金が第一で、自分だけが儲ければ良いと、人間を消耗品扱いする大企業の経営者・政治家・官僚ばかりの世の中になってしまった様に思います。
AI がこの様なプログラムを瞬時に作ってくれる時代が近づいているのでしょうか？


私の学生時代は、「ユークリッド幾何学の難しいことをやっても評価されない」から、
「皆がやっている最前線の難しい現代的な数学を研究しないといけない」と言われていましたが、
「高次元ユークリッド幾何学」の分野もそれなりに難しく、不思議な絵が描け、楽しい分野です。勿論、本で解説されている事は既に数学的には解決している事で、
単なる道楽・暇つぶしだと言えるとは思いますが、数学教育の材料・教材としては貴重な分野だと思います。
結晶学などに重要な応用があり、数学者より著名な物理学者や化学者が研究してきた数学の分野です。ちなみに昔は数学者と物理学者は同一人物でした。
現在は安価なパソコンで誰でも楽しめる数学の分野になっています。誰の言葉か忘れましたが、「勉強ではなく、学問をせよ！」です。
国語教育で有名な大村はまさんのやっていたことも「勉強ではなく、学問をせよ！」と生徒達に教えていたと思います。
囲碁や将棋も手が全然読めなくなっているし、読みかけの「The Girl with the Dragon Tattoo」も読む時間がありません。
外国語も本箱で埃を被っていた池田修著「アラビア語入門」みたいな昔の岩波書店の参考書達の方が昭和の人間の私にはあっているみたいです。
最近、机の上で使うために「ヒバ」の９路盤・13路盤を手に入れましたが、「ヒバ」が中学生の時、担任の先生が話していた「あすなろ」だったとは。
碁盤や将棋盤は「カヤ」が有名で、柾目盤などはびっくりするほど高額ですが、高知市にも全国的に知られた碁盤店があり、100年先、200年先を見据えて
カヤの植林もしています。高知の囲碁界では一番強く有名であった中国人が店番もして、強くもないのに定年退職記念にその人から
一番安い「カヤ」の碁盤を普通通販なのに、店にわざわざ来てくれたからと安くしてもらって購入しましたが、その人は中国に帰国しました。
私の碁盤が部屋の隅で泣いています。
能登の「ヒバ」も有名で、輪島塗の材料でもあるそうです。暫くお休みです。
ブックオフの入口の目に付く棚に渡辺京二著「逝きし世の面影」平凡社があり、なんとなく手に取ると面白そうな本なので購入しました。
普段なら絶対読まない本のカテゴリーに属する本ですが、ちょっと読んで見ると面白い本です。
最近、和歌（小説と違い短いのが良いです。高校の詩人でもある現代国語の先生は俳句や短歌より詩の方が文学として高く評価されると言っていたと思いますが。
私の生まれた小さな集落の一つか二つ年下の知人は多分年取ってから短歌や俳句に楽しさ・才能を見出し、良く高知新聞の短歌の欄に作品が載っています。）や
歴史の本が面白いです。平田雅博著「英語の帝国　ある島国の言語の１５００年史」講談社選書メチエもブックオフで見つけました。
帯びに、「イングランドから大英帝国へ、そして日本へ。いかに世界を征服したか？文明化の使命を担い、教養と出世をもたらす言語ー
熱望したのは、いつも」「親たち」だった！」と刺激的なキャッチコピーが書いてあります。
私達の世代は高校で一様、日本史も世界史も地理も政経も倫理もすべて必修科目でしたが、イギリスがどんな国なのかも全然分かっていませんでした。
面白い本です。フランス語が勢力を伸ばしたのも同じような歴史を辿ったのでしょうか？知らないことが多すぎます。
同い年のタレントさんが階段を昇れなくなったと報道されるようになりましたが、歩けなくなると大変だと今まで良く行っていた弥右衛門公園から更に
足を伸ばし、かなり急な陸橋を歩いてブックオフまで歩いています。ブックオフは私にとっては宝の山です。読もうと思う本が積みあがるだけですが。
最近は大谷選手のトレーニングの様子が連日テレビで放映されています。車の運転をしながら聴いていたラジオで「筋トレ」の専門家が話をしていて、
メインはスポーツ選手の筋トレの話ですが、老人の歩行の話にも触れていて、足の筋肉を付けるには「背伸びの運動」だけで良く、背伸びをする時、
人は無意識に小指の側に体重をかけている。それは親指の側に体重をかけるときついからである。これは力学（てこの原理）で説明できるそうです。
老人が歩き続ける為には負荷のかかる親指に体重をかける背伸びをして、筋肉を維持することが大事だそうです。人は、皆、学校で習うことは
実生活では役に立たないと声高に言いますが、
特別な専門職に就く人たちばかりでなく一般の人たちにも役に立つのにその使い方・役立て方を単に知らないだけだと教えられました。
又、ペットボトルのブラックコーヒーを年のせいか、病気では無いと思いますが、急にキツイと感じるようになりました。手間は掛かりますが、
通販で手に入れた生豆をタマゴ焼き用のフライパンと最近見かけなくなった電気コンロで焙煎し、
当然ムラのある焙煎になりますが、サイフォンで入れて飲む回数を増やしています。これは贅沢をしたくてしているいる訳ではなく、
若者で溢れているスターバックスで飲むコーヒーの多分二十分の一位で済むので経済的です。


今日：３月１日近くの公園で面白いものを見ました。夕方の散歩の帰路の途中で、近くの公園の外の歩道のベンチに腰を降ろすと
公園のブランコの一方の鎖が短くなっていて、何が起こったんだろうと見ていると、小学低学年だと思われる女の子（多分次女）が乗って遊んでいましたが、
飛び降りた後、自力では乗れなくなって、もう一人の少し背の高い多分年長の女の子（多分長女）が手伝って載せようと手で足を支えたり色々するが
乗せることができず、最後は両手を地面について、背中を踏み台にして乗せました。自力では漕ぐことが出来ず、押してやっていました。
多分三女だと思う女の子も近くで遊んでいて二人の面倒を見ていました。最後、どうするだろうと思って見ていると
感心なことに、腰を掛ける板をくるくる回転させて短くしていたブランコを元の状態に次女だと思う女の子が戻してから帰っていきました。
子供は教えなくても遊びを工夫します。多分。


今日：3月4日の高知新聞に「地方女子　地元進学指向強く」昨年、東京大学の学生が行った調査では「女子は地元（で進学）」との意識の根強さも浮かんだ。
「地方女子」を阻むハードルとは？との記事が出ていましたが、人間の評価を大学に合格できる能力と言う一つの指標だけで評価する一面的な記事だと思います。
東京大学に合格できた人間だけが偉いと言う傲慢さが表現されています。東京大学は他の国立大学に比べ卒業生も多いので、活躍している人も多いですが、
世の中には音楽・美術など芸術やスポーツや農業・畜産や漁業・養殖や演劇・芸能や伝統産業・手工業や建設・土木や観光などのサービス業や運輸業などなどもあり、
日本を支えている分野は多彩ですが、それぞれの分野で実際に現場で役に立つ高度な技術を持って活躍している東大卒業生の割合はそんなに多くないはずです。
更に、女子だけでなく、東京大学の合格者の大部分は実際は東京都の裕福な家庭の子弟で、全国の高校生の数に対して異常に多いと言う事実を無視しています。
例えば、農業でも、都会育ちの指導者たちはアメリカの言いなりで、大規模農業でないと利益は上げられないと思っていますが、少ない農地で工夫をし、
自分で値段を付けることの出来る販売所も増えてきたので、ブランド価値のある作物を栽培することで、収穫期には一日で１００万円の売り上げを得ている農家も
高知県にも沢山います。東京育ちの政治家・官僚・マスコミや金儲けだけ考えている塾や予備校が「東京の大学に進学できなければ人生終った」と宣伝し、
例えば、箱根駅伝も東京圏の大学しか参加できないの大々的に全国放送し、兎も角、有名になりたければ、金を稼ぎたければ、東京に来いです。
東京或いは大阪だけに投資を集中するので、地方は疲弊するばかりで、地方は先人が苦労して開墾した農地も林野に戻っていっています。
あらゆることを欧米の真似をするのではなく、しかも政治家に取って都合の良い処だけ
全体を無視して欧米ではこの様にしていると国民を騙しているのではないか思われる政策が行われている様に思います。
例えば、農業でも英国は土地が余っていたから規模拡大で収入を上げ、日本は土地がないから世界にもまれな肥沃な土地を生かし労働力を集約する事で日本人を
食べらしてきたと言われています。アメリカの言いなりで、アメリカの農業を補助・補完する政策ではなく、日本の実体にあった日本人の為の政策を取るべきです。


パソコンが壊れて、新しいパソコンを購入すると Kindle for PC では洋書は読めなくなっていましたが、「Strange Prisoners」が安かったので購入し、
 Kindle for PC で試してみると読めるようになっていました。他の洋書も Kindle でも Kindle for PC でも読めるようになっていました。
 Kindle for PC は字が大きいのでずっと家にいる老人には助かります。


一松信著「正多面体を解く」の第４章準正多面体も必要なデータはすべて与えてくれていますが我々凡人には難解です。
先ずは最初のページの写真の様に模型を作ってみるのが良いみたいです。
写真の様な巧妙な模型は素人には作れないし、今話題の多面体の模型を作るための商品は高額で、沢山の模型を作るには経済的負担が大きく、
また、大きさや作れる多面体が制限されていますが、「ストローの模型」を作れば良いことをインターネットの動画で教えてもらったので、
作ってみます。






これらは準正多面体の「ストローの模型」です。紙の模型も作ってみると良いです。
「準正多面体の双対多面体」も解説してくれていますが、展開図を提示してくれているので、紙の模型から作って行くと良いです。






「三方四面体」、「三方八面体」、「四方六面体」、「五方十二面体」だけしかまだ作っていません。
これらは、展開図から作った方が綺麗に作れるとは限りません。






は「五方十二面体」の展開図ですが、「正十二面体」の展開図






で、「正五角形」を次の「二等辺三角形５個のパーツ」で置き換えたものをです。







又、５個の二等辺三角形から成るこのパーツや






の「二等辺三角形」や






の展開図の半分のパーツを印刷して、組み立てる方が楽かも。

「三方二十面体」は「二等辺三角形３個のパーツ」を作ってみるとほぼ「正三角形」と同じで、








の様に隙間が僅かで、正二十面体の展開図の正三角形を「二等辺三角形３個のパーツ」で置き換えた展開図は






の様になります。これは表4.12 準正多面体の双対多面体の表と表4.13 型Iの双対多面体より

import numpy as np

y = 6/5
x = (2*np.sqrt(2))/(5*np.sqrt(3))
theta = np.arccos((5/2)/3)*180/np.pi

print('三方四面体: 底辺=2, 斜辺=', y, '楊心の持ち上げ量=', x)
print('二等辺三角形の底角=', theta, '合計=', (180-2*theta)*3)
print()

y = 3/2
x = np.sqrt(11/12)
theta = np.arccos((4/2)/3)*180/np.pi
print('四方六面体: 底辺=2, 斜辺=', y, '楊心の持ち上げ量=', x)
print('二等辺三角形の底角=', theta, '合計=', (180-2*theta)*4)
print()

y = 4-2*np.sqrt(2)
x = 2*(3-2*np.sqrt(2))/np.sqrt(3)
theta = np.arccos(((2+np.sqrt(2))/2)/2)*180/np.pi
print('三方八面体: 底辺=2, 斜辺=', y, '楊心の持ち上げ量=', x)
print('二等辺三角形の底角=', theta, '合計=', (180-2*theta)*3)
print()

y = 3*(9+np.sqrt(5))/19
x = (2/19)*np.sqrt((65+22*np.sqrt(5))/5)
theta = np.arccos(((9-np.sqrt(5))/2)/6)*180/np.pi
print('五方十二面体: 底辺=2, 斜辺=', y, '楊心の持ち上げ量=', x)
print('二等辺三角形の底角=', theta, '合計=', (180-2*theta)*5)
print()

y = (15-np.sqrt(5))/11
x = (5*np.sqrt(5)-9)/(11*np.sqrt(3))
theta = np.arccos(((3+(1/np.sqrt(5)))/2)/2)*180/np.pi
print('三方二十面体: 底辺=2, 斜辺=', y, '楊心の持ち上げ量=', x)
print('二等辺三角形の底角=', theta, '合計=', (180-2*theta)*3)


を実行すれば

三方四面体: 底辺=2, 斜辺= 1.2 楊心の持ち上げ量= 0.3265986323710905
二等辺三角形の底角= 33.55730976192071 合計= 338.65614142847573

四方六面体: 底辺=2, 斜辺= 1.5 楊心の持ち上げ量= 0.9574271077563381
二等辺三角形の底角= 48.189685104221404 合計= 334.48251916622877

三方八面体: 底辺=2, 斜辺= 1.1715728752538097 楊心の持ち上げ量= 0.19811529142685025
二等辺三角形の底角= 31.399714809919047 合計= 351.6017111404857

五方十二面体: 底辺=2, 斜辺= 1.7741159964473354 楊心の持ち上げ量= 0.5030510688294035
二等辺三角形の底角= 55.69063953440601 合計= 343.0936046559399

三方二十面体: 底辺=2, 斜辺= 1.1603574565909283 楊心の持ち上げ量= 0.11443816554294514
二等辺三角形の底角= 30.480324565355676 合計= 357.11805260786593


であることより理解できます。

インターネット：https://www7b.biglobe.ne.jp/~geomzome/ArchimedianDual/08_3_10_10/08_3_10_10.html に「三方二十面体」の「紙の模型」を作る為の型紙






を示してくれています。この型紙１０個を使って組み立てる為には、このホームページの型紙で示しているように、それぞれどの頂点と辺が同じか指示する必要があります。
この型紙をどの様にして見つけたか書いていませんが、例えば、






の様な展開図があることに気が付けば良いです。コンピュータで探索出来ますが、
プログラムは作ろうと思えば作れると思いますが、我々貧乏人の貧弱なパソコンでは出来ないような気がします。
即ち、「三方二十面体」の頂点、辺、面の隣接関係の情報を求め、６０個の「二等辺三角形」の各面に頂点、辺、面の一連番号を振り、
６個づつ接続してブロックを作った時、１０個の合同なものが選べるかコンピュータで探索すれば、理論上は、可能です。

「ストローの模型」も作ってみると良いです。「紙の模型」と「ストローの模型」の二種類、全部、作るのは結構時間が掛かります。
次に、準正多面体と準正多面体の双対多面体をパソコンのコンピュータグラフィックスとして、実現し、パソコンで計算しながら、
図4.28、図4.29、図4.30、図4.31、図4.32などのコンピュータグラフィックスを実際に描画しながら一松信さんの解説を読んでみれば良いです。
どうすれば数学が分かったと思うかは人それぞれなのですが、自分がわかったと思うまで、本の解説の順序の逆に、最後に解説している様に、
「準正多面体の双対多面体」から「準正多面体」をプログラミングしてみるなど気のすむまでやってみれば良いです。余裕が有ればですが。
この様な図形は伝統的に日本人の美的感覚にないものですから、我々凡人は時間を掛けて学ぶ必要があるように思います。


簡単な型 I の準正多面体の双対多面体のコンピュータグラフィックス






などを作ってみると「四方六面体」が「紙の模型」と異なって描画されたので、
表4.13 「型 I の双対多面体」の「四方六面体」の x の値は 1/2 のミスプリントであることに気が付きました。
これは表4.12 の「準正多面体の双対多面体の表」の「辺の比」を使って、「三平方の定理」で計算できます。
「二面角」を計算するとこの表の値と一致するので、これが正しい値です。一松信さんの様な大数学者の本にもミスプリントがあるので、
一つ一つ自分で納得できるまで確かめる必要があります。
後は、これから「準正多面体」を作り、







更に、「準正多面体から双対多面体」を作り、描画してみる必要があります。
先ず「準正多面体」に球面が外接する事を確かめます。






最後に、一松信著「正多面体を解く」の第４章準正多面体では「準正多面体の双対多面体」の定義として解説していますが






が「準正多面体」の各頂点の外接球の接平面で構成される多面体として「準正多面体の双対多面体」を構成したものです。
静止画では本当に正しく構成できているか良く分かりませんが、動画なら両者の関係が良く分かります。
なお変則的な連立方程式を沢山解く必要がありますが、Sympy を使えば簡単にプログラミング出来ます。
手計算では大変ですが、アルゴリズムをパソコンに教えると一瞬で計算してくれ、結果を描画してくれます。
良い時代になりました。勿論、直接、正多面体から準正多面体を構成することも可能で、その前に解説してくれています。
昔、その部分は読んで、色々なプログラムを作ったので、今回は逆の順序で構成してみたかったのです。
「正多面体の双対多面体」も同じ方法でも作れるはずです。
「ストローの模型」も作ってみると良いです。
例えば、「凧形二十四面体」の「ストローの模型」を作る時、我々凡人は一松信著「正多面体を解く」の１１５ページの図と
展開図を見て作るのはかなり難しいです。インターネットで「凧形二十四面体」を探索するとフリー百科事典「ウィキペディア（Wikipedia）」に
五角二十四面体（ごかくにじゅうしめんたい、英: pentagonal icositetrahedron）の展開図として






の様な展開図を載せてくれています。これを印刷し、「紙の模型」を作ることが出来ますが、この展開図を見ると
「立方体の展開図」との類似性に誰でも気付きます。即ち、「立方体」の各面に「凧形４個」から成る屋根を
乗せた多面体が「凧形二十四面体」だと言うイメージを持つことが出来れば、容易に「ストローの模型」を作る
事が出来ます。優秀な人が「じっと眺めていれば分かる」と言うのは、多分、眺めていてこの様なイメージが浮かべば、
容易に理解できると言っているのだと思います。「タイパ」だけでなく、時間を掛けて、検討してみる事も必要です。
但し、一松信さんは一松信著「正多面体を解く」の１１２ページの図4.31 「凧形２E面体」の図を掲げてくれているので、
これを眺めて記憶に残っていれば、上の様な展開図に出会わなくても上に書いたイメージが出来ているハズではあり、
具体的な「凧形二十四面体」の「ストローの模型」を作る時、そのイメージを元に迷うことなく作成できるハズですが、
我々凡人は「一般的な概念」からではなく、具体的な例達を通してイメージを作り、その「帰納」として、
「一般的な概念」を理解するので、上の様な混乱が起こるのではないかと思います。多分。
五角二十四面体（ごかくにじゅうしめんたい、英: pentagonal icositetrahedron）なども同様です。
我々凡人はほんのちょっとしたことで、理解できたり、理解できなくなったりするみたいで、教育は本当は難しいです。

外国語の場合も澤井康佑著「中学英語「再」入門」の様な復習・整理の仕方をすれば、英語のモヤモヤが解消する人達もいると
思います。更に続けて、澤井康佑著「英文法再入門」を読めば、もっと英語がわかった気がする人達もいるハズです。
英文法と表題にありますが、中身は「英文を作る為のアルゴリズム」を解説してくれています。
中学校で受身などの練習はしましたが、あらゆる英文に対して「英文を作る為のアルゴリズム」を解説してくれているので、
数学を学ぶ時と同じ勉強法を使うことが出来ます。
「英文を作る為のアルゴリズム」の一つ一つを定着するまで、何を練習しているか意識しながら繰り返し練習すれば良いです。多分。
昔、薬袋善郎さんの沢山出版されている本や大西泰斗さんの本を読もうとしましたが、私には合わず読み切れませんでしたが、
（正確に書くと例えば「ゼロからわかる英語ベーシック教本」などは鉛筆で線を引いているので全体に目を通したはずですが、
この本の価値がその時は理解できなかったみたいで、内容を何も記憶していません。
今読むとコンピューターの「言語理論」と同じような事を書いていると思います。
即ち、NIKLAUS WIRTH 著「Alorithms + Data Structures = Programs」の 5 LANGUAGE STRUCTURES AND COMPILERS の
人工的な言語の理解と同じような理解も自然言語でも必要だとその時は思い至らなかったです。
又、「言語理論とオートマトン」で「文脈自由文法」とか「文脈依存文法」とか少し齧っていれば意識的に考えることが出来ます。
NIKLAUS WIRTH さんの別の本で Pascal の「メタ言語」による完全な記述がなされていましたが、今は Pascal は使われていないので、
上の本の様な単純な言語で良いですが、その言語で許されるプログラムの構造は何かの「抽象的な記述」と「意味の理解」
（我々凡人はこの様な簡略化でないと言語の構造を理解できない事を忘れていました）と
Pascal のプログラムの分解に依るプログラムの理解、即ち、ディープラーニング以前のコンピューターの自然言語の理解を
（この部分が薬袋善郎さんの沢山出版されている本でやっていることです）、
優秀な人達が書いている方法で上手くいかなければ、我々凡人もこうやってみれば良いのではないかと言うことです。
この本（NIKLAUS WIRTH 著「Alorithms + Data Structures = Programs」）は翻訳は無理だと思いますが、
原著なら古本でまだ入手できるかも？
私はこの本で現代的なプログラミングの基本を教わりました。Pascal を考案した著者による Pascal の本です。）
少しは英語が出来るようになったのか、
牧野智一著「一度読んだら絶対に忘れない英文法の教科書」は読み切ることが出来ました。面白かったです。
今流行りの外国語の勉強法で上手くいかなければ、読んで試してみると良いです。
更に、薬袋善郎さんの本達を引っ張り出して、今、読んで見ると面白いです。我々凡人には本を読む順序があるみたいです。
今は分からない英文はインターネットで調べると意味・訳は分かるけど何でそんな訳になるか知りたいです。
でないと、皆がこうしろと言う丸暗記では、我々凡人は覚えられずにすぐ忘れ、ずっとモヤモヤが残ります。
数学やコンピューターの本は専門用語と数学やコンピューターの知識で外国語の本が読めますが、
一般の書籍はずっとモヤモヤが残ったままです。優秀な人達のこうすれば良いと言う方法では我々貧乏な凡人は上手くいきません。
訳もなく何でもかんでも丸暗記を続けることが出来ません。毎日少しづつも続きません。最低限、何を丸暗記すれば良いか、
幾つかの参考書を眺めて、自分でもできる方法を探す必要があります。
例えば、「英文読解の透視図」の別冊「英文読解再入門」の最後の動詞表１，２，３を毎日書き写し、
丸暗記し、 O1, O2, O, C に何が入るか？修飾語がどの様にくっ付くか？名詞や形容詞や副詞だけでなく、「完了動名詞」や
「前置詞＋名詞で構成される形容詞句または副詞句」とか・・・も可能だと
適切な他の文法書で補い、「英文がどの様に構成されている」か整理し、丸暗記すべきことを最低限に整理し、
更には「英文のこの様な構造を認識する」方法を学び、無意識に判断できるまで、集中して練習する必要があるみたいです。
この年になって、私が外国語を理解するにはこの様にすれば良いのではないかと思うようになりました。
無駄な努力をしていたみたいです。本当は数学やコンピューターの勉強に比べ、全然努力してなかったですが。

最近出版された林松涛著「一度読んだら絶対忘れない中国語の教科書」で中国語の文章の生成規則を解説してくれています。
逆は、高校生の時は余り興味がなかったので、椙本神社の神主さんに習った事しか覚えていませんが、折角、漢文を習っているので、
どの大学受験の参考書でも良いですが、例えば、「寺師の漢文をはじめからていねいに」を読めば、中国語の解釈の勉強が出来ます。
難点は「読み下し文」が「古文」であることです。「古文」の勉強も必要ですが、どうせ、老人の暇つぶしだから問題はないですが。
後は、発音（ピーイン）と簡体字と基本単語を覚えれば、中国語も何とかなるのでは？多分。やってはいませんが。


私の記憶はいい加減で、私の最初に読んだ囲碁の本は、八段　岩本薫　校閲　五段　下田源一郎著
「新書　碁の打ち方」虹有社刊でした。実家の本箱で最近偶然見つけました。。
偶然本屋で目に付いて読んだのが高校卒業直後だったので、所謂「易しい囲碁入門」の様な本ではなく、
この様な硬派の解説書に最初に出会ったので、本を読むことによって囲碁に興味を持つことが出来たと思います。
有名な本達を集めるだけで、全然読んでなく、勉強の絶対量が足りないので、３級ぐらいで上達は止まったままですが。

更に、上で、「一般的に３次元の凸多面体に関して、どの辺のペアに対して、面を調べるべきかを決定することが出来るアルゴリズムを見つけることが出来ました。」
と書きましたが、「四方六面体」の面の隣接関係を計算させると想定外の事が起こり、アルゴリズムが間違っていることに気が付きました。

    def get_cyclic_pair(self, e_list, v):
        print('##################### get_cyclic_pair ####### e_list=', e_list)
        print('v=', v)
        
##        a1 = self.v[self.e[e_list[0]][0]][0]
##        a2 = self.v[self.e[e_list[0]][1]][0]
##        b1 = self.v[self.e[e_list[1]][0]][0]
##        b2 = self.v[self.e[e_list[1]][1]][0]
##        print('a1=', a1, ' a2=', a2)
##        print('b1=', b1, ' b2=', b2)
##        if self.same_vectorP(a1, v):
##            e1 = np.array(a2) - np.array(a1)
##        else:
##            e1 = np.array(a1) - np.array(a2)
##        if self.same_vectorP(b1, v):
##            e2 = np.array(b2) - np.array(b1)
##        else:
##            e2 = np.array(b1) - np.array(b2)
##        print('e1=', e1, ' e2=', e2)
##        cross = np.cross(e1, e2)
##        print('cross=', cross)
##        n = (1/np.sqrt(np.dot(cross, cross))) * cross

        n = (1/np.sqrt(np.dot(np.array(v), np.array(v)))) * np.array(v)
        


と修正すれば、原点が凸多面体の内部にあれば計算してくれるはずです。


これらのプログラムは、先ず、一松信著「高次元の正多面体」のページ２，３の
5種類の正多面体の頂点の座標の情報を使って、5種類の正多面体の頂点、辺、面の隣接関係を計算し、
OpenGL を使って描画するプログラムを作ります。これを、「5種類の正多面体の頂点、辺の情報を計算するモジュール」と
「多面体の頂点、辺の情報から多面体の頂点、辺、面の隣接関係を計算するモジュール」と
「多面体の頂点、辺、面の隣接関係の情報を使って描画するモジュール」に分割します。
次に、5種類の正多面体の頂点、辺、面の隣接関係と表4.13 型 I の双対多面体のデータを使って、
型 I の双対多面体の頂点、辺の情報を計算し、「多面体の頂点、辺の情報から多面体の頂点、辺、面の隣接関係を計算するモジュール」を
使って、型 I の双対多面体の頂点、辺、面の隣接関係を計算し、「多面体の頂点、辺、面の隣接関係の情報を使って描画するモジュール」を
使って、型 I の双対多面体の描画を行います。次に、型 I の双対多面体の頂点、辺、面の隣接関係の情報を使って、各二等辺三角形の面の
内心を計算し、対応する型 I の準正多面体の頂点、辺の情報を計算し、
「多面体の頂点、辺の情報から多面体の頂点、辺、面の隣接関係を計算するモジュール」を使って、
対応する型 I の準正多面体の頂点、辺、面の隣接関係を計算し、「多面体の頂点、辺、面の隣接関係の情報を使って描画するモジュール」を
使って対応する型 I の準正多面体の描画します。最後に、対応する型 I の準正多面体の頂点、辺、面の隣接関係の情報を使って、
各頂点での接平面の方程式を計算し、辺で隣接する二つの接平面の交線の方程式を変数の数より式の数が少ない連立方程式を Sympy で解き、
更に、隣接する二つの交線の交点を計算して、対応する型 I の双対多面体の頂点、辺の情報を計算し、
「多面体の頂点、辺の情報から多面体の頂点、辺、面の隣接関係を計算するモジュール」を使って、
対応する型 I の双対多面体の頂点、辺、面の隣接関係を計算し、
「多面体の頂点、辺、面の隣接関係の情報を使って描画するモジュール」を使って、描画しているだけです。
注意：接平面を変数の数より式の数が少ない連立方程式を Sympy で解いていますが、その解は不可解で、どんな表現になるか予想が付かず、
その方程式を文字式で表現しようとして半日努力しましたが結局諦めました。欲しいのは隣接する接平面の交線達の交点の座標ですから、
そのままどの変数が媒介変数になっているか調べて、交点を求める今度は変数の数より式の数が多い連立方程式を作り、
Sympy で解けば交点の座標が求まります。
「多面体の頂点、辺の情報から多面体の頂点、辺、面の隣接関係を計算するモジュール」に不備が見つかる度に
改良しています。Python のクラスを使って、モジュール化して、同じような事を繰り返しているだけです。
何時でも「5種類の正多面体の頂点、辺の情報」から計算をしていて無駄な事をしていて、
効率の良いプログラムではないですが現在の安価なパソコンでもデータの準備に時間が掛かりますが
実用に足るアニメーションの描画をしてくれます。全体のプログラムはごちゃごちゃしていて、
使い方を解説するのが厄介で、人様に見せるようなものではないですし、かなり大量のコードがあります。
こんな単純なプログラムでも思い通りにアニメーションが始まると嬉しいものです。
高度な数学の知識は必要ないので、是非、自分でやってみて下さい。


推理小説ではないですが、明治依吹著「アルゴリズムの乙女たち」徳間文庫が近くの本屋で目に付き、購入しました。
この様な本が出版された事は、インターネットで見つけることは難しく、矢張り、新刊書を並べたリアルな本屋があることが必要です。


沢山「ストローの模型」を色々な材料で色々工夫して作っていると段々上手に作れるようになります。多分。






先ずは、誰でも簡単にできる「模型」を作ることから始めます。
面が三角形でも針金の芯を入れると綺麗に作れます。ストローは様々な太さのものを購入できますが、
太いストローには太いアルミの針金、細いストローには細い銅の針金が不器用な老人には使い易いです。
大分上の写真の細いストロー：「キャンドゥ」の「 Mini drinking straw pastel color 120p」は至る所で売っていますが、
少し値が張りますが同じ太さの透き通ったストロー：大和物産株式会社「まがるミニストロー70本入り」も近くのスーパーにありました。
今回の更に細い透き通ったストロー：「セイワ・プロ」の「お子様ミニストロー先斜カット１５０本入」は殆ど売っている処がありません。
業務用食品スーパーの中の余り有名でない百均で、偶然見つけました。自分の美的感覚に合う模型を作れば良いです。
これを見ると田舎育ちの私は子供たちがイネ科の多年草「ジュズダマ」の果実を集めて糸に通して「数珠」を作って遊んでいたことを思い出します。

最後に、「準正多面体の双対多面体」をより良く理解するためには我々凡人は、与えられた図を眺めるだけでなく。どうしても、
残りの型 II、型 III、型 IV、型 V の「準正多面体の双対多面体」も順次、座標の計算方法を調べ、
他の多面体との関連をコンピュータで描画することにより、同様に調べる必要があります。結構大変です。















は図4.29を見ながら「正八面体」から「菱形十二面体」を構成したものと「正二十面体」から「菱形三十面体」を構成したものです。
一松信著「正多面体を解く」の表 4.14 の「型 II の双対多面体」の (p,q)=(3,4) の x の値は 1/np.sqrt(6) ではないかと思います。
上の二つの動画はこの x の値を使ってプログラミングしています。
ここで、一松信著「正多面体を解く」は2002年5月20日　第1版第1刷発行　東海大学出版会です。
「正八面体」から「菱形十二面体」を構成したものを使っても「立方体」から「菱形十二面体」を構成したものを使っても
「菱形十二面体」から「正方八面体」を作ってくれます。






 (p,q)=(3,4) の x の値は 1/np.sqrt(6) ではと言う計算は正しいと思います。
又、「正十二面体」から「菱形三十面体」を構成したものを使っても「正二十面体」から「菱形三十面体」を構成したもの使っても
「菱形三十面体」から「二十面十二面体」を作ってくれます。






最後に、「正方八面体」から「菱形十二面体」を構成するプログラム






と「二十面十二面体」から「菱形三十面体」を構成するプログラム






を作ります。このプログラムを作る時、型 I で考えたアルゴリズムが馬鹿げたものであったことに気が付きました。
3つの接平面の交点の座標を直接連立方程式を解くことで求めればよかったです。

型 III、型 IV、型 V の「準正多面体の双対多面体」は同様に計算できるはずですが、
一松信さんは計算結果を提示してくれていませんので、解説の図（図4.30、図4.31、図4.32）と「ストローの模型」を
見比べ全部自分で計算する必要があります。
基本的には同じ考え（類比）でアルゴリズムを考えれば良いはずですが、段々厄介になります。


型 III の「準正多面体の双対多面体」はインターネットで調べると面の辺の比の正確な値を得ることが出来るので、
「面楊心」と「辺楊心」の持ち上げ量を計算するための連立方程式は簡単に作れますが、私には解けません。
仕方がないので、「準正多面体」から「双対多面体」の定義通り構成することにします。
一松信著「正多面体を解く」を読めば、頂点の座標を決定できますが、手を抜いて、
昔作った「準正多面体」や「星形正多面体」を「正多面体」から構成する様子を見る C++ のプログラムから
大分上で作成した Pyton のモジュール archimedes.pyd を使って、「準正多面体」の頂点と辺のデータを取り出すプログラム

import sympy
import numpy as np
import archimedes

class MakeTypeIIISemiRegular:
    def __init__(self, dim, n, kind):
        print('start MakeDual')
            
        self.n = n
        self.dim = dim
        if n == 4:
            type = 0
        elif n == 6:
            type = 1
        elif n == 8:
            type = 2
        elif n == 12:
            type = 3
        elif n == 20:
            type = 4
            
        self.poly = archimedes.POLY(type, 0, 0)
        self.basic_length = self.poly.length
        self.basic_f_list = self.poly.get_face()
        self.basic_n_face = self.poly.n_face
        self.basic_v_list = self.poly.get_vertex()
        self.get_basic_inf()
        print()
        print('len(self.basic_v)=', len(self.basic_v))
        print('self.basic_v=', self.basic_v)
        print('len(self.basic_e)=', len(self.basic_e))
        print('self.basic_e=', self.basic_e)
        
        self.kind = kind
        if kind == 1:
            if n == 4:
                index = 3
            elif n == 6:
                index = 7
            elif n == 8:
                index = 5
            elif n == 12:
                index = 19
            elif n == 20:
                index = 11
        elif kind == 2:
            if n == 4:
                index = 3
            elif n == 6:
                index = 7
            elif n == 8:
                index = 5
            elif n == 12:
                index = 19
            elif n == 20:
                index = 11
        elif kind == 3:
            if n == 4:
                index = 9
            elif n == 6:
                index = 19
            elif n == 8:
                index = 17
            elif n == 12:
                index = 49
            elif n == 20:
                index = 41
        elif kind == 4:
            if n == 4:
                index = 9
            elif n == 6:
                index = 19
            elif n == 8:
                index = 17
            elif n == 12:
                index = 49
            elif n == 20:
                index = 41
        elif kind == 5:
            if n == 4:
                index = 19
            elif n == 6:
                index = 37
            elif n == 8:
                index = 37
            elif n == 12:
                index = 91
            elif n == 20:
                index = 91
        print('type=', type, 'kind=', kind, 'indes=', index)
        self.poly = archimedes.POLY(type, kind, index)
        self.length = self.poly.length
        print('self.length=', self.length)
        self.f_list = self.poly.get_face()
        self.n_face = self.poly.n_face
        self.v_list = self.poly.get_vertex()
        self.get_poly_inf()
        ratio = self.get_size()
        print('ratio=', ratio)
        kk = self.get_basic_size()
        print('basic_ratio=', kk)
        ratio = ratio/kk
        for k in range(len(self.basic_v)):
            self.basic_v[k] = ratio*(np.array(self.basic_v[k]))
        
        print()
        print('len(self.v)=', len(self.v))
        print('self.v=', self.v)
        print('len(self.e)=', len(self.e))
        print('self.e=', self.e)
        print()
        print('len(self.basic_v)=', len(self.basic_v))
        print('self.basic_v=', self.basic_v)
        print('len(self.basic_e)=', len(self.basic_e))
        print('self.basic_e=', self.basic_e)

    def new_basic_vertexP(self, V):
        for k in range(len(self.basic_v)):
            if np.abs(V[0]-self.basic_v[k][0])<0.0001 and \
                   np.abs(V[1]-self.basic_v[k][1])<0.0001 and \
                   np.abs(V[2]-self.basic_v[k][2])<0.0001 :
                return False
        return True

    def get_basic_inf(self):
        self.basic_v = []
        
        for i in range(self.basic_n_face):
            for k in range(len(self.basic_f_list[i])-1):
                if self.new_basic_vertexP(self.basic_v_list[self.basic_f_list[i][k]]):
                    self.basic_v.append(self.basic_v_list[self.basic_f_list[i][k]])
        self.basic_e = []
        min_length = 1000
        for i in range(len(self.basic_v)):
            for k in range(i+1, len(self.basic_v)):
                a = np.array(self.basic_v[i]) - np.array(self.basic_v[k])
                dis = np.dot(a, a)
                if dis < min_length:
                    min_length = dis
        for i in range(len(self.basic_v)):
            for k in range(i+1, len(self.basic_v)):
                a = np.array(self.basic_v[i]) - np.array(self.basic_v[k])
                dis = np.dot(a, a)
                if np.abs(dis-min_length)<0.001:
                    self.basic_e.append([i, k])
                    
    def new_vertexP(self, V):
        for k in range(len(self.v)):
            if np.abs(V[0]-self.v[k][0])<0.0001 and \
                   np.abs(V[1]-self.v[k][1])<0.0001 and \
                   np.abs(V[2]-self.v[k][2])<0.0001 :
                return False
        return True

    def get_basic_size(self):
        if self.n == 4:
            n_sides = 3
        elif self.n == 6:
            n_sides = 4
        elif self.n == 8:
            n_sides = 3
        elif self.n == 12:
            n_sides = 5
        elif self.n == 20:
            n_sides = 3

        index = 0
        g = np.array([0.0, 0.0, 0.0])
        for k in range(n_sides):
             g = g + np.array(self.basic_v_list[self.basic_f_list[index][k]])
        g = (1/n_sides)*g
        return np.sqrt(np.dot(g, g))

    def get_size(self):
        if self.n == 4:
            if self.kind == 1:
                n_sides = 6
            elif self.kind == 2:
                n_sides = 3
            elif self.kind == 3:
                n_sides = 3
            elif self.kind == 4:
                n_sides = 6
            elif self.kind == 5:
                n_sides = 3
        elif self.n == 6:
            if self.kind == 1:
                n_sides = 8
            elif self.kind == 2:
                n_sides = 4
            elif self.kind == 3:
                n_sides = 4
            elif self.kind == 4:
                n_sides = 8
            elif self.kind == 5:
                n_sides = 4
        elif self.n == 8:
            if self.kind == 1:
                n_sides = 6
            elif self.kind == 2:
                n_sides = 3
            elif self.kind == 3:
                n_sides = 3
            elif self.kind == 4:
                n_sides = 3
            elif self.kind == 5:
                n_sides = 3
        elif self.n == 12:
            if self.kind == 1:
                n_sides = 10
            elif self.kind == 2:
                n_sides = 5
            elif self.kind == 3:
                n_sides = 5
            elif self.kind == 4:
                n_sides = 10
            elif self.kind == 5:
                n_sides = 5
        elif self.n == 20:
            if self.kind == 1:
                n_sides = 6
            elif self.kind == 2:
                n_sides = 3
            elif self.kind == 3:
                n_sides = 3
            elif self.kind == 4:
                n_sides = 6
            elif self.kind == 5:
                n_sides = 3

        index = 0
        for i in range(self.n_face):
            if len(self.f_list[i])-1 == n_sides:
                index = i
                break
        g = np.array([0.0, 0.0, 0.0])
        for k in range(len(self.f_list[index])-1):
             g = g + np.array(self.v_list[self.f_list[index][k]])
        g = (1/n_sides)*g
        return np.sqrt(np.dot(g, g))
        
    def get_poly_inf(self):
        self.v = []
        
        for i in range(self.n_face):
            for k in range(len(self.f_list[i])-1):
                if self.new_vertexP(self.v_list[self.f_list[i][k]]):
                    self.v.append(self.v_list[self.f_list[i][k]])
        self.e = []
        min_length = 1000
        for i in range(len(self.v)):
            for k in range(i+1, len(self.v)):
                a = np.array(self.v[i]) - np.array(self.v[k])
                dis = np.dot(a, a)
                if dis < min_length:
                    min_length = dis
        for i in range(len(self.v)):
            for k in range(i+1, len(self.v)):
                a = np.array(self.v[i]) - np.array(self.v[k])
                dis = np.dot(a, a)
                if np.abs(dis-min_length)<0.001:
                    self.e.append([i, k])
        
if __name__ == '__main__':

    cube = MakeTypeIIISemiRegular(3, 6, 4)



を作り、例えば、型 III の「大菱形立方八面体」の頂点と辺の情報を得る為に作ったプログラム

    cube = MakeTypeIIISemiRegular(3, 6, 4)


を実行した時、表示されるデータ

ratio= 0.40114868709940155

len(self.v)= 48
self.v= [
[-0.25224077608295226, -0.10448154791755498, 0.4], [-0.10448155063403142, -0.25224077389690075, 0.4], 
[0.10448154927579331, -0.25224077445950144, 0.4], [0.2522407749899265, -0.10448154980621827, 0.4], 
[0.2522407751774601, 0.1044815504143222, 0.4], [0.10448155078938925, 0.25224077533281797, 0.4],
 [-0.10448154943115101, 0.2522407758954187, 0.4], [-0.2522407751452844, 0.10448155124213543, 0.4], 
[0.2522407755203515, -0.10448154927579334, -0.4], [0.10448154927579328, -0.25224077445950144, -0.4], 
[-0.1044815506340315, -0.25224077389690075, -0.4], [-0.2522407755525271, -0.10448154844798008, -0.4], 
[-0.2522407746148594, 0.10448155177256044, -0.4], [-0.10448154943115107, 0.2522407758954187, -0.4], 
[0.10448155078938937, 0.25224077533281797, -0.4], [0.25224077570788506, 0.10448154988389724, -0.4], 
[0.4000000004527461, 0.10448154948607843, -0.25224077512253273], [0.40000000058535234, 0.2522407745371804, -0.10448154993882447], 
[0.40000000058535234, 0.25224077453718047, 0.10448154993882444], [0.4000000004527461, 0.10448154948607843, 0.25224077512253273], 
[0.40000000026521254, -0.1044815502040371, 0.25224077512253273], [0.4000000001326063, -0.252240775255139, 0.10448154993882458], 
[0.4000000001326063, -0.25224077525513894, -0.10448154993882461], [0.40000000026521254, -0.10448155020403704, -0.25224077512253273], 
[-0.10448154876811983, 0.4000000006402797, -0.25224077512253273], [-0.25224077381922183, 0.4000000010380985, -0.10448154993882455], 
[-0.2522407738192219, 0.4000000010380985, 0.10448154993882441], [-0.10448154876811988, 0.4000000006402797, 0.25224077512253273], 
[0.10448155092199568, 0.40000000007767894, 0.25224077512253273], [0.2522407759730976, 0.39999999967986016, 0.10448154993882447], 
[0.2522407759730975, 0.39999999967986016, -0.10448154993882461], [0.10448155092199557, 0.40000000007767894, -0.25224077512253273], 
[-0.40000000082781323, -0.1044815480501613, -0.25224077512253273], [-0.40000000149084447, -0.25224077310126325, -0.1044815499388245], 
[-0.40000000149084447, -0.2522407731012633, 0.10448154993882447], [-0.40000000082781323, -0.10448154805016127, 0.25224077512253273], 
[-0.3999999998901454, 0.10448155163995429, 0.25224077512253273], [-0.3999999992271141, 0.25224077669105627, 0.10448154993882453], 
[-0.3999999992271141, 0.25224077669105627, -0.10448154993882455], [-0.3999999998901454, 0.1044815516399542, -0.25224077512253273], 
[0.10448154914318708, -0.39999999920436247, -0.25224077512253273], [0.25224077472471396, -0.39999999960218124, -0.10448154993882455], 
[0.252240774724714, -0.39999999960218124, 0.10448154993882455], [0.10448154914318697, -0.39999999920436247, 0.25224077512253273], 
[-0.10448155129706282, -0.3999999986417618, 0.25224077512253273], [-0.25224077687858976, -0.39999999824394306, 0.10448154993882441], 
[-0.2522407768785897, -0.39999999824394306, -0.10448154993882458], [-0.10448155129706291, -0.3999999986417618, -0.25224077512253273]]
len(self.e)= 72
self.e= [[0, 1], [0, 7], [0, 35], [1, 2], [1, 44], [2, 3], [2, 43], [3, 4], [3, 20], [4, 5], 
[4, 19], [5, 6], [5, 28], [6, 7], [6, 27], [7, 36], [8, 9], [8, 15], [8, 23], [9, 10], 
[9, 40], [10, 11], [10, 47], [11, 12], [11, 32], [12, 13], [12, 39], [13, 14], [13, 24], [14, 15], 
[14, 31], [15, 16], [16, 17], [16, 23], [17, 18], [17, 30], [18, 19], [18, 29], [19, 20], [20, 21], 
[21, 22], [21, 42], [22, 23], [22, 41], [24, 25], [24, 31], [25, 26], [25, 38], [26, 27], [26, 37], 
[27, 28], [28, 29], [29, 30], [30, 31], [32, 33], [32, 39], [33, 34], [33, 46], [34, 35], [34, 45], 
[35, 36], [36, 37], [37, 38], [38, 39], [40, 41], [40, 47], [41, 42], [42, 43], [43, 44], [44, 45], 
[45, 46], [46, 47]]

len(self.basic_v)= 8
self.basic_v= [array([ 0.40114869, -0.40114869,  0.40114869]), array([0.40114869, 0.40114869, 0.40114869]), 
array([-0.40114869,  0.40114869,  0.40114869]), array([-0.40114869, -0.40114868,  0.40114869]), 
array([ 0.40114869, -0.40114869, -0.40114869]), array([-0.40114869, -0.40114868, -0.40114869]), 
array([-0.40114869,  0.40114869, -0.40114869]), array([ 0.40114869,  0.40114869, -0.40114869])]
len(self.basic_e)= 12
self.basic_e= [[0, 1], [0, 3], [0, 4], [1, 2], [1, 7], [2, 3], [2, 6], [3, 5], [4, 5], [4, 7], [5, 6], [6, 7]]


を使って、プログラミングします。






「大菱形立方八面体」の動画が出来ました。上のプログラムの数値を変えるともう一つの
型 III の「準正多面体」：「大菱形二十面十二面体」の動画






を作ることが出来ます。

同様に、型 IV の「準正多面体」：「小菱形立方八面体」と「小菱形二十面十二面体」の動画












と型 V の「準正多面体」：「変形立方体」と「変形十二面面体」の動画














も描画できます。後はこれらを使って上と同じことをすれば良いだけです。
「準正多面体の双対多面体」は

import sympy
import numpy as np
import re
from numpy.linalg import solve
import copy
import tkinter.simpledialog as simpledialog
import os
import time

from AllTypeSemiRegularPolyhedron import *
from Frame import *

class Rotate:
    def rotate(self, n, r, theta):
        n = (1/np.sqrt(np.dot(n, n))) * n
        n_dot = np.dot(r, n)
        n_cross = np.cross(n, r)
        w = np.cos(theta)*r+n_dot*(1-np.cos(theta))*n+np.sin(theta)*n_cross
        return w
    def matrix(self, n, theta):
        t_mtx = []
        m1 = self.rotate(n, np.array([1.0, 0.0, 0.0]), theta)
        m2 = self.rotate(n, np.array([0.0, 1.0, 0.0]), theta)
        m3 = self.rotate(n, np.array([0.0, 0.0, 1.0]), theta)
        t_mtx.extend(m1)
        t_mtx.extend(m2)
        t_mtx.extend(m3)
        mtx = np.array(t_mtx, dtype=float).reshape(3, 3) 
        return mtx
            
class CreateAllTypeSemiRegular:
    def __init__(self, dim, n, kind):
        print('start MakeDual')
            
        self.n = n
        self.dim = dim
        self.kind = kind

        self.poly = MakeTypeIIISemiRegular(dim, n, kind)
        self.frame = MakeFrame(dim, self.poly.v, self.poly.e)
        self.v = self.frame.v
        self.e = self.frame.e
        self.f = self.frame.f

        print()
        print('len(self.v)=', len(self.v))
        print('self.v=', self.v)
        print('len(self.e)=', len(self.e))
        print('self.e=', self.e)
        print('len(self.f)=', len(self.f))
        print('self.f=', self.f)

        self.get_semiregular_inf()
        print()
        print('len(self.semi_v)=', len(self.semi_v))
        print('self.semi_v=', self.semi_v)
        print('len(self.semi_e)=', len(self.semi_e))
        print('self.semi_e=', self.semi_e)
        
    def get_line_eq2(self, sol):       
        x = sympy.Symbol('x')
        y = sympy.Symbol('y')
        z = sympy.Symbol('z')

        print('############################ sol=', sol)
        key_list =  list(sol.keys())
        print('key_list=', key_list) ## 例： key_list = [x]
        if not ( x in key_list):
            print('x not in')
            return [x, sol[y], sol[z]]
        if not ( y in key_list):
            print('y not in')
            return [sol[x], y, sol[z]]
        if not ( z in key_list):
            print('z not in')
            return [sol[x], sol[y], z]
        
    def find_semi_v(self, V):
        print('V=', V)
        for k in range(len(self.semi_v)):
            err0 = np.abs(V[0]-self.semi_v[k][0])
            err1 = np.abs(V[1]-self.semi_v[k][1])
            err2 = np.abs(V[2]-self.semi_v[k][2])
            print('k=', k, 'self.semi_v[k]=', self.semi_v[k])
            print('err0=', err0,'err1=', err1, 'err2=', err2) 
            if err0 < 0.001 and err1 < 0.001 and err2 < 0.001:
                return k
        return -1

    def semi_e_containedP(self, pair):
        for k in range(len(self.semi_e)):
            if self.semi_e[k][0] == pair[0] and self.semi_e[k][1] == pair[1]:
                return True
            if self.semi_e[k][0] == pair[1] and self.semi_e[k][1] == pair[0]:
                return True
        return False

    def semi_v_P(self, V, W):
        err0 = np.abs(V[0]-W[0])
        err1 = np.abs(V[1]-W[1])
        err2 = np.abs(V[2]-W[2])
            
        if err0 < 0.001 and err1 < 0.001 and err2 < 0.001:
            return True
        return False
        
    def same_vectorP(self, v, w):
        for k in range(len(v)):
            if np.abs(v[k]-w[k])>0.0001:
                return False
        return True
    
    def firstP(self, e1, e2):
        if (e1[0] >= 0 and e1[1] >= 0):
            if (e2[0] >= 0 and e2[1] >= 0):
                if e1[0] > e2[0]:
                    return True
                else:
                    return False
            else:
                return True
        elif (e1[0] < 0 and e1[1] >= 0):
            if (e2[0] >= 0 and e2[1] >= 0):
                return False
            elif (e2[0] < 0 and e2[1] >= 0):
                if e1[0] > e2[0]:
                    return True
                else:
                    return False
            else:
                return True
        elif (e1[0] < 0 and e1[1] < 0):
            if (e2[0] >= 0 and e2[1] >= 0):
                return False
            elif (e2[0] < 0 and e2[1] >= 0):
                return False
            elif (e2[0] < 0 and e2[1] < 0):
                if e1[0] < e2[0]:
                    return True
                else:
                    return False
            else:
                return True
        else:
            if (e2[0] >= 0 and e2[1] >= 0):
                return False
            elif (e2[0] < 0 and e2[1] >= 0):
                return False
            elif (e2[0] < 0 and e2[1] < 0):
                return False
            else:
                if e1[0] < e2[0]:
                    return True
                else:
                    return False

    def get_cyclic_pair(self, e_list, v):
        print('##################### get_cyclic_pair ####### e_list=', e_list)
        print('v=', v)

        n = (1/np.sqrt(np.dot(np.array(v), np.array(v)))) * np.array(v)
        
        space = Space(self.dim, n)
        x = space.x
        y = space.y
        print('x=', x, ' y=', y)
        v_list = []
        ind = 0
        for e in e_list:
            print('e=', e)
            print('self.e[e]=', self.e[e])
            a1 = self.v[self.e[e][0][0]][0]
            a2 = self.v[self.e[e][0][1]][0]
            print('a1=', a1, ' a2=', a2)
            if self.same_vectorP(a1, v):
                e1 = np.array(a2) - np.array(a1)
            else:
                e1 = np.array(a1) - np.array(a2)
            print('e1=', e1)
            V = np.array([np.dot(x, e1), np.dot(y, e1)])
            print('V=', V)
            V = (1/np.sqrt(np.dot(V, V)))*V
            v_list.append([e_list[ind], V])
            ind = ind+1
        print('#### len(v_list)=', len(v_list))
        print('v_list=', v_list)
        for k in range(len(v_list)):
            for i in range(k+1, len(v_list)):
                if self.firstP(v_list[i][1], v_list[k][1]):
                    temp = v_list[k]
                    v_list[k] = v_list[i]
                    v_list[i] = temp
        result2 = []
        for k in range(len(v_list)):
            if k < len(v_list)-1:
                if v_list[k][0] < v_list[k+1][0]:
                    result2.append([v_list[k][0], v_list[k+1][0]])
                else:
                    result2.append([v_list[k+1][0], v_list[k][0]])
            else:
                if v_list[k][0] < v_list[0][0]:
                    result2.append([v_list[k][0], v_list[0][0]])
                else:
                    result2.append([v_list[0][0], v_list[k][0]])
        e_order = []
        head = result2.pop(0)
        e_order.extend(head)
        t_e = head[1]
            
        for j in  range(len(e_list)-2):
            for pair in result2:
                if t_e in pair:
                    if pair[0] == t_e:
                        e_order.append(pair[1])
                        t_e = pair[1]
                    else:
                        e_order.append(pair[0])
                        t_e = pair[0]
                    result2.remove(pair)
        return e_order
                
    def get_semiregular_inf(self):
        x = sympy.Symbol('x')
        y = sympy.Symbol('y')
        z = sympy.Symbol('z')

        self.semi_v = []
        self.semi_e = []

        if self.kind == 2 or self.kind == 3:
            for k in range(len(self.v)):
                v = self.v[k][0]
                e_list = self.v[k][1][0] ## 今度は菱形又は凧形
                result = self.get_cyclic_pair(e_list, v)
                print('### result=', result)
                w1 = self.v[self.e[result[0]][0][1]][0]
                if self.semi_v_P(v, w1) == True:
                    w1 = self.v[self.e[result[0]][0][0]][0]
                w2 = self.v[self.e[result[1]][0][1]][0]
                if self.semi_v_P(v, w2) == True:
                    w2 = self.v[self.e[result[1]][0][0]][0]
                w3 = self.v[self.e[result[2]][0][1]][0]
                if self.semi_v_P(v, w3) == True:
                    w3 = self.v[self.e[result[2]][0][0]][0]
                w4 = self.v[self.e[result[3]][0][1]][0]
                if self.semi_v_P(v, w4) == True:
                    w4 = self.v[self.e[result[3]][0][0]][0]
                
                eqn0 =v[0]*x+v[1]*y+v[2]*z-v[0]*v[0]-v[1]*v[1]-v[2]*v[2]
                eqn1 =w1[0]*x+w1[1]*y+w1[2]*z-w1[0]*w1[0]-w1[1]*w1[1]-w1[2]*w1[2]
                eqn2 =w2[0]*x+w2[1]*y+w2[2]*z-w2[0]*w2[0]-w2[1]*w2[1]-w2[2]*w2[2]
                eqn3 =w3[0]*x+w3[1]*y+w3[2]*z-w3[0]*w3[0]-w3[1]*w3[1]-w3[2]*w3[2]
                eqn4 =w4[0]*x+w4[1]*y+w4[2]*z-w4[0]*w4[0]-w4[1]*w4[1]-w4[2]*w4[2]
        
                sol = sympy.solve([eqn0, eqn1, eqn2]) ## sol は辞書
                V = []
                V.append([sol[x], sol[y], sol[z]])
                sol = sympy.solve([eqn0, eqn2, eqn3]) ## sol は辞書
                V.append([sol[x], sol[y], sol[z]])
                sol = sympy.solve([eqn0, eqn3, eqn4]) ## sol は辞書
                V.append([sol[x], sol[y], sol[z]])
                sol = sympy.solve([eqn0, eqn4, eqn1]) ## sol は辞書
                V.append([sol[x], sol[y], sol[z]])
                print('V[0]=', V[0])
                print('V[1]=', V[1])
                print('V[2]=', V[2])
                print('V[3]=', V[3])
                ind0 = self.find_semi_v(V[0])
                if ind0 == -1:
                    ind0 = len(self.semi_v)
                    self.semi_v.append(V[0])
                ind1 = self.find_semi_v(V[1])
                if ind1 == -1:
                    ind1 = len(self.semi_v)
                    self.semi_v.append(V[1])
                ind2 = self.find_semi_v(V[2])
                if ind2 == -1:
                    ind2 = len(self.semi_v)
                    self.semi_v.append(V[2])
                ind3 = self.find_semi_v(V[3])
                if ind3 == -1:
                    ind3 = len(self.semi_v)
                    self.semi_v.append(V[3])
                
                if self.semi_e_containedP([ind0, ind1]) == False:
                    self.semi_e.append([ind0, ind1])
                if self.semi_e_containedP([ind1, ind2]) == False:
                    self.semi_e.append([ind1, ind2])
                if self.semi_e_containedP([ind2, ind3]) == False:
                    self.semi_e.append([ind2, ind3])
                if self.semi_e_containedP([ind0, ind3]) == False:
                    self.semi_e.append([ind0, ind3])
        elif self.kind == 1 or self.kind == 4:
            for k in range(len(self.v)):
                v = self.v[k][0]
                e_list = self.v[k][1][0] ## 今度は三角形
                result = self.get_cyclic_pair(e_list, v)
                print('### result=', result)
                w1 = self.v[self.e[result[0]][0][1]][0]
                if self.semi_v_P(v, w1) == True:
                    w1 = self.v[self.e[result[0]][0][0]][0]
                w2 = self.v[self.e[result[1]][0][1]][0]
                if self.semi_v_P(v, w2) == True:
                    w2 = self.v[self.e[result[1]][0][0]][0]
                w3 = self.v[self.e[result[2]][0][1]][0]
                if self.semi_v_P(v, w3) == True:
                    w3 = self.v[self.e[result[2]][0][0]][0]
                
                eqn0 =v[0]*x+v[1]*y+v[2]*z-v[0]*v[0]-v[1]*v[1]-v[2]*v[2]
                eqn1 =w1[0]*x+w1[1]*y+w1[2]*z-w1[0]*w1[0]-w1[1]*w1[1]-w1[2]*w1[2]
                eqn2 =w2[0]*x+w2[1]*y+w2[2]*z-w2[0]*w2[0]-w2[1]*w2[1]-w2[2]*w2[2]
                eqn3 =w3[0]*x+w3[1]*y+w3[2]*z-w3[0]*w3[0]-w3[1]*w3[1]-w3[2]*w3[2]
        
                sol = sympy.solve([eqn0, eqn1, eqn2]) ## sol は辞書
                V = []
                V.append([sol[x], sol[y], sol[z]])
                sol = sympy.solve([eqn0, eqn2, eqn3]) ## sol は辞書
                V.append([sol[x], sol[y], sol[z]])
                sol = sympy.solve([eqn0, eqn3, eqn1]) ## sol は辞書
                V.append([sol[x], sol[y], sol[z]])
                print('V[0]=', V[0])
                print('V[1]=', V[1])
                print('V[2]=', V[2])
                ind0 = self.find_semi_v(V[0])
                if ind0 == -1:
                    ind0 = len(self.semi_v)
                    self.semi_v.append(V[0])
                ind1 = self.find_semi_v(V[1])
                if ind1 == -1:
                    ind1 = len(self.semi_v)
                    self.semi_v.append(V[1])
                ind2 = self.find_semi_v(V[2])
                if ind2 == -1:
                    ind2 = len(self.semi_v)
                    self.semi_v.append(V[2])
                
                if self.semi_e_containedP([ind0, ind1]) == False:
                    self.semi_e.append([ind0, ind1])
                if self.semi_e_containedP([ind1, ind2]) == False:
                    self.semi_e.append([ind1, ind2])
                if self.semi_e_containedP([ind0, ind2]) == False:
                    self.semi_e.append([ind0, ind2])
        elif self.kind == 5:
            for k in range(len(self.v)):
                v = self.v[k][0]
                e_list = self.v[k][1][0] ## 今度は五角形
                result = self.get_cyclic_pair(e_list, v)
                print('### result=', result)
                w1 = self.v[self.e[result[0]][0][1]][0]
                if self.semi_v_P(v, w1) == True:
                    w1 = self.v[self.e[result[0]][0][0]][0]
                w2 = self.v[self.e[result[1]][0][1]][0]
                if self.semi_v_P(v, w2) == True:
                    w2 = self.v[self.e[result[1]][0][0]][0]
                w3 = self.v[self.e[result[2]][0][1]][0]
                if self.semi_v_P(v, w3) == True:
                    w3 = self.v[self.e[result[2]][0][0]][0]
                w4 = self.v[self.e[result[3]][0][1]][0]
                if self.semi_v_P(v, w4) == True:
                    w4 = self.v[self.e[result[3]][0][0]][0]
                w5 = self.v[self.e[result[4]][0][1]][0]
                if self.semi_v_P(v, w5) == True:
                    w5 = self.v[self.e[result[4]][0][0]][0]
                
                eqn0 =v[0]*x+v[1]*y+v[2]*z-v[0]*v[0]-v[1]*v[1]-v[2]*v[2]
                eqn1 =w1[0]*x+w1[1]*y+w1[2]*z-w1[0]*w1[0]-w1[1]*w1[1]-w1[2]*w1[2]
                eqn2 =w2[0]*x+w2[1]*y+w2[2]*z-w2[0]*w2[0]-w2[1]*w2[1]-w2[2]*w2[2]
                eqn3 =w3[0]*x+w3[1]*y+w3[2]*z-w3[0]*w3[0]-w3[1]*w3[1]-w3[2]*w3[2]
                eqn4 =w4[0]*x+w4[1]*y+w4[2]*z-w4[0]*w4[0]-w4[1]*w4[1]-w4[2]*w4[2]
                eqn5 =w5[0]*x+w5[1]*y+w5[2]*z-w5[0]*w5[0]-w5[1]*w5[1]-w5[2]*w5[2]
        
                sol = sympy.solve([eqn0, eqn1, eqn2]) ## sol は辞書
                V = []
                V.append([sol[x], sol[y], sol[z]])
                sol = sympy.solve([eqn0, eqn2, eqn3]) ## sol は辞書
                V.append([sol[x], sol[y], sol[z]])
                sol = sympy.solve([eqn0, eqn3, eqn4]) ## sol は辞書
                V.append([sol[x], sol[y], sol[z]])
                sol = sympy.solve([eqn0, eqn4, eqn5]) ## sol は辞書
                V.append([sol[x], sol[y], sol[z]])
                sol = sympy.solve([eqn0, eqn5, eqn1]) ## sol は辞書
                V.append([sol[x], sol[y], sol[z]])
                print('V[0]=', V[0])
                print('V[1]=', V[1])
                print('V[2]=', V[2])
                print('V[3]=', V[3])
                print('V[4]=', V[4])
                ind0 = self.find_semi_v(V[0])
                if ind0 == -1:
                    ind0 = len(self.semi_v)
                    self.semi_v.append(V[0])
                ind1 = self.find_semi_v(V[1])
                if ind1 == -1:
                    ind1 = len(self.semi_v)
                    self.semi_v.append(V[1])
                ind2 = self.find_semi_v(V[2])
                if ind2 == -1:
                    ind2 = len(self.semi_v)
                    self.semi_v.append(V[2])
                ind3 = self.find_semi_v(V[3])
                if ind3 == -1:
                    ind3 = len(self.semi_v)
                    self.semi_v.append(V[3])
                ind4 = self.find_semi_v(V[4])
                if ind4 == -1:
                    ind4 = len(self.semi_v)
                    self.semi_v.append(V[4])
                
                if self.semi_e_containedP([ind0, ind1]) == False:
                    self.semi_e.append([ind0, ind1])
                if self.semi_e_containedP([ind1, ind2]) == False:
                    self.semi_e.append([ind1, ind2])
                if self.semi_e_containedP([ind2, ind3]) == False:
                    self.semi_e.append([ind2, ind3])
                if self.semi_e_containedP([ind3, ind4]) == False:
                    self.semi_e.append([ind3, ind4])
                if self.semi_e_containedP([ind0, ind4]) == False:
                    self.semi_e.append([ind0, ind4])
                
if __name__ == '__main__':
    
    cube = CreateAllTypeSemiRegular(3, 12, 3)



の様なプログラムで必要なデータを生成できます。ここで

from AllTypeSemiRegularPolyhedron import *
from Frame import *


は上の「準正多面体」の頂点と辺のデータを計算するプログラムと頂点と辺のデータから
「頂点、辺、面の隣接関係」のデータを計算するプログラムです。




































などが描画出来るようになりました。

「準正多面体」の正確な頂点の座標を一松信著「正多面体を解く」の解説を読んで計算し、
「双対多面体」の定義通り、三個の接平面の交点の座標を連立方程式を使って計算してみれば、
型 III の「準正多面体の双対多面体」の「面楊心」と「辺楊心」の持ち上げ量を計算することが
出来るハズです。興味があればやってみて下さい。
上のプログラムを少し修正すれば






の様な一松信著「正多面体を解く」の「図 4.30 面楊心と辺楊心を結んでできる六方 F 面体」を
描画出来ます。しかし、描画を工夫すべきです。
これを描画したデータを使えば、
「６方８面体」の「面楊心」と「辺楊心」の持ち上げ量の近似値を計算することが出来ます。
但し、

        if self.n == 6 and self.kind == 4:
            a = np.array(self.basic_v[0])-np.array(self.basic_v[1])
            r_b = np.sqrt(np.dot(a,a))
            b = np.array(self.semi_v[2])-np.array(self.semi_v[4])
            n = np.dot(b, b)
            r_s = np.sqrt(np.array(n, dtype=np.float64))
            for k in range(len(self.basic_v)):
                self.basic_v[k] = (r_s/r_b)*np.array(self.basic_v[k])


とプログラムする必要がありました。
何でエラーになるのか理解不能な事が起こりましたが、エラーメッセージをインターネットで探索すると
対策が分かります。良い世の中になりました。
作っているプログラムの全体を暗記していないですが、多分、C++ で計算した不動点実数の数値を使っていると、
今まで問題の無かった numpy の関数で、エラーメッセージが出るようになっているみたいで、厄介です。
「準正多面体」の頂点、辺の情報から「頂点。辺。面の隣接関係」を求める時は問題なかったのに、それから計算した
「準正多面体の双対多面体」の頂点、辺の情報から「頂点。辺。面の隣接関係」を求める時はエラーメッセージが
でます。
今まで問題なかったコードが適用範囲を拡大するとエラーになるので、「何が本質的な問題か？」即ち、

        if self.n == 6 and self.kind == 4:
            a = np.array(self.basic_v[0][0])-np.array(self.basic_v[1][0])
            r_b = np.sqrt(np.dot(a,a))
            b = np.array(self.semi_v[2])-np.array(self.semi_v[4])
            n = np.dot(b.astype(np.float64), b.astype(np.float64))
            r_s = np.sqrt(n)
            for k in range(len(self.basic_v)):
                self.basic_v[k][0] = (r_s/r_b)*np.array(self.basic_v[k][0])


の様な変換が「何時必要になるか？」、「それで正しい答えが計算できているか？」、
「本当はどの時点で対応すべきか」、キチンと numpy を勉強する必要があります。
同様に、「図 4.28 」や「図 4.29 」や「図 4.31 」や「図 4.32 」
























なども描画できます。これらを理解するために必要な数学は高校までの数学で十分です。
この様な簡単な Python のプログラムが作れるなら、色々実験し、より良く数学を理解できます。
例えば、「図 4.28 」や「図 4.29 」や「図 4.30 」や「図 4.31 」や「図 4.32 」を最初に見つけた人は
どの様にして見つけたのだろうか？それは我々凡人には分かりませんが、
自分もこの様にすれば、見つけることが出来ると言うことが分かります。
この様な経験を積み重ねば、我々凡人でも何か新しいことを発見・発明できるかも？
更に、






正八面体に内接する正二十面体（正八面体の各辺を黄金比に分割する点が正十二面体の頂点）や






立方体に内接する正二十面体（各面の対辺の中点を結ぶ線分の中点の両側を黄金比に分割する二点が正十二面体の頂点）や







正十二面体に内接する立方体
（立方体の各面に屋根を付けると正十二面体（正五角形の辺と対角線の比は１対 tau=(1+np.sqrt(5)/2 即ち tau^(-1) 対 1）や







直交する三枚の辺の比が黄金比である矩形が内接する正二十面体の様な動画も作れます。
これらから一松信著「高次元の正多面体」の３ページの「正二十面体」や「正十二面体」の座標が
どの様にして見つけたものか、そして、それがユークリッドの「原論」の作図法だと気が付きます。
座標の数値の並びだけを暗記するのは我々凡人には難しいですが、
これらの図形と一緒に学び、この図を覚えていれば、我々凡人でも容易にこれらの座標を導くことが出来ます。多分。
あらゆる事を丸暗記しなければいけない訳でなく、必要になれば覚えていることから導いたり、
インターネットや辞書や参考書で調べる方法を練習して置き、必要になればその都度調べれば良いこともあります。多分。

小・中学校の先生はこの様な多面体の複合の「ストローの模型」を作って、教室に展示して置けば、
数学・幾何学に興味を持つ生徒たちも出てくると思います。文部省は、小・中学校の先生には、
この様な勉強が自由に出来る時間的余裕を与えるべきです。
念願の「日教組」を潰すことには成功しましたが、副作用として「公教育」も潰してしまい、
公立学校の教員のブラック職業化を招き、教員志望者が少なくなってしまったのでは？。

難点はこの様なプログラミングはお金にならないので、必要な事だけ最短で学ぶための参考書が無いことです。

「準正多面体の双対多面体」は綺麗な多面体だと思わなかったので、昔は
プログラミングして描画していなかったので、今回、やってみました。
誰でも出来るこんな事ばかりやっていても詰まりませんから、
本来の「高次元の超立方体の充填形からのタイリングの構成」に
速く到達出来るよう「星形多面体」もありますが三次元の多面体はもうやめ、
一松信著「高次元の正多面体」などを読む必要があるので暫くお休みです。
N. Bourbaki, Elements de mathematique, Algebre VII, Hermann 1976 も読む必要があるみたいです。


放送大学テレビにも面白い講義が一杯あり、知らない分野の学問を教えて貰えます。
大学卒の学位が欲しい訳でなければ、外国語とか情報系とか物理・化学・生物学・地学とか心理学とか文学とか
面白いと思ったものだけ見れば良いです。
講義を聴くだけでは大雑把な事しか分かりませんが、チャンと学ぶためには、どの様な本を読めば良いか分かります。
３万円位の安く小さいテレビでもUSBハードディスクを繋いで、予約録画して置けば何時でも見ることが出来ます。
唯、安いテレビのせいか原因は不明ですが、放送大学ラジオは映らないし、新聞のテレビ欄と異なるところがあります。

物理や化学はさっぱり理解できません。「量子力学」の理解が必須みたいです。「物理のためのベクトルとテンソル」
(違法アップロードではないと思いますが、原著「A Student's Guide to Vectors and Tensors」は pdf ファイルで
インターネットからゲットでき、無料の PC kindle で読むことが出来ます。)を
読んで見ると要は昔習った「微分幾何学」みたいですが、数学では抽象的すぎて良く理解できていなかったので、すっかり忘れました。
例えば、サラッと結果だけ書いてあるこの本の５６ページの発散の円柱座標系の公式 (2.36) や球座標系の公式 (2.37) なども
物理的には明らかな公式かも知りませんが、強引に計算すれば数学的な証明は私にも出来ますが、私がやればかなりの計算量です。
数学と物理両方学ぶのは大変ですが、
我々凡人には、何でそんなことをやっているか理解しながら数学をキチンと学ぶためには本当は必要な事だったかも？
昔は数学者は物理学者を兼ねていました。現在は学ぶべきことが多くなって分離しましたが。多分。


「正三角両角錐」、「正五角両角錐」、「三重増正三角柱」、「蛇腹正四角両角錐」、「双子の十二面体」の
「凸三角面体」を描画する方法を考えていて、上の中ほどで記述したプログラム : usegeneralkite.py を実行すると


Traceback (most recent call last):
  File "H:/PythonSrc/OpenGL/一松信/第４章準正多面体/タートルグラフィックス/Kite/usegeneralkite.py", line 11, in 
    from tetra import *
ModuleNotFoundError: No module named 'tetra'


の様なエラーメッセージが表示されることに気が付きました。


from tetra import *


は必要なく、コメントアウト（削除）しておくべきでした。
なんかの拍子にコメントアウトしていたのがはずれ、古いプログラムの断片が残っていました。

この様な多面体はタートルグラフィックスで描画して、各頂点の座標を表示して、openGL のプログラムを
作るのが、直接手計算で頂点の座標を計算するより楽かも？好みの問題ですが？


弥右衛門公園の「ヤマモモの木」に赤い小さな実が沢山なっているのに気が付きました。県外では「ヤマモモ」は余り
食べられていないみたいですが、高知県では沢山ある果物（文旦と新高梨が高知を代表する果物で、今の時期は小夏が旬です）の一つです。
もうすぐスーパーにも並ぶハズです。


二十数年前に作った Archimedes.exe のソフトを作った時のメモをバインダーに纏めておいたものがあることに気が付いたので補足しておきます。






不鮮明な写真ですが、「正六面体」の「捩じり切り」の為の3次元方程式の求め方をメモに書いてありました。
４次元以上と異なり、３次元では模型が作れるので、出来上がりの模型と正多面体の「捩じり切り」がどの様なものであるか分かるように
紙の模型に切り取った時に出来る辺を描いて見ます。そうすれば、「正六面体」と「正八面体」、「正十二面体」と「正二十面体」で
同じ準正多面体が出来る理由も理解できますし、どの辺の長さが等しいとして方程式を見つけるべきかが理解できます。

「準正多面体」の「捩じり切り」のデータの計算は厄介ですが、描画するだけなら、一松信著「正多面体を解く」の表 4.7 の数値
「正六面体」:「b/a=0.43759329, α=16.467560555555554」と「正十二面体」「b/a=0.56212196, α=13.106402777777777」を使えば、













の様に「正六面体」と「正十二面体」を削って作る準正多面体は作れますが、「正四面体」、「正八面体」及び「正二十面体」を「捩じり切り」
する為には、それぞれ、「b/a=0.270091, α=22.2388」、 「b/a=0.336462, α=20.315」、「b/a=0.363856, α=19.5109」の値を使えば、


















を描画できます。残っていたメモには「正六面体」の計算方法しか書いてなくて、


import sympy as sp
import numpy as np

u = sp.Symbol('u')
v = sp.Symbol('v')

a1 = u
a2 = v
a3 = 0
b1 = 1-v
b2 = u
b3 = 0
c1 = v
c2 = 1-u
c3 = 0
d1 = 0
d2 = u
d3 = v
e1 = 0
e2 = 1-v
e3 = u
f1 = v
f2 = 0
f3 = u
g1 = 1-u
g2 = 0
g3 = v

ab = (a1-b1)**2+(a2-b2)**2+(a3-b3)**2
ac = (a1-c1)**2+(a2-c2)**2+(a3-c3)**2
ad = (a1-d1)**2+(a2-d2)**2+(a3-d3)**2
ae = (a1-e1)**2+(a2-e2)**2+(a3-e3)**2
af = (a1-f1)**2+(a2-f2)**2+(a3-f3)**2
bf = (b1-f1)**2+(b2-f2)**2+(b3-f3)**2
bg = (b1-g1)**2+(b2-g2)**2+(b3-g3)**2
ce = (c1-e1)**2+(c2-e2)**2+(c3-e3)**2

print('ab=', sp.expand(ab))
print('ac=', sp.expand(ac))
print('ad=', sp.expand(ad))
print('ae=', sp.expand(ae))
print('af=', sp.expand(af))
print('bf=', sp.expand(bf))
print('bg=', sp.expand(bg))
print('ce=', sp.expand(ce))

print('ab-ac=', sp.expand(ab-ac))
print('ab-ad=', sp.expand(ab-ad))
print('ab-ae=', sp.expand(ab-ae))
print('ab-af=', sp.expand(ab-af))
print('ab-ae=', sp.expand(ab-bf))
print('ab-ae=', sp.expand(ab-bg))
print('ab-ce=', sp.expand(ab-ce))

eq = 2*v**3-4*v**2+4*v-1
s = sp.solve(eq, v)
print()
print('s=', s)
s1 = 2/3 + 2/(3*(-1/2 - np.sqrt(3)*1j/2)*(13/4 + 3*np.sqrt(33)/4)**(1/3)) \
- (-1/2 - np.sqrt(3)*1j/2)*(13/4 + 3*np.sqrt(33)/4)**(1/3)/3
s2 = 2/3 - (-1/2 + np.sqrt(3)*1j/2)*(13/4 + 3*np.sqrt(33)/4)**(1/3)/3 \
     + 2/(3*(-1/2 + np.sqrt(3)*1j/2)*(13/4 + 3*np.sqrt(33)/4)**(1/3))
s3 = -(13/4 + 3*np.sqrt(33)/4)**(1/3)/3 \
     + 2/(3*(13/4 + 3*np.sqrt(33)/4)**(1/3)) + 2/3
print()
print('s1=', s1)
print('s2=', s2)
print('s3=', s3)
print()
print('v=', s3)
print('u=', -s3**2+s3)
print()
b_2 = ab.subs([(u, 0.22815549365396184 ), (v, 0.3522011287389577)])
print('b_2=', b_2)
b =np.sqrt(0.191487883953119) 
print('b/a=', b)
pi = 4*np.arctan(1)
alpha = pi/4 - np.arccos(np.sqrt(2)*(1/2-0.22815549365396184)/b)
print('alpha=', alpha*180/pi)
print('alpha=', alpha)

theta = np.arccos(np.sqrt(2)*(1/2-0.22815549365396184)/b)
print('theta=', np.arccos(np.sqrt(2)*(1/2-0.22815549365396184)/b))
print('theta=', np.arccos(np.sqrt(2)*(1/2-0.22815549365396184)/b)*180/pi)
print(-1.072811312155226+ pi/2 )
print(theta-pi/2)
print((pi/4-theta)*180/pi)


の様なプログラムで


ab= 2*u**2 - 2*u + 2*v**2 - 2*v + 1
ac= 2*u**2 - 2*u + 2*v**2 - 2*v + 1
ad= 2*u**2 - 2*u*v + 2*v**2
ae= 2*u**2 + 4*v**2 - 4*v + 1
af= 2*u**2 - 2*u*v + 2*v**2
bf= 2*u**2 + 4*v**2 - 4*v + 1
bg= 2*u**2 - 2*u*v + 2*v**2
ce= 2*u**2 - 2*u*v + 2*v**2
ab-ac= 0
ab-ad= 2*u*v - 2*u - 2*v + 1
ab-ae= -2*u - 2*v**2 + 2*v
ab-af= 2*u*v - 2*u - 2*v + 1
ab-ae= -2*u - 2*v**2 + 2*v
ab-ae= 2*u*v - 2*u - 2*v + 1
ab-ce= 2*u*v - 2*u - 2*v + 1

s= [2/3 + 2/(3*(-1/2 - sqrt(3)*I/2)*(13/4 + 3*sqrt(33)/4)**(1/3)) - (-1/2 - sqrt(3)*I/2)*(13/4 + 3*sqrt(33)/4)**(1/3)/3, 
2/3 - (-1/2 + sqrt(3)*I/2)*(13/4 + 3*sqrt(33)/4)**(1/3)/3 + 2/(3*(-1/2 + sqrt(3)*I/2)*(13/4 + 3*sqrt(33)/4)**(1/3)), 
-(13/4 + 3*sqrt(33)/4)**(1/3)/3 + 2/(3*(13/4 + 3*sqrt(33)/4)**(1/3)) + 2/3]

s1= (0.8238994356305211+0.8607166186235682j)
s2= (0.823899435630521-0.8607166186235682j)
s3= 0.3522011287389577

v= 0.3522011287389577
u= 0.22815549365396184

b_2= 0.191487883953119
b/a= 0.43759328600096115
alpha= 16.467560400386297
alpha= 0.28741314875777657
theta= 0.4979850146396717
theta= 28.532439599613703
0.4979850146396705
-1.072811312155225
16.467560400386297


の結果を得ます。但し、このプログラムは、計算結果を見ながら、書き足し書き足して作っています。
sympy で得た数値を使わないと numpy で変数のままではそのまま使えません。又は、データの変換をすれば良いです。
「類比」（真似をして）で一松信さんのヒント通り（斜交座標を使い、正多面体の二つの面の正p角形の頂点の座標を(u,v)で表現し、
直交座標に変換し、更に隣接する一方の面を2φだけx軸の周りに回転し、頂点間の距離が等しいとして連立方程式を求める）
やれば良いはずですが、二十数年前にどうやってこれらの値を求めたか今では不明です。
図4.9 「互いに鏡像をなす右手系と左手系の立体」とあるように２種類あるので、「正四面体」から作られる「正二十面体」以外は、
正多面体の隣接関係のデータで、各面に隣接する頂点（と辺）を「反時計回り」に並べておく必要があります。
私のプログラムでは、Frame.py を更に作り直す必要がありました。
泥縄的に継ぎ足し継ぎ足しで、綺麗に整理してからでなければ、とても人様に見せるような代物ではありません。
これらだけ描画するなら、正多面体の隣接関係のデータを手作業でセットすれば良いです。
「捩じり切り」以外の準正多面体の x, y の値等の値は簡単に導けると思います。

P.R.クロムウェル著「多面体」には












の様な包含関係が図示（図 2.22 ：「切頭立方体、立方八面体、それに切頭八面体はすべて立方体か
正八面体を切り取ることで得られる。」）されています。
これを見れば誰でも「類比」（真似をすること）で、「切頭十二面体、二十・十二面体、それに切頭二十面体は
すべて正十二面体か正二十面体を切り取ることで得られる。」に気付きます。実際。












の様に可能です。他にも色々な多面体の包含関係があります。
この様に、我々凡人でも、ポリアさんが教えてくれた「帰納」と「類比」で考え、それを「プログラミング」で検証すれば、
時間はかかりますが、数学を理解することが出来ます。多分。

これは簡単な例で、才能ある優秀な人達は図をじーっと眺めれば全て理解すると思いますが、我々凡人は
切頭八面体の正方形が立方体の各面に一つづつ乗っている（及び切頭八面体の正三角形が正八面体の各面に一つづつ乗っている）のを見て、
もしやと思い、（準正多面体は立方体・正八面体と正十二面体・正二十面体のペアで同じ多面体が作れるので）調べると
切頭二十面体の正五角形の配置が正十二面体の各面の配置、切頭十二面体の正三角形の配置が正二十面体の各面の配置が対応しているから、
同じことが成り立つのではと思います。正十二面体と正二十面体の展開図を打ち出し、紙の模型を作り、
それぞれの各面に小さな正五角形と正三角形を描き、隣接する面の頂点を辺になる線分の投影図を描けば、
確信になります。正確な大きさを計算し、その結果を確かめる為に、プログラミングして見ます。
プログラミングが出来れば、先生がいなくても、計算結果が正しいか正しくないか自分一人で判断できます。
この様なプロセスを踏めば、理解できた・分かったと自分自身を納得させることが出来、自信になります。多分。

優秀な人達とのこの違いは、丸岡章著「概説　人工知能　ディープラーニングから生成 AI へ」で解説されている
カーネマンのシステム１とシステム２で説明出来ると思います。システム１：瞬時に無意識のうちに下す判断、
システム２：意識して判断を下す時に用いるもので、図をじーっと眺めて理解できるのは、システム２を繰り返し、
練習した結果、システム１で判断できる様になった可能性もあると思います。
我々凡人でも、詰将棋や詰碁を「何を考えれば良いか意識しながら」只管練習すれば、簡単なものは一瞬で解けるように。
我々凡人は練習が足りないから、システム２を使う必要があります。多分。才能の違いもあるとは思いますが。

次はP.R.クロムウェル著「多面体」に掲載されている「正多角形を面に持つ凸多面体」の一部の「ストローの模型」です。








有名な3次元多面体の一覧は http://polyhedra.html.xdomain.jp/polyhedron_table.html で見ることが出来ます。
中国人が作成したものなのか「中国語を翻訳しますか」と表示されます。
老人のボケ防止の為に暇を見つけてコレクションを増やせば良いです。平面に投影した図だけですから、
辺の長さの比が不明なものもあり、自分で計算する必要な物もありますし、複雑な多面体は図をよく見て、
考え考え作る必要な物もあります。

この様な情報は簡単に得ることが出来るようになりましたが、かって批判された「詰め込み教育」は何が駄目だったかと考えます。
唯、この様な単なる事実だけを只管覚えさせられた事なのかな？例えば、院政が始まったとは習いましたが、何で、院政が始まったかは
習わなかったように思います。藤原氏などの摂関家が娘を天皇に嫁がせて、孫を天皇にすることで権勢を得ていたのを、
天皇が自分の直系の子孫を天皇にする為に、天皇や皇太子を早めに決めて、自分は法王として権力を維持していたという
最近語られるようになった支配階級の権力争いの解説があれば、単なる出来事の羅列ではなく、それが起こった理由の説明・解説があれば、
即ち、今までのあらゆる教科の公式の丸暗記ではなく、公式の解説・理解を伴った「詰め込み教育」なら悪いものではないのではないかと思います。
現在の政治家たちの権力争いの構図も理解できるのでは？全部、自分で考えるべきだと言っても、訓練しないと難しいです。
我々は本当に知るべき事の教育・考え理解する教育を受けてこなかったんだなあと最近よく思います。
だから、皆、支配者階級の頭の良い人達にころっと騙されます。

ミステリーなどの低俗なものは読まないと言う有名人もいますが、ミステリーから色々な事を学ぶこともあります。
今、初めて台湾の作家の「炒飯狙撃手」を読んでいます。面白いです。
「・・・　「軍人を生業とするなら、給料をもらって突っ立っているだけでいい。退役するまでな。
その点、わしは何か言うつもりはない。だが軍人を志すのであれば、何より集中力が必要だ。
軍人だったら集中できるはずだ。わしの声がはっきり聞こえているか？
ちっぽけなシラミが、車輪の大きさに見えてくるまで、ひたすら練習しろ。・・・」
「家というのはですね、いいですか。上にある「宀」というのが、煙突のある屋根を意味するんです。
最新の考古学的証拠によると、陝西省西安には、紀元前五千年前から煙突があったことが判明しています。
屋根の左右に、二本の柱がある。そして屋根の下には「豕」がある。この文字は、豚の古語でしてね」
・・・「家が「宀」と「豕」でできているのには、二つ、理由があってね。
一つは、古代人が蛇や狼などの獣を避けるために家の下で豚を飼い、人は上階で寝たとする説だね。
豚を育てるということはつまり、いよいよ農耕社会になってきたということさ。
社会には食料が十分あり、生活が保障されている。そして生活の保障の上に家族が形成される」
・・・　
今の日本で全ての国民に「生活の保証」が本当になされているだろうか？

「狡知ある者が必ず愚かな者をだますことができ、強者が必ず弱者をいじめることができるのが、
自然規則である。自然規則に従えば、人道は行きづまってしまう。
それ故、人為規則が自然規則の弊害を正すことによってはじめて、民衆は生存できるのである」
（「両京十五日」の訳者あとがきにある清末の章炳麟さんの言葉）

支配者階級の頭の良い人達は個人の「自己責任」として、見え見えの手を使って、国民を誘導し、
国公立大学の授業料の大幅値上げを画策するなど、日本が生き残っていくために必要不可欠な
幅広い人材育成の為の教育政策など放棄して、東京（大阪も？）の富裕層だけ良ければ良いと考えているのでは？

更に、東日本大震災の復興予算と能登震災の復興予算の違いは、能登の様な僻地を復興する価値がないと
更に大阪万博の準備の障害になると考えているだけでなく、「珠洲は原発に反対したんや」と、地元で、
だから「報復している」と受け取れる発言したと報道されている
首相候補と自他ともに認める有力政治家もいます。政治家を生業としている政治家はまだ実害は少ないですが、
この様な事を酒の席とは言え平気で言う有力政治家を全力で失脚させないと日本の将来は更に惨めなものでは？
東京暮らしの政治家は兎も角、阪神・淡路の有権者たちは 29年前の阪神・淡路大震災で全国から
支援を受けたことをもう忘れたのでしょうか？恩を忘れ、能登の人たちを敵視・無視する政治家が立候補する
今度の衆議院議員選挙で兵庫県の有権者がどの様な投票行動をするか、全国の国民が注視する思います。


Michael Baake and Uwe Grimm 著「APERIODIC ORDER」を読むためには、我々凡人は予備知識として
J.W.S.Cassels 著「An Introduction to the Geometry of Numbers」
（線形代数は係数が R や C ですが、Z に一般化した論文達を整理し、as self-contained as possible に解説した本です。
この様な一般化を考えることで沢山の人たちが数学の論文を書くことが出来ます。）を読めば良いと思います。

更に、読む時、
大学受験などの受験勉強をしている時や誰も知らないことを研究している時とは当然読み方が異なります。
受験勉強は数学は満点が取れる教科ですが、必ずしも満点を取る必要はなく、他の教科の点数と合算して、
合格に必要な点数以上を取れば良いです。誰も知らないことを研究している時は、先日も高知大学の研究者が
「20年間研究を続けて」、大発見をし、外国の有名な学術誌に掲載されたと新聞に大きく報道されていましたが、
誰も知らないことを見つけるのは大変な時間と努力が必要で、２，３年の期限付きで成果を挙げよと
命令されている身分の不安定な若手研究者は可哀そうです。研究が何たるか知らない人達が制度設計をしているのでは
ないだろうか？それに対して、既に知られている数学を学ぶ時は、自分に合った適切な参考書に出会うことが出来れば、
誰でも時間をかければ理解できます。

例えば、この本の１３ページの Corollary 1 の B の証明は Similar. の一言です。
Similar. と書いているので、 「Corollary 1 の A の証明と同じことをすれば良い（類比）」と言うことですが
我々凡人には何が同じか直ぐには分かりません。直ぐに思いつくことをやってみると計算が複雑になり過ぎ、
とても「Corollary 1 の A の証明と同じ分量に収まりませんから、これは Similar. ではないことに気が付きます。
ある程度やってみて出来なければ、散歩に行ったり、推理小説を読んだりしてその日は止めて、
次の日、元の Theorem I の A, B の証明から読み直します。
何日か、ああでもない、こうでもないとやって、やっと「Corollary 1 の A の証明と逆」に
$$
b_1 = b'_1, b_2=t_{21}b'_1+b'_2, \cdots, b_n=t_{n1}b'_1+\cdots+t_{n,n-1}b'_{n-1}+b'_n
$$
と置けば良いことに気付きました。これなら「Corollary 1 の A の証明と同じ分量」に収まり、
同じ方法・技法で証明が出来ます。
こうゆう処を「まあいいや」とキチンと理解しないままに飛ばすと、私の場合。確実にその本が読めなくなります。
ちゃんとした自分の能力に合った参考書は時間を掛ければ理解できるので、自分が分かったと思うまで
粘って見ます。それが出来ない参考書は、本当は良い本で有っても少なくても現時点では、自分には必要ない参考書です。

処が、In some contexts we shall need the following more speialized corollay 
which follows at once from Crollay 3. と書いていて、Corollary 4 の証明は Proof. Clear. と書いてあります。
数学の clear や trivial は厄介で、私はこれは著者の勘違い？ではないかと思います。
Corollay 3 と Corollay 4 が関係あるとは思えません。Corollay 4 は正しい命題のハズで、
既にキチンと証明されているハズです。必要条件は私でも一般的に証明できますが、
十分条件は m=n, n-1, n-2, ... と順番に帰納的に考え、basis を構成する必要がありますが、
m=n の場合は明らかで、m=n-1 の場合は、具体例を色々やってみて、一般的に証明出来ましたが、
m=n-2 場合は m=n-1 の場合の構成法を組み合わせ、「最大公約数に関する２個の予想」を証明できれば、
一般的に証明出来ますし、それが出来れば、一般の m 場合にどの様に basis を構成すれば良いか帰納出来そうですが、
「最大公約数に関する２個の予想」の証明を思い付きません。この方針が間違っているのか、疲れました。
これは保留にして置き、本の続きを読み、 Corollay 4 が必要になれば、もう一度挑戦した方が良いみたいです。

処が、次のLemma 1 の証明も本に書いてある情報だけでは直ぐに理解できず、具体的なΛとMに対して計算してみて、
どの様に証明すればよいかやっと理解できました。
この本は普通の数学の参考書ではなく、どうも情報を与える事典のような本です。
1959年の出版で、私は古本で購入しましたが、最初は8970円で販売するつもりっだたものを売れないので5600円に値段を下げたものを
私が購入したみたいです。三宅香帆著「なぜ働いていると本が読めなくなるのか」で解説されている現在売れる本である
「情報」を手軽に得ることの出来る本と同じようなものです。これをいちいち証明を付けていたら何時読み終わるか分かりません。
通して読むのは止めて、Michael Baake and Uwe Grimm 著「APERIODIC ORDER」を読みながら、必要になったら、
J.W.S.Cassels 著「An Introduction to the Geometry of Numbers」の必要な箇所だけ読むべきでした。

我々凡人には矢張り数式ばかりの本より、Michael Baake and Uwe Grimm 著「APERIODIC ORDER」のような
図形ばかりの本が眺めていて楽しいですし、コンピュータでその図を描けば規則も見えてきます。多分。
その図形に含まれる法則をキチンと数学的な裏付けを持って教えて貰うには、
J.W.S.Cassels 著「An Introduction to the Geometry of Numbers」のような代数関連の数式ばかりの本や
更には Fourier transform のような解析関連の本も読む必要があり、数学のあらゆる分野が関連していますが、
先ずはどの様な図形（現在の関心事は Tilings ですが）が既に知られているか目を通すのが多分良いです。

ちなみに、三宅香帆著「なぜ働いていると本が読めなくなるのか」もそうだったんだと面白くて一気に読みましたが、
現在売れている本のトレンドそのままに手軽に「情報」を得る為の本ですが、著者がこの本を書くためには
大変な努力が必要っだった事も分かりますし、この本に書いてあることを検証するにも大変な労力が必要です。

icosidodecahedron の座標は
$$ (\pm 1, 0, 0), \frac{1}{2}(\pm 1, \pm \tau', \pm \tau) \  where \  \tau'=1-\tau $$
の全ての偶置換が座標になると言う情報も root system や Weyl group H3 を求める為に必要です。
この座標で作られる準正多面体は


from Frame import *

def even_permutationP(permutaton):
        p = 1
        for i in range(len(permutaton)):
            for k in range(i+1, len(permutaton)):
                p = p*(permutaton[i]-permutaton[k])
        if p > 0:
            return True
        else:
            return False

def get_even_perm(r, l, s, k):
        if len(s)==k:
            if even_permutationP(s):
                r.append(s)
            return
        for e in l:
            old_s = s[:]
            s.append(e)
            new_l = l[:]
            new_l.remove(e)
            get_even_perm(r, new_l, s, k)
            s = old_s

def get_even_symmetry_group(n):
        l = []
        r = []
        k = n
        l = [i for i in range(n)]
        get_even_perm(r, l, [], k)
        return r

def even_f(ind, i):
    T = (1+np.sqrt(5))/2
    IT = 1/T
    if ind == 0:
        return i
    elif ind == 1:
        return 0
    elif ind == 2:
        return 0

def even_f2(ind, i, j, k):
    T = (1+np.sqrt(5))/2
    IT = 1/T
    if ind == 0:
        return i/2
    elif ind == 1:
        return j*IT/2
    elif ind == 2:
        return k*T/2

class GeneralCube:
    def __init__(self, dim):
        self.dim = dim
        self.v =[]
        self.e = []
        self.v, self.e = self.get_single_polytope_inf()
        print('self.v=', self.v)
        print('self.e=', self.e)
        
        self.frame = MakeFrame(self.dim, self.v, self.e)
        
    def get_single_polytope_inf(self):
        if self.dim == 3: 
            ## Aperiodic order
            v = []
            lst = get_even_symmetry_group(3)
            print('lst=', lst)
            for i in range(1,-2,-2):
                for s in range(len(lst)):
                        v.append(np.array([even_f(lst[s][0], i),\
                                               even_f(lst[s][1], i),\
                                               even_f(lst[s][2], i)]))
            print('v=', v)
            for i in range(1,-2,-2):
                for j in range(1,-2,-2):
                    for k in range(1,-2,-2):
                        for s in range(len(lst)):
                            v.append(np.array([even_f2(lst[s][0], i, j, k),\
                                               even_f2(lst[s][1], i, j, k),\
                                               even_f2(lst[s][2], i, j,k)]))
            min_l = 100
            for i in range(len(v)):
                for j in range(i+1, len(v)):
                    w = v[i]-v[j]
                    l = np.dot(w, w)
                    if np.abs(l-min_l) < 0.001:
                        continue
                    if l < min_l:
                        min_l = l
            e = []
            for i in range(len(v)):
                for j in range(i+1, len(v)):
                    w = v[i]-v[j]
                    l = np.dot(w, w)
                    if np.abs(l-min_l) < 0.001:
                        e.append([i, j])
            return v, e


と言ったプログラムを作れば、既に作っているプログラムと併せて








と icosidodecahedron (semi-regular polyhedron) とその双対多面体 triacontrahedron (Kepler's body) を描画できます。

この本には様々な事を書いていますが、何が本当に必要か兎も角全体をざっと読み通してみる必要があります。
人生は以外に短く、我々凡人はあらゆることを知ることは出来ません。

又、この本を読んでいて具体例が理解できなければ、人に見せるための凝った図でなくても良いですから












の様な図を描いてみれば、Example 3.1 やその直前の dual lattice や dual basis の定義が何を言っているか？
又、この二つの lattices （original と dual）が相似であることも我々凡人でも容易に理解できます。
良く理解できなければ、自分で図を描いてみれば良いです。
「物理のためのベクトルとテンソル」を同時に読んで見ると dual basis が何であるか分かります。
「ベクトル」は元々物理の研究から考えられたものらしいですから、若い時に物理も学んでおくべきでした。

「犯人はすごい専門知識を持っているのに、こういう基礎課程の講習に参加する必要があったのかな？」
とテキ（羽＋隹）巡査部長が言う。
「誰でも最初は初心者なんだし、基本的なやり方を学ぶ必要があっただろう。インターネットで A から Z まで
すべて勉強するのは不可能だよ。台湾ではこういうワークショップは本当に少ない。おれがそいつだったら、
こういうチャンスがあったら、きっと参加する」
「「修業は一人でするものだが、入門には師匠が必要」っていいますからね」。小趙が言う。
（紀蔚然著「台北プライベートアイ」）

Harriss E. and Frettloh D. (wds.) Tilings Encyclopedia, available at http://tilings.math.uni-bielefeld.de/
に沢山の aperiodic tilings の画像が集められています。
更に、見たことのなかった一次元の tilings も沢山掲載されています。
「帰納」と「類比」と「プログラミング」で考えるには一次元の tilings の情報も貴重です。

「aperiodic order」の chapter 7 Projection Method and Model Sets まで読むのが当面の目標ですが矢張り難しくて大変です。
素人目には簡単に見える tilings の様な事にも広範囲の深い数学の知識・技能が必要で、
知らないことや昔は出来たはずなのにすっかり忘れてしまったことが多すぎます。ボケ防止と思って少しづつ読んでいます。

aperiodic tilings との関連はまだ不明ですが、 p-adic number に関する情報は英文なら各大学が載せている情報がインターネットに沢山あります。
有理数の p-adic number を手計算で計算するのは厄介ですが、ごちゃごちゃしていて良いプログラムではないですが、


from fractions import Fraction
import numpy as np

def extended_gcd(a, b):
    s = 0
    old_s = 1
    r = b
    old_r = a
         
    while r != 0:
        quotient = old_r // r
        old_r, r = r, old_r - quotient * r
        old_s, s = s, old_s - quotient * s
    
    if b != 0:
        bezout_t = (old_r - old_s * a) // b
    else:
        bezout_t = 0
    ## a * old_s = old_r + b * ( -bezout_t )
    return old_s, - bezout_t, old_r

def get_valuation(n, radix):
    m = n
    v_n = 0
    p = 1
    while m % radix == 0:
        m = m // radix
        v_n = v_n + 1
        p = p * radix
    return v_n, n // p
        
def step_of_p_adic_number(F, radix, k):
    original_m = F.numerator
    original_n = F.denominator
    if original_m > 0:
        m = original_m
    else:
        m = - original_m
    n = original_n
    v_m, m = get_valuation(m, radix)
    v_n, n = get_valuation(n, radix)
    v = v_m - v_n
    q, h, gcd = extended_gcd(n, radix)
    k = m*q // radix
    a = m*q % radix
    new_m = k * n - h * m
    if original_m > 0:
        if new_m > 0:
            new_v_m, m = get_valuation(new_m, radix)
        else:
            new_v_m, m = get_valuation(-new_m, radix)
            m = -m
        next_v = v + 1 + new_v_m
        return a, v, next_v, m, n
    ## original_m is negative:
    a = - a
    new_m = - new_m
    p = a // radix
    q = a % radix
    a = q
    m = p * radix *n + radix**(v+1) * new_m
    if m > 0:
        new_v_m, m = get_valuation(m, radix)
    else:
        new_v_m, m = get_valuation(-m, radix)
        m = -m
    v_n, new_n = get_valuation(n, radix)
    next_v = v + new_v_m    
    return a, v, next_v, m, new_n
    
def get_p_adic_number(F, radix, k):
    A = []
    ## first step
    original_m = F.numerator
    original_n = F.denominator
    print('original_m=', original_m, 'original_n=', original_n)
    if original_n == 1:
        if original_m != 0:
            m = original_m
            print('m=', m)
            start_v = 0
            count = 0
            while m != 0:
                a = m % radix
                m = m // radix
                A.append(a)
                count = count+1
                if count > k:
                    break
            print('start_v=', start_v)
            print('A=', A)
            return
        else:
            start_v = 0
            A.append(0)
            print('start_v=', start_v)
            print('A=', A)
            return
    a, v, next_v, new_m, n = step_of_p_adic_number(F, radix, k)
    start_v = v
    A.append(a)
    for j in range(next_v-1-v):
        A.append(0)
    for i in range(k):
        F = Fraction(new_m, n) 
        a, v, next_v, new_m, n = step_of_p_adic_number(F, radix, k)
        A.append(a)
        for j in range(next_v-1-v):
            A.append(0)
    print('start_v=', start_v)
    print('A=', A)    

F =  Fraction(1, 3)      
radix = 5
k= 30
get_p_adic_number(F, radix, k)
F =  Fraction(1, 5)      
radix = 3
k= 30
get_p_adic_number(F, radix, k)
F =  Fraction(1, 7)      
radix = 5
k= 30
get_p_adic_number(F, radix, k)
F =  Fraction(18, 5)      
radix = 3
k= 30
get_p_adic_number(F, radix, k)
F =  Fraction(1, 45)      
radix = 3
k= 30
get_p_adic_number(F, radix, k)
F =  Fraction(5, 1)      
radix = 3
k= 30
get_p_adic_number(F, radix, k)
F =  Fraction(-1, 1)      
radix = 3
k= 30
get_p_adic_number(F, radix, k)
F =  Fraction(-5, 1)      
radix = 3
k= 30
get_p_adic_number(F, radix, k)
F =  Fraction(0, 1)      
radix = 3
k= 30
get_p_adic_number(F, radix, k)


の様なプログラムを作れば、本当は無限系列になりますが


original_m= 1 original_n= 3
start_v= 0
A= [2, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1]
original_m= 1 original_n= 5
start_v= 0
A= [2, 0, 1, 2, 1, 0, 1, 2, 1, 0, 1, 2, 1, 0, 1, 2, 1, 0, 1, 2, 1, 0, 1, 2, 1, 0, 1, 2, 1, 0, 1, 2, 1, 0, 1, 2, 1, 0, 1, 2, 1, 0]
original_m= 1 original_n= 7
start_v= 0
A= [3, 3, 0, 2, 1, 4, 2, 3, 0, 2, 1, 4, 2, 3, 0, 2, 1, 4, 2, 3, 0, 2, 1, 4, 2, 3, 0, 2, 1, 4, 2, 3, 0, 2, 1, 4, 2]
original_m= 18 original_n= 5
start_v= 2
A= [1, 1, 2, 1, 0, 1, 2, 1, 0, 1, 2, 1, 0, 1, 2, 1, 0, 1, 2, 1, 0, 1, 2, 1, 0, 1, 2, 1, 0, 1, 2, 1, 0, 1, 2, 1, 0, 1, 2, 1, 0]
original_m= 1 original_n= 45
start_v= -2
A= [2, 0, 1, 2, 1, 0, 1, 2, 1, 0, 1, 2, 1, 0, 1, 2, 1, 0, 1, 2, 1, 0, 1, 2, 1, 0, 1, 2, 1, 0, 1, 2, 1, 0, 1, 2, 1, 0, 1, 2, 1, 0]
original_m= 5 original_n= 1
m= 5
start_v= 0
A= [2, 1]
m= -1
start_v= 0
A= [2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2]
original_m= -5 original_n= 1
m= -5
start_v= 0
A= [1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2]
original_m= 0 original_n= 1
start_v= 0
A= [0]


と指定したところまで計算してくれます。まだバグが残っているかもしれませんが、これらの例では正しい答えが出ていて、
規則性（有理数（分数）を小数で表現した時の循環小数の様に循環していること）が見て取れます。
これらは各有理数の p-adic series の同値類の normalized  p-adic series 代表元を表示したものです。
我々凡人はこの様な具体的な例で理解します。良い時代になりました。但し、証明は抽象的な定義に基づいて証明する必要があります。
完備化(completion)は有理数から実数を作った時のように、この様に循環しているものを含む循環していないもの全体に拡張することです。
「類比」に依れば、多分。専門が代数ではないので全くの出鱈目かも？代数も学ぶべきことが多くて難しいです。
（五十数年前の学生時代に一通り代数も基本的なことは教わりましたが、必要がなかったので、今ではすっかり忘れてしまいました。
本当に必要なら昔の参考書等を眺めれば、多分、直ぐに思い出すとは思いますが。）
そうすれば、aperiodic なものが出てくるのかな？

Haar measure も現在は欧米の各有名な大学が解説の文書の pdf ファイルをインターネットにアップしてくれているので、自分が読んでわかるものを
読めば良いです。例えば、UMEA UNIVERSITY と言うスウェーデンの有名な大学の
「The Existaence and Uniqueness of the Haar Mesure」
は Topology, Measure Theory, Locally Compact Groups の定義から必要な事を解説してくれています。
但し、積分の詳しい解説はないので、必要なら、別途、理解できる解説の文書の pdf ファイル又は参考書を探す必要があります。
この解説には Donald Cohn, Measure theory, 2nd ed., Springer, 2013 を読みなさいと書いてあります。
この様な解析は面倒な定義、定理の羅列になり一つ一つ暗記・理解しながら読むのは大変なので、
家で独学するには手頃な大きさのホワイトボード（百均にも３００円位でホワイトボードがありますが私が使うには小さいです）を2枚手に入れて、
覚えるべきことを一枚に箇条書きし、もう１枚でそれを見ながら必要な証明を繰り返し練習すれば良いです。多分。
「証明を丸暗記する」為ではなく、「証明に使われている（独特な）目玉になっているアイデア・技法・テクニックを発見し身につける」為に繰り返し練習します。
それが結果として「証明を丸暗記する」ことになるかも？
しかし、最初から「証明の丸暗記」を目標にするわけではなく、「何に気が付けば私でも解けるか？」を見つけようとします。
私が「ルベーグ積分」を教わった冨田先生は原稿もメモも無しでチョークの箱だけ持ってブラーとやってきてその場で考えながら講義して下さりました。
本当に才能ある優秀な人とはこの先生の様な人達を言うのだと思います。我々凡人には真似ができません。
Donald Cohn, Measure theory, 2nd ed., Springer, 2013 は Birkhauser からも出版されています。
必要な予備知識は Appendix に簡潔に纏められていて、例や演習問題も多く、Haar Measure を含む広範囲の話題が取り上げられています。
文字が小さいですが４００ページ位の本で、まだ始めの方しか読んでいませんが、論理のギャップが少なく今まで手に取った
Measure Theory ・ルベーグ積分 の本の中で最も読みやすい参考書です。
但し、全ての演習問題を解くには、殆どの問題がそれまでに学んだ事を使えば解けるように教育的配慮がされていて、
暫く考えれば殆ど解けますが、私には随分時間が掛かります。
英語も、例えば「Show that the set of points that belong to A_k for infinitely many values of k has measure zero under μ.」は
瞬時には私には意味が取れませんが、解説の流れから言って、数学的に何が証明できるはずかを考えれば、意味を掴むことが私にも出来ます。
もう現役を引退した老人の暇つぶしではありますが。
我々凡人には、要点だけ簡潔に解説した日本人の良くある参考書ではなく、
全ての定義を明確に解説してくれていて、（知っているはずだとして、定義を書いてくれていない参考書も多いです）、
この様な沢山の例を挙げてくれている本が望ましいです。多分。
何を言っているかと言うと「修業は一人でするものだが、入門には師匠が必要」で、我々凡人は「修行」出来るように配慮してくれている
参考書に出会えるかどうかで運命が決まります。教育的配慮がなされた参考書は、演習問題は必ず本文の対応する部分の「類比（真似）」で
解けるようになっています。まず、練習問題に含まれる言葉の定義を遡って書き出し、練習問題に対応・類似の定理の記述と証明を書き出し、
その証明の真似をすれば、我々凡人でも証明できるようになっています。多分。この様な「修行」を一人黙々とやっていれば、
厄介な解析学を攻略する解析学特有の考え方・方策・思考パターンが少しづつ身についていきます。多分。
我々凡人はそうするしかないです。多分。そのような読み続けることが出来る自分に合った参考書に出会えるかどうかです。多分。
「General Topology」（例えば、John L. Kelley 著「General Topology」は私が昔学んだ時より難しいこと
例えば、「Baire Category Theorem」などを一杯書いています。また、表紙にパイプを咥えた写真が掲載されています。）と共に、
数学のあらゆる分野の理解に必要な知識・技能ですから、本当は、一定期間ごとに、繰り返し、復習しておくべきでした。

「前提条件が間違っている」と「間違った結論」を導きますが、我々凡人は「前提条件が間違っている」ことに（なかなか）気がつきません。



数学の参考書を読むだけでは、疲れるので、息抜きに、丸岡章著「人工知能」ちくま学芸文庫の「ルート描画パズル」をプログラミングしてみました。



import tkinter as tk
from tkinter import *
import numpy as np
import random
from tkinter import font
import os
from tkinter import filedialog
import copy
import re

sol = []

def sub_search(pos, field, path):
    global sol
    
    if len(field) == 0:
        if pos == 29 or pos == 34:
            s = copy.deepcopy(path)
            sol.append(s)
            if len(sol) >= 2:
                print('found at least two solutions!')
                return True
        return False
    x = pos % 6
    y = pos // 6
    if x > 0 and pos-1 in field:
        new_pos = pos - 1
        new_field =  copy.copy(field)
        new_field.remove(new_pos)
        path.append(new_pos)
        if sub_search(new_pos, new_field, path) == True:
            return True
        path.pop()
    if x < 5 and pos+1 in field:
        new_pos = pos + 1
        new_field =  copy.copy(field)
        new_field.remove(new_pos)
        path.append(new_pos)
        if sub_search(new_pos, new_field, path) == True:
            return True
        path.pop()
    if y > 0 and pos-6 in field:
        new_pos = pos - 6
        new_field =  copy.copy(field)
        new_field.remove(new_pos)
        path.append(new_pos)
        if sub_search(new_pos, new_field, path) == True:
            return True
        path.pop()
    if y < 5 and pos+6 in field:
        new_pos = pos + 6
        new_field =  copy.copy(field)
        new_field.remove(new_pos)
        path.append(new_pos)
        if sub_search(new_pos, new_field, path) == True:
            return True
        path.pop()
    return False
        
def search(barrier):
    global sol
    
    field = []
    sol = []
    for i in range(1, 35):
        if i in barrier:
            continue
        field.append(i)
    path = []
    return sub_search(0, field, path)

def get_barrier(n, l, b, path_w):
    global sol
    
    if l == n:
        print('in get_barrier(n, l, b): barrier=', b) 
        search(b)
        if len(sol) == 1:
            print('barrier=', b, 'sol=', sol)
            with open(path_w, mode='a') as f:
                sol_l = []
                sol_l.append(str(b))
                f.writelines(sol_l)
                f.write('\n')
                sol_l = []
                for i in range(len(sol)):
                    sol_l.append(str(sol[i]))
                f.writelines(sol_l)
                f.write('\n')
            f.close()
    else:
        if len(b) == 0:
            s = 1
        else:
            s = b[len(b)-1]+1
        for k in range(s, 35):
            if k in b:
                continue
            new_b = copy.copy(b)
            new_b.append(k)
            get_barrier(n, l+1, new_b, path_w)
    
def getPuzzle(fileName):
    global sol

    path = os.getcwd()
    path_w = path + '/' + fileName
    if os.path.isfile(path_w) == True:
        os.remove(path_w)
    
    for n in range(3, 4):
        b = []
        l = 0
        get_barrier(n, l, b, path_w )

def drawFrame(barrier):
    canvas.create_rectangle(0, 0, 640, 640, fill='WHITE')
    for k in range(1, 8):
        canvas.create_line(80, 80*k, 560, 80*k, fill = "Blue", width = 5)
        canvas.create_line(80*k, 80, 80*k, 560, fill = "Blue", width = 5)
    font1 = font.Font(family='Helvetica', size=20, weight='bold')
    id = canvas.create_text(120, 120, text="start" \
                            , width=100, font=font1)
    id = canvas.create_text(520, 520, text="goal" \
                            , width=100, font=font1)
    color = 'RED'
    for pos in barrier:
        x = pos % 6 + 1
        y = pos // 6 + 1
        canvas.create_rectangle(x*80, y*80, (x+1)*80, (y+1)*80, fill=color)
 
def button1_clicked(): # 「全ての問題作成」をクリックした時の処理
    fileName = txt.get()
    getPuzzle(fileName)

def button2_clicked(): # 「問題の読み込み」をクリックした時の処理

    n = int(txt2.get())
    typ = [('全てのファイル','*.*')] 
    dir = os.getcwd()
    fle = filedialog.askopenfilename(filetypes = typ, initialdir = dir)
    if fle[-4:] == '.txt':
        cnt = 0
        with open(fle) as f:
            for s_line in f:
                if cnt // 2 == n-1 and cnt % 2 == 0:
                    barrier = s_line
                    cnt = cnt + 1
                elif cnt // 2 == n-1 and cnt % 2 == 1:
                    solution = s_line
                    cnt = cnt + 1
                    break
                else:
                    cnt = cnt + 1
                    
        print('n=', n, 'barrier=', barrier, 'solution=', solution)
        txt3.delete(0, tk.END)
        txt3.insert(tk.END, barrier)
    else:
        textBox.insert(END, '\nファイルがテキストファイルではありません')
        print('file=', fle)
 
def button3_clicked(): # 「問題図の描画」をクリックした時の処理
    s_barrier = txt3.get()
    str_l = re.findall(r'\d+', s_barrier)
    barrier = []
    for e in str_l:
        barrier.append(int(e))
    drawFrame(barrier)

def get_xy(pos):
    x = pos % 6
    y = pos // 6
    x = 120 + 80 * x
    y = 120 + 80 * y
    return x, y
    
def button4_clicked(): # 「問題の正解表示」をクリックした時の処理
    global sol
    
    s_barrier = txt3.get()
    str_l = re.findall(r'\d+', s_barrier)

    barrier = []
    for e in str_l:
        barrier.append(int(e))
    drawFrame(barrier)
    search(barrier)
    print('sol=', sol)
    old_pos = 0
    for pos in sol[0]:
        ox, oy = get_xy(old_pos)
        tx, ty = get_xy(pos)
        canvas.create_line(ox, oy, tx, ty, fill = "Black", width = 5)
        old_pos = pos
    ox, oy = get_xy(old_pos)
    tx, ty = get_xy(35)
    canvas.create_line(ox, oy, tx, ty, fill = "Black", width = 5)

searchFlag = False
searchPath = []

def button5_clicked(): # 「解答開始」をクリックした時の処理
    global searchFlag, searchPath

    searchFlag = True
    searchPath = [0]
    lbl5["text"] = "◆マウスクリック可" 
    s_barrier = txt3.get()
    str_l = re.findall(r'\d+', s_barrier)

    barrier = []
    for e in str_l:
        barrier.append(int(e))
    drawFrame(barrier)

def leftClick(event):
    global searchFlag, searchPath

    if searchFlag == False:
        return
    x = event.x // 80 - 1
    y = event.y // 80 - 1
    pos = x + 6 * y
    if pos in searchPath:
        return
    old_pos = searchPath[len(searchPath)-1]
    ox, oy = get_xy(old_pos)
    tx, ty = get_xy(pos)
    if pos == old_pos + 6:
        canvas.create_line(ox, oy, tx, ty, fill = "Black", width = 5)
        searchPath.append(pos)
        return
    if pos == old_pos - 6:
        canvas.create_line(ox, oy, tx, ty, fill = "Black", width = 5)
        searchPath.append(pos)
        return
    if pos == old_pos - 1 and oy == ty:
        canvas.create_line(ox, oy, tx, ty, fill = "Black", width = 5)
        searchPath.append(pos)
        return
    if pos == old_pos + 1 and oy == ty:
        canvas.create_line(ox, oy, tx, ty, fill = "Black", width = 5)
        searchPath.append(pos)
        return   

def button6_clicked(): # 「解答終・断念了」をクリックした時の処理
    global searchFlag, searchPath

    searchFlag = False
    searchPath = [0]
    lbl5["text"] = "探索：解答開始ボタン" 

def button7_clicked(): # 「一手戻す」をクリックした時の処理
    global searchFlag, searchPath

    pos = searchPath.pop()
    
    s_barrier = txt3.get()
    str_l = re.findall(r'\d+', s_barrier)

    barrier = []
    for e in str_l:
        barrier.append(int(e))
    drawFrame(barrier)
    old_pos = 0
    for pos in searchPath:
        ox, oy = get_xy(old_pos)
        tx, ty = get_xy(pos)
        canvas.create_line(ox, oy, tx, ty, fill = "Black", width = 5)
        old_pos = pos
            
if __name__ == '__main__':
            
    W = 640
    H = 640
    root = tk.Tk()
    root.title('丸岡章著「人工知能」のルート描画パズル')
    root.geometry("900x640")
    canvas = tk.Canvas(root, width = W, height=H)
    ## キャンバス表示
    canvas.pack(anchor = tk.W)
    canvas.bind('', leftClick)

    
    lbl = tk.Label(text='書き込むファイル名', font=("MSゴシック", "15", "bold"))
    lbl.place(x=670, y=0)
    txt = tk.Entry(width=15, font=("MSゴシック", "15", "bold"))
    txt.place(x=670, y=30)
    lbl2 = tk.Label(text='障害物、解', font=("MSゴシック", "15", "bold"))
    lbl2.place(x=670, y=60)
    button1 = tk.Button(root, width=15, height=1, text="全ての問題作成",
                        font=("MSゴシック", "15", "bold"),
                        command=button1_clicked)
    button1.place(x=670, y=90)
    
    lbl3 = tk.Label(text='ファイルの何番の問題', font=("MSゴシック", "15", "bold"))
    lbl3.place(x=650, y=145)
    txt2 = tk.Entry(width=15, font=("MSゴシック", "15", "bold"))
    txt2.place(x=670, y=180)
    button2 = tk.Button(root, width=15, height=1, text="問題の読み込み",
                        font=("MSゴシック", "15", "bold"),
                        command=button2_clicked)
    button2.place(x=670, y=210)
    
    lbl4 = tk.Label(text='現在の障害物の位置', font=("MSゴシック", "15", "bold"))
    lbl4.place(x=670, y=270)
    txt3 = tk.Entry(width=15, font=("MSゴシック", "15", "bold"))
    txt3.place(x=670, y=305)
    button3 = tk.Button(root, width=15, height=1,text="問題図の描画",
                        font=("MSゴシック", "15", "bold"),
                        command=button3_clicked)
    button3.place(x=670, y=340)
    
    button4 = tk.Button(root, width=15, height=1,text="問題の正解表示",
                        font=("MSゴシック", "15", "bold"),
                        command=button4_clicked)
    button4.place(x=670, y=590)
    
    lbl4 = tk.Label(text='マウスクリックで解答', font=("MSゴシック", "15", "bold"))
    lbl4.place(x=660, y=390)
    
    lbl5 = tk.Label(text='探索：解答開始ボタン', font=("MSゴシック", "15", "bold"))
    lbl5.place(x=660, y=415)
    
    button5 = tk.Button(root, width=15, height=1,text="解答開始",
                        font=("MSゴシック", "15", "bold"),
                        command=button5_clicked)
    button5.place(x=670, y=455)

    button6 = tk.Button(root, width=15, height=1,text="解答終了・断念",
                        font=("MSゴシック", "15", "bold"),
                        command=button6_clicked)
    button6.place(x=670, y=545)

    button7 = tk.Button(root, width=15, height=1,text="一手戻す",
                        font=("MSゴシック", "15", "bold"),
                        command=button7_clicked)
    button7.place(x=670, y=500)
   
    barrier = [1, 5, 33]
    txt3.delete(0, tk.END)
    txt3.insert(0, barrier)
    drawFrame(barrier)

    root.mainloop()









が実行画面です。「書き込むファイル名」の下の「Entry」に「保存したいファイル名」を入力し、「全ての問題作成」のボタンをクリックすると、
コンピュータで見つけた問題を保存します。既に、カレントディレクトリに「書き込むファイル名」のファイルがあれば、
黙って削除されるので、注意が必要です。
今の設定は６×６の盤で、出発点が左上隅で終点が右下隅、「障害物」が３個の場合の解が一通りの問題を全て見つけてくれますが、
「障害物」の可能な配置の全体：34×33×32/6＝5984 個の中から解がユニークに決まるものを探しますから、結構時間が掛かります。
途中で止めたら、それまでに見つけた問題の障害の位置と解のパスが保存されています。
私の計算では、６×６の盤で、障害物が３個で、左上隅から右下隅への唯一のルートを求めるこの問題は５２個存在します。
但し、問題の画面の対称性は考慮に入れていません。 、出発点(start) と 終点(goal) の位置を変更して、調べるとパズルとして面白くなるかも？
上のプログラムの簡単な修正で可能です。更に、マジックナンバーを大域変数(global)に変更し、盤のサイズや出発点(start) と 終点(goal) の位置や
障害物の個数を入力して指定できるようにプログラムを修正すれば、自分で楽しみ、このパズルを探求するには便利です。
但し、他人に使ってもらうには、使い方が複雑になり、使ってもらえない可能性が出てきます。
この様にして作ったファイルがある場合、「ファイルの何番の問題」の下の「Entry」に問題の番号を入力し、
「問題の読み込み」のボタンをクリックすると、「現在の障害物の位置」下の「Entry」に「障害物」の３個の位置をリストで表示します。
上の様にファイルから、又は、正しい問題の「障害物」の３個の位置のリストがあるなら手作業で「現在の障害物の位置」下の「Entry」に入力し、
「現在の障害物の位置」下の「Entry」に「障害物」の３個の位置のリストがセットされていれば、「問題の正解表示」の
ボタンをクリックすると、「障害物」の３個の位置のリストが解がユニークに決まる問題のものならば画面の様な表示がされます。
この場合は新たに解をコンピュータが探索しています。実際は解が2個以上ある場合もその内の最初に見つけた解が描画されます。
解がない場合はエラーメッセージが表示されます。この部分は他人に使ってもらうためには本当は適切に対処すべきです。
マウスを使って、手動で解を探すことも出来ます。「解答開始」ボタンをクリックすれば、マウスで次の進むべきセルをクリックすれば、
start からのパスを伸ばすことが出来ます。無効なセルをクリックしても何も起きません。最初は start (０番目のセル)に隣接するセルを
クリックします。「一手戻す」で一手取り消せます。
解を求めることが出来たか、嫌になったら、「解答終了・断念」をクリックします。この後、続きを継続できません。
「解答開始」ボタンをクリックして、最初からやり直してください。
このパズルの通常の人間の「鉛筆パズル」的な解き方の考え方は「巻末注」の２に書いてあります。
このパズルに関連する著者たちの論文の掲載雑誌も書いてありますが、多分、「学習曲線に関するもの」で、門外漢が手に入れるのは厄介です。
上のプログラムは強引に「バックトラッキング」の虱潰しの探索で解を求めています。
他人にこのプログラムを使ってもらうためには、start からパスを入力するのではなく、
人間がこのパズルを攻略するように部分的な解（パス）の断片を入力できるようにすべきかも？多分。
又、時間の掛かる探索の部分を C++ でプログラミングすれば、高速になりますが、やりだせば切りがないので止めです。
興味があれば自由に作り直してください。
（この本の「ディープラーニング」までの部分は、我妻幸長著「はじめてのディープラーニング」SB Creative 
に掲載の Python プログラムを実行しながら読むと良く理解できると思います。
我々凡人は「数式の無い数学書」を読んでも数学が出来るようにならないように、「プログラムの無いプログラミングの解説書」を
読んでもプログラミングが出来るようになりません。独学だとこの様な2種類の本が必要です。多分。
例えば、５.９　のプログラムを



import tkinter as tk
from tkinter import *
import numpy as np
import random
from tkinter import font
import matplotlib.pyplot as plt

wb_width = 0.01  # 重みとバイアスの広がり具合

# -- 中間層 --
class MiddleLayer:
    def __init__(self, n_upper, n):  # 初期設定
        global wb_width
        
        self.w = wb_width * np.random.randn(n_upper, n)  # 重み（行列）
        self.b = wb_width * np.random.randn(n)  # バイアス（ベクトル）
        
    def forward(self, x):  # 順伝播
        self.x = x
        u = np.dot(x, self.w) + self.b
        self.y = 1/(1+np.exp(-u))  # シグモイド関数
        
##        print('self.w=', self.w)
##        print('self.b=', self.b)
##        print('self.x=', self.x)
##        print('self.y=', self.y)
        
    def backward(self, grad_y):  # 逆伝播
        delta = grad_y * (1-self.y)*self.y  # シグモイド関数の微分
        
        self.grad_w = np.dot(self.x.T, delta)
        self.grad_b = np.sum(delta, axis=0)
        
##        print('self.y=', self.y)
##        print('grad_y=', grad_y)
##        print('中間層:delta=', delta)
        
        self.grad_x = np.dot(delta, self.w.T) 
        
    def update(self, eta):  # 重みとバイアスの更新
        self.w -= eta * self.grad_w
        self.b -= eta * self.grad_b

# -- 出力層 --
class OutputLayer:
    def __init__(self, n_upper, n):  # 初期設定
        global wb_width
        
        self.w = wb_width * np.random.randn(n_upper, n)  # 重み（行列）
        self.b = wb_width * np.random.randn(n)  # バイアス（ベクトル）
    
    def forward(self, x):  # 順伝播
        self.x = x
        u = np.dot(x, self.w) + self.b
        self.y = u  # 恒等関数
    
    def backward(self, t):  # 逆伝播
        delta = self.y - t
        self.grad_w = np.dot(self.x.T, delta)
        self.grad_b = np.sum(delta, axis=0)

        print('self.y=', self.y)
        print('t=', t)
        print('出力層:delta=', delta)
        
        self.grad_x = np.dot(delta, self.w.T)
        
    def update(self, eta):  # 重みとバイアスの更新
        self.w -= eta * self.grad_w
        self.b -= eta * self.grad_b

def shuffle_data(data_list, index_random):
    changed = []
    for k in range(len(data_list)):
        changed.append(data_list[index_random[k]])
    return np.array(changed)
    
def button1_clicked(): # 「一手戻す」をクリックした時の処理
    global wb_width

    # -- 各設定値 --
    n_in = 1  # 入力層のニューロン数
    n_mid = 3  # 中間層のニューロン数
    n_out = 1  # 出力層のニューロン数

    wb_width = 0.01  # 重みとバイアスの広がり具合
    eta = 0.1  # 学習係数
    epoch = 2001
    interval = 200  # 経過の表示間隔

    n_mid = int(txt1.get())
    
    eta = float(txt2.get())
    
    interval = int(txt3.get())
    
    epoch = int(txt4.get())
    
    wb_width = float(txt5.get())
    
    batch_size = int(txt6.get())

    n_func = v1.get()
    
##    batch_size = 2
    
    original_input_data = np.linspace(0, np.pi*2, 120)  # 入力
    if n_func == 1:
       original_correct_data = np.sin(original_input_data)  # 正解
    else:
       original_correct_data = np.cos(original_input_data)  # 正解
    original_input_data = (original_input_data-np.pi)/np.pi  # 入力を-1.0-1.0の範囲に収める
    input_data = original_input_data.copy()
    correct_data = original_correct_data.copy()
    n_data = len(correct_data)  # データ数

    # インデックスをシャッフル
    if batch_size > 1:
        index_random = np.arange(n_data)
        np.random.shuffle(index_random)
        input_data = shuffle_data(input_data, index_random)
        correct_data = shuffle_data(correct_data, index_random)
    
    input_data = input_data.reshape(n_data//batch_size, batch_size)
    correct_data = correct_data.reshape(n_data//batch_size, batch_size)

    # -- 各層の初期化 --
    middle_layer = MiddleLayer(n_in, n_mid)
    output_layer = OutputLayer(n_mid, n_out)

    # -- 学習 --
    for i in range(epoch):

        # インデックスをシャッフル
        index_random = np.arange(n_data//batch_size)
        np.random.shuffle(index_random)
    
        # 結果の表示用
        total_error = 0
        plot_x = []
        plot_y = []
        plot_z = []
    
        for idx in index_random:
        
            x = input_data[idx:idx+1]  # 入力
            t = correct_data[idx:idx+1]  # 正解
        
            # 順伝播
            middle_layer.forward(x.reshape(batch_size, n_in))  # 入力を行列に変換
            output_layer.forward(middle_layer.y)  

            # 逆伝播
            output_layer.backward(t.reshape(batch_size, n_in))  # 正解を行列に変換
            middle_layer.backward(output_layer.grad_x)
        
            # 重みとバイアスの更新
            middle_layer.update(eta)
            output_layer.update(eta)
    
            if i%interval == 0:
##                print('output_layer.y=', output_layer.y)
                y = output_layer.y.reshape(-1)  # 行列をベクトルに戻す
                # 誤差の計算
                total_error += 1.0/2.0*np.sum(np.square(y - t))  # 二乗和誤差
            
                # 出力の記録
                plot_x.append(x)
                plot_y.append(y)

##                print('x=', x, 'y=', y)
##                print('middle_layer.x=', middle_layer.x)
##                print('middle_layer.y=', middle_layer.y)
                
                z = middle_layer.y.reshape(-1)  # 行列をベクトルに戻す
                plot_z.append(z)
                
##                print('z=', z)
            
        if i%interval == 0:
            # 出力のグラフ表示
            plot_x = np.array(plot_x)
            plot_x = plot_x.reshape(batch_size, n_data//batch_size)
            polt_x = plot_x.T
            plot_y = np.array(plot_y)
            plot_y = plot_y.reshape(batch_size, n_data//batch_size)
            polt_y = plot_y.T
            
            plt.plot(original_input_data, original_correct_data, linestyle="dashed")
            
##            print('plot_x=', plot_x)
##            print('plot_y=', plot_y)

            for k in range(batch_size):
                plt.scatter(plot_x[k], plot_y[k], marker="+")

##            print('plot_x=', plot_x)
##            print('plot_z=', plot_z)
                
            plot_z = np.array(plot_z).reshape(-1)
            plot_z = plot_z.reshape(n_data//batch_size, batch_size*n_mid)
            
            plot_z = plot_z.transpose()
            plot_zz = []
            plot_xx = []
            for k in range(n_mid):
                plot_zz.append([])
                plot_xx.append([])
            for p in range(batch_size):
                for k in range(n_mid):
                    plot_zz[k].extend(plot_z[p*n_mid+k])
                    plot_xx[k].extend(plot_x[p])
                    
##            print('plot_xx=', plot_xx)
##            print('plot_zz=', plot_zz)

            for k in range(n_mid):
                if k == 0:
                    mk = 'x'
                elif k == 1:
                    mk = 's'
                elif k == 2:
                    mk = 'o'
                elif k == 3:
                    mk = '1'
                else:
                    mk = '2'
                plt.scatter(plot_xx[k], plot_zz[k], marker=mk)
                
            plt.show()
        
            # エポック数と誤差の表示
            print("Epoch:" + str(i) + "/" + str(epoch), "Error:" + str(total_error/n_data))
            
if __name__ == '__main__':
            
    root = tk.Tk()
    root.title('バックプロパゲーションの実装：回帰')
    root.geometry("300x550")

    lb1 = tk.Label(text='中間層の個数', font=("MSゴシック", "15", "bold"))
    lb1.place(x=50, y=10)
    txt1 = tk.Entry(width=15, font=("MSゴシック", "15", "bold"))
    txt1.place(x=50, y=40)
    txt1.delete(0, tk.END)
    txt1.insert(0, 3)

    lb2 = tk.Label(text='学習係数', font=("MSゴシック", "15", "bold"))
    lb2.place(x=50, y=70)
    txt2 = tk.Entry(width=15, font=("MSゴシック", "15", "bold"))
    txt2.place(x=50, y=100)
    txt2.delete(0, tk.END)
    txt2.insert(0, 0.1)

    lb5 = tk.Label(text='重みとバイアスの広がり具合', font=("MSゴシック", "15", "bold"))
    lb5.place(x=10, y=130)
    txt5 = tk.Entry(width=15, font=("MSゴシック", "15", "bold"))
    txt5.place(x=50, y=160)
    txt5.delete(0, tk.END)
    txt5.insert(0, 0.01)

    lb6 = tk.Label(text='バッチサイズ', font=("MSゴシック", "15", "bold"))
    lb6.place(x=50, y=190)
    txt6 = tk.Entry(width=15, font=("MSゴシック", "15", "bold"))
    txt6.place(x=50, y=220)
    txt6.delete(0, tk.END)
    txt6.insert(0, 1)

    lb3 = tk.Label(text='経過の表示間隔', font=("MSゴシック", "15", "bold"))
    lb3.place(x=50, y=250)
    txt3 = tk.Entry(width=15, font=("MSゴシック", "15", "bold"))
    txt3.place(x=50, y=280)
    txt3.delete(0, tk.END)
    txt3.insert(0, 200)

    lb4 = tk.Label(text='エポックの総数', font=("MSゴシック", "15", "bold"))
    lb4.place(x=50, y=310)
    txt4 = tk.Entry(width=15, font=("MSゴシック", "15", "bold"))
    txt4.place(x=50, y=340)
    txt4.delete(0, tk.END)
    txt4.insert(0, 2001)

    lb7 = tk.Label(text='学習する関数', font=("MSゴシック", "15", "bold"))
    lb7.place(x=50, y=380)
    # Radiobutton 1
    v1 = tk.IntVar()
    v1.set(1)
    rb1 = tk.Radiobutton(
        root,
        text='sin 関数を使用',
        value=1, font=("MSゴシック", "15", "bold"),
        variable=v1)
    rb1.place(x=40, y=410)

    # Radiobutton 2
    rb2 = tk.Radiobutton(
        root,
        text='cos 関数を使用',
        value=2, font=("MSゴシック", "15", "bold"),
        variable=v1)
    rb2.place(x=40, y=440)

    button1 = tk.Button(root, width=15, height=1, text="結果表示",
                        font=("MSゴシック", "15", "bold"),
                        command=button1_clicked)
    button1.place(x=50, y=480)

    root.mainloop()


の様に修正すれば、「中間層の個数」、「学習係数」、 「経過の表示間隔」、
「バッチの個数」、「エポックの総数」などを変更できるし、
「中間層の出力の変化」も表示し、







の様に調べることも出来ます。プログラムは参考書の解説の通り作っているつもりですが、
「中間層の出力の変化」の表示はバッチの個数＝２の時は上手く表示できていません。まだ、何か勘違いしているかも？
また、我々凡人は Python のコマンドも直ぐ忘れてしまうので、radio buttonn などこの様な機会を見つけて、繰り返し使ってみます。
最もこれらは趣味のプログラミングでは本質ではなく、その都度、インターネットで調べると良いですが。
また、それなりに時間を費やしたはずだが、全然モノになっていない「ロシア語」や「アラビア語」などの語学も、
我々凡人は繰り返し学び直しする必要があります。これらは実際の仕事には必要なかったですが、
辞書を引けば何とかなるではなく、矢張り覚えるべきものはキチンと覚える必要があったみたいです。
昔から、語学は、３キ、アンキ（暗記）、コンキ（根気）、ネンキ（年季）だと言われていて、
学習初期の決め手はアンキだそうです。
残念ながら意識して覚えようと努力しないと覚えることは出来ません。当たり前のことですが。
独学で、入門書や文法書ばかり読んで見ても嫌になりますが、宮本雅之著「中級アラビア語読本」が出版されたので、
読んで見ようかな？この様な参考書がないとまだ辞書と文法を自分なりにまとめたカードの束を見るだけではまだまだ難しいですから。
アラビア語の有名な古本を集めて、独学したので、音声が手に入らなかったし、外国に行くこともないだろうから発音は良いだろうと言う
教育を受けた世代ですが、只管、ネイティブスピーカーの音声を聴く必要があるみたいです。
佐藤純一著「NHK （新）ロシア語入門」もCDの普及とともに、少しづつ音声が多くなっていきまし、岩波書店が語学書を出版しなくなりました。
また、高校生時代、生物の授業で流行っていた「サブノート」と師匠の「図書カード」のメモの真似をして、
暗記すれば良いのに、LaTeX を使いたくて、アラビア語の文法のカードの束を作りました。
ArabTeX は私でも何とか使いこなせます。ArabluaTeX というのもありますが私には使えません。無駄な努力ばかりしています。多分。
現在は情報が多すぎます。恐竜の専門家がラジオで参考書が少なかったから一冊の本を隅から隅まで読むことが出来たと話していました。
囲碁のプロになった女流棋士は本因坊秀策さんの全集を子供の時買ってもらって全局暗記したそうです。
私も「本因坊秀策全集」も持っていますが、持っている本が多過ぎ、どれも読んでいません。
趣味の本は仕事についてお金が少し自由になってから購入したので、読むためではなく、集めることが目的になってしまいました。
語学も沢山の参考書を集めるのではなく自分に適した暗記する価値のある一つの本を何回も読んで丸暗記すべきでした。それが難しいですが。多分。
後期高齢者になり、これといってするべきことが無くなったので、それぞれの分野のどれか一つの本に決めて繰り返し読んで見れば良いだけですが。
一番最初に購入し本箱で埃を被っていた池田修著「アラビア語入門」も入門書ではなかったですが、テープは駄目になっていますが、
今読むと文法の全体像がそれなりにつかめているので面白いですし、池田修・竹田新編「現代アラビア語小辞典」も語数が多く今の私には結構役に立ちます。
「パスポート初級アラビア語事典」から「THE HANS WEHR DICTIONARY OF MODERN WRITTEN ARABIC」へ移行する前に使うと良いと思います。
ロシア語の参考書も日本語訳を見る前に、Oxford Essential Russian Dictionary (英国の辞書は英国の政策で補助金を出し、円安でも安価です。)
を引いて、訳してみます。
知らない英語の単語、例えば、голод や орошать の訳の famine や irrigate など英和辞典を更に引かなければ意味が分かりませんが、
有難いことに今は時間が一杯あります。

今は見る影もありませんが、日本も一時期はそれなりに豊かな時期がありました。欧米に働き過ぎだと攻撃され、政府は慌てふためき、
「ゆとり教育」や「新自由主義」の導入など、様々な拙い対応する中で日本の中間層は消滅し、なかなか立ち直れなくなっています。多分。

現在の世界の情勢は「欧米」、「ロシア」、「中国」、「イスラム圏」、「その他のかって欧米に略奪された国々」に
分かれて勢力争いをしています。多分、欧米がNATOを東方に拡大し、ロシアの恐怖を煽り、ウクライナ戦争になりました。多分。
ロシアに核兵器を使わせずに、ロシアを壊滅させるにはどうすれば良いか、欧米各国は戦略を巡らせているみたいです。
キリスト教圏ではない国々が発展・繁栄することが我慢ならない欧米は昔から一貫して非キリスト教世界を攻撃、侵略、破壊し続けていますし、
キリスト教圏ではない日本も米国の意のままそれに加担しようとし、米軍の先陣を仰せつかって中国と戦うために軍備の増強に勤しんでいるように見えます。
「欧米」側の恣意的な情報だけでなく、「ロシア」、「中国」、「イスラム圏」、「インド（・トルコ）、その他のかって欧米に略奪された国々」の言い分も
吟味してみる必要があります。その為には、欧米の言語だけでなく、それぞれの国の言語が正確に理解できる日本人達を増やす必要があります。

直ぐに仕事に役立ち、お金を生み出す複雑なプログラムの例が欲しい人や
単に数学的原理が知りたいだけで単純な原理が理解できるプログラムの例が欲しい人など世の中には色々な人達がいるので、
何をしたいかによって話は勿論変わってきますが、偶然手に取る本でその人の運が決まります。多分。
手に入れたプログラムを様々に修正して実験してみれば、時間は掛かりますが、知りたいことを知ることが出来ます。多分。
上の図は中間層が4個の場合ですが、二つの中間層のニューロンの出力が同じような出力なので、この例の場合には、
他の設定値は同じで、中間層を4個に一つ増やしても無意味であったことが見て取れると思います。多分。
ちなみに







が中間層が3個の場合です。非常に単純な場合で、図示すると誰の目にも明らかですが、これが極値である事が数学的に証明できるだろうか？
或いは既に証明されているだろうか？この図の数学的根拠が説明できるか？こんな事が意味があることか不安を抱えながら調べて見るのが研究です。多分。
研究者のすそ野が広ければ、直ぐにはお金になる成果を挙げれなくとも一見無駄とも思えることをしている人達の誰かが面白い成果を挙げると思います。
この様にプログラミングの勉強は、我々貧乏人の安価なコンピュータでもコンピュータが答え（正しいか間違っていっるか）を教えてくれるので、
現在は他の勉強に比べ非常に楽です。多分。但し、お金を稼ぐには GPU 付きの高価なコンピュータが必要です。多分。
又、５.１０　のプログラムを



import tkinter as tk
from tkinter import *
import numpy as np
import random
from tkinter import font
import matplotlib.pyplot as plt

# -- 座標 --
X = np.arange(-1.0, 1.1, 0.1)
Y = np.arange(-1.0, 1.1, 0.1)

# -- 入力、正解データを作成 --
input_data = []
correct_data = []
for x in X:
    for y in Y:
        input_data.append([x, y])
##        if y < np.sin(np.pi * x):  # y座標がsinカーブよりも下であれば
##            correct_data.append([0, 1])  # 下の領域
        if y < np.cos(np.pi * x):  # y座標がsinカーブよりも下であれば
            correct_data.append([0, 1])  # 下の領域
        else:
            correct_data.append([1, 0])  # 上の領域
            
n_data = len(correct_data)  # データ数

input_data = np.array(input_data)
correct_data = np.array(correct_data)
            
# -- 各設定値 --
n_in = 2  # 入力層のニューロン数
n_mid = 6  # 中間層のニューロン数
n_out = 2  # 出力層のニューロン数

wb_width = 0.01  # 重みとバイアスの広がり具合
eta = 0.1  # 学習係数
epoch = 101
interval = 10  # 経過の表示間隔

# -- 中間層 --
class MiddleLayer:
    def __init__(self, n_upper, n):
        self.w = wb_width * np.random.randn(n_upper, n)  # 重み（行列）
        self.b = wb_width * np.random.randn(n)  # バイアス（ベクトル）

    def forward(self, x):
        self.x = x
        u = np.dot(x, self.w) + self.b
        self.y = 1/(1+np.exp(-u))  # シグモイド関数
    
    def backward(self, grad_y):
        delta = grad_y * (1-self.y)*self.y
        
        self.grad_w = np.dot(self.x.T, delta)
        self.grad_b = np.sum(delta, axis=0)
        
        self.grad_x = np.dot(delta, self.w.T) 
        
    def update(self, eta):
        self.w -= eta * self.grad_w
        self.b -= eta * self.grad_b

# -- 出力層 --
class OutputLayer:
    def __init__(self, n_upper, n):
        self.w = wb_width * np.random.randn(n_upper, n)  # 重み（行列）
        self.b = wb_width * np.random.randn(n)  # バイアス（ベクトル）
    
    def forward(self, x):
        self.x = x
        u = np.dot(x, self.w) + self.b
        self.y = np.exp(u)/np.sum(np.exp(u), axis=1, keepdims=True)  # ソフトマックス関数
    
    def backward(self, t):
        delta = self.y - t
        
        self.grad_w = np.dot(self.x.T, delta)
        self.grad_b = np.sum(delta, axis=0)
        
        self.grad_x = np.dot(delta, self.w.T) 

    def update(self, eta):
        self.w -= eta * self.grad_w
        self.b -= eta * self.grad_b

def button1_clicked(): # 「結果表示」をクリックした時の処理
    global n_in, n_mid, n_out, eta, interval, epoch, wb_width, batch_size
    global input_data, correct_data, n_data

    n_mid = int(txt1.get())
    
    eta = float(txt2.get())
    
    interval = int(txt3.get())
    
    epoch = int(txt4.get())

        
    # -- 各層の初期化 --
    middle_layer = MiddleLayer(n_in, n_mid)
    output_layer = OutputLayer(n_mid, n_out)

    # -- 学習 --
    ##sin_data = np.sin(np.pi * X) # 結果の検証用
    cos_data = np.cos(np.pi * X) # 結果の検証用
    for i in range(epoch):

        # インデックスをシャッフル
        index_random = np.arange(n_data)
        np.random.shuffle(index_random)
    
        # 結果の表示用
        total_error = 0
        x_1 = []
        y_1 = []
        x_2 = []
        y_2 = []
        zx = []
        zy = []
        zx_1 = []
        zy_1 = []
        zx_2 = []
        zy_2 = []
        # 中間層の表示用
        for k in range(n_mid):
            zx.append([])
            zy.append([])
            zx_1.append([])
            zy_1.append([])
            zx_2.append([])
            zy_2.append([])
       
        for idx in index_random:
        
            x = input_data[idx]
            t = correct_data[idx]

            # 順伝播
            middle_layer.forward(x.reshape(1,2))
            output_layer.forward(middle_layer.y)

            # 逆伝播
            output_layer.backward(t.reshape(1,2))
            middle_layer.backward(output_layer.grad_x)
        
            # 重みとバイアスの更新
            middle_layer.update(eta)
            output_layer.update(eta)
        
            if i%interval == 0:
            
                y = output_layer.y.reshape(-1)  # 行列をベクトルに戻す

                z = middle_layer.y.reshape(-1)  # 行列をベクトルに戻す

                # 誤差の計算
                total_error += - np.sum(t * np.log(y + 1e-7)) # 交差エントロピー誤差
            
                # 確率の大小を比較し、分類する
                if y[0] > y[1]:
                    x_1.append(x[0])
                    y_1.append(x[1])
                else:
                    x_2.append(x[0])
                    y_2.append(x[1])

                for k in range(n_mid):
                    zx[k].append(x[0])
                    zy[k].append(z[k])
                    if z[k] > 0.5:
                        zx_1[k].append(x[0])
                        zy_1[k].append(x[1])
                    else:
                        zx_2[k].append(x[0])
                        zy_2[k].append(x[1])
                    
            
        if i%interval == 0:
        
            # 出力のグラフ表示
            plt.plot(X, cos_data, linestyle="dashed")
            plt.scatter(x_1, y_1, marker="+")
            plt.scatter(x_2, y_2, marker="x")
            plt.suptitle("output_layer")
            plt.show()

            for k in range(n_mid):
                plt.plot(X, cos_data, linestyle="dashed")
                plt.scatter(zx[k], zy[k], marker="x")
                plt.suptitle("middle_layer"+str(k))
                plt.show()
            for k in range(n_mid):
                plt.plot(X, cos_data, linestyle="dashed")
                plt.scatter(zx_1[k], zy_1[k], marker="+")
                plt.scatter(zx_2[k], zy_2[k], marker="x")
                plt.suptitle("middle_layer"+str(k))
                plt.show()
            
            # エポック数と誤差の表示
            print("Epoch:" + str(i) + "/" + str(epoch), "Error:" + str(total_error/n_data))
            
if __name__ == '__main__':
            
    root = tk.Tk()
    root.title('丸岡章著「人工知能」のルート描画パズル')
    root.geometry("300x400")

    lb1 = tk.Label(text='中間層の個数', font=("MSゴシック", "15", "bold"))
    lb1.place(x=50, y=10)
    txt1 = tk.Entry(width=15, font=("MSゴシック", "15", "bold"))
    txt1.place(x=50, y=50)
    txt1.delete(0, tk.END)
    txt1.insert(0, 6)

    lb2 = tk.Label(text='学習係数', font=("MSゴシック", "15", "bold"))
    lb2.place(x=50, y=90)
    txt2 = tk.Entry(width=15, font=("MSゴシック", "15", "bold"))
    txt2.place(x=50, y=120)
    txt2.delete(0, tk.END)
    txt2.insert(0, 0.1)

    lb3 = tk.Label(text='経過の表示間隔', font=("MSゴシック", "15", "bold"))
    lb3.place(x=50, y=160)
    txt3 = tk.Entry(width=15, font=("MSゴシック", "15", "bold"))
    txt3.place(x=50, y=200)
    txt3.delete(0, tk.END)
    txt3.insert(0, 10)

    lb4 = tk.Label(text='エポックの総数', font=("MSゴシック", "15", "bold"))
    lb4.place(x=50, y=240)
    txt4 = tk.Entry(width=15, font=("MSゴシック", "15", "bold"))
    txt4.place(x=50, y=280)
    txt4.delete(0, tk.END)
    txt4.insert(0, 101)

    button1 = tk.Button(root, width=15, height=1, text="結果表示",
                        font=("MSゴシック", "15", "bold"),
                        command=button1_clicked)
    button1.place(x=60, y=320)

    root.mainloop()


の様に修正すれば、「中間層の個数」、「学習係数」、 「経過の表示間隔」及び 「エポックの総数」を変更できるし、
「中間層の出力の変化」も表示し、中間層の個数＝２で十分で






























の様な表示が得られます。

多分、アメリカの命令で増やした軍事費（バイデン大統領が時々自慢しています？）を少し削って、地方国立大学（もう国立大学ではないので、
文部省・官僚。政治家の意識では私立大学と同じで、国がお金の面倒を見る必要は無くなったし、欧州の各国の様に大学の教育研究に使うお金はないから、
米国の大学は教育費がいかに高額かを宣伝し、「教育は自己責任」（？）だから、米国の様に「学費を大幅に値上げして対処しろ」でしょうが。）
の予算を元に戻すべきです。東京等の大規模な国立大学は米国の大学のように沢山いる成功した卒業生達に寄付してもらえば良いです。
しかし、例えば、杉良太郎さんのボランティア活動などを「売名行為」だと罵る人だらけの国で、「日本では、少なくとも昔は、民衆の苦しみを
救うために志を立てたエライ人というのがおよそいない。つねに民衆ぬきだからかなわない。ビアフラの飢えた民衆のための寄付者は、
日本では高校生が大部分だといいます。なかなかエライもんです。」だそうですから、皆、他人を蹴落とすのに必死で、期待は出来ないでしょうが。

地方の店も大企業の系列店ばかりになり、地方の富が大都市に吸い上げられて地方は衰退するばかりです。地方に再配分すべきです。
佐渡の金山も石見の銀山も掘りつくし、世界遺産になりましたし、石炭も時代遅れになったので、人材だけが日本の唯一の資源です。
）
買い貯めた数学等の参考書・本を読む時間や外国語を勉強する時間が無くなります。

本当は、この様な既に知られているパズルではなく、新しいパズルを考案しないといけないですが、プログラミングの練習にはなります。
このパズルを一般化し、N×M の盤で、小さい N とM の値に対して、start, goal,の位置、 障害物の個数・位置のどの様な組み合わせで、
全てのセルを一度だけ通り start から goal に辿り着ける解が唯一つである問題が何個あるか虱潰しに
（手作業が大変なら、上のプログラムの比較的簡単な修正で、パソコンで虱潰しの探索が出来ます。）調べ上げれば、
「小学生・中学生の夏休みの自由研究」になるのでは？私がやっても、時間さえ掛ければ出来るに決まっているので、意味がないですが？
但し、何らかの一般的な法則を発見できれば、欧米ではそれなりに評価されると思いますが、日本ではアマチアの数学愛好家のやる事と思われそうです？
スマホのパズルにすることも容易ですが、広告無し、課金無しのフリーソフトでは、プラットフォームのお金にはならないので、無視されます。多分。

中国製の易占いの正八面体２個と立方体１個のサイコロを手に入れたが、立方体は初、二、三、四、五、上の文字が書いてあり、
正八面体は赤と黒で下の左の漢字だけ書いてあり、右ではないので初心者には厄介です。
二進数表記で最上位を１の位、真ん中を２の位、最下位を４の位と考えて、

7＝乾（けん）…　天

6＝兌（だ）　…　沢

5＝離（り）　…　火

4＝震（しん）…　雷

3＝巽（そん）…　風

2＝坎（かん）…　水

1＝艮（ごん）…　山

0＝坤（こん）…　地

と解釈すれば、（学生時代、黄小娥さんの本で十円玉６個を使って占う時には、下から並べるように教わったのですが、
逆の解釈でも良いですが。陽が１の方が多分良い？）、漢字が書いてあるサイコロなら占っている雰囲気が
ありますが、正多面体５種類各１個とデルタ多面体の１０面体２個（１の位と１０の位用）を１グループに様々な色のサイコロを
セットにした市販品でも私の持っている易の解説書で簡単に占うことが出来そうです。
黄小娥さんが風穴を開けてから、十円玉５個と百円玉１個で占う方法とか色々な本がその後出版されています。
考えれば、色々な事が可能ですが、我々凡人は覚えるのに必死で、別の考え・方法もあるとなかなか考えようとしません。
岩波文庫の「易経」（上下）を眺めると

1＝乾（けん）…　天

2＝兌（だ）　…　沢

3＝離（り）　…　火

4＝震（しん）…　雷

5＝巽（そん）…　風

6＝坎（かん）…　水

7＝艮（ごん）…　山

8＝坤（こん）…　地

と６５ページに書いてあります。二進数表記で最上位を１の位、真ん中を２の位、最下位を４の位と考えて、
陰を１、陽を０として計算して、１を加えるのが筮竹による占いに対応しているみたいです。
この本の易の解説の順番も不思議な気がします。暇を見つけて、岩波文庫の「易経」（上下）も読んで見る必要があります。

学生時代と言えば、天神で良く詰将棋の大道将棋をよく見かけましたが、現在は森さんのこの解説書も出版され、
私も持っていますが、読まないと何にもなりません。何か一つに決めて集中できれば良いのですが。

Donald Cohn, Measure theory, 2nd ed., Springer, 2013 は 円安で、英語の本が高価になっていますが、
この本の pdf ファイルをインターネットでゲットでき、Kindle for  PC で読むことも出来ます。

解析と言うと大学の一般教養で習う「微分積分」が真っ先に頭に浮かびますし、高校までの数学はこの「微分積分」を
理解させる為のカリキュラムが組まれていると言われていますが、数学が好きである・出来るとは「微分積分」を
理解している事とほぼ同値ではあり、「微分積分」が理解できていなければ話にはなりませんし、
「幾何学」（プログラミングも専門と言っても良いかな？）が専門だと言っても、学生さんに「微分積分」も質問されるので、
就職してから「微分積分」もそれなりに勉強しましたが、それで十分ではなく、
現代数学（の解析学・統計学）はこの「Measure theory」の理解から始まると思います、
解析が得意とは「Measure theory」が頭の中で構成できていることではないかと私は思います。私は専門外でまだ出来ていませんが。
恐竜を研究している専門家が「恐竜の研究」がいかにお金を生み出すか、縷々、ラジオで解説していたり、
平安時代の女流作家の研究をしている研究者が目に見える「お金を生まない研究」も大切で、
「源氏物語」や「枕草子」などをずっと書き写し、戦乱の中でも後世に残す努力をしてきた人々のおかげで、今日、
それらを我々は読むことが出来、日本の文化として世界に誇ることが出来るし、西洋の学問一辺倒になった明治時代に、
与謝野晶子さん達文学者が江戸時代の数学・和算の書籍の保存に努力したことも知られています。
和算が日本で発展したのは、中国の暦法やその為の数学が理解できなかったから、何とかしたいと努力した結果だそうですが。
第二次世界大戦前後の期間の欧州における民族の大移動の研究などもお金になる研究ではないと思いますが、
現在の世界の状況を理解するための貴重な情報・知識になります。たまたま見た放送大学で解説していました。
「無駄の排除」は聞こえの良い言葉で苦しい生活を強いられている民衆の心に響きますが、
蟻が生き残る為に、半分の蟻は無駄な行動をしている様に、優秀な官僚？がマニュアルを作り、その通り行動しているか
膨大な報告書を作らせ、例えば、公立学校の教員達を、監視する今の制度より、犯罪を犯しているのでなければ、
お金にならない、多くの人には無駄だと思われる・見えてしまう事をしている人達をそれなりに抱えているのが健全ではないでしょうか？

陸秋槎著「文学少女対数学少女」の解説が面白いです。推理小説の作者たちが何を考えて来たか解説してくれています。
又、最近翻訳されるようになってきた（と思われる）中国や台湾の推理小説を読むと見たことの無い漢字が無数に出てきます。
楽譜を描こうと思って、昔、MusicTeX や MusiXTeX を触ったことがあったと思い出して、MuteXTeX を使おうとすると
全然使い方が分からない。インターネット上の情報は２０年位前のものが多くて、多くがアクセスできませんと表示される。
Windows の TeX Live では MusiXTeX+PMX+M-Tx が自動的に使えるみたいだが、最初に見つけた情報通りコンパイルすると、
.mtx のサンプルプログラムは簡単に、.pdf ファイルが作れたが、他の二つはまだ出来ない。
M-Tx のプログラムを PMX のプログラムに翻訳して、更に、TeX のプログラムに翻訳して、実行しているみたいです。
.mtx に書き込むコードの解説書がインターネット上で見つからない。日本語の解説は殆どが現在は削除されている。
.pmx ファイルはエラーは出るがコンパイル出来ている様な気はしますが、コードの書き方を理解してないし、
マニュアルは見つけたが、そもそも中学校までの知識で、音楽を理解していないので、読んで理解できるか不明だし、
更に難しそうな MusiXTeX のサンプルプログラムは ptex でコンパイルできるが、楽譜が左側に偏り、
バランスいい配置にならず、楽譜の描画が上手くいかない。何か修正が必要と書いてあるが理解できない。
理解したければ、キチンと「TeX book」を読んで、 MusiXTeX のサンプルプログラムの何処が問題か調べれば良いだけですが、
自分にとって、そこまでする価値が本当にあるかです。即ち、日常的に楽譜の描画が自分にとって必要かです。
更に、LaTeX ではなく  TeX で処理する必要があり、日本語フォントの使い方も難しそうです。
PMX の基本的マニュアルは手に入れたが、どうも「TeXbook」を理解していることが前提条件みたい。
囲碁や将棋のスタイルファイルのようなレベルの難しさでは全然ないです。困った！矢張り手書きが一番か？
機械語・アセンブリ言語を理解していれば C 言語の理解が容易だったように、
即ち、コンピューターは最終的には機械語・アセンブリ言語のプログラムで動いているので、
C のコンパイラの作るアセンブリ言語のプログラムを読めば、C のやっていることが理解できた様に、
（本当は、マイコンの黎明期には、８ビットマイコンには回路図が添付されていて、
マイコン関連の雑誌には８ビットマイコンの機械語のプログラムが溢れ、ハンドアセンブルをしたり、
エディターでマイコンの動きを覗くことが出来ました。
当時は CPU は３種類あり、その比較や優劣が雑誌で議論されていて、BASIC もスタックの使い方に差がありました。
その後、インテルの機械語・アセンブリ言語の参考書である「増補版 the 8086 primer 8086 入門」が出版され、
メモリーのアドレスを指定する様々なアドレッシングモードのやり方が使われていることを 学びました。
又、種々の単純な言語の処理系が作られ、それら処理系のプログラム・情報
（図を描くロボット言語やスタック指向の FORTH や関数型プログラミング言語 LISP や
論理型プログラミング言語 PROLOG などの仕組み・原理が理解できる単純なプログラムが雑誌「bit」などに掲載されていました。
子供用の言語として開発され、一時流行った LOGO は LISP をベースに図を描くロボット言語を組み込み、手続き型言語の糖衣をまぶしたもので、
Scrach は最新の技術を取り入れた LOGO の改良版だと思います。
全学生にパソコンを購入させているので、メールと Excel と Word の基本を教えて終わりでは申し訳ないと思ったので、
LOGO が流行り出すと小学校の教員免許の為の選択必修の「初等数学」で LOGO で図形の描き方も教えていましたし、
LOGO が下火になると私の作った「LOGO もどき」（「数学を改善する為のソフト開発」にアップしてあります。）で、
パソコンによる図形の描き方も教えていました。
高知大学教育学部学校教育教員養成課程一年生達が平成１５年後期の「初等数学Ｂ］の「子供の喜ぶ絵を描く」という課題でプログラミングした作品の例を
 https://www.cc.kochi-u.ac.jp/~tyamag/kite/gallary.htmlPython にアップしてあります。
プログラミングの学び始めに、「再帰」などの基本概念を理解するのに、我々凡人には。、描かれた図を見ることで理解できる有難い機能です。）、
が出版されていたり、現在と違い、コンパイラやオートマトン・言語理論の参考書が沢山出版されていたこともあります。
教育学部に新課程の情報関係のコースが新設されることになった時、責任者になった教授にどの様な教員が必要か質問されましたが、
ホップ代数（Steenrod algebra）のコホモロジーを計算するプログラムしか考えてなかったので、何も答えられず、
情報科学科で教えているカリキュラムを調べて、コンパイラやオートマトン・言語理論なども独学で学びました。
言語理論の本は、定義・定理・証明の羅列で、現代数学の本と同じだと思いましたが、それらが役に立ったかどうかは不明です。
特に、PASCAL を考案した Niklaus Wirth さんの「アルゴリズム＋データ構造＝プログラム」を
繰り返し読んでいたことが大きかったようにも思うので、
（更には、開発者自身が解説した「プログラミング言語 C」（コンピューターのある処には必ず置いていると言われていました）や
「プログラミング言語 C++」（初版は薄い本でした）が直ちに翻訳され、出版されたこと、
「再帰をほどく方法が解説された本」も翻訳して、出版されました。
OS が Windows になった時には、全ての Windows のプログラムはこの本のプログラムをコピーして作られていると言われていた本の
翻訳が出版され、（実家の本箱に入れていたら、ネズミの住家になり、齧られて、この本は駄目になっていました。
ネズミにも何冊もあった同じような本の中でどの本が最も貴重な本か判断できるのかな？）
プログラミングのやり方が１８０度変更になり、「使って天国、作って地獄」と言われていた頃で、一年がかりで苦労して読みました。
その後、C ではなく、Delphi や C++ のオブジェクト指向言語でプログラミングするようになって、
GUI で必要になる部品がクラスで提供されるようになり、誰でも簡単に Windows のプログラムを作成できるようになりました。
若い人たちから見ると我々の世代は無駄な努力を繰り返してきたみたいです。　
プログラミングは数学と異なり、その特殊性で私達団塊の世代が学んで来たことを繰り返さなくても、
適切な師匠について、それぞれの学びたい分野に上手く入門する事が出来れば、最新の技術から学び始める事が出来ると思います。
将棋（や囲碁）のプログラミングの発展の様子が分かる一連の書籍や人工知能やゲームの本がが出版されたこと：
どれも中途半端な理解でしたが、世の中で何が起こっているかはそれなりに知ることが出来ました。
「ゆわゆる入門書を書いても評価されない」から書くなと先生から言われたと話している高知大の京大出身の先生もいましたが、
良くできた入門書を書いたり、翻訳してくれる優秀な人達が沢山いたから、
独学することが出来ました。）、これだとは言い切れませんが。
我々老人の世代は（二つの専門を持てる様に、誰でも、即ち、地方国立大学の教育学部にいても、
（本当は、誰も期待していない地方国立大学の教育学部にいたから、（何処にいても生きていると実際は様々な事が起こりますが、）
即ち、弱小地方国立大学の教育学部にいて教員の専門がバラバラで、私が何をしているか誰も（誰もではなかったかも）気にしていませんでしたので、
自由にやりたいことが出来たかも分かりませんが、
（但し、「幾何学」などの教育学部の幼稚園・小学校/中学校・高校の免許の為の数学と全学部対象の共通教育の数学
（所謂、教養部の解体により、教育学部の私達も共通教育の講義も在職中の後半には持たされましたが、
教育学部の学生は教員免許の為の講義で流用していて、多分、トータルでも教育学部の学生は一人受講しただけだったと思います。）
（「微分積分」と「線形代数」は理学部の担当で、農学部や人文学部の学生さんも対象なので、私の専門の「位相幾何学：トポロジー」の
話をする訳にもいかないと思ったので、何をすれば良いか試行錯誤して、付け焼刃で、「グラフ理論」や何種類かの「暗号解読」
（「解読するためのプログラムを自作して、（この時作ったプログラム達は、確か防衛大学の関係者が書いた一連の古典的な暗号の解説書を
元に作ったもので、まだバグが残っているものもある気がしますし、公表するレベルの物ではないです。）パソコンを使った古典的な暗号解読」や
「良く知られている整数論を使った暗号」（暗号と言いながら整数論だと言われました。
補助のプログラムの作成など、キチンと勉強して講義をすべきでしたし、専門分野でもないのに、私を教えて下さった教授達の真似をして、
ノート無しで講義し、失敗もしました。私の師匠は他人が見ると暗号みたいなカードを見ながら良く講義していましたが。））などやってみましたが、
最後にやった「ゲームの世界」だけが上手くできた講義（受講生が数倍になり教室一杯になりました）だったように思います。
その時のプログラムは「数学教育を改善するためのソフト開発」：https://www.cc.kochi-u.ac.jp/~tyamag/sugaku.html にアップしています。
更に、毎週レポートの課題を出していましたが、https://www.cc.kochi-u.ac.jp/~tyamag/sokoban/sokoban.html の「倉庫番」のプログラムには、
高知大学の平成２０年度の共通教育の授業「ゲームの世界」の 受講生たちが作った問題と
高知大学の平成２１年度の共通教育の授業「ゲームの世界」の 受講生たちが作った問題の良い問題と思ったものを組み込んでいます。）の講義のほかに、
数学の教員免許の為に必修のプログラミングを教える「情報数学」の講義
（私が教育学部にいる間に、時代遅れの「測量」が廃止され、「コンピュータ」が数学の必修科目に変更になりました）や
（市販のパッケジプログラムを使いだすまで）大学の入試のデータ作成の為のプログラム作成の委員を
その間継続して勤めていたので「遊んでいた」訳ではなく、ある意味、必要以上の学びをしていただけですが。））、
独学で、（芸術家やスポーツ選手などの独学と異なり、直接講義を聴いて、指導してもらっていなくても、
間接的に、本や雑誌を通して、優秀な一流の人達に教わっています。）
数学の研究・教育の合間に、昔は、世の中、なんとなく時間がゆったり流れ、余裕があったので、
（今は、全世界が弱肉強食の世の中で、（例えば、米国は本当に見習うべき民主主義国だろうか？
私の大学時代は「大学では米国の歴史を教えることが禁止されている」と一般教養の歴史の先生が話していたと記憶しています。
日本では、誰も責任を取りたくないので、証拠が残らないよう記録を残すことをしませし、残していても真っに塗りつぶした記録しか開示しませんが、
欧米ではあらゆる記録を残しているので、秘密にされていたものが開示された時や古い資料を発掘した時など、時々、
世界史（日本史も）の大きな修正が起きます。）、
日本の政策も全部強者の為の政策で、国の予算も基本は強者にまず配分し、中抜きした後で、一部を弱者に配分する政策ばかりで、
それを正当化するために強者は弱者を如何に騙すか必死に知恵を絞っている様にしか見えませんが。
「何処で騙しているか」は強者達が主張するその根拠としている暗黙の「前提条件」が本当に正しいか考えてみることです。
「間違った前提条件からは、どんな馬鹿げた結論でも論理的に導ける」ことが数学的に知られています。
例えば、「富裕層の所得・富が著しく増大する一方で、大半の所得層では生活水準が低迷している状態と言える」と言った世界的な
状況を無視し、富裕層から低所得層へ・都市部から地方への富の再分配をすることなしに、老人達と若者達の分断を煽り、
「低所得者からの税金だけ」をどの様にするかの議論ばかりです。富裕層に課税すると外国に逃げると盛んに主張されてきましたが、
「少子高齢化が問題」と言いながら、政治の無策で、日本では食べていけない、十分な給料を得ることのできない、
何らかの技術を持った若者達が外国に次々と逃げ出しています。）
パソコンの発展と共に基本的な理論を学ぶことが出来ましたが、
若い人たちはもっと効率的な学び方があると思います。
（又、「中学校で数学の落ちこぼれであったのに、２年生の夏休みから、急に数学が出来るようになった」と
成績が悪いと居残りの補習を一度、一緒に受けた同級生に言われるようになったか、
大学の学部に進級すると教養部の先生に「出来るそうでね」と不思議そうに言われた理由は、
（自分が何で数学が出来る様になったか考えたことなかったですが、）
大学の場合は、この年になって考えると色々な数学の本を読んできましたが、
「現代数学概説I」を大学１年と２年の間の春休みに只管読んだことが、その後の数学を理解する上で大きかったと思います。
残念ながら、最後まで読み終わりませんでしたが、最後まで読んでいれば良かった！　何時もすることが中途半端です。
更に追加すると１年生の時、他の自主ゼミより遅れて、高知から唯一人の学生だった（数学科に高知から私以前に行ったのは二人だそうです。
その三人全員が高知大に一時期、集まったとその一人の野町先生（非常勤として来ていて「確率過程」を教わったハズです）が言っていました。）
私を誘ってくれたて始まったチューターの２年生の梅野さんと森さんと３人だけの小さな自主ゼミで
コルモゴロフ・フォーミン著「函数解析の基礎」を少し齧っていたり、
他の自主ゼミで読んでいたポントリャーギン著「連続群論」の最初を自分で少し読んでいたから、また、
外国語など色々やることが多くて、熱心に勉強したとは言えませんが一般教養の「微分積分」と「線形代数」の講義を一様聴いていたので、
「現代数学概説 I」、又、後に「現代数学概説 II」を一人で読むことが出来たような気がします。
「現代数学概説 I」（や「現代数学概説 II」）が他の参考書と異なるのは、「帰納と類比」の重要性を教えてくれる本であり、
この本を読むために、他の参考書を参照する必要が無いように、（ほぼ）完全に必要なことはこの本で解説してくれていて、
中学や高校の数学の参考書・問題集の様に（解答はないですが、難しいいものにはヒントがある）大量の「例題」の形で、
我々凡人でも、コツコツ解いていけば、数学の概念を理解できるように強制的に理解すべきことを練習できるようになっていることです。
例えば、p.313 の定理１１の証明がどうしてこの様なめんどくさいことをしなければいけないか、多重線形写像の定義と
定理９（及び証明）とTensor 積の定義などと与えられた前提条件から納得いく答えが得られるまで、我々凡人は、考え続ける必要があります。
「先生に質問しに行けば、簡単に分かるのに、先生はその為にいる。（しかし、進学校で教員のアルバイトをしたことのある数学の教授が、
「新学期に、生徒たちが次々に質問に来るから、分からないから聞きに来るのだと思っていたら、ぴったり質問に来なくなった。
どうも新しい先生の実力を値踏みに来ていただけで、実力があることが分かれば先生に興味がなくなり、先生を無視し、自分で勉強しだした。」と
話をしていたことがあります。）」と思うと思いますが、自分で気づくことに意味があります。多分。
熱心に指導して下さった先生方には申し訳ないですが、先生の話を聴いているだけでは、我々凡人は数学も出来るようにはならないです。
暗記力に問題があるので、記憶する気がないだけかも分かりませんが、一人で、かなり大量の練習問題を集中してこなさないと
「誰でも出来るようになるハズの数学」でも出来るようになりません。
中学校の場合は、中学で「算数」から「数学」に変わった時、解答付きの例題があり、その直後に、その例題が理解できれば解けるはずの問題が
適切な個数並んでいる参考書で、その例題の解法の為の「目玉になるアイデア」を見つけ、
（即ち、このことに気が付けば、自分でも自力でこの例題が解けたはずだと思えるアイデア：
他人に教えられたものでなく、自分で見つけたものは宝物になります。）、
問題が解けなければ例題の解答を読み返し、
「魚の捕り方」を自然と学ぶことが我々凡人には必要だった様に、大学で学び始める「現代数学」でも、「集合に順序や位相や代数構造を
入れるという新しい概念（アブストラクト・ナンセンスとも言われますが、定義にもとづき、前提条件から厳密な・論理的な議論をすること）」に
なじむためには、「現代数学概説 I」や「現代数学概説 II」の様な参考書が我々凡人には必要でした。
大学の数学では、例えば、高校までと異なり、個々の関数を研究するのではなく、関数全体の集合を研究対象にし、その構造を研究し始めます。
それぞれの分野の入門期には、我々凡人には、適切な師匠が、多分、必要で、上手く入門出来れば、後は一人で出来ます。
記憶力の良い優秀な人達には通用しない事で、馬鹿げた考えだと思いますが。多分。
どの様な巡り合わせになるか、どの様な人達、どの様な本達に巡り合うか、
何で「現代数学概説 I」を読もうと思ったか、著者の一人に日本初のフィールズ賞受賞者の小平邦彦さんの名前があったからか、
更に、何で「ドイツ語の亀の子文字（装飾文字）」で半分ぐらい解説してあるドイツ語の入門書を古本屋で高校生の時、手に入れたか、
（この頃の数学の本には、「ドイツ語の亀の子文字（装飾文字）」が記号として、沢山使われています。）
今となっては不明ですが、この本で現代数学を学ぶための基礎を学ぶことが出来ましたが、人生は結局、運です。多分。
「修業は一人でするものだが、入門には師匠が必要」で、上手く入門出来れば、後は「独学」で知識・技術の習得は出来ますが、
それを他人・世間に認めてもらうのは「資格試験に合格する」などしなければ難しいですが、有名な大学や大学院で学べば、
知識・技術の習得だけでなく、朋友などの人脈形成や学閥の有形・無形の支援などを受けることが出来るようになります。多分。）
MusiXTeX の様な複雑な画像を作成するためには、
最終的には Knuth さんの作った TeX のコマンド・プログラムを元に描画しているので、
大本の TeX の理解（「TeXbook」の理解）から始めるのが早道みたいです。

M-Tx の真の配布元から「M-Tx: Music from Text Version 0.62 User’s Guide」を見つけた。
これは M-Tx の作者自身が書いた解説書です。所謂一次資料で、良いものが見つかった。
マニュアルではないので、出来る事全てを書いている訳ではないと思いますが、
オリジナルな楽譜を描きたい訳ではなく、描きたい楽譜の通り描ければ良いだけですが、
中学までの音楽の知識しかないので、読んで理解できると良いのですが？
43ページの解説書ですが、インターネット上の二次的な情報では不明だった事がチャンと解説されています。
これらは人工的な物なので、幾ら考えても分からず、具体的に例で M-Tx の作者から教えて貰う必要があります。

簡単な例は


Title: Riff in C
Composer: W. A. Mozart (1756 -- 1791)
Style: piano
Width: 120mm

c2+ e4 g | b4d- c1 d c2 |
c8 g+ e g c- g+ e g | d g f g c- g+ e g |


を mtx_example2.mtx とする時、


prepmx mtx_example2
pmxab mtx_example2
euptex mtx_example2
musixflx mtx_example2
ptex2pdf -e -u mtx_example2


を実行すれば、mtx_example2.pdf のファイルに、楽譜を描いてくれます。






コンパイルに失敗した時は、中間で作成された mtx_example2.mtx 以外のファイルを
削除してから、再コンパイルする必要があります。次の例、（作者は PMX は lyrics(歌詞)が
表示できないから、M-Tx を作ったと書いていますが、）


Title: Net soos ek is
Composer: Charlotte Elliott
Style: SATB
Sharps: 2
Meter: 3/4
Space: 9

f f f | e2s e4 | f2 b4 | a2d | g4 g g | f2 f4 | g2 c4n | b2d |
d d d | d2r d4r | d2 d4 | d2d | e4 e e | d2s d4 | e2 f4 | f2d |
L: 1. Net soos ek is, geen hulp na-by, al-leen U bloed ge-stort vir my,
L: 2. Net soos ek is, nooi U vir my, ver-ge-we, rei-nig en be-vry.
L: 3. Net soos ek is, U lief-de teer werp al-le hin-der-pa-le neer.
a a a | g2s g4 | a2 g4 | a2d | b4 b b | c2n c4 | b2 e4 | ds2d |
d d d | d2 d4 | d2 g4 | f2d | e4 e e | a2 a4 | g2 g4 | b2d |


もチャンとコンパイルできます。

プロのミュージシャンでない音楽に関して素人である我々は,
「M-Tx: Music from Text Version 0.62 User’s Guide」を読んで、
 M-Tx が理解できれば、多分、必要な楽譜は作れます。
上の例は、この pdf の最初のプログラミングの例です。平易な英文で解説してくれています。
最初に作りたかった楽譜の断片は作れたが、デジタルの時代だと言っても、
音楽の知識がない人間は、複雑な楽譜は本の楽譜をコピーするのが矢張り一番簡単です。
何の為にそのような楽譜が欲しいかが、本当は本質的な問題です。

暑かった季節も終わり、高知の公園にも小さな子だも達の歓声が戻ってきました。

お寺からお札が送られてきたので、久しぶりに佐川に帰ると昔購入していた「エスペラント四週間」が見つかった。
「・・・　ところが、外国語は、どれもむずかしし、それを完全にモノにすることは、ふつうの人にはほとんどできない。
だいいち、カネと時間がかかりすぎる。それに、ひとつの外国語だけで世界じゅうのどこの国の人をも
相手にするわけにはいかない。・・・」
「・・・　そうは言っても、ひとりでコツコツ語学を学ぶのは、なかなかシンドイことである。
はじめは、かなりスラスラと調子よくいっても、しばらくすると、かならずぶつかって立ち往生するのがふつうである。
もしそこで、あきらめて止めてしまっては、それまでの骨折りが水の泡になってしまう。
その努力をムダにしないためには、心機一転、またはじめから出なおすのが、いちばんよい。
しばらくの冷却期間をおくなり、ほかのことをなにかやるなり、カベにぶつかって、とまどった気持ちが
なくなるのを待って、気分をあらたにして、また出なおすのである。
　そうすれば、はじめぶつかったカベのところへ行くまで、すこぶる快調にすすむことができ、
その調子でいきおいよくそのカベをつきやぶって、さきへすすむことができる。
するとまたあたらしいカベにぶつかって、まごつき、イヤになるかもしれない。
そうしたら、また、はじめからやりなおして、いきおいをつけて、そのカベをつきやぶるのである。
　こうした手順をくりかえしていけば、たくさんの単語や文型、文法のきまりに、
だんだんとなじむことができ、エスペラントをモノにすることができるようになる。
　おおくの人は、この努力をしないので、せっかくの志が中途でくじけ、
独習書はいたずらに本箱のかざりものになってしまうのである。
つまり、語学の勉強に必要な条件のひとつは、根気よくやることである。・・・」
と書いてあります。私の本箱に何故本達が溢れているかの原因・理由を書いてあります。
　エスペラントの特殊性か、他の語学の独習書の様な「我々凡人にとって無茶な要求」は書いていません。
広く語学には、国語（日本語）、外国語（英語やロシア語やアラビア語など無数にあります）、数学（科学の為の言語）、
プログラミング言語（計算機に命令するための言語）があり、私は主としてこれらを学んできましたが、
プログラミング言語の学習が一番楽でした。人工的な言語で、文法に例外がなく、
覚えるべき予約語（外国語の単語、数学における定義に相当）と構文（文法規則とその意味）が少なかったのがその理由です。
但し、これはプログラミング言語の基本について述べているだけで、例えば、Python のライブラリーも対象にすると
無数とも言えるライブラリーがあるので、興味のある分野のライブラリーについて、
当然、膨大な学びが必要になる場合もありますし、Niklaus Wirth さんの「アルゴリズム＋データ構造＝プログラム」で教えて増らった様に、
（最もこの本は原著も翻訳も絶版になっているし、PASAL も消滅したので、これからプログラミングを学ぶ人たちには意味のない情報ですが）、
プログラミングは「データ構造」を使って、「アルゴリズム」を実装する事ですから、
データ構造とプログラミングしたい分野の膨大なアルゴリズムの学びが別途必要で、こっちの方が本当は大事です。
エスペラントも人工的な言語で、文法に例外がなく、動詞の人称変化もなく、原型、現在形、未来形、過去形、
命令形も語幹＋ -i, -as, -os, -is, -u で良いとか、男性・女性名詞と言った区別がないとか、単純で覚えやすいです。
しかし、単語は矢張り大量暗記する必要がありますが、今まで学んで来た外国語で、
なんとなく予想できる単語が多そうではありますが。まず、エスペラントで自分も出来ると自信を付けるのがいい気もします。
今は「ファスト教養」の時代で、無駄を省き、「すぐにお金になる事」が大切だと上も下も考える世の中で、
特に若い世代には息苦しく、住みにくい世の中で、能登の復興など無駄だと公然と発言する政治家が再選する世の中ですが、
エスペラントの様な明らかに学んでもお金になりそうなものではなく、
無駄とも思えるロシア語のお勉強も優秀な人達のようにはいかなくても、今は you tube で ロシア語と日本語の短文を次々表示しながら、
発音してくれるのもあるので、それを繰り返し見ながら、
　Я хочу пить.
  Что бы ты хотел выпить ?
　Ты хочешь выпить вино?  
　Я бы хотел по пить воду.
の様な役に立ちそうな短文を暗記するべく努力し、пить の仲間の выпить や по пить などが何であったか、
私の様な凡人は大学で先生に土曜日の午後２コマ一年間教えて貰っても、文法書で何度読んでも纏めては暗記出来ないので、
出てくるたび文法書で調べていく必要があります。
アラビア語は更に厄介で、動詞の変化も複雑だし、単語の造語法もヨーロッパの言語と異なります。
小池百合子著「３日でおぼえるアラビア語」を見て、政治家がこんな嘘を書いたらいかんと言った人がいますが、
（尤も３日と言えば、１日１０時間勉強するとすれば３０時間で、大学の半期一コマの講義に相当し、
「３日でおぼえるフランス語」など随分色々な事を書いていて、覚えるべき単語の数も多く、
３日で読み終える、ましてや覚えることなど私には不可能ですが、
何度も何度も繰り返し読んで最初に覚えるべき基本的な事柄を書いてはいるとは思います。
中国語は方言の上海語、広東語、福建語などありますが、普通話（北京語を元にした共通語）を普通最初に学ぶと思いますが、
アラビア語も地域ごとに異なる方言（話し言葉：アーンミーヤ）があり、エジプト方言、マグレブ方言（北アフリカ）、
レバント方言（シリア。パレスチナほか）、湾岸方言（サウジアラビアほか）などと標準的な共通語（フスハー）が
ありますが、小池百合子著「３日でおぼえるアラビア語」は、標準的な共通語（フスハー）ではなく、エジプト方言の参考書です。
要するに、凡人である一般人は、外国語で食べていくのでなければ、
「外国語の勉強は自分が聞いたり・話したりする必要のある文・事だけをまず繰り返し只管練習すれば良いのだ！」
と言うことを書いていると思います。
どうもフランス語の方が英語より易しく、動詞の現在変化だけが複雑で、現在は音声付きの参考書が沢山出版されているので、
覚えようと努力しないと我々凡人は覚えられないので、各人が欲しいものを他人・専門家に準備してもらうと高額のお金が必要ですから、
（例えば、多面体の模型も市販のキットを使えば、想定されている立体は簡単に作れますが、１セット１万円とか掛かりますし、
それを使って講習会をしても、受講者に作ったものを持ち帰らせれば、幾らお金があっても足りません。
ストローと針金とタコ糸で作れば、どんな立体でも作れ、作成に時間は掛かりますが、費用は僅かで済みますし、
講習会の受講者に各自が講習会で作ったものを持って帰ってもらえます。
勿論、多面体の模型のアメリカ製の市販のキットを購入し、構造を研究することで、新たな金儲けのアイデアを得る可能性もありますが。）
覚えたい部分を自分で編集して、例えば、


from pydub import AudioSegment
from pydub.playback import play

n = 1
m = 10

for i in range(10):
    print("No.", i+1)
    print("01_au_francais_nyumon_1080210401_25.mp3")
    sound = AudioSegment.from_mp3("01_au_francais_nyumon_1080210401_25.mp3")
    print('etre の活用')
    print('etre：～だ、～である')
    sound0 = sound[:14000] ## 単位ミリ秒
    sound0 = sound0*m
    play(sound0)
    print("01_au_francais_nyumon_1080210401_30.mp3")
    sound = AudioSegment.from_mp3("01_au_francais_nyumon_1080210401_30.mp3")
    print('avoir の活用')
    print('avoir ：～を持っている')
    sound0 = sound[:13000] ## 単位ミリ秒
    sound0 = sound0*m
    play(sound0)
    print("01_au_francais_nyumon_1080210401_36.mp3")
    sound = AudioSegment.from_mp3("01_au_francais_nyumon_1080210401_36.mp3")
    print('parler の活用')
    print('parler ：話す')
    sound0 = sound[:18000] ## 単位ミリ秒
    sound0 = sound0*m
    play(sound0)
　・・・


の様なプログラムを作って、このプログラムと同じ順序で動詞の活用表を LaTeX で作って、印刷し、
それを見ながら、毎日聴いていれば嫌でも覚えますし、発音の規則も少しづつ分かってきます。
覚えたい例文も同じことをすれば良いです。現在はそれほどお金を掛けなくても色々なことが学べます。
私にような凡人は、覚えたというような曖昧な基準ではなく、
例えば、後で古本屋に売ろうなどとはとは考えず、鉛筆で線を引いたり、辞書で調べたことを書きこんだり、
大事だと思ったことを書き写すと言う客観的な作業をすることで、兎も角一冊本を最後まで読む事が大切です。多分。
そうでないと本の最初を何度か読むだけで、我々凡人は覚えられないと本を読むのを止めてしまいます。
多分。そして、我々凡人は２回も読めば、本を読んだ・随分・十分勉強したと思って、安心しますが、
東大を首席で卒業したという人が教えてくれているように、最低でも７回は繰り返す必要が有りそうです。
尤も彼女は読むだけで良かったと思いますが。
昔の人は「読書百遍意自ずから通ず」と言っています。しかし、今の自分に適した本を読まないと駄目・無駄だと思いますが。
同じ本を読むのに飽きたら、別の同じレベルの本達でも良いです。多分。
我々凡人には難しい話ではありますが、囲碁のトップ棋士なども表題に名前が載っている本
を読むとそれぞれの分野でそれ以上の努力をしているみたいです。
又、英語もペーパーバックを読んでいて、意味不明なら、手間を厭わず片っ端から辞書を引いて見れば良いです。
In these notebooks he had recorded in an impeccable hand his own speculations, theories, digressions.
Blomkvist leafed through them. ( : leaf through a book : 本にざっと目を通す)
Ice had formed on the sound and inside the old harbour, ( sound: 入り江、瀬戸)
Blomkvist kept reading until the small hours and did not get up until late on Epiphany Day.
(small hours : [the small hours] 夜ふけ、夜中（午前１時から４時ごろまで）)
Leblanc died in Perpignan in southern France near the Spanish border. It was November 6,
1942 and he was a month shy of seventy-six. (His hit was one meter shy of a home run.:
彼のヒットはホームランに１メートル足りなかった。)
It did not mean, however, that she behaved herself. (他：(～ oneself):Behave yourself! : 
行儀よくしなさい：多分、この様な場合、フランス語は「代動」se comporter や se tenir と書いてある）
など意外なことが書いてあります。勿論、優秀な人達は前後関係から予想できるとは思いますが。
英語のニュアンスや語源を纏めた参考書を読んで見ても今一つなら、
辞書の大きい文字のページ数の多い項目を例文ごと何度も読んで見れば良いですし、
（私達の学生時代と異なり、現在は、探せば良い紙の辞書が見つかる良い時代になっています。
私は主として、今は製造中止で手に入らない Made in China の SII の電子辞書を使っていますが、
良く分かっていると思っていた小・中学校で身に着けたい語：約１１５０語に出会った時、意味が取れなければ、
「アクシスジーニアス英和辞典」の解説を読んでいます。宣伝されている本より、辞書が一番便利だと思います。
即ち、ペーパーバックを読んでいて、意味が取れない時、文法書を引っ張り出さなくても、
重要単語に関する事柄であれば、適切な辞書を読めば良い場合が現在は英語の場合は多いです。
そんなに高価ではないので（３０００円位）、実際に本屋に行って、
大きなフォントの自分がよく理解していると思っている no 、或いは自信の無い would などの解説を読んで見て、
自分に何が足りないかは、多分、自分で分かっていると思うので、自分に合った学習用の辞書を購入すれば良いです。
我々凡人にはランダムハウス英和大辞典だけが何時でも良い辞典でもないです。
最も現在は、インターネットで質問している人がいて、それに対する答えとしても探索出来ますが。）
revient が revenir と revoir のどっちか迷えば、より基本的な venir と voir の活用を思い出し、
それに re- を付けたものだと思い当れば、わざわざ語源の本を購入して悪戦苦悩することもないです。
電子辞書は便利ですが、次々製造中止になっていっています。大事に使わなくては。
英語も数学やプログラミングの本は易しい英語で書かれていますが、(ドイツ語やフランス語も同様です。
ロシア語はポントリャーギンの「常微分方程式」を買いに行ったら、先ずこれを読んで見ろとロシアの
高校の数学の教科書を買わされ、暫く時間を置いて行くと欲しい本を売ってくれました。
柴垣先生の授業の教科書だったので、翻訳で間に合わせ、まだ読んでいないですが。
ポントリャーギンの「連続群論」の原著も、一年生の時、読んだのは翻訳で、本箱で埃を被ったままです。)。
ミステリーは厄介な本があります。
例えば、Donald E. Westlake 著「Watch Your Back!」（木村二郎訳「うしろにご用心！」）などは、
"What gets me is this fruitcake Muslim Heaven with the seventy-two virgins."
易しい単語ばかりですが、訳せません。What gets me をインターネットで調べると意味を教えてくれます。
答えが分かると文法の知識を元に暫く考えているとそう言うことかと思いますが。丸暗記ではなく、理解できるよう、
色々なパターンを沢山練習して、瞬時に理解できるようになれば、聴いても理解できるようになるはずです。多分。
何を書いているかと言うと
((What gets me) is ((this fruitcake)=((Muslim Heaven)( with the seventy-two virgins)))).
の構造をしている文で、What gets me も主語と動詞と目的語があるはずで、gets は動詞で me は主語ではないので、
What が主語のはずである。だから、「何かが私をゲットした」。「その何かはこのフルーツケーキの
様なムスリムの天国で、そこには７２人のヴァージンがいる。」と（文法を元に考えて）理解すべきであった。
この様な訓練の為の本として薬袋善郎さんの一連の本がありますが、いきなりこれらの本を読んでも私の様な凡人は
英文法の基礎が出来ていないので、「猫に小判」（使い方が間違っているかも？）で、ずっと後に出版された
澤井康佑著「一生モノの英文法 COMPLETE」を読んで、（長時間の音声データが添付されているので聴いてか？）、
やっと英語の勉強はどうすべきが分かった気がします。
(「英文法を勉強しろ」と言う人と「勉強しなくても良い」と言う人がいると言うことは、多分、英文法には、
学ばなければいけない部分(「構文の仕組み」・「文や句や節がどの様な種類の単語の組み合わせ・語順により成り立っているか、
どのような意味的・文法的役割を果しているか」)と
気にしなくても良い部分（「辞書を引けば分かること」: 勿論、暗記しておけば、辞書を引く回数をへせますが、
現在は電子辞書など便利なものがあります。但し、話したり、聞いたり出来るためには、
瞬時に反応する必要があり、辞書を引く余裕がないので、語彙と発音の学習が必要です。
日本にやって来た外国人の子供が日本語を喋り出すのに、日本語を聞いているだけで、
半年間から一年間の何も喋らない期間が必要だと分かったそうですが、日本人が大人になって外国語を学ぶ時も同じで、
「構文の仕組み」を文法書を読んで理解できる為には、まず入門書で、学びたい外国語の沢山の文になじむ必要があるみたいです。
多分。）があると言うことで、
例えば、英語なら、澤井康佑著「一生モノの英文法 COMPLETE」に書いてあることだけで、
「英文を読むため」には、基本的に・プロになるのではければ、十分だと言うことだと思います。
ドイツ語の勉強のやり直しには鷲巣由美子著「これならわかるドイツ語文法」、フランス語の勉強のやり直しなら
六鹿豊著「これならわかるフランス語文法」が比較的最近(2016年)出版された本で入手しやすく、良いのではと私は思います。
我々凡人は、「(1)変化表を暗記し、(2)例文の文法的説明を理解し、(3)日本語訳から元の例文が
再現できるまで練習を繰り返すことです。」など、一回読むだけで、一気加勢に、出来るわけないですから、数回に分け、
一回目は、例えば、辞書を引きながら、すべての例文を訳して、参考書の訳文と比較するだけを兎も角最後までやってみれば良いです。
「構文の仕組み：文の成り立ち・組み立て方」の全体像を掴んでから、
後は、やりたいことに焦点を当てて、繰り返し読むことで、勉強すればいいです。多分。
私にはもう必要ありませんが、私の様な貧乏人が、独学で、たいしてお金を掛けずに、「英語などを話せるようになるため」には、
中川浩一著「総理通訳の外国語勉強法」が参考になると思います。マネできる処だけマネすれば。多分。)
ちなみに
((What gets me) is ((this fruitcake)=(Muslim Heaven with the seventy-two virgins))).
の様な分解・解析は、コンピューターに英文を理解させるために Prolog のプログラミングで
一時期盛んに研究されていました。
また、この様な Pascal の完全な構文は、Niklaus Wirth さんの本で私は学ぶことが出来ました、
この様な研究の一般論が、多分、チョムスキーさんが始めたとされるオートマトン・言語理論の
「言語理論」で、定義・定理・証明の羅列で、完全に現代数学と同じだと私は思いました。
「プログラミング言語」はこの言語理論で良いと思いますが、「自然言語の理解」は、様々な人達が色々な事を言っていて、
様々な主張が入り乱れていて、何が正しいか私には良く分かりません。現在の AI の限界もそんな処にあるかも？
fruitcake も勿論、フルーツケーキそのものではありません。例え・比喩です。
こっちの方は学生の時、手に入れた「THE POCKET DICTIONARY OF AMERICAN SLANG」にも載っていますが。
私が大学生の時にはどうしようもなかったですが、良い時代にはなっています。何をしたいかで何をすべきかが決まります。
アラビア語も最近、中川浩一著「総理通訳の外国語勉強法」では、自分のした勉強法を詳しく解説してくれていますし、
師岡カリーマ・エルサムニー著「これからはじめるアラビア語入門」など独学でも何とか出来そうな気にしてくれる本が出版されています。
こんな本を書く人達は全て恵まれた環境で学んだ人（国のお金で勉強させてもらったとか、父親がエジプト人で母親が日本人とか、
小さい会社（？）の社長をしている私の大学の同級生は子供を米国に留学させるのに、月１００万円送っていたと話していました。）ですが、
お金がない我々でもマネできることがないか考えて、アラビア人と話す必要があるか？千夜一夜物語を原書で読みたいだけか？
アルジャジーラを見て理解できるようになりたいか？
フランス語なら子供の頃読んだアルセーヌ・ルパンを今なら安価（200円？）で手に入る原書で読みたいとか、
（半過去形や条件法・接続法の理解も必要でハードルは高いですが、修行中なので、英語を学んだ時の様に、
現在は市内の複数のブックオフを回り、古本で購入するなどする必要があるものが多いですが、
堀口大学さん（「強盗紳士」新潮文庫　他）や平岡敦さん（「怪盗紳士ルパン」ハヤカワ文庫　他）や
竹内英夫さん（「怪盗紳士ルパン」偕成社文庫　他）の翻訳と見比べながら読んで見れば良いです。
全部を手元に置いておく必要はなく、本屋や図書館や今では至る所にあるブックオフの様な古本屋で、
実際に手に取って読んで見て、元が一つと思えないほど、訳文のトーンが異なっているので、
自分の好きな本一冊あれば良いです。高知にも日本で最後の県として「ドン・キホーテ」が開店しましたが、
全国チェーンの店ばかりになり、（家の近くの「MAC」が「2nd STREET」(Reuse store) に代わり、
「2nd STREET」に注意が向くようになると「2nd STREET」も市内に沢山出来ていることに気が付きました。
近所の「2nd STREET」の開店日に行くと私位の年の老人が「日本人なのに鰻が食べれなくなった。」と呟いていました。
私の子供の頃は冬には近所の小さな川で私でも鰻が採れていました。
今は鰻の生態が分かり、河口で稚魚が一斉に捕獲されてしまいますが、この老人はそういうことを言っているのではなく、
一部の金持ちと大多数の貧乏人の格差が拡大し、多くの人が私の子供時代のように貧乏に成り、
一部の人だけが富を独占する国になってしまいました。
尤も、鰻の稚魚の密漁も盛んに行われているみたいで、多分、鰻は完全養殖ではないので、
稚魚の乱獲で、資源が減ってきていて、日本鰻が食べれなくなってきているかも？
昔は、今みたいに、鰻も一年中食べてはいなかったと思いますが？）、 
地方のお金が大都会や米国に吸い上げられる一方で、地方には地方交付金や
ふるさと納税で僅かばかりのお金しか戻ってきません。地産地消も限られています。
農家が農産物を持ちより販売している「とさのさと」には、始めてみる柑橘（文旦より大きいみかん）があります。
購入しているお婆さんがいたので、「それ美味しいですか？」と聞くと「美味しいよ。
家で植えているけど実がならない。」と言っていました。最近のブドウやイチゴの様に、庶民は食べれなくなりますが、
（最近の国産のブドウは高価ですが、スーパーでは安価なオーストラリア産のブドウが売られています。
オーストラリアは知りませんが、昔、スペインでは、日本の様に棚を作って大切に栽培せずに、そのまま地面に這わしていました。
スペインで食べたブドウも、屋台でミキサーで目の前で作って売っていた生の果物ジュースも美味しかったですが。）
地域にまだあるこの様な品種を基に、外国で作れないもの・栽培の難しいものを日本の技術で生産し、外国へ輸出すれば、
米国やオーストラリアのような大規模な農業でなくても、小規模な日本の農家の収入を高めることが出来るはずです。
沖縄復帰の日から琉球大学理工学部の助手に採用してもらいましたが、その頃、雑談で、
「本土（大和）では、田圃の畔（あぜ）で大豆を栽培している。」と復帰に際して本土（大和）の事を勉強した数学の教授が
言ったことを覚えています。昔は、少ない土地を最大限活用して、農業をしていましたが、
米国のマネなのか、地理的環境差を無視した農業は大規模でないといけないと言うことになり、この様な風景も農村から消えました。
「やらせ」かも知れませんが、テレビで、「今の日本は親が必死で貯めた財産を放蕩息子が使い潰している状態だ。」と
言う趣旨の発言を日本に長く住んでいるアジア系のお婆さんがしていたのが印象に残りました、
田舎出身の首相は何を考えているのだろう？
勿論、対訳ではないので、フランス語をチャンと学ばないと原著は正確には読めませんが。
更に、Penguin Classic の「Arsene Lupin, Gentleman-Thief」や「Arsene Lupin, Der Gentleman-Dieb」などもあります。
良く分からないですが、これらは洋書ですが、「Printed in Japan」と書いてあって、円安の今でも安価で手に入ります。
著作権が切れているのだろうか？日本の製本の品質が良く、日本の中小企業の労働者の賃金が異常に低い上に円安が続いているので、
費用が安く抑えられるので米国などがアウトソーシングしているのかな？
「ルパン三世」を生み出した日本がフランスに次いでルパンの人気あるそうで、この様にルパンの翻訳が沢山あるみたいです。
推理小説の本場とも言える米国では不当に過小評価されているそうです。英国とフランスが本当は仲が悪いのは有名ですが。米国も？
この分野（翻訳ミステリー）は英米の作家がほとんどでしたが、最近は北欧や中国（や台湾）の作家も日本で人気になっています。
フランスには「黄色い部屋の秘密」のガストン・ルルー（Gaston Leroux)やジョルジュ・シムノン（Georges Simenon)
（私の学生時代に流行っていた作家で、フランス人だと思っていましたが、ベルギー出身のフランス語で書く推理作家だそうです）がいますし、
最近は「その女アレックス」のピエール・ルメートルがいます。
ドイツやロシアやスペインやイタリヤには日本で有名な推理小説の作家はいないみたいです。
私が知らなかっただけで、「ミステリマガジン」の「２１世紀翻訳ミステリベスト！」には
ドイツやスペインや韓国の作家の作品が翻訳されているとそれらの作品が紹介されていました。
ロシアにも推理小説の作家がいるとNHKのラジオ講座で話していたと記憶しています。
ルブラン原作、南洋一郎文「怪盗紳士」ポプラ社は翻訳ではなく子供向けに書き下ろした本です。
ハヤカワ「ミステリマガジン」で松江松恋さんが面白いことを書いていました。

「推理とは何でしょうか。
ミステリの訳語は第二次世界大戦後に探偵小説から推理小説に変わりました。辞書で推理を引くと、
「ある事実を基にして、まだ知られていない事柄を推し量ること」というような意味が出てきます。
推理のためには何か前提がないといけないということがわかります。それが考えるための手がかりであり、
論を立てた後でそれを支えてくれる証拠です。
手がかりや証拠がないときに突然ひらめきが降ってきて、得られた結論が事実と照らし合わせて正しかったとしても、
推理が行われたとは言えません。それは単なる思いつきでしょう。
一人だけの世界で完結するものは推理とは認められません。同じ手がかりが与えられれば、考える人が代わっても
同じ結論に到達できる、そういうものが推理です。」

これが所謂高尚な文学作品との違いです。吉見俊哉著「アメリカ・イン・ジャパン」で解説されているように
有島武郎著「在る女」や谷崎潤一郎著「痴人の愛」が何を書いているかを読み取るのは我々凡人には難しいです。
何を言っているかと言うとこれら所謂高尚な文学作品を優秀な人達の言う様に理解するためには、
作品そのものに実際に書かれていることだけでなく、作者の文化的素養・生活体験などの作家個人の背景知識や
文学界の流れ・流行・歴史や当時の社会背景など様々な知識が必要になります。多分。
勿論、我々凡人は、そんなこと気にせず、面白いと思ったものを好きなように読めば良いとは思いますが。

また、大学院入試や仏検対策でなく、単に楽しみ・暇つぶしに学んでいるなら、重要な動詞変化や単語はしょっちゅ出てくるので、
色々な人達が書いている様に、その都度、辞書を引いたり、文法書を調べるようにし、
シャカリキになって纏めて覚えなくても良いようにも思います。
本当は、学生時代に「力学」を習った先生の様に、息抜きに、モンテーニュの「随想録」を読むのが望ましいでしょうが。
どうも、それぞれの先生に何を習ったか、その内容は全然覚えていませんが、それぞれの先生の雑談だけは覚えています。）、
何をしたいかで何をすべきかが決まります。多分。棋士の米長邦雄さんも何を目指すかで、勉強の仕方が全く異なると書いていました。
兎も角、ファン・推しの人の本だけでなく、色々な人の体験談を読んで見ると良いです。
「本物を見分けるためには、一流の物だけ見なさい」という人と
「良い映画を見るためには、全ての映画を見なさい」と言う人とがいます。
どちらも我々、貧乏人の凡人には、実行不可能な事ではありますが。
我々凡人の貧乏人に役に立つことを書いている人は少ない（即ち。置かれている環境・前提条件が違いすぎたり、
我々凡人が知りたいと思っていることを当人は当たり前のことだと思っていて、或いは、無意識にやっていて、
それを書くことが殊更重要だと思っていなくて、わざわざ書くまでもないと思っている可能性もあります）とは思いますが、
自分でも使うことのできる教材とプログラミングで、工夫すれば何ができるか考えれば良いです。多分。







但し、私の様に、人が面白そうな事をしていれば何でもやってみたくなると何もなさずに終わりますが。
また、英語にはドイツ語が一番近いと思い込んでいましたが、中川浩一著「総理通訳の外国語勉強法」の
（参考２）アメリカ国務省付属の語学機関による語学難易度には
カテゴリー I (英語に近い言語）イタリア語、スペイン語、フランス語、・・・
カテゴリー II (カテゴリー I より英語から遠い言語）ドイツ語、インドネシア語、・・・
カテゴリー III (難しい言語、英語とは大きな隔たりのある言語）ロシア語、タイ語、トルコ語、ヘブライ語、・・・
カテゴリー IV (非常に難しい言語）アラビア語、中国語、韓国語、日本語
と書いてあります。同じセム語族で、同じく母音を省略するヘブライ語がアラビア語より易しいと言うのが良く分からないですが。

トランプ大統領はカナダやメキシコなどからの麻薬流入を止める為に関税の強化が必要だと力説していますが、ドン・ウィンズロウ著「犬の力」
の解説には、「・・・　アメリカの CIA は中南米の共産化を防ぐためという大義に基づき各国への工作を行ったが、負の遺産として
現地で深刻な社会問題を引き起こしている。麻薬カルテルの拡大もその一つで、長期的に見ればアメリカは自分で自分の首を
締めたのだ。・・・」と書いています。「江戸時代に落語」が果たしていた役割を「現在は推理小説」が果たしている様な気がします。
世の中で起こっていることはそんなに単純ではないみたいです。
）、
現代はもっとすごくて、「１０分で答えが欲しい人たち」ばかりになっているそうです。若い人たちが可哀そうです。
一時期、日本の家電品や半導体が世界の市場を席巻していましたが、欧州や米国の圧力もあって、米国の属国である悲しさもあって、
昔の面影もない発展途上国に逆戻りしてしまいましたが、優秀な官僚や政治家や大企業の社長の皆さんはこのような現状を、
自分達だけが生き残るには好都合だと思っているので、現状の「自己責任」で「弱肉強食」で、米国やドイツや
江戸時代の藩が存在した時代の日本の様なある程度、地方が自立している状況でない現在の中央集権的な国家で、「地方切り捨て」
の政策を推進しているのでしょうが、一般の国民にとって望ましいことだと本当に思っているのでしょうか？
どうも私は日本人なので普通のアルファベットではなく、不思議な文字を使っている言語が好きみたいです。
　老後は、「やり残したことをする」のが良いそうで、皆は「山登り」や「旅行」や「新しい趣味」などを始めるみたいですが、
本箱で埃を被ったままの本達を「上の緩やかな考え」で、再度、読んで見るのが、お金もかからず、良いみたいです。

「修業は一人でするものだが、入門には師匠が必要」の例は、強化学習(Reinforcement Learning)を学んでみたいと思っても、
我々凡人には、参考書に書いてあることが抽象的すぎて全く理解できません。
書いてある数式をプログラムに変換できれば、理解できたと言えると思いますが、
その数式が理解できるように今まで読んで見ようとした本達には書いてありません。多分。
読み方が不十分であったかも分かりませんが。
又、Berkeley の有名な「パックマン(PacMan)」の　PacMan ai project というのもあり、そのプログラムをゲット出来ますし、
YouTube の沢山の動画もありますが、我々凡人には、プログラムが複雑すぎて、
また、私のコンピュータの能力・私の能力が低すぎるのか、そのプログラムを上手く実行できなくて、理解できません。
我々凡人には、先ずは、原理が分かる単純な例・プログラムが欲しいです。
やっと、Sudharsan Ravichandiran 著「Deep Reinforcement Learning with Python」の p.99 の単純な例を元に


import  numpy as np

dynamics = np.array([
    [[0, 0, 0, 0.1, 0], [0, 0, 1, 0.8, -1], [0, 0, 2, 0.1, 1]],
    [[0, 1, 0, 0.1, 0], [0, 1, 1, 0.0, -1], [0, 0, 2, 0.9, 1]],
    [[1, 0, 0, 0.1, 0], [1, 0, 1, 0.5, -1], [1, 0, 2, 0.3, 1]],
    [[1, 1, 0, 0.1, 0], [1, 1, 1, 0.7, -1], [1, 1, 2, 0.2, 1]],
    [[2, 0, 0, 0.1, 0], [2, 0, 1, 0.2, -1], [2, 0, 2, 0.7, 1]],
    [[2, 1, 0, 0.1, 0], [2, 1, 1, 0.6, -1], [2, 1, 2, 0.3, 1]]
    ])
Q = np.array([
    [0, 0, 0.0],[0, 1, 0.0],
    [1, 0, 0.0],[1, 1, 0.0],
    [2, 0, 0.0],[2, 1, 0.0],
    ])
V = np.array([0.0, 0.0, 0.0])
gamma = 1.0

def calc_Q(s, a):
    q = 0
    for i in range(3):
        ns = (int)(dynamics[2*s+a][i][2])
        q += dynamics[2*s+a][i][3] * \
             (dynamics[2*s+a][i][4] + gamma * V[ns])
    return q

def calc_V():
    global V

    nV = np.array([0.0, 0.0, 0.0])
    for s in range(3):
        Q0 = calc_Q(s, 0)
        Q1 = calc_Q(s, 1)
        nV[s] = max(Q0, Q1)
    V = nV

def value_iteration():
    global V, Q
    
    num_iteration = 10
    for n in range(num_iteration):
        old_V = V.copy()
        calc_V()
        for s in range(3):
            for a in range(2):
                Q[2*s+a][2] = calc_Q(s, a)
        print('V=', V)
        print('Q=', Q)
        if np.amax(np.abs(old_V-V)) < 0.001:           
            break

value_iteration()


と p.118 の単純な例を元に


import  numpy as np

dynamics = np.array([
    [[0, 0, 0, 0.1, 0], [0, 0, 1, 0.8, -1], [0, 0, 2, 0.1, 1]],
    [[0, 1, 0, 0.1, 0], [0, 1, 1, 0.0, -1], [0, 0, 2, 0.9, 1]],
    [[1, 0, 0, 0.1, 0], [1, 0, 1, 0.5, -1], [1, 0, 2, 0.3, 1]],
    [[1, 1, 0, 0.1, 0], [1, 1, 1, 0.7, -1], [1, 1, 2, 0.2, 1]],
    [[2, 0, 0, 0.1, 0], [2, 0, 1, 0.2, -1], [2, 0, 2, 0.7, 1]],
    [[2, 1, 0, 0.1, 0], [2, 1, 1, 0.6, -1], [2, 1, 2, 0.3, 1]]
    ])
Q = np.array([
    [0, 0, 0.0],[0, 1, 0.0],
    [1, 0, 0.0],[1, 1, 0.0],
    [2, 0, 0.0],[2, 1, 0.0],
    ])
V = np.array([0.0, 0.0, 0.0])
P = np.array([1, 0, 1])
gamma = 1.0


def calc_Q(s, a):
    global V
    
    q = 0
    for i in range(3):
        ns = (int)(dynamics[2*s+a][i][2])
        q += dynamics[2*s+a][i][3] * \
             (dynamics[2*s+a][i][4] + gamma * V[ns])
    return q

        
def calc_V():
    global V

    nV = np.array([0.0, 0.0, 0.0])
    for s in range(3):
        nV[s] = calc_Q(s, P[s])
    V = nV

def get_next_policy():
    global V, Q, P
    
    num_iteration = 50
    for n in range(num_iteration):
        old_V = V.copy()
        calc_V()
        if np.amax(np.abs(old_V-V)) < 0.001:           
            break
    for s in range(3):
        for a in range(2):
            Q[2*s+a][2] = calc_Q(s, a)
    for s in range(3):
        P[s] = 0 if Q[2*s][2]>Q[2*s+1][2] else 1
        print('V=', V)
        print('Q=', Q)
        print('P=', P)

def policy_iteration():
    global P
    
    num_iteration = 50
    for n in range(num_iteration):
        old_P = P.copy()
        get_next_policy()
        if old_P[0]==P[0] and old_P[1]==P[1] and old_P[2]==P[2]: 
            break
    print('P=', P)
    
policy_iteration()


の様なプログラムを作ってみることで、やっと参考書に書いていることを、抽象的な議論を、理解する糸口を得ました。
今の場合、本に書いてあった式は適当な初期値を与え、繰り返し修正し、安定になった時の式を与えていたみたいです。
即ち、強化学習の本の数式は、通常の数式ではなく、アルゴリズムを背負った数式であるという認識が必要でした。
但し、この本には完全なデータを与えてくれていないので、上のプログラムは間違っているかも分かりませんが、
心理的なバリヤーが取れ、拒否反応が無くなり、GYM というライブラリーを使っていて、その部分がブラックボックスで、
プログラムを全部・完全には見せてくれませんし、Frozen Lake problem でも optimal policy が


[0. 3. 3. 3. 0. 0. 0. 0. 3. 1. 0. 0. 0. 2. 1. 0.]


が何を言っているか理解するためには


for s in range(16):
    for a in range(4):
        print('P[',s,'][',a,']=', env.P[s][a])


を実行して


P[ 0 ][ 0 ]= [(0.3333333333333333, 0, 0.0, False), (0.3333333333333333, 0, 0.0, False), (0.3333333333333333, 4, 0.0, False)]
P[ 0 ][ 1 ]= [(0.3333333333333333, 0, 0.0, False), (0.3333333333333333, 4, 0.0, False), (0.3333333333333333, 1, 0.0, False)]
P[ 0 ][ 2 ]= [(0.3333333333333333, 4, 0.0, False), (0.3333333333333333, 1, 0.0, False), (0.3333333333333333, 0, 0.0, False)]
P[ 0 ][ 3 ]= [(0.3333333333333333, 1, 0.0, False), (0.3333333333333333, 0, 0.0, False), (0.3333333333333333, 0, 0.0, False)]
P[ 1 ][ 0 ]= [(0.3333333333333333, 1, 0.0, False), (0.3333333333333333, 0, 0.0, False), (0.3333333333333333, 5, 0.0, True)]
P[ 1 ][ 1 ]= [(0.3333333333333333, 0, 0.0, False), (0.3333333333333333, 5, 0.0, True), (0.3333333333333333, 2, 0.0, False)]
P[ 1 ][ 2 ]= [(0.3333333333333333, 5, 0.0, True), (0.3333333333333333, 2, 0.0, False), (0.3333333333333333, 1, 0.0, False)]
P[ 1 ][ 3 ]= [(0.3333333333333333, 2, 0.0, False), (0.3333333333333333, 1, 0.0, False), (0.3333333333333333, 0, 0.0, False)]
・・・
P[ 14 ][ 0 ]= [(0.3333333333333333, 10, 0.0, False), (0.3333333333333333, 13, 0.0, False), (0.3333333333333333, 14, 0.0, False)]
P[ 14 ][ 1 ]= [(0.3333333333333333, 13, 0.0, False), (0.3333333333333333, 14, 0.0, False), (0.3333333333333333, 15, 1.0, True)]
P[ 14 ][ 2 ]= [(0.3333333333333333, 14, 0.0, False), (0.3333333333333333, 15, 1.0, True), (0.3333333333333333, 10, 0.0, False)]
P[ 14 ][ 3 ]= [(0.3333333333333333, 15, 1.0, True), (0.3333333333333333, 10, 0.0, False), (0.3333333333333333, 13, 0.0, False)]
P[ 15 ][ 0 ]= [(1.0, 15, 0, True)]
P[ 15 ][ 1 ]= [(1.0, 15, 0, True)]
P[ 15 ][ 2 ]= [(1.0, 15, 0, True)]
P[ 15 ][ 3 ]= [(1.0, 15, 0, True)]


を表示して見る必要がありました。本文にはこんなことは書いていないので、
（本当は読み返すと一部のデータは書いてくれています。Table 2.1 Four discrete actions :


Number  Action
0  Left
1  Down
2  Right
3  Up


の数字と誤解していました。
自分で作ったプログラムでないので、「プログラム」や「やろうとしていること」の理解が不十分だとこの様な勘違いをします。
我々凡人は、入門期には、ほんのチョットしたことで躓きます。師匠がいればスムーズに入門出来ると思います。）
我々凡人には独学で強化学習に入門するにはハードルがけっこう高いです。
ここまで何とか理解できれば、この本のプログラムは私の貧弱なパソコンでも今の処、実行できるので、
いきなり目覚ましい応用例の解説ではなく、一歩一歩、少しづつ解説してくれている、この本なら読めそうと言う気にはなります。
例えば、Chapter 4 の Every-visit MC prediction with blackjack game のプログラミングを gym を使わず、


import random
import pandas as pd
from collections import defaultdict

class Blackjack:
    def __init__(self, threshold):
        self.threshold = threshold

    def open_deal(self):
        card1 = random.randint(1, 13)
        card2 = random.randint(1, 13)
        card_sum = card1 if card1<10 else 10
        card_sum += card2 if card2<10 else 10
        if card1==1 or card2==1:
            card_flag = True
        else:
           card_flag = False
        if card_sum == 11 and card_flag == True:
            card_sum == 21
            natural21_flag = True
        else:
           natural21_flag = False
           if card_flag == True:
               if card_sum + 10 > 17:
                  card_sum += 10
        num_card1 = card1 if card1<10 else 10
        num_card2 = card2 if card2<10 else 10
        
        return [card_sum, num_card1, num_card2, card_flag, natural21_flag]
            
    def reset(self):
        self.player_deal = self.open_deal()
        self.dealer_deal = self.open_deal()
        self.state = (self.player_deal[0], self.dealer_deal[1], self.player_deal[3])
    def policy(self, state):
        return 0 if state[0] >= self.threshold  else 1

    def next_deal(self, sum, flag, who):
        card = random.randint(1, 13)
        card_sum = card if card<10 else 10
        if card==1:
            card_flag = True
        else:
            card_flag = False
        if flag == True or card_flag == True:
            if who == 0 and sum + card_sum + 10 > self.threshold and sum + card_sum + 10 <= 21:
                card_sum = sum + card_sum + 10
            elif who == 1 and sum + card_sum + 10 >= 17 and sum + card_sum + 10 <= 21:
                card_sum = sum + card_sum + 10
            else:
                card_sum = sum + card_sum           
        else:
            card_sum = sum + card_sum
        card_flag = flag or card_flag
        return [card_sum, card_flag]
            
    def  step(self, action):
        self.episode = []
        if action == 0: ## stand
            if self.player_deal[4] == True: ## player is natural 21
                if self.dealer_deal[4] == True: ## dealer is natural 21
                    self.episode.append((self.state, 0, 0.0))
                else:
                    self.episode.append((self.state, 0, 2.5))
            if self.dealer_deal[0] >= 17:
                if self.player_deal[0] > self.dealer_deal[0]:
                    self.episode.append((self.state, 0, 1.0))
                elif self.player_deal[0] < self.dealer_deal[0]:
                    self.episode.append((self.state, 0, -1.0))
                else:
                    self.episode.append((self.state, 0, 0.0))
            else: ## dealer must draw card
                while True:
                    new_card = self.next_deal(self.dealer_deal[0], self.dealer_deal[3], 1)
                    self.dealer_deal[0] = new_card[0]
                    self.dealer_deal[3] = new_card[1]
                    if self.dealer_deal[0] >= 17:
                        break
                if self.dealer_deal[0] > 21:
                    self.episode.append((self.state, 0, 1.0))
                elif self.player_deal[0] > self.dealer_deal[0]:
                    self.episode.append((self.state, 0, 1.0))
                elif self.player_deal[0] < self.dealer_deal[0]:
                    self.episode.append((self.state, 0, -1.0))
                else:
                    self.episode.append((self.state, 0, 0.0))
        else: ## action == 1: hit
            while True:
                new_card = self.next_deal(self.player_deal[0], self.player_deal[3], 0)
                self.player_deal[0] = new_card[0]
                self.player_deal[3] = new_card[1]
                if self.player_deal[0] >= self.threshold:
                    break
                self.episode.append((self.state, 1, 0.0))
                new_state = list(self.state).copy()
                new_state[0] = new_card[0]
                new_state[2] = new_card[1]
                self.state = tuple(new_state)
            if self.player_deal[0] > 21:
                self.episode.append((self.state, 1, -1.0))

            else: ## dealer must draw card
                self.episode.append((self.state, 1, 0.0))
                new_state = list(self.state).copy()
                new_state[0] = new_card[0]
                new_state[2] = new_card[1]
                self.state = tuple(new_state)              
                while True:
                    new_card = self.next_deal(self.dealer_deal[0], self.dealer_deal[3], 1)
                    self.dealer_deal[0] = new_card[0]
                    self.dealer_deal[3] = new_card[1]
                    if self.dealer_deal[0] >= 17:
                        break
                if self.dealer_deal[0] > 21:
                    self.episode.append((self.state, 0, 1.0))
                elif self.player_deal[0] > self.dealer_deal[0]:
                    self.episode.append((self.state, 0, 1.0))
                elif self.player_deal[0] < self.dealer_deal[0]:
                    self.episode.append((self.state, 0, -1.0))
                else:
                    self.episode.append((self.state, 0, 0.0))
        return self.episode   

env = Blackjack(19)

total_return = defaultdict(float)
N = defaultdict(int)

num_iterations = 500000

#then, for every iteration
for i in range(num_iterations):
    env.reset() 
    action =  env.policy(env.state)
    episode = env.step(action)
    
    #store all the states, actions, rewards obtained from the episode
    states, actions, rewards = zip(*episode)
    
    #then for each step in the episode 
    for t, state in enumerate(states):
        
            #compute the return R of the state as the sum of reward
            R = (sum(rewards[t:]))
            
            #update the total_return of the state
            total_return[state] =  total_return[state] + R
            
            #update the number of times the state is visited in the episode
            N[state] =  N[state] + 1

total_return = pd.DataFrame(total_return.items(),columns=['state', 'total_return'])

N = pd.DataFrame(N.items(),columns=['state', 'N'])

df = pd.merge(total_return, N, on="state")

print()
print(df.head(10))

df['value'] = df['total_return']/df['N']

print()
print(df.head(10))


の様なプログラムをでっち上げ、実行すると


             state  total_return      N
0   (13, 3, False)       -1722.0   3829
1   (19, 3, False)        1634.0   4407
2   (19, 9, False)        2149.0   4659
3  (16, 10, False)       -9192.0  16907
4  (20, 10, False)       16447.0  26407
5   (17, 5, False)       -2569.0   4412
6   (20, 5, False)        4362.0   6583
7   (12, 8, False)       -1431.0   3857
8   (15, 8, False)       -2047.0   4076
9  (19, 10, False)        7120.0  17806

             state  total_return      N     value
0   (13, 3, False)       -1722.0   3829 -0.449726
1   (19, 3, False)        1634.0   4407  0.370774
2   (19, 9, False)        2149.0   4659  0.461258
3  (16, 10, False)       -9192.0  16907 -0.543680
4  (20, 10, False)       16447.0  26407  0.622827
5   (17, 5, False)       -2569.0   4412 -0.582276
6   (20, 5, False)        4362.0   6583  0.662616
7   (12, 8, False)       -1431.0   3857 -0.371014
8   (15, 8, False)       -2047.0   4076 -0.502208
9  (19, 10, False)        7120.0  17806  0.399865


の様になります。この様に時間を掛けて読んでいくと何をやっているか少しづつ理解できて来ている気がします。
「注」上のプログラムで dictionary（辞書）のキーにする為には、state や episode は内容を変更できる list でなく、
面倒ですが、内容を変更できない tuple を使う必要があります。
勿論、どの様になれば、理解できたと思うかは人それぞれで、こうであるべきだとは言えませんが。多分。
更に、ライブラリー gym の中身を知らずに作っているので、今の場合はこれで良いはずですが、
このプログラムは自分の手札の合計点数の閾値を固定して hit と stand の行動を決めていますが、
p.179 の Implementing on^policy MC control を gym を使わずにプログラミングする為には、
ディーラーの手と自分の手に１が含まれているかも参考に行動を決めれるような柔軟なプログラムにしておく必要があり、
戦術(policy)に応じて、行動(action)を変えることが出来るように、Blackjack の class を作り変える必要があります。
ここで、ライブラリー gym を使わないでプログラミングしようとしているのは、自分の興味ある課題を
強化学習(Reinforcement Learning)で解こうとした時には、ライブラリー gym は使えず、
自分で、自分の課題に対応する gym に当たるものを作成する必要があるので、この段階から作ってみているのです。
（ライブラリーには、中身を理解できなくてもその使い方を理解するだけで使えば差し当たっていいもの
（実際は、優秀な人達はそのようなライブラリーもどの様に作っているか知っていて、作ろうと思えば自分で作れるはずですが）と
教育の為に作られ、原理を説明するコードが短くて済むように使われているモノがあり、学んだ事を自分で応用しようとすると
そのライブラリーの中身が予想・理解できないと上手く応用出来なくて我々凡人は困るものがあります。）
このような時、強化学習(Reinforcement Learning)に詳しい人（師匠になってくれる人）に教われば、即ち、
障害になっていることを質問することが出来れば、ほんのちょっとしたことなので、それさえわかれば、簡単に、
我々凡人でも、強化学習(Reinforcement Learning)に入門できるのではないかと思います。
入門さえできれば、後は一人で勉強出来ます。但し、AI の本格的な勉強には高価なコンピュータが必要みたいですが。
又、ある程度の基礎が出来れば、インターネット上の情報を有効に使えるようになりますが、殆どが断片的な情報なので、
（例えば、from collections import defaultdict の defaultdict が普通の dictionary とどう違うかや
import pandas as pd で  pd.DataFrame() の使い方：


data = {
    '名前' :['田中', '山田', '高橋'],
    '役割' : ['営業部長', '広報部', '技術責任者'],
    '身長' : [178, 173, 169]
    }
df = pd.DataFrame(data, columns=["名前", "役割", "身長"])
print(df)


などを教えて貰うことや
 Python の pyttsx3 を使ったテキストを読み上げてくれるプログラムなど
や beta distribution のグラフを描く Python のプログラム：


import numpy as np
from scipy.stats import beta
import matplotlib.pyplot as plt

a, b = 2, 3
x = np.linspace(0, 1, 100)
y = beta.pdf(x, a, b)

plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('Probability density')
plt.title('Beta distribution with a=2, b=3')
plt.show()


やベータ分布からのランダムサンプリングでヒストグラムを作成し、表示する


import numpy as np
import matplotlib.pyplot as plt

a = 2
b = 3
sample_size = 1000
beta_samples = np.random.beta(a, b, size=sample_size)

plt.hist(beta_samples)
plt.xlabel('x')
plt.ylabel('Probability density')
plt.title('Beta distribution with a=2, b=3')
plt.show()


などはインターネットで簡単に見つかります。それが正しいかどうかは実行してみれば分かります。）、
入門期には、我々凡人には、独学で学ぶためには、纏まった情報を与えてくれる・
単純な例で原理と必要な数学・アルゴリズムとコードをステップバイステップで教えてくれる・
自分が読んで理解出来そうな優れた入門書を読むことが必要だと思います。
どうすれば、例えば、私にとっての強化学習(Reinforcement Learning)における
Sudharsan Ravichandiran 著「Deep Reinforcement Learning with Python」を
見つけることが出来たかは運だと思いますが、色々な強化学習の参考書を漁って、
何年も経って、やっと見つけました。
勿論、強化学習(Reinforcement Learning)は人工知能の一つの分野として大分前からよく知られているので、
適切な師匠が居れば、直ちに、適切な参考書を紹介してくれたと思いますが、独学は運任せです。



最も、強化学習(Reinforcement Learning)も内容が豊富になって来て、応用できる範囲が広範囲になり、
研究者以外のそれを理解することを必要とする人達が増えたので、
強化学習(Reinforcement Learning)の発展を歴史的に整理し、私の様な素人にも独学で理解できる
Sudharsan Ravichandiran 著「Deep Reinforcement Learning with Python」
のような基本的な参考書を書いてくれる人がやっと出てきたのかも分かりませんが。



CTAN で cchess.sty を見つけた。


\documentclass{jarticle}

\usepackage{cchess}

\begin{document}
 \smallboard
\begin{position}
   \piece{a}{1}{r}  \piece{i}{1}{r}
   \piece{b}{1}{n}  \piece{h}{1}{n}
   \piece{c}{1}{b}  \piece{g}{1}{b}
   \piece{d}{1}{g}  \piece{f}{1}{g}
   \piece{e}{5}{c}  \piece{e}{7}{c}
   \piece{a}{4}{p}  \piece{c}{4}{p}
   \piece{e}{4}{p}  \piece{g}{4}{p}
   \piece{i}{4}{p}  \piece{e}{1}{k}
   \piece{a}{9}{R}  \piece{i}{10}{R}
   \piece{a}{8}{N}  \piece{g}{8}{N}
   \piece{c}{10}{B} \piece{g}{10}{B}
   \piece{d}{10}{G} \piece{f}{10}{G}
   \piece{b}{8}{C}  \piece{h}{8}{C}
   \piece{a}{7}{P}  \piece{c}{7}{P}
   \piece{g}{7}{P}
   \piece{i}{7}{P}  \piece{e}{10}{K}
\end{position}

 \normalboard
% \largeboard
\begin{position}
   \piece{a}{1}{r}  \piece{i}{1}{r}
   \piece{b}{1}{n}  \piece{h}{1}{n}
   \piece{c}{1}{b}  \piece{g}{1}{b}
   \piece{d}{1}{g}  \piece{f}{1}{g}
   \piece{e}{5}{c}  \piece{e}{7}{c}
   \piece{a}{4}{p}  \piece{c}{4}{p}
   \piece{e}{4}{p}  \piece{g}{4}{p}
   \piece{i}{4}{p}  \piece{e}{1}{k}
   \piece{a}{9}{R}  \piece{i}{10}{R}
   \piece{a}{8}{N}  \piece{g}{8}{N}
   \piece{c}{10}{B} \piece{g}{10}{B}
   \piece{d}{10}{G} \piece{f}{10}{G}
   \piece{b}{8}{C}  \piece{h}{8}{C}
   \piece{a}{7}{P}  \piece{c}{7}{P}
   \piece{g}{7}{P}
   \piece{i}{7}{P}  \piece{e}{10}{K}
\end{position}

\end{document}


で






を作ってくれます。
Jacques Richer さんが METAFONT でフォントと描くための LaTeX のプログラム（cchessboard.tex）を作ったのを
Frank Mittelbach さんがそのフォントを利用して、分り易い cchess.sty を作ったそうです。
cchessboard.tex は私のコンピューターでは駒の無い盤面だけを表示しますが、
まだコードが理解できません。
chinesechess.pdf(中国象棋棋?排版 chinesechess 宏包耿楠 ) という cchessboard.tex の
マニュアルらしきものもありますが、中国語で、今の処、何を書いているか分かりません。
中国ドラマの与君歌ではハン・ドンさんとシュエン・ルーさんとミッキー・ホーさんが、
互いに策略を巡らしている象徴・小道具として、象棋（中国将棋）を一人で良くやっていますが、
（囲碁ではなく象棋なのは、一人の行動や軍隊の行動ではなく、仲間・手下をどの様に動かすかを熟慮するので、象棋です。）
駒が普通に安価に手に入れる事の出来る大きなおはじきの様なものではなく立体的な立派な駒を使っています。
入門書は中村千鶴著「シャンチー入門とその先へ」マイナビが現在はあります。
象棋はチェスと同じく駒が盤上から次々消えていきますが、ジョッシュ・ウェイッキンさんの勉強法と同じ順序で
中村千鶴著「シャンチー入門とその先へ」では解説されています。
誰か強い象棋のPC用のソフトを作ってくないかな。中国製は無料な強いものあったみたいですが、
私はブロックされて入手出来ません。スマホ用はあるかもしれませんが老人には画面の大きいPC用が良いです。
まあ、時間は一杯あるから強化学習(Reinforcement Learning)をチャンと勉強して自分で作れば良いですが、
問題は若い時のようにはいかないのと私の貧弱なパソコンで強いのが作れるか疑問な事です。
（「Use PyTorch for GPU-accelerated tensor computations」と書いてある GPU を装備したパソコンを想定した参考書も
現在は沢山出版されていますが、私のパソコンには GPU の機能の一部が CPU に組み込まれているだけで、単独の GPU がないです。
藤井聡太さんのコンピューターが１００万円、渡辺明さんのコンピューターが１５０万円と報道されている様に、
最新の研究のプログラミングを学ぶには、また数学をプログラミンを元に研究するには、それなりのお金が現在は必要です。
「パソコン工房」も高知から撤退したし、パソコンを購入する時、現在はチャンとした GPU が必須だと気が回らなかったです。
例えば、オーストラリアの群論の研究者達の様に、自分達の研究に必要なコンピューターを（安価に）自作できる人達も
世の中には勿論いますが、私の様な不器用で、自作のラジオも単にキットの部品を半田付け無しに繋ぐ以外、
鳴ったことの無い（技術教室の教授達は半田付けなんて簡単で、うちの学生もすぐ出来るようになると話していましたが、
簡単にできる人達が教授になっていて、その指導の元で訓練すれば出来るようになるのであって）
凡人が独学で個人でするのは無理です。）
色々面白いものがインターネット上には今はあります。


やっと「飛車落ち」で最強ではない古い将棋ソフトに勝てた。
シャンチー入門の本だと思って購入したら、中国語のチェスの本だった。表紙の絵をよく見れば気が付いたはずだが。
チェスの本は、ロシアが本場だと思って、「ШАХМАТЫ　уроки　лучшей　игры」を持っていて、
思い出したら辞書を引きながら少しづつ読んでいます。
ロシア語の本は、「最初に学ぶべきだとジョッシュ・ウェイッキンさんが言う事」が最後に書いているみたいです。
中国語の本は女性の有名なチェスプレイヤーの書いた本で、これも子供用の本ですが、図を眺めると良い本みたいです。
米国も強いみたいで、英語なら沢山のチェスの参考書があります。。
最近、注意力が散漫になっていて、将棋も「飛車落ち」でなかなか勝てなかった。次は「角落ち」。
囲碁の「棋譜並べ」も思い出したらやってみないと本は一杯集めています。磁石付きの碁盤の方が膝の上で出来るので便利です。
思い出したらやっている、詰碁は頭の中ですべきですが、韓国のドリルはどう考えても複数の解があるのもあり、
桂の９・１３路盤で、木の盤だと日本棋院お勧めの９・７路盤の石では軽すぎてグラグラするので、
プチ贅沢して６・９路盤用の薄い蛤・那智黒（各４０個）の碁石を使って、狭い机の上でするのが私にとっては良いです。
勿論、本気で強くなりたければ、盤など使わず、頭の中に盤を描いて、そこで石を打たなければいけないようです。
退職の記念に買った薄い榧の１９路盤と多分蛤・那智黒の碁石は大きく重いので部屋の隅で、
囲碁の本やコーヒーの生豆の置き場所になっています。

ジョッシュ・ウェイッキン著「The Art of Learning 習得への情熱ーチェスから武術へー　上達するための、僕の意識的学習法」
みすず書房が面白い本です。チェスだけでなく、色々な事の学習にとって示唆に富む本だと思います。

Sudharsan Ravichandiran 著「Deep Reinforcement Learning with Python」の p.179 の the on-policy Monte Carlo method のプログラムは


import random
import pandas as pd
from collections import defaultdict

Q = defaultdict(float)
total_return = defaultdict(float)
N = defaultdict(int)

class Blackjack:
    def __init__(self, epsilon):
        self.epsilon = epsilon

    def open_deal(self):
        card1 = random.randint(1, 13)
        card2 = random.randint(1, 13)
        card_sum = card1 if card1<10 else 10
        card_sum += card2 if card2<10 else 10
        if card1==1 or card2==1:
            card_flag = True
        else:
           card_flag = False
        if card_sum == 11 and card_flag == True:
            card_sum == 21
            natural21_flag = True
        else:
           natural21_flag = False
        num_card1 = card1 if card1<10 else 10
        num_card2 = card2 if card2<10 else 10
        return [card_sum, num_card1, num_card2, card_flag, natural21_flag]
            
    def reset(self):
        self.player_deal = self.open_deal()
        self.dealer_deal = self.open_deal()
        self.state = (self.player_deal[0], self.dealer_deal[1], self.player_deal[3])

    def epsilon_greedy_policy(self, Q):
        if random.uniform(0,1) < self.epsilon:
            if random.uniform(0,1) < 0.5:
                return 0
            else:
                return 1
        else:
            action = 0 if Q[(self.state, 0)] > Q[(self.state, 1)] else 1
            return action

    def next_deal(self, sum, flag):
        card = random.randint(1, 13)
        card_sum = card if card<10 else 10
        if card==1:
            card_flag = True
        else:
            card_flag = False
        card_flag = flag or card_flag
        card_sum = sum + card_sum
        return [card_sum, card_flag]

    def dealer_play(self):
        if self.player_deal[3] == True:
            if self.player_deal[0] + 10 <= 21:
                self.player_deal[0] += 10
        while True:
            new_card = self.next_deal(self.dealer_deal[0], self.dealer_deal[3])
            self.dealer_deal[0] = new_card[0]
            self.dealer_deal[3] = new_card[1]
            if self.dealer_deal[0] >= 17:
                break
            elif self.dealer_deal[3] == True:
                if self.dealer_deal[0] + 10 >= 17:
                    break
        if self.dealer_deal[0] > 21:
            self.episode.append((self.state, 0, 1.0))
        else:
            if self.dealer_deal[3] == False:
                if self.player_deal[0] > self.dealer_deal[0]:
                    self.episode.append((self.state, 0, 1.0))
                elif self.player_deal[0] < self.dealer_deal[0]:
                    self.episode.append((self.state, 0, -1.0))
                else:
                    self.episode.append((self.state, 0, 0.0))
            else: ## self.dealer_deal[3] == True
                if self.dealer_deal[0] + 10 <= 21:
                    if self.player_deal[0] > self.dealer_deal[0] + 10:
                        self.episode.append((self.state, 0, 1.0))
                    elif self.player_deal[0] < self.dealer_deal[0] + 10:
                        self.episode.append((self.state, 0, -1.0))
                    elif self.player_deal[0] == self.dealer_deal[0] + 10:
                        self.episode.append((self.state, 0, 0.0))
                else:
                    if self.player_deal[0] > self.dealer_deal[0]:
                        self.episode.append((self.state, 0, 1.0))
                    elif self.player_deal[0] < self.dealer_deal[0]:
                        self.episode.append((self.state, 0, -1.0))
                    elif self.player_deal[0] == self.dealer_deal[0]:
                        self.episode.append((self.state, 0, 0.0))

    def generate_episode(self, Q):
        self.episode = []
        self.reset() ## 最初の self.state をセット
        action = self.epsilon_greedy_policy(Q)
        
        if action == 0: ## stand
            if self.player_deal[4] == True: ## player is natural 21
                if self.dealer_deal[4] == True: ## dealer is natural 21
                    self.episode.append((self.state, 0, 0.0))
                else:
                    self.episode.append((self.state, 0, 2.5))
            if self.dealer_deal[0] >= 17:
                if self.player_deal[0] > self.dealer_deal[0]:
                    self.episode.append((self.state, 0, 1.0))
                elif self.player_deal[0] < self.dealer_deal[0]:
                    self.episode.append((self.state, 0, -1.0))
                else:
                    self.episode.append((self.state, 0, 0.0))
            else: ## dealer must draw card
                self.dealer_play()
        else: ## action == 1: hit
            while True:
                new_card = self.next_deal(self.player_deal[0], self.player_deal[3])
                self.player_deal[0] = new_card[0]
                self.player_deal[3] = new_card[1]
                if self.player_deal[0] > 21:
                    break
                self.episode.append((self.state, 1, 0.0))
                new_state = list(self.state).copy()
                new_state[0] = new_card[0]
                new_state[2] = new_card[1]
                self.state = tuple(new_state)
                new_action = self.epsilon_greedy_policy(Q)
                if new_action == 0:
                    break
            if self.player_deal[0] > 21:
                self.episode.append((self.state, 1, -1.0))
            else: ## dealer must draw card
                self.episode.append((self.state, 1, 0.0))
                new_state = list(self.state).copy()
                new_state[0] = new_card[0]
                new_state[2] = new_card[1]
                self.state = tuple(new_state)              
                self.dealer_play()
        return self.episode   

env = Blackjack(0.5)

num_iterations = 500000

#for each iteration
for i in range(num_iterations):
    
    #so, here we pass our initialized Q function to generate an episode
    episode = env.generate_episode(Q)
    
    #get all the state-action pairs in the episode
    all_state_action_pairs = [(s, a) for (s,a,r) in episode]
    
    #store all the rewards obtained in the episode in the rewards list
    rewards = [r for (s,a,r) in episode]

    #for each step in the episode 
    for t, (state, action, reward) in enumerate(episode):

        #if the state-action pair is occurring for the first time in the episode
        if not (state, action) in all_state_action_pairs[0:t]:
            
            #compute the return R of the state-action pair as the sum of rewards
            R = sum(rewards[t:])
            
            #update total return of the state-action pair
            total_return[(state,action)] = total_return[(state,action)] + R
            
            #update the number of times the state-action pair is visited
            N[(state, action)] += 1

            #compute the Q value by just taking the average
            Q[(state,action)] = total_return[(state, action)] / N[(state, action)]

df = pd.DataFrame(Q.items(),columns=['state_action pair','value'])

print(df.head(11))


の様なもので多分良いです。

Sudharsan Ravichandiran 著「Deep Reinforcement Learning with Python」の p.184 の the off-policy Monte Carlo method のプログラムは


import random
import pandas as pd
from collections import defaultdict

Q = defaultdict(float)

PI = defaultdict(float)
C = defaultdict(float)

total_return = defaultdict(float)

N = defaultdict(int)

class Blackjack:
    def __init__(self, epsilon):
        self.epsilon = epsilon

    def open_deal(self):
        card1 = random.randint(1, 13)
        card2 = random.randint(1, 13)
        card_sum = card1 if card1<10 else 10
        card_sum += card2 if card2<10 else 10
        if card1==1 or card2==1:
            card_flag = True
        else:
           card_flag = False
        if card_sum == 11 and card_flag == True:
            card_sum == 21
            natural21_flag = True
        else:
           natural21_flag = False
        num_card1 = card1 if card1<10 else 10
        num_card2 = card2 if card2<10 else 10
        
        return [card_sum, num_card1, num_card2, card_flag, natural21_flag]
            
    def reset(self):
        self.player_deal = self.open_deal()
        self.dealer_deal = self.open_deal()
        self.state = (self.player_deal[0], self.dealer_deal[1], self.player_deal[3])

    def epsilon_greedy_policy(self, Q):
        if random.uniform(0,1) < self.epsilon:
            if random.uniform(0,1) < 0.5:
                return 0
            else:
                return 1
        else:
            action = 0 if Q[(self.state, 0)] > Q[(self.state, 1)] else 1
            return action

    def next_deal(self, sum, flag):
        card = random.randint(1, 13)
        card_sum = card if card<10 else 10
        if card==1:
            card_flag = True
        else:
            card_flag = False
        card_flag = flag or card_flag
        card_sum = sum + card_sum
        return [card_sum, card_flag]

    def dealer_play(self):
        if self.player_deal[3] == True:
            if self.player_deal[0] + 10 <= 21:
                self.player_deal[0] += 10
        while True:
            new_card = self.next_deal(self.dealer_deal[0], self.dealer_deal[3])
            self.dealer_deal[0] = new_card[0]
            self.dealer_deal[3] = new_card[1]
            if self.dealer_deal[0] >= 17:
                break
            elif self.dealer_deal[3] == True:
                if self.dealer_deal[0] + 10 >= 17:
                    break
        if self.dealer_deal[0] > 21:
            self.episode.append((self.state, 0, 1.0))
        else:
            if self.dealer_deal[3] == False:
                if self.player_deal[0] > self.dealer_deal[0]:
                    self.episode.append((self.state, 0, 1.0))
                elif self.player_deal[0] < self.dealer_deal[0]:
                    self.episode.append((self.state, 0, -1.0))
                else:
                    self.episode.append((self.state, 0, 0.0))
            else: ## self.dealer_deal[3] == True
                if self.dealer_deal[0] + 10 <= 21:
                    if self.player_deal[0] > self.dealer_deal[0] + 10:
                        self.episode.append((self.state, 0, 1.0))
                    elif self.player_deal[0] < self.dealer_deal[0] + 10:
                        self.episode.append((self.state, 0, -1.0))
                    elif self.player_deal[0] == self.dealer_deal[0] + 10:
                        self.episode.append((self.state, 0, 0.0))
                else:
                    if self.player_deal[0] > self.dealer_deal[0]:
                        self.episode.append((self.state, 0, 1.0))
                    elif self.player_deal[0] < self.dealer_deal[0]:
                        self.episode.append((self.state, 0, -1.0))
                    elif self.player_deal[0] == self.dealer_deal[0]:
                        self.episode.append((self.state, 0, 0.0))

    def generate_episode(self, Q):
        self.episode = []
        self.reset() ## 最初の self.state をセット
        action = self.epsilon_greedy_policy(Q)
        
        if action == 0: ## stand
            if self.player_deal[4] == True: ## player is natural 21
                if self.dealer_deal[4] == True: ## dealer is natural 21
                    self.episode.append((self.state, 0, 0.0))
                else:
                    self.episode.append((self.state, 0, 2.5))
            if self.dealer_deal[0] >= 17:
                if self.player_deal[0] > self.dealer_deal[0]:
                    self.episode.append((self.state, 0, 1.0))
                elif self.player_deal[0] < self.dealer_deal[0]:
                    self.episode.append((self.state, 0, -1.0))
                else:
                    self.episode.append((self.state, 0, 0.0))
            else: ## dealer must draw card
                self.dealer_play()
        else: ## action == 1: hit
            while True:
                new_card = self.next_deal(self.player_deal[0], self.player_deal[3])
                self.player_deal[0] = new_card[0]
                self.player_deal[3] = new_card[1]
                if self.player_deal[0] > 21:
                    break
                self.episode.append((self.state, 1, 0.0))
                new_state = list(self.state).copy()
                new_state[0] = new_card[0]
                new_state[2] = new_card[1]
                self.state = tuple(new_state)
                new_action = self.epsilon_greedy_policy(Q)
                if new_action == 0:
                    break
            if self.player_deal[0] > 21:
                self.episode.append((self.state, 1, -1.0))

            else: ## dealer must draw card
                self.episode.append((self.state, 1, 0.0))
                new_state = list(self.state).copy()
                new_state[0] = new_card[0]
                new_state[2] = new_card[1]
                self.state = tuple(new_state)              
                self.dealer_play()
        return self.episode   

def initialize_Q_and_C():
    for p in range(2, 22, 1):
        for d in range(1, 11, 1):
            state = (p, d, True)
            for action in range(0, 2):
                Q[(state, action)] = random.uniform(-1, 1)
                C[(state, action)] = 0
            state = (p, d, False)
            for action in range(0, 2):
                Q[(state, action)] = random.uniform(-1, 1)
                C[(state, action)] = 0
    
env = Blackjack(0.5)
initialize_Q_and_C()

num_iterations = 500000
##num_iterations = 5

#for each iteration
for i in range(num_iterations):
    
    #so, here we pass our initialized Q function to generate an episode
    episode = env.generate_episode(Q)
    
    #store all the rewards obtained in the episode in the rewards list
    rewards = [r for (s,a,r) in episode]
    T = len(episode)
    W = 1
    episode_reversed = list(reversed(episode))
    for t, (state, action, reward) in enumerate(episode_reversed):
        R = sum(rewards[(T-t-1):])
        C[(state, action)] = C[(state, action)] + W
        Q[(state, action)] = Q[(state, action)] + W*(R-Q[(state, action)]) \
                             / C[(state, action)]
        PI[state] = 0 if  Q[(state, 0)]>Q[(state, 1)] else 1
        if action !=  PI[state]:
            break
        W = W / env.epsilon * 2

df = pd.DataFrame(Q.items(),columns=['state_action pair','value'])

print(df.head(11))

df = pd.DataFrame(PI.items(),columns=['state','action'])

print(df.head(11))


の様なもので多分良いです。実行結果の例は


     state_action pair     value
0    ((2, 1, True), 0) -0.858824
1    ((2, 1, True), 1) -1.000000
2   ((2, 1, False), 0)  0.692051
3   ((2, 1, False), 1) -0.109458
4    ((2, 2, True), 0) -0.327044
5    ((2, 2, True), 1) -1.000000
6   ((2, 2, False), 0) -0.713299
7   ((2, 2, False), 1)  0.342702
8    ((2, 3, True), 0) -0.454545
9    ((2, 3, True), 1) -0.500000
10  ((2, 3, False), 0) -0.641912
              state  action
0    (17, 1, False)       0
1   (12, 10, False)       1
2    (16, 6, False)       0
3    (11, 1, False)       1
4    (15, 5, False)       0
5    (17, 9, False)       1
6    (8, 10, False)       1
7    (17, 8, False)       1
8     (17, 2, True)       1
9    (11, 2, False)       1
10    (21, 9, True)       0


です。間違っていることに気が付けば、その時、修正すれば良いだけです。兎も角、数をこなすことです。多分。
本を読む時、一回目では良く理解できていないこともよくあり、（ある優秀な人は本は７回読めと言っています。
誰に対して、どの様な分野の本に対して述べているか不明ですが、
（ブックオフで手に入れた前野直彬著「精講漢文」ちくま学芸文庫などはまだ数十ページしか読んでいませんが、
知らなかった事ばかり書いてあって面白いですが、例えば、漢音や呉音など日本に入ってきた時期によって
日本の漢字の音読みが違うことぐらいは知っていましたが、
中国語には同音異義語が多いがアクセントの付け方によってある程度区別がつくが、
この中国語の「四声」が昔と現在の標準語である北京語とでは全然別の物であることなど、
何回読み返せば記憶に残るだろうと思う本ではあります。）
私が若かった頃、数学の免許の為の必修の単位数が現在の２倍であった頃の話ですが、
教育学部は数学の教員が３人（小学校課程の増員で、私が行く前は２人）しかいなかったので、
昔は理学部の授業を教育学部の学生も受講させてもらっていましたが、
理学部の位相幾何学専門の先生が「教育学部の学生は優秀で、理学部の数学の学生が嫉妬し、自信を無くす。」とこぼしていましたが、
何のことない・当たり前の話で、私が教育学部で「位相空間」の講義をし、理学部でその続きの講義を聞いてくればいいのに、
理学部でも「位相空間」の最初からの講義を取るので、はじめて聞く理学部の学生さんより
教育学部の学生さんの方が良く理解でき、良く出来ていただけです。）
先の方まで読めば、最初の方で理解が間違っていたことに気が付く事もあります。
具体的には、Sudharsan Ravichandiran 著「Deep Reinforcement Learning with Python」で言えば、
５章 Understanding Temporal Difference Learning で、それまで学んで来た Dynamic programming(DP) と Monte Carlo method(MC) 
（とTD learning algorithm の TD prediction と TD control ）の advantage  と disadvantage を解説してくれていて、
これから学ぶ TD learning を解説していきますが、これを読むと DP で良く理解できなかった事
（確率の分布をどの様に決めたか？ : dynamic programming(DP) は model-based method で、
Monte Carlo method は model-free だと書いて、Blackjack の例は Monte Carlo method の例として適切だったと思ったのですが、
Frozen Lake の例は DP のアルゴリズムを説明するには単純な問題で、アルゴリズムは理解できましたが、
Frozen Lake の問題は探索で簡単に解ける問題で、DP では私は解けているとは思えなかったので、DP で解ける単純な例がなかったのかも？）
又、６章 Case Study - The MAB Prolem の the multi-armed bandit は大分前、在職中に知ってプログラミングしてみたことがありました。
しかし、この本で MAB Prolem に対しても
Epsilon-greedy
Softmax exploration
Upper confidence bound
Thompson sampling
と様々な方法が考え出されていることを教えて貰えます。答えは一つではないです。どれが自分にとって最善かは別ですが。
この本は私の様な初心者が理解できるように、
単純な例で、概念、手計算、アルゴリズム、実装と丁寧に、歴史に沿って最新の結果まで解説してくれています。
本を何日で読んだかを誇ることもありますが、ざっと振り返る為に、ここで、最初から読み返してみることも我々凡人には有益です。多分。
更に、本を2回読むとか、自分で前もってそれなりに勉強して置いて、
その分野の先生の講義を聴くことが出来れば、更に良く理解できます。多分。

白石勇一著「やさしく語る　棋譜並べ上達法」で、
「ところで、世の中には様々なプロがいて、憧れの的にもなっていますね。「あんなことができたらいいな」と思って、
真似してみることもあるでしょう。例えば、スポーツが好きな方は贔屓の選手のフォームを真似するかもしません。
絵が好きな方は名作を模写するかもしれません。音楽が好きな方は、名曲を演奏するかもしれません。
ですが、決して本人と同じことはできないでしょう。情報の整理が難しいということもありますが、
なにより再現には高い技術が必要になるからです。
　ですが、囲碁ではそれが可能です。例え初心者であっても、棋譜を見ながらであれば棋士同士の対局を完全に再現できるのです。」
と書いてありますが、数学の計算・証明もプログラミングも（完全に）真似をすれば、プロと同じことが出来、
誰がやっても同じ結果が得られます。難しいのは誰もやったの無いこと・オリジナルな事・答えがあるかどうか分からない事を
自力・独力でやり遂げることです。

シャンチー（象棋）の局面を LaTeX で描くプログラムを作りたくて、インターネットで見つけた象棋の画像から、
象棋の駒と盤の画像を作りたくて、youtube で「GIMPによる画像を切り抜いて背景を透明化（透過）する３つの方法」
１．自由選択して画像を切り抜く方法
２．パスで選択して画像を切り抜く方法
３．前景抽出選択で選択して画像を切り抜く方法
と別の youtube で
「スタンプで描画ツール」を使って、駒を消して、何もない盤を作る方法
を教えて貰ったが、駒は丸いから２．パスで選択して画像を切り抜く方法が良いと思ったが上手くいかなかった。
持っている象棋の大きな駒と盤の写真を撮って、作業した方が良いかも？著作権が問題になりますが、自分で使うだけですから。
更に、METAPOST で作る方法もありますが複雑な漢字を美しい駒になるように自作するのは楽ではないと思います。
カナダの Jacques Richer さんが METAFONT で作ったシャンチーの駒のフォントのプログラムもゲット出来ていますが、
1173行もあるし、苦労して作ったみたいですが、私は美しい駒だと思わないので、そのままコピーペーストして Metapost の
プログラムに変換しても余り嬉しくないし、これを参考に駒の画像を作れば良いですが、大変な労力が必要なことが予想されます。
「GIMP」の様な手動で画像作成・画像加工は「枯れた技術」で誰でも知っていて使えて当然の技術になっていると思いますが、
（というか。人工知能の成果を使えば、もはや時代遅れの技術になっているかも分かりませんが、）
私の様な不器用な人間にはやり方を丁寧に教えて貰ってもすぐには youtube の解説者の様には上手く使えません。
これが「熟練の技術が必要な手動の作業・手作業」と「誰がやっても同じものが作れるプログラミング」の違うところです。

しかし、昔（２０数年前の2001年に作っています）作った弱くてどうしようもない象棋（中国将棋）のプログラムは






の様な画面でした。現在も動きますが、強化学習(Reinforcement Learning)などの人工知能を学んで、作り直すには、
Borland C++ Builder で作っているので、現在は VC++ で作るしかなく、初めから作り直す必要があります。
チェスや






（昔スペインで購入したキリスト教徒とイスラム教徒の対戦を模したチェスのセットなども持っていましたが、
ポーランド製の木製の小さなマグネットのチェスのセットが狭い机の上で入門書で学ぶには良いです。
処で、クイーンを一組余計に付けてくれているセットもあることに気が付いて思ったのですが、
ポーンが昇格（プロモーション）した時、駒を実際には替えずに、替えたことを覚えているのかな？
「プロモーションで、ポーンが昇格できるのは次の４つの駒です。クイーン、ルーク、ビショップ、ナイト。
ふつうは最も強力なクイーンになります。
コンピュータ上では自動的に選んだ駒に変わってくれますが、
実際に盤と駒を使用しているときは自分の手で駒を変える必要があります。
プロモーションを行う時点では、相手がこちらの駒をたくさん手に入れていることがほとんどですから、
取られたクイーンの駒を再使用します。
　もしも、同じ色のクイーンが２つ存在するような状況になったときは、
ルークを逆さまに置いてクイーンの代わりとするのが一般的です。」
とインターネットで調べると書いてあった。便利な世の中になりました。
何でもスマホで調べればよいという世の中になり、一日中スマホばかり見ている人達ばかりの世の中になりましたが、
昭和生まれの私などは、この様な情報を書き込んでいる人達はどの様にしてこの情報を得たのだろうと思ってしまいます。
スマホ・パソコンで調べて、書き込んでいるのではなく、実際にチェスをやっているか、書籍を読んで知ったのでは？
毎日、１００通以上の迷惑メールが届くし、パソコンには様々な警告メッセージが引っ切り無しに表示されたり、
強制終了しなければならない事態も時々起こるし、時々、変な電話もかかってくるし、結構大変な世の中です。）
チェッカー






も昔（これらも象棋と同じ頃に作っています）作った弱いプログラムはあります。大したものではないので、
昔、卒論ゼミの学生さん達にやらしてみただけで、私のパソコンの中で眠っていて、
動かすのに rtl60.bpl と vcl60.bpl をインストールする必要がありました。
最近の強化学習(Reinforcement Learning)などの人工知能の発展が早すぎて、学ばなければいけないことが多過ぎて大変です。
高次元多面体や Tiling (「APERIODIC ORDER」：知らないこと、忘れてしまっていることが多過ぎる )など、
他にもやりたいことが一杯あり、様々なことを、思い出したら、衰えも隠せないので、少しづつやっています。




私が講義の為にプログラムを一杯作っていたのは、学生に背を向けノートを黒板に書き写す代わりに、
私が教えて貰った先生がたの真似をして、専門分野でないものまで、ノート無しで講義をしてみて失敗ばかりしていたから、
プロジェクターという便利なものがあるので、パソコンを操作して、準備したプログラムを見せていただけみたいな気もします。
唯、学生さんが「子供が喜ぶ絵を KITE で描け」や「倉庫番の問題をつくれ」という課題などだど、
いやいやだったかも分かりませんがそれなりにやってくれましたが、
（最も過去の学生さんたちがやった例を沢山見せるとやる気が失せ駄目みたいでしたが）、
最後の講義で、Scratch で簡単なゲームの作り方を教えても真似してやってくれる学生さんは一人しかいませんでした。
SNS の影響で、「すぐにお金になる事」や「１０分で分かる事」だけにしか興味がなくなったのか、
学生の興味が変化したのかも分かりませんが？
最近は、世の中の動きの変化を分析して教えてくれる
三宅香帆著「なぜ働いていると本が読めなくなるか」集英社新書
レジー著「ファスト教養　１０分で答えが欲しい人たち」集英社新書
のような若い世代の著者による面白い本が幾つか出版されています。

よく調べて見ると Jacques Richer さんが METAFONT で作ったシャンチーの駒のフォントは、読む気もしない命令の羅列ですが、
unfilldraw とか見たことない命令など使われていますが、draw に変えて、一つの漢字「将」だけ、どの様に描画させているか調べると、
どうもサイズが固定されていて、即ち、使う時に Large や Huge で自由に拡大・縮小が出来ず、
漢字の知識がない状態で作り始めたのか、９０度回転していて、汎用的ではないみたいで、
漢字の縁取りの図を描き、一つ一つ短い（曲）線を繋いで描いています。







象棋の駒に使われている様な装飾的な漢字のフォントを作るには、やっぱり、描きたい漢字を紙に大きく描き、
座標を細かく計算して、描くしかないみたいです。
将棋の .sty の様に、カナダ人には漢字の既成のフォントが使えなかったかもしれませんが、
無駄な努力をするより、妥協して既存の漢字のフォントを使う方が遥かに楽で、自分で象棋用の .sty を作った方が良いみたいです。

象棋用のスタイルファイルを作っていて、白く塗りつぶした円の描き方が分からず、
（METAPOST と異なり、 Donald E. Knuth 著「METAFONT ブック」を見ると METAFONT には、この様な機能はないみたいです。）
用事があって外出して、線の交点に石を置く囲碁のスタイルファイルのやり方をふと思い出して、
これは作る必要ないのではとの考えが頭にふと浮かびました。（全てのプログラムの共通部分はスタイルファイルにすべきですが。）
将棋や象棋の局面を作成する C++ のプログラム内で、配列を使って盤に駒を配置してから、LaTeX のプログラムを打ち出せば、
TeX や LaTeX のコマンドで悩む必要は無くなります。将棋のプログラムから作り直してから、象棋です。

久しぶりに VC++ のプログラムを作りましたが、私の「カードゲームを作ってみよう！」
https://www.cc.kochi-u.ac.jp/~tyamag/jyohou/whist.pdf
と同じようなプログラムです。これを見ながら、VC++ でGUIを使う方法
（これだと黒いウインドウにcoutで変数値を表示出来るのでデバッグが楽です。）と画像を表示する方法を思い出し、
「情報数学のテキスト（数独）」
https://www.cc.kochi-u.ac.jp/~tyamag/jyohou/suudoku2.pdf
で、ファイルの読み書きをどの様にしたかを思い出し、
「Pythonによる音声データの有効活用とLaTeXによる将棋・囲碁カード作成補助のC#のソフト作成とカード画像作成」
https://www.cc.kochi-u.ac.jp/~tyamag/jyohou/kifumodify.pdf
で、どの様なソフトを作ったか、思い出します。この C# で作ったソフトは、時々、奇妙な動きをします。
即ち、不慣れなC#を使ったので、バグが残っていますが、私の手を離れているので、簡単には修正できません。
C++そのものは Bjarne Stroustrup 著「プログラミング言語 C++」を読めば良いだけですが、VC++ で GUI のプログラミングを
する為には、更に、マイクロソフト独特の ref class を理解し、通常の class との併用の方法の理解が必要ですが、
残念ながら適切な参考書がありません。自作のダイアログボックスを作り、利用する方法をインターネットで
丸一日探してみましたが見つけることが出来ませんでした。
ref class を使っているので、画像のデータなどを保存する配列などは


		array＜Bitmap^＞^ komas = gcnew array＜Bitmap^＞(29);
		array＜int＞^ iban = gcnew array＜int＞(81);
		array＜int＞^ black_captured = gcnew array＜int＞(8);
		array＜int＞^ white_captured = gcnew array＜int＞(8);
		array＜String^＞^ basiclist = gcnew array＜String^＞(90);
		array＜String^＞^ komalist = gcnew array＜String^＞(14);


や


		array＜int＞^ xpos = gcnew array＜int＞(64);
		array＜int＞^ ypos = gcnew array＜int＞(64);
		// using namespace std; を宣言するとエラーになるので注意！
		array＜int, 2＞^ c = gcnew array＜int, 2＞(2, 3);
		int iLen = c->GetLength(1);	// １次の配列の個数  (= 3)
		int jLen = c->GetLength(0);	// ０次の配列の個数　(= 2)

		for (int j = 0; j < jLen; j++)
		{
			for (int i = 0; i < iLen; i++)
			{
				c[j, i] = j * 10 + i;
			}
		}
		//c[0, 0] = 0	c[0, 1] = 1	c[0, 2] = 2
		//c[1, 0] = 10	c[1, 1] = 11	c[1, 2] = 12



の様に宣言する必要があること（半角だと消えるので全角の＜＞を使っています。）を見つけるのに、丸一日費やしました。
昔は調べても適切な情報が見つからなかったですが、現在は、気長に探すと見つかります。
良い時代になりましたが、世間では VC++ の時代は終わったみたいで、新しい参考書も出版されません。、
何時も我々凡人がやっと理解した頃にはそのブームは終わっている事が多いですが、私には現役のプログラミング言語で、
現在でもチャンとプログラミングすることが出来、チャンと動きますから、費やした時間とお金の元を取らなくては。

将棋用の局面を作るプログラムは、画質が悪いですが






の様なプログラムで、この局面を LaTeX で描けるように


\documentclass[10pt, a4paper]{ jarticle}
\usepackage[dvips]{ graphicx}
\usepackage[dvips]{ color}
\usepackage{xparse}

\begin{document}

\font\sgsign=sgsign scaled 2000

\huge

\begin{center}

\setlength\unitlength{1truecm}
\thicklines
\begin{picture}(14,13)(0,0)
\multiput(2,0)(1,0){10}{\line(0,1){9}}
\multiput(2,0)(0,1){10}{\line(1,0){9}}
\put(2.3, 9.3) { \textcolor{blue}{9} }
\put(3.3, 9.3) { \textcolor{blue}{8} }
\put(4.3, 9.3) { \textcolor{blue}{7} }
\put(5.3, 9.3) { \textcolor{blue}{6} }
\put(6.3, 9.3) { \textcolor{blue}{5} }
\put(7.3, 9.3) { \textcolor{blue}{4} }
\put(8.3, 9.3) { \textcolor{blue}{3} }
\put(9.3, 9.3) { \textcolor{blue}{2} }
\put(10.3, 9.3) { \textcolor{blue}{1} }
\put(11.3, 8.3) { \textcolor{blue}{一} }
\put(11.3, 7.3) { \textcolor{blue}{二} }
\put(11.3, 6.3) { \textcolor{blue}{三} }
\put(11.3, 5.3) { \textcolor{blue}{四} }
\put(11.3, 4.3) { \textcolor{blue}{五} }
\put(11.3, 3.3) { \textcolor{blue}{六} }
\put(11.3, 2.3) { \textcolor{blue}{七} }
\put(11.3, 1.3) { \textcolor{blue}{八} }
\put(11.3, 0.3) { \textcolor{blue}{九} }
\put(12.4, 8.3) { \mbox{{\sgsign 1}} }
\put(12.3, 7.5) { \textcolor{blue}{持} }
\put(12.3, 6.8) { \textcolor{blue}{駒} }
\put(12.3,5.3 ){ \textcolor{blue}{角} }
\put(12.3,4.3 ){ \textcolor{blue}{桂} }
\put(12.3,3.3 ){ \textcolor{blue}{歩} }
\put(0.6, 0.7) { \mbox{ \rotatebox{180}{ {\sgsign 0}} } }
\put(0.7, 1.7) { \textcolor{blue}{\rotatebox{ 180 }{持}} }
\put(0.7, 2.7) { \textcolor{blue}{\rotatebox{ 180 }{駒}} }
\put(0.7,4.7 ){ \textcolor{blue}{\rotatebox{ 180 }{桂}} }
\put(2.15,8.7) {\textcolor{blue} {\rotatebox{180}{香}}}
\put(3.15,8.7) {\textcolor{blue} {\rotatebox{180}{桂}}}
\put(10.15,8.7) {\textcolor{blue} {\rotatebox{180}{香}}}
\put(4.15,7.7) {\textcolor{blue} {\rotatebox{180}{玉}}}
\put(6.15,7.7) {\textcolor{blue} {\rotatebox{180}{金}}}
\put(9.15,7.7) {\textcolor{blue} {\rotatebox{180}{金}}}
\put(3.15,6.7) {\textcolor{blue} {\rotatebox{180}{歩}}}
\put(4.15,6.7) {\textcolor{blue} {\rotatebox{180}{歩}}}
\put(5.15,6.7) {\textcolor{blue} {\rotatebox{180}{歩}}}
\put(6.15,6.7) {\textcolor{blue} {\rotatebox{180}{銀}}}
\put(7.15,6.7) {\textcolor{blue} {\rotatebox{180}{銀}}}
\put(9.15,6.7) {\textcolor{blue} {\rotatebox{180}{歩}}}
\put(2.15,5.7) {\textcolor{blue} {\rotatebox{180}{歩}}}
\put(6.15,5.7) {\textcolor{blue} {\rotatebox{180}{歩}}}
\put(7.15,5.7) {\textcolor{blue} {\rotatebox{180}{歩}}}
\put(8.15,5.7) {\textcolor{blue} {\rotatebox{180}{歩}}}
\put(10.15,5.7) {\textcolor{blue} {\rotatebox{180}{歩}}}
\put(2.15,3.2) {\textcolor{blue} {歩}}
\put(4.15,3.2) {\textcolor{blue} {歩}}
\put(6.15,3.2) {\textcolor{blue}{銀}}
\put(8.15,3.2) {\textcolor{blue} {歩}}
\put(10.15,3.2) {\textcolor{blue} {歩}}
\put(3.15,2.2) {\textcolor{blue} {歩}}
\put(5.15,2.2) {\textcolor{blue} {歩}}
\put(6.15,2.2) {\textcolor{blue} {歩}}
\put(8.15,2.7) {\textcolor{blue} {\rotatebox{180}{角}}}
\put(9.15,2.2) {\textcolor{blue} {歩}}
\put(4.15,1.2) {\textcolor{blue} {玉}}
\put(6.15,1.2) {\textcolor{blue} {金}}
\put(7.15,1.2) {\textcolor{blue} {飛}}
\put(2.15,0.2) {\textcolor{blue} {香}}
\put(3.15,0.2) {\textcolor{blue} {桂}}
\put(4.15,0.2) {\textcolor{blue}{銀}}
\put(5.15,0.2) {\textcolor{blue} {金}}
\put(10.15,0.2) {\textcolor{blue} {香}}
\end{picture}
\end{center}
\end{document}


の様な LaTeX のコードをファイルに打ち出す様に作っています。兎も角、半日ででっち上げたもので、汎用性を持たせるには、
画像のサイズを調整できるように修正する必要があります。
象棋用もこの様なプログラムなら簡単に作れるはずです。そこで、






の様なプログラムを作り、局面（出鱈目ですが）を表示する LaTeX のコードをファイルに打ち出します。
九宮に駒がいる時、線が切れているとか、（picture 内のコマンドでは短い線を表示してくれなかった。
これも下で述べている様に、長さの単位を拡大すると小数の値を指示すると描画してくれる場合もあります。厄介です。）、
拡大・縮小出来ないとか問題だらけですが、（実はダメもとでやってみて、


\setlength\unitlength{1truecm}


を


\setlength\unitlength{1.3truecm}


の様に長さの単位を変えれば、枠組みが拡大します。ここに整数だけでなく、小数も使えることに今気が付きました。
小さな子供のように、片っ端から思ったことを、何でも、やってみることです。）、



\newcount\XPos
\newcount\YPos

\NewDocumentCommand{\CellA}{m m }{%
\XPos= #1
\YPos= #2
\put(\the\XPos,\the\YPos){\line(1,0){5}}
\put(\the\XPos,\the\YPos){\line(0,-1){5}}
}

\NewDocumentCommand{\CellB}{m m }{%
\XPos= #1
\YPos= #2
\put(\the\XPos,\the\YPos){\line(-1,0){5}}
\put(\the\XPos,\the\YPos){\line(0,-1){5}}
}

・・・

\NewDocumentCommand{\CellR}{m m }{%
\XPos= #1
\YPos= #2
\put(\the\XPos,\the\YPos){\line(1,0){5}}
\put(\the\XPos,\the\YPos){\line(-1,0){5}}
\put(\the\XPos,\the\YPos){\line(0,1){5}}
\put(\the\XPos,\the\YPos){\line(0,-1){5}}
\put(\the\XPos,\the\YPos){\line(-1,-1){5}}
}

\NewDocumentCommand{\WaA}{m m }{%
\XPos= #1
\YPos= #2
\put(\the\XPos,\the\YPos){\circle{10}}
}


を china.sty とし、


\documentclass[10pt, a4paper]{ jarticle}
\usepackage[dvips]{ graphicx}
\usepackage[dvips]{ color}
\usepackage{ xparse}
\usepackage{ china}

\begin{document}

\Huge

\begin{center}
\setlength\unitlength{1truemm}
\thicklines
\begin{picture} (90, 100) (0, 0)

\WaA{5}{5}
\put(0,2){\textcolor{red}{車}}
\CellE{15}{5}
\WaA{25}{5}
\put(20,2){\textcolor{red}{相}}
\WaA{35}{5}
\put(30,2){\textcolor{red}{仕}}
\WaA{45}{5}
\put(40,2){\textcolor{red}{帥}}
\WaA{55}{5}
\put(50,2){\textcolor{red}{仕}}
\WaA{65}{5}
\put(60,2){\textcolor{red}{相}}
\WaA{75}{5}
\put(70,2){\textcolor{red}{車}}
\CellD{ 85 }{5}
\CellF{ 5 }{15}
\CellI{15}{15}
\CellI{25}{15}

・・・
\CellI{ 65 }{85}
\CellI{ 75 }{85}
\CellG{ 85 }{85}
\WaA{5}{95}
\put(0,92){\textcolor{black}{車}}
\WaA{15}{95}
\put(10,92){\textcolor{black}{馬}}
\CellH{ 25 }{95}
\WaA{35}{95}
\put(30,92){\textcolor{black}{士}}
\WaA{45}{95}
\put(40,92){\textcolor{black}{將}}
\WaA{55}{95}
\put(50,92){\textcolor{black}{士}}
\WaA{65}{95}
\put(60,92){\textcolor{black}{象}}
\CellH{ 75 }{95}
\WaA{85}{95}
\put(80,92){\textcolor{black}{車}}
\end{picture}
\end{center}

\end{document}


の様なコードを保存しています。chain.sty のコマンドの内容をフォントにすると良いと思います。
こんなことしなくても上の VC++ のプログラムだけ作り、画面をコピーして、画像で貼り付ければ済むことではありました。
まあ、それでも、少しは経験値が上がったかな？


\newcount\counterX
\newcount\counterY

\NewDocumentCommand{\WaB}{m m }{%
\counterX = #1
\counterY = #2
\put(\counterX,\counterY){\circle{10}}
\advance\counterX by 5
\advance\counterY by -5
\put(\counterX,\counterY){\line(-1,1){2.3}}
}
・・・
を china.sty に追加して、拡大した場合の結果は






です。

注意：



\newcount\XPos
\newcount\YPos

\NewDocumentCommand{\CellA}{m m }{%
\XPos= #1
\YPos= #2
\put(\the\XPos,\the\YPos){\line(1,0){5}}
\put(\the\XPos,\the\YPos){\line(0,-1){5}}
}


の様に定義していますが、これは


\newcommand{\CellA}[2]{
\put(#1,#2){\line(1,0){5}}
\put(#1,#2){\line(0,-1){5}}
}


でも良かったです。偶々、インターネットで見つけた情報を良く理解せずにそのまま使っていました。
矢張り、「１０分で答えを知ること」は私には無理です。
最後に、china.sty に


\makeatletter
\newenvironment{xiangqi}[1][]%
{
\setlength\unitlength{#1 truemm}
\thicklines
\begin{center}
\begin{picture}(90,100)(0,0)
}
{ 
\end{picture} 
\end{center}
}
\makeatother 


を追加し、


\documentclass[10pt, a4paper]{ jarticle}
\usepackage[dvips]{ graphicx}
\usepackage[dvips]{ color}
\usepackage{ xparse}
\usepackage{ china}

\begin{document}

\Huge

\begin{xiangqi}[1.2]

\WaA{5}{5}
\put(0,2){\textcolor{red}{車}}
\CellE{15}{5}
\WaA{25}{5}
\put(20,2){\textcolor{red}{相}}
・・・
\CellH{ 75 }{95}
\WaA{85}{95}
\put(80,92){\textcolor{black}{車}}
\end{xiangqi}

\end{document}


を保存するようにすれば、


\begin{xiangqi}[1.2]


の引数の値の変更と


\Huge


の変更で欲しい図を得ることが出来るようになります。

更なる微調整も必要ですが、リグれば切りがないですが、自分だけが使うプログラムですから、
こればかりやっている訳にはいかないので、一先ず完成したことにします。

昔作った囲碁の局面の LaTeX のコードを保存するプログラムは現在でも動きますが、チェスのプログラムは
ウイルス対策ソフトでブロックされ動かなくなっていた。私が作ったプログラムなのにどうしてだろう？不可解です。
チェスの強いフリーソフト Stockfish も現在も使え、強い将棋のフリーソフトと同じくエンジンソフトなので
表示するための Arena もダウンロードして、そのエンジンとして Stockfish を組み込む必要があります。
インターネットでインストールの方法が解説されているので、その通りやれば良いです。簡単です。
昔手に入れた Stockfish も現在も使え、WinBoard に組み込んで使っているみたいですが、良いソフトです。
インターネットで調べると色々なソフトが無料で利用可能みたいです。趣味は一つにとも言いますが、良い世の中です。
VC++ による GUI のプログラミングのやり方を覚えている内に作り直して置くのが良いみたいです。
昔はソフトを作るだけで、将棋や囲碁やチェスや象棋などやる時間的余裕がなかったが、今はあるので。

https://www.cc.kochi-u.ac.jp/~tyamag/jyohou/kifumodify.pdf のチェスの為のプログラムの作り方の解説は
今読んで見ると酷いものでした。
当時はチェスのカードを作る事しか考えてなかったのですが、もっと単純な分り易い解説にすべきでした。
プログラムを作る為の画像の名前が変わっている？ものもあったのですが、何でだろう。
最近、良く分からない事が起こります。作り直しました。






skak.sty の使い方は


\documentclass[12pt]{jarticle}
\usepackage{skak}

\begin{document}

\newgame

\mainline{1.e4 e5 2. Nf3 Nc6 3.Bb5}

\begin{center}

\showboard

\end{center}

\end{document}


の様に、チェスの手順を指示すると最後の局面を描画してくれることです。
一方、skak.sty の作者が作っているフォントを使わして貰って


\documentclass[a4paper,10pt]{jarticle}
\pagestyle{plain}
 
\begin{document}
   
\font\remark=skak30 scaled\magstep1
 \centerline{
 \hbox{\vrule
 \vbox{\hrule
 \hbox{\remark r m b l k a 0 s }
 \hbox{\remark o p o p Z p o p }
 \hbox{\remark 0 Z 0 Z 0 m 0 Z }
 \hbox{\remark Z 0 Z 0 o 0 Z 0 }
 \hbox{\remark 0 Z 0 Z P Z 0 Z}
 \hbox{\remark Z 0 Z 0 Z N Z 0 }
 \hbox{\remark P O P O 0 O P O }
 \hbox{\remark S N A Q J B Z R }
 \hrule }
 \hskip-7pt \vrule }
 }
 
 \end{document}


の様に使うことです。0 Z N n などがどのフォントに対応しているかは


\documentclass[a4paper,10pt]{jarticle}
 \font\remark=skak30 scaled\magstep5
 \pagestyle{plain}
 
 \begin{document}
 
 \font\remark=skak30 scaled\magstep5
 \noindent{\remark 0 Z K k J j}
 \noindent{\remark Q q L l R r}
 \noindent{\remark S s B b A a}
 \noindent{\remark N n M m P p}
 \noindent{\remark O o}

 \end{document}


を実行してみれば、理解できます。因みに、初期配置は


\documentclass[10pt, a4paper]{ jarticle}
\font\remark=skak30 scaled\magstep2
\pagestyle{plain}

\begin{document}

\centerline{
\hbox{\vrule
\vbox{\hrule
\hbox{\remark r m b l k a n s }
\hbox{\remark o p o p o p o p }
\hbox{\remark 0 Z 0 Z 0 Z 0 Z }
\hbox{\remark Z 0 Z 0 Z 0 Z 0 }
\hbox{\remark 0 Z 0 Z 0 Z 0 Z }
\hbox{\remark Z 0 Z 0 Z 0 Z 0 }
\hbox{\remark P O P O P O P O }
\hbox{\remark S N A Q J B M R }
\hrule}
\hskip-7pt\vrule }
}
\end{document}


で得られます。だから、手作業でこの様なコードを作成しても大した手間ではありませんでした。

skak.sty は使い易いし、詰将棋・詰碁の類は頭の中で解くべきであって、こんなプログラムはそもそも不要だったみたいです。
久しぶりに佐川に帰ると雪が積もっていて、本箱を調べると「ボビー・フィッシャーのチェス入門」や「定本大山の振り飛車」や
真部一男著「升田将棋の世界」や蛸島彰子著「将棋かくしふで」や橋本宇太郎解説　二口外義編集「詰碁を解くカギ」などの
懐かしい憧れの人達の古い本が見つかりました。持っているだけでなく、繰り返し読んで見なければ！！
「ボビー・フィッシャーのチェス入門」の新しい本が予約になっていますが、「BOBBY FISCHER TEACHES CHESS」も同じ位の値段で、
新書位の大きさで、英語も易しく、持ち歩くには便利です。

昔C#で作った囲碁の局面をLaTeXのコードで保存するプログラムを使ってみると使い勝手が良くないので作り直そうと思って、
https://www.cc.kochi-u.ac.jp/~tyamag/jyohou/crosscram.pdfのプログラムの FLTK を使っているものをコンパイルしようと
思うと出来なくて、「ストラウストラップのプログラミング入門」を引っ張り出して、何とかコンパイル出来るようにしましたが、
FLTK の開発は中止になった思っていましたが、続いているみたいで、新しいバージョンの FLTK が作られていました。
調べていると FLTK で openGL が使えるようになったみたいですが、インターネットで調べたプログラムがどれもコンパイルできない。
unix/linux 用のコードみたいだし、fltk 1.4.1 の lib が空で、自分でコンパイルしなさいとの事だがやり方が分からない。
師匠や朋友がいないので、大変です。囲碁のプログラムには関係ないし、openGL は Python で使えるから、支障はないですが、
他の人が使っているのに、私だけ理解できないのは癪です。windows 10 では、駄目だろうか？
今の処、VC++ 2019 では、基本的には「ストラウストラップのプログラミング入門」に書いてある様にすれば、即ち、
https://www.cc.kochi-u.ac.jp/~tyamag/jyohou/crosscram.pdfの FLTK のプログラミングの解説通りで良いですが、
VC++ 2022 では、私はまだ、コンパイル出来ていません。VC++ 2019 と設定の違いを比較して調べる必要があります。
VC++ 2019 で作ったプログラムもプロジェクトファイルをダブルクリックすると勝手に VC++ 2022 が立ち上がり、
聞いてくる何かの変更を指示すると VC++ 2022 でコンパイル・実行できるので、VC++ 2019 では 32 ビットのソフトを、
 VC++ 2022 では 64 ビットのソフトを作っていたので、プロパティでその設定の違いを修正すれば多分できます。
基本的な FLTK のプログラミングや openGL のプログラミングを忘れているので、思い出すのに時間が掛かり、疲れ果てます。
VC++ による GUI も FLTK のプログラミングも時代遅れの様な気もしますが、それなりに、面白いですし、時間をかけたものだから。
昔に比べ FLTK の情報は多いですが、windows 用のサンプルプログラムはなく、それぞれの部品のマニュアルの情報ですから、
それをどの様にプログラムに組み込めばよいのかが理解できる単純なサンプルプログラムを探すのが難しいですが、幸いなことに、
https://www.cc.kochi-u.ac.jp/~tyamag/jyohou/crosscram.pdfの FLTK のプログラミングの解説があるので、何とかなります。
しかし、 FLTK には円を描く機能や塗りつぶした矩形を描く機能はありますが、塗りつぶした円を描く機能はどうもないみたいで、
矩形の塗りつぶしか、多分、石の画像を貼り付ける（昔は windows では出来なかったはずですが？）しかないみたいです。






の様なものは出来ましたが、


\documentclass[a4paper, 12pt]{jarticle}
\usepackage{go2}
 \begin{document}
 \inifulldiagram
 \pos{b}{3}=\white.
 \pos{c}{2}=\black.
 \pos{c}{3}=\black.
 \pos{c}{4}=\white.
 \pos{c}{5}=\white.
 \pos{c}{10}=\white.
 \pos{c}{15}=\black.
 \pos{d}{4}=\black.
 \pos{d}{6}=\white.
 \pos{d}{17}=\black.
 \pos{e}{3}=\black.
 \pos{f}{4}=\black.
 \pos{g}{17}=\white.
 \pos{h}{4}=\white.
 \pos{k}{17}=\white.
 \pos{l}{3}=\black.
 \pos{o}{3}=\black.
 \pos{o}{17}=\black.
 \pos{q}{3}=\white.
 \pos{q}{16}=\black.
 \pos{r}{4}=\white.
 \pos{r}{14}=\white.
\begin{figure}
\gofontsize{20}
\showfulldiagram
\end{figure}
\end{document}


を指定したファイルに打ち出させ、LaTeX で図を描かせると






になります。FLTK には、保存するファイルを見つけるダイアログボックスはないみたいで、ファイル名を入力して、
メニューの保存をクリックして、保存しています。
ファイル名を入力して、エンターキーを押せば保存できるようにもプログラムを修正出来ます。。
囲碁の本の図は複雑なものがあり、FLTK は久しぶりで、この様な単純な図を描かせるだけでも結構大変でした。
打ち間違えた時、一手づつ戻す機能とか、番号や記号を一部の石に表示できる様にするとか、どの様な図が欲しいかに応じて、
やろうと思えば、幾らでも出来ますが、これは当分、もうやめです。
GUI のプログラミングも VC++ の　GUI と FLTK と二通りのやり方が使えると便利です。
FLTK のプログラミングは linux でのプログラミングの練習みたいなものですが、FLTK の開発者は linux で開発していて、
windows で使えるようにするのは、余興みたいなので、FLTK では純粋に C++ の知識だけで良いというメリットだけみたいです。
Python や C# や Java などでも作れるので、自分の得意な言語で、興味があれば、作ってみれば良いです。

将棋の学び方でも何を目指しているかに依って、違うはずですが、升田幸三著「すぐ強くなる将棋の必勝法」には、
「飛車落戦法についても、その一手一手ごとが千変万化、変化は無限大であり、幾百冊の講義を続けても解き切れるものではない、
しかし棋術の深奥に秘められた理法をば身につけると、説明をきかなくとも、局面局面を見れば瞬間に大勢の判断がつくものである、
この境地はアマの方々といえどもある程度まで到達し得るしそれから先は”読み”の深浅いかんということにかかる。」
とありますが、本を読むと局面から棋譜で変化を書いてあり、頭の中で、駒を動かすか、将棋盤で駒を動かすか、が普通でしょうが、
上で作ったようなソフトを使えば、一つ一つの局面の変化を目で見えるように出来ますし、そのような局面を最初から駒を動かして、
何度も何度も作ることが定跡を理解・暗記する手助けに私の様な凡人にはなります。
本当に強くなりたければ、全部、頭の中で将棋盤を思い浮かべ、その上で駒を動かすべきだとは思いますが。
様々、思い付いたことをやってみれば良いです。多分。
現在は、大学共通テストでも、知識の量ではなく、自ら考えることを要求される様になっているみたいです。

橋本宇太郎解説　二口外義編集「詰碁を解くカギ」を私の様な凡人が読むためにも
昔作った VC++ のプログラムの記録が残っている
https://www.cc.kochi-u.ac.jp/~tyamag/jyohou/crosscram.pdf
を見ながら、必要な情報が殆ど得られなくなっているので、何とかでっち上げて






の様な .pdf ファイルを作って、この本の「死活の基本的な筋２０項」を自分なりに編集する必要があるみたいです。

更に、 Hanna Kolodziejska さんの作った go.sty は、例えば、複数の棋譜を並べて表示するにはどうすればよいかなど、
凡人の私には使いにくいので、チェスのプログラムでやったように、
フォントを使わして貰って、作りたい局面の画像を LaTex で作ることを考えます。
go.mf, go1black.mf, go2black.mf, go1white.mf, go2white.mf 及び go.sty を眺めていれば、


\documentclass[a4paper,10pt]{jarticle}
\pagestyle{plain}
 
\begin{document}
   
\font\remark=go10 at 20truept
\font\blackfontOne=go1bla10 at 20truept
\font\blackfontTwo=go2bla10 at 20truept
\font\whitefontOne=go1whi10 at 20truept
\font\whitefontTwo=go2whi10 at 20truept

 \centerline{
 \hbox{\vrule
 \vbox{\hrule
 \hbox{\remark  \char6  \char4  \char4 \char4  \char4  \char4 \char7}
 \hbox{\remark  \char2  {\whitefontOne \char0}  \char1 \char1  \char1  \char1 \char3}
 \hbox{\remark  \char2  \char1  \char1 \char1  \char1  \char1 \char3}
 \hbox{\remark  \char2  \char1  {\whitefontOne \char1} \char1  \char1  \char1 \char3}
 \hbox{\remark  \char2  \char0  \char1 \char1  \char1  \char1 \char3}
 \hbox{\remark  \char2  \char1  \char1 \char1  {\blackfontOne \char0 }  \char1 \char3}
 \hbox{\remark  \char2   \char1 \char1 {\blackfontOne \char4 }  \char1  \char1 \char3}
 \hbox{\remark  \char2  \char1  \char1 \char1  \char1  \char1 \char3}
 \hbox{\remark  \char8  \char5  \char5 \char5  \char5  \char5 \char9}
 \hbox{\whitefontTwo \char127  \whitefontTwo \char126}
 \hbox{\blackfontTwo \char127   \char126}
 \hbox{\remark \char10   \char11 \char12}
 \hbox{\remark \char13   \char14 \char15}
 \hbox{\remark \char16   \char17 \char18}
\hrule }
 \hskip-7pt \vrule }
 }
 \hbox{\blackfontOne \char0   \char1 \char2 \char3 \char4}
 \hbox{\whitefontOne \char0   \char1 \char2 \char3 \char4}
 \hbox{\blackfontTwo \char0   \char1 \char2 \char3 \char4}
 \hbox{\whitefontTwo \char0   \char1 \char2 \char3 \char4}

\end{document}


を LaTeX で実行してみれば、 Hanna Kolodziejska さんの作ったフォントの使い方が理解でき、






と描画・表示してくれるので、チェスの場合と同様、囲碁の局面を描画するLaTeX のコードを打ち出すプログラムが容易に作れます。






のような描画が出来るようになりました。 Hanna Kolodziejska さんの go.sty と使用目的に応じて使い分ければ良いです。

手作業で、１９路盤なら上の様な指示を３６１個並べるのは大変ですが、補助の VC++ のプログラムを作り、
コンピューターに作らせるならこの様に楽をすることが出来ます。
LaTeX のコードが長くなり、お除けないですが、これを .sty ファイルとして使う様に改良すれば見た目は単純になります。
即ち、保存するファイル名を mySSS.sty とした時、作った VC++ のプログラムで、


\makeatletter
\newenvironment{mySSS}[2][]%
{
\begin{center}

\font\ban=go10 at #1truept
\font\blO=go1bla10 at #1truept
\font\blT=go2bla10 at #1truept
\font\whO=go1whi10 at #1truept
\font\whT=go2whi10 at #1truept

\hspace*{#2mm} \hbox{\ban \char6 \char4 \char4 {\blO \char1} {\whO \char2} {\whO \char0} \char4 {\whO \char0} \char4 \char4 \char4 \char4 }
\hspace*{#2mm} \hbox{\ban \char2 \char1 {\blO \char0} {\whO \char0} {\whO \char4} \char1 {\blO \char5} {\whO \char0} {\blO \char0} \char1 \char1 \char1 }
\hspace*{#2mm} \hbox{\ban \char2 \char1 {\blO \char0} {\whO \char0} {\blO \char3} {\whO \char0} {\whO \char0} {\whO \char0} {\blO \char0} \char1 \char1 \char1 }
\hspace*{#2mm} \hbox{\ban \char2 \char1 {\blO \char0} {\blO \char0} {\blO \char0} {\blO \char0} {\blO \char0} {\blO \char0} {\blO \char0} \char0 \char1 \char1 }
\hspace*{#2mm} \hbox{\ban \char2 \char1 \char1 \char1 \char1 \char1 \char1 \char1 \char1 \char1 \char1 \char1 }
\hspace*{#2mm} \hbox{\ban \char2 \char1 \char1 \char1 \char1 \char1 \char1 \char1 \char1 \char1 \char1 \char1 }
\hspace*{#2mm} \hbox{\ban \char2 \char1 \char1 \char1 \char1 \char1 \char1 \char1 \char1 \char1 \char1 \char1 }
\hspace*{#2mm} \hbox{\ban \char2 \char1 \char1 \char1 \char1 \char1 \char1 \char1 \char1 \char1 \char1 \char1 }
\hspace*{#2mm} \hbox{\ban \char2 \char1 \char1 \char1 \char1 \char1 \char1 \char1 \char1 \char1 \char1 \char1 }
\hspace*{#2mm} \hbox{\ban \char2 \char1 \char1 \char0 \char1 \char1 \char1 \char1 \char1 \char0 \char1 \char1 }
\hspace*{#2mm} \hbox{\ban \char2 \char1 \char1 \char1 \char1 \char1 \char1 \char1 \char1 \char1 \char1 \char1 }

}
{
\end{center}
}
\makeatother


の様な内容の mySSS.sty を打ち出せば、


\documentclass[12pt, a4paper]{ jarticle}
\pagestyle{plain}
\usepackage{mySSS}
\begin{document}

\begin{mySSS}[20]{5}

\end{mySSS}
\Large
「詰碁を解くカギ」基本の考え方：問題７
\end{document}


の様な LaTeX のコードで、欲しい局面を描画できます。ここで、数字の２０は盤のサイズ、５は左の空白の指示です。
更に、\picture 環境で、、\put 命令で、空の盤を描いた後で、\put 命令で、石を上書き配置することも可能です。
様々な方法が可能なので、自分で実験してみて下さい。

コンピューター囲碁の基本的な理論およびプログラミングは少し古い(AlphaGo が出る直前)ですが、
youtube に２０１５年に開催された「電気通信大学コンピューター囲碁講習会」
の模様を録画したものが
https://www.youtube.com/watch?v=UIlIVAn1WOg
https://www.youtube.com/watch?v=kWlOrPZjEgQ
https://www.youtube.com/watch?v=MZMov82KjP8
にアップされていて、今でも見ることが出来ます。
この講習会の山下宏さんのサンプルプログラムは、（講義の最後の「９路盤のデータをどの様にして手に入れるか？」
の質問の記憶があるので、多分）、２０１５年にゲットしていたはずで、私は持っていますが、
どうも現在は入手が困難みたいです。
（わざとバグを入れている（間違えている）ので、ソースコードを良く読んで、何をやっているか理解し。
自分でデバッグする（間違いを修正する）必要があります。）
UCB・UCT の理解には、講義を聴くのが一番ですし、コードの例を見せてもらうことが、私の様な凡人には有難いです。
抽象的な理論の理解と実際にコードに落とし込むことの間には、私の様な凡人には大きなギャップがあります。
この様な応用範囲の広い「基本的な雛型」を教えて貰うと、私の様な凡人でも、囲碁は終わったと思いますが、
ボケないためにも、様々なゲームに対して適応してみる事・実験して見る事が可能になります。多分。
「修業は一人でするものだが、入門には師匠が必要」そのものですが、師匠は youtube 上の師匠でも良いです。
８時間の入門講義をしてくれていて、当時のコンピュータ囲碁の専門家の常識となっている事を様々教えてくれています。

＜注意＞ 現在、サンプルプログラムの go10.c を go10.cpp として VC++ 2022 でコンパイルするとエラーメッセージが表示され、
コンパイル・実行出来ないですが、
例えば、



#include＜string＞


を追加し、


//char* pattern3x3[] = {
std::string pattern3x3[] = {
  "XO?"  // "X" ... black,  black "X" to play at the center.
  "..."  // "O" ... white
  "???", // "." ... empty
    // "#" ... out of board
"OX."  // "?" ... dont care
"..."
"?.?",

"XO?"
"..X"
"?.?",

"X.."
"O.."
"###",

//NULL
""
};

#define EXPAND_PATTERN_MAX  (8*100)
int e_pat_num = 0;
int e_pat[EXPAND_PATTERN_MAX][9];      // rotate and flip pattern
int e_pat_bit[EXPAND_PATTERN_MAX][2];  // [0] ...pattern, [1]...mask
int dir_3x3[9] = { -WIDTH - 1, -WIDTH, -WIDTH + 1,  -1, 0, +1,  +WIDTH - 1, +WIDTH, +WIDTH + 1 };

void expand_pattern3x3()
{
    int n, i, j;
    e_pat_num = 0;
    for (n = 0; ; n++) {
        int i, j;
//        char* p = pattern3x3[n];
        std::string p = pattern3x3[n];
//        if (p == NULL) break;
        if (p == "") break;
        if (e_pat_num > EXPAND_PATTERN_MAX - 8) { prt("e_pat_num over Err\n"); exit(0); }

        for (i = 0; i < 9; i++) {
            int m = 0;
//            char c = *(p + i);
            char c = p[i];
            if (c == '.') m = 0;
            if (c == 'X') m = 1;
            if (c == 'O') m = 2;
            if (c == '#') m = 3;
            if (c == '?') m = 4;
            e_pat[e_pat_num][i] = m;
        }

    ・・・・・

    prt("pattern3x3 num=%d, e_pat_num=%d\n", n, e_pat_num);
}


の様に、C の


char* 


を C++ の


std::string


を使う様に変更すれば、コンパイル・実行出来る様になります。


又、これ以前のコンピューター囲碁のソースを公表して下さっていた gnugo も、私は持っていますが、
どうも現在は入手が困難みたいです。現在でも GoGui で動かすことが出来ます。
C 言語のソースコードを持っているだけでは駄目で、読んで、理解しないと何にもなりませんが、
囲碁では、強くするためには、セキやウッテガエシやオイオトシや５目中手など複雑な手筋の局面の考察が実際は必要で、
他人の物凄く長くて複雑な C 言語のプログラムを読むのは、私の様な凡人には難しいです。
この様なゲームソフトを開発する人達は、実行を高速化する為に、
流石にすべて機械語・アセンブリ言語で書くと言うことはしてないと思いますが、
コンピューターに細かな指示が可能な C 言語でプログラミングしているみたいです。
私の様な凡人は C 言語のトリッキーな表現・技術の習得まではしていないので、
学習時間の長い C++ の方が楽なので、C++ に書き直してみることも勉強になります。多分。

最近のゲームプログラミングの話題は、伊藤毅志編著「ゲームAI研究の新展開」があります。

上の囲碁の局面の LaTeX のコードを打ち出すプログラムでもこの山下さんの C の囲碁のルール通り打つプログラムの
コードを C++ に変換して勝手に使わしてもらっています。
即ち、全ての囲碁の盤に関する関数・データを閉じ込めた class Go を作り、


private: System::Void pictureBox1_MouseClick(System::Object^ sender, System::Windows::Forms::MouseEventArgs^ e) {
	static Go game(19);

	if (startFlag == true) {
		game = Go(19);
		startFlag = false;
		draw(game);
		return;
	}
・・・
		draw(game);
	}
	else
	{
		return;
	}
}


の様に通常の class を使い、static で保存して、一つの関数内で保持して置き、（グローバル変数として使えないので）、
盤の石の配置の情報 game.board[], game.board2[] を ref class の配列


		array＜int, 2＞^ iban = gcnew array＜int,2＞(21,21);
		array＜int, 2＞^ iban2 = gcnew array＜int, 2＞(21, 21);


にも game の情報が更新されるたびに、コピーして置き、
例えば、 game の情報にアクセスできない関数である、ファイルに盤の配置を打ち出す時使っています。
VC++ の GUI で C++ の class と VC++ の ref class を同時に使うのは結構厄介です。
別の解決方法もあると思いますが、現在は VC++ の GUI に関する情報は極端に少なくなっています。多分。

囲碁は１９路盤、１３路盤、９路盤など色々あって厄介です。最終的には







の様なプログラムを作りました。ごちゃごちゃしていますが、自分で使うだけですから、これで良いです。
図面は、橋本宇太郎解説　二口外義編集「詰碁を解くカギ」の１６．ツケコシ・ワリコミの手筋の問題２です。
又、最近は囲碁も「１，３，５手の詰碁」と言った本が出版されるようになりました。
詰碁も詰将棋と同様、純粋なパズルとして楽しむことが出来ます。何も考えず、沢山解いてみなければ。

これで、これらの課題のプログラム：将棋、象棋、チェス、囲碁の局面描画は何とかでっち上げることが出来ました。


放送大学の講義で、「小学校や中学校の情報教育」の話をしていましたが、ソフト単独ではなく、ロボットを動かす教育を
解説していましたが、あんな精巧なおもちゃのロボットを誰が作ったんだろうと思いました。
小中学生の教育内容の改正だけでなく、それに耐えられる教員の能力の育成も必要なわけで、その教員養成に特化した
教育学部の教員も、どの様な教育をしたいかに応じて、そのようなロボットを準備しなければなら、お金も必要な技術の習得も大変です。
文部省も冷遇されている地方の国立大学の教育学部にも、
（教育学部の名称が変わり、これからは馬鹿にされなくなると喜んでいたある大学の教員もいました。
「教育学部の数学何て、高校の数学の教科書を教えればよい。俺でも出来る。」が一般の認識かも分かりません。
私も理工学部から教育学部に移った時、学生に何でこんな難しことを学ぶ必要があるんだと良く質問されました。
「１００教える必要がある時、ギリギリの１００だけ知っている先生と１０００知っている先生と
君はどちらの先生に習いたいんだ？君に教わることになる生徒も同じことを思うはずだよ。」と質問すると黙りました。
昔は有名国立大学の文科系学部の学生たちがグループで自分の大学志望者の為の通信添削のアルバイトをしていました。
誰かに雇われていた訳ではないので、アルバイトは適切ではないかも。
数学の問題は自分の大学の一般教養の数学の教授の書いた大学の教科書から問題を見繕って出題していました。
実際、大学に入学すると一般教養の数学の教科書（「微積分」と「線形代数」）に見覚えのある問題が幾つかありました、
昔は文系の学生でも大学で数学も学んでいるので、大学レベルの数学（？）の問題の解答の添削が出来るんだと思いました。
大学の入試問題は高校の教科書を読んで作っている訳ではなく、大学の授業で出会ったこれは使えると思った問題を
高校の数学の範囲で解けるように修正して出題しているはずです。多分。
尤も、高校の教科書に名を連ねている大学の先生はどうか知りませんが。私が聴いていた深夜のラジオ講座でも、例えば、
東北大学の勝浦捨造さんなどが講師をして人気だったし、最近でも、秋山仁さんがNHKの高校講座の講師をしていました。）
中央集権的な、現場を知ろうとしない官僚の権力を見せつけるだけの？、
無駄な大量の文書を作成する必要のある競争的な資金の請求しなくても使える、
各大学の自由裁量で使える通常の経常的な予算をもっと配分すべきです。


２月２日には、高知で藤井聡太棋王（7冠）対増田康宏八段の棋王戦第１局行われ、大盤解説会に行っていました。２１年ぶりの高知開催で、
その時も大盤解説会に行きましたが、プロの将棋の世界だけでなく、将棋を楽しむ人達が増え、将棋 AI は元より、情報通信機器の発達などで、
大盤解説の仕方も激変し、(高知では大きなホールでの開催で、大盤解説解説会なのに舞台上に将棋の大盤が置いていないので、
どうやって解説するのだろうと思っていると、解説者と聞き手の3名（佐藤 天彦九段が来ていました）だけが舞台に上がり、多分遠隔操作で、
解説に合わして盤面を舞台のスクリーンに映していました。それで、報道関係者も１階ではなく２階席へ行かされていました。)、
世の中随分変わったなーと実感しました。おやつの当てクイズで、両対局者の配慮で、殆どの人が正解で、
私は次の連続テレビ小説「あんぱん」にちなんで新作したという「ぼくらはみんないきている」という命名の
小さなアンパンの形をしたお饅頭が当たりました。
知り合いは誰もいなかったとは思いますが、名前が呼ばれ、来ていることが参加者全員に知られてしまいました。
次の一手のクイズは、この様な真剣勝負をしている時、すぐに手を指さず長く考えている時は、殆ど「その他の手」が正解になるみたいです。

キャベツが高いと騒いでいますが、大都会にいて、農業を知らない人達ばかりに成ったのではないでしょうか？
野菜も一年中いつでも収穫できるものではなく、露地栽培では収穫できる時期が決まっています。
百姓がスーパーで野菜を買っていたと驚いた時期もありましたが、元々は「旬の食材」を愛でていたのが日本人です。
経済効率を考え、地方を切り捨てるべきだ。能登の復興などとんでもないと言う主張も出てきています。
北方領土問題や尖閣諸島問題や竹島問題は大騒ぎするのに、本当はシンガポールのような都市国家が理想で、
日本の地方は中国人や米国人やロシア人に売り渡せば良いと考えているのでしょうか？単なる受け狙いの発言でしょうか？
幸いなことに「政治家」だけは選挙によって入れ替えることが出来ます。
各「政治家」がどの様な考えを持っているかよく調べ、家柄が良いとか、かっこいいとかでなく、次の参院選等で主体的に投票すべきです。
老い先短い私などは良いですが、（同年代の人達が次々亡くなっていますが、遺伝的に見て、後２０年ぐらいは多分大丈夫だとは思いますが）
若い人たちは、如何にすれば国民を騙せるかばかり考え、それを生きがいにしている優秀な人達に騙されないようにしないと、
所謂単純な詐欺はすぐに被害が判明しますが、優秀な人達の行う合法的な詐欺行為は我々凡人に被害が判明するのに時間が掛かるので、
(場合によっては数十年以上、数百年で、歴史の見直しが起きてから判明することも多いです。)、厄介で、
権威を傘に、通常の詐欺グループより大規模な集団で協力し合い、巧みな話術を駆使するので、凡人は気付かないことが多く、
気が付いた時には、格差が拡大した悲惨な未来が待っていますよ。
相場英雄著「アンダークラス」の帯の「金がないか、心がないか。本当の下層はどっちだ？ー藻谷浩介」が・・・

トランプ大統領による関税が連日報道され、株価や円相場が乱高下していますが、フランス人が巧妙に考え出した
「付加価値税」＝「消費税」は国内的には「安定財源」ですが、対外的（特に消費税のない米国に対して）には、
第２の関税になっているそうです。輸入品にも消費税税が掛かり、輸出品には消費税分が企業に払い戻されているからだそうです。
欧州各国が農業に補助金を出すことなどの対策で、必死に自国の食料自給率確保を行っていますし、
逆に農業に補助金を出すことなどの対策で農産物の輸出を有利にしている国もあります。これも間接的な関税です。
世の中、どうも昔から優秀な人達による壮絶な騙し合いの世界みたいです。

私達の学生時代には米国の歴史を大学で教えることは禁止されていたようですが、最近やっと
吉見俊哉著「アメリカ・イン・ジャパン」岩波新書の様な我々凡人にも読んで理解できる本が出版される様になりましたが、
最近は本を読む人が少なくなり、皆、スマホに夢中で、インフルエンサーの金儲けに協力しています。
米国にも色々な人がいて、マイケル・サンデル著「実力も運のうち　能力主義は正義か？」も面白い本です。
ハヤカワ文庫もミステリ・SF だけでなく、結構、価値ある本・読み応えのある本を出版してくれています。

馬伯庸著「両京十五日」が面白かったので、同じ作者の「西遊記事変」を読もうと思ったら、
元の「西遊記」を先ず読んだ方が良いとのことで、昔、平凡社版の「西遊記」を読んだことがありましたが、
実家に置いていたら行方不明になってしまいました。ブックオフで小野忍訳の岩波文庫版の１・２を安価で
手に入れましたが、３はアマゾンで出品されていますが、
一万円以上の値がついていて、中国文学の専門家でもないので、そこまでの価値があるとは思えず買えません。
中野美代子訳は新刊として１～１０が書店で手に入ります。平凡社版の「西遊記」と岩波文庫版の「西遊記」は
基にしている本が簡本と繁本と異なっていますが、昔、何を読んでいたか、「西遊記」てこんな本だったのかと思っています。
最近、宗教が問題になる事が多いですが、同じ系列であるはずのユダヤ教・キリスト教・イスラム教だけでなく、
仏教も複雑怪奇で、まともに学んだことの無い我々凡人には複雑で難しすぎます。

「富める者が富めば、貧しい者にも自然に富がこぼれ落ち、経済全体が良くなる」とする経済理論である
トリクルダウン理論が有効でないことが分かったので、与野党とも「富める者」を優遇する政策を
修正し、財源はどうすると脅迫している、隠れ関税としてフランスで考え出されたと言う消費税を
減税するための財源は、GAFA（ガーファ）の躍進の基礎でもある金儲けの原則で、
インフルエンサーの資金源でもある、貧乏人から広くかき集めるのを止め、
今まで優遇してきた「富める者」に大分の負担をしてもらえば良いはずですが、政策決定する人達は、
（「富める者」達の支持で生活している与野党の政治家やマスコミを含め）、
自分自身が「富める者」の一部を構成しているので、自らの身を切る発想は浮かばないみたいです。
少し前には、自分ぐらい偉い政治家なら企業の経営者並みに年収１億円貰って当然だと
発言した人も居たぐらいですから。

ジョージ・ポリアさんは
「いかにして問題をとくか（How to Solve It）」、
「数学の問題の発見的解き方」、
「数学における発見はいかになされるか　第１巻：帰納と類比」
「数学における発見はいかになされるか　第２巻：発見的推論ーそのパターン」
の４冊の啓蒙書を書いています。
日本では、「いかにして問題をとくか（How to Solve It）」が重要視されているみたいですが、
最近皆が言い出した「考える力」を培うには、「問題を解くためのマニュアル集」であると
私には思われる「いかにして問題をとくか（How to Solve It）」ではなく、
「数学における発見はいかになされるか　第１巻：帰納と類比」の
方が重要ではないかと私は思います。（こう考えるのは、訳者の柴垣先生に教わったからかも？）
数学は暗記科目と理解せれていて、素早く公式を丸暗記し、それを使って、問題を素早く解ける人が
優秀とされています。
「分からないでなければ、分った」だと普通は思うので、こんなこと考えないと思いますが、
「数学が分かるとはどういうことか？」と先生に質問したら、
「君は哲学的なことを考えるんだね」と答えを教えてくれなかったと不満を漏らしている人が居ました。
例えば、九九を覚える時、九九を唱えさせて覚えさせるのが一般的だと思いますし、
「九九を覚えることが出来た人は誰でも将棋でアマの３段までは行く」と書いていたプロ棋士も居ました。）
しかし、九九を暗記する方法は、九九を唱えるだけでなく、九九の仕組み・掛け算の定義から、
サン・イチがサンは良いとして、サン・ニがロクをサン・イチがサンのサンとサンを暗算で足し算し、ロクと唱え、
サ・ザンがキュウをサン・ニがロクのロクとサンを暗算で足し算し、キュウと唱え、・・・と繰り返し練習し
暗記しても良いはずです。台形の面積の公式：（「上底」足す「下底」）掛ける「高さ」割る「２」も
（何度も）唱えることで素早く暗記できる人が優秀だとされますが、長方形、平行四辺形、三角形、台形と
新聞紙を切って、それぞれの図形を作り、切り貼りしたり、２個をくっ付けたりするのを見せてもらって、
互いに関連しているとやっと納得して、それら一連の操作を通してなら覚えることが出来る人たちもいます。
２次方程式の解の公式も中学校で結論の公式そのものを丸暗記するよう指導されました。
しかし、平方根の定義は何か、平方完成をすれば、平方根の定義から公式が導けると言う流れを理解して、
その一連の操作を頭の中ですることが出来るように練習して、公式を唱えることが数学を理解することではないでしょうか？
「２次方程式と言うと平方完成からする学生がいるよね」と話していた数学の教授たちがいましたが、
数学は確かに暗記科目だと思いますが、暗記させる事柄が間違っているのでは？考える材料や推論の仕方を教えるべきでは？
この年になって考えると
「前提条件は何か？それらをキチンと確かめ、それらを元に推論し、正しい結論を得ることが出来れば、
更に、現在は、コンピューターを誰でも使えるので、プログラミングで結果を自分で検証できれば、
理解できたと言えるのではないでしょうか？」が「数学が理解できた！」ではないかと私は思いますが？
「これらを教えなくても、自分で考え出せるように！」が教育学者や心理学者の悲願みたいで、
様々なソフトの開発などがなされていますが、上手くいっていないと思います。
子供の時、これ様な経験を一杯して、考える材料がたまれば、ポリアさんの言う「類比」が可能になるのではと思います。
算数・数学が出来るようになるには、「結論の公式の丸暗記」が唯一の方法ではないと思います。
前提条件があって、それらから論理的に推論するのが、算数・数学で、誰がやっても同じ結論を得るものです。
最初の前提条件が間違っていれば、どんな出鱈目な結論でも、論理的に導けるので、注意が必要です。




情報数学のテキストの為のソフト





  チューリングマシン

  チューリングマシン for Windows 8.1


  和田秀男著「計算数学」の小さなコンピュータ TinyCom


  Knuth の仮想計算機 Mix


  ４０００語のMix for Windows 8.1


  TinyBasic.jar のダウンロ ード 


  Hopf algebra の cohomology


  正二十面体の展開図の個数の求め方


  LaTeX で囲碁の作図をするために必要なこと


  ボヘミアン・シュナイダーのゲーム


  古い線画のAchimedes





  情報数学の資料


  数学教育を改善するためのソフト開発