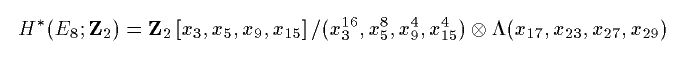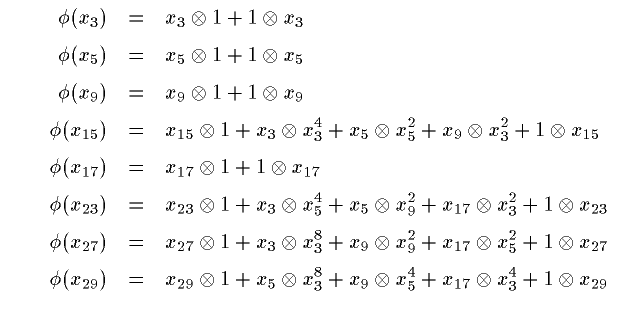最終更新日 2009年7月7日
Hopf 代数のコホモロジー
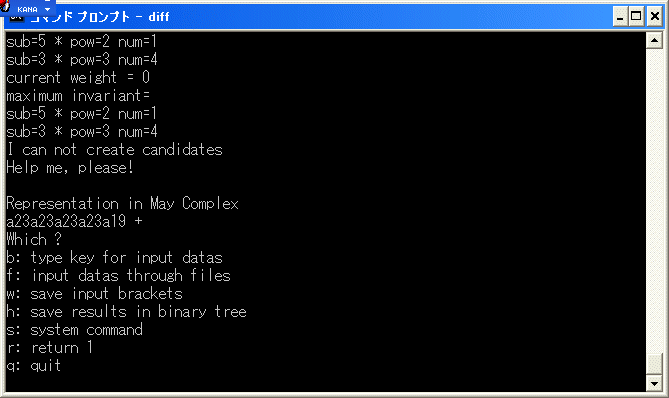
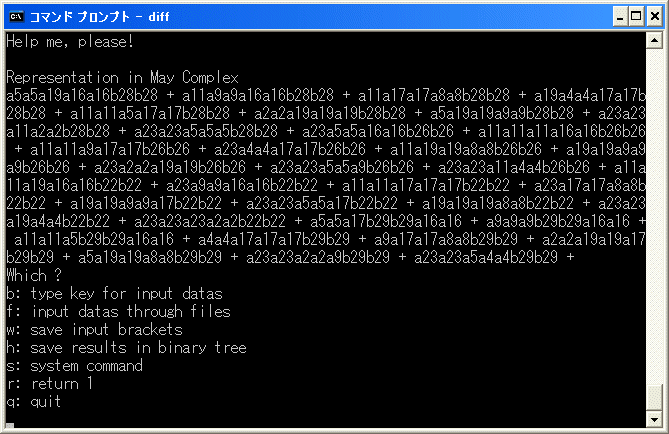
HZ2*(E8)のcohomology

リー群 E8の Z2 cohomology の cohomology の
計算を出来るところまで計算してみます。
まず、出発点は E1 term の決定です。これは May complex で与えられます。
なので、代数としては cobar construction で
[x3], [x5], [x3^2], [x9], [x5^2], [x3^4], [x15], [x17], [x9^2],
[x5^4], [x23], [x3^8], [x27], [x29], [x15^2]
で表される元で生成される polynomial algebra です。これらを
a2, a4, a5, a8, a9, a11, b14, a16, a17, a19, b22, a23, b26, b28, b29
で表現することにします。
微分は
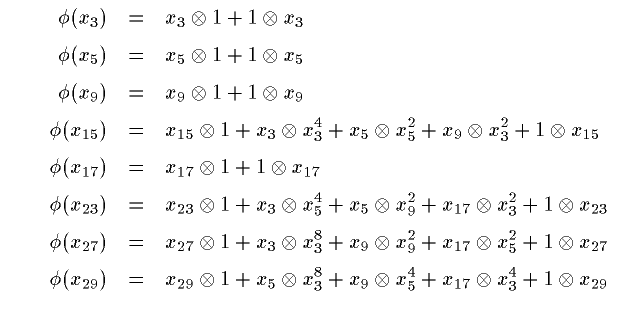
なので、 cobar construction で
d[x3]=0,
d[x5]=0,
d[x3^2]=0,
d[x9]=0,
d[x5^2]=0,
d[x3^4]=0,
d[x15]=[x3/x3^4]+[x5/x5^2]+[x9/x3^2],
d[x17]=0,
d[x9^2]=0,
d[x3^4]=0,
d[x23]=[x3/x5^4]+[x5/x9^2]+[x17/x3^2],
d[x27]=[x3/x3^8]+[x9/x9^2]+[x17/x5^2],
d[x29]=[x5/x3^8]+[x9/x5^4]+[x17/x3^4],
d[x15^2]=[x3^2/x3^8]+[x5^2/x5^4]+[x9^2/x3^4]
となるので、
d1(a2)=0,
d1(a4)=0,
d1(a5)=0,
d1(a8)=0,
d1(a9)=0,
d1(a11)=0,
d1(b14)=a2a11+a4a9+a8a5,
d1(a16)=0,
d1(a17)=0,
d1(a19)=0,
d1(b22)=a2a19+a4a17+a16a5,
d1(a23)=0,
d1(b26)=a2a23+a8a17+a16a9,
d1(b28)=a4a23+a8a19+a16a11,
d1(b29)=a5a23+a9a19+a17a23
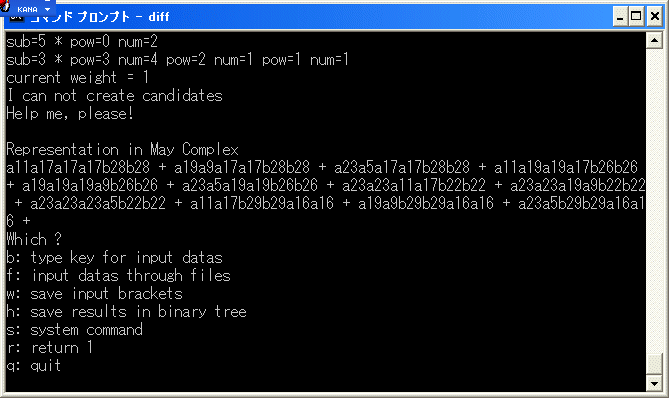
で与えられます。E1 term の微分代数としての構造が決まりましたので、all.exe というソフトで
ホモロジーの構造を決定します。all.exe は gen.dat と rel.dat という二つのファイルに
微分代数の情報をセットして実行します。gen.dat には
生成元と微分の情報を deg, dim, weight, name, differential の順に並べます。
deg は通常と異なり、degree - dimension を deg としています。
これは all.exe を使って私が本当に計算したい A2 の cohomology を計算するとき、
球面の安定ホモトピー群と旨く対応させるためにこのようにしています。
name はメモリを少なくするために、
0=[x3], 1=[x5], 2=[x3^2], 3=[x9], 4=[x5^2], 5=[x3^4], 6=[x15], 7=[x17], 8=[x9^2],
9=[x5^4], 10=[x23], 11=[x3^8], 12=[x27], 13=[x29], 14=[x15^2]
と数字で表現しています。また、cocycle の場合 differential には E をセットしています。
今の場合、gen.dat は次のようになります。
2 1 0 0 E
4 1 0 1 E
5 1 0 2 E
8 1 0 3 E
9 1 0 4 E
11 1 0 5 E
14 1 1 6 0*5+1*4+3*2
16 1 0 7 E
17 1 0 8 E
19 1 0 9 E
22 1 1 10 0*9+1*8+2*7
23 1 0 11 E
26 1 1 12 0*11+3*8+4*7
28 1 1 13 1*11+3*9+5*7
29 1 1 14 2*11+4*9+5*8
rel.dat は relation の情報を degree, dimension, weight, =0 無しの relation の順で並べますが、今の場合、
polynomial algebra なので、relation は無いので、空のファイルとします。
all.exe は all weight dim または all -r deg weight dim の形式で実行します。これは、
indecomposable elements と defining relations を探索する範囲を指定するための引数です。
weight は微分の weight の差を指定します。dim は探索する dimension の上限を指定します。
-r deg は主として A2 のための指定で、探索する degree の上限を指定します。
この微分代数のホモロジーの indecomposable elements と defining relations が存在しうる範囲を
予想し、この場合、十分余裕をとっても dim <= 9 で大丈夫のはずであるので、
コマンドプロンプトで
all 1 9
を実行します。
ここで、1 は E1 term のホモロジーを計算するので differential の weight の差 1 を指定します。
約40分で終了します。
この微分代数のホモロジー(E2 term)の indecomposable elements と defining relations が
ind.dat と def.dat にセットされます。ind.dat は次のようになっています。
0 0 1 2 0
1 1 1 4 0
2 2 1 5 0
3 3 1 8 0
4 4 1 9 0
5 5 1 11 0
6 7 1 16 0
7 8 1 17 0
8 9 1 19 0
9 11 1 23 0
10 6^2 2 28 2
11 6*7+3*10+1*12+0*13 2 30 1
12 6*8+2*12+0*14+4*10 2 31 1
13 6*9+5*10+2*13+1*14 2 33 1
14 6*11+5*12+4*13+3*14 2 37 1
15 10^2 2 44 2
16 9*12+10*11+7*14+8*13 2 45 1
17 12^2 2 52 2
18 13^2 2 56 2
19 14^2 2 58 2
20 6*9*12+6*10*11+5*10*12+6*8*13+2*12*13+1*12*14+0*13*14+3*10*14+4*10*13+6*7*14 3 59 2
name, representative, dimension, degree, weight の順に並んでいます。
10 6^2 2 28 2
は 10 と名前を付けた gen.dat の元を使った表現で 6^2 で表される dim = 2 deg = 28 weight = 2 の
indecomposable element があることを
表していて、E2 term には cobar construction での表現で [x15/x15] から始まる indecomposable element が
あることを表しています。同じく
11 6*7+3*10+1*12+0*13 2 30 1
は 11 と名前を付けた gen.dat の元を使った表現で 6*7+3*10+1*12+0*13 で表される dim = 2 deg = 30 weight = 1 の
indecomposable element があることを表していて、E2 term には cobar construction での表現で
[x15/x17]+[x9/x23]+[x5/x27]+[x3/x29] から始まる indecomposable element があることを表しています。
def.dat は次のようになっています。ind.dat で与えた indecomposable elements が満たす defining relationas が
与えられています。
2*3+1*4+0*5 2 13 0
2*6+1*7+0*8 2 21 0
4*6+3*7+0*9 2 25 0
5*6+3*8+1*9 2 27 0
5*7+4*8+2*9 2 28 0
2*11+1*12+0*13 3 35 1
4*11+3*12+0*14 3 39 1
5*11+3*13+1*14 3 41 1
5*12+4*13+2*14 3 42 1
7*11+6*12+0*16 3 47 1
8*11+6*13+1*16 3 49 1
8*12+7*13+2*16 3 50 1
9*11+6*14+3*16 3 53 1
9*12+7*14+4*16 3 54 1
9*13+8*14+5*16 3 56 1
11^2+6^2*10+3^2*15+1^2*17+0^2*18 4 60 2
11*12+6*7*10+3*4*15+1*2*17+0*20 4 61 2
12^2+7^2*10+4^2*15+2^2*17+0^2*19 4 62 2
11*13+6*8*10+3*5*15+1*20+0*2*18 4 63 2
12*13+7*8*10+4*5*15+2*20+0*1*19 4 64 2
13^2+8^2*10+5^2*15+2^2*18+1^2*19 4 66 2
11*14+6*9*10+3*20+1*5*17+0*4*18 4 67 2
12*14+7*9*10+4*20+2*5*17+0*3*19 4 68 2
13*14+8*9*10+5*20+2*4*18+1*3*19 4 70 2
14^2+9^2*10+5^2*17+4^2*18+3^2*19 4 74 2
11*16+6*20+3*9*15+1*8*17+0*7*18 4 75 2
12*16+7*20+4*9*15+2*8*17+0*6*19 4 76 2
13*16+8*20+5*9*15+2*7*18+1*6*19 4 78 2
14*16+9*20+5*8*17+4*7*18+3*6*19 4 82 2
11*20+6*10*16+3*14*15+1*13*17+0*12*18 5 89 3
16^2+9^2*15+8^2*17+7^2*18+6^2*19 4 90 2
12*20+7*10*16+4*14*15+2*13*17+0*11*19 5 90 3
13*20+8*10*16+5*14*15+2*12*18+1*11*19 5 92 3
14*20+9*10*16+5*13*17+4*12*18+3*11*19 5 96 3
16*20+9*14*15+8*13*17+7*12*18+6*11*19 5 104 3
20^2+9^2*10*15+8^2*10*17+7^2*10*18+6^2*10*19+5^2*15*17+4^2*15*18+3^2*15*19+2^2*17*18+1^2*17*19+0^2*18*19 6 118 4
relation, dimension, degree, weight の順に並んでいます。
結果を見ると all 1 7 で良かったことが分かります。これなら約3分で終了します。
all 1 8 なら約10分で終了します。all 1 10 なら約60分でメモリーが足りなくなって異常終了します。
計算時間を犠牲にして、必要最小限度のデータを記憶するようにして使用記憶容量が少なくてすむように
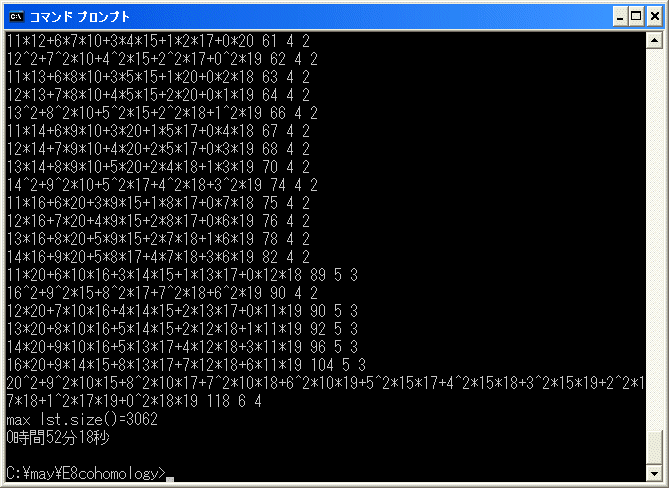
修正した all.exe を使って計算すると all 1 5 で4秒、all 1 6 で22秒、
all 1 7 で1分47秒、all 1 8 なら8分39秒、all 1 9 なら52分18秒かかります。
必要記憶容量の目安になる最大要素数は all 1 5 では 90, all 1 6 では 248,
all 1 7 では 616, all 1 8 では 1377, all 1 9 では 3062 で、
それぞれ概数ですが 90*5, 248*6, 616*7, 1377*8,
3062*9 に比例したメモリーが必要だったと思われます。大して計算時間が変わっていないように見えますが、
探索する範囲が広がれば広がるほど無駄な同じ計算を繰り返しますから、これから先の計算では
原理的に計算時間が大量に必要になり計算時間は改善されていません。尤も計算出来なければ話に
なりませんから、これは以下の計算のためには必要不可欠な改良になっています。
つぎのステップは微分代数 E2 term を決定するために、代数構造は分かりましたから、微分を決定します。
indecomposable elements 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 16 は weight が1以下ですから
微分 d2 は 0 です。したがって、
10 : [x15/x15], 15 : [x23/x23], 16 : [x5^4/x27]+[x23/x3^8]+[x17/x15^2]+[x9^2/x29], 17 : [x27/x27],
18 : [x29/x29], 19 : [x15^2/x15^2], 20 : [x15/x5^4/x27]+[x15/x23/x3^8]+[x3^4/x23/x27]+[x15/x9^2/x29]
+[x3^2/x27/x29]+[x5/x27/x15^2]+[x3/x29/x15^2]+[x9/x23/x15^2]+[x5^2/x23/x29]+[x15/x17/x15^2] の微分を
決定すればいいです。
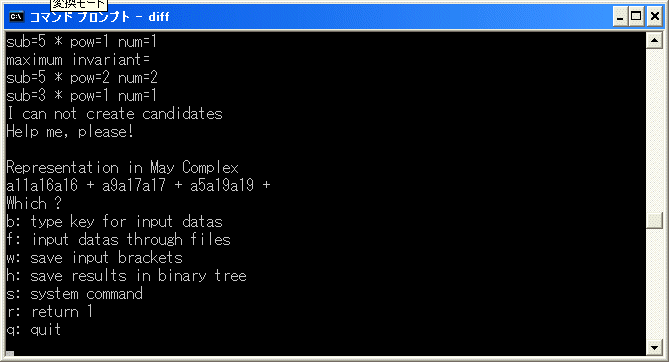
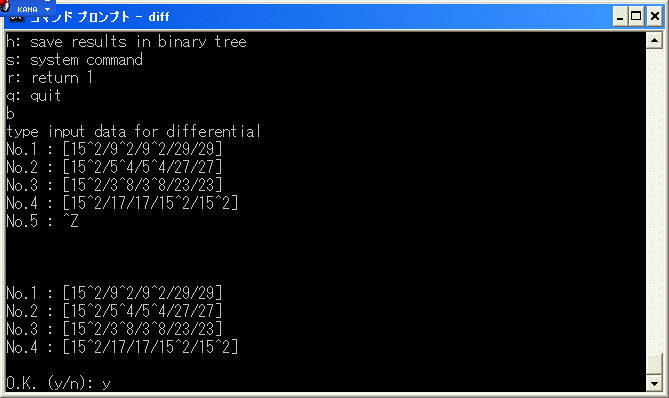
d2(10) を決定します。diff.exe を使います。diff.exe を実行します。b を選択し、[15/15] を入力します。
y を入力すると計算を始めます。直ちに停止します。
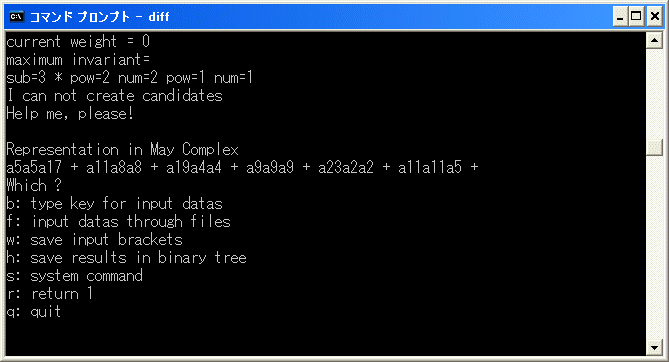
a5a5a17+a11a8a8+a19a4a4+a9a9a9+a23a2a2+a11a11a5 は weight 0 の元で、cocycle ですから
d2(10)=2^2*7+5*3^2+8*1^2+4^3+9*0^2+5^2*2 であることが分かりました。
d2(15) を決定します。diff.exe を実行します。b を選択し、 [x23/x23] を入力します。
y を入力すると計算を始めます。直ちに停止します。
a11a16a16+a9a17a17+a5a19a19 は weight 0 の元で、cocycle ですから
d2(15)=5*6^2+4*7^2+2*8^2 であることが分かりました。
d2(16) を決定します。diff.exe を実行します。b を選択し、 [x5^4/x27]+[x23/x3^8]+[x17/x15^2]+[x9^2/x29] を
入力します。
y を入力すると計算を始めます。直ちに停止します。
cocycle と表示して終了したので、16 は permanent cocycle です。
d2(17) を決定します。diff.exe を実行します。b を選択し、 [x27/x27] を入力します。
y を入力すると計算を始めます。直ちに停止します。
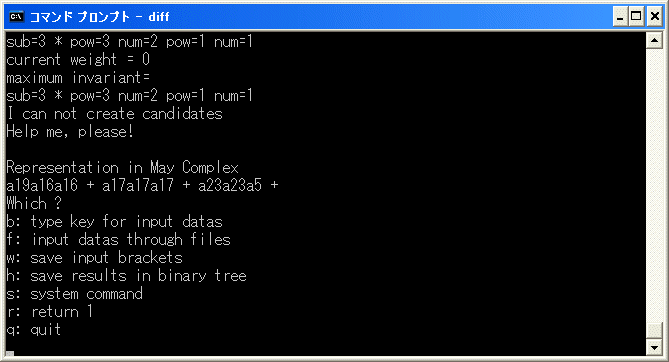
a19a16a16+a17a17a17+a23a23a25 は weight 0 の元で、cocycle ですから
d2(17)=8*6^2+7^3+9^2*2 であることが分かりました。
d2(18) を決定します。diff.exe を実行します。b を選択し、[x29/x29] を入力します。
y を入力すると計算を始めます。直ちに停止します。
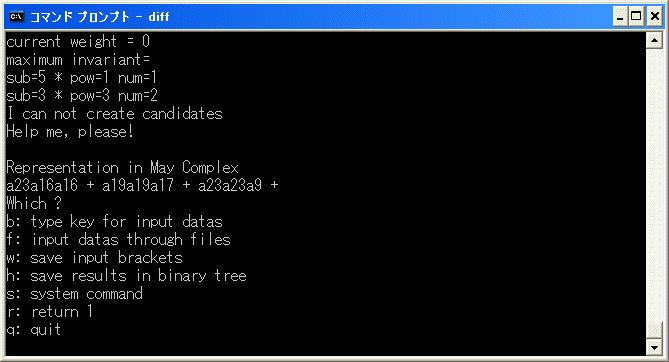
a23a16a16+a19a19a17+a23a23a9 は weight 0 の元で、cocycle ですから
d2(18)=9*6^2+8^2*7+9^2*4 であることが分かりました。
d2(19) を決定します。diff.exe を実行します。b を選択し、[x15^2/x15^2] を入力します。
y を入力すると計算を始めます。直ちに停止します。
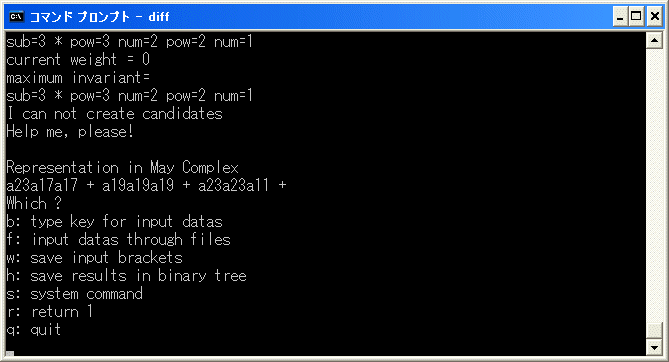
a23a17a17+a19a19a19+a23a23a11 は weight 0 の元で、cocycle ですから
d2(19)=9*7^2+8^3+9^2*5 であることが分かりました。
d2(20) を決定します。diff.exe を実行します。b を選択し、
[x15/x5^4/x27]+[x15/x23/x3^8]+[x3^4/x23/x27]+[x15/x9^2/x29]
+[x3^2/x27/x29]+[x5/x27/x15^2]+[x3/x29/x15^2]+[x9/x23/x15^2]+[x5^2/x23/x29]+[x15/x17/x15^2] を入力します。
y を入力すると計算を始めます。直ちに停止します。
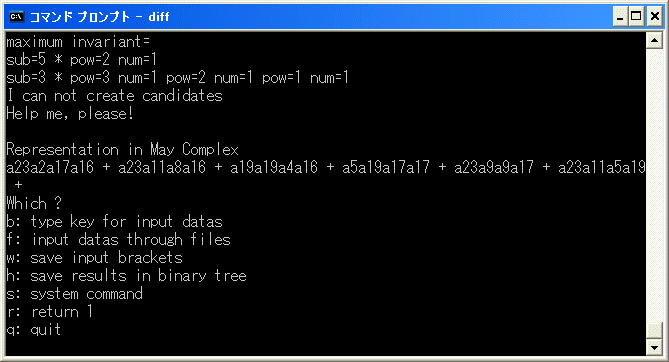
a23a2a17a16+a23a11a8a16+a19a19a4a16+a5a19a17a17+a23a9a9a17+a23a11a5a19 は weight 0 の元で、cocycle ですから
d2(20)=9*0*7*6+9*5*3*6+8^2*1*6+2*8*7^2+9*4^2*7+9*5*2*8 であることが分かりました。
E4 term を計算する準備が整いました。
次の gen.dat は上で計算した ind.dat を書き換えて、次のようにします。
2 1 0 0 E
4 1 0 1 E
5 1 0 2 E
8 1 0 3 E
9 1 0 4 E
11 1 0 5 E
16 1 0 6 E
17 1 0 7 E
19 1 0 8 E
23 1 0 9 E
28 2 2 10 2^2*7+5*3^2+8*1^2+4^3+9*0^2+5^2*2
30 2 1 11 E
31 2 1 12 E
33 2 1 13 E
37 2 1 14 E
44 2 2 15 5*6^2+4*7^2+2*8^2
45 2 1 16 E
52 2 2 17 8*6^2+7^3+9^2*2
56 2 2 18 9*6^2+8^2*7+9^2*4
58 2 2 19 9*7^2+8^3+9^2*5
59 3 2 20 9*0*7*6+9*5*3*6+8^2*1*6+2*8*7^2+9*4^2*7+9*5*2*8
また、次の rel.dat は上で計算した def.dat を書き換えて、次のようにします。
13 2 0 2*3+1*4+0*5
21 2 0 2*6+1*7+0*8
25 2 0 4*6+3*7+0*9
27 2 0 5*6+3*8+1*9
28 2 0 5*7+4*8+2*9
35 3 1 2*11+1*12+0*13
39 3 1 4*11+3*12+0*14
41 3 1 5*11+3*13+1*14
42 3 1 5*12+4*13+2*14
47 3 1 7*11+6*12+0*16
49 3 1 8*11+6*13+1*16
50 3 1 8*12+7*13+2*16
53 3 1 9*11+6*14+3*16
54 3 1 9*12+7*14+4*16
56 3 1 9*13+8*14+5*16
60 4 2 11^2+6^2*10+3^2*15+1^2*17+0^2*18
61 4 2 11*12+6*7*10+3*4*15+1*2*17+0*20
62 4 2 12^2+7^2*10+4^2*15+2^2*17+0^2*19
63 4 2 11*13+6*8*10+3*5*15+1*20+0*2*18
64 4 2 12*13+7*8*10+4*5*15+2*20+0*1*19
66 4 2 13^2+8^2*10+5^2*15+2^2*18+1^2*19
67 4 2 11*14+6*9*10+3*20+1*5*17+0*4*18
68 4 2 12*14+7*9*10+4*20+2*5*17+0*3*19
70 4 2 13*14+8*9*10+5*20+2*4*18+1*3*19
74 4 2 14^2+9^2*10+5^2*17+4^2*18+3^2*19
75 4 2 11*16+6*20+3*9*15+1*8*17+0*7*18
76 4 2 12*16+7*20+4*9*15+2*8*17+0*6*19
78 4 2 13*16+8*20+5*9*15+2*7*18+1*6*19
82 4 2 14*16+9*20+5*8*17+4*7*18+3*6*19
89 5 3 11*20+6*10*16+3*14*15+1*13*17+0*12*18
90 4 2 16^2+9^2*15+8^2*17+7^2*18+6^2*19
90 5 3 12*20+7*10*16+4*14*15+2*13*17+0*11*19
92 5 3 13*20+8*10*16+5*14*15+2*12*18+1*11*19
96 5 3 14*20+9*10*16+5*13*17+4*12*18+3*11*19
104 5 3 16*20+9*14*15+8*13*17+7*12*18+6*11*19
118 6 4 20^2+9^2*10*15+8^2*10*17+7^2*10*18+6^2*10*19+5^2*15*17+4^2*15*18+3^2*15*19+2^2*17*18+1^2*17*19+0^2*18*19
本来はこの微分代数のホモロジーの indecomposable elements と defining relations が存在しうる範囲を
予想し、コマンドプロンプトで
all 2 20
ぐらいを実行すべきですが、いままで使っていた all.exe では all 1 9 が限界でしたので、
ここでは計算時間を犠牲にして、使用記憶容量が少なくてすむように修正した all.exe を
使って all 2 11 を計算します。
ここで、2 は E2 term のホモロジーを計算するので differential の weight の差 2 を指定します。
148時間59分24秒で終了します。どの程度の結果が得られているか調べてみます。
ind.dat は次のようになっています。
0 0 1 2 0
1 1 1 4 0
2 2 1 5 0
3 3 1 8 0
4 4 1 9 0
5 5 1 11 0
6 6 1 16 0
7 7 1 17 0
8 8 1 19 0
9 9 1 23 0
10 11 2 30 1
11 12 2 31 1
12 13 2 33 1
13 14 2 37 1
14 16 2 45 1
15 6*15+3*17+1*18+0*19 3 60 2
16 7*15+4*17+2*18 3 61 2
17 8*15+5*17+2*19 3 63 2
18 9*15+5*18+4*19 3 67 2
19 9*17+7*19+8*18 3 75 2
20 10^2 4 56 4
21 15^2 4 88 4
22 15*16+14*17+12*19+13*18 4 89 3
23 17^2 4 104 4
24 18^2 4 112 4
25 19^2 4 116 4
26 9*15*17+2*18*19+4*17*19+8*15*18+5*17*18+7*15*19 5 119 4
27 9^2*10*15+8^2*10*17+6^2*10*19+5^2*15*17+3^2*15*19+7^2*10*18+1^2*17*19+0^2*18*19+2^2*17*18+4^2*15*18 6 118 4
28 6^2*10*20+3*11*14*15+1^2*17*20+1*6*8*10*17+0*3*4*15*18+0*11*12*18 7 119 4
29 7^2*10*20+4*12*14*15+2^2*17*20+0*3*4*15*19+0*11*12*19+2*7*8*10*17 7 121 4
30 8^2*10*20+2^2*18*20+1*3*5*15*19+1*11*13*19+2*7*8*10*18+5*13*14*15 7 125 4
31 9^2*10*20+5*13*14*17+4^2*18*20+4*7*9*10*18+1*3*5*17*19+3*11*14*19 7 133 4
32 5*8^2*15*18+7^2*18*20+3*6*9*15*19+1*6*8*17*19+6*11*16*19+2*8*9*15*19+2*5*8*18*19+4*8^2*15*19+5*9*18*20+3^2*8*18*19+1*3*9*18*19+4^2*7*18*19+4*9*19*20+8*13*16*17 7 149 4
33 9^2*10*15*20+8^2*10*17*20+7^2*10*18*20+6^2*10*19*20+1*11*13*17*19+2*12*13*17*18+3*11*14*15*19+4*12*14*15*18+5*13*14*15*17+0*11*12*18*19 9 177 6
E4 term の indecomposable elements が34個見つかっています。最後のものが dim = 9 なので、
多分全部見つかっていると思います。
def.dat は次のようになっています。
2*3+1*4+0*5 2 13 0
2*6+1*7+0*8 2 21 0
4*6+3*7+0*9 2 25 0
5*6+3*8+1*9 2 27 0
4^3+3^2*5+2*5^2+1^2*8+0^2*9+2^2*7 3 27 0
5*7+4*8+2*9 2 28 0
2*10+1*11+0*12 3 35 1
4*10+3*11+0*13 3 39 1
5*10+3*12+1*13 3 41 1
5*11+4*12+2*13 3 42 1
4*7^2+2*8^2+1*6*9+3*6*8 3 43 0
7*10+6*11+0*14 3 47 1
8*10+6*12+1*14 3 49 1
8*11+7*12+2*14 3 50 1
7^3+6^2*8+2*9^2 3 51 0
9*10+6*13+3*14 3 53 1
9*11+7*13+4*14 3 54 1
7*8^2+6^2*9+4*9^2 3 55 0
9*12+8*13+5*14 3 56 1
8^3+7^2*9+5*9^2 3 57 0
4^2*7*9+2*7^2*8+2*5*8*9+1*6*8^2+1*3*9^2+0*6*7*9+3^2*8*9 4 58 0
2*15+1*16+0*17 4 65 2
4*15+3*16+0*18 4 69 2
5*15+3*17+1*18 4 71 2
4*11^2+2*12^2+2^2*16+1*10*13+1^2*17+3*10*12+0^2*18 5 71 2
5*16+4*17+2*18 4 72 2
7*15+6*16+0*19 4 77 2
8*15+6*17+1*19 4 79 2
7*11^2+4^2*16+2*13^2+1*10*14+3^2*17+6*10*12+0^2*19 5 79 2
8*16+7*17+2*19 4 80 2
9*15+6*18+3*19 4 83 2
4*13^2+3*10*14+2*5*18+1^2*19+7*12^2+3^2*18+6*10*13+4*5*17 5 83 2
9*16+7*18+4*19 4 84 2
8*12^2+5*13^2+5^2*17+4*11*14+2^2*19+4^2*18+7*11*13 5 85 2
9*17+8*18+5*19 4 86 2
4^2*11*13+2*7*11*12+1*3*13^2+1*6*12^2+1*3*5*17+1^2*12*14+3^2*12*13+2*4^2*17+2*5*12*13+2^2*4*18+0*3*4*18+0*6*11*13+0*2*8*15+0*2*6*17+0^2*13*14+0*4*10*14 6 86 2
11*15+10*16+0*22 5 91 3
12*15+10*17+1*22 5 93 3
12*16+11*17+2*22 5 94 3
7^2*16+2*14^2+6^2*17 5 95 2
13*15+10*18+3*22 5 97 3
13*16+11*18+4*22 5 98 3
4*14^2+7*8*17+6^2*18+2*8*19 5 99 2
13*17+12*18+5*22 5 100 3
8^2*17+5*14^2+7^2*18 5 101 2
4*7*11*14+3*6*12*14+2*8*12*14+1*9*10*14+1*6*8*17+1*3*14^2+0*6*7*18+2*7^2*17+2^2*7*19 6 102 2
14*15+10*19+6*22 5 105 3
14*16+11*19+7*22 5 106 3
7*14^2+6^2*19+4*9*19+7*9*18 5 107 2
14*17+12*19+8*22 5 108 3
8*14^2+7^2*19+5*9*19+8*9*18 5 109 2
7^2*11*14+6^2*12*14+5*9*11*14+4*9*12*14+4^2*7*19+3*5*6*19+2*8^2*18+1*6*14^2+1*6*9*18+0*6*7*19 6 110 2
14*18+13*19+9*22 5 112 3
9*14^2+9^2*18+8^2*19 5 113 2
4*9*13*14+4*8*9*17+1*6*8*19+2*8*9*18+7*8*12*14+3*6*9*18+3*6*14^2+6^2*13*14 6 114 2
8^2*12*14+5*9*13*14+5^2*8*19+7^2*13*14+3*6*7*19+0*6*9*19+4^2*9*19+2*7*8*19+5*8^2*18 6 116 2
15^2+6^2*21+3^2*23+1^2*24+0^2*25 6 120 4
10^4+6^4*20+3^4*21+1^4*23+0^4*24 8 120 4
15*16+6*7*21+3*4*23+1*2*24+0*26 6 121 4
10^3*11+6^3*7*20+3^3*4*21+1^3*2*23+0*28 8 121 4
16^2+7^2*21+4^2*23+2^2*24 6 122 4
10^2*11^2+6^2*7^2*20+3^2*4^2*21+0^2*27+1^2*2^2*23 8 122 4
15*17+6*8*21+3*5*23+1*26+0*2*25 6 123 4
11^2*16+4^2*7*21+2*27+3^2*8*21+1^2*5*23+10^2*17+2^2*4*23+0^2*26 7 123 4
10*11^3+1*2^3*23+0*29+2*6*9^2*20+3^3*5*21+1*4*5^2*21+1*2*4*7*21+0*5^3*21+0*2*4*8*21+0*2^2*9*21+1^2*3*8*21+0^2*3*9*21+6^3*8*20 8 123 4
10^3*12+1*28+6^3*8*20+3^3*5*21+0^3*2*24 8 123 4
16*17+7*8*21+4*5*23+2*26 6 124 4
10^2*11*12+2*28+0*1*27+3^2*4*5*21+6^2*7*8*20 8 124 4
11^4+6^2*7*8*20+2*7*9^2*20+2^4*23+3^2*4*5*21+1^2*2*9*21+0^2*4*9*21+1^2*5*7*21+2^2*4*7*21+2*4*5^2*21+0^4*25 8 124 4
10*11^2*12+6*7^2*8*20+3*4^2*5*21+1*29+0*2*27 8 125 4
17^2+8^2*21+5^2*23+2^2*25 6 126 4
10^2*12^2+3^2*5^2*21+1^2*27+0^2*2^2*24+6^2*8^2*20 8 126 4
11^3*12+6^2*8^2*20+2*8*9^2*20+0^3*1*25+2*29+3^2*5^2*21+2*5^3*21+2^2*4*8*21+2^3*9*21+1^2*5*8*21+0^2*5*9*21 8 126 4
15*18+6*9*21+3*26+1*5*24+0*4*25 6 127 4
4*27+2*12*22+2^3*24+1^2*26+0^2*5*24+2*5*9*21+4*5*8*21+11*12*17+3^2*9*21+10^2*18 7 127 4
10*11*12^2+3*4*5^2*21+1*2*27+3*7*9^2*20+0*9^3*20+6^3*9*20+0*30 8 127 4
10^3*13+3*28+6^3*9*20+0^3*4*24+1^3*5*23 8 127 4
16*18+7*9*21+4*26+2*5*24 6 128 4
10^2*11*13+4*28+0*3*27+1^2*2*5*23+6^2*7*9*20 8 128 4
11^2*12^2+6^2*7*9*20+4*7*9^2*20+4^2*5^2*21+0^2*1^2*25+2^2*27 8 128 4
12^2*17+5*27+4^2*9*21+2^2*26+0^2*4*25+11^2*18+5^2*8*21+1^2*2*25 7 129 4
10*11^2*13+3*29+1*2^2*5*23+6*7^2*9*20+0*2*12*22+0*2*5*9*21+0*1*15*17+0*1*6*8*21+0*1*3*5*23+0^3*5*24+0*2^3*24+0*3^2*9*21+0*4*5*8*21+0*10^2*18+0*11*12*17+0^2*1*2*25 8 129 4
10*12^3+3*5^3*21+1*30+0*2^3*24+3*8*9^2*20+1*9^3*20+6*7^2*9*20 8 129 4
17*18+8*9*21+5*26+2*4*25 6 130 4
10^2*12*13+2*30+2*11^2*17+2^2*11*22+2*4^2*8*21+2^2*4*9*21+1*3*27+0^2*2*4*24+1*3*5*8*21+1*10*12*17+0*3*4*9*21+0*2*6*8*21+0*1*16*17+0^2*17^2+0^2*2^2*25+0*10*11*18+0^2*5^2*23+0*1*4*5*23+4*29+6^2*8*9*20 8 130 4
11*12^3+4*5^3*21+6^2*8*9*20+4*8*9^2*20+0*1^3*25+2*30 8 130 4
11^3*13+4*29+6^2*8*9*20+4*8*9^2*20+5*7*9^2*20+2^3*5*23+0^3*3*25 8 130 4
5*28+2*30+2*11^2*17+2^2*11*22+2*4^2*8*21+2^2*4*9*21+1*3*5*8*21+1*10*12*17+0*3*4*9*21+0*2*6*8*21+0*1*16*17+0^2*17^2+0^2*2^2*25+0*10*11*18+0^2*5^2*23+0*1*4*5*23+4*29 8 130 4
11^2*12*13+5*29+7^2*8*9*20+2*4*27+0^2*1*3*25 8 132 4
12^4+7^2*8*9*20+5*8*9^2*20+5^4*21+1^4*25+2^2*16^2+2^2*7^2*21+2^2*4^2*23 8 132 4
10*12^2*13+6*8^2*9*20+3*30+1*5*27+0*2^2*4*24 8 133 4
18^2+9^2*21+5^2*24+4^2*25 6 134 4
10^2*13^2+6^2*9^2*20+3^2*27+0^2*4^2*24+1^2*5^2*23 8 134 4
11*12^2*13+4*30+4*9^3*20+6^2*9^2*20+0*1^2*3*25+2*5*27 8 134 4
15*19+6*26+3*9*23+1*8*24+0*7*25 6 135 4
7*27+11*13*18+4*13*22+2*4^2*24+1^2*9*23+0^2*8*24+3^2*26+4*5^2*23+10^2*19 7 135 4
10*11*13^2+6*7*9^2*20+4*12^2*15+2*10*12*18+0*31+0*2*16*18+0*2*7*9*21+0*2*4*26+0^2*3*5*24+1*11*12*18+1*2^2*4*24+1^2*15*18+1^2*6*9*21+1^3*5*24+0*1*2*3*25+0^2*1*5*25+3^3*9*21+3*5^2*7*21+1*2*5^2*23+3*10^2*18 8 135 4
10^3*14+6*28+3^3*9*21+1^3*8*23+0^3*7*24 8 135 4
16*19+7*26+4*9*23+2*8*24 6 136 4
10^2*11*14+7*28+3^2*4*9*21+1^2*2*8*23+0*6*27 8 136 4
11^2*13^2+7^2*9^2*20+4*12^2*16+3*11*13*15+3*4*10*22+0*13^2*15+2^3*4*24+4^2*5*8*21+3^2*4*9*21+2*4*5*9*21+2^2*5^2*23+1*2*15*18+1*2*6*9*21+1^2*2*5*24+0*5*15*17+0*5*6*8*21+0*3*5^2*23+0*2^2*3*25+0^2*3^2*25+0^2*4*5*24 8 136 4
12^3*13+5*30+5*9^3*20+7^2*9^2*20+2^3*4*24+1^3*3*25 8 136 4
8*27+12*13*18+5*13*22+4^2*26+2^2*9*23+1*3*4*25+0*3*5*25+5^3*23+11^2*19+0^2*7*25 7 137 4
10*11^2*14+6*29+1*2^2*8*23+3*4^2*9*21+0*11*13*18+0*4*13*22+0*4*5^2*23+0*10^2*19+0*3^2*26+0*2*4^2*24+0*1*5*6*23+0^3*8*24+0*1*3*8*23 8 137 4
10*12*13^2+6*8*9^2*20+1*31+3*5*27+0*2*4^2*24 8 137 4
17*19+8*26+5*9*23+2*7*25 6 138 4
10^2*12*14+1*10*13*18+0^2*2*7*24+1*3*5^2*23+0*10*11*19+0*2*3*8*23+0*3*4*26+4^2*11*22+2*4^2*5*23+0*2*5*6*23+1*6*27+2*31+3*5*10*22+2*12^2*18+0^2*18^2+1^2*17*18+2^2*16*18+7*29+3^2*5*9*21 8 138 4
11*12*13^2+7*8*9^2*20+0*1*3^2*25+2*31+4*5*27 8 138 4
11^3*14+7*29+3^2*5*9*21+2^3*8*23+2*5^2*9*21+1^2*8*9*21+0^2*9^2*21+2^2*7*9*21+0^3*6*25 8 138 4
8*28+1*10*13*18+1*3*5^2*23+0*10*11*19+0*2*3*8*23+0*3*4*26+4^2*11*22+2*4^2*5*23+0*2*5*6*23+2*31+3*5*10*22+2*12^2*18+0^2*18^2+1^2*17*18+2^2*16*18+7*29 8 138 4
11^2*12*14+8*29+4^2*5*9*21+0^2*1*6*25+2*7*27 8 140 4
12^2*13^2+8^2*9^2*20+2^2*4^2*24+1^2*3^2*25+5^2*27 8 140 4
13^2*18+9*27+4^2*5*24+3^2*4*25+5^2*26+1^2*7*25+12^2*19+2^2*8*24 7 141 4
10*12^2*14+6*30+3*5^2*9*21+1*5*13*22+1*4*16*18+1*4*7*9*21+1*2^2*9*23+1^2*3*4*25+0*1*3*5*25+0^2*1*7*25+1*5^3*23+1*11^2*19+1*12*13*18+1*2*4*5*24+0*2^2*7*24 8 141 4
10*13^3+6*9^3*20+3*31+0*8*15^2+0*6^2*8*21+0*3^2*8*23+0*3^2*5*24+0*5*16*18+0*5*7*9*21+0*4*5*26+0^3*9*24+0^2*2*6*25+0^2*1*7*25+1*5^3*23+0*2^2*7*24 8 141 4
18*19+9*26+5*8*24+4*7*25 6 142 4
10^2*13*14+4*31+3*6*27+3*10*13*18+0*3*4*5*24+0*1*2*8*24+1*3*17*18+0*2*3*5*25+1*5*6*9*21+1^2*18^2+1^2*5^2*24+1*10*12*19+1^2*5*8*23+2^2*4*5*24+0^2*4*7*24+4*12*13*17+7*30+2*12*13*18+0^2*5^2*25 8 142 4
11*12^2*14+7*30+4*5^2*9*21+0*1^2*6*25+2*12*13*18+2*11^2*19+2*5*13*22+2*4^2*26+1^2*4^2*25+0^2*5^2*25+2*5^3*23+2^3*9*23+0^2*2*7*25 8 142 4
11*13^3+7*9^3*20+4*31+0*3^3*25+2*5^3*23 8 142 4
9*28+4*31+3*10*13*18+0*3*4*5*24+0*1*2*8*24+1*3*17*18+0*2*3*5*25+1*5*6*9*21+1^2*18^2+1^2*5^2*24+1*10*12*19+2^2*4*5*24+4*12*13*17+7*30+2*12*13*18+0^2*5^2*25 8 142 4
11^2*13*14+5*31+5^2*12*22+5*12^2*18+2^2*5*8*23+1^2*4*5*25+0*1*5^2*25+2*4*17*18+2*4*8*9*21+1*2*15*19+0*8*15*17+0*6*17^2+0*2^2*6*25+4^2*13*22+2^2*9^2*21+2*11*12*19+0^2*2*8*25+0^2*3*6*25+0^2*5*7*24+1^2*7*26+3^2*4*26+1*3*4*5*24+0*3*18^2+0*3*9^2*21+4^2*5^2*23+2^2*18^2+4*10^2*19+8*30+2^3*7*24 8 144 4
12*13^3+8*9^3*20+1*3^3*25+1^2*4*9*23+0^2*4*8*24+1^2*7*26+2^3*7*24+2^2*5^2*24+1*3*4*5*24+0*3*18^2+0*3*9^2*21+0*3*4^2*25+0^2*5*7*24+1*2*15*19+0*8*15*17+0*6*17^2+5*31 8 144 4
12^3*14+8*30+5^3*9*21+2^3*7*24+1^3*6*25 8 144 4
9*29+5*31+5^2*12*22+5*12^2*18+1^2*4*5*25+0*1*5^2*25+2*4*17*18+2*4*8*9*21+1*2*15*19+0*8*15*17+0*6*17^2+0*2^2*6*25+4^2*13*22+2^2*9^2*21+2*11*12*19+0^2*2*8*25+8*30+0*3*14*22+0*9*10*22+3^2*16*18+0*3*4^2*25+3*10*14*16+4^2*17^2+2^2*5^2*24+6*11*13*15+7*12^2*16 8 144 4
12^2*13*14+9*30+5*11^2*19+2^2*4*7*24+4^2*17*18+4^2*8*9*21+5^2*13*22+5^4*23+5*12*13*18+1^2*2*8*25+2^2*5^2*25+0^2*4*8*25+2^2*17*19+2^2*8*26+1^2*3*6*25 8 148 4
13^4+9^4*20+3^4*25+5^4*23+3^2*4*5*24+2*7*17^2+2*6^2*9*21+2*4*18^2+1*3*4*5*25+0*3*5^2*25+0^2*5*7*25+1^2*2*8*25+2^2*5^2*25+1^2*4*8*24+0^2*4*9*24+2^2*4*7*24+0^2*4*8*25+2*4*5*8*23+2^2*17*19+2^2*8*26+2^3*7*25 8 148 4
15*22+10*26+6*14*21+3*13*23+1*12*24+0*11*25 7 149 5
10*13^2*14+6*31+3*9*27+1*5^2*8*23+0*4^2*7*24 8 149 4
10*28+6^3*14*20+3^3*13*21+1^3*12*23+0^3*11*24 9 149 5
19^2+9^2*23+8^2*24+7^2*25 6 150 4
16*22+11*26+7*14*21+4*13*23+2*12*24 7 150 5
10^2*14^2+6^2*27+0^2*7^2*24+3^2*9^2*21+1^2*8^2*23 8 150 4
11*13^2*14+7*31+0*3^2*6*25+2*5^2*8*23+4*5^2*26+4*12^2*19+8*12*13*16+6*13^2*15+4*5*17*18+2*5*18^2+1^2*18*19+1^2*5*8*24+0^2*5*9*24+2*5^3*24+3^2*9^2*21+2^2*4*8*24+2^2*5*7*24+1^2*4*7*25+3^2*14*22+3*10*13*19+4*12*14*17+5*11*12*19+2*9*12*22 8 150 4
11*28+6^2*7*14*20+3^2*4*13*21+0*10*27+1^2*2*12*23 9 150 5
11*14*19+7*14*22+2*7^2*24+6^2*26+4*8^2*23+7*18^2+4*18*19+4*9*26+2*5*9*24 7 151 4
10*11*14^2+7*13^2*15+0*9*13*22+0*32+0*2*4*9*24+1*4^2*7*24+0^2*6*8*24+1^2*6*9*23+1*2*8^2*23+1*5*16*19+1*5*7*26+3*8*16*17+1*8*16*18+1*7*8*9*21+1*3*5*6*24+6*10^2*19+3*6*15*18 8 151 4
10*29+6*7^2*14*20+3*4^2*13*21+0*11*27+1*2^2*12*23 9 151 5
17*22+12*26+8*14*21+5*13*23+2*11*25 7 152 5
11^2*14^2+0^2*6^2*25+0^2*7*8*24+1*2*6*9*23+0*3*8^2*23+0*5*6*8*23+2^2*8^2*23+2*4^2*7*24+2*5*16*19+2^2*5*8*24+3*4*15*19+1*4*5*6*24+0*6*18^2+0*3*5*8*24+4*8*16*17+3*9*15*16+0^2*4*9*25+2^2*9*26+6*11*14*15+6*7*10*22+0*14^2*15+7*13^2*16 8 152 4
12*13^2*14+8*31+1*3^2*6*25+8*12*13*17+7*13^2*16+5*12*14*17+5^2*8*9*21+4^2*14*22+4*8*16*17+4^2*5*8*23+3*9*15*16+3^2*4*9*23+1^2*4*9*24+0*9*15*18+2*5*7*26+4*11*13*19+1^2*2*9*25+2*4^2*7*24 8 152 4
11*29+6^2*8*14*20+2^3*12*23+3^2*5*13*21+0*4*6*13*21+0*3*7*13*21+1^2*8*13*21+2^2*7*13*21+2*5^2*13*21+2*9^2*14*20+0^3*10*25 9 152 5
12*28+0^2*2*11*24+1*10*27+6^2*8*14*20+3^2*5*13*21 9 152 5
12*14*19+8*14*22+5*8^2*23+1*6*7*25+0*6*8*25+7^2*26+8*18^2+5*18*19+5*9*26+2*4*9*25 7 153 4
10*12*14^2+8*13^2*15+1*9*13*22+0*3*5*6*25+1*32+1*5*17*19+1*2*5*7*25+0^2*6*7*25+2^2*6*9*23+0*2*7^2*24+3*4*16*19+0*4*5*8*24+3*8*17^2+1*8*17*18+1*8^2*9*21+1*5*8*26+0*2*5*8*25+3*9*16^2+0*9*16*18+0*7*9^2*21+6*11*14*16+6*7*11*22 8 153 4
11*12*14^2+8*13^2*16+5*11*13*19+4*12*13*19+7^2*11*22+2*4*7*8*23+0*1*4*9*25+1*10*14*19+0*6*7*26+6*12*14*15+1*14^2*15+4^2*16*19+0^2*19^2+0*2*6*8*24+4*8*17^2+1*9*15*18+0*1*7*8*24+0*1*6^2*25+1*5^2*6*24+1*3*8^2*23+3*9*15*17+1^2*5*9*24+0*4*5*6*25+1*6*18^2+2^3*9*25+2*4^2*8*24+2^2*5*7*25 8 154 4
2*32+7^2*11*22+6*8*10*22+4^2*16*19+0^2*19^2+1*9*15*18+2*4*7*8*23+1^2*8*9*23+1*5^2*6*24+1*3*8^2*23+1*10*14*19+3*5*15*19+2*8*17*18+0*6*7*26+0*4*5*6*25+2*9*13*22+2*4*5*7*24+2^2*5*7*25+2^3*9*25 8 154 4
12*29+7^2*8*14*20+4^2*5*13*21+0^2*1*10*25+2*11*27 9 154 5
10*30+6*8^2*14*20+3*5^2*13*21+1*12*27+0*2^2*11*24 9 155 5
18*22+13*26+9*14*21+5*12*24+4*11*25 7 156 5
12^2*14^2+1^2*6^2*25+0^2*7*8*25+2^2*8*9*23+4*5*16*19+4^2*5*9*23+2*9*16*18+1*2*3*9*25+1*6*7*26+0*6*8*26+2*4*8^2*23+5^3*8*23+2*5^2*7*24+5^2*9^2*21+7*8*11*22+7*12*14*16+8*13^2*17+1*4*5*6*25+0*5^2*6*25 8 156 4
13^3*14+9*31+5^3*8*23+3^2*5*7*24+2*5^2*7*24+1^2*7*8*24+0^2*7*9*24+2^2*7^2*24+3^3*6*25 8 156 4
11*30+6^2*9*14*20+4*9^2*14*20+4*5^2*13*21+0*1^2*10*25+2*12*27 9 156 5
13*28+0^2*4*11*24+1^2*5*12*23+3*10*27+6^2*9*14*20 9 156 5
13*14*19+9*14*22+9^3*21+4*7*8*24+2*7*9*24+8^2*26+3*6*7*25+0*6*9*25 7 157 4
10*13*14^2+6*9*27+3*13^2*19+3*5*17*19+3*4*5*7*24+3^3*7*25+0*3^2*9*25+1*4*5*7*25+0*5^2*7*25+3*32+1*5*8^2*23+3*9*13*22+3*5^2*9*23+0*2*8^2*24+0*5*6^2*24 8 157 4
11*13*14^2+7*9*27+6*13*14*15+4*5^2*9*23+3*14^2*15+3^2*18*19+0*3*6^2*25+7*12*14*17+4*9*17^2+2*7^2*26+1*6*8*26+0*3*7*8*24+0*2*6*9*24+0^2*8*9*24+3*6*18^2+3^2*9*26+1*3*5*9*24+2*9*17*18+4^2*7*8*23+3^2*8^2*23+2*7*16*19+1^2*9^2*23+2*12*14*19+3*10*14*19+0*3*4*9*25+2*5*9*26 8 158 4
4*32+6*9*10*22+4*9*13*22+2*5^2*8*24+1^2*19^2+3^2*4*7*25+4^2*5*7*24+7*8*12*22+4*9*17^2+1*6*8*26+0*3*7*8*24+0*2*6*9*24+0^2*8*9*24+3*6*18^2+3^2*9*26+1*3*5*9*24+2*9*17*18+2*12*14*19+3*10*14*19+2^2*7*8*24 8 158 4
12*30+7^2*9*14*20+5*9^2*14*20+5^3*13*21+1^3*10*25+2^3*11*24 9 158 5
13*29+11^2*12*17+10^2*13*16+4^2*8*12*21+3^2*9*11*21+3*10*11*22+0*10*13*22+0^2*2*13*24+0^2*4*12*24+1*2*10*26+0*12*15*17+0*6*8*12*21+0*3*5*12*23+2^2*5*12*23+0^2*3*10*25+2*11*12*22+2*5*9*11*21+2*4*8*13*21+0^2*2*12*25+7^2*9*14*20+2^3*11*24 9 158 5
12*13*14^2+8*9*27+1^2*7*8*25+2^2*5*9*25+8^2*12*22+0*1*8^2*25+3*6*16*19+3^2*7*9*23+1^2*7*9*24+0*9*15*19+4^2*8^2*23+2*7*8*26+1*5*6*7*24+0*5*6*8*24+4*11*14*19+0*4*6*7*25+0^2*7*9*25+5*8*17*18+5^3*9*23+1*3*6^2*25+4^2*18*19+7*9*11*22+6^2*16*18+7^2*17^2+5*13^2*19 8 160 4
5*32+0*1*8^2*25+4*5^2*7*24+5*9*13*22+8^2*12*22+4*11*14*19+5*8*17*18+7*9*11*22+6^2*16*18+7^2*17^2+5^2*17*19+4^2*18*19+3^2*5*7*25+4^2*8^2*23+2*4*5*8*25+1^2*7*8*25+0*3*5*9*25+2*7*8*26+3*6*16*19+3^2*7*9*23+1^2*7*9*24+2^2*8^2*24+0*9*15*19+0*4*6*7*25+0^2*7*9*25 8 160 4
13*30+8^2*9*14*20+1^2*3*10*25+2^2*4*11*24+5*12*27 9 162 5
10*31+6*9^2*14*20+0*4^2*11*24+3*13*27+1*5^2*12*23 9 163 5
19*22+14*26+9*13*23+8*12*24+7*11*25 7 164 5
13^2*14^2+9^2*27+5^2*9*26+3^2*6^2*25+4*7*17*19+4^2*8*9*23+3^2*7*8*24+2*4*19^2+1*3*7*9*24+0*5*6*9*24+2*7*9*26+1*5*6*7*25+0*5*6*8*25+5*8*18^2+5^2*18*19+2*4*5*9*25+5*14^2*17 8 164 4
11*31+7*9^2*14*20+0*3^2*10*25+2*5*9*13*21+1^2*13*26+0^2*5*13*24+3^2*9*13*21+4*5^2*14*21+4*5*9*12*21+11*12*13*17+2*12*13*22+2^2*5*11*24+2^2*4*12*24+10^2*13*18+2*5^2*12*23 9 164 5
14*28+6*10*27+0^2*7*11*24+3^2*9*13*21+1^2*8*12*23 9 164 5
14^2*19+8^2*9*23+7^2*8*24+6^2*7*25+9^2*26 7 165 4
10*14^3+6*13*14*18+6*32+1*9*17*19+1*7^2*9*23+0*4*8^2*25+2^2*6*9*25+0*5*7*9*24+0*2*9^2*24+0*6^2*8*24+3*8*17*19+3*5*8*9*23+3*5*7^2*24+3^2*6*7*25+1*4*7*8*25+0*3*6*9*25+3*9^3*21 8 165 4
11*14^3+0*6^3*25+7*13*14*18+2*4*7*9*24+6*10*14*19+0*6*7*8*24+4*8*17*19+2*5*19^2+3*6*18*19+1*5*6*9*24+0*4*6*9*25+1*6*8*9*23+2*7^2*9*23+2^2*7*9*25+4*9*14*22 8 166 4
7*32+6*10*14*19+0*6*7*8*24+4*8*17*19+2*5*19^2+4*13*14*19+3*6*18*19+1*5*6*9*24+1*6*8*9*23+2*9*17*19+2*4*7*9*24 8 166 4
12*31+8*9^2*14*20+2*4^2*11*24+2*4*12*26+4^2*9*13*21+2*5*11*26+11^2*13*18+0^2*4*13*25+12^3*18+5*12^2*22+1^2*2*13*25+5^2*8*13*21+1*3^2*10*25 9 166 5
14*29+0^2*6*10*25+11^2*13*18+4*11*13*22+0*10*18^2+0*9^2*10*21+0*3*5*12*24+0^2*4*13*25+4^2*9*13*21+4*5^2*11*23+6*10*11*22+10^2*14*16+3*4*10*26+0*13*15*18+0*4^2*10*25+0*10*14*22+0*6*9*13*21+2^2*8*12*23+2*4^2*11*24+1*2*9*10*23+0*5*6*12*23+0*3*8*12*23+0^2*7*12*24+0^2*2*14*24 9 166 5
12*14^3+1*6^3*25+4*7*18*19+2*7*8*9*23+2*5*7*9*24+7^2*14*22+6^2*7*26+4^2*19^2+4^2*9^2*23+2^2*9^2*24+0*6*7^2*25+7^2*18^2+5*9*14*22+5*8*17*19+2^2*8*9*25+4*7*8^2*23+8*13*14*18+1*3*7*9*25+0*1*9^2*25+0*5*6*9*25 8 168 4
8*32+4*7*18*19+2*7*8*9*23+2*7^3*24+7^2*14*22+6^2*7*26+4^2*19^2+4^2*9^2*23+4*7*8^2*23+0*6*7^2*25+7^2*18^2+5*8*17*19+2^2*8*9*25+5*13*14*19+2^2*9^2*24+0*5*6*9*25 8 168 4
13*31+9^3*14*20+3^3*10*25+3^2*5*11*24+2*5^2*11*24+1^2*8*11*24+0^2*7*13*24+0^2*4*14*24+2^2*7*11*24+5^3*12*23 9 170 5
14*30+5^2*9*13*21+12^2*13*18+5*12*13*22+1*4*5*10*25+0*5^2*10*25+2^2*8*13*23+2^2*5*14*23+4*5*11*26+2*13*16*18+2*7*9*13*21+1*2*3*13*25+0^2*7*12*25+5^3*12*23+11^2*14*17+7*11*12*22+2*11*14*22+2^2*5*13*24+2^2*7*11*24+1^2*6*10*25 9 170 5
13*14^3+9^2*13*22+3*6^3*25+5*8*18*19+4^2*8*9*24+2*6^2*9*24+2*4*8*9*25+3^2*7*9*25+0*3*9^2*25+8^2*18^2+8^2*14*22+7^2*8*26+3*6*7*8*24+1*6*7*9*24+2*7*8^2*24+0*6*8^2*25+9*13^2*19 8 172 4
9*32+5*8^3*23+0*6*8^2*25+8^2*18^2+8^2*14*22+7^2*8*26+2*7*8^2*24+5^2*19^2+5^2*9^2*23+2^2*9^2*25 8 172 4
10*11*12*13*14+6*7*8*9*14*20+3*4*5*9*13*21+0*2^2*19*22+3*5^3*11*23+1^2*14*15*17+0*2*7*12*26+3^2*5*10*26+1*4^2*5*11*24+0*4^3*11*25+1^2*8*15*22+0*5^2*12*26+0*2*8*11*26+7*12^3*15+3*5*12*16*17+0*4*7*9*13*21+3*4*13*16^2+3^2*5*15*22+0*4*13*16*18+6*10*12*13*15+1*3*10*14*22+1*2*5*8*12*23+1*4*8^2*13*21+2^2*4*6*13*23+2*5^2*15*22+2*5*12*15*18+0*2*4*5*12*25+1*3*6*9*13*21+0^2*3*9*13*23+0*2*4*7*11*24+2*9*10*27+0*1*3*6*10*25+0^2*6*9*14*21+0*5^3*13*23+1*5^2*16*22+1^2*3*5*14*23+0*1*2*8*10*25+0^2*3*8*12*24+1*2^2*6*10*25+0*6*11*15*18+1^2*2*6*11*25+0^2*3*7*11*25+0*6*10*16*18+0^2*6*13*26+0*4^2*13*26+3*10^2*12*19+3*10^2*14*17+2*6*13*27+1*7*13*27+1*11*12^2*19+2*10*12^2*19+0^2*5*6*12*24 10 176 5
22^2+14^2*21+13^2*23+12^2*24+11^2*25 8 178 6
14*31+9*13*27+5^2*8*12*23+3^2*6*10*25+4^2*7*11*24 9 178 5
10^2*27+0^2*11^2*24+6^2*14^2*20+3^2*13^2*21+1^2*12^2*23 10 178 6
15*26+6*19*21+3*18*23+1*17*24+0*16*25 8 179 6
10*32+2*4*6*13*24+1*4*9*11*24+3*5*9*12*23+1*4*8*11*25+0*4*5*14*24+4^2*8*10*24+3^2*7*10*25+0*3*9*10*25+6*14*27+10*13*14*18+1*4*7*13*24+3*9^2*13*21+1*8^2*12*23+5*10*17*19+2^2*9*10*25+1*5*9*13*23+0*4*8*12*25+0*7^2*11*24 9 179 5
16*27+7*13^2*21+3^2*19*21+2*11^2*24+1^2*18*23+0^2*17*24+10^2*26+4*12^2*23 9 179 6
10*11*27+6*9^2*16*20+0*33+6^3*19*20+3^3*18*21+3*6*10*13*21+3*8*11*12*21+3^2*10*14*21+3*5^2*16*21+1*8*11*13*21+1*7*12*13*21+1^2*6*18*21+1^2*9*15*21+2*5*10*14*21+1*2*12^2*23 10 179 6
15*28+10^3*22+6^3*19*20+3^3*18*21+0^3*16*24+1^3*17*23 10 179 6
14^4+6^4*25+9^4*21+7^2*8*9*23+5*8*9^2*23+6^2*7*8*24+2*7*9^2*24 8 180 4
16*26+7*19*21+4*18*23+2*17*24 8 180 6
11*32+0*6^2*10*25+4*9^2*13*21+4*12*17*19+4^2*8*11*24+0^2*8*14*24+1*5*6*13*24+3^2*7*11*25+2*4*8*11*25+2*4*7*13*24+2^2*9*11*25+4*13*14*22+0*4*6*13*25+4*5*8*13*23+3^2*9*13*23+1^2*9*13*24+2^2*7*13*25+10^2*14*19+0*4*9*10*25+3*10*18*19+3*9*10*26+3^2*19*22+2*8*13*26+2*7*9*11*23+1*6*8*13*23+2*7^2*13*23+3*8^2*10*23+4*7*8*11*23 9 180 5
11^2*27+7^2*9*18*20+2^2*12^2*23+4*7*9*19*20+4*8*11*12*21+3*9*10*11*21+2*5*11*14*21+2*4*5*18*21+2^2*13*14*21+1*2*9*15*21+1*2*6*18*21+0*9*10*13*21+0^2*10^2*25+0*5*8*15*21+0*5*6*17*21+3^2*4*18*21+4^2*5*17*21+6^2*7*19*20 10 180 6
16*28+10^2*11*22+6^2*7*19*20+3^2*4*18*21+0*15*27+1^2*2*17*23 10 180 6
17*27+8*13^2*21+5*12^2*23+1*10*11*25+4^2*19*21+11^2*26+2^2*18*23+0*10*12*25+0^2*16*25 9 181 6
10*12*27+6*9^2*17*20+1*33+6*7^2*19*20+3*5*13^2*21+0*2*11^2*24 10 181 6
15*29+1*2^2*17*23+3*4^2*18*21+6*7^2*19*20+10*11^2*22+4^2*10*14*21+3*4*11*14*21+0*2*11^2*24+0*5*11*12*23+0*1*5*15*23+1*2*11*13*23+2^2*10*13*23+0*10^2*26+0*3*9*15*21+0*3*6*18*21+0*1*3*17*23+0*9*11*13*21+0^3*17*24 10 181 6
17*26+8*19*21+5*18*23+2*16*25 8 182 6
12*32+1*6^2*10*25+5*12*17*19+4^2*7*11*25+3^2*7*12*25+2*4*8*12*25+2^2*9*12*25+1*3*7*13*25+5*13*14*22+5^2*8*13*23+2^2*9*14*23+1*4*9*10*25+0*5*6*13*25+7*11*14*22+4*9*16*22+4*9*11*26+5*9^2*13*21+6*14*15*16+6*7*15*22+3*7*9*10*23+1*7*8*10*24+4*8^2*11*23+1^2*7*14*24+0*10*19^2+0*6*9*13*23+0*8^2*10*24+1*2*6*14*24+7*13*16*18+4*11*18*19+4^2*9*13*23+2^2*9*13*24 9 182 5
11*12*27+7*9^2*17*20+2*9^2*19*20+2*33+4*5*13^2*21+0*1*10^2*25+6^2*8*19*20 10 182 6
11^3*22+10^2*12*22+1*3*12^2*23+1^2*12*13*23+0*10*11*26+0*2*3*17*23+0*2*5*15*23+0*4*9*15*21+4*7*11*13*21+3*5*10*14*21+0*4*6*18*21+3^2*5*18*21+1*15*27+0^2*2*16*24+3*9*10*12*21+2*4*11*12*23+2*9^2*19*20+2*33+2^3*17*23+4^3*18*21+0^3*15*25 10 182 6
16*29+10^2*12*22+1*3*12^2*23+1^2*12*13*23+0*10*11*26+0*2*3*17*23+0*2*5*15*23+0*4*9*15*21+4*7*11*13*21+2*4*11*12*23+2*33+6^2*8*19*20+0*4*6*18*21+3^2*5*18*21+3*5*10*14*21+1*15*27+0^2*2*16*24+3*9*10*12*21 10 182 6
17*28+10^2*12*22+6^2*8*19*20+3^2*5*18*21+1*15*27+0^2*2*16*24 10 182 6
12^2*27+8^2*9*18*20+5*8*9*19*20+1^2*10^2*25+5^2*13^2*21+2^2*11^2*24+7^2*8*19*20 10 184 6
17*29+4^2*5*18*21+11^2*12*22+7^2*8*19*20+2*16*27+0^2*1*15*25 10 184 6
18*27+9*13^2*21+5^2*19*21+2*11*13*24+2^2*17*24+12^2*26+1^2*16*25+4*11*12*24+3*10*11*25+0*10*13*25 9 185 6
10*13*27+3*33+6*9^2*18*20+6*8^2*19*20+1*5*12^2*23+0^3*18*24+0*3^2*17*23+0*15^2*17+0*5*10^2*24+0*6^2*17*21+0*2*12^2*24+0*2^2*16*24+0^2*2*15*25+0^2*1*16*25 10 185 6
15*30+3*5^2*18*21+1*4*9*16*21+6*8^2*19*20+10*12^2*22+5^2*10*14*21+3*5*12*14*21+0*1*10*12*25+0^2*1*16*25+1*11^2*26+1*9*12*13*21+1*5*12^2*23+1^2*10*11*25+1*2^2*18*23+0*2^2*16*24+1*4*7*18*21 10 185 6
18*26+9*19*21+5*17*24+4*16*25 8 186 6
13*32+3*6^2*10*25+2*8^2*11*24+1*6*9*11*24+0*5*6*14*24+0*1*9*14*24+3*7*8*10*24+2*4*9*13*24+0*6*8*12*25+0*3*9*13*25+3^2*9*11*25+4^2*9*12*24+8*13*17*18+8*12*14*22+5*9*17*22+2*4*9*12*25+7*14*16*17+7*8*16*22+4*8*9*11*23+1*7*8*10*25+2*11*19^2+2*7^2*11*25+2*7*9*13*23+5*12*18*19+5^2*19*22 9 186 5
11*12^2*22+4*33+4*9^2*19*20+4*5^2*18*21+0*1^2*15*25+2^2*11*12*24+10^2*13*22+3*15*27+3*6*13^2*21+0^2*4*16*24+1*5*9*15*21+1*5*6*18*21+1^2*5*17*23+0*2*10*13*24+0*15*16*17+0*6*7*17*21+0*3*4*17*23+0*2*15*26+0*1*16*26+1*10*12*26+2*9*12*13*21+2*17*27+4*9*12^2*21+0*3*11*12*24+0^2*12*13*24+3^2*13*14*21+4*5*12*14*21 10 186 6
11*13*27+7*9^2*18*20+2^2*5*16*23+4^2*11*12*23+3^2*12^2*23+2*4*11*13*23+0^2*5*18*23+1^2*13^2*23+1^2*5*17*23+0*3*10^2*25+4*33+4*9^2*19*20+6^2*9*19*20 10 186 6
16*30+10^2*13*22+3*15*27+3*6*13^2*21+0^2*4*16*24+1*5*9*15*21+1*5*6*18*21+0*2*10*13*24+0*15*16*17+0*6*7*17*21+0*3*4*17*23+0*2*15*26+0*1*16*26+1*10*12*26+2*9*12*13*21+4*9*12^2*21+0*3*11*12*24+0^2*12*13*24+3^2*13*14*21+4*33+4*5*12*14*21+6^2*9*19*20+2^2*11*12*24+1^2*5*17*23 10 186 6
18*28+10^2*13*22+6^2*9*19*20+3*15*27+0^2*4*16*24+1^2*5*17*23 10 186 6
12*13*27+5*33+8*9^2*18*20+7^2*9*19*20+5*9^2*19*20+2^3*16*24+2^2*12^2*24+1*5*10*11*24+0*5*10*12*24+0^2*2*18*24+1^2*2*17*24+1*3*10^2*25 10 188 6
12^3*22+5*33+5*9^2*19*20+1^2*11*12*25+11^2*13*22+2^2*5*17*23+2*5*9*16*21+0*1*2*16*25+2*5*7*18*21+0^2*5*16*24+3^2*4*19*21+4^2*12^2*23+0*4*10*11*25+3*10*11*26+1*2*3*18*23+0*3*5*17*23+0*5^2*15*23+0^2*3*15*25+0*10*13*26+5^3*18*21+0*1*12^2*25+5*8*12*13*21+1^3*15*25+4^2*13*14*21+2*11*12*26+2^2*12^2*24+1*5*10*11*24+0*5*10*12*24+1^2*2*17*24 10 188 6
17*30+11^2*13*22+2^2*5*17*23+2*5*9*16*21+0*1*2*16*25+2*5*7*18*21+0^2*5*16*24+3^2*4*19*21+4^2*12^2*23+0*4*10*11*25+3*10*11*26+1*2*3*18*23+0*3*5*17*23+0*5^2*15*23+0^2*3*15*25+5*8*12*13*21+2*11*12*26+4^2*13*14*21+0*10*13*26+5*33+0*1*12^2*25+1^2*11*12*25+7^2*9*19*20+2^3*16*24+2^2*12^2*24+1*5*10*11*24+0*5*10*12*24+1^2*2*17*24 10 188 6
18*29+11^2*13*22+2^2*5*17*23+0^2*5*16*24+4^2*12^2*23+3*10*11*26+0*3*5*17*23+0^2*3*15*25+7^2*9*19*20+2^3*16*24+1*5*10*11*24+0*5*10*12*24+0*10*13*26+2*4*8*18*21+1*2*15*26+0*15*17^2+0*6*8*17*21+0*2^2*15*25+3^2*9*16*21+4^2*8*17*21+7*9*10^2*21+8^2*11^2*21+2^2*22^2+2^2*11^2*25+2^2*13^2*23+2*5*9*16*21+0*1*2*16*25 10 188 6
13^2*27+9^3*18*20+8^2*9*19*20+3^2*10^2*25+5^2*12^2*23+3^2*11*12*24+1*3*11*13*24+0*5*10*13*24+0^2*4*18*24+1^2*4*17*24+2*5*11*12*24+2^2*12*13*24+2^2*4*16*24 10 192 6
18*30+12^2*13*22+8^2*9*19*20+1^2*3*15*25+5^2*12^2*23+4*11*12*26+2*11*13*26+0^2*5*16*25+4^2*5*19*21+2^2*4*16*24+5*8*13^2*21+2*4*11^2*25+2^2*17*26+2^2*12^2*25+1^2*2*17*25+2^2*8*19*21+0*2*4*15*25+0*2*3*16*25 10 192 6
19*27+8*12*13*23+13^2*26+7*11*12*24+2*11*14*24+4^2*17*24+0*10*14*25+5^2*18*23+6*10*11*25+3^2*16*25+5*12*14*23 9 193 6
10*14*27+6*33+3*9*13^2*21+0*8*10^2*24+0*4^2*16*24+0*3^2*17*24+0*2*13^2*24+0^3*19*24+1*2*4*17*24+1*16^2*18+1*9*11^2*23+1*7^2*18*21+1*5*13^2*23+1*5^2*17*23+1*2*5*16*24+1*2^2*19*23 10 193 6
15*31+3*9*13^2*21+6*9^2*19*20+3*12^2*26+3*5^2*19*21+1^2*4*15*25+0*1*5*15*25+0*1*3*17*25+0*2*5*17*24+3*5*11^2*24+3^2*10*11*25+10*13^2*22+1*2*4*17*24+1*5^2*17*23+0*3*10*13*25+0*4^2*16*24 10 193 6
19*26+9*18*23+8*17*24+7*16*25 8 194 6
14*32+8*9*17*22+7^2*9*12*23+2*7*9*12*25+8*14*17*18+5*14*17*19+6^3*10*25+6^2*8*11*24+4*8*9*11*24+3*7*9*10*25+0*9^2*10*25 9 194 5
11*13^2*22+7*33+7*9^2*19*20+0*2*10*14*24+3*10*13*26+0*3*4*17*24+0*2*5*15*25+1*5*10*14*23+1*6*8*18*21+0*2*3*17*25+2*7^2*18*21+2^2*7*17*23+1*6*12*13*23+4^2*11*12*24+3^2*11^2*25+0*3^2*15*25+10^2*14*22+0^2*12*14*24+6*15*27+0*6*11*12*24+0^2*7*16*24+1^2*13*14*23+0^2*13^2*25+4*5*9*17*21+4*5^2*19*21+2*5*9*18*21+8^2*11*13*21+4*12*17*22+9^2*10^2*21+2*4*11*12*25+4*16^2*17+3*15*17^2+0^2*5*17*25+0*4*6*17*23+0*3*7*17*23 10 194 6
11*14*27+7*33+0*6*10^2*25+1^2*4*16*25+4*5*9*17*21+3^2*9*18*21+1*3*17*26+1*5*15*26+2*5*9*18*21+8^2*11*13*21+4*12*17*22+4*5*12*13*23+4*12^2*26+2*5*13^2*23+2^2*5*16*24+9^2*10^2*21+2*4*11*12*25+4*16^2*17+3*15*17^2+0^2*5*17*25+2*16^2*18+0*4*6*17*23+0*3*7*17*23+1^2*8*17*23+1*15*17*18+2*9*11^2*23+2^2*8*16*23 10 194 6
16*31+7*33+3^2*9*18*21+1*3*17*26+1*5*15*26+1^2*8*17*23+1*15*17*18+0*2*10*14*24+3*10*13*26+0*3*4*17*24+0*2*5*15*25+1*5*10*14*23+1*6*8*18*21+0*2*3*17*25+1*6*12*13*23+2*4*11*13*24+10^2*14*22+0^2*12*14*24+6*15*27+0*6*11*12*24+0^2*7*16*24+1^2*13*14*23+4*5*12*13*23 10 194 6
19*28+10^2*14*22+6*15*27+3^2*9*18*21+0^2*7*16*24+1^2*8*17*23 10 194 6
12*13^2*22+8*33+8*9^2*19*20+1*3^2*15*25+4*11*13*26+2*7*12*13*23+2*16*17*18+2*7*8*18*21+0*1*13^2*25+11^2*14*22+9^2*11^2*21+2^2*8*17*23+0*3*8*17*23+3*4*15*26+0*9^2*15*21+0*6*9*18*21+7*10^2*26+0^2*6*15*25+2*5*16*26+2*4*17*26+5^2*12*13*23+4^2*9*18*21+4*5^2*16*23+4^2*11^2*25+0*3*5*17*24+1*8*10*11*24+0*8*10*12*24+0^2*8*16*24+4^2*22^2+3*9*10*11*23+1*2*9*15*23+0*9*10*13*23+0*5*6*17*23+2^2*13*14*23+2*5*11*14*23+1*3*11*13*25+5*18*27+0*5*10*13*25+4^2*12^2*24+2^2*13^2*24+0*7*10*11*25 10 196 6
12*14*27+8*33+1*6*10^2*25+5^2*9*17*21+1^2*4*17*25+5^2*8*18*21+5*12^2*26+2*5*16*26+2*4*17*26+2^2*9*19*21+4*16*17^2+3*15*16*18+1*4*5*15*24+0*15*18^2+0*4^2*15*25+0*3*5*17*24+1*8*10*11*24+0*8*10*12*24+0*3*4*16*25+0^2*7*17*24+0^2*8*16*24+4*8*11*12*23+4^2*22^2+4^2*11^2*25+3*9*10*11*23+1*2*9*15*23+0*9*10*13*23+1*2*6*18*23+0*5*6*17*23+0*5*8*15*23+2^2*13*14*23+2*4^2*16*24+2*5*11*14*23+1^2*2*18*25+1*3*11*13*25+5*18*27+3^2*11*12*25+0*5*10*13*25 10 196 6
17*31+8*33+2*5*16*26+2*4*17*26+0*3*5*17*24+1*8*10*11*24+0*8*10*12*24+0^2*8*16*24+4^2*22^2+4^2*11^2*25+3*9*10*11*23+1*2*9*15*23+0*9*10*13*23+0*5*6*17*23+2^2*13*14*23+2*4^2*16*24+2*5*11*14*23+1*3*11*13*25+0*5*10*13*25+5^2*12*13*23+4*11*13*26+2*7*12*13*23+2*16*17*18+2*7*8*18*21+0*7*10*11*25+0*1*13^2*25+11^2*14*22+9^2*11^2*21+2^2*8*17*23+0*3*8*17*23+3*4*15*26+0*9^2*15*21+0*6*9*18*21+2^2*13^2*24+4^2*9*18*21+7*10^2*26+0^2*6*15*25+4*5^2*16*23+4^2*12^2*24 10 196 6
19*29+11^2*14*22+9^2*11^2*21+2^2*8*17*23+0*3*8*17*23+3*4*15*26+0*9^2*15*21+0*6*9*18*21+0*3*5*17*24+2^2*13^2*24+2*4^2*16*24+0*3*4*16*25+0^2*8*16*24+4^2*9*18*21+7*10^2*26+0*8*10*12*24+1*8*10*11*24+0^2*6*15*25+4*5^2*16*23+4^2*22^2+4^2*12^2*24+4^2*11^2*25+3*9*10*11*23+1*2*9*15*23+0*9*10*13*23+0*5*6*17*23 10 196 6
13*14*27+9*33+5^3*17*23+2^2*9*17*23+4*9*11*12*23+1*9*10*11*24+0*5*10*14*24+2*6*10*13*24+1*6*11*13*24+0*1*13*14*24+0^2*7*18*24+4*8*10^2*24+2*9*11*13*23+1^2*7*17*24+2^2*12*14*24+5^2*13^2*23+2^2*8*18*23+4^2*5*18*23+2*8*11*12*24+2^2*7*16*24+3*6*10^2*25 10 200 6
13^3*22+12^2*14*22+9*33+2^2*9*17*23+4*9*11*12*23+9^2*12^2*21+5^2*9*18*21+1^2*6*15*25+4*5*16*26+0^2*7*17*25+2*7*9*18*21+8*11^2*26+2*7*11^2*25+5^2*22^2+5^2*12^2*24+4^2*12^2*25+2*16*18^2+2*9*11*13*23+9^3*19*20+3^2*11*13*25+0*3*13^2*25+5*12*13*26+4^2*12*13*24+1*8*10*11*25+3^3*15*25+3^2*4*17*24+2*5^2*16*24+0^2*4*19*24+1*9*10*11*24+0*5*10*14*24+2*6*10*13*24+1*6*11*13*24+1^2*7*17*24+0*1*13*14*24+0^2*7*18*24+2^2*12*14*24+1*2*10*14*25+0*3*5*17*25+1*2*3*18*25 10 200 6
18*31+12^2*14*22+9*33+5^3*17*23+2^2*9*17*23+4*9*11*12*23+9^2*12^2*21+5^2*9*18*21+1^2*6*15*25+4*5*16*26+2*7*9*18*21+8*11^2*26+5^2*22^2+5^2*12^2*24+4^2*12^2*25+2*16*18^2+2*9*11*13*23+3^2*11*13*25+0*3*13^2*25+2^2*7*16*24+0*3*5*17*25+5*12*13*26+4^2*12*13*24+2*4*13^2*24+2*5^2*16*24+2*8*11*12*24+1*2*3*18*25+2*7*11^2*25+0^2*7*17*25+1*2*10*14*25+1*8*10*11*25 10 200 6
19*30+2^2*7*16*24+12^2*14*22+9^2*12^2*21+5^2*9*18*21+1^2*6*15*25+4*5*16*26+0^2*7*17*25+2*7*9*18*21+2^2*5*18*24+8*11^2*26+2*7*11^2*25+5^2*22^2+5^2*12^2*24+4^2*12^2*25+2*16*18^2+1*4*5*15*25+0*5^2*15*25+1*2*3*18*25+5^3*17*23+2*9*11*13*23+2^2*9*17*23+4*9*11*12*23 10 200 6
6*7*8*9*19*20+10*12*13*14*16+6*11*12*13*22+3*11*12*14*22+3*8*16*27+3*4*5*9*18*21+0*2*4*7*16*24+1*4*5*17*26+2*3*8*11^2*24+1^2*2*7*15*25+0*4*7*11^2*25+2*9*15*27+1*7*9*13^2*21+1*2*8*11^2*25+1*2^2*11*14*25+0^2*4*7*15*25+0*5*8*11^2*24+0*2^2*7*16*25+1*7*12^2*26+1*2*5^2*17*24+1*5*16*17*18+1*2*9*11^2*24+1*2^2*7*17*24+0*5*7*10^2*25+0^2*3*7*16*25+1*9*16*27+1*2*5*8*17*23+0*1*3*6*15*25+1*4*7*10^2*25+1*11*13*14*22+1*5*7*8*18*21+2^2*7*10*12*25 11 206 6
10*33+1*12^3*23+6*14^3*20+3*13^3*21+0*11^3*24 11 207 7
22*26+14*19*21+13*18*23+12*17*24+11*16*25 9 208 7
14^2*27+9^2*13^2*21+7^2*12*13*23+5*8*22^2+5*8*12^2*24+2^2*8*19*23+2*9*11*14*23+4^2*8*18*23+4*7*12*14*23+5^2*8*17*23+4*7*12^2*25+2*9*11*12*25+5*14*17*22+5^2*13*14*23+5*12*14*26+2*4*12*14*25+6^2*11*12*24+4^2*7*16*24+3^2*7*17*24+1*6*11*14*24+0*8*10*14*24+0^2*7*19*24+2*7*13^2*24+6^2*10^2*25 10 208 6
19*31+13^2*14*22+9^2*13^2*21+9*12^2*26+0*3*8*17*25+5^2*18*26+5^2*13^2*24+4^2*5*18*24+4^2*13^2*25+3^2*4*18*25+2^2*8*18*24+5*8*12^2*24+4*7*12^2*25+5^2*8*17*23+4^2*7*16*24+3^2*6*15*25+1*2*6*18*25+0*5*8*15*25 10 208 6
11*33+7*9*14*18*20+4*9*14*19*20+7*12^2*13*21+6*10*13^2*21+4*5*13*17*21+2*5*13*18*21+1^2*13*19*21+2*12^3*23+3^2*13*18*21+3*10*13*14*21+6^2*14*19*20+0*10^3*25 11 208 7
22*28+6^2*14*19*20+10*15*27+3^2*13*18*21+1^2*12*17*23+0^2*11*16*24 11 208 7
14^2*26+8^2*18*23+9^2*19*21+7^2*17*24+6^2*16*25 9 209 6
15*32+10*14^2*22+6*13*18*22+6*9*12^2*23+6*8*11^2*24+6^2*10*11*25+3*8*12*13*24+3*7*11*13*25+1*9*12*13*24+5^2*10*14*24+4^2*10*14*25+3*14*18*22+1*5*14^2*23+2*4*6*18*24+0*4*5*19*24+1*9*17*26+2^2*9*15*25+0*5*7*17*25+1*7^2*18*23+1*5*8*17*24+0*3*6*18*25+0*9*11*13*25+0*6*10*14*25+0*6^2*17*24+0*2*14^2*24+0*2*8*18*25 10 209 6
11*14^2*22+7*13*18*22+2*4^2*19*24+0^2*8*19*24+4*8*12*14*23+2*7*11*14*24+0*6*7*17*24+2*7^2*18*23+0*3*4*19*25+1^2*9*18*24+2*4*8*16*25+2*4*7*17*25+0*6^2*15*25+6*10*19*22+3*9*10*14*23+1*8*10*14*24+5^2*11*14*24+4^2*11*14*25+4*17^2*19+3*9*15*26+3^2*19*26+1*5*9*15*24+3*4*7*15*25+3^2*7*16*25+4*9*22^2+3^2*9*18*23+4*7*8*16*23+3*8^2*15*23+2*7*9*16*23+0*7*10*14*25 10 210 6
16*32+6*10*19*22+3*9*10*14*23+3^2*14^2*23+6^2*11^2*25+6^2*13^2*23+6^2*12^2*24+1*8*10*14*24+1^2*14^2*24+0*6*7*17*24+1^2*9*18*24+3^2*9*18*23+2*4*8*16*25+2*4*7*17*25+0^2*14^2*25+0*7*10*14*25+4*8*12*14*23+4^2*7*17*24+2*5*8*17*24+2*4*9*16*24+2*7*11*14*24+2*4^2*19*24+5^2*11*14*24+4^2*11*14*25+4*14*18*22+6*15*18^2+3^2*19*26+1*3*5*19*24+3*4*7*15*25+0^2*9*18*25+7*17^2*18+2*9*17*26+1*6*8*18*23 10 210 6
12*33+8*9*14*18*20+5*9*14*19*20+5*13^3*21+7^2*14*19*20+2*11^3*24+1*10^3*25 11 210 7
22*29+7^2*14*19*20+2*11^3*24+0^2*10*15*25+3*4*10*19*21+0*9*13*15*21+0*6*13*18*21+7*11*13^2*21+10^2*16*22+6*10*11*14*21+3*10*11*13*23+1*10*11*12*24+0*10*22^2+0*10*11^2*25+4*11*12^2*23+2^2*12*17*23+4^2*13*18*21+1*2*10*18*23+0*5*12*15*23+0*3*12*17*23+0^2*11*17*24 11 210 7
12*14^2*22+1*6^2*15*25+7*11*19*22+2*7*8*18*23+4*9*16*26+2*5*9*16*24+2^2*9*18*24+4*9*11*14*23+2*8*11*14*24+0*7^2*15*25+1*6*11*14*25+4^2*8*17*24+0*8*10*14*25+8*13*18*22+5*9*22^2+2^2*9*19*23+5*8*12*14*23+4^2*7*16*25+1*4*9*15*25+5^2*12*14*24+0*5*9*15*25+4^2*12*14*25+0*5*6*18*25+1*4*6*18*25+5*17^2*19+2^2*8*18*25+2^2*9*17*25+2*7^2*16*24+0*1*14^2*25 10 212 6
17*32+7*11*19*22+7^2*12^2*24+6^2*11*12*25+2*7*8*18*23+7^2*13^2*23+4*9*16*26+4^2*19*26+4*9*11*14*23+4^2*14^2*23+2*8*11*14*24+2*7^2*16*24+1*7*8*15*24+1*2*6*19*24+0*8^2*15*24+0*7^2*15*25+5*14*18*22+5^2*12*14*24+0*5*9*15*25+5^2*8*18*23+5*9^2*18*21+0*1*14^2*25+5*8*12*14*23+4^2*12*14*25+2*4*13*14*25+2*9*11*13*25+2^2*8*18*25+2*4*8*17*25+1*4*6*18*25+1*3*7*18*25 10 212 6
13*33+9^2*13*19*20+9^3*20*22+3*10*11*12*24+2^2*11*16*24+1*10*11*13*24+0^2*11*18*24+1*2*10*17*24+0*1*12*17*24+8^2*14*19*20+5*12^3*23+2*11*12^2*24+3*10^3*25 11 214 7
22*30+8^2*14*19*20+8*12*13^2*21+1^2*10*15*25+5^2*13*18*21+1*10*11*12*25+5*12^3*23+11^2*17*22+7*11*12*14*21+4*11*12*13*23+4*5*11*19*21+2*11*22^2+2*7*13*18*21+2*9*13*16*21+0*10*12^2*25+0^2*12*16*25+2^2*12*18*23+2^2*11*16*24+2*11*12^2*24 11 214 7
13*14^2*22+3*6^2*15*25+9*13*18*22+5^2*19*26+4^2*5*19*24+5*8^2*17*23+5^2*13*14*24+4^2*13*14*25+3*7*8*15*24+1*6*9*16*24+0*5*6*19*24+0*1*9*19*24+3^2*4*19*25+2*9*11*14*24+8*12*19*22+5*9*17*26+5^2*9*18*23+2*4*9*17*25+2^2*9*18*25+5*9*12*14*23+2*7*12*14*25+1*6*7*17*25+0*6*8*17*25+0*8^2*15*25+2*8^2*16*24+2*6^2*18*24+0*3*14^2*25+4*7*12*14*24+3*6*11*14*25+0*9*10*14*25 10 216 6
18*32+9^2*12^2*23+8*12*19*22+7^2*12^2*25+3*6*11*14*25+0*3*14^2*25+0*8^2*15*25+1^2*7*19*25+5*9*12*14*23+5^2*19*26+5^2*9*18*23+4^2*5*19*24+4^2*9*17*24+2^2*9*18*25+8^2*12^2*24+2^2*8*19*24+1*6*7*17*25+0*6*8*17*25+5^2*13*14*24+4*7*12*14*24+3^2*7*18*25+2*6^2*18*24+2*9*11*14*24+2*7*12*14*25+2*4*9*17*25+4^2*13*14*25+0*9*10*14*25+0*3*9*18*25+2*4*9*18*24 10 216 6
14*33+6*10^3*25+9*13^3*21+7*11*12*13*23+5*12*13^2*23+4*11*12*14*23+2^2*12*19*23+4*5*11*18*23+2*4*13*18*23+5^2*12*17*23+6*10*11*12*24+4^2*11*16*24+3^2*11*17*24+2*11*13^2*24+1*10*11*14*24+0^2*11*19*24 11 222 7
22*31+9^2*14*19*20+3^2*10*15*25+9*13^3*21+2*11*13^2*24+5*12*13^2*23+1*2*13*15*25+0*10*13^2*25+0*5*10*17*25+0*3*12*17*25+4*11*12*13*24+4^2*11*16*24+12^2*18*22+8*12*13*14*21+5^2*12*17*23+5*12*22^2+2*11*12*13*25+5^2*13*19*21+2^2*13*17*24+3*10*11*13*25 11 222 7
14^3*22+6^3*15*25+6^2*11*14*25+9*13*19*22+9^2*13^2*23+8^2*13^2*24+7^2*13^2*25+7^2*12*14*24+5*8*19*26+4^2*8*19*24+2*4*8*19*25+5*8*13*14*24+4*7*13*14*25+0*6*14^2*25+1*6*7*19*24+0*6*8*19*24+9^3*18*21+8^2*13*14*23+7^2*9*17*23+6^2*8*16*24+2*9^2*16*24+4*7*8*19*23+4^2*14^2*25+5^2*14^2*24+2*7*9*19*23+2*7*8*18*25+0*6*9*18*25+3*4*6*19*25 10 224 6
19*32+0*6*14^2*25+2*9^2*16*24+1*6*7*19*24+0*6*8*19*24+0*6*9*18*25+6^2*11*14*25+8^2*13*14*23+7^2*12*14*24+5*8*13*14*24+4*7*13*14*25+4*7*8*19*23+5*17*19^2+2^2*9*19*25+4*7*8*18*24+3*7*9*15*25+3*4*6*19*25+0*9^2*15*25+2*7*9*19*23+2*4*8*19*25 10 224 6
26*27+13^2*19*21+11^2*17*24+10^2*16*25+3^2*7*21*25+12^2*18*23+5^2*9*21*23+0^2*2*24*25+1^2*4*23*25+2^2*5*23*24+4^2*8*21*24 11 237 8
26^2+9^2*21*23+8^2*21*24+7^2*21*25+5^2*23*24+4^2*23*25+2^2*24*25 10 238 8
22*32+7*11*12*14*24+6*10*11*14*25+7^2*12*18*23+6^2*10*15*25+8*9*12*19*21+6^2*11*17*24+5*12*19*26+5*12*13*14*24+4*5*11*19*24+2*7*13*18*24+0*10*14^2*25+0*9*10*18*25+2*9*11*18*24+8*12*13*14*23+3*4*10*19*25+0*6*13*18*25+4*11*13*14*25+2*4*8*22*25+2*4*12*19*25+2^2*9*22*25+2^2*13*19*25 11 238 7
E4 term の defining relations は all 2 9 では198個でしたが、all 2 10 では250個、
all 2 11 では262個見つかります。
dim = 9 のindecomposable element があるので、少なくとも dimension = 18 まで探索する必要があり,
defining relations はまだまだ沢山あるはずです。修正した all.exe では2ギガのメモリーで
どこまで計算できるかまだ分かりません。
もとの all.exe は効率よく計算するためにすべてのデータを保持していましたが、
修正した all.exe は必要最小限度のデータしか保持しないようにして、かなり使用メモリーを減らしましたが、
焼け石に水です。
計算時間は all 2 4 が1秒、all 2 5 が11秒、all 2 6 が1分24秒、all 2 7 が9分48秒、
all 2 8 が1時間6分48秒、all 2 9 が5時間45分、all 2 10 が29時間56分9秒、
all 2 11 が148時間59分24秒です。
必要記憶容量の目安になる最大要素数は all 2 4 では 19, all 2 5 では 46, all 2 6 では 110,
all 2 7 では 300, all 2 8 では 721, all 2 9 では 1616 で、all 2 10 では 3369 で、all 2 11 では 6568 で、
それぞれ概数ですが 19*4=76, 46*5=230, 110*6=660, 300*7=2100, 721*8=5768,1616*9=14544, 3369*10=33690,
6568*11=72248 に比例したメモリーが必要だったと思われます。
したがって、私のアルゴリズムでは E4 term を決定するだけでも膨大な計算時間と
膨大な記憶容量が必要でパソコンでは計算不可能です。
更に、diff.exe で [15/15/15/15] の微分を計算してみると
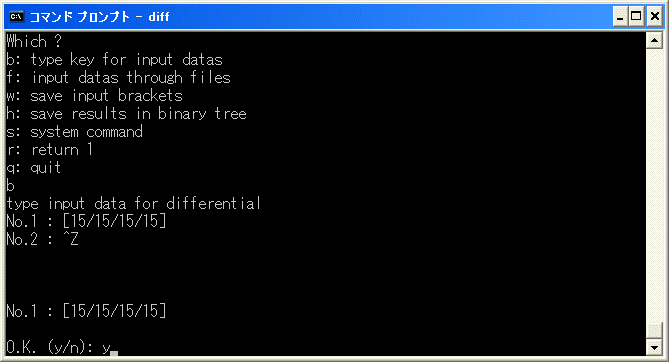
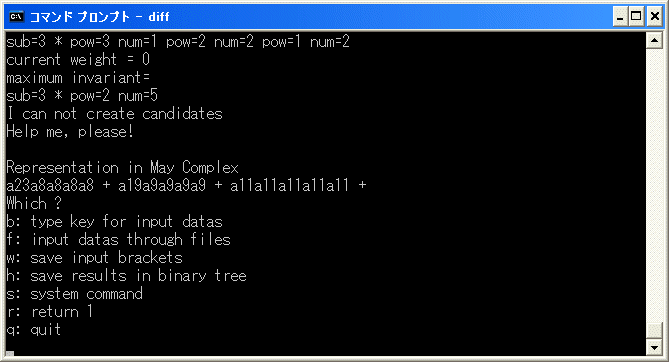
a23a8a8a8a8+a19a9a9a9a9+a11a11a11a11a11 は cocycle ですから、E4 term で
d4(20)=9*3^4+8*4^4+5~5 となるので、E4 term で May Spectral Sequence の計算が終わった訳ではなく、
当然 d8(20^2)=? 等が問題になるので、少なくとも E8 term を計算する必要があります。
64ビットの計算機を使わずに、これ以上どうしても計算したければ、計算機に随分助けてもらったと考え、
後は手計算で indecomposable elements が他にないかのチェックと defining relations の組合せ的探索を
すればいいです。そうすれば、次のステップ(d4 の決定および E6 term の部分的な決定等)でまた計算機に
助けてもらえます。diff.exe の本質的な改良は思いつかないので、多分、高次の微分はメモリー不足で
計算不可能だと思いますし、もしこのようにして May Spectral Sequence を計算できたとしても、
defining relations の修正は記憶容量が足りず、すべてを diff.exe でチェックすることは不可能ですし、
cobar construction を使っては計算機で出来ないものは手計算は勿論不可能で、 bar construction を
使った手計算も経験的に言ってものすごく大変な作業になると思います。ただ、微分の計算は、
Steenrod operation を使う手法や matric Massey bracket を使う手法など別の方法も知られています。
人間が直感的に計算しているプロセスをアルゴリズム化できればいいですが、いつでも正しいすべての答えが得られる
ような旨いアルゴリズムはかなり考えましたがまだ発見できません。
すでに述べたように完全な構造を求めることは不可能ですが、部分的な結果なら求めることが出来ます。
出来るところまで計算してみます。
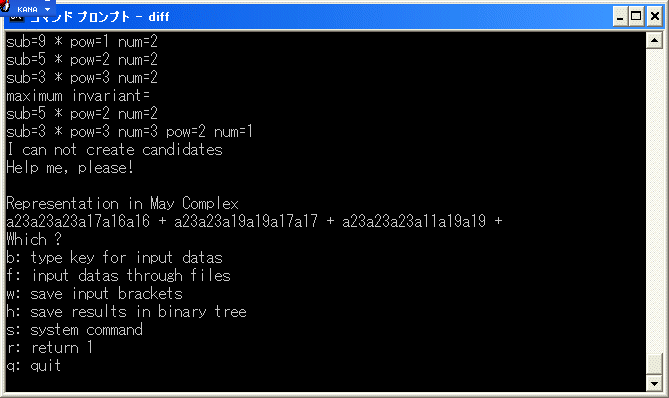
d4(20)=9*3^4+8*4^4+5~5 は求めたので、d4(21) を計算します。
diff.exe で [23/23/23/23] の微分を計算してみると
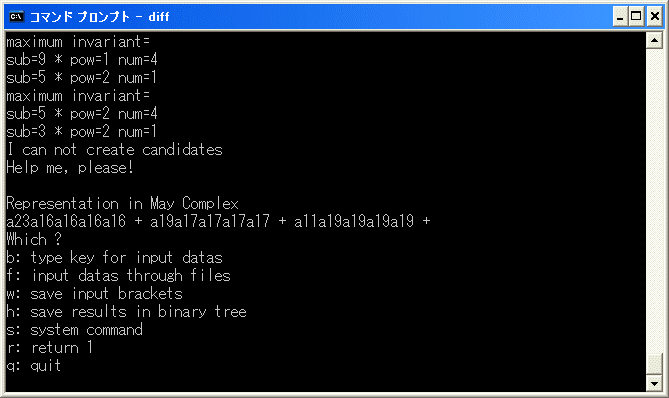
a23a16a16a16a16+a19a17a17a17a17+a11a19a19a19a19 は cocycle ですから、E4 term で
d4(21)= 9*6^4+8*7^4+5*8^4 となります。
d4(22) = 0 を計算します。
diff.exe で
[23/23/5^4/27]+[23/23/3^8/23]+[23/23/17/15^2]+[23/23/9^2/29]
+[3^8/15/27/27]+[3^4/27/27/27]+[5^2/29/27/27]+[9/15^2/27/27]
+[15/9^2/15^2/15^2]+[3^2/27/15^2/15^2]+[3/15^2/15^2/15^2]+[5^2/23/15^2/15^2]
+[15/5^4/29/29]+[3^4/23/29/29]+[3^2/29/29/29]+[5/15^2/15^2/15^2]
の微分を計算してみるとすぐに中断します。
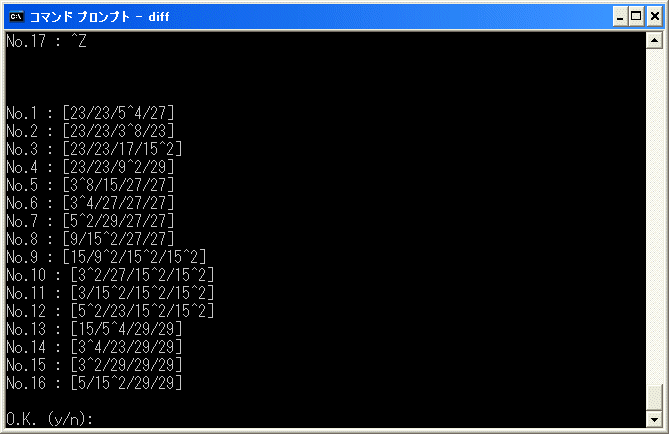
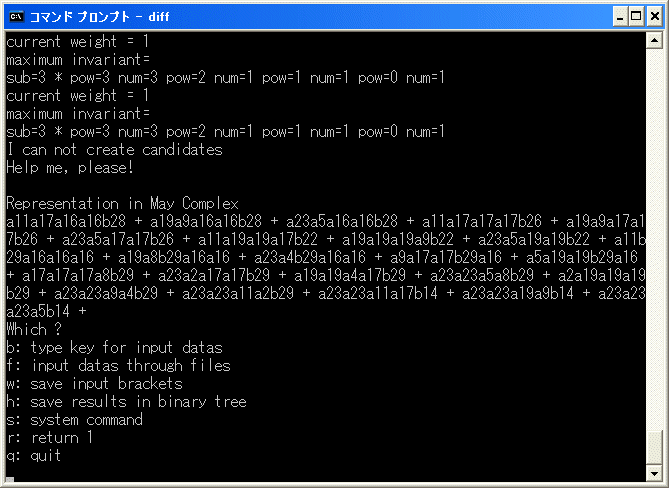
a11a17a16a16b28+a19a9a16a16b28+a23a5a16a16b28+a11a17a17a17b26+a19a9a17a17b26+a23a5a17a17b26
+a11a19a19a17b22+a19a19a19a9b22+a23a5a19a19b22+a11a16a16a16b29+a19a8a16a16b29+a23a4a16a16b29
+a9a17a17a16b29+a5a19a19a16b29+a17a17a17a8b29+a23a2a17a17b29+a19a19a4a17b29+a23a23a5a8b29
+a2a19a19a19b29+a23a23a9a4b29+a23a23a11a2b29+a23a23a11a17b14+a23a23a19a9b14+a23a23a23a5b14
=d1(a16^2b28b29+a17^2b26b29+a19^2b22b29+a23^2b14b29)
なので
[17/17/29/15^2]+[9^2/9^2/7/15^2]+[5^4/5^4/23/15^2]+[3^8/3^8/15/15^2]
を追加します。
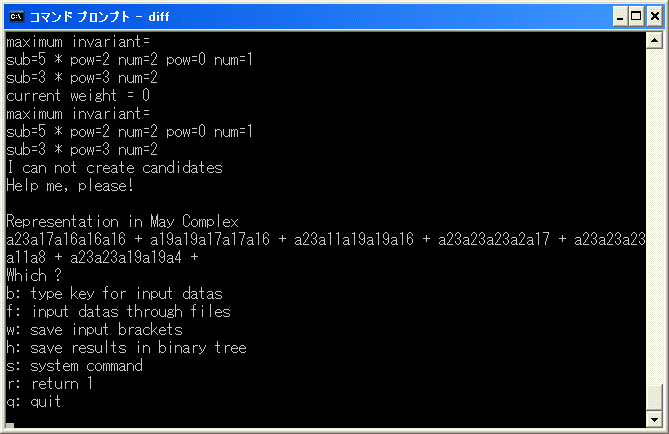
a23a17a16^3+a19^2a17^2a16+a23a11a19^2a16+a23^3a2a17+a23^3a11a8+a23^2a19^2a4
=d1(b28a19^2a23+b26a17a23^2)+d2(a16a17b28^2+a8a23b29^2)
なので
[29/5^4/5^4/3^8]+[27/9^2/3^8/3^8]+[17/9^2/29/29]+[9/3^8/15^2/15^2]
を追加します。
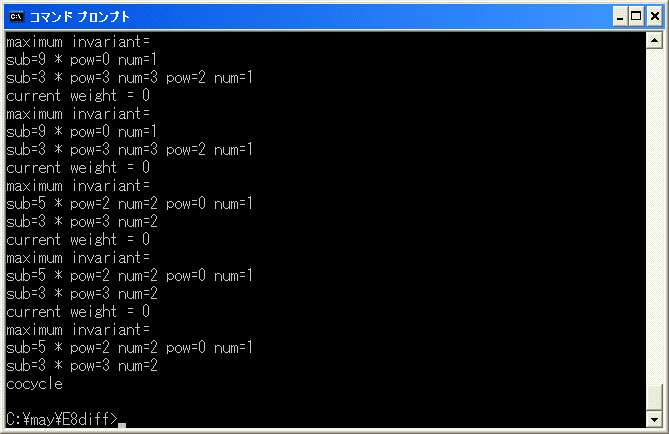
cocycle になったので、d3(22)= d4(22) = 0 です。
d4(23) を計算します。
diff.exe で [27/27/27/27] の微分を計算してみると
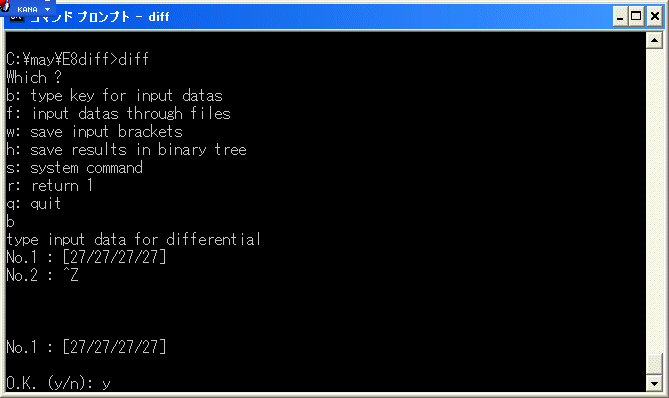
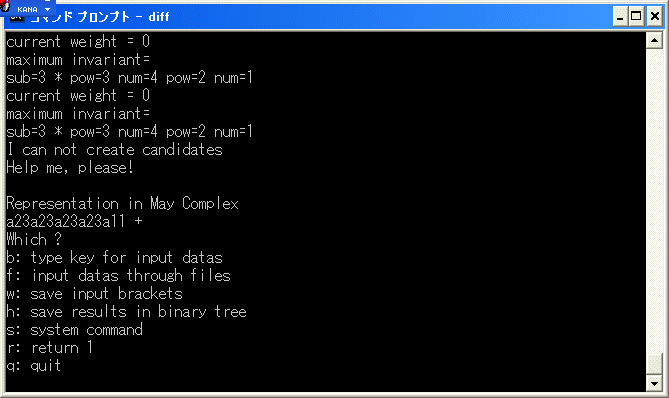
a23a23a23a23a11 は cocycle ですから、E4 term で
d4(23)= 5*9^4 となります。
d4(24) を計算します。
diff.exe で [29/29/29/29] の微分を計算してみると
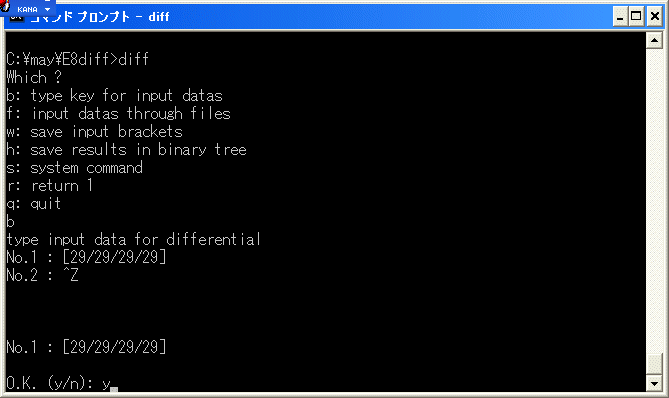
a23a23a23a23a19 は cocycle ですから、E4 term で
d4(24)= 8*9^4 となります。
d4(25) を計算します。
diff.exe で [15^2/15^2/15^2/15^2] の微分を計算してみると
a23a23a23a23a23 は cocycle ですから、E4 term で
d4(25)= 9^5 となります。
d4(26) を計算します。
diff.exe で
[3^8/23/23/27/27]+[3^2/29/29/15^2/15^2]+[5^2/27/27/15^2/15^2]
+[5^4/23/23/29/29]+[3^4/27/27/29/29]+[9^2/23/23/15^2/15^2]
の微分を計算してみると約2分30秒で中断します。
a17^2(a11a17+a9a19+a5a23)b28^2+a19^2(a11a17+a9a19+a5a23)b26^2
+a23^2(a11a17+a9a19+a5a23)b22^2+a16^2(a11a17+a9a19+a5a23)b29^2
は d1(b29(a17^2b28^2+a19^2b26^2+a23^2b22^2+a16^2b29^2)) ですから
[15^2/9^2/9^2/29/29]+[15^2/5^4/5^4/27/27]+[15^2/3^8/3^8/23/23]+[15^2/17/17/15^2/15^2]
で消去できることを教えます。
a23^3a17a16^2+a23^2a19^2a17^2+a23^3a11a19^2 は cocycle ですから、E4 term で
d4(26) = 9^2(6^2*7*9+7^2*8^2+5*8^2*9) となります。
d4(27) を計算します。
diff.exe で
[3^8/3^8/15/15/23/23]+[5^4/5^4/15/15/27/27]+[17/17/15/15/15^2/15^2]+[3^4/3^4/23/23/27/27]
+[9/9/23/23/15^2/15^2]+[9^2/9^2/15/15/29/29]+[5/5/27/27/15^2/15^2]+[3/3/29/29/15^2/15^2]
+[3^2/3^2/27/27/29/29]+[5^2/5^2/23/23/29/29]
の微分を計算してみると数分で中断します。
(a5^2a19a16^2+a11a9^2a16^2+a11a17^2a8^2+a19a4^2a17^2+a11^2a5a17^2
+a2^2a19^3+a5a19^2a9^2+a23^2a11a2^2+a23^2a5^3)b28^2
+(a23a5^2a16^2+a11^3a16^2+a11^2a9a17^2+a23a4^2a17^2+a11a19^2a8^2
+a19^2a9^3+a23a2^2a19^2+a23^2a5^2a9+a23^2a11a4^2)b26^2
+(a11^2a19a16^2+a23a9^2a16^2+a11^2a17^3+a23a17^2a8^2+a19^2a9^2a17
+a23^2a5^2a17+a19^3a8^2+a23^2a19a4^2+a23^3a2^2)b22^2
+(a5^2a17a16^2+a9^3a16^2+a11^2a5a16^2+a4^2a17^3+a9a17^2a8^2
+a2^2a19^2a17+a5a19^2a8^2+a23^2a2^2a9+a23^2a5a4^2)b29^2
=d2(a9^2b22^2b28^2+a5^2b26^2b28^2+a2^2b29^2b28^2+a11^2b22^2b26^2+a4^2b29^2b26^2+a8^2b22^2b29^2)
+(a17^2b28^2+a19^2b26^2+a23^2b22^2+a16^2b29^2)d2(b14^2)
で、a17^2b28^2+a19^2b26^2+a23^2b22^2+a16^2b29^2 は cocycle なので
[5^2/5^2/23/23/29/29]+[3^2/3^2/27/27/29/29]+[3/3/15^2/15^2/29/29]+[3^4/3^4/23/23/27/27]
+[5/5/15^2/15^2/27/27]+[9/9/23/23/15^2/15^2]+[9^2/9^2/29/29/15/15]+[5^4/5^4/27/27/15/15]
+[3^8/3^8/23/23/15/15]+[17/17/15^2/15^2/15/15]
で消去できることを教えます。数分で終了します。
d4(27) = 0 となります。
また、直前の計算は、手計算では気づきませんでしたが、計算機で連立方程式を解くと
(a5^2a19a16^2+a11a9^2a16^2+a11a17^2a8^2+a19a4^2a17^2+a11^2a5a17^2
+a2^2a19^3+a5a19^2a9^2+a23^2a11a2^2+a23^2a5^3)b28^2
+(a23a5^2a16^2+a11^3a16^2+a11^2a9a17^2+a23a4^2a17^2+a11a19^2a8^2
+a19^2a9^3+a23a2^2a19^2+a23^2a5^2a9+a23^2a11a4^2)b26^2
+(a11^2a19a16^2+a23a9^2a16^2+a11^2a17^3+a23a17^2a8^2+a19^2a9^2a17
+a23^2a5^2a17+a19^3a8^2+a23^2a19a4^2+a23^3a2^2)b22^2
+(a5^2a17a16^2+a9^3a16^2+a11^2a5a16^2+a4^2a17^3+a9a17^2a8^2
+a2^2a19^2a17+a5a19^2a8^2+a23^2a2^2a9+a23^2a5a4^2)b29^2
=d1(a2a19a19b22+a4a17a19b22+a5a16a19b22+a2a11a23b26+a8a11a17b26+a9a11a16b26+a5a5a23b29+a5a9a19b29+a5a11a17b29)b28b28
+d1(a2a19b22a23+a4a17b22a23+a5a16b22a23+a4a11a23b28+a8a11a19b28+a11a11a16b28+a5a9a23b29+a9a9a19b29+a9a11a17b29)b26b26
+d1(a2a23a23b26+a8a17a23b26+a9a16a23b26+a4a19a23b28+a8a19a19b28+a11a16a19b28+a5a17a23b29+a9a17a19b29+a11a17a17b29)b22b22
+d1(a4b14a19a23+a8b14a19a19+a11b14a16a19+a2a17a19b22+a4a11b22a23+a4a17a17b22+a5a16a17b22+a8a11a19b22+a11a11a16b22+a2a9a23b26+a8a9a17b26+a9a9a16b26+a4a5a23b28+a4a9a19b28+a4a11a17b28)b29b29
なので
[3/5^4/5^4/23/29/29]+[5/9^2/5^4/23/29/29]+[3^2/17/5^4/23/29/29]+[3/3^4/3^8/27/29/29]+
[9/3^4/9^2/27/29/29]+[5^2/3^4/17/27/29/29]+[3^2/3^2/3^8/15^2/29/29]+[3^2/5^2/5^4/15^2/29/29]+
[3^2/3^4/9^2/15^2/29/29]+[3/5^4/23/3^8/27/27]+[5/9^2/23/3^8/27/27]+[3^2/17/23/3^8/27/27]+
[5/3^4/3^8/29/27/27]+[9/3^4/5^4/29/27/27]+[3^4/3^4/17/29/27/27]+[3^2/5^2/3^8/15^2/27/27]+
[5^2/5^2/5^4/15^2/27/27]+[5^2/3^4/9^2/15^2/27/27]+[3/3^8/3^8/27/23/23]+[9/9^2/3^8/27/23/23]+
[5^2/17/3^8/27/23/23]+[5/5^4/3^8/29/23/23]+[9/5^4/5^4/29/23/23]+[3^4/17/5^4/29/23/23]+
[3^2/9^2/3^8/15^2/23/23]+[5^2/9^2/5^4/15^2/23/23]+[3^4/9^2/9^2/15^2/23/23]+[5/15/5^4/3^8/15^2/15^2]+
[9/15/5^4/5^4/15^2/15^2]+[3^4/15/17/5^4/15^2/15^2]+[3/9^2/5^4/23/15^2/15^2]+[5/3^4/23/3^8/15^2/15^2]+
[5/9^2/9^2/23/15^2/15^2]+[3^2/17/9^2/23/15^2/15^2]+[9/3^4/5^4/23/15^2/15^2]+[3^4/3^4/17/23/15^2/15^2]+
[3/5^2/3^8/27/15^2/15^2]+[9/5^2/9^2/27/15^2/15^2]+[5^2/5^2/17/27/15^2/15^2]+[5/3^2/3^8/29/15^2/15^2]+
[5/5^2/5^4/29/15^2/15^2]+[5/3^4/9^2/29/15^2/15^2]
で消去できることを教えます。数分で中断します。
a11a11a17a17a17a16b28+a11a19a9a17a17a16b28+a11a5a19a19a19a16b28+a23a23a11a11a5a16b28+
a11a19a17a17a17a8b28+a19a19a9a17a17a8b28+a23a23a5a4a17a17b28+a11a19a19a19a4a17b28+
a23a23a11a11a4a17b28+a5a19a19a19a19a8b28+a23a23a11a5a19a8b28+a19a19a19a19a9a4b28+
a23a23a11a19a9a4b28+a11a19a19a9a17a16b26+a19a19a19a9a9a16b26+a23a5a19a19a9a16b26+
a11a19a19a17a17a8b26+a19a19a19a9a17a8b26+a23a5a19a19a17a8b26+a23a11a2a19a19a17b26+
a23a2a19a19a19a9b26+a23a23a5a2a19a19b26+a23a11a11a17a17a16b22+a23a23a11a5a17a16b22+
a11a11a19a19a19a16b22+a23a23a5a19a9a16b22+a23a23a23a5a5a16b22+a23a23a11a11a11a16b22+
a23a11a19a17a17a8b22+a23a23a19a9a4a17b22+a23a23a11a2a19a17b22+a23a23a23a5a4a17b22+
a11a19a19a19a19a8b22+a23a23a11a11a19a8b22+a23a11a19a19a19a4b22+a23a23a2a19a19a9b22+
a23a23a23a5a2a19b22+a23a23a23a11a11a4b22+a11a11a17a17b29a16a16+a19a19a9a9b29a16a16+
a23a23a5a5b29a16a16+a23a11a19a17a17b14a16+a11a19a19a19a19b14a16+a23a23a11a11a19b14a16+
a23a19a19a17a17a8b14+a23a23a19a4a17a17b14+a19a19a19a19a19a8b14+a23a23a11a19a19a8b14+
a23a19a19a19a19a4b14+a23a23a23a11a19a4b14
=d1(a11b14a19a23a23+b14a17a17a19a23+b14a19a19a19a19+a11a11b22a23a23+a11a17a17b22a23+a11a19a19a19b22+a5a17a17a23b28+a9a17a17a19b28+a11a17a17a17b28)b28
+d1(a5a19a19a23b26+a9a19a19a19b26+a11a17a19a19b26)b26
+d1(a5b22a23a23a23+a9a19b22a23a23+a11a17b22a23a23+a11a11a23a23b28+a11a17a17a23b28+a11a19a19a19b28)b22
+d1(a2a19b22a23a23+a4a17b22a23a23+a5a16b22a23a23+a2a19a19a23b26+a8a17a19a19b26+a9a16a19a19b26+a4a17a17a23b28+a8a17a17a19b28+a11a16a17a17b28)b29
+d1(a11a19a23a23b28+a17a17a19a23b28+a19a19a19a19b28)b14
=d1(a11a19a23a23+a17a17a19a23+a19a19a19a19)b14b28
+d1(a11a11a23a23+a11a17a17a23+a11a19a19a19)b22b28
+d1(a5a17a17a23b28+a9a17a17a19b28+a11a17a17a17b28)b28
+d1(a5a19a19a23b26+a9a19a19a19b26+a11a17a19a19b26)b26
+d1(a5b22a23a23a23+a9a19b22a23a23+a11a17b22a23a23)b22
+d1(a2a19b22a23a23+a4a17b22a23a23+a5a16b22a23a23+a2a19a19a23b26+a8a17a19a19b26+a9a16a19a19b26+a4a17a17a23b28+a8a17a17a19b28+a11a16a17a17b28)b29
=d1((a11a19a23a23+a17a17a19a23+a19a19a19a19)b14b28)
+d1((a11a11a23a23+a11a17a17a23+a11a19a19a19)b22b28)
+(a17b14+a9b22+a5b26+a2b29)d1(a19b22a23a23)
+(a19b14+a11b22+a5b28+a4b29)d1(a17b22a23a23)
+(a23b22+a19b26+a17b28+a16b29)d1(a5b22a23a23)
+(a17b14+a9b22+a5b26+a2b29)d1(a19a19a23b26)
+(a23b14+a11b26+a9b28+a8b29)d1(a17a19a19b26)
+(a23b22+a19b26+a17b28+a16b29)d1(a9a19a19b26)
+(a19b14+a11b22+a5b28+a4b29)d1(a17a17a23b28)
+(a23b14+a11b26+a9b28+a8b29)d1(a17a17a19b28)
+(a23b22+a19b26+a17b28+a16b29)d1(a11a17a17b28)
で、a17b14+a9b22+a5b26+a2b29、a19b14+a11b22+a5b28+a4b29、a23b14+a11b26+a9b28+a8b29、a23b22+a19b26+a17b28+a16b29 は cocycle なので、
[3^4/5^4/3^8/3^8/15/29]+[9^2/9^2/5^4/3^8/15/29]+[5^4/5^4/5^4/5^4/15/29]+
[3^4/3^4/3^8/3^8/23/29]+[3^4/9^2/9^2/3^8/23/29]+[3^4/5^4/5^4/5^4/23/29]+
[9^2/15/5^4/23/3^8/3^8]+[5^2/23/5^4/23/3^8/3^8]+[3^2/29/5^4/23/3^8/3^8]+[3/15^2/5^4/23/3^8/3^8]+
[5^4/15/9^2/23/3^8/3^8]+[3^4/23/9^2/23/3^8/3^8]+[3^2/29/9^2/23/3^8/3^8]+[5/15^2/9^2/23/3^8/3^8]+
[3^8/23/3^2/23/3^8/3^8]+[5^4/27/3^2/23/3^8/3^8]+[9^2/29/3^2/23/3^8/3^8]+[17/15^2/3^2/23/3^8/3^8]+
[9^2/15/5^4/5^4/3^8/27]+[5^2/23/5^4/5^4/3^8/27]+[3^2/27/5^4/5^4/3^8/27]+[3/15^2/5^4/5^4/3^8/27]+
[3^8/15/9^2/5^4/5^4/27]+[3^4/27/9^2/5^4/5^4/27]+[5^2/29/9^2/5^4/5^4/27]+[9/15^2/9^2/5^4/5^4/27]+
[3^8/23/5^2/5^4/5^4/27]+[5^4/27/5^2/5^4/5^4/27]+[9^2/29/5^2/5^4/5^4/27]+[9/15^2/5^2/5^4/5^4/27]+
[5^4/15/9^2/9^2/3^8/29]+[3^4/23/9^2/9^2/3^8/29]+[3^2/29/9^2/9^2/3^8/29]+[5/15^2/9^2/9^2/3^8/29]+
[3^8/15/9^2/9^2/5^4/29]+[3^4/27/9^2/9^2/5^4/29]+[5^2/29/9^2/9^2/5^4/29]+[9/15^2/9^2/9^2/5^4/29]+
[3^8/23/3^4/9^2/9^2/29]+[5^4/27/3^4/9^2/9^2/29]+[9^2/29/3^4/9^2/9^2/29]+[17/15^2/3^4/9^2/9^2/29]
で消去できることを教えます。
a23a23a5a5a19a16b28+a23a23a5a19a4a17b28+a23a23a5a2a19a19b28+
a11a19a19a9a17a16b26+a19a19a19a9a9a16b26+a23a5a19a19a9a16b26+
a23a23a5a5a19a16b26+a11a19a19a9a17a8b26+a23a23a5a19a4a17b26+
a19a19a19a9a9a8b26+a23a5a19a19a9a8b26+a23a23a5a2a19a19b26+
a23a23a5a19a9a16b22+a23a23a11a5a19a16b22+a23a23a5a19a17a8b22+
a23a23a5a19a19a8b22+a23a23a23a5a19a4b22+a23a23a23a5a2a19b22+
a19a19a9a9b29a16a16+a19a19a9a17a8b29a16+a19a19a9a9a8b29a16+a23a2a19a19a9b29a16+
a19a19a9a17a8a8b29+a23a2a19a19a9a8b29
d4(28) を計算します。
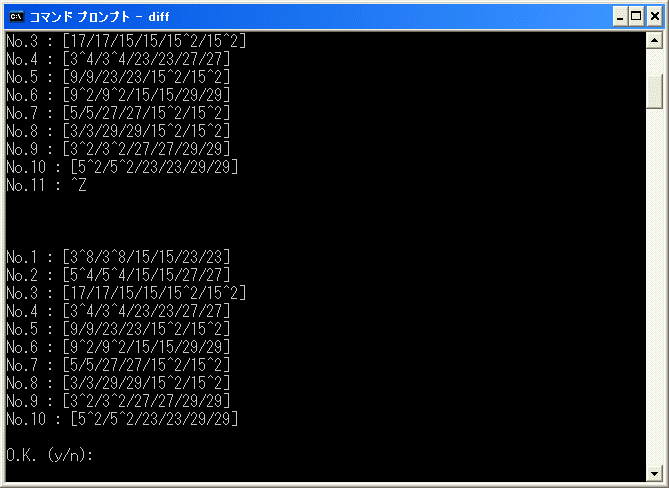
diff.exe で
[17/17/15/15/15/5^4/27]+[17/17/15/15/15/23/3^8]+[17/17/15/15/3^4/23/27]+[17/17/15/15/15/9^2/29]+
[17/17/15/15/3^2/27/29]+[17/17/15/15/5/27/15^2]+[17/17/15/15/3/29/15^2]+[17/17/15/15/9/23/15^2]+
[17/17/15/15/5^2/23/29]+[17/17/15/15/15/17/15^2]+[9/15/17/15/3^8/23/23]+[9/15/17/3^4/27/23/23]+
[9/15/17/5^2/29/23/23]+[9/15/17/9/15^2/23/23]+[9/9/23/15/3^8/23/23]+[9/9/23/3^4/27/23/23]+
[9/9/23/5^2/29/23/23]+[9/9/23/9/15^2/23/23]+[9/5/27/15/3^8/23/23]+[9/5/27/3^4/27/23/23]+
[9/5/27/5^2/29/23/23]+[9/5/27/9/15^2/23/23]+[9/3/29/15/3^8/23/23]+[9/3/29/3^4/27/23/23]+
[9/3/29/5^2/29/23/23]+[9/3/29/9/15^2/23/23]+[5/5/27/27/15/5^4/27]+[5/5/27/27/15/23/3^8]+
[5/5/27/27/3^4/23/27]+[5/5/27/27/15/9^2/29]+[5/5/27/27/3^2/27/29]+[5/5/27/27/5/27/15^2]+
[5/5/27/27/3/29/15^2]+[5/5/27/27/9/23/15^2]+[5/5/27/27/5^2/23/29]+[5/5/27/27/15/17/15^2]+
[5/17/5^4/15/15/27/27]+[3/9/5^2/23/23/29/29]+[3/15/17/15/9^2/29/29]+[3/15/17/3^2/27/29/29]+
[3/15/17/3/15^2/29/29]+[3/15/17/5^2/23/29/29]+[3/9/23/15/9^2/29/29]+[3/9/23/3^2/27/29/29]+
[3/9/23/3/15^2/29/29]+[3/9/23/5^2/23/29/29]+[3/5/27/15/9^2/29/29]+[3/5/27/3^2/27/29/29]+
[3/5/27/3/15^2/29/29]+[3/5/27/5^2/23/29/29]+[3/3/29/15/9^2/29/29]+[3/3/29/3^2/27/29/29]+
[3/3/29/3/15^2/29/29]+[3/3/29/5^2/23/29/29]
の微分を計算してみると約7時間で中断します。
a5a5a5a17a16a16b26b28+a11a5a8a8a16a16b26b28+a11a9a4a8a16a16b26b28+a11a11a2a8a16a16b26b28+
a5a9a9a9a16a16b26b28+a11a11a5a5a16a16b26b28+a5a4a4a17a17a17b26b28+a9a9a4a17a17a8b26b28+
a11a2a9a17a17a8b26b28+a5a2a2a19a19a17b26b28+a5a19a19a9a4a8b26b28+a11a5a2a19a19a8b26b28+
a23a23a5a2a2a9b26b28+a23a23a5a5a4a4b26b28+a5a5a9a17a16a16b22b28+a9a9a9a9a16a16b22b28+
a11a11a5a9a16a16b22b28+a9a4a4a17a17a17b22b28+a9a9a17a17a8a8b22b28+a2a2a19a19a9a17b22b28+
a5a19a19a9a8a8b22b28+a23a23a2a2a9a9b22b28+a23a23a5a9a4a4b22b28+a11a9a8b14a16a16a16b28+
a5a5a2a17b29a16a16b28+a2a9a9a9b29a16a16b28+a11a11a5a2b29a16a16b28+a5a5a17a17b14a16a16b28+
a11a17a8a8b14a16a16b28+a9a9a9a17b14a16a16b28+a11a11a5a17b14a16a16b28+a23a11a2a8b14a16a16b28+
a9a9a17a17a8b14a16b28+a5a19a19a9a8b14a16b28+a2a4a4a17a17a17b29b28+a2a9a17a17a8a8b29b28+
a2a2a2a19a19a17b29b28+a5a2a19a19a8a8b29b28+a23a23a2a2a2a9b29b28+a23a23a5a2a4a4b29b28+
a4a4a17a17a17a17b14b28+a23a2a9a17a17a8b14b28+a2a2a19a19a17a17b14b28+a23a23a2a2a9a17b14b28+
a23a23a5a4a4a17b14b28+a23a5a2a19a19a8b14b28+a11a11a4a8a16a16b26b26+a23a5a2a4a16a16b26b26+
a5a5a19a4a17a16b26b26+a23a2a4a4a17a16b26b26+a11a19a4a8a8a16b26b26+a23a11a4a4a8a16b26b26+
a19a9a9a9a4a16b26b26+a23a2a2a19a4a16b26b26+a11a11a5a19a4a16b26b26+a11a9a4a17a17a8b26b26+
a5a19a4a4a17a17b26b26+a5a2a19a19a4a17b26b26+a23a9a9a4a4a17b26b26+a11a5a19a19a4a8b26b26+
a23a11a5a19a4a4b26b26+a23a23a5a2a9a4b26b26+a11a5a5a17a16a16b22b26+a23a5a2a8a16a16b22b26+
a11a9a9a9a16a16b22b26+a23a2a9a4a16a16b22b26+a23a11a2a2a16a16b22b26+a11a11a11a5a16a16b22b26+
a11a4a4a17a17a17b22b26+a11a9a17a17a8a8b22b26+a5a2a19a19a17a8b22b26+a2a19a19a9a4a17b22b26+
a11a5a19a19a8a8b22b26+a23a23a5a2a9a8b22b26+a23a23a2a9a9a4b22b26+a23a23a11a5a4a4b22b26+
a11a11a8b14a16a16a16b26+a23a5a2b14a16a16a16b26+a5a5a4a17b29a16a16b26+a9a9a9a4b29a16a16b26+
a11a11a5a4b29a16a16b26+a5a5a19a17b14a16a16b26+a23a2a4a17b14a16a16b26+a11a19a8a8b14a16a16b26+
a23a11a4a8b14a16a16b26+a19a9a9a9b14a16a16b26+a23a2a2a19b14a16a16b26+a11a11a5a19b14a16a16b26+
a11a9a17a17a8b14a16b26+a5a2a19a19a17b14a16b26+a11a5a19a19a8b14a16b26+a23a23a5a2a9b14a16b26+
a4a4a4a17a17a17b29b26+a9a4a17a17a8a8b29b26+a2a2a19a19a4a17b29b26+a5a19a19a4a8a8b29b26+
a23a23a2a2a9a4b29b26+a23a23a5a4a4a4b29b26+a19a4a4a17a17a17b14b26+a23a9a4a17a17a8b14b26+
a2a19a19a4a17a17b14b26+a23a23a2a9a4a17b14b26+a23a5a19a19a4a8b14b26+a23a23a5a19a4a4b14b26+
a23a2a9b14a16a16a16b22+a5a5a17a8b29a16a16b22+a9a9a9a8b29a16a16b22+a11a11a5a8b29a16a16b22+
a23a2a17a8b14a16a16b22+a23a5a5a17b14a16a16b22+a23a9a9a9b14a16a16b22+a23a23a2a2b14a16a16b22+
a23a11a11a5b14a16a16b22+a2a19a19a9a17b14a16b22+a23a23a2a9a9b14a16b22+a4a4a17a17a17a8b29b22+
a9a17a17a8a8a8b29b22+a2a2a19a19a17a8b29b22+a5a19a19a8a8a8b29b22+a23a23a2a2a9a8b29b22+
a23a23a5a4a4a8b29b22+a23a4a4a17a17a17b14b22+a23a9a17a17a8a8b14b22+a2a19a19a17a17a8b14b22+
a23a23a2a9a17a8b14b22+a23a5a19a19a8a8b14b22+a23a23a23a5a4a4b14b22+a5a5a17b29b14a16a16a16+
a9a9a9b29b14a16a16a16+a11a11a5b29b14a16a16a16+a5a19a17a17b14b14a16a16+a23a9a9a17b14b14a16a16+
a23a11a5a19b14b14a16a16+a4a4a17a17a17b29b14a16+a9a17a17a8a8b29b14a16+a2a2a19a19a17b29b14a16+
a5a19a19a8a8b29b14a16+a23a23a2a2a9b29b14a16+a23a23a5a4a4b29b14a16+a19a4a17a17a17b14b14a16+
a23a9a17a17a8b14b14a16+a2a19a19a17a17b14b14a16+a23a23a2a9a17b14b14a16+a23a5a19a19a8b14b14a16+
a23a23a5a19a4b14b14a16
これを見ると呆然としますが、ともかく
[3/17/17/3^8/15/23/27]+[3/5^2/3^8/3^8/15/23/27]+[3/9^2/5^4/5^4/15/23/27]+[5/3^4/5^4/3^8/15/23/27]+
[3^4/3^4/17/5^4/15/23/27]+[5/3^4/9^2/3^8/15/23/29]+[5/5^2/5^4/3^8/15/23/29]+[9/3^4/17/17/15/27/29]+
[3/5^2/9^2/3^8/15/27/29]+[3/3^4/5^4/5^4/15/27/29]+[5/3^2/5^4/3^8/15/27/29]+[5/3^4/9^2/5^4/15/27/29]+
[5^2/5^2/17/9^2/15/27/29]+[3/17/9^2/5^4/15/23/15^2]+[5/5/3^8/3^8/15/23/15^2]+[5/17/9^2/9^2/15/23/15^2]+
[3^2/17/17/9^2/15/23/15^2]+[9/3^4/17/5^4/15/23/15^2]+[3/5^2/17/3^8/15/27/15^2]+[5/5/5^4/3^8/15/27/15^2]+
[5/9/5^4/5^4/15/29/15^2]+[5/3^4/17/5^4/15/29/15^2]+[9/5^2/17/9^2/15/27/15^2]+[5^2/5^2/17/17/15/27/15^2]+
[5/5/9^2/3^8/15/29/15^2]+[5/3^4/17/9^2/15/29/15^2]+[3/5^2/5^2/3^8/23/27/29]+[5/3^2/3^4/3^8/23/27/29]+
[9/5^2/5^2/9^2/23/27/29]+[5^2/5^2/5^2/17/23/27/29]+[5/5^2/3^4/5^4/23/27/29]+[5/5/5^2/3^8/23/29/15^2]+
[5/9/5^2/5^4/23/29/15^2]+[5/9/3^4/9^2/23/29/15^2]+[5/5/3^2/3^8/27/29/15^2]+[5/5/5^2/5^4/27/29/15^2]+
[5/5/3^4/9^2/27/29/15^2]
の微分を追加してみます。
d4(29) を計算します。
diff.exe で
[9^2/9^2/15/15/15/5^4/27]+[9^2/9^2/15/15/15/23/3^8]+[9^2/9^2/15/15/3^4/23/27]+[9^2/9^2/15/15/15/9^2/29]+
[9^2/9^2/15/15/3^2/27/29]+[9^2/9^2/15/15/5/27/15^2]+[9^2/9^2/15/15/3/29/15^2]+[9^2/9^2/15/15/9/23/15^2]+
[9^2/9^2/15/15/5^2/23/29]+[9^2/9^2/15/15/15/17/15^2]+[5^2/15/9^2/15/3^8/23/23]+[5^2/15/9^2/3^4/27/23/23]+
[5^2/15/9^2/5^2/29/23/23]+[5^2/15/9^2/9/15^2/23/23]+[5^2/3^2/27/15/3^8/23/23]+[5^2/3^2/27/3^4/27/23/23]+
[5^2/3^2/27/5^2/29/23/23]+[5^2/3^2/27/9/15^2/23/23]+[5^2/3/15^2/15/3^8/23/23]+[5^2/3/15^2/3^4/27/23/23]+
[5^2/3/15^2/5^2/29/23/23]+[5^2/3/15^2/9/15^2/23/23]+[5^2/5^2/23/15/3^8/23/23]+[5^2/5^2/23/3^4/27/23/23]+
[5^2/5^2/23/5^2/29/23/23]+[5^2/5^2/23/9/15^2/23/23]+[3^2/3^2/27/27/15/5^4/27]+[3^2/3^2/27/27/15/23/3^8]+
[3^2/3^2/27/27/3^4/23/27]+[3^2/3^2/27/27/15/9^2/29]+[3^2/3^2/27/27/3^2/27/29]+[3^2/3^2/27/27/5/27/15^2]+
[3^2/3^2/27/27/3/29/15^2]+[3^2/3^2/27/27/9/23/15^2]+[3^2/3^2/27/27/5^2/23/29]+[3^2/3^2/27/27/15/17/15^2]+
[3/9/5^2/23/23/15^2/15^2]+[3/15/17/15/9^2/15^2/15^2]+[3/15/17/3^2/27/15^2/15^2]+[3/15/17/3/15^2/15^2/15^2]+
[3/15/17/5^2/23/15^2/15^2]+[3/9/23/15/9^2/15^2/15^2]+[3/9/23/3^2/27/15^2/15^2]+[3/9/23/3/15^2/15^2/15^2]+
[3/9/23/5^2/23/15^2/15^2]+[3/5/27/15/9^2/15^2/15^2]+[3/5/27/3^2/27/15^2/15^2]+[3/5/27/3/15^2/15^2/15^2]+
[3/5/27/5^2/23/15^2/15^2]+[3/3/29/15/9^2/15^2/15^2]+[3/3/29/3^2/27/15^2/15^2]+[3/3/29/3/15^2/15^2/15^2]+
[3/3/29/5^2/23/15^2/15^2]+[3^2/9^2/5^4/15/15/27/27]
の微分を計算してみると数時間で中断します。
結論 : リー群 E8の Z2 cohomology の cohomology の決定は非常に困難な問題で、
私の手に負えるようなものではありませんでした。
高知大学名誉教授
中村 治
osamu@mg.pikara.ne.jp