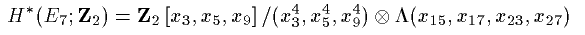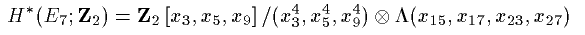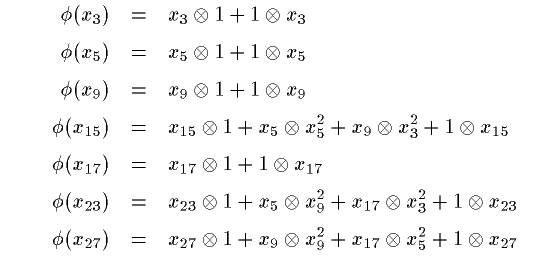最終更新日 2009年6月11日

Hopf 代数のコホモロジー

HZ2*(E7)のcohomology

　リー群 E７の Z2 cohomology の cohomology ぐらいの計算量の比較的少ない 計算は私のパソコン（３２ビットの２ギガバイトの記憶容量のパソコン）でも計算できます。 以下、計算のステップを紹介します。

　まず、出発点は E1 term の決定です。これは May complex で与えられます。

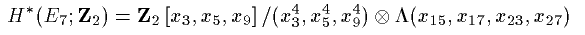
なので、代数としては cobar construction で
　[x3], [x5], [x3^2], [x9], [x5^2], [x15], [x17], [x9^2], [x23], [x27]
で表される元で生成される polynomial algebra です。これらを
　a2, a4, a5, a8, a9, b14, a16, a17, b22, b26
で表現することにします。
　微分は

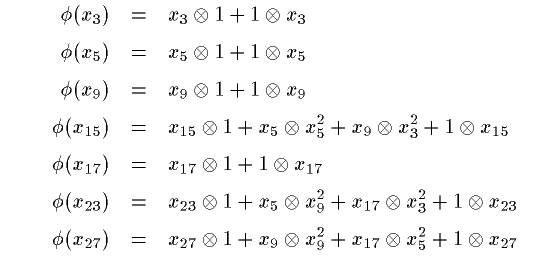
なので、 cobar construction で
d[x3]=0, d[x5]=0, d[x3^2]=0, d[x9]=0, d[x5^2]=0, d[x15]=[x5/x5^2]+[x9/x3^2], d[x17]=0, d[x9^2]=0, d[x23]=[x5/x9^2]+[x17/x3^2], d[x27]=[x9/x9^2]+[x17/x5^2] となるので、
d1(a2)=0, d1(a4)=0, d1(a5)=0, d1(a8)=0, d1(a9)=0, d1(b14)=a4a9+a8a5, d1(a16)=0, d1(a17)=0, d1(b22)=a4a17+a16a5, d1(b26)=a8a17+a16a9 で与えられます。E1 term の微分代数としての構造が決まりましたので、all.exe というソフトで ホモロジーの構造を決定します。all.exe は gen.dat と rel.dat という二つのファイルに 微分代数の情報をセットして実行します。gen.dat には 生成元と微分の情報を deg, dim, weight, name, differential の順に並べます。name はメモリを 少なくするために、
　0=[x3], 1=[x5], 2=[x3^2], 3=[x9], 4=[x5^2], 5=[x15], 6=[x17], 7=[x9^2], 8=[x23], 9=[x27]
と数字で表現しています。また、cocycle の場合 differential には E をセットしています。 今の場合、gen.dat は次のようになります。
2 1 0 0 E 4 1 0 1 E 5 1 0 2 E 8 1 0 3 E 9 1 0 4 E 14 1 1 5 1*4+3*2 16 1 0 6 E 17 1 0 7 E 22 1 1 8 1*7+6*2 26 1 1 9 3*7+6*4 　rel.dat は relation の情報を degree, dimension, weight, =0 無しの relation の順で並べますが、今の場合、 polynomial algebra なので、relation は無いので、空のファイルとします。

　all.exe は all weight dim または all -r deg weight dim の形式で実行します。これは、 indecomposable elements と defining relations を探索する範囲を指定するための引数です。 weight は微分の weight の差を指定します。dim は探索する dimension の上限を指定します。 -r deg は主として A2 のための指定で、探索する degree の上限を指定します。
　この微分代数のホモロジーの indecomposable elements と defining relations が存在しうる範囲を 予想し、この場合、十分余裕をとっても dim <= 6 で大丈夫のはずであるので、 コマンドプロンプトで
　all 1 6
を実行します。ここで、1 は E1 term のホモロジーを計算するので differential の weight の差 1 を指定します。

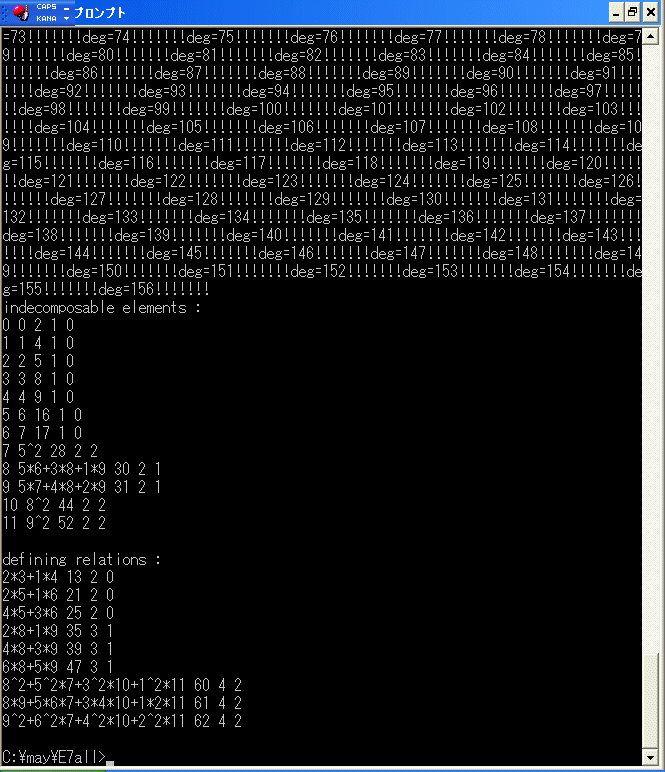
　数秒で、この微分代数のホモロジー（E2 term）の indecomposable elements と defining relations が ind.dat と def.dat にセットされます。ind.dat は次のようになっています。

0 0 1 2 0 1 1 1 4 0 2 2 1 5 0 3 3 1 8 0 4 4 1 9 0 5 6 1 16 0 6 7 1 17 0 7 5^2 2 28 2 8 5*6+3*8+1*9 2 30 1 9 5*7+4*8+2*9 2 31 1 10 8^2 2 44 2 11 9^2 2 52 2 　name, representative, dimension, degree, weight の順に並んでいます。
7 5^2 2 28 2
は 7 と名前を付けた gen.dat の元を使った表現で 5^2 で表される dim = 2 deg = 28 weight = 2 の indecomposable element があることを 表していて、E2 term には cobar construction での表現で [x15/x15] から始まる indecomposable element が あることを表しています。同じく
8 5*6+3*8+1*9 2 30 1
は 8 と名前を付けた gen.dat の元を使った表現で 5*6+3*8+1*9 で表される dim = 2 deg = 30 weight = 1 の indecomposable element があることを表していて、E2 term には cobar construction での表現で [x15/x17]+[x9/x23]+[x5/x27] から始まる indecomposable element があることを表しています。
　def.dat は次のようになっています。ind.dat で与えた indecomposable elements が満たす defining relationas が 与えられています。

2*3+1*4 2 13 0 2*5+1*6 2 21 0 4*5+3*6 2 25 0 2*8+1*9 3 35 1 4*8+3*9 3 39 1 6*8+5*9 3 47 1 8^2+5^2*7+3^2*10+1^2*11 4 60 2 8*9+5*6*7+3*4*10+1*2*11 4 61 2 9^2+6^2*7+4^2*10+2^2*11 4 62 2 　relation, dimension, degree, weight の順に並んでいます。

　つぎのステップは微分代数 E2 term を決定するために、代数構造は分かりましたから、微分を決定します。 indecomposable elements 0, 1, 2, 3, 4, 5, 6, 8, 9 は weight が１以下ですから微分 d2 は 0 です。したがって、 7 : [x15/x15], 10 : [x23/x23], 11 : [x27/x27] の微分を決定すればいいです。

　コマンドプロンプトで
　diff
を実行します。

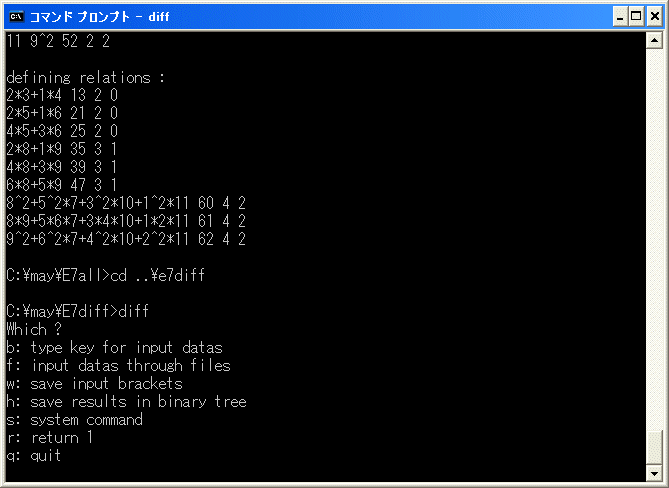
　b を選択し、[15/15] を入力します。

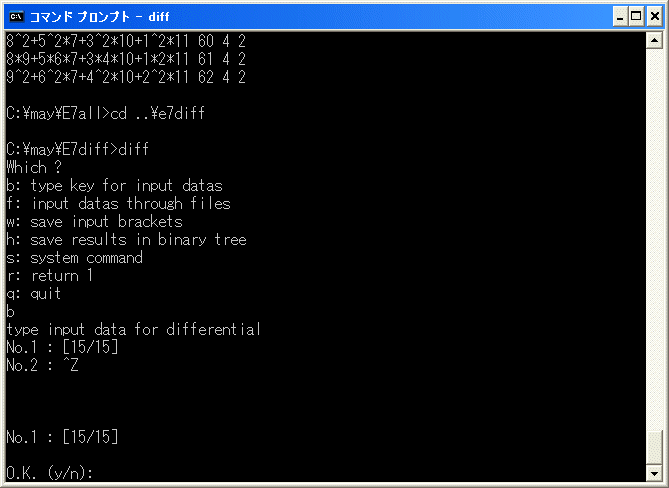
　y を入力すると直ちに

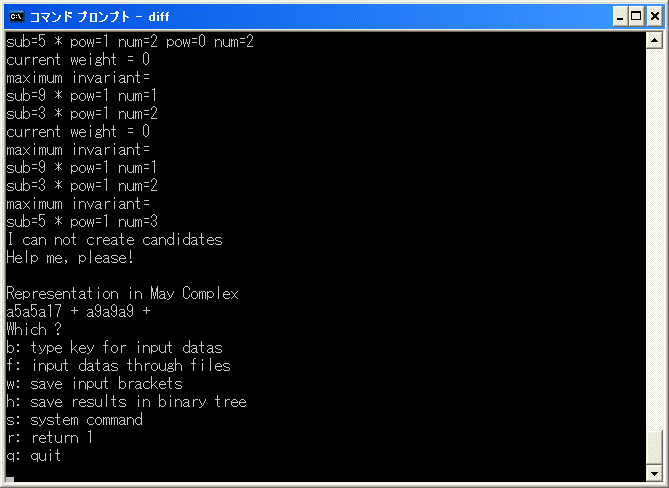
で中断します。
Representation in May Complex a5a5a17+a9a9a9+ は主要部分が [x3^2/x3^2/x9^2]+[x5^2/x5^2/x5^2] となるところで自動計算が出来なくなったことを示しています。
　diff.exe が何をしたかを追跡して見ると、diff.exe は与えられた [15/15] を元に、自動的に次のようなブラッケトを生成し、 weight=1 のものはすべて消去し、 weight=0 の [x3^2/x3^2/x9^2]+[x5^2/x5^2/x5^2] に辿り着いたと言っています。
2 [15/15] 2 [15/3^2*9] 2 [3^2*9/15] 2 [3^2*15/9] 2 [3^2/9*15] 2 [15/5^3] 2 [5^3/15] 2 [5^2*15/5] 2 [5^2/5*15] 2 [3^2*9/3^2*9] 2 [3^2*5^2*9/5] 2 [3^2*9/5^3] 2 [3^2/5^3*9] 2 [5^2/3^2*5*9] 2 [5^3/3^2*9] 2 [3^2*5^2/5*9] 2 [3^2*5^3/9] 2 [5^3/5^3] 1 [3^2/3^2*9^2] 　したがって、d2(7) = 4^3+2^2*6 であることが決定できました。
　次に、d2(10) を決定します。 diff.exe を実行し、b を選択し、[23/23] を入力します。直ちに

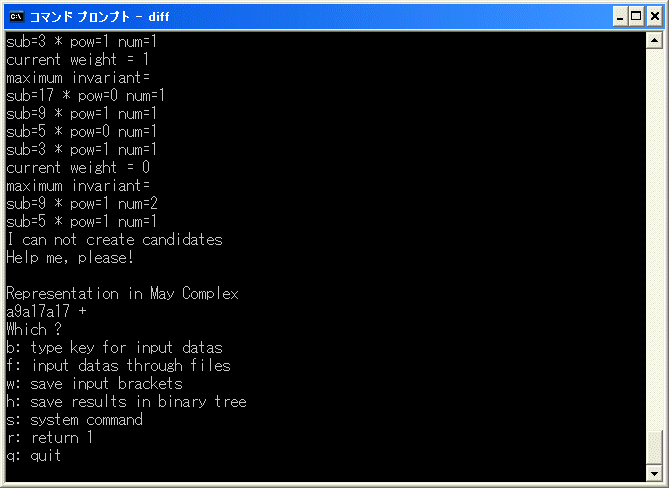
で中断します。
Representation in May Complex a9a17a17 は主要部分が [x5^2/x9^2/x9^2] となるところで自動計算が出来なくなったことを示しています。 したがって、d2(10) = 4*6^2 であることが決定できました。
　次に、d2(11) を決定します。 diff.exe を実行し、b を選択し、[27/27] を入力します。直ちに

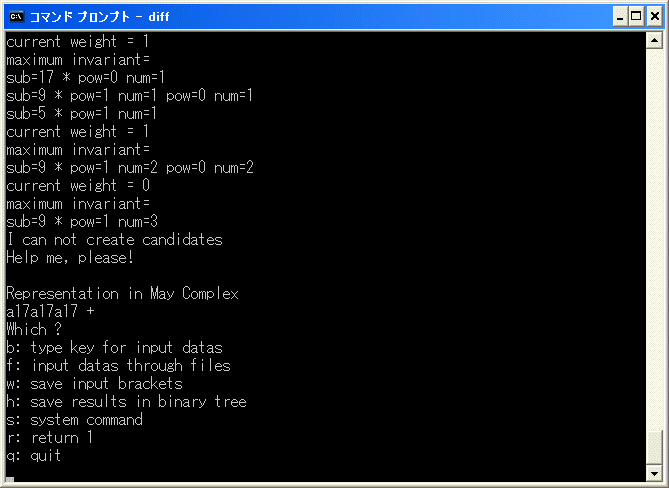
で中断します。
Representation in May Complex a17a17a17 は主要部分が [x9^2/x9^2/x9^2] となるところで自動計算が出来なくなったことを示しています。 したがって、d2(11) = 6^3 であることが決定できました。

　E4 term を計算する準備が整いました。
　次の gen.dat は上で計算した ind.dat を書き換えて、次のようにします。
2 1 0 0 E 4 1 0 1 E 5 1 0 2 E 8 1 0 3 E 9 1 0 4 E 16 1 0 5 E 17 1 0 6 E 28 2 2 7 4^3+2^2*6 30 2 1 8 E 31 2 1 9 E 44 2 2 10 4*6^2 52 2 2 11 6^3 　また、次の rel.dat は上で計算した def.dat を書き換えて、次のようにします。
13 2 0 2*3+1*4 21 2 0 2*5+1*6 25 2 0 4*5+3*6 35 3 1 2*8+1*9 39 3 1 4*8+3*9 47 3 1 6*8+5*9 60 4 2 8^2+5^2*7+3^2*10+1^2*11 61 4 2 8*9+5*6*7+3*4*10+1*2*11 62 4 2 9^2+6^2*7+4^2*10+2^2*11
　この微分代数のホモロジーの indecomposable elements と defining relations が存在しうる範囲を 予想し、この場合、十分余裕をとって dim <= 10 で大丈夫のはずであるので、コマンドプロンプトで
　all 2 10
を実行します。ここで、2 は E2 term のホモロジーを計算するので differential の weight の差 2 を指定します。

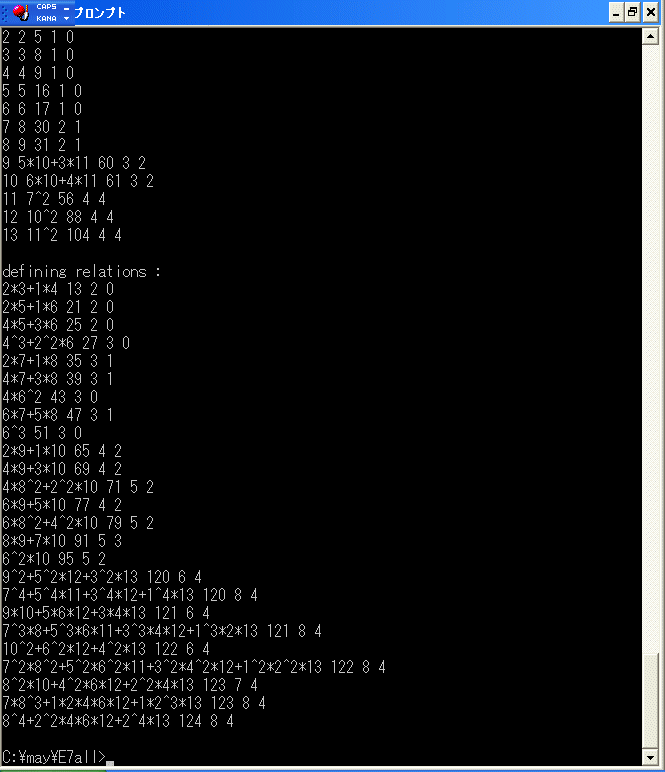
　１分ぐらいで、この微分代数のホモロジーの indecomposable elements と defining relations が ind.dat と def.dat に セットされます。ind.dat は次のようになっています。
0 0 1 2 0 1 1 1 4 0 2 2 1 5 0 3 3 1 8 0 4 4 1 9 0 5 5 1 16 0 6 6 1 17 0 7 8 2 30 1 8 9 2 31 1 9 5*10+3*11 3 60 2 10 6*10+4*11 3 61 2 11 7^2 4 56 4 12 10^2 4 88 4 13 11^2 4 104 4 　def.dat は次のようになっています。ind.dat で与えた indecomposable elements が満たす defining relationas が 与えられています。
2*3+1*4 2 13 0 2*5+1*6 2 21 0 4*5+3*6 2 25 0 4^3+2^2*6 3 27 0 2*7+1*8 3 35 1 4*7+3*8 3 39 1 4*6^2 3 43 0 6*7+5*8 3 47 1 6^3 3 51 0 2*9+1*10 4 65 2 4*9+3*10 4 69 2 4*8^2+2^2*10 5 71 2 6*9+5*10 4 77 2 6*8^2+4^2*10 5 79 2 8*9+7*10 5 91 3 6^2*10 5 95 2 9^2+5^2*12+3^2*13 6 120 4 7^4+5^4*11+3^4*12+1^4*13 8 120 4 9*10+5*6*12+3*4*13 6 121 4 7^3*8+5^3*6*11+3^3*4*12+1^3*2*13 8 121 4 10^2+6^2*12+4^2*13 6 122 4 7^2*8^2+5^2*6^2*11+3^2*4^2*12+1^2*2^2*13 8 122 4 8^2*10+4^2*6*12+2^2*4*13 7 123 4 7*8^3+1*2*4*6*12+1*2^3*13 8 123 4 8^4+2^2*4*6*12+2^4*13 8 124 4 　次のステップの為に、indecomposable elements の微分を計算します。 weight の考察から、計算しなければならないのは、 11 7^2 4 56 4 12 10^2 4 88 4 13 11^2 4 104 4 の３個です。

　d4(11) を計算します。[15/15/15/15] から始めます。

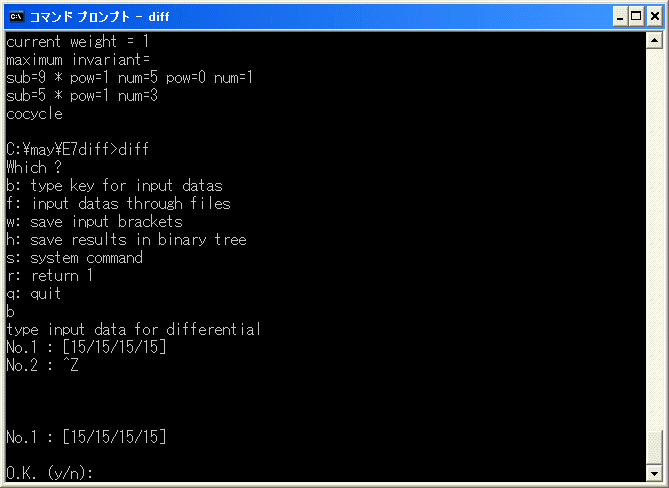
直ちに終了します。

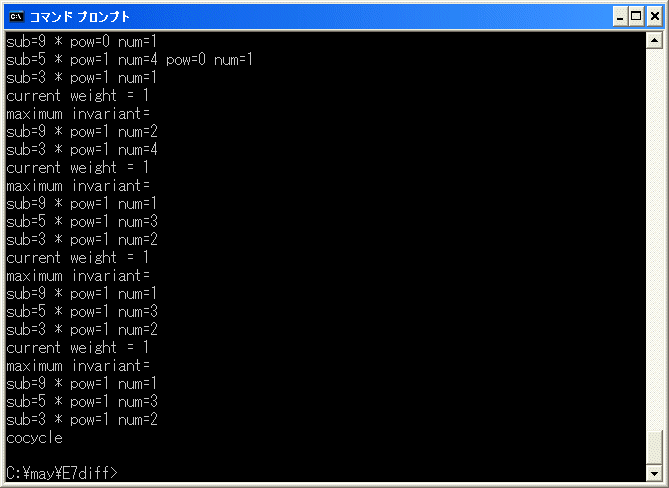
11 は cocycle であることが分かりました。したがって、d4(11) = 0 です。

　d4(12) を計算します。[23/23/23/23] から始めます。

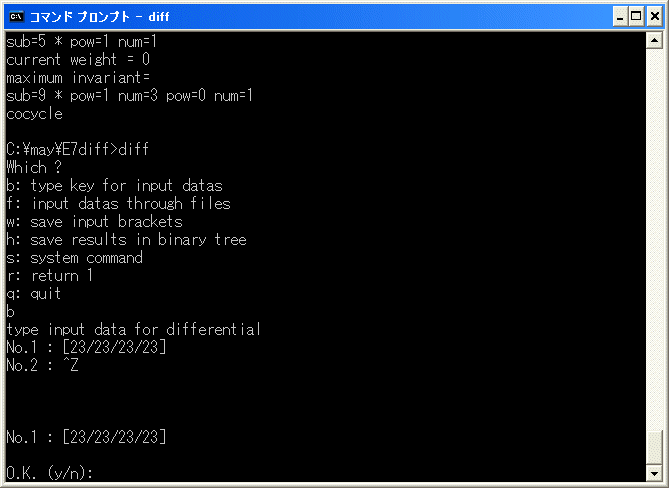
直ちに終了します。

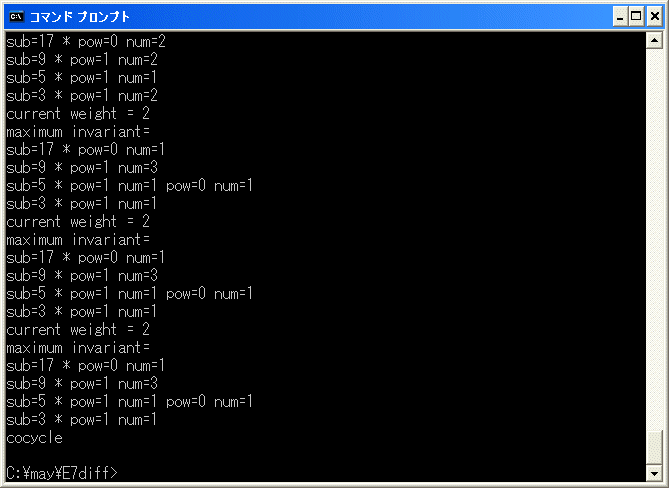
12 は cocycle であることが分かりました。したがって、d4(12) = 0 です。

　d4(13) を計算します。[27/27/27/27] から始めます。

直ちに終了します。

13 は cocycle であることが分かりました。したがって、d4(13) = 0 です。
　すべての indecomposable elements が permanent cocycle であることが分かりました。 したがって、Spectral Sequence の計算はおわりました。

　最後のステップは def.dat の defining relations
2*3+1*4 2 13 0 2*5+1*6 2 21 0 4*5+3*6 2 25 0 4^3+2^2*6 3 27 0 2*7+1*8 3 35 1 4*7+3*8 3 39 1 4*6^2 3 43 0 6*7+5*8 3 47 1 6^3 3 51 0 2*9+1*10 4 65 2 4*9+3*10 4 69 2 4*8^2+2^2*10 5 71 2 6*9+5*10 4 77 2 6*8^2+4^2*10 5 79 2 8*9+7*10 5 91 3 6^2*10 5 95 2 9^2+5^2*12+3^2*13 6 120 4 7^4+5^4*11+3^4*12+1^4*13 8 120 4 9*10+5*6*12+3*4*13 6 121 4 7^3*8+5^3*6*11+3^3*4*12+1^3*2*13 8 121 4 10^2+6^2*12+4^2*13 6 122 4 7^2*8^2+5^2*6^2*11+3^2*4^2*12+1^2*2^2*13 8 122 4 8^2*10+4^2*6*12+2^2*4*13 7 123 4 7*8^3+1*2*4*6*12+1*2^3*13 8 123 4 8^4+2^2*4*6*12+2^4*13 8 124 4 を正しい relations に修正することです。

　まず、diff.exe を使って、indecomposable elements の cobar construction における表現を 求めます。名前が n の indecomposable elements の表現を cn というファイルにセットしておきます。

c0 : [x3] c1 : [x5] c2 : [x3^2] c3 : [x9] c4 : [x5^2] c5 : [x17] c6 : [x9^2] は明らかです。
c7 を求めるために、diff.exe で [15/17]+[9/23]+[5/27] の微分を計算します。
w: save input brackets を選択し、生成したブラケットを保存するファイル名 c7 を指示します。

データを入力します。

　y を入力すると

となります。最後の cocycle は自動計算していたら、微分が 0 になったことを示しています。
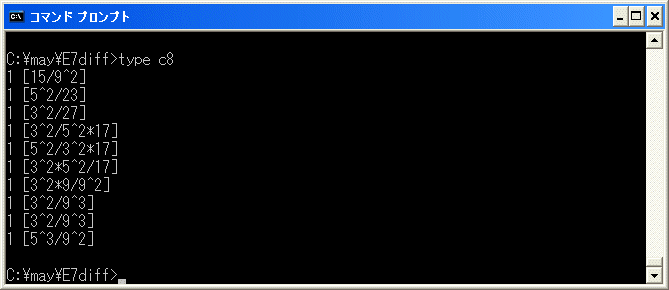
type c7 でファイル c7 を覗いてみると

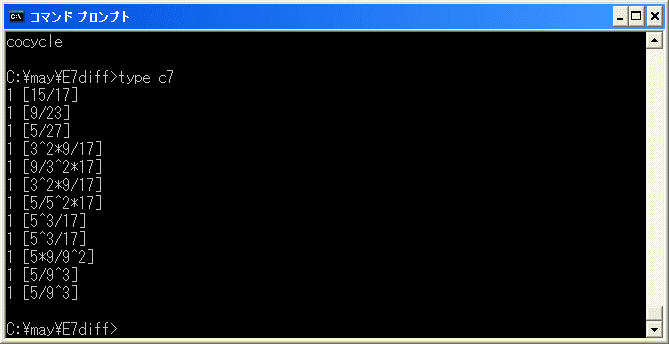
となっています。
1 [15/17] 1 [9/23] 1 [5/27] 1 [3^2*9/17] 1 [9/3^2*17] 1 [3^2*9/17] 1 [5/5^2*17] 1 [5^3/17] 1 [5^3/17] 1 [5*9/9^2] 1 [5/9^3] 1 [5/9^3] を [15/17]+[9/23]+[5/27] を基にして、自動生成しています。これは cobar construction で
d([x15/x17]+[x9/x23]+[x5/x27]+[x3^2*x9/x17]+[x9/x3^2*x17]+[x3^2*x9/x17]+[x5/x5^2*x17]+[x5^3/x17] +[x5^3/x17]+[x5*x9/x9^2]+[x5/x9^3]+[x5/x9^3]) = 0
であることを示しています。[x5/x9^3] が重複していますが、 計算スピードを上げようとするとこのような重複が出てしまいます。結果は正しいです。 したがって、7 の cobar construction での 表現が [x15/x17]+[x9/x23]+[x5/x27]+[x3^2*x9/x17]+[x9/x3^2*x17]+[x3^2*x9/x17]+[x5/x5^2*x17]+[x5^3/x17] +[x5^3/x17]+[x5*x9/x9^2](+[x5/x9^3]+[x5/x9^3]) であることを示しています。
　同様にして、8 : [x15/x9^2]+[x5^2/x23]+[x3^2/x27]　の cobar construction での表現を c8 にセットします。 [x15/x9^2]+[x5^2/x23]+[x3^2/x27]　の微分を diff.exe で計算してみます。実行すると

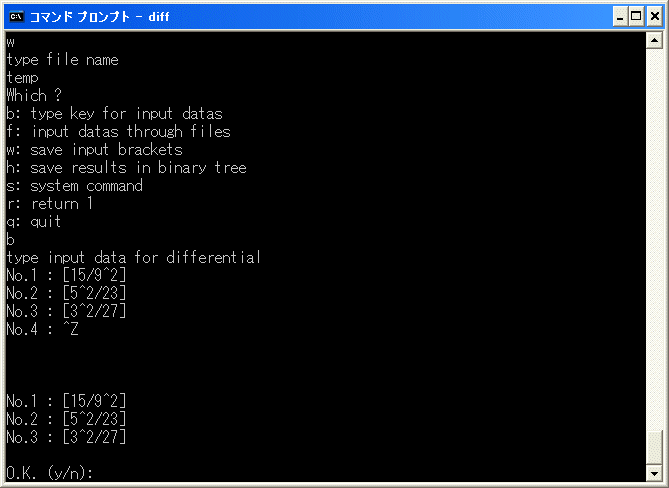
となります。したがって、8 の cobar construction での表現が
[x15/x9^2]+[x5^2/x23]+[x3^2/x27]+[x3^2/x5^2*x17]+[x5^2/x3^2*x17] +[x3^2*x5^2/x17]+[x3^2*x9/x9^2](+[x3^2/x9^3]+[x3^2/x9^3])+[x5^3/x9^2]
になることを示しています。

9 : [x17/x23/x23]+[x9/x27/x27] の cobar construction での表現を c9 にセットします。 [x17/x23/x23]+[x9/x27/x27] の微分を diff.exe で計算します。実行すると

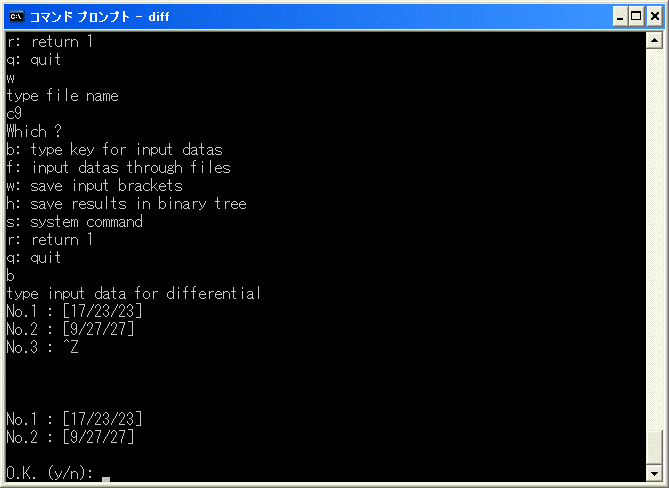
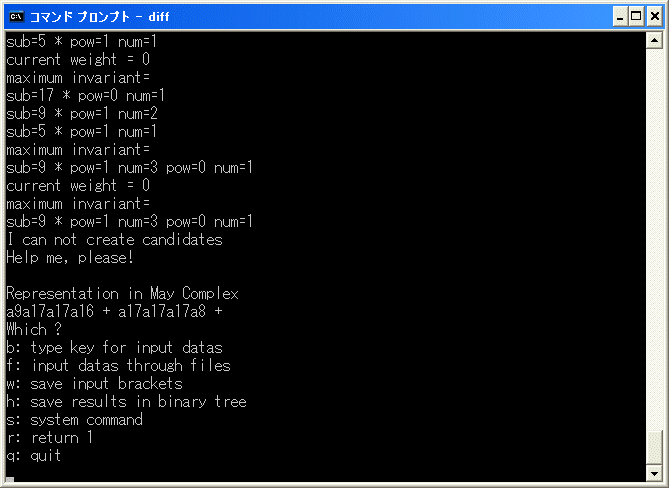
で中断します。
Representation in May Complex a9a17a17a16+a17a17a17a8+ は主要部分が [x5^2/x9^2/x9^2/x17]+[x9^2/x9^2/x9^2/x9] となるところで自動計算が 出来なくなったことを示しています。a9a17a17a16+a17a17a17a8 は E1 term の表現で、 7^2(3*7+6*4) = d1(7^2*9) ですから、[x9^2/x9^2/x27] の微分を追加するため、

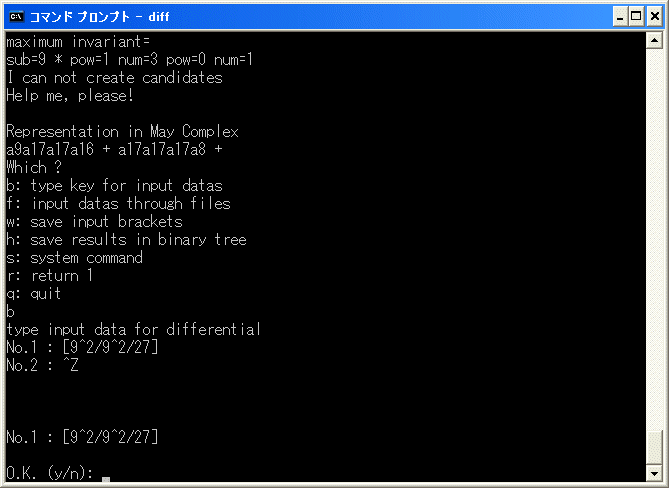
　y を入力すると

となります。微分が 0 になりました。完全自動に出来れば良いですが、 すべての計算過程を記憶していて、厄介な計算をしなければならないし、今でも記憶容量不足で 苦労しているので、このような人間による介入は仕方が無いです。
c9 に 9 の cobar construction での表現がセットされています。
10 : [x9^2/x23/x23]+[x5^2/x27/x27] の cobar construction での表現を c10 にセットします。 [x9^2/x23/x23]+[x5^2/x27/x27] の微分を diff.exe で計算します。実行すると

c10 に 10 の cobar construction での表現がセットされました。
11 : [x15/x15/x15/x15] の cobar construction での表現を c11 にセットします。 [x15/x15/x15/x15] の微分を diff.exe で計算します。実行すると

c11 に 11 の cobar construction での表現がセットされました。

　同じようにして、c12, c13 にそれぞれ 12 と 13 の cobar construction での表現をセットします。

　次の relations は weight=0 だから正しい relations です。 2*3+1*4 2 13 0 2*5+1*6 2 21 0 4*5+3*6 2 25 0 4^3+2^2*6 3 27 0 6^3 3 51 0 4*6^2 3 43 0 2*7+1*8 3 35 1
の修正をします。diff.exe を実行します。f を選択します。

5 を選択し、2*7 の cobar construction における表現を c2c7 にセットします。

4 を選択し、2*7 の cobar construction における表現を diff の binary tree にセットします。

5 を選択し、1*8 の cobar construction における表現を c1c8 にセットし、 4 を選択し、1*8 の cobar construction における表現を diff の binary tree にセットします。

6 を選択し、f のセッションを終わります。

r を選択し、binary tree にセットした cocycle 2*7+1*8 を diff.exe に消去させます。直ちに停止します。

Representation in May Complex a5a8b22+a9a4b22+a5b14a16+a4a17b14+ の a5a8b22+a9a4b22+a5b14a16+a4a17b14 は主要部分が E1 term の表現で、 2*3*8+4*1*8+2*5*6+1*7*6 = (2*3+4*1)*8+(2*5+1*7)*6 = d1(6*8) となるところで自動計算が 出来なくなったことを示しています。b を選択し、[15/23] を入力し、計算を再開させると直ちに停止します。

Representation in May Complex a9a9a17+ の a9a9a17 は主要部分が E1 term の表現で、4*4*7 の元を表しています。これは E4 term の cocycle で 4*4*6 と表現されています。これは 2*7+1*8 の weight 1 より weight の小さい weight 0 の 元で、0 でないですから、f を選択して、4*4*6 の cobar construction の表現を diff の binary tree に追加します。

r を選択し、計算を続行させます。

cocycle で終了し、binary tree が空になったので、2*7+1*8+4^2*6=0 が正しい relation です。
4*7+3*8 3 39 1
の修正をします。diff.exe を実行します。f を選択し、c4*c7 を c4c7 に、c3*c8 を c3c8 にセットし、 c4c7 と c3c8 を binary tree に追加します。

r を選択して、削除を試みます。

Representation in May Complex a5a8b26+a9a4b26+a9b14a16+a17a8b14+ の a5a8b26+a9a4b26+a9b14a16+a17a8b14 は a5a8b26+a9a4b26+a9b14a16+a17a8b14 = d1(b14b26) なので、b を選択し、[15/27] を入力します。

y を入力します。

Representation in May Complex a5a17a17+ の a5a17a17 は E4 term の cocycle で 2*6*6 と表現されています。これは 4*7+3*8 の weight 1 より weight の小さい weight 0 の 元で、0 でないですから、f を選択して、2*6*6 の cobar construction の表現を diff の binary tree に追加します。

再開すると終了します。

したがって、4*7+3*8+2*6^2 を消去することが出来たので、 4*7+3*8+2*6^2=0 が正しい relation です。
6*7+5*8 3 47 1
の修正をします。diff.exe を実行します。f を選択し、c6*c7 を c6c7 に、c5*c8 を c5c8 にセットし、 c6c7 と c5c8 を binary tree に追加し、r を選択して、削除を試みます。

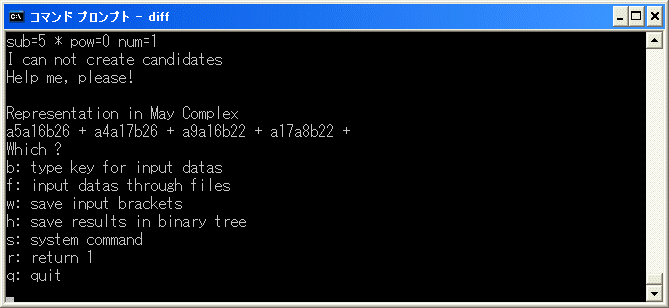
　a5a16b26+a4a17b26+a9a16b22+a17a8b22 = d1(b26b22) なので、[23/27] を追加して、

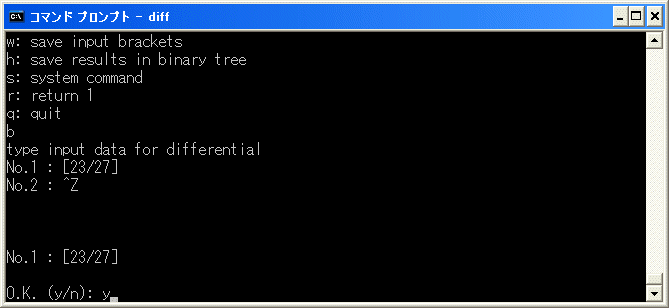
再開します。

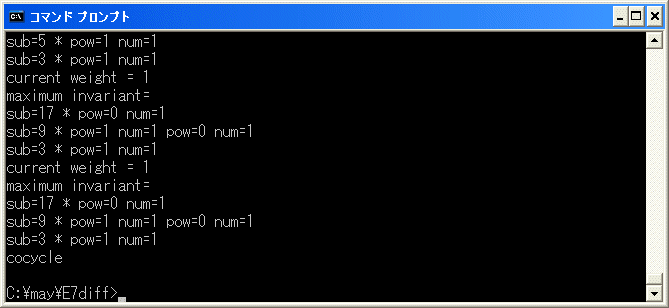
cocycle で終了したので、6*7+5*8=0 は正しい relation です。
2*9+1*10 4 65 2
の修正をします。diff.exe を実行し、f を選択し、2*9+1*10 を binary tree に追加し、r を選択して、削除を試みます。

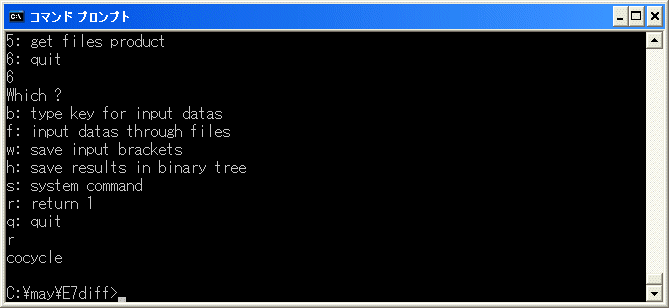
cocycle で終了したので、2*9+1*10=0 は正しい relation です。
4*9+3*10 4 69 2
の修正をします。diff.exe を実行し、f を選択し、4*9+3*10 を binary tree に追加し、r を選択して、削除を試みます。

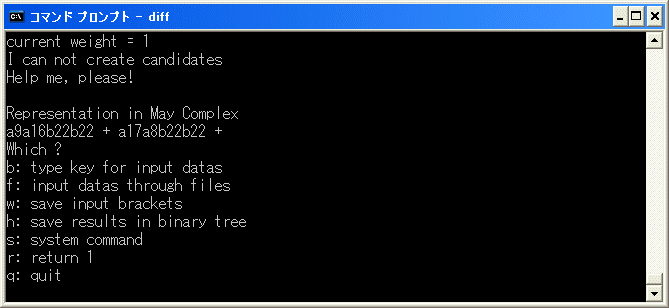
　a9a16b22b22+a17a8b22b22 = d1(b26b22b22) なので、b を選択し、[27/23/23] を入力します。

y を入力し、再開します。

cocycle で終了したので、4*9+3*10=0 は正しい relation です。
4*8^2+2^2*10 5 71 2
の修正をします。diff.exe を実行し、f を選択し、4*8^2+2^2*10 を binary tree に追加し、r を選択して、削除を試みます。

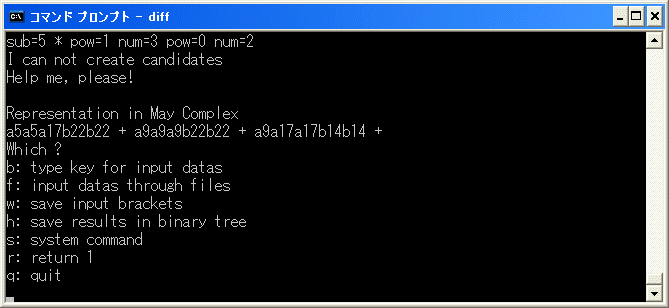
　a5a5a17b22b22+a9a9a9b22b22+a9a17a17b14b14 は E2 term で (4^3+2^2*6)*10+4*6^2*7 = d2(7*10) なので、b を選択し、[15/15/23/23] を入力します。

y を入力し再開します。

cocycle で終了したので、4*8^2+2^2*10=0 は正しい relation です。
6*9+5*10 4 77 2
の修正をします。diff.exe を実行し、f を選択し、6*9+5*10 を binary tree に追加し、r を選択して、削除を試みます。

　a9a16b26b26+a17a8b26b26 = d1(b26b26b26) なので、b を選択し、[27/27/27] を入力し、再開します。

cocycle で終了したので、6*9+5*10=0 は正しい relation です。

6*8^2+4^2*10 5 79 2
の修正をします。diff.exe を実行し、f を選択し、6*8^2+4^2*10 を binary tree に追加し、r を選択して、削除を試みます。

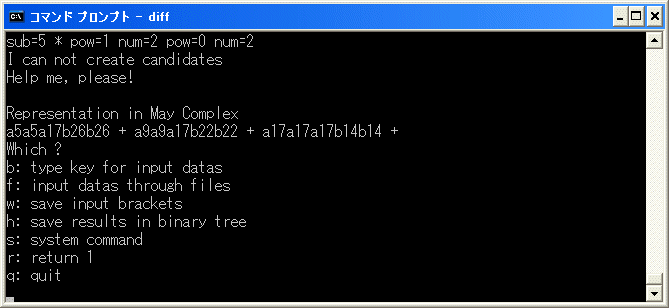
　a5a5a17b26b26+a9a9a9b26b26+a17a17a17b14b14 は E2 term で (4^3+2^2*6)*11+6^3*10=d2(7*11) なので、b を選択し、[15/15/27/27] を入力し、再開します。

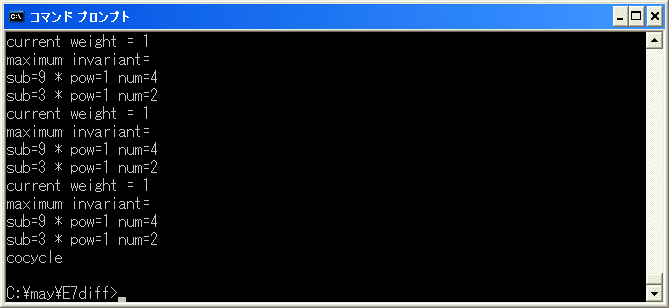
cocycle で終了したので、6*8^2+4^2*10=0 は正しい relation です。
8*9+7*10 5 91 3
の修正をします。diff.exe を実行し、f を選択し、c8*c9 を c8c9 に、c7*c10 を c7c10 にセットし、 c8c9 と c7c10 を binary tree に追加し、r を選択して、削除を試みます。

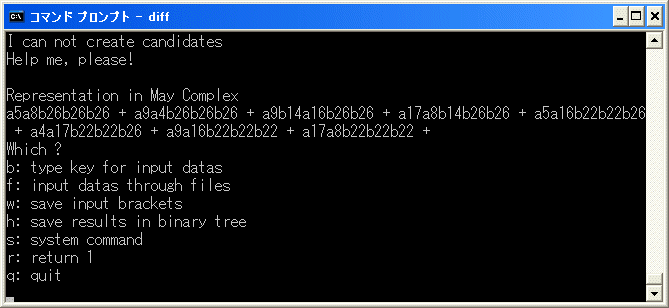
　 a5a8b26b26b26+a9a4b26b26b26+a9b14a16b26b26+a17a8b14b26b26+a5a16b26b22b22 +a4a17b26b22b22+a9a16b22b22b22+a17a8b22b22b22=d1(b14b26b26b26+b22b26b22b22) なので、 b を選択し、[15/27/27/27]+[23/27/23/23] を入力し、再開します。

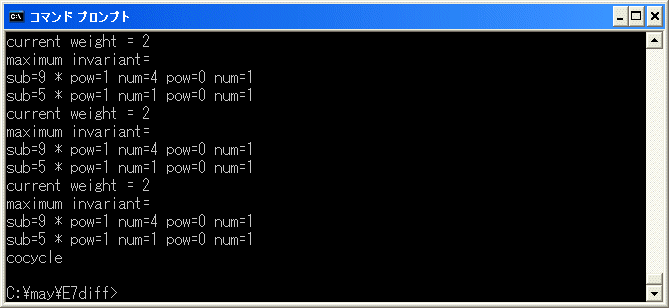
cocycle で終了したので、8*9+7*10=0 は正しい relation です。
6^2*10 5 95 2
の修正をします。diff.exe を実行し、f を選択し、6^2*10 を binary tree に追加し、r を選択して、削除を試みます。

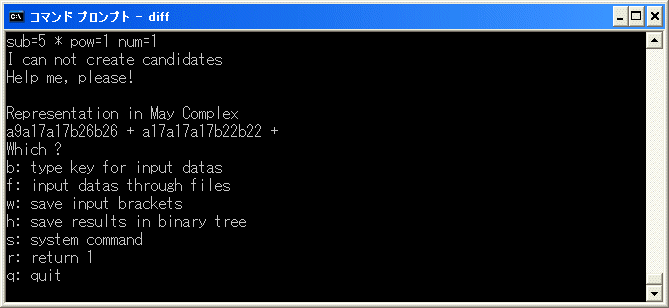
　a9a17a17b26b26+a17a17a17b22b22 は E2 term で、 4*6^2*11+6^3*10=d2(10*11) なので、 b を選択し、[23/23/27/27] を入力し、再開します。

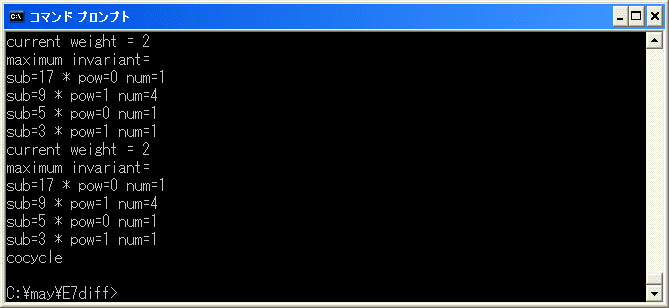
cocycle で終了したので、6^2*10=0 は正しい relation です。
9^2+5^2*12+3^2*13 6 120 4
の修正をします。diff.exe を実行し、f を選択し、9^2+5^2*12+3^2*13 を binary tree に追加し、r を選択して、削除を試みます。

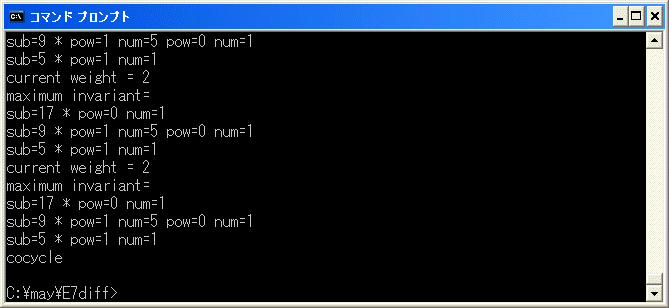
cocycle で終了したので、9^2+5^2*12+3^2*13=0 は正しい relation です。

7^4+5^4*11+3^4*12+1^4*13 8 120 4
の修正をします。diff.exe を実行し、f を選択し、7^4+5^4*11+3^4*12+1^4*13 を binary tree に追加し、r を選択して、削除を試みます。 約３０分の計算で中断します。

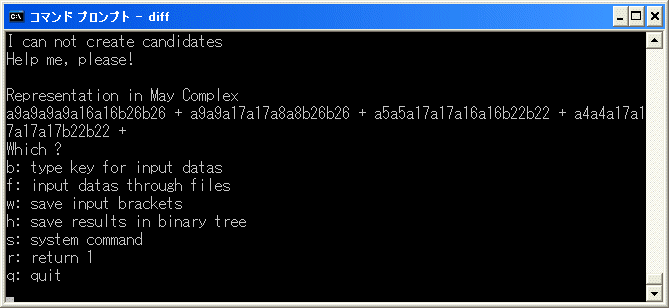
　a9a9a9a9a16a16b26b26+a9a9a17a17a8a8b26b26+a5a5a17a17a16a16b22b22+a4a4a17a17a17a17b22b22 =d1(a9a9(a9a16+a17a8)b26b26b26+a17a17(a5a16+a4a17)b22b22b22) なので、b を選択し、 [5^2/5^2/5^2/17/27/27/27]+[5^2/5^2/9^2/9/27/27/27]+[9^2/9^2/3^2/17/23/23/23]+[9^2/9^2/5/9^2/23/23/23] を入力し、再開します。直ちに終了します。

cocycle で終了したので、7^4+5^4*11+3^4*12+1^4*13=0 は正しい relation です。
9*10+5*6*12+3*4*13 6 121 4
の修正をします。diff.exe を実行し、f を選択し、c9*c10 を c9c10 に、 c5*c6*c12 を c5c6c12 に、c3*c4*c13 を c3c4c13 にセットし、 c9c10, c5c6c12, c3c4c13 を binary tree に追加し、r を選択して、削除を試みます。

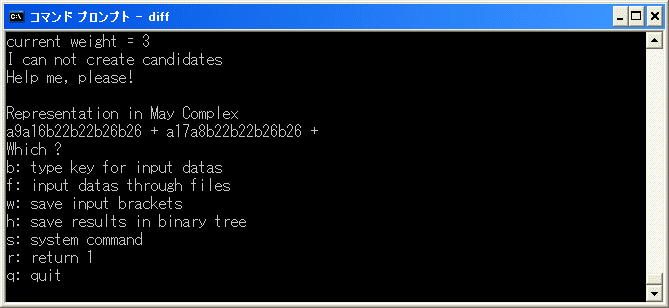
Representation in May Complex a9a16b22b22b26b26+a17a8b22b22b26b26+
a9a16b22b22b26b26+a17a8b22b22b26b26=d1(b26b22b22b26b26) なので、b を選択し、 [27/23/23/27/27] を入力し、再開します。直ちに終了します。

cocycle で終了したので、9*10+5*6*12+3*4*13=0 は正しい relation です。
7^3*8+5^3*6*11+3^3*4*12+1^3*2*13 8 121 4
の修正をしてみます。diff.exe を実行し、7^3*8+5^3*6*11+3^3*4*12+1^3*2*13 を binary tree にセットします。 diff.exe にこれを kill させてみると、４０分ぐらい計算すると

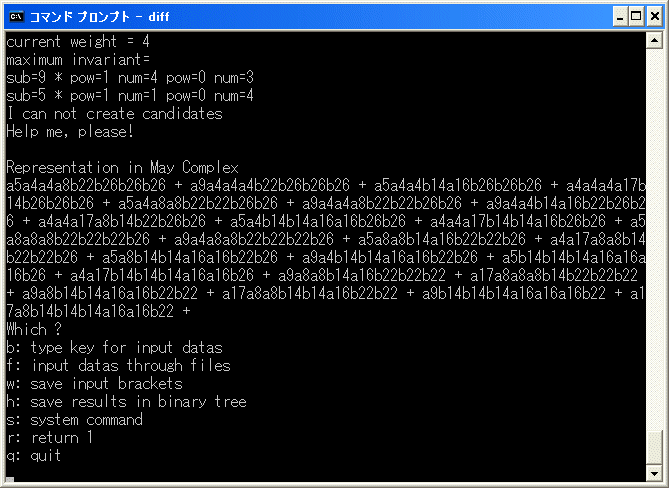
と表示して、停止します。

a5a4a4a8b22b26b26b26+a9a4a4a4b22b26b26b26+a5a4a4b14a16b26b26b26+a4a4a4a17b14b26b26b26 +a5a4a8a8b22b22b26b26+a9a4a4a8b22b22b26b26+a9a4a4b14a16b22b26b26+a4a4a17a8b14b22b26b26 +a5a4b14b14a16a16b26b26+a4a4a17b14b14a16b26b26+a5a8a8a8b22b22b22b26+a9a4a8a8b22b22b22b26 +a5a8a8b14a16b22b22b26+a4a17a8a8b14b22b22b26+a5a8b14b14a16a16b22b26+a9a4b14b14a16a16b22b26 +a5b14b14b14a16a16a16b26+a4a17b14b14b14a16a16b26+a9a8a8b14a16b22b22b22+a17a8a8a8b14b22b22b22 +a9a8b14b14a16a16b22b22+a17a8a8b14b14a16b22b22+a9b14b14b14a16a16a16b22+a17a8b14b14b14a16a16b22

は、E1 term の微分 d1 を使って

a4a4b14b22b26b26b26+a4a8b14b22b22b26b26+a4a16b22b14b14b26b26+a8a8b14b22b26b22b22 +a16a16b14b22b26b14b14+a8a16b26b14b14b22b22

で kill することが出来るので、これで消去できることをコンピュータに教えるために

[5/5/15/23/27/27/27]+[5/9/15/23/23/27/27]+[5/17/23/15/15/27/27]+[9/9/15/23/27/23/23] +[17/17/15/23/27/15/15]+[9/17/27/15/15/23/23]

を入力します。

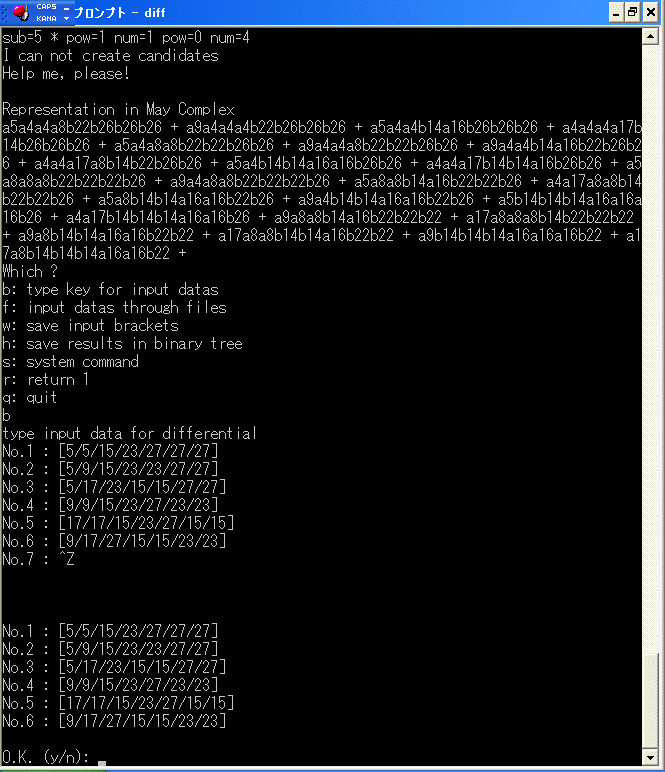
y を入力し、計算を再開させます。すると１時間３０分ぐらい計算すると

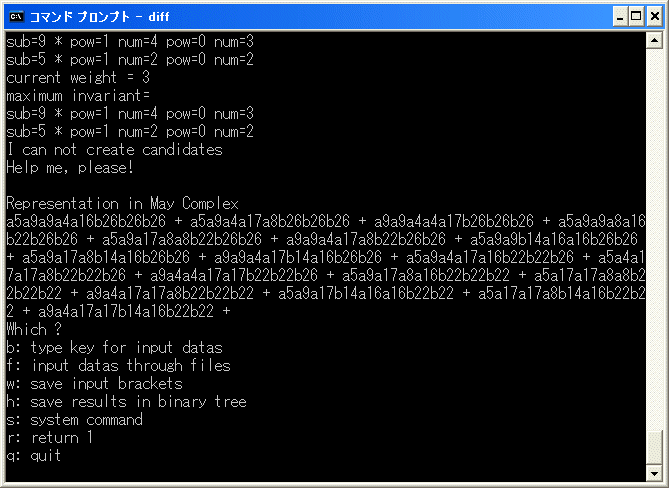
と表示して、停止します。

a5a9a9a4a16b26b26b26+a5a9a4a17a8b26b26b26+a9a9a4a4a17b26b26b26+a5a9a9a8a16b22b26b26 +a5a9a17a8a8b22b26b26+a9a9a4a17a8b22b26b26+a5a9a9b14a16a16b26b26+a5a9a17a8b14a16b26b26 +a9a9a4a17b14a16b26b26+a5a9a4a17a16b22b22b26+a5a4a17a17b22b22b26+a9a4a4a17a17b22b22b26 +a5a9a17a8a16b22b22b22+a5a17a17a8a8b22b22b22+a9a4a17a17a8b22b22b22+a5a9a17b14a16a16b22b22 +a5a17a17a8b14a16b22b22+a9a4a17a17b14a16b22b22

は因数分解すると E4 term の indecomposable elements で
2*4*5*7*10+2*3*6*7*10+1*4*6*7*10
であることが分かります。したがって、これらの cobar construction における表現を binary tree に追加します。

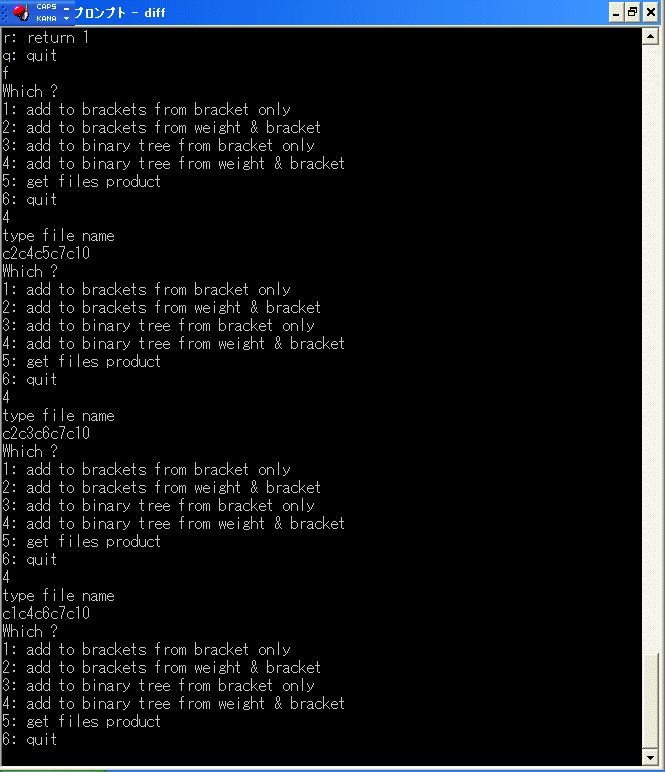
そして、更なる計算を再開させます。３分ぐらいで

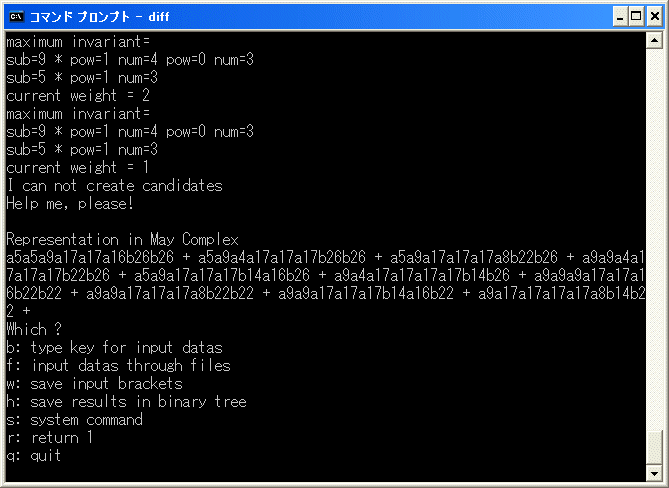
と表示して停止します。

a5a5a9a17a17a16b26b26+a5a9a4a17a17a17b26b26+a5a9a17a17a17a8b22b26+a9a9a4a17a17a17b22b26 +a5a9a17a17a17b14a16b26+a9a4a17a17a17a17b14b26+a9a9a9a17a17a16b22b22+a9a9a17a17a17a8b22b22 +a9a9a17a17a17b14a16b22a+a9a17a17a17a17a8b14b22

は E1 term の微分 d1 で
b22a5a9a17a17b26b26+a9a9a17a17b26b22b22+a9a17a17a17b14b22b26
で消去できるので、コンピュータに
[23/3^2/5^2/9^2/9^2/27/27]+[5^2/5^2/9^2/9^2/27/23/23]+[5^2/9^2/9^2/9^2/15/23/27]
で消去できることを教えます。

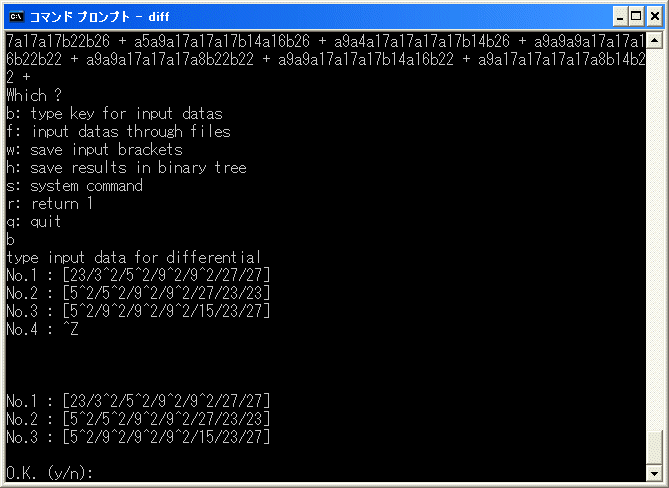
今度は直ちに

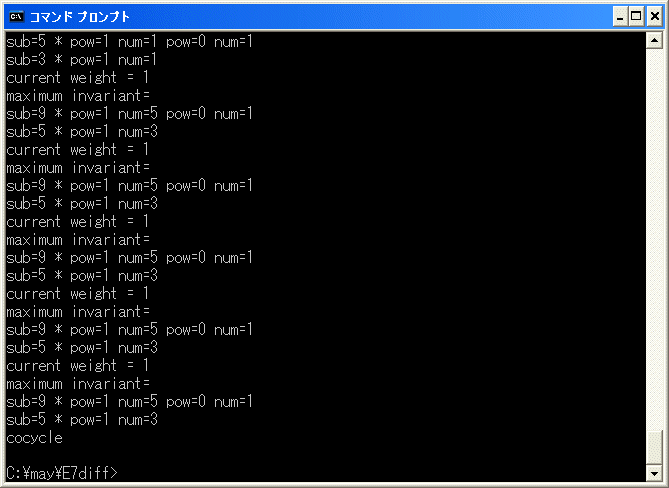
と表示して終了します。これで、正確な relation は
7^3*8+5^3*6*11+3^3*4*12+1^3*2*13+2*4*5*7*10+2*3*6*7*10+1*4*6*7*10=0
であることが分かりました。ここで、2*3+1*4=0 という relation があるので
7^3*8+5^3*6*11+3^3*4*12+1^3*2*13+2*4*5*7*10=0
と簡単に出来ます。。

10^2+6^2*12+4^2*13 6 122 4
の修正をします。diff.exe を実行し、10^2+6^2*12+4^2*13 を binary tree に追加し、r を選択して、削除を試みます。

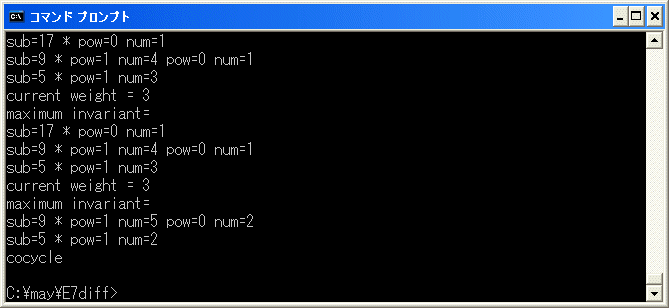
cocycle で終了したので、10^2+6^2*12+4^2*13=0 は正しい relation です。

7^2*8^2+5^2*6^2*11+3^2*4^2*12+1^2*2^2*13 8 122 4
の修正をします。diff.exe を実行し、f を選択し、7^2*8^2+5^2*6^2*11+3^2*4^2*12+1^2*2^2*13 を binary tree に追加し、r を選択して、削除を試みます。 約２０分の計算で中断します。

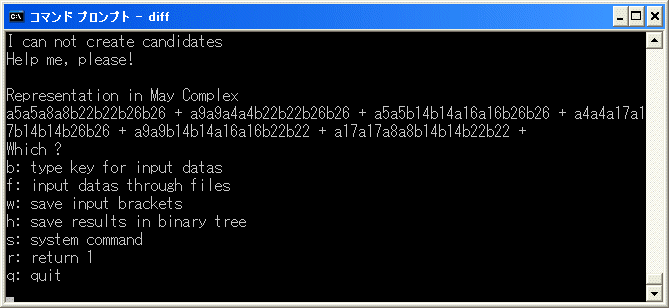
a5a5a8a8b22b22b26b26+a9a9a4a4b22b22b26b26+a5a5a16a16b14b14b26b26+a4a4a17a17b14b14b26b26 +a9a9a16a16b14b14b22b22+a17a17a8a8b14b14b22b22 =d1((a5a8+a9a4)b14b22b22b26b26+(a5a16+a4a17)b22b14b14b26b26+(a9a16+a8a17)b26b14b14b22b22) ですから、b を入力し、 [3^2/9/15/23/23/27/27]+[5^2/5/15/23/23/27/27]+[3^2/17/23/15/15/27/27] +[5/9^2/23/15/15/27/27]+[5^2/17/27/15/15/23/23]+[9/9^2/27/15/15/23/23] を入力し、計算を再開します。 約２０分の計算で中断します。

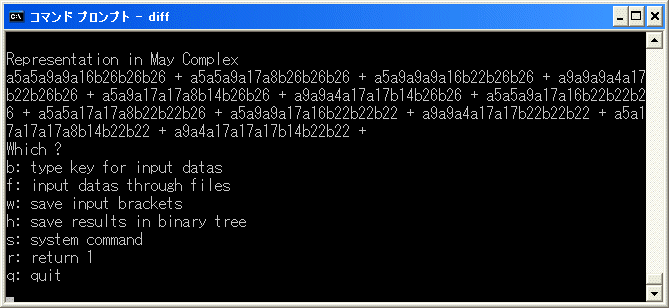
a5a5a9a9a16b26b26b26+a5a5a9a17a8b26b26b26+a5a9a9a9a16b22b26b26+a9a9a9a4a17b22b26b26 +a5a9a17a17a8b14b26b26+a9a9a4a17a17b14b26b26+a5a5a9a17a16b22b22b26+a5a5a17a17a8b22b22b26 +a5a9a9a17a16b22b22b22+a9a9a4a17a17b22b22b22+a5a17a17a17a8b14b22b22+a9a4a17a17a17b14b22b22 は E4 term の表現で 10*(2*4*5*8+2*3*6*8+1*4*6*8+2*4*6*7) ですから、 10*(2*4*5*8+2*3*6*8+1*4*6*8+2*4*6*7) を binary tree に追加し、再開します。 約３分で終了します。

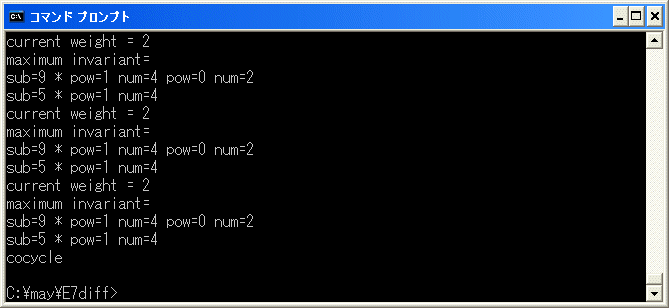
したがって、正しい relation は
7^2*8^2+5^2*6^2*11+3^2*4^2*12+1^2*2^2*13+10*(2*4*5*8+2*3*6*8+1*4*6*8+2*4*6*7)=0
です。ここで、2*3+1*4=0 という relation があるので
7^2*8^2+5^2*6^2*11+3^2*4^2*12+1^2*2^2*13+10*(2*4*5*8+2*4*6*7)=0
と簡単に出来ます。
8^2*10+4^2*6*12+2^2*4*13 7 123 4
の修正をします。diff.exe を実行し、f を選択し、8^2*10+4^2*6*12+2^2*4*13 を binary tree に追加し、r を選択して、削除を試みます。約３分で中断します。

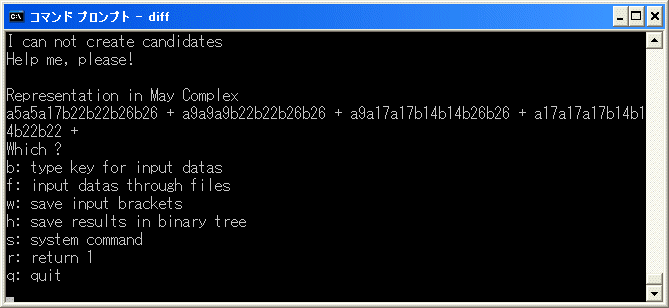
a5a5a17b22b22b26b26+a9a9a9b22b22b26b26+a9a17a17b14b14b26b26+a17a17a17b14b14b22b22 =d2(b14b14b22b22b26b26) なので、b を入力し、[15/15/23/23/27/27] を入力して、計算を再開します。 約２分で終了します。

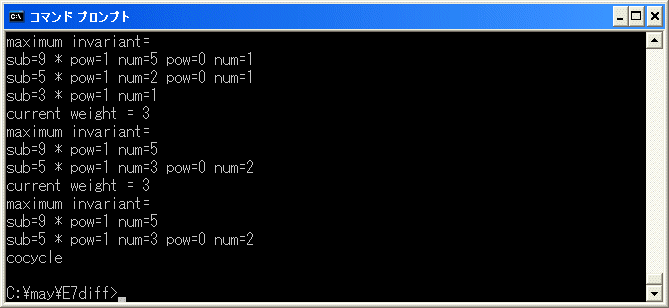
したがって、8^2*10+4^2*6*12+2^2*4*13=0 は正しい relation です。
7*8^3+1*2*4*6*12+1*2^3*13 8 123 4
の修正をします。diff.exe を実行し、f を選択し、7*8^3+1*2*4*6*12+1*2^3*13 を binary tree に追加し、r を選択して、削除を試みます。約３５分で中断します。

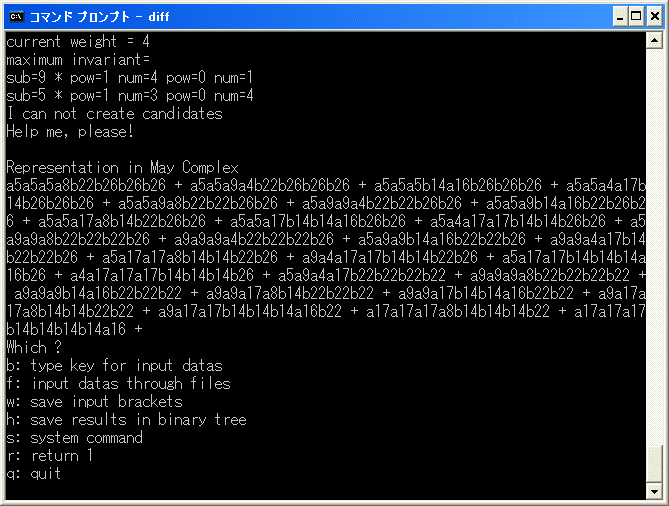
a5a5a5a8b22b26b26b26+a5a5a9a4b22b26b26b26+a5a5a5a16b14b26b26b26+a5a5a4a17b14b26b26b26 +a5a5a9a8b22b22b26b26+a5a9a9a4b22b22b26b26+a5a5a9a16b14b22b26b26+a5a5a17a8b14b22b26b26 +a5a5a17a16b14b14b26b26+a5a4a17a17b14b14b26b26+a5a9a9a8b22b22b22b26+a9a9a9a4b22b22b22b26 +a5a9a9a16b14b22b22b26+a9a9a4a17b14b22b22b26+a5a17a17a8b14b14b22b26+a9a4a17a17b14b14b22b26 +a5a17a17a16b14b14b14b26+a4a17a17a17b14b14b14b26+a5a9a4a17b22b22b22b22+a9a9a9a8b22b22b22b22 +a9a9a9a16b14b22b22b22+a9a9a9a17a8b14b22b22b22+a9a9a17a16b14b14b22b22+a9a17a17a8b14b14b22b22 +a9a17a17a16b14b14b14b22+a17a17a17a8b14b14b14b22+a17a17a17a16b14b14b14b14
=d1(a5a5b14b22b26b26b26+a5a9b14b22b22b26b26+a5a17b22b14b14b26b26+a9a9b14b22b26b22b22 +a17a17b14b22b26b14b14+a9a17b26b14b14b22b22+a5a17b14b22b22)
+d2(b14b14a8b22b22b22b22+b26b26a16b14b14b14b14)
なので、
[3^2/3^2/15/23/27/27/27]+[3^2/5^2/15/23/23/27/27]+[3^2/9^2/23/15/15/27/27]+[5^2/5^2/15/23/27/23/23] +[9^2/9^2/15/23/27/15/15]+[5^2/9^2/27/15/15/23/23]+[3^2/9^2/15/23/23/23/23] +[15/15/9/23/23/23/23]+[27/27/17/15/15/15/15]
を入力して、計算を再開します。やく１時間で中断します。

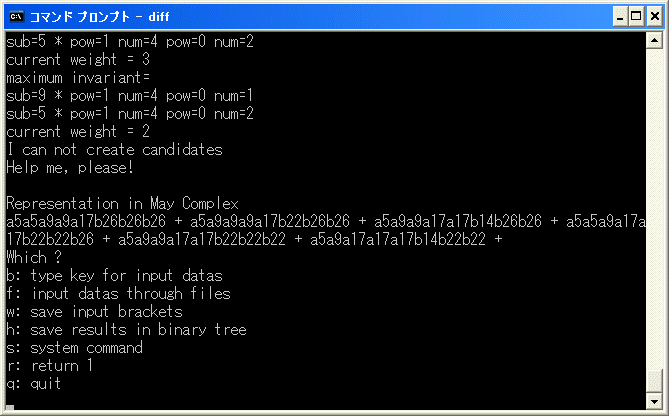
a5a5a9a9a17b26b26b26+a5a9a9a9a17b22b26b26+a5a9a9a17a17b14b26b26 +a5a5a9a17a17b22b22b26+a5a9a9a17a17b22b22b22+a5a9a17a17a17b14b22b22
=2*4*6*8*10
なので、2*4*6*8*10 を binary tree に追加して、計算を再開します。 直ちに終了します。

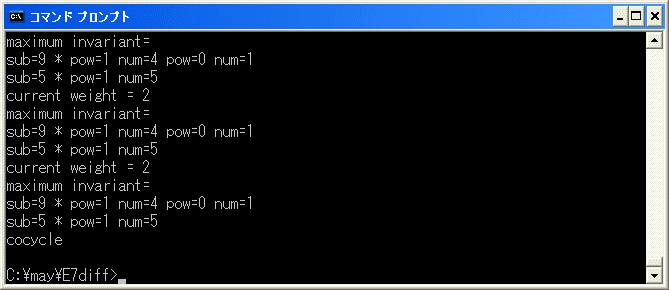
したがって、正しい relation は
7*8^3+1*2*4*6*12+1*2^3*13+2*4*6*8*10=0
です。

8^4+2^2*4*6*12+2^4*13 8 124 4
の修正をします。diff.exe を実行し、f を選択し、8^4+2^2*4*6*12+2^4*13 を binary tree に追加し、r を選択して、削除を試みます。 約２０分で中断します。

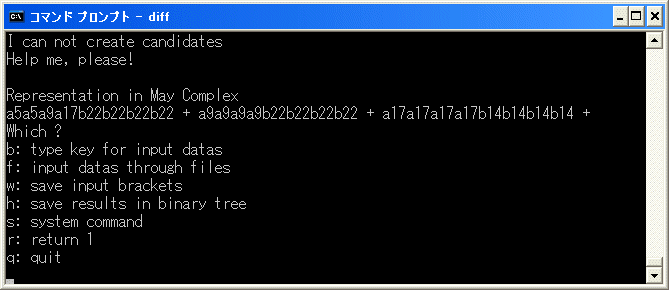
a5a5a9a17b22b22b22b22+a9a9a9a9b22b22b22b22+a17a17a17a17b14b14b14b14=
d2(b14b14a9b22b22b22b22+b26b26a17b14b14b14b14)
だから
[15/15/5^2/23/23/23/23]+[27/27/9^2/15/15/15/15]
を追加して、計算を再開する。約４５分で終了します。

したがって、8^4+2^2*4*6*12+2^4*13=0 は正しい relation です。

　すべての def.dat の defining relations を修正することが出来ました。

2*3+1*4=0 2*5+1*6=0 4*5+3*6=0 4^3+2^2*6=0 2*7+1*8+4^2*6=0 4*7+3*8+2*6^2=0 4*6^2=0 6*7+5*8=0 6^3=0 2*9+1*10+6^2*8=0 4*9+3*10=0 4*8^2+2^2*10=0 6*9+5*10=0 6*8^2+4^2*10=0 8*9+7*10=0 6^2*10=0 9^2+5^2*12+3^2*13=0 7^4+5^4*11+3^4*12+1^4*13=0 9*10+5*6*12+3*4*13=0 7^3*8+5^3*6*11+3^3*4*12+1^3*2*13+2*4*5*7*10=0 10^2+6^2*12+4^2*13=0 7^2*8^2+5^2*6^2*11+3^2*4^2*12+1^2*2^2*13+2*4*5*8*10+2*4*6*7*10=0 8^2*10+4^2*6*12+2^2*4*13=0 7*8^3+1*2*4*6*12+1*2^3*13+2*4*6*8*10=0 8^4+2^2*4*6*12+2^4*13=0 が最終的な defining relations となります。これですべて終了しました。完全な結果をうることが出来ました。
generators が次の１４個で
0 0 1 2 0 1 1 1 4 0 2 2 1 5 0 3 3 1 8 0 4 4 1 9 0 5 5 1 16 0 6 6 1 17 0 7 8 2 30 1 8 9 2 31 1 9 5*10+3*11 3 60 2 10 6*10+4*11 3 61 2 11 7^2 4 56 4 12 10^2 4 88 4 13 11^2 4 104 4 次の２５個の relations を満たす代数の構造をしています。
2*3+1*4=0 2 13 0 2*5+1*6=0 2 21 0 4*5+3*6=0 2 25 0 4^3+2^2*6=0 3 27 0 2*7+1*8+4^2*6=0 3 35 1 4*7+3*8+2*6^2=0 3 39 1 4*6^2=0 3 43 0 6*7+5*8=0 3 47 1 6^3=0 3 51 0 2*9+1*10+6^2*8=0 4 65 2 4*9+3*10=0 4 69 2 4*8^2+2^2*10=0 5 71 2 6*9+5*10=0 4 77 2 6*8^2+4^2*10=0 5 79 2 8*9+7*10=0 5 91 3 6^2*10=0 5 95 2 9^2+5^2*12+3^2*13=0 6 120 4 7^4+5^4*11+3^4*12+1^4*13=0 8 120 4 9*10+5*6*12+3*4*13=0 6 121 4 7^3*8+5^3*6*11+3^3*4*12+1^3*2*13+2*4*5*7*10=0 8 121 4 10^2+6^2*12+4^2*13=0 6 122 4 7^2*8^2+5^2*6^2*11+3^2*4^2*12+1^2*2^2*13+2*4*5*8*10+2*4*6*7*10=0 8 122 4 8^2*10+4^2*6*12+2^2*4*13=0 7 123 4 7*8^3+1*2*4*6*12+1*2^3*13+2*4*6*8*10=0 8 123 4 8^4+2^2*4*6*12+2^4*13=0 8 124 4

高知大学名誉教授
中村　治
osamu@mg.pikara.ne.jp

Hopf 代数のコホモロジーのページに戻る